Capítulo 3 Datos funcionales para estadísticos.
3.1 Introducción
Una variable funcional \(X\) es solo una variable aleatoria que toma valores en un espacio funcional \(\mathcal{E}\).
Entonces, ¿Qué es un espacio funcional y porque en todos los textos aparecen los Espacios de Hilbert?.
Pensemos entonces, en el conjunto de los polinomios \(P(x)=\{a+bx^2: (a,b) \in \mathbb{R}\}\), es decir, el conjunto \[\begin{equation} P(x)=\{1+x^2, 2+2x^2, 2+3x^2, \dots, 10+300 x^2 \} \end{equation}\]
Según la definición de espacio funcional, este conjunto pertenece al espacio funcional y además puede ser representado por la pareja \((a, b)\) en el plano cartesiano conocido por todos, con ejes \(x\) y \(y\).
Ahora, considere el conjunto de los polinomios \(P(x)=\{a+bx^2+cx^3: (a,b, c) \in \mathbb{R}\}\): \[\begin{equation} P(x)=\{1+ x^2+x^3, 2+2x^2+2x^3, 2+3x^2+4x^2, \dots, 10+300 x^2+54x^3 \} \end{equation}\]
con todas las combinaciones que se le pueda ocurrir de la tripla \((a,b,c)\), la cual se puede representar en el espacio \(\mathbb{R}^3\) o en los ejes \(x\), \(y\) y \(z\). Estos polinomios tambien pertenecen al espacio funcional. Pero, el conjunto de polinomios: \[\begin{equation} P(x)=\{a+bx+cx^2+dx^3+\dots : (a,b,c, \dots) \in \mathbb{R}\}: \end{equation}\] en donde, el grado puede llegar a infinito, tambien pertence al espacio funcional. Entonces, se puede representar por \((a,b,c\dots)\) infinitos puntos.
Entonces, es aquí donde necesitamos los espacios de Hilbert.
Resulta que las matemáticas que trabajan en dimensiones finitas, como el caso de los dos polinomios de grado finito, están definidas bajo el Espacio Euclidiano, el que todos conocemos, en el que medimos distancia utilizando la diferencia. Pero, cuando trabajamos con dimensiones infinitas, los espacios euclidianos no nos alcanzan para entender cómo vamos a medir y como vamos a tomar distancia. El Espacio de Hilbert generalizan la noción de espacio euclidiano, básicamente nos da las reglas para trabajar con ejes infinitos. El espacio L^2(S) es el conjunto de funciones de valor complejo e integrables cuadradas en los reales. Es decir, son todas las funciones \(f\) tal que \(|f|^2\) es integrable. También es un espacio de Hilbert.
Entonces, el espacio funcional se supone que es un espacio métrico normado o semi-normado, es decir, que se puede definir una norma vectorial (nos interesa conocer la longitud de los elementos). Y si el espacio funcional es un espacio de Hilbert, entonces los datos funcionales se pueden representar utilizando una base.
Un dato funcional se puede entender como la realización de un proceso estocástico o una curva, que esta en funcion del tiempo continuo y cuyas trayectorias pertenecen al espacio L^2(S). Una base de datos funcionales no es más que diferentes realizaciones de este proceso. Los datos son curvas. Para presentar un ejemplo, primero presentamos el paquete de R que utilizaremos.
3.2 Paquete de R: fda.
Para el estudio de datos funcionales, vamos a utilizar el paquete de R, fda, publicado por Febrero-Bande and Oviedo de la Fuente (2012) . En práctica, esta paquete proyecta un espacio dimensional infinito en uno finito. Sin embargo, si el espacio funcional \(\mathcal{E}\) no es de Hilbert, el paquete provee una representación más flexible de los datos funcionales: fdata. Esta nueva clase utiliza solo los valores evaluados en una cuadrícula \(\{t_1, \dots, t_m\}\) de puntos discretos ubicados a distancias diferentes.
El paquete fda define un objeto denominado fdata como una lista de los siguientes componentes:
- datos: Normalmente una matriz de \((n, m)\) dimensión que contiene un conjunto de \(n\) curvas discretizadas en \(m\) en puntos o argvals.
- argvals: Ubicaciones de los puntos de discretización, de forma predeterminada: \(\{t_1=1, \dots, t_m=m\}\).
- rangeval: Rango de puntos de discretización, por defecto es el mismo rango de argvals.
- names: Lista opcional con tres componentes: main, un título general, xlab, un título para el eje \(x\) y ylab, un título para el eje \(y\).
El paquete fda incluye en el formato fdata algunos conjuntos de datos populares de datos funcionales.
3.3 De datos reales a datos funcionales
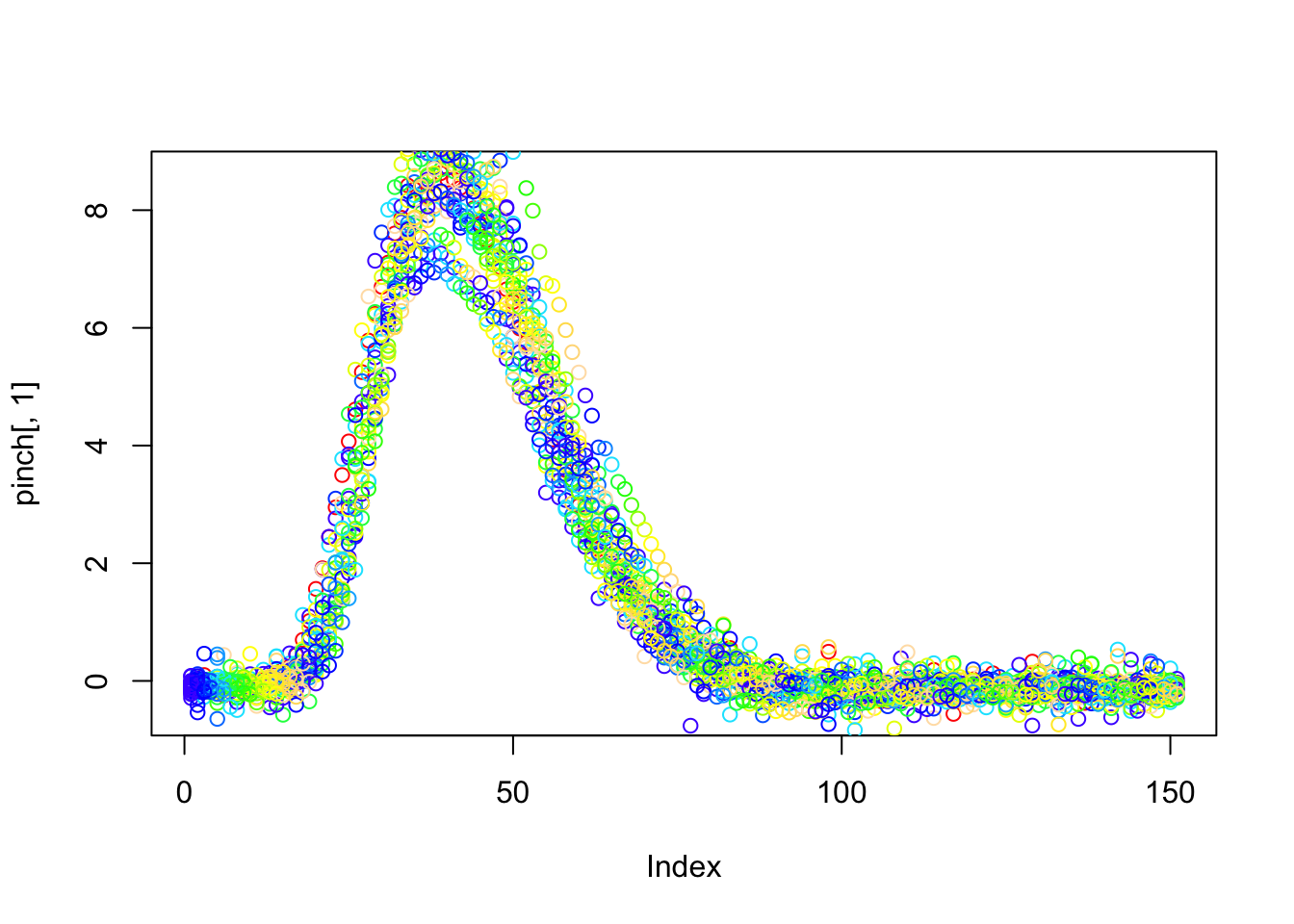
Aquí está el problema. Queremos una descripción matemática de una curva o cualquier conjunto de datos. Normalmente, los datos son recolectados a traves del tiempo o el espacio (Por ejemplo, datos de temperatura por meses, datos de acciones, datos de algún evento aleatorio por días) y por lo general se ven así (Tomamos los datos llamados pinch):
p<-data(pinch) #Es un conjunto de datos incluido en el paquete fda. Consiste en 151 mediciones de fuerza de pellizco para 20 repeticiones.
plot(pinch[,1], col="red")
i=1
for( i in 2:19){
points(pinch[,i], col=topo.colors(i))
}
Entonces debemos construir la forma funcional, porque estos son puntos y necesitamos curvas. Claro que no pueden ser cualquier curva, debe:
Permitir la evaluación del registro en cualquier momento,
Evaluar las tasas de cambio,
Reducir ruído,
Permitir el registro en una escala de tiempo común
Esta técnica se llama suavizamiento. Cuanto tomamos datos a lo largo del tiempo, inherente a esta recopilación existe alguna forma de variación aleatoria. Existen métodos para reducir la cancelación del efecto debido a la variación aleatoria. Esto llama, suavizar y cuando se aplica adecuadamente, revela más claramente los componentes cíclicos, estacionales y de tendencia subyacentes. La suavidad será un aspecto clave del análisis cuando estemos interesados en análisis funcional. En muchos de estos casos, el interés no sólo será la estimación de las curvas, sino en la estimación de las derivadas e integrales de estas curvas.
Para realizar esta técnica, necesitamos una base.
3.4 ¿Qué es una función base?
Entonces, nuestros datos son:
\[\begin{equation} \{x_n (t): t \in [T_1, T_2], n=1,2,\dots, N\} \end{equation}\] \([T_1, T_2]\) es el intervalo de espacio o tiempo de estudio. \(N\) es el número de réplicas o potenciales curvas. \(x_n (t)\) es la realización de la \(n-\)ésima réplica en tiempo \(t\).
La flexibilidad es un tema central ya que generalmente no podemos decir de antemano qué tan compleja será la curva, ni especificar algunas de sus características. Tampoco tenemos el tiempo ni la paciencia para buscar en un manual de funciones conocidas una que se parezca a lo que queremos estudiar.
Necesitamos, por lo tanto, un conjunto de bloques de construcción funcionales básicos que puedan apilarse uno encima del otro para tener las características que necesitamos. Entonces, denotamos \(\phi_k (t)\) las fichas para apilar, estas son las bases. Son funciones que pertencen a \(L^2\), como por ejemplo \(sen(wt)\) y \(cos(wt)\).
Por “apilar” en matemáticas nos referimos a sumar cosas, posiblemente después de multiplicar cada una de ellas por su propia constante. Así que construiremos una función \(X_{n}(t)\) usando \(K\) de estos bloques o bases.
\[\begin{equation} X_{n}(t)=a_1 \phi_1 (t)+a_2 \phi_2 (t)+\dots+a_K \phi_k (t). \tag{3.1} \end{equation}\]
En matemáticas, esta es una “combinación lineal”. La construcción de una función real se convierte en una cuestión de asignar valores a las \(K\) constantes \(a_k\).
En el paquete fda encontramos funciones en R para realizar estas representaciones:
- Constante: \(\phi(t)=1\).
- Polinomio: \(1, x, x^2, x^3, \dots\)
- Potencias: \(t^{\lambda_1}, t^{\lambda_2}, t^{\lambda_3}, \dots\)
- Exponencial: \(\exp^{t{\lambda_1}}, \exp^{t{\lambda_2}}, \exp^{t{\lambda_3}}, \dots\)
- Fourier: \(1, sen(wt), cos(wt), sen(2wt), cos(2wt), \dots\)
Pero en esta guía, solo mostramos dos: La base de Fourier y B splines.
3.4.1 Base de Fourier
Las funciones bases son las funciones seno y coseno de frecuencia creciente:
\[\begin{equation} 1, sen(wt), cos(wt), sen(2wt), cos(2wt), \dots \end{equation}\]
con \(w=2 \pi/P\) donde \(P\) es el periodo de oscilación.
Sin embargo, esta base usualmente es utilizada para datos periódicos. Veamos un ejemplo:
- Primero K=5, es decir, un pequeño número de bases.
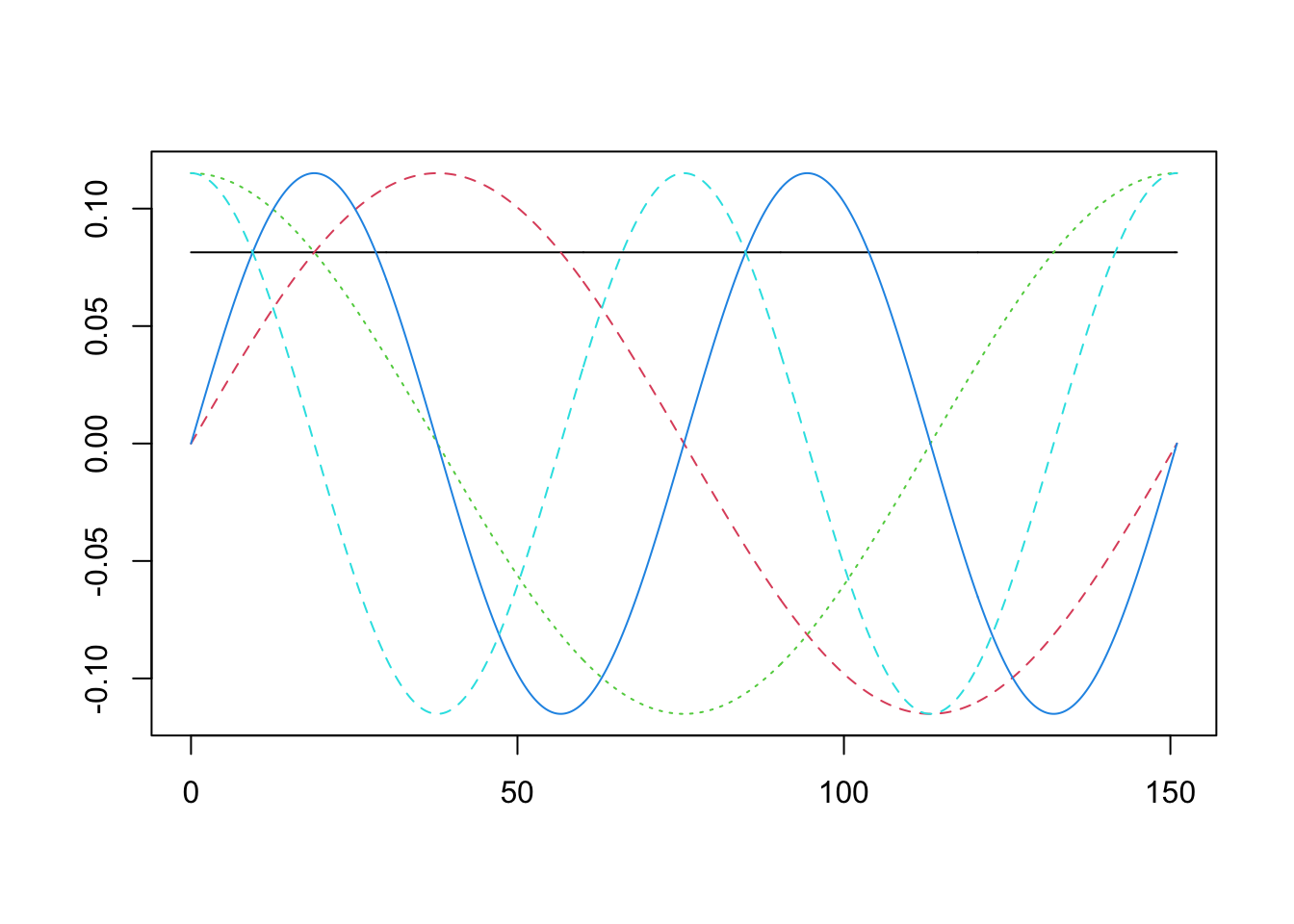
- Segundo K=15, es decir, un grande número de bases.
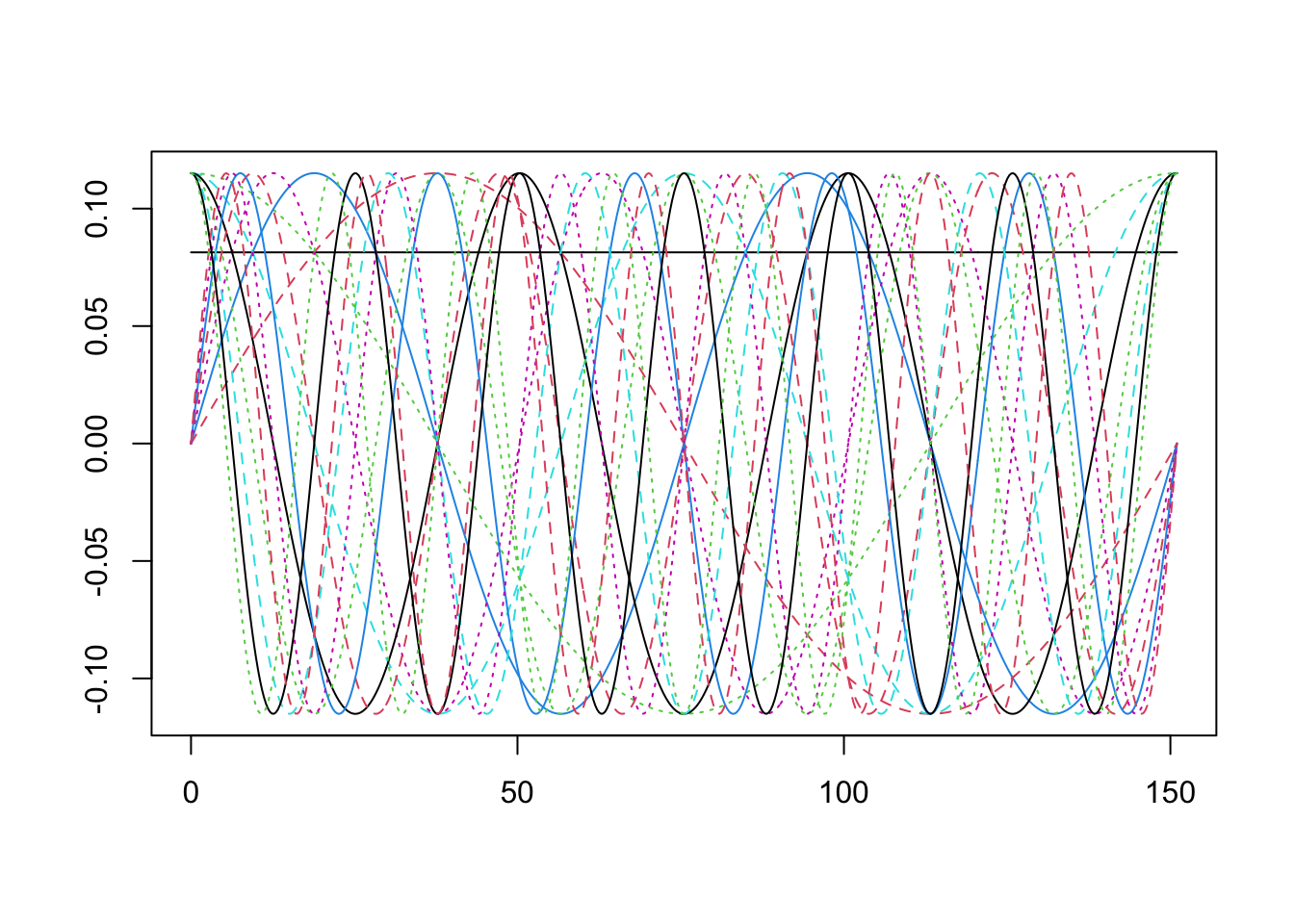
La base de Fourier usualmente es utilizada para datos periódicos. Veamos otro ejemplo bases, los B-Splines
3.4.2 Base B-Spline
Este tipo de suavizamiento se traduce como: “penalización de rugosidad”. En este caso, el objetivo es estimar una función no periódica basada en observaciones discretas con ruido, dispuestas en un vector \(y\).
Los Splines son segmentos polinomiales unidos de extremo a extremo,
Los segmentos están limitados para ser suaves en las uniones,
Los puntos en los que los segmentos se unen se llaman NUDOS,
El orden \(m\) es el orden del polinomio.
Por ejemplo, en R:
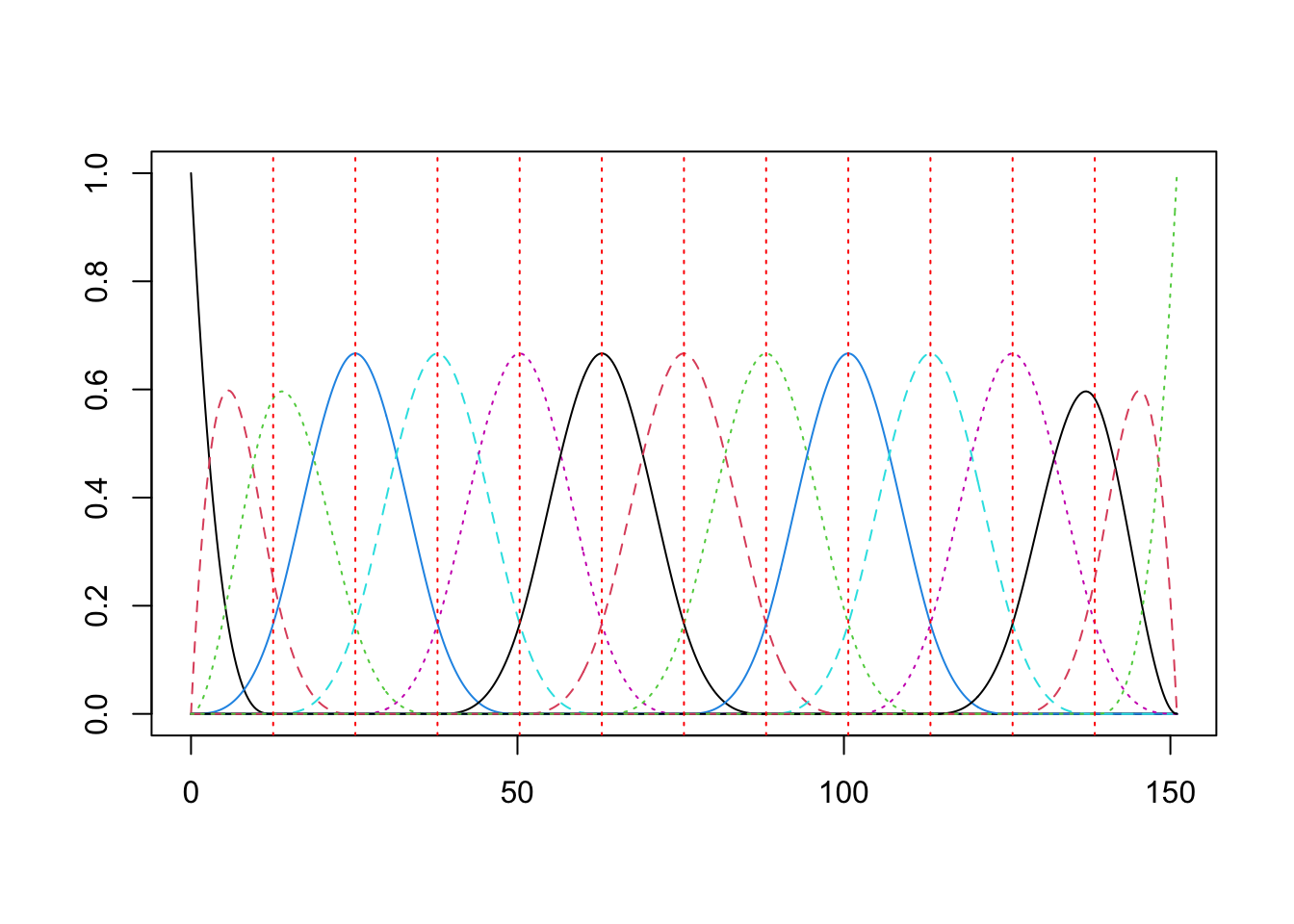
3.5 Suavizamiento
La primera etapa en un análisis de datos funcionales consiste en definir la función \(X_n (t)\), definida en (3.1) a partir de dichas observaciones reales, este proceso se conoce como suavizamiento de la función.
Entonces, se asume que las observaciones para una sola curva sigue un modelo de regresión:
\[\begin{equation} Y_i=X_n (t)+\epsilon \end{equation}\]
donde los residuos \(\epsilon\) son independientes de \(X_n (t)\), podemos recuperar la señal original \(X_n (t)\) usando un suavizador lineal,
\[\begin{equation} X_n (t) \approx \sum_{j=1}^K c_j \phi_j(t) \end{equation}\]
y podemos estimar \(c_j\) por minimos cuadrados, como en una regresión tradicional.
3.5.1 ¿Qué queremos decir con suavidad?
Lo que realmente queremos hacer es eliminar pequeños movimientos en los datos para que conserven la forma correcta.
El paquete de R presenta el comando smooth.basis, este nos ayuda a estimar los coeficientes \(c_j\) y nos permite suavizar la curva. Esto permitirá un mejor ajuste del modelo a los datos.
Sin embargo, se debe tener cuidado con el suavizamiento, no queremos que sea muy suave:
n = 100
N=1
W.mat=matrix(0, ncol=N, nrow=100) #Simule algunos datos
W.mat=cumsum(rnorm(100))
argvals = seq(0,1,len=n)
K = 2
y<-W.mat
basisobj = create.fourier.basis(c(0,1), K) # forme una base
ys = smooth.basis(argvals=argvals, y=y, fdParobj=basisobj) #suavícela
xfd = ys$fd
par(mfrow = c(1, 2))
plot(basisobj)
plotfit.fd(y, argvals, xfd)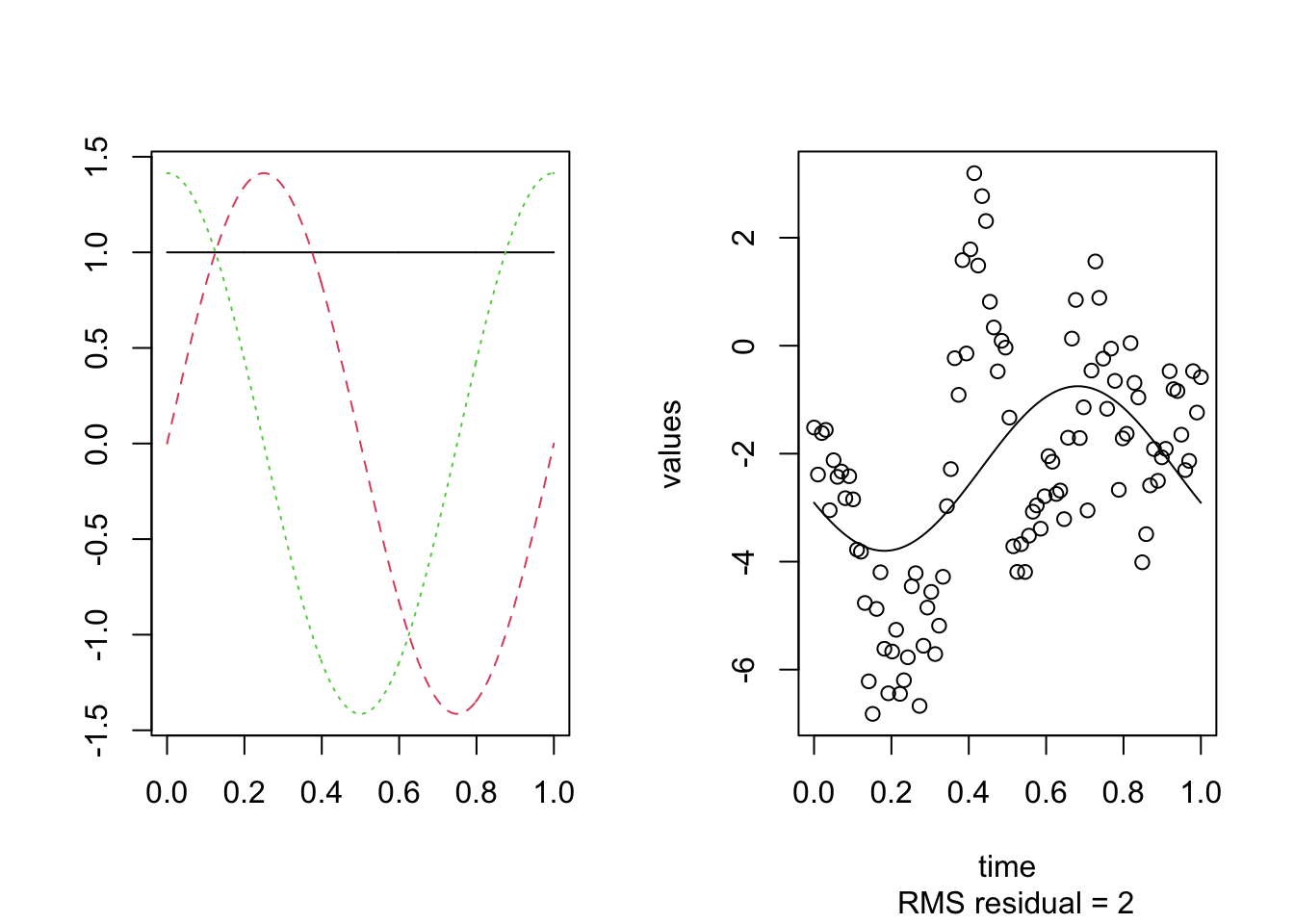
o muy duro:
n = 100
N=1
W.mat=matrix(0, ncol=N, nrow=100) #Simule algunos datos
W.mat=cumsum(rnorm(100))
argvals = seq(0,1,len=n)
K = 20
y<-W.mat
basisobj = create.fourier.basis(c(0,1), K) # forme una base
ys = smooth.basis(argvals=argvals, y=y, fdParobj=basisobj) #suavícela
xfd = ys$fd
par(mfrow = c(1, 2))
plot(basisobj)
plotfit.fd(y, argvals, xfd)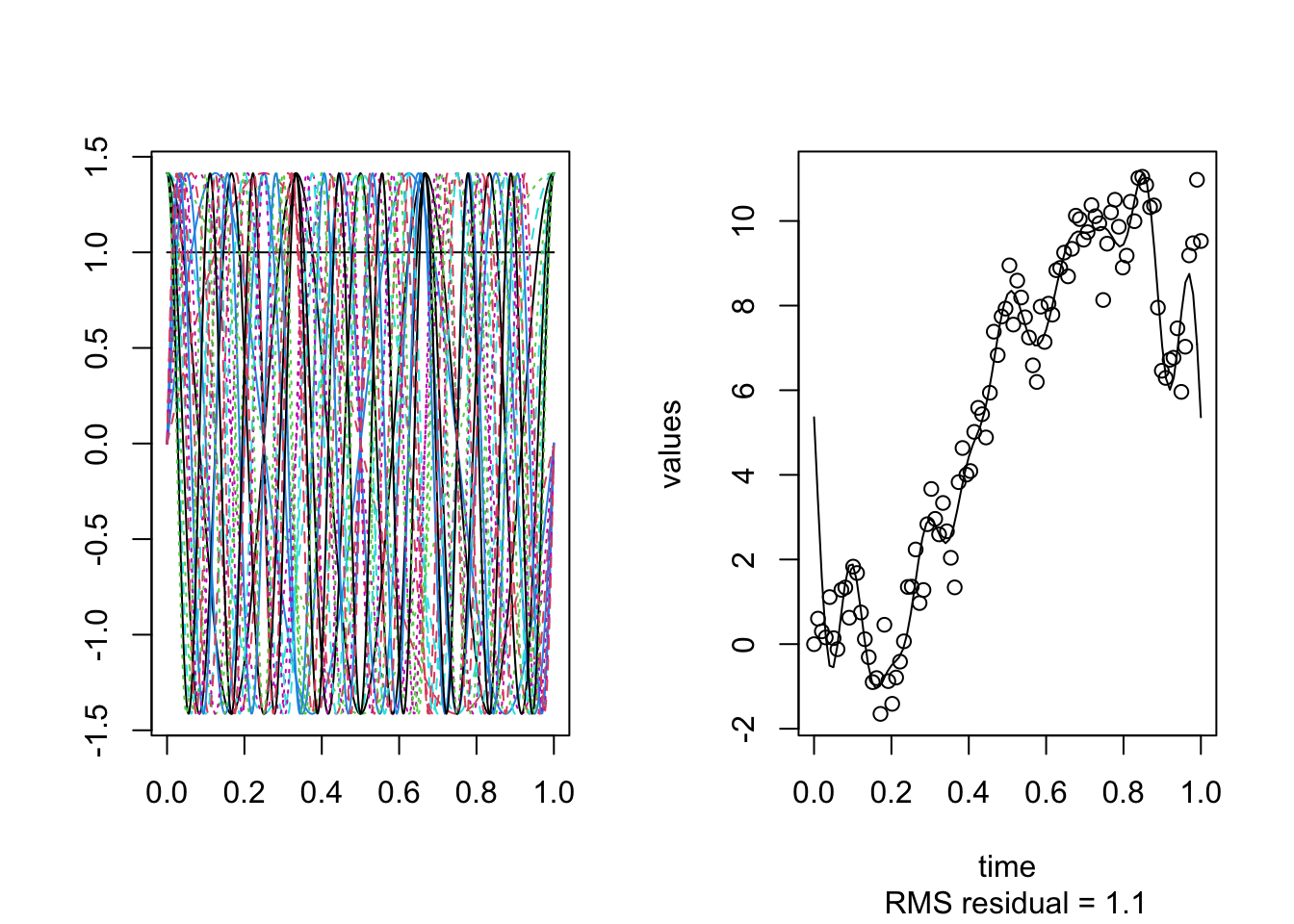
Si no que sea apenitas:
n = 100
N=1
W.mat=matrix(0, ncol=N, nrow=100) #Simule algunos datos
W.mat=cumsum(rnorm(100))
argvals = seq(0,1,len=n)
K = 7
y<-W.mat
basisobj = create.fourier.basis(c(0,1), K) # forme una base
ys = smooth.basis(argvals=argvals, y=y, fdParobj=basisobj) #suavícela
xfd = ys$fd
par(mfrow = c(1, 2))
plot(basisobj)
plotfit.fd(y, argvals, xfd)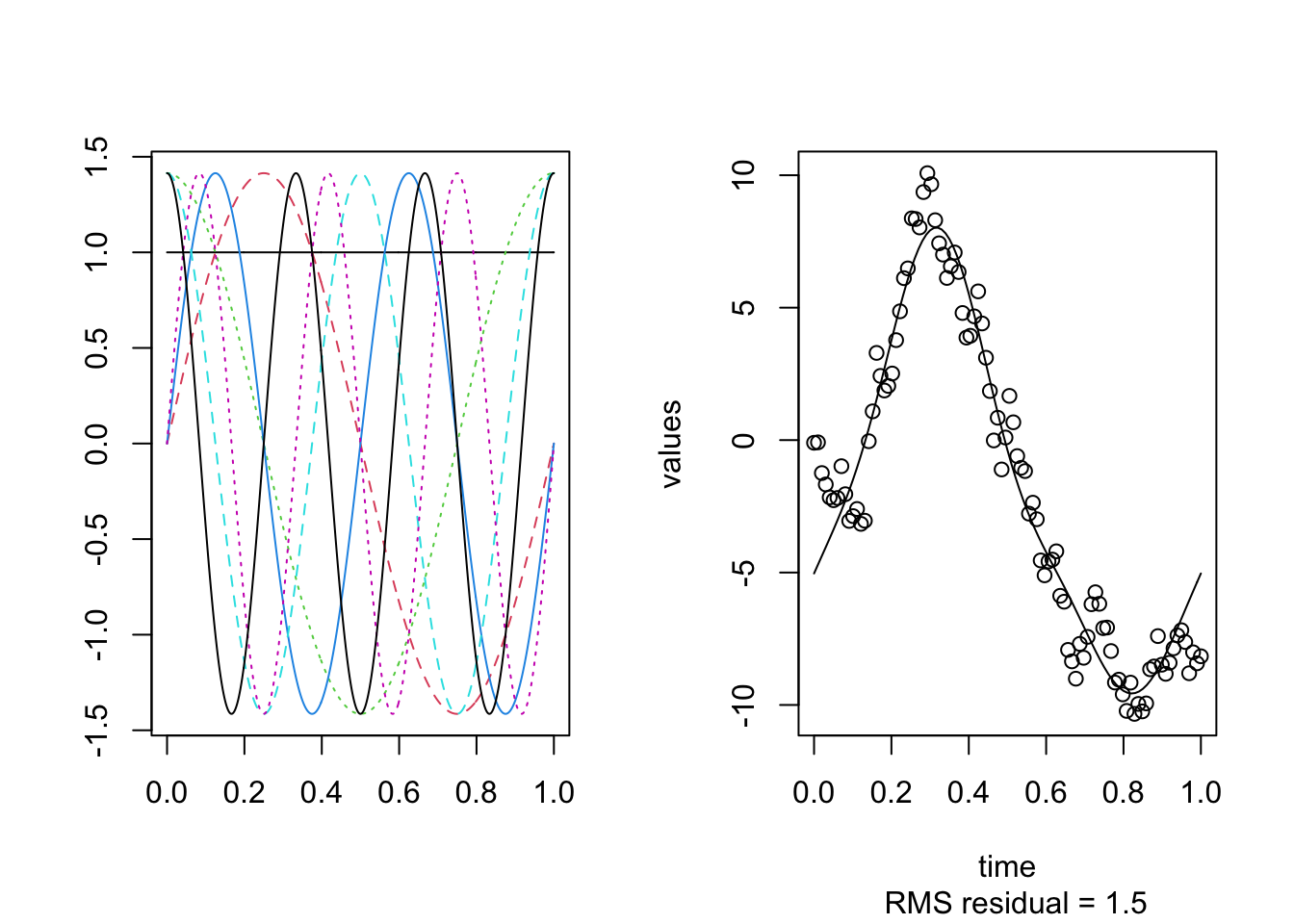
Note que esto depende del tipo de funciones utilizadas para la base y del número \(K\), es decir, el número de bases. Tambien note que la función calcula el error cuadrático medio (RMSE). Lógicamente, queremos el menor RMSE, pero también queremos el menor número \(K\) de funciones bases, que en este caso son los grados de libertad para el error \((df)\). Un \(df\) pequeño implica una estimación estable. Por lo tanto, no es aconsejable usar el suavizado más duro, aunque tiene un valor RMSE más bajo (0.78), necesito 20 bases para obtenerlo. En la vida real, se puede tener un error de \(1.6\) con 7 funciones de base.
Ahora, suponga que vamos a utilizar una base para los datos Pinch, que no son periodicos, pero que aún asi intentamos con la base de Fourier.
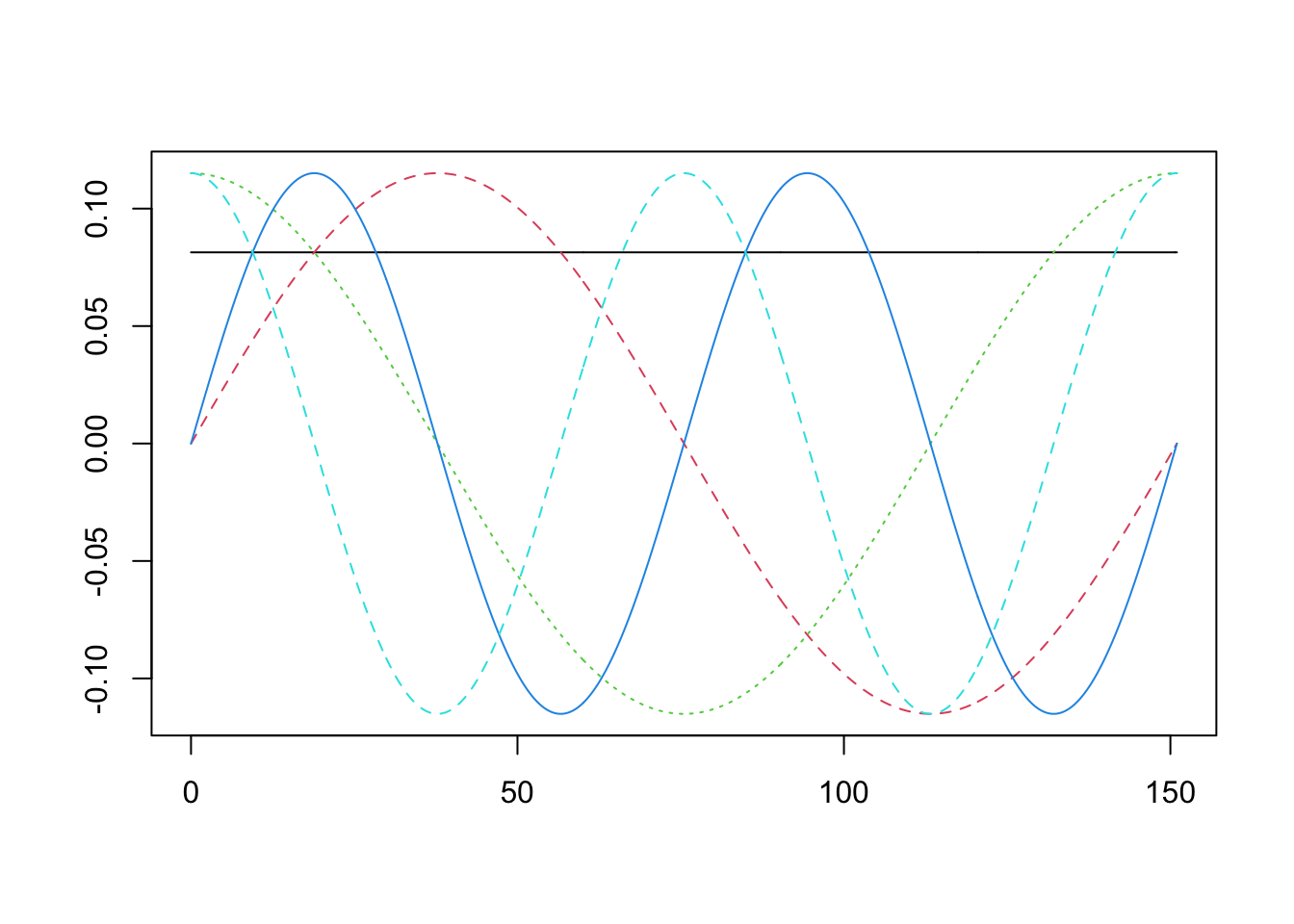
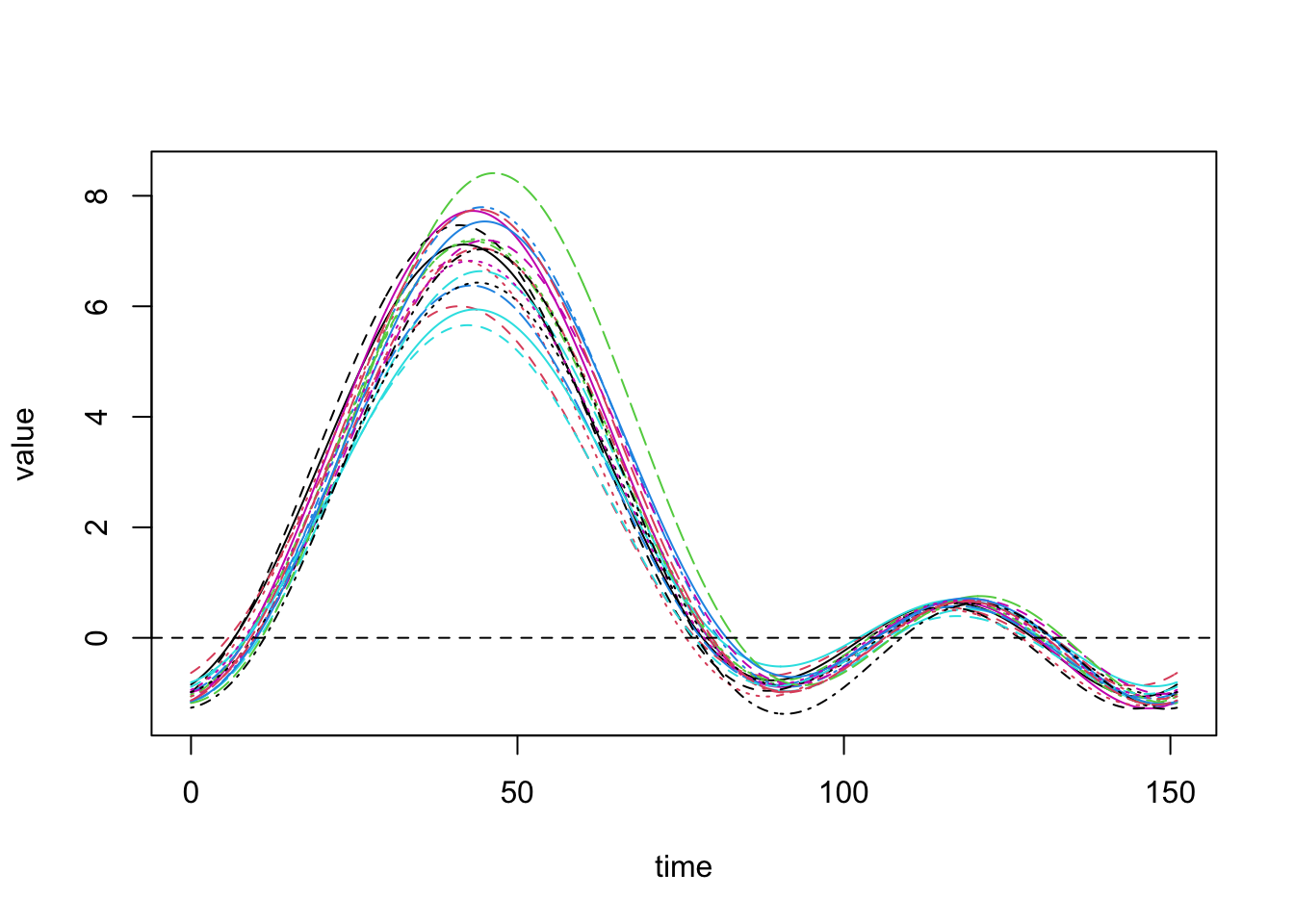
- Segundo K=15, es decir, un grande número de bases.
fourier.basis=create.fourier.basis(rangeval=c(0,151), nbasis=15)
pinch.fd=smooth.basis(y=pinch, fdParobj=fourier.basis)
plot(pinch.fd)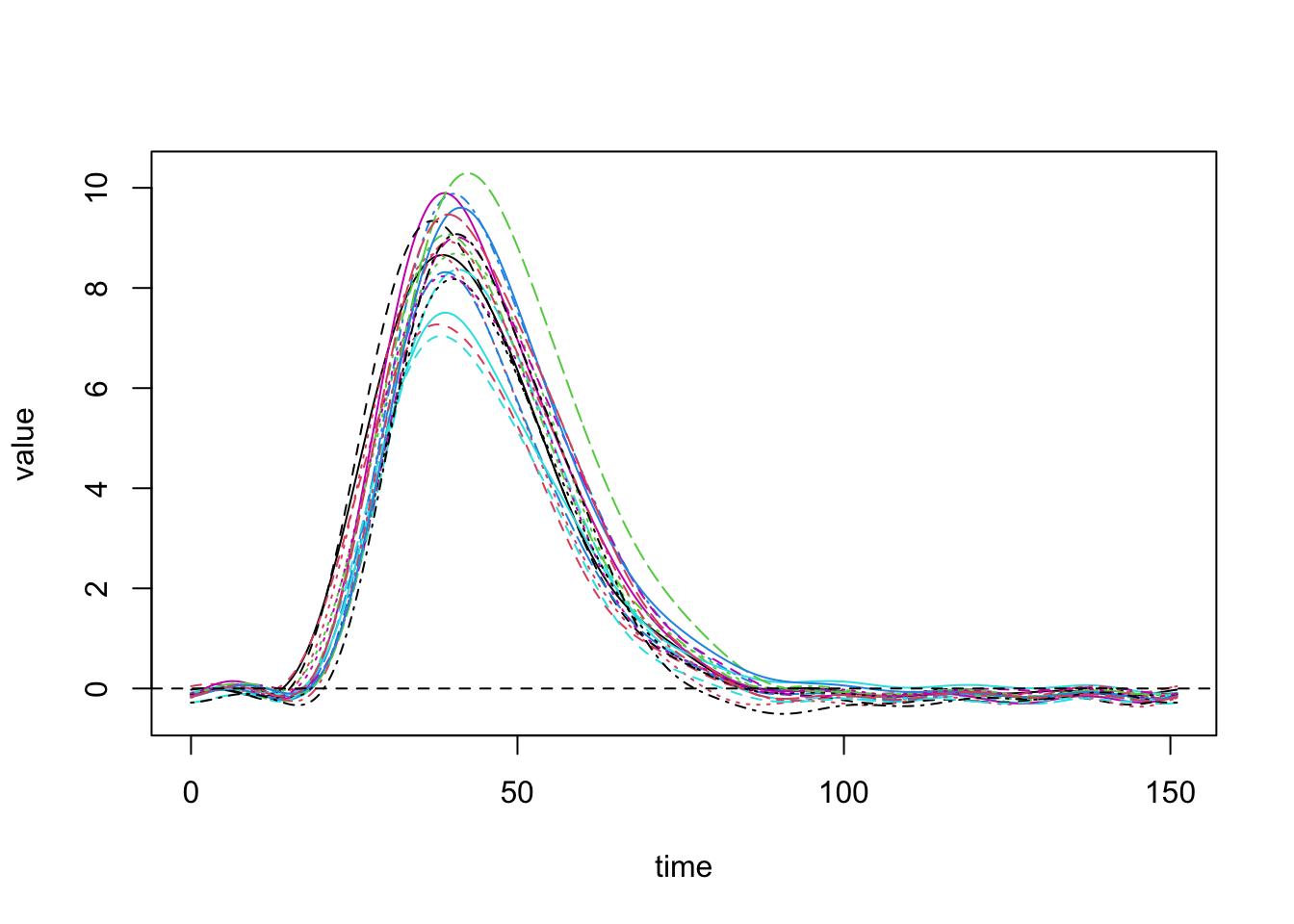
bspline.basis=create.bspline.basis(rangeval=c(0,151), nbasis=15)
pinch.fd=smooth.basis(y=pinch, fdParobj=bspline.basis)
plot(pinch.fd)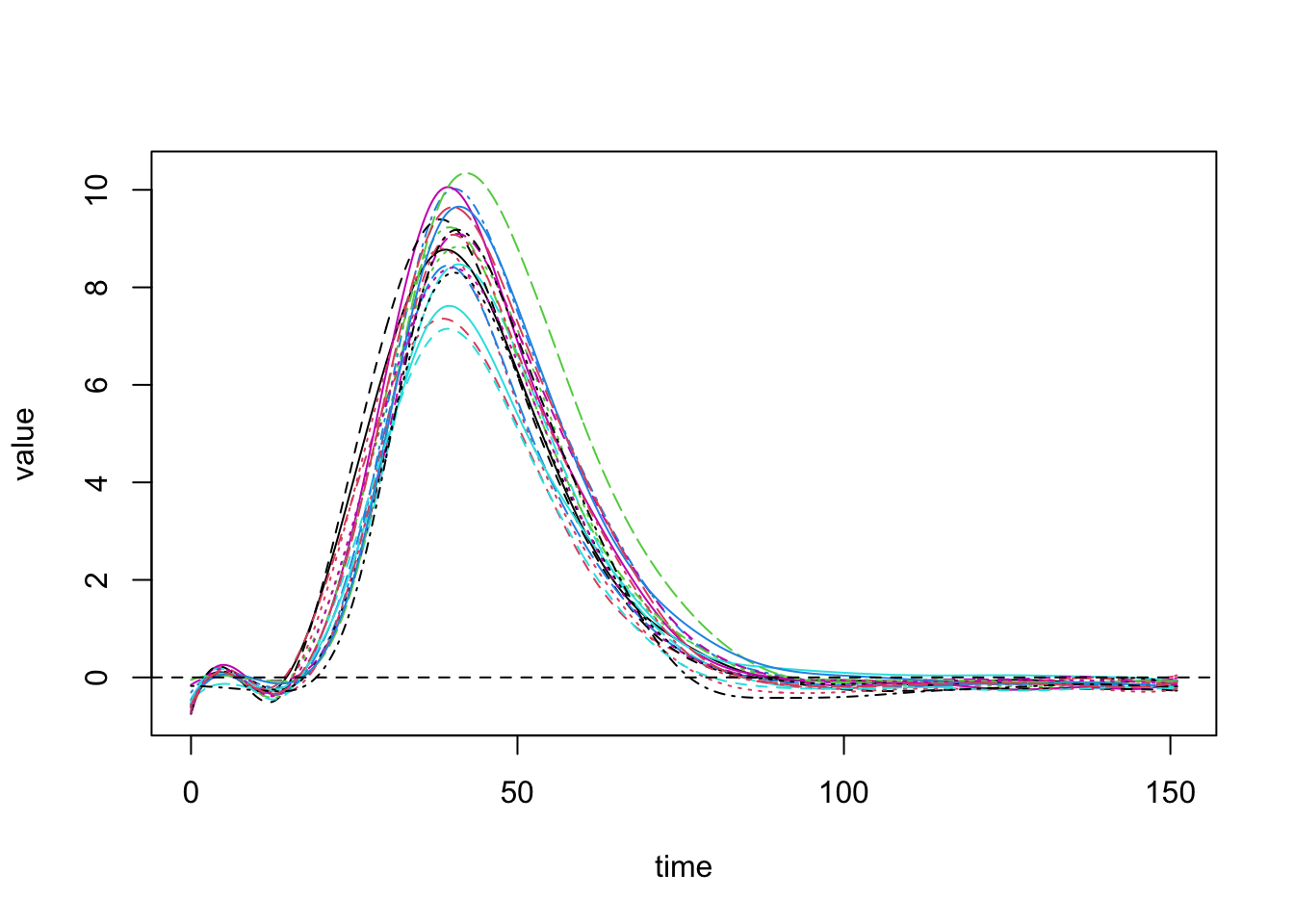
3.6 Media y covarianza
Ahora suponemos que los datos se han convertido en objetos funcionales mediante una base adecuada, posiblemente con suavizado adicional, y podemos trabajar con datos funcionales de la forma. Las estadísticas de resumen más simples son la media puntual y la desviación estándar puntual:
\[\begin{equation} \bar{X}_{N}(t)=\frac{1}{N}\sum_{n=1}^N X_{n}(t), \end{equation}\]
\[\begin{equation} SD_{X}(t)=\{\frac{1}{N-1} \sum_{n=1}^N (X_{n}(t)-\bar{X}_{N}(t))^2\}^{1/2} \end{equation}\]
Note que las formas son idénticas a las fórmulas usuales.
El siguiente código se usó para producir la siguiente Figura. La salida de la función smooth.basis es una lista. Los valores de las funciones se extraen usando $fd. Siguiendo el ejemplo de los datos pinch,
## Warning in mean.default(pinch.fd$fd): argument is not numeric or logical: returning NA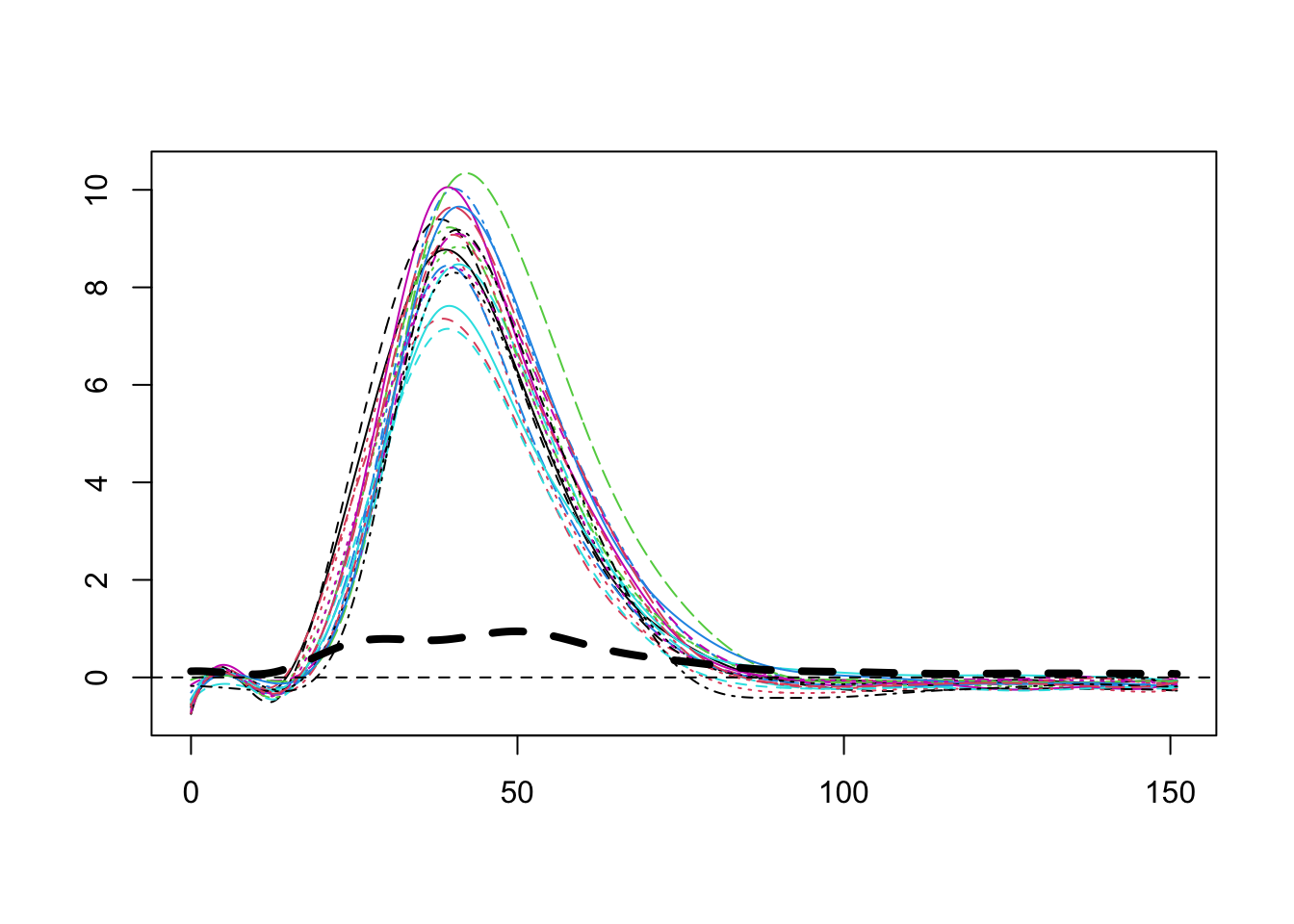
La desviación estándar de la muestra puntiaguda nos da una idea sobre la variabilidad típica de las curvas en cualquier punto \(t\), pero no proporciona información sobre cómo los valores de las curvas en el punto \(t\) se relacionan con otros puntos en el tiempo, llamado \(s\). Una formula que se usa ampliamente en la fda es la función de covarianza de muestra definida como:
\[\begin{equation} \hat{c}(t,s)=\frac{1}{N-1} \sum_{n=1}^N (X_{n}(t)-\bar{X}_{N}(t))(X_{n}(t)-\bar{X}_{N}(s)). \end{equation}\]
La interpretación de los valores de \(\hat{c}(t,s)\) es la misma que para la matriz de varianza-covarianza habitual.Por ejemplo, los valores grandes indican que \(X_n (t)\) y \(X_n (s)\) tienden a estar simultáneamente por encima o por debajo de los valores promedio en estos puntos. Es decir, una correlacion positiva.
El siguiente código calcula las funciones de covarianza de los datos pinch y genera la siguiente Figur. En este caso, el diagrama de contorno es particularmente interesante.
P.cov=var.fd(pinch.fd$fd)
grid=(1:5)*5
P.cov.mat=eval.bifd(grid, grid, P.cov)
persp(grid, grid, P.cov.mat, xlab="s", ylab="t", zlab="c(s,t)")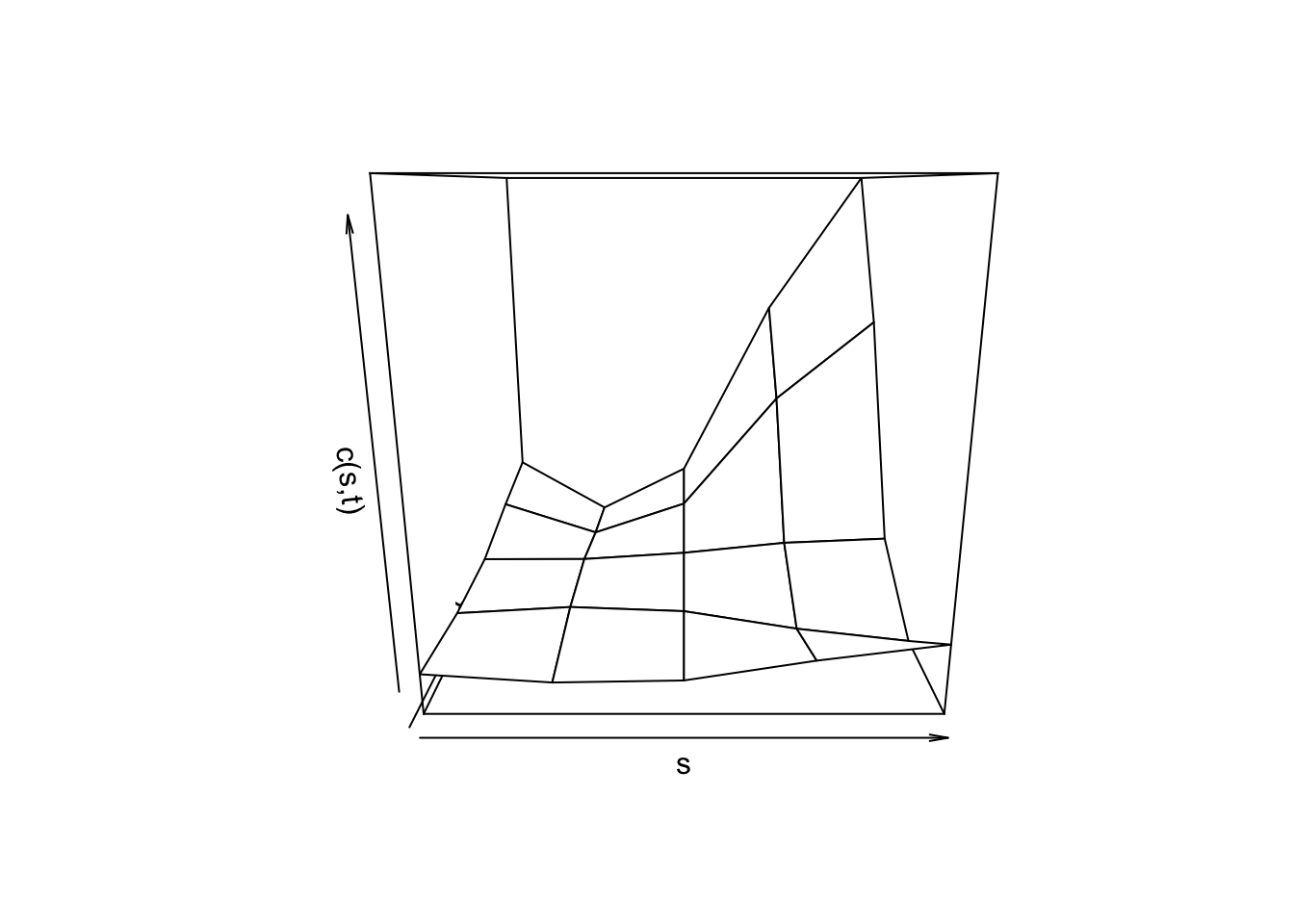
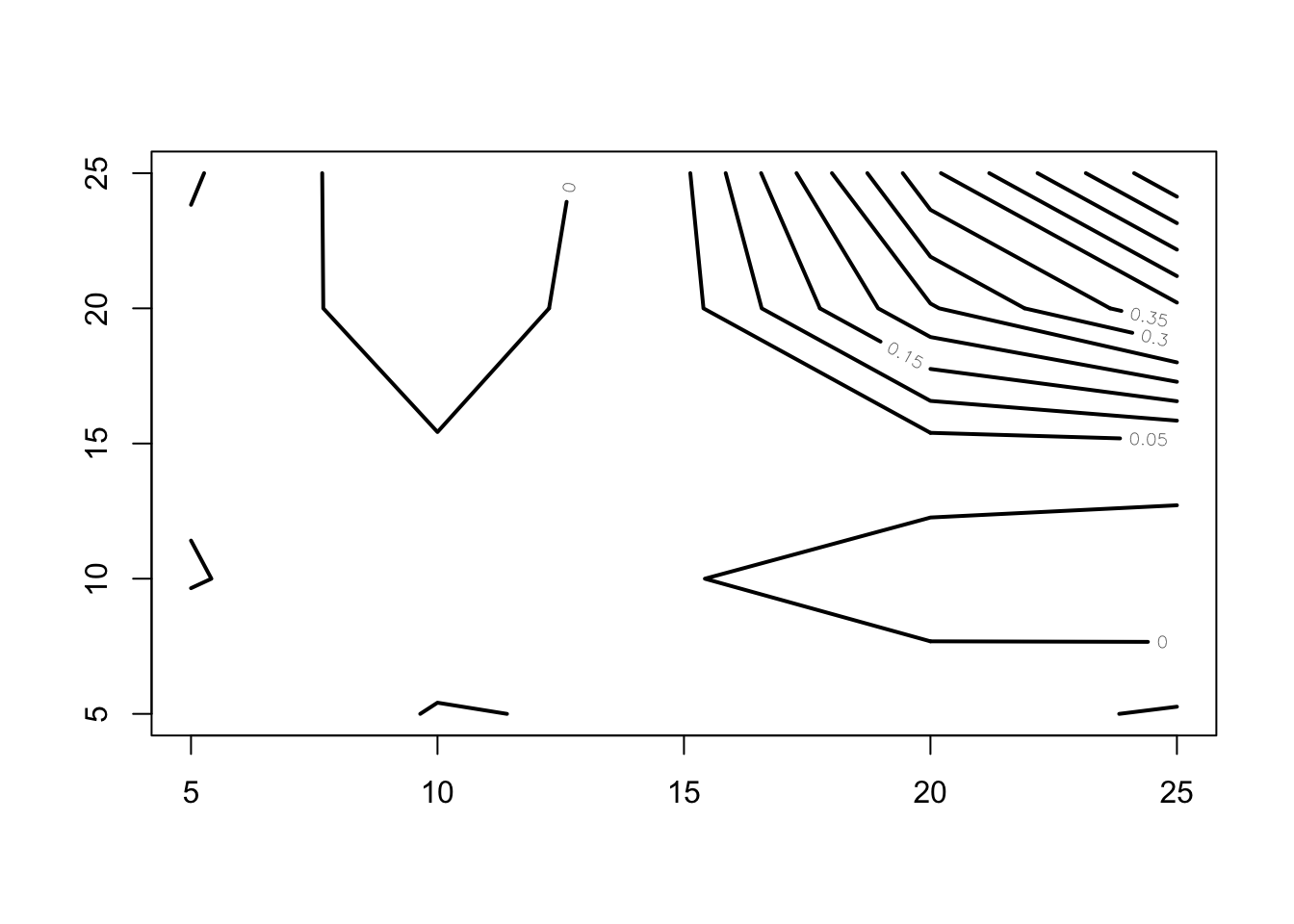
Tenemos una gráfica de contornos, ya que esta es una función bivariada, que depende de \(t\) y \(s\). En la gráfica de contornos nos muestra que para valores \(t\) y \(s\) cercanos a 25 la covarianza es mucho mayor, en comparación con los primeros valores.
3.7 Ejemplo de datos simulados
Tomado de Kokoszka (2018). Este libro tiene varios ejemplos y aplicaciones.
N=50
W.mat=matrix(0, ncol=N, nrow=10000)
n=1
for(n in 1:N){
W.mat[, n]=cumsum(rnorm(10000))/100
}
B25.basis=create.bspline.basis(rangeval=c(0,10000), nbasis=25)
W.fd=smooth.basis(y=W.mat, fdParobj=B25.basis)
plot(W.fd, ylab="", xlab="",col="gray",lty=1)
W.mean=mean(W.fd$fd)## Warning in mean.default(W.fd$fd): argument is not numeric or logical: returning NA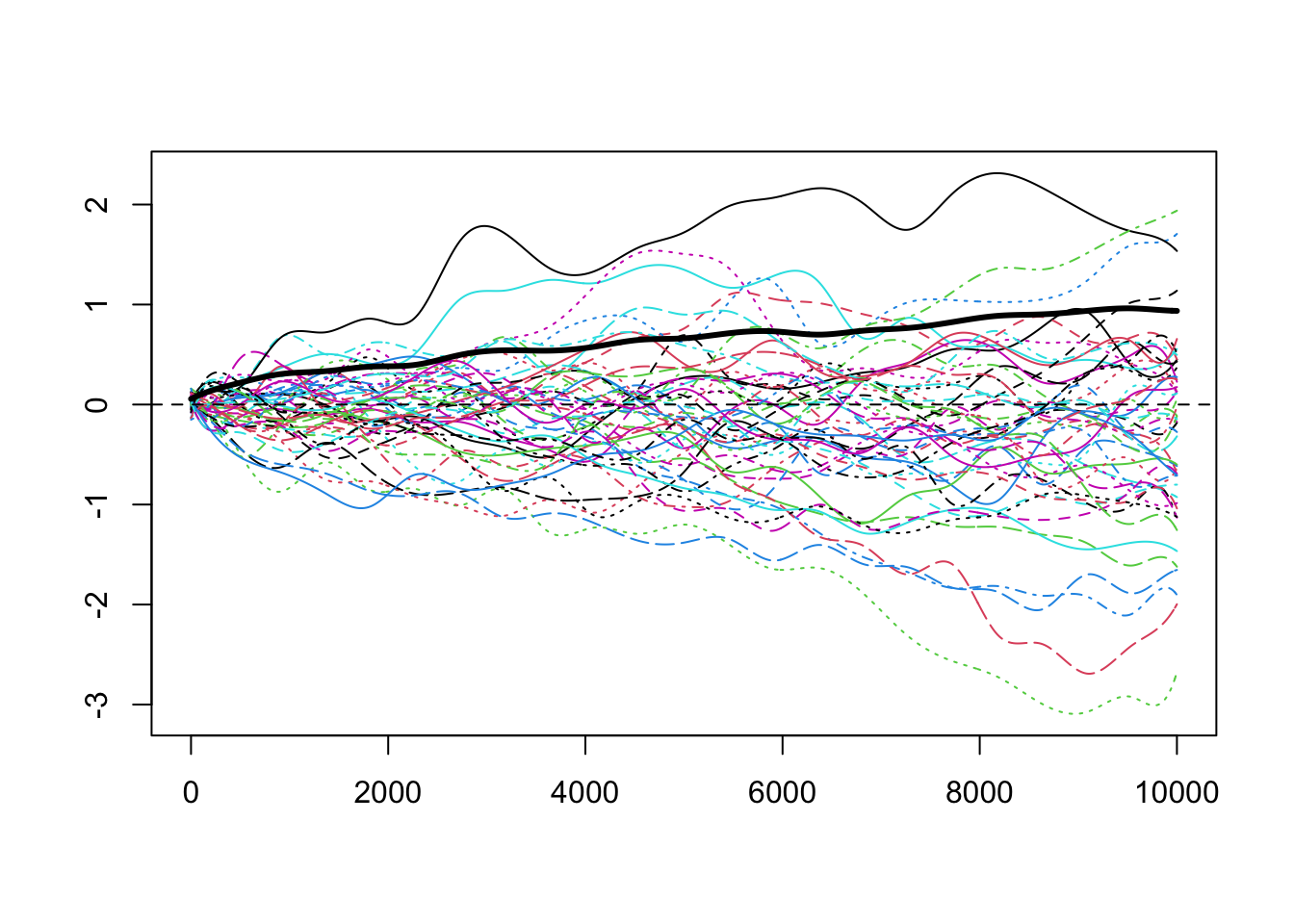
3.8 Aplicación: Corrupción en Colombia.
Uno de los más poderosos venenos, cánceres y maldiciones de un país, es la corrupción, aunque no hace falta datos para mostrar que Colombia es corrupta, vamos a estudiar que tan corrupta es. Vamos a utilizar los datos de [http://www.anticorrupcion.gov.co/Paginas/indicador-sanciones-penales.aspx], en esta página muestra el número de sanciones penales desde el 2008 hasta el 2018, por departamento y distritos especiales, de modo que sea posible saber cuál es el delito contra la administración pública asociado a la corrupción que se presenta con mayor frecuencia y cuál es el departamento en el que se presentan más sanciones. Los delitos son:
Mal uso del poder para obtener provecho personal,
Detrimento patrimonial,
Perjuicio social significativo.
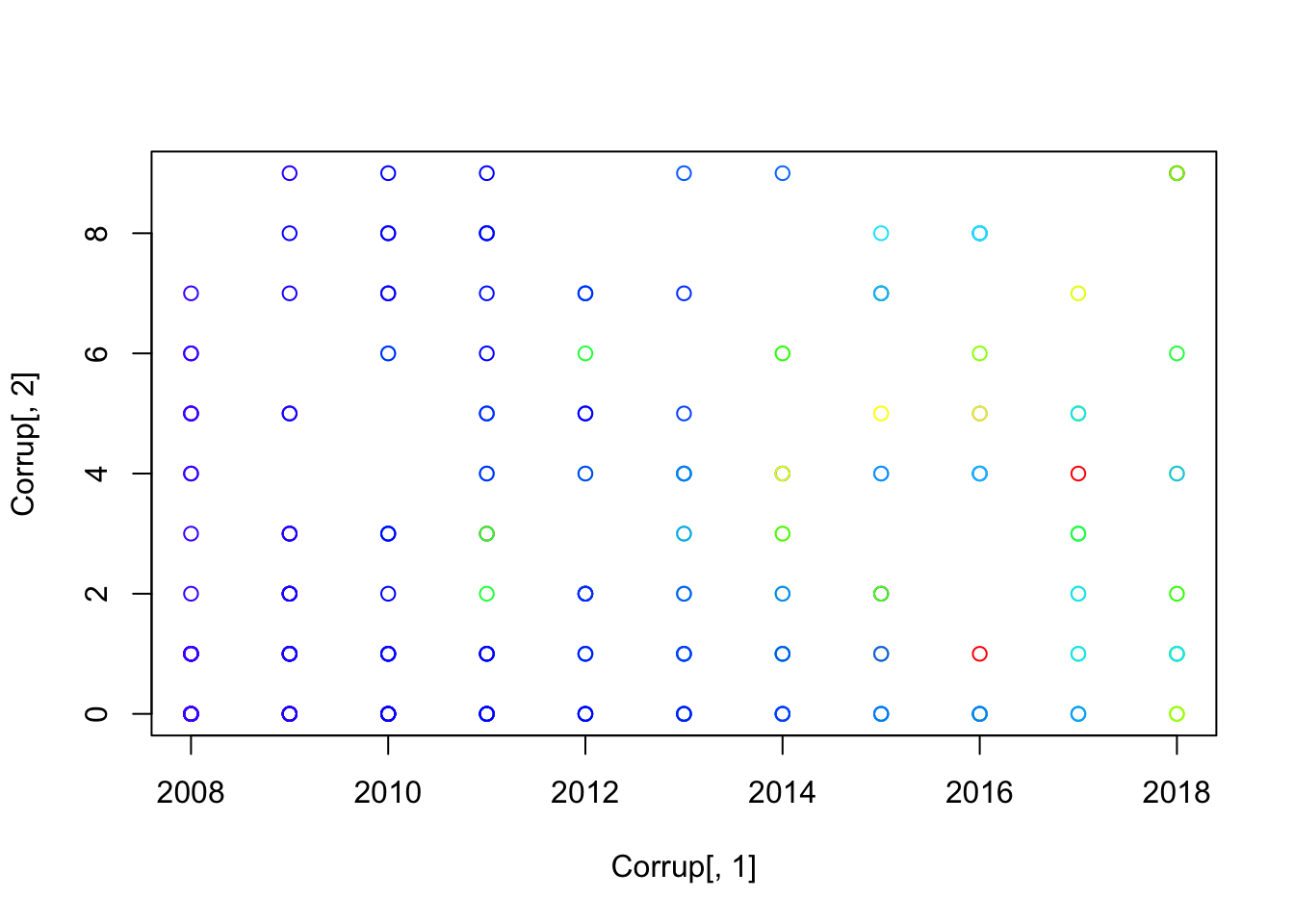
Los datos discretos se ven de la siguiente forma:
Corrup <- read.table("bases_de_datos/corrupcionSerieTiemp.csv",
header = TRUE,
sep = ";")
plot(Corrup[,1], Corrup[,2], col="red")
i=3
for( i in 3:34){
points(Corrup[,1], Corrup[,i], col=topo.colors(i))
}
Y aplicando el suavizado obtenemos: nam
x<-Corrup[, 1]
names<-names(Corrup)[2:34]
fdnames=list(Años=Corrup[, 1], Departamento=names, value='height')
fourier.basis=create.fourier.basis(rangeval=c(0,11), nbasis=6)
Corrup.fd=smooth.basis(y=as.matrix(Corrup[, 2:34]), fdParobj=fourier.basis, fdnames=fdnames)
plot(Corrup.fd, xlim=c(-1, 11), ylab="", xlab="",col="gray", pch=1:33, lty=1)## [1] "done"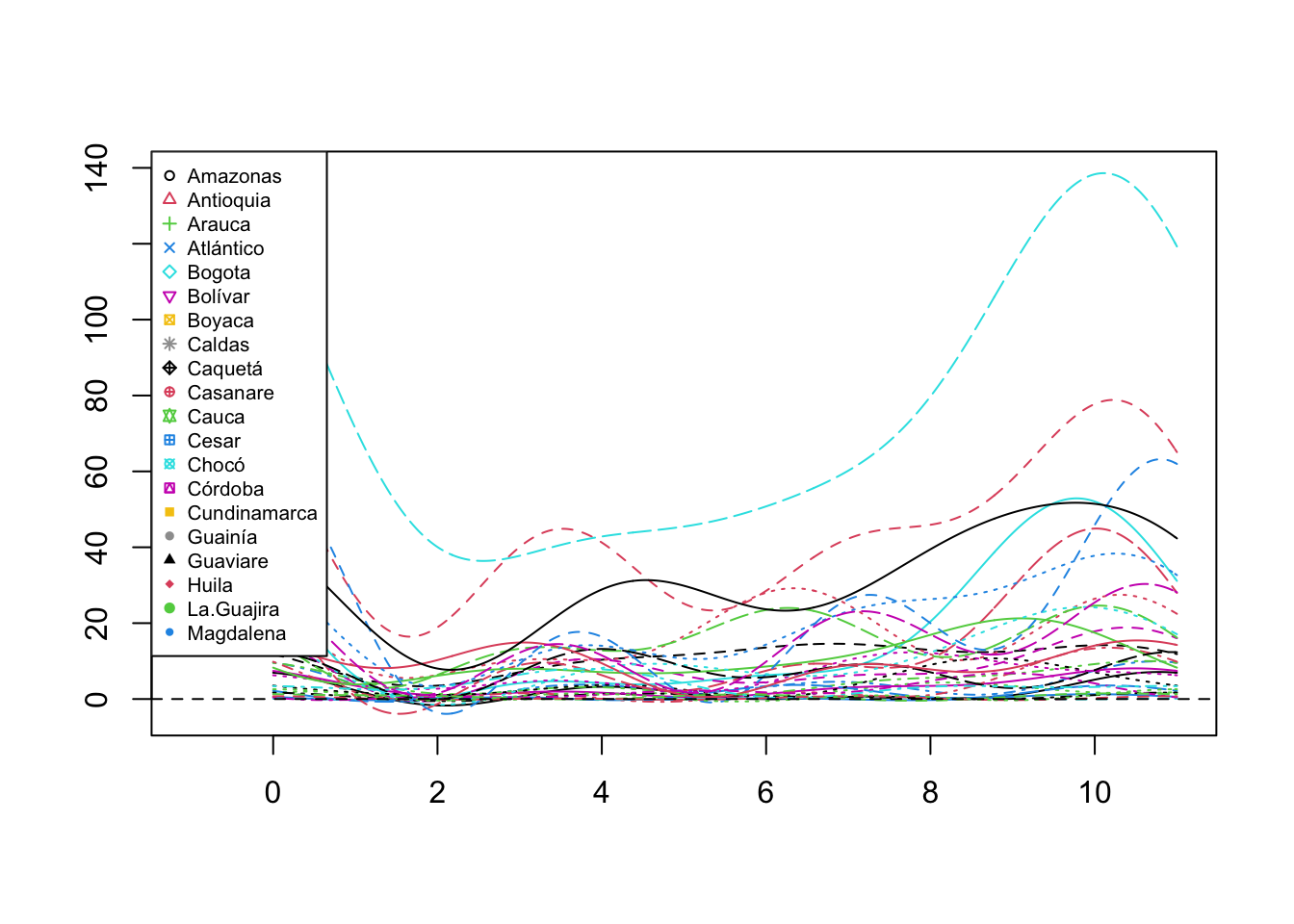
Bogotá encabeza el número de sanciones, seguido de Antioquia. El suavizamiento parece correcto. Algunas estadística descriptivas:
## Warning in mean.default(Corrup.fd$fd): argument is not numeric or logical: returning NA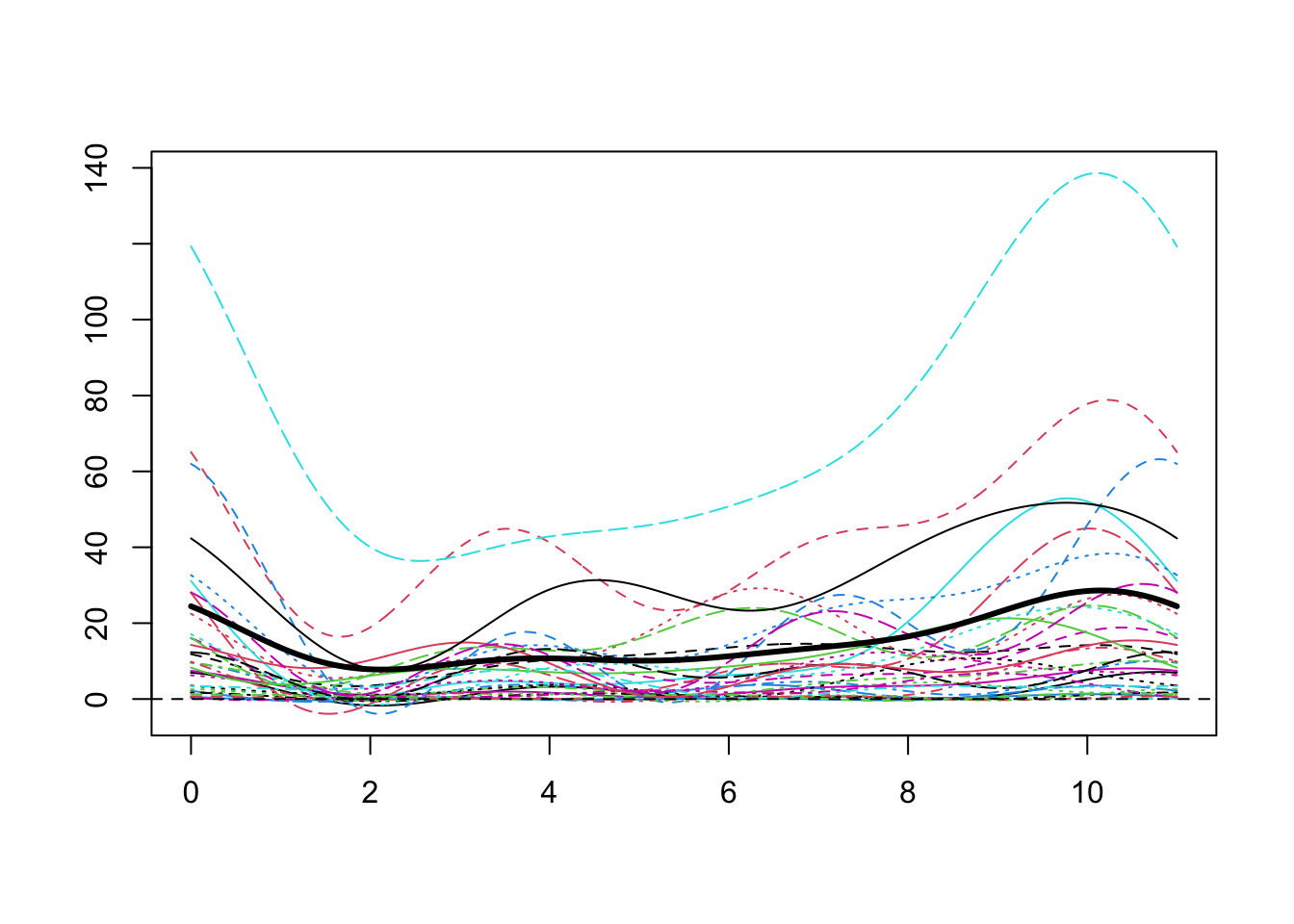
En realidad, la corrupción no ha bajado, desde el 2008 al 2018, siempre hemos tenido políticos corruptos, en toda Colombia, veamos la curva negra y continua, se mantiene casi estable a lo largo de los años.
Aunque los datos y las curvas que se muestran arriba se conocen comúnmente como “curvas de crecimiento”, el término crecimiento en realidad significa cambio. Entonces es la velocidad \(V (t)\), que mide la tasa de cambio de altura en el tiempo \(t\), que es la curva de crecimiento real, para esto, se debe calcular la derivada. También podemos calcular la segunda derivada, es decir la aceleración.
Para calcular la derivada, el paquete fda ofrece una opción rápida, pero primero debemos convertir los objetos a fdata:
bsp1 <- create.fourier.basis(c(1,33),21)
fd1 <- Data2fd(1:33,y=t(as.matrix(Corrup[, 2:34])),basisobj=bsp1)
fdataobj=fdata(fd1)
class(fdataobj)## [1] "fdata"Entonces, la velocidad a la que nos roban se mantiene estable:
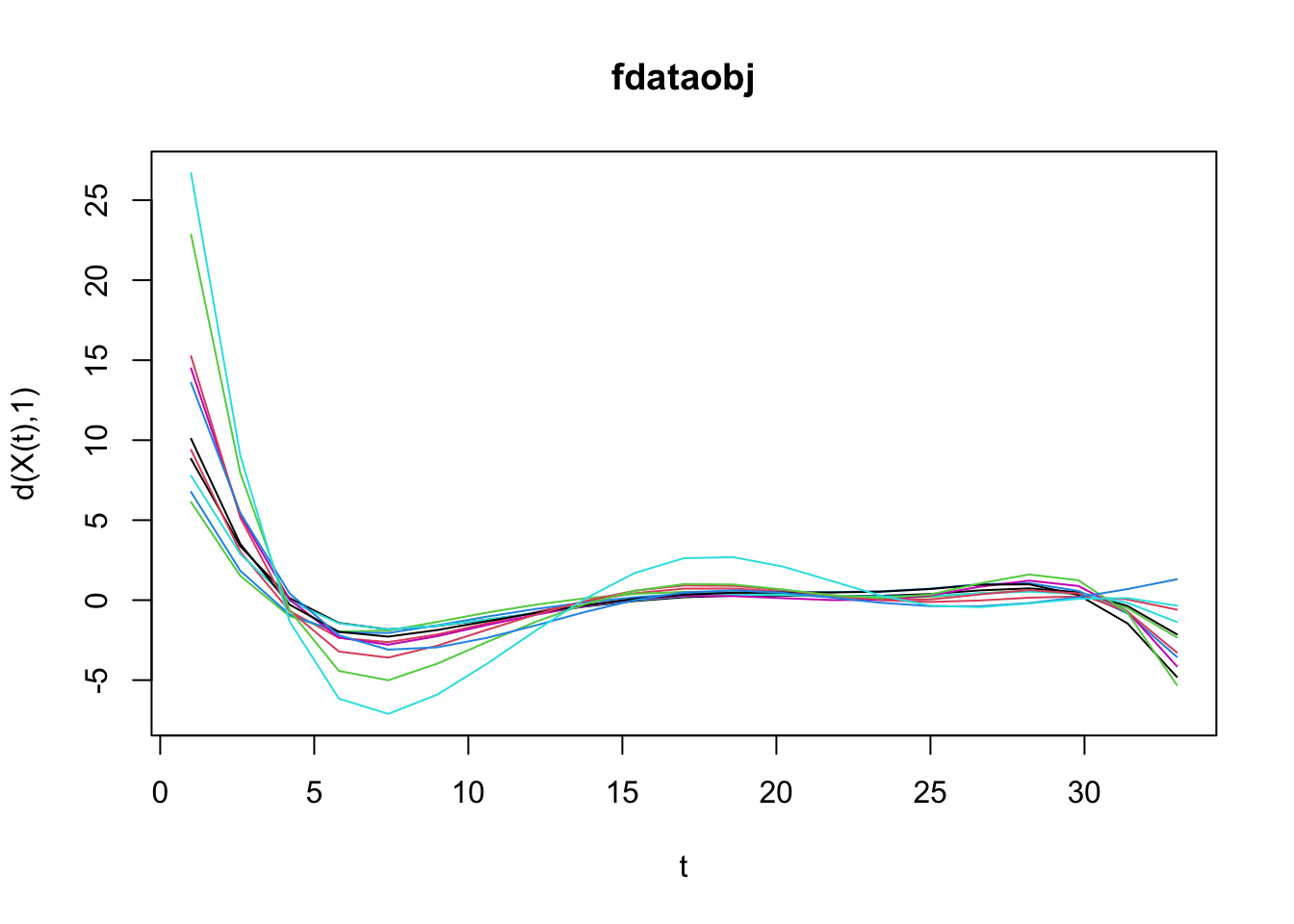Pero se aceleró con el tiempo:
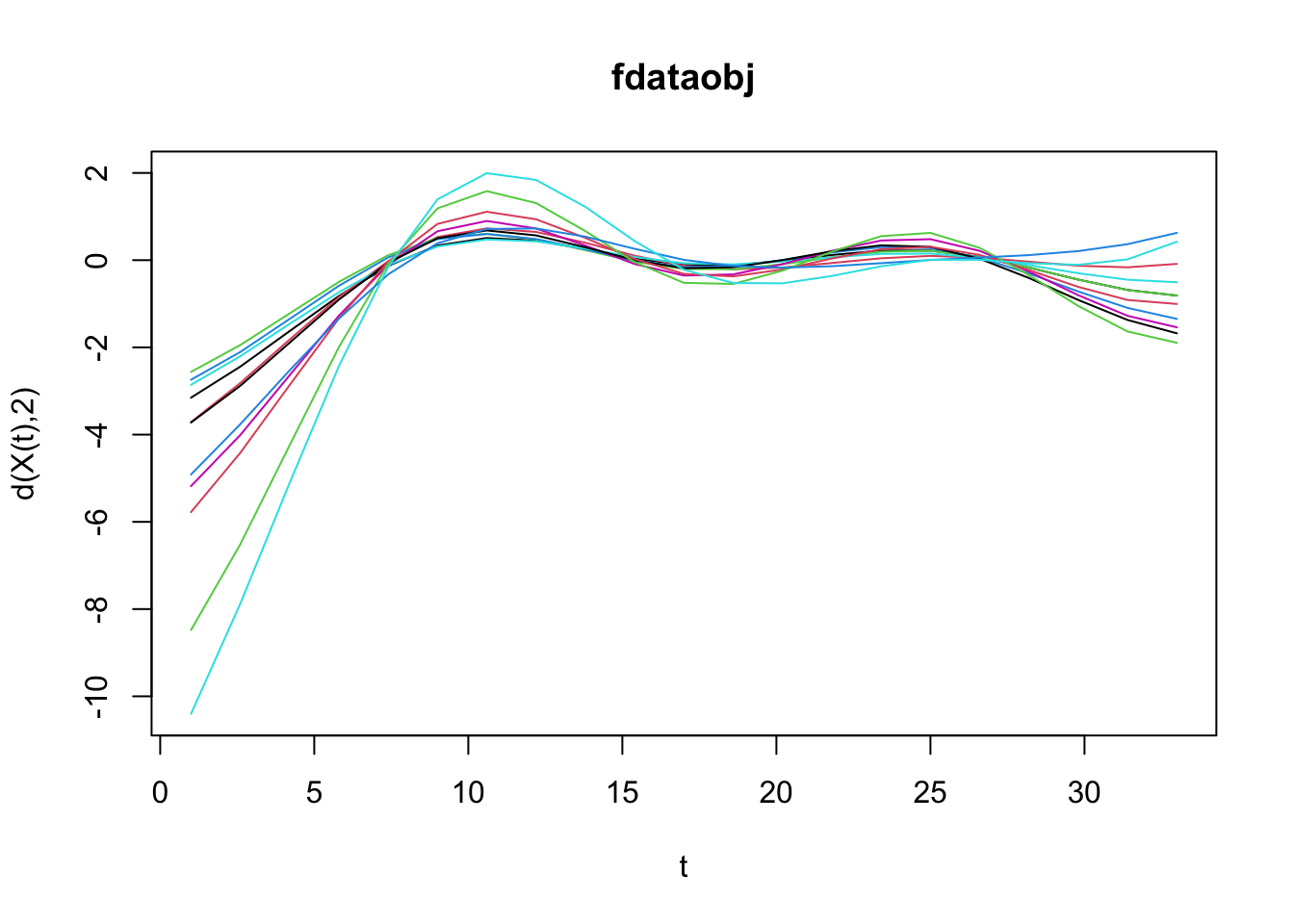
Esta sección fue revisada por: Anita.
Bibliografía
Febrero-Bande, Manuel, and Manuel Oviedo de la Fuente. 2012. “Statistical Computing in Functional Data Analysis: The R Package Fda.usc.” Journal of Statistical Software 51 (October): 1–28. https://doi.org/10.18637/jss.v051.i04.
Kokoszka, Reimherr, P. 2018. Introduction to Functional Data Analysis. New York: Chapman; Hall/CRC.