4 Models and assumptions
In this chapter, we’ll take a close look at the assumptions we make when using statistical models, and how we decide if assumptions are reasonable for practical purposes. More generally, we’ll consider the distinction between answering scientific (or “real world”) questions and answering statistical questions.
Chapter 4 readings
Statistical Inference: The Big Picture (Kass 2011)
Statistical Modeling: The Two Cultures (Breiman 2001)
Beyond objective and subjective in statistics (Gelman and Hennig 2017)
Consumption of low-calorie sweetened beverages is associated with higher total energy and sugar intake among children (Sylvetsky et al. 2019)
Disentangling bias and variance in election forecasts (Shirani-Mehr et al. 2018)
4.1 What are models, and why do we use them?
To make useful inferences from data, we typically require a model. Statistical models describe, mathematically, a data generating process. Consider for instance the simple linear regression model:
\[ \begin{align} Y_i&=\beta_0+\beta_1x_i+\varepsilon_i \\ \varepsilon_i &\sim Normal(0,\sigma^2) \\ i&=1,...,n \end{align} \]
This model says that the value \(Y_i\) is generated as a linear function \(x_i\), defined by the intercept \(\beta_0\) and slope \(\beta_1\), plus a value \(\varepsilon_i\) that is taken at random from a normal distribution with mean \(\mu=0\) and variance \(\sigma^2\).
If we assign values to \(\beta_0\), \(\beta_1\), and \(\sigma^2\), and we have values for \(x_1,\dots,x_n\), we can use this model to generate values for \(Y_1,\dots,Y_n\).
If we observe values \(x_1,y_1\dots x_n,y_n\), we can use these data to calculate parameter estimates \(\hat\beta_0,\hat\beta_1,\text{and } \hat\sigma^2\).
From this model, we can say things like:
- The expected (mean) value of \(Y_i\) given \(x_i\) is \(\beta_0+\beta_1x_i\).
- The estimated mean value of \(Y_i\) given \(x_i\) is \(\hat\beta_0+\hat\beta_1x_i\).
- If we observe two values of \(x\) that are one unit apart, their expected \(Y\) values will be \(\beta_1\) units apart.
- If we repeatedly observe values of \(Y\) at some particular value of \(X\), we expect that the standard deviation of these values will be \(\sqrt{\sigma^2}\).
- If we repeatedly collect new samples of size \(n\) and for each sample calculate \(\hat{\beta_1} \pm t_{( \alpha/2,df=n-2)}\cdot \sqrt{\hat{Var}(\hat{\beta_1})}\), then in \((1-\alpha)\cdot 100\%\) of repeated samples, \(\beta_1\) will be contained inside this interval.
4.1.1 Inference requires models; models require assumptions
All of the statements above are made within the context of a model. If we suppose that our data were generated according to the rules of our model, we get to make these claims. But, of course, our data were not actually generated the way the model says.
The model describes the data generating process in a way that imposes strong restrictions, which we treat as “assumptions” about how our data came to be. Here are some some assumptions impled by the simple linear regression model:
- We assume that, the population level, average value of \(Y\) is a linear function of \(X\).
- We assume that each observed \(y_i\) value was drawn independently from an infinitely large population characterized by a normal distribution centered on \(\beta_0+\beta_1x_i\).
- We assume that the variance in values of \(Y\) given \(x\) is \(\sigma^2\) for all \(x\).
Are these assumptions “true”? To the extent that this question even makes sense, the answer is no. The “true” (or “real world) process that created our data is almost certainly more complex that our model claims.
Here are some more assumptions of this model that we rarely say out loud:
We assume that there is actually some population from which our data are a sample, and that if we wanted we could take more samples from this population.
We assume that the “true parameter values” we are trying to estimate exist in the real world.
It is extremely difficult to respect this distinction when interpreting statistical results. When we see a p-value of 0.001 next to an estimated regression slope (call it \(\hat{\beta_1}\)) and interpret this as “the probability of getting a test statistic at least as large as ours, if the null hypothesis was true”, we are implicitly assuming our model is true. When we interpret \(\hat{\beta_1}\) as “the estimated average difference in Y corresponding to a one unit difference in X”, we are relying on the assumption of linearity. That assumption is almost certainly false, and so our slope interpretation isn’t a description of the real world - it’s a description of our model of the real world.
“All models are wrong but some are useful” - George Box
The Wikipedia page for “All models are wrong” gives an excellent overview of this principle, including many more quotes from Box and other statisticians.
When we use models that make assumptions, we are accepting a burden: the quality of our inferences may depend upon the correctness of our assumptions. To the extent that our assumptions are false, aspects of our inferences may also be false (we’ll look more into this next).
Why would we choose to burden ourselves this way? Can’t we just “let the data speak” rather than impose these risky assumptions?
The first answer is that data only metaphorically “speak” in response to the specific questions we ask of them. The result of any statistical analysis can be thought of as our data’s answer to a particular question. Change the question, even slightly, and the answer may also change.
The second answer is that our assumptions allow us to make inferences. We could not talk about, for instance, “the change in our estimated outcome \(Y\) associated with a 1-unit difference in \(x_1\) when the values of \(x_2\) and \(x_3\) are held constant” if we did not first establish the model relating them. We could not use standard errors to quantify the likely amount of error in our estimates without first establishing the quantity being estimated (assumed to exist for an assumed population from which we assume our sample is one of infinitely many that could be taken), and then establishing the conditions under which we can guarantee our estimation procedure has certain properties.
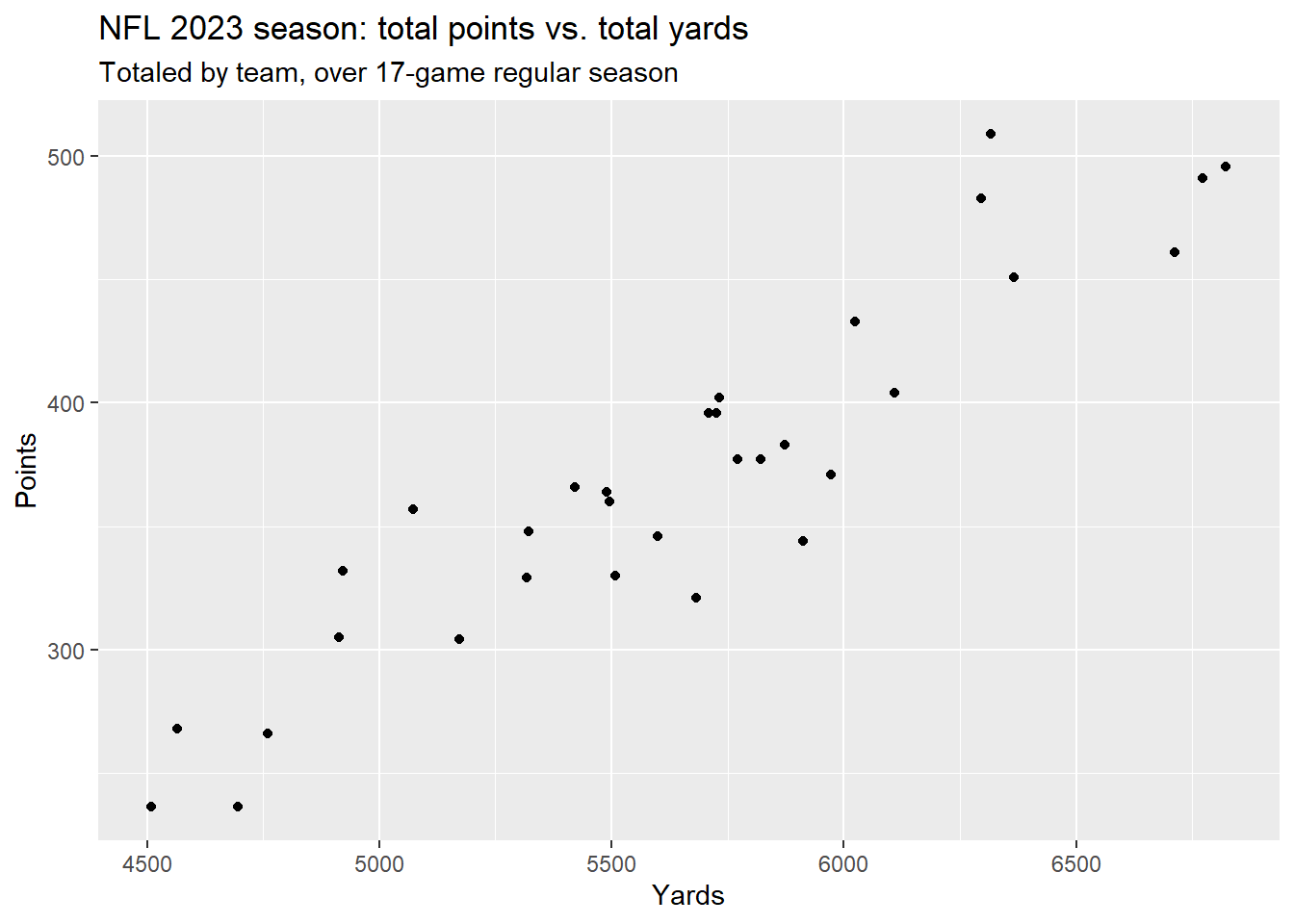
4.1.2 Example: Points vs. Yards in the NFL
Here is a plot of some data from the 2023 regular season of the NFL (National Football League):
This looks like a strong linear trend. Let’s fit the simple linear regression model:
\[ \begin{align} Points_i&=\beta_0+\beta_1Yards+\varepsilon_i \\ \varepsilon_i &\sim Normal(0,\sigma^2) \end{align} \]
options(scipen=1) # gets rid of scientific notation in estimates
NFL_model <- lm(Points~Yds,data=NFL)
summary(NFL_model,digits=3)
Call:
lm(formula = Points ~ Yds, data = NFL)
Residuals:
Min 1Q Median 3Q Max
-55.497 -16.430 -0.755 16.915 66.163
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -233.151854 46.082852 -5.059 1.97e-05 ***
Yds 0.107011 0.008128 13.166 5.31e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 28.06 on 30 degrees of freedom
Multiple R-squared: 0.8525, Adjusted R-squared: 0.8476
F-statistic: 173.4 on 1 and 30 DF, p-value: 5.312e-14So, the fitted model is:
\[ \begin{align} \hat{Points_i}&=-233.152+0.107(Yards_i) \\ \hat{\sigma}_{\varepsilon}&=28.06 \end{align} \]
Note
The estimated standard deviation of \(\varepsilon_i\) is \(\hat{\sigma}_{\varepsilon}=28.06\). It is referred to as “residual standard error” in the summary regression output. This is unfortunate; it ought to be called something like “residual standard deviation” or “estimated standard deviation of the errors”. From the R help documentation for sigma():
The misnomer “Residual standard error” has been part of too many R (and S) outputs to be easily changed there.
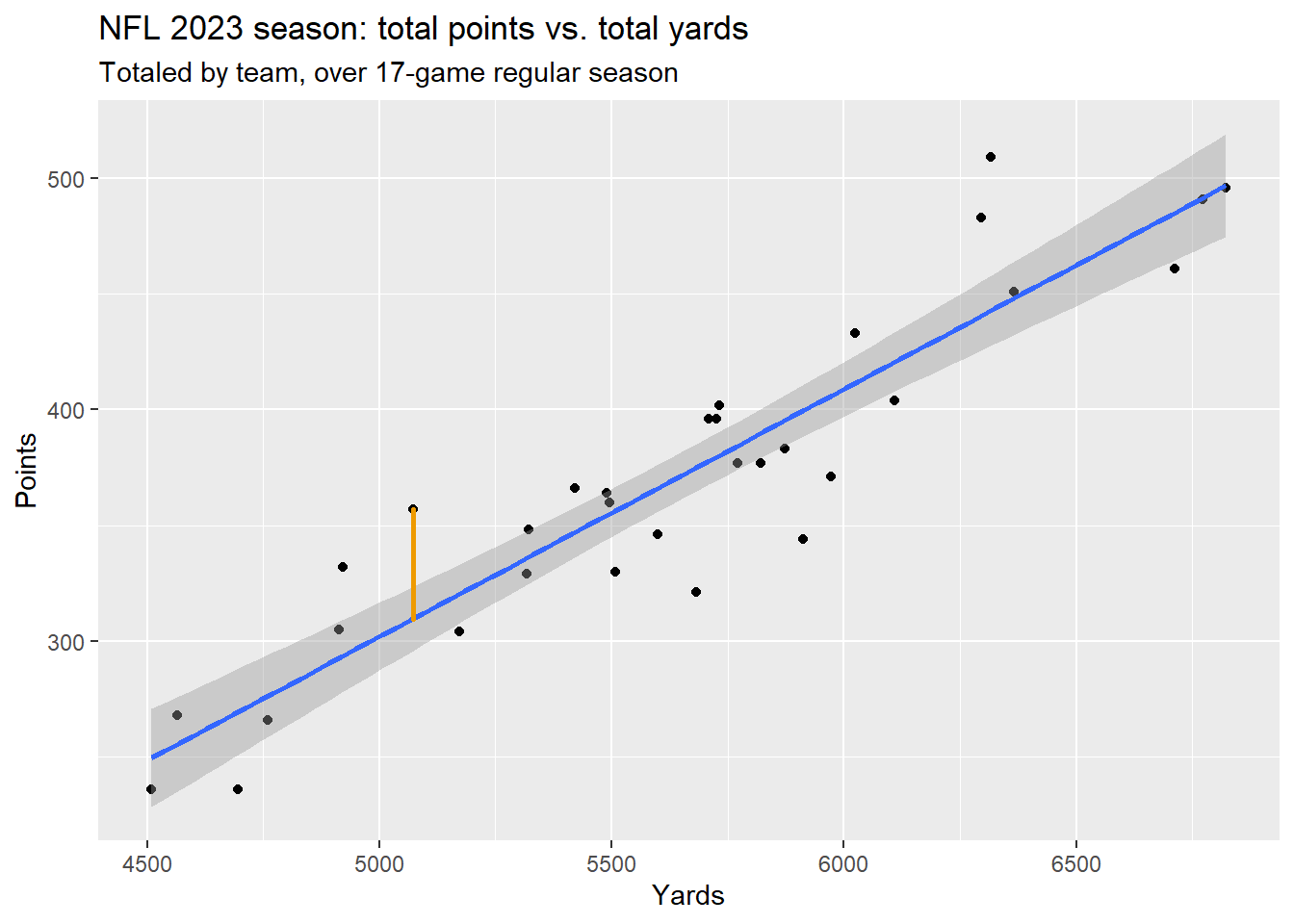
The Denver Broncos had 5,072 yards and 357 points. If we plug 5072 into \(\hat{Points_i}=-233.152+0.107(Yards_i)\), we get \(\hat{Points}=-233.152+0.107\times 5072=309.552\), which is the value that puts us on the line. The difference between 357 and 309.55 is the residual for the Broncos, drawn in orange on the plot above.
So, according to this model, here’s how the Denver Broncos’ 357 total regular season points came into being:
- First, their 5,072 total regular season yards came into being, somehow.
- Next, this value was plugged into the estimated equation \(\hat{Points_i}=-233.152+0.107(Yards_i)\) , giving us an estimated population average point total of 309.55 for all teams who accumulated 5,072 yards over the season.1
- Then, a value of \(\varepsilon\) was realized from a normal distribution that has a mean of zero and estimated standard deviation of 28.06. This turned out to be \(\hat{\varepsilon}=\) 47.448.
- Finally, \(\hat{\varepsilon}=\) 47.448 wass added to \(\hat{Points}=\) 309.552, giving 309.552 + 47.448 = 357 points.
This, of course, isn’t really how those 357 total regular season points came into being. The true process involved hundreds of football players and coaches and referees (each with their own personal history that brought them to the NFL), a variety of weather conditions, subtle interactions between cleats and patches of grass, moments of intense crowd noise, split-second strategic choices, lots of lucky (and unlucky) guesses about what other players would do, long summer days spent in weight rooms, etc. The complete set of real-world forces that combined to create those 357 points are far too vast and complex for any person to comprehend.
But, it seems like we can fake the real-world outcomes pretty well with a straight line and numbers pulled randomly from a normal distribution. Let’s see how the model performs if we use it to generate new simulated point totals, given the observed yard totals:
set.seed(335)
simulated_errors <- rnorm(n=32,mean=0,sd=28.06)
NFL$simulated_points <- predict(NFL_model) + simulated_errors
ggplot(NFL,aes(x=Yds,y=simulated_points)) +
geom_point() +
xlab("Actual Yards") +
ylab("Simulated Points") +
ggtitle("Simulated total points vs. actual total yards",
subtitle = "Simulated points come from regression model fit to actual data ")
Not bad! Despite the real-world process that generated each team’s points being incomprehensibly complex, a very simple statistical model can generate simulated points that look awfully similar.
4.2 Simulating model violations
In this section, we’ll look at examples of simulating data in ways such that assumptions are violated, and then examining the consequences.
4.2.1 Violating equal variance for a t-test
The two-sample t-test assumes that the data in each of the two groups being compared came from normal distributions. This assumption allows us to mathematically prove that the long-run Type I error rate when testing \(H_0:\mu_1-\mu_2=0\) is controlled by \(\alpha\).
This code simulates running a two-sample t-test when \(H_0\) is true:
set.seed(335)
N <- 50
group1 <- rnorm(n=N,mean=10,sd=1)
group2 <- rnorm(n=N,mean=10,sd=1)
t.test(group1,group2)$p.value[1] 0.02181207How about that, it’s a Type 1 error! Let’s try again.
N <- 50
group1 <- rnorm(n=N,mean=10,sd=1)
group2 <- rnorm(n=N,mean=10,sd=1)
t.test(group1,group2)$p.value[1] 0.265644Now, let’s do this 10,000 times and see how often we get \(p<0.05\).
reps <- 1e4
pvals <- rep(0,reps)
N <- 50
for (i in 1:reps) {
group1 <- rnorm(n=N,mean=10,sd=1)
group2 <- rnorm(n=N,mean=10,sd=1)
pvals[i] <- t.test(group1,group2)$p.value
}
sum(pvals<0.05)/reps[1] 0.0464This is close enough to the \(\alpha=0.05\) rate we expect.
Now let’s violate the assumption of equal variance:
reps <- 1e4
pvals <- rep(0,reps)
N <- 50
for (i in 1:reps) {
group1 <- rnorm(n=N,mean=10,sd=3)
group2 <- rnorm(n=N,mean=10,sd=1)
pvals[i] <- t.test(group1,group2)$p.value
}
sum(pvals<0.05)/reps[1] 0.0479This doesn’t seem to have done much. Let’s violate it more severely:
reps <- 1e4
pvals <- rep(0,reps)
N <- 50
for (i in 1:reps) {
group1 <- rnorm(n=N,mean=10,sd=10)
group2 <- rnorm(n=N,mean=10,sd=1)
pvals[i] <- t.test(group1,group2)$p.value
}
sum(pvals<0.05)/reps[1] 0.049Huh, seems like this should have done something… oh wait! R defaults to using Welch’s t-test, which relaxes the assumption of equal variances. Here’s code for Student’s t-test, which assumes equal variances:
reps <- 1e4
pvals <- rep(0,reps)
N <- 50
for (i in 1:reps) {
group1 <- rnorm(n=N,mean=10,sd=10)
group2 <- rnorm(n=N,mean=10,sd=1)
pvals[i] <- t.test(group1,group2,var.equal=TRUE)$p.value
}
sum(pvals<0.05)/reps[1] 0.0466Our Type 1 error rate is still where it should be. Does this assumption matter at all? Let’s try changing the sample sizes so that they aren’t equal (aka “balanced”):
reps <- 1e4
pvals <- rep(0,reps)
N1 <- 30
N2 <- 70
for (i in 1:reps) {
group1 <- rnorm(n=N1,mean=10,sd=10)
group2 <- rnorm(n=N2,mean=10,sd=1)
pvals[i] <- t.test(group1,group2,var.equal=TRUE)$p.value
}
sum(pvals<0.05)/reps[1] 0.2056Oh my. Now the Type 1 error rate has quadrupled. Let’s swap which group gets the larger sample:
reps <- 1e4
pvals <- rep(0,reps)
N1 <- 70
N2 <- 30
for (i in 1:reps) {
group1 <- rnorm(n=N1,mean=10,sd=10)
group2 <- rnorm(n=N2,mean=10,sd=1)
pvals[i] <- t.test(group1,group2,var.equal=TRUE)$p.value
}
sum(pvals<0.05)/reps[1] 0.0049Now the test is far too conservative.
Just to check to see how Welch’s t-test deals with this…
reps <- 1e4
pvals <- rep(0,reps)
N1 <- 30
N2 <- 70
for (i in 1:reps) {
group1 <- rnorm(n=N1,mean=10,sd=10)
group2 <- rnorm(n=N2,mean=10,sd=1)
pvals[i] <- t.test(group1,group2,var.equal=FALSE)$p.value
}
sum(pvals<0.05)/reps[1] 0.0482Remember, Welch’s t-test doesn’t assume equal variances. With no assumption violation anymore, we shouldn’t be surprised to see the correct Type I error rate.
4.2.2 Violating the normality assumption
The two-sample t-test assumes data for both groups came from a normal distribution. Similarly, ordinary least squares (OLS) regression assumes that residuals come from a normal distribution. If we want to model a violation, we need to draw from a non-normal distribution. There are many options when modeling non-normality; we’ll look at one here.
The gamlss.dist package for R lets us draw values from a “sinh-arcsinh” distribution, which is a 4 parameter distribution in which the normal is a special case. The additional 2 parameters are nu (skewness) and tau (kurtosis).
library(gamlss.dist)
normal_data <- rSHASHo(n=1000,mu=10,sigma=3,nu=0,tau = 1)
hist(normal_data,breaks=20)
skewed_data <- rSHASHo2(n=1000,mu=10,sigma=3,nu=0.5,tau = 1)
hist(skewed_data,breaks=20)
skewed_data <- rSHASHo(n=1000,mu=10,sigma=3,nu=-1,tau = 1)
hist(skewed_data,breaks=20)
heavy_tailed_data <- rSHASHo(n=1000,mu=10,sigma=3,nu=0,tau = 0.5)
hist(heavy_tailed_data,breaks=20)
light_tailed_data <- rSHASHo(n=1000,mu=10,sigma=3,nu=0,tau = 1.5)
hist(light_tailed_data,breaks=20)
Now we can try out the same kinds of simulations as before:
reps <- 1e4
pvals <- rep(0,reps)
N <- 10
for (i in 1:reps) {
group1 <- rSHASHo(n=N,mu=10,sigma=3,nu=0,tau = 0.5)
group2 <- rSHASHo(n=N,mu=10,sigma=3,nu=0,tau = 1)
pvals[i] <- t.test(group1,group2,var.equal=TRUE)$p.value
}
sum(pvals<0.05)/reps[1] 0.0519reps <- 1e4
pvals <- rep(0,reps)
N1 <- 10
N2 <- 20
for (i in 1:reps) {
group1 <- rSHASHo(n=N1,mu=10,sigma=3,nu=0,tau = 0.5)
group2 <- rSHASHo(n=N2,mu=10,sigma=3,nu=0,tau = 1)
pvals[i] <- t.test(group1,group2,var.equal=TRUE)$p.value
}
sum(pvals<0.05)/reps[1] 0.15074.2.3 Extreme non-normality: the Cauchy distribution
The Cauchy distribution can be used to simulate data from a distribution that takes on extreme outliers. The Cauchy distribution has no population mean or variance; the Law of Large Numbers and Central Limit Theorem do not “work” with the Cauchy distribution insofar as the sample mean never converges to a population mean, regardless of sample size. Here’s an example of data from a Cauchy distribution:
set.seed(335)
cauchy_data <- rcauchy(n=200,location=0,scale=1)
hist(cauchy_data,breaks=20)
And again:
cauchy_data <- rcauchy(n=200,location=0,scale=1)
hist(cauchy_data,breaks=20)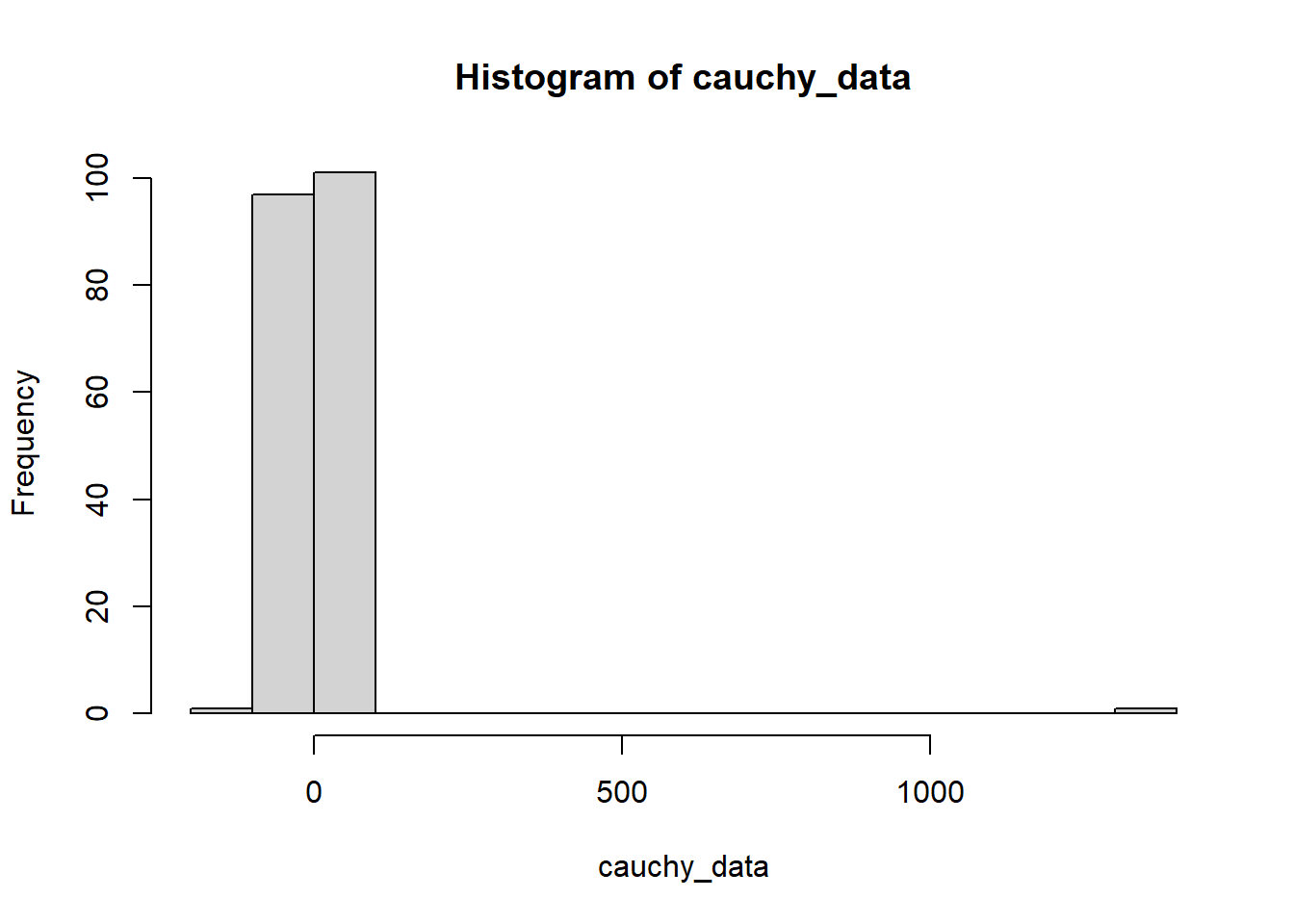
A Cauchy random variable can also be constructed as the ratio of two standard normal random variables:
normal_numerators <- rnorm(200)
normal_denominators <- rnorm(200)
Cauchy_from_normals <- normal_numerators/normal_denominators
hist(Cauchy_from_normals,breaks=20)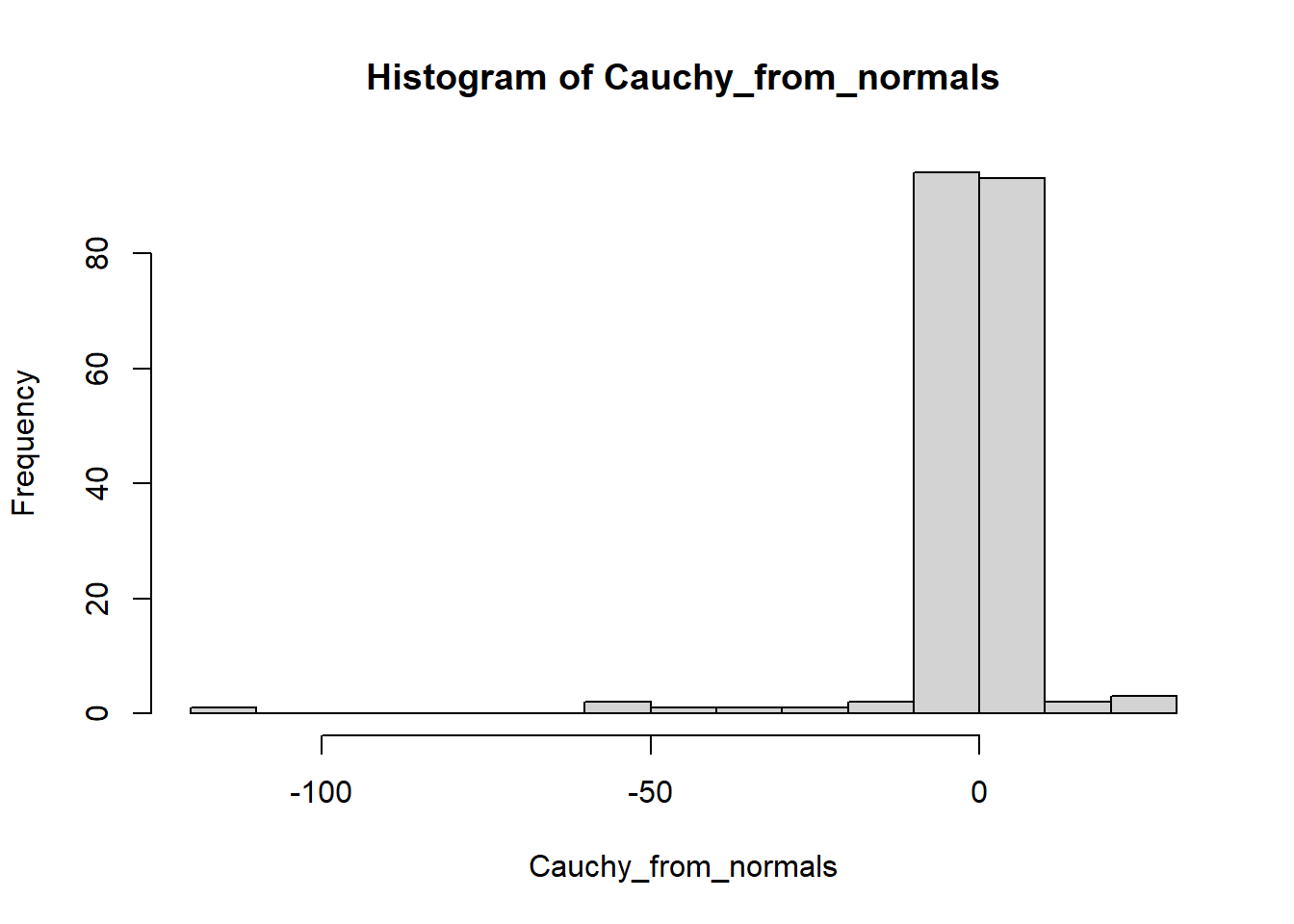
The Cauchy distribution’s “location” parameter is its median. Since the median isn’t sensitive to outliers, this parameter can be defined and is quite stable; the sample median is an unbiased estimator of the population median.
The Cauchy distribution’s “scale” parameter is its inter-quartile range. The IQR encloses the central 50% of values in a data set.
Let’s re-do our simulations, this time using the Cauchy distribution to model extreme non-normality:
reps <- 1e4
pvals <- rep(0,reps)
tstats <- rep(0,reps)
N <- 10
for (i in 1:reps) {
group1 <- rcauchy(n=N,location=0,scale=1)
group2 <- rcauchy(n=N,location=0,scale=1)
test_results <- t.test(group1,group2,var.equal=TRUE)
pvals[i] <- test_results$p.value
tstats[i] <- test_results$statistic
}
sum(pvals<0.05)/reps[1] 0.0213This is conservative. Changing the sample size won’t do anything. For fun, let’s look at the distribution of test statistics from this simulation:
hist(tstats)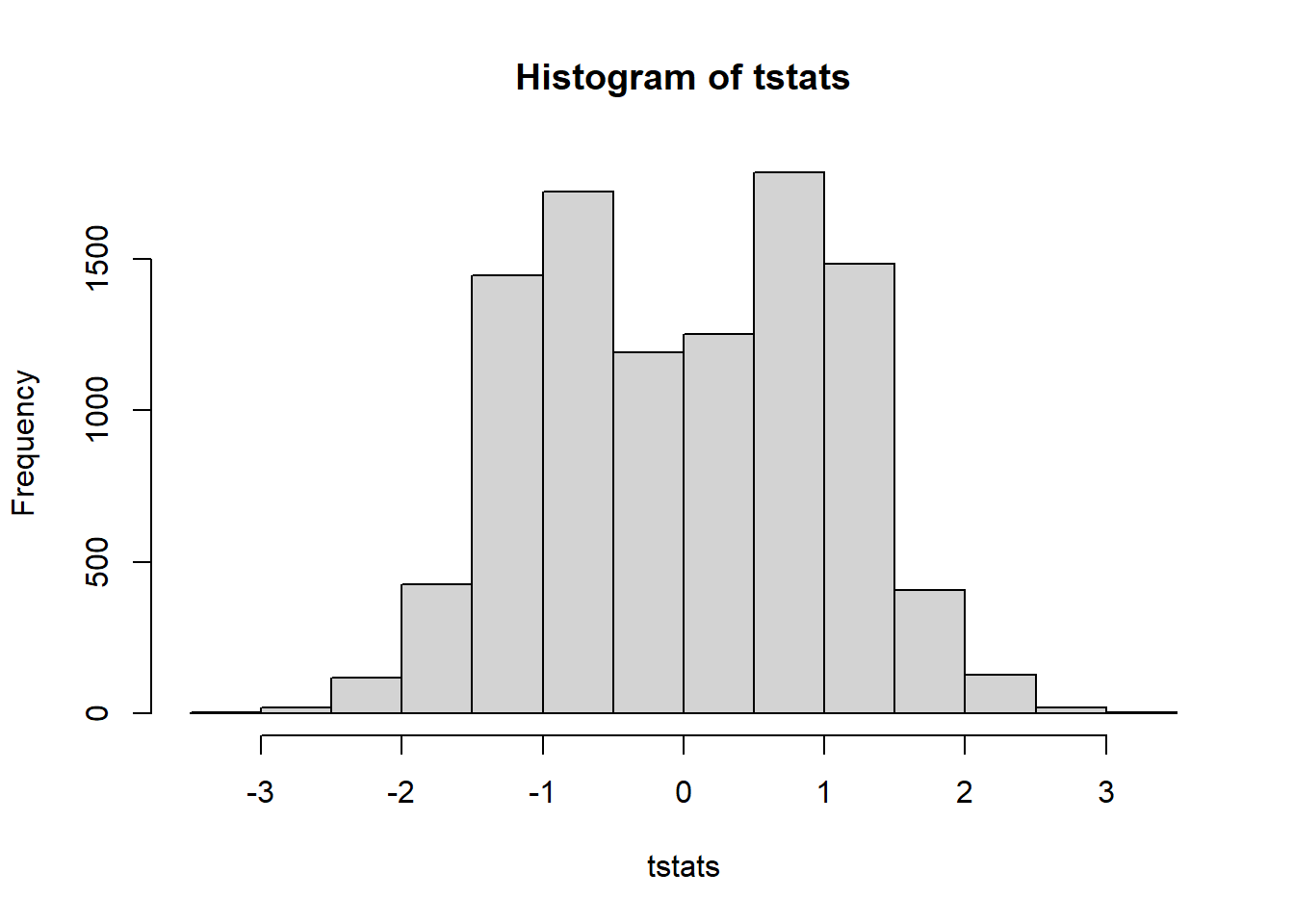
The Cauchy distribution is “heavy-tailed”: it produces outliers in both directions. There is also a “half-Cauchy” distribution that produces only positive values, and a “skewed Cauchy” with an adjustable skew parameter. But we’ll stop here.
4.2.4 Beware “tests” of assumptions!
We’ve seen a few examples of model assumptions being broken in ways that aren’t consequential for the purpose of drawing inference on parameters (note: they’d be consequential if we were just making predictions!). This presents a danger in using formal tests to check assumptions. A test might correctly convey that an assumption is violated, even if that violation is not consequential. For example:
Levene’s Test tests against the null hypothesis that population variance is the same for all values of our predictor variable. It can be found in the R package lawstat, function levene.Test().
The Shapiro-Wilk test tests against the null hypothesis that a set of data came from a normal distribution. The function shapiro.test implements this.
Exercise: Go back to previous examples in this section and include these tests in the simulations. See if there are cases in which the tests report “significant” violations of model assumptions that are, nonetheless, inconsequential. We’ll do this for Shapiro-Wilk test here.
First, we’ll try it on normal data:
set.seed(335)
test_shapiro <- rnorm(n=100,mean=0,sd=1)
shapiro.test(test_shapiro)
Shapiro-Wilk normality test
data: test_shapiro
W = 0.98606, p-value = 0.3773Now we’ll check that its Type I error rate is correct:
N <- 100
reps <- 1e4
shapiro_pvals <- rep(0,reps)
for (i in 1:reps) {
test_shapiro <- rnorm(n=N,mean=0,sd=1)
shapiro_pvals[i] <- shapiro.test(test_shapiro)$p.value
}
sum(shapiro_pvals<0.05)/reps[1] 0.0472Now let’s try it out on some non-normal data:
N <- 100
reps <- 1e4
shapiro_pvals <- rep(0,reps)
for (i in 1:reps) {
test_shapiro <- rSHASHo(n=N,mu=10,sigma=3,nu=0,tau = 0.5)
shapiro_pvals[i] <- shapiro.test(test_shapiro)$p.value
}
sum(shapiro_pvals<0.05)/reps[1] 0.9714That’s some high power! Let’s use it now on the residuals from one of our previous t-test simulations:
reps <- 1e4
pvals <- rep(0,reps)
shapiro_pvals <- rep(0,reps)
N <- 10
for (i in 1:reps) {
group1 <- rSHASHo(n=N,mu=10,sigma=3,nu=0,tau = 0.5)
group2 <- rSHASHo(n=N,mu=10,sigma=3,nu=0,tau = 1)
test_results <- t.test(group1,group2,var.equal=TRUE)
pvals[i] <- test_results$p.value
resids <- c(group1-mean(group1),group2-mean(group2))
shapiro_pvals[i] <- shapiro.test(resids)$p.value
}
sum(pvals<0.05)/reps[1] 0.05sum(shapiro_pvals<0.05)/reps[1] 0.561In this case, the Shapiro-Wilk test has about 57% power to reject the null of normality. Also, in this case, violating the assumption of normality didn’t do anything bad to our Type I error rate.
4.2.5 Meta assumption violations
Simulation is a powerful tool for exploring the consequences of assumption violations, but don’t forget that these simulations are themselves models. Just as real data are not generated from normal distributions, they also are not generated from Cauchy or “sinh-arcsinh” distributions.
The same principle holds for our Type I error rate simulations. We used a data generating model that violated the equal variance assumption, and observed how often the null hypothesis \(H_0:\mu_1-\mu_2=0\) is rejected when it is true. But this null can’t really be true; it is a statement about the values of parameters in a model! The population means \(\mu_1\) and \(\mu_2\) are no more real than a straight line drawn on a scatterplot.
There are two kinds of simplifications in this example:
To guarantee a Type I error rate of \(\alpha=0.05\), we make the false assumptions that our data consist of independent draws from two normal distributions, and that these distributions have the same variance. Violating these assumptions can bias the Type I error rate, so that our true \(\alpha\) level is not what we claim it to be.
Type I errors are defined as occurring when a null hypothesis is true. Our null hypothesis is that two fictitious population parameters have the same value. It cannot be true.
So, in order to investigate the potential consequences of a model assumption being false, we created a new model, which also makes false assumptions. We then compared the values of an imaginary quantity, generated separately under each model, to see if they differ by more than we’d like.
4.2.6 A bunch of apps
Here are some apps for exploring the potential consequences of violating model assumptions:
4.3 Let’s make a diagram of statistical inference!
We will now take a big step back and consider what the “process” of statistical inference looks like.
4.3.1 The intro to statistics diagram
In “Statistical Inference: The Big Picture” (2006), Robert Kass presents a typical diagram:
The idea here is that our data are sampled from a population, and we want to use the data to learn about the population. “Inference” is the process by which we go from sample to population.
Typically this takes the form of drawing inference on the values of unknown parameters, using sample statistics. For instance, we might be interested in the mean of the population from which our data were sampled. We call this mean \(\mu\), and we treat its value as unknown. We estimate \(\mu\) using the mean of our data, \(\bar{y}\), which is a statistic. The statistic estimates the value of the unknown parameter: \(\hat{\mu}=\bar{y}\). This is the presentation almost everyone gets in their introductory statistics class. For instance, here’s an image from CSU’s STAT 301 (Introduction to Statistical Methods):
Note the absence of any mention of a model. We simply assert that \(\mu\) exists at the population level, and we use data to infer its value. Later in the semester, we may begin to look at models explicitly, such as the simple linear regression model:
\[ Y_i = \beta_0 + \beta_1x_i + \varepsilon_i \\ \varepsilon_i\sim Normal(0,\sigma^2) \]
Now the story of inference is something like “we are interested in the value of \(\beta_1\), which is unknown, so we estimate it using our data:
\[ \hat{\beta_1} = \frac{\sum{(y_i-\bar{y})}\sum{(x_i-\bar{x})}}{\sum(x_i-\bar{x})^2} \]
What is not clear from the diagram above is that this statistic estimates a parameter in a model of the real-world process that created our data. Students are taught that \(\beta_1\) is a feature of the population from which we sampled.
4.3.2 Kass’s “Big Picture” diagram
Kass presents an alternative:
A distinction is made between the “real” and “theoretical” worlds. Statistical and scientific models exist in the “theoretical” world. Data exist in the “real” world, and are fit to statistical models. The inferential conclusion we come to are informed by both the models and the data directly.
The Kass paper is a reading assignment for this class; we’ll discuss it in more detail in person.
4.3.3 Fisher’s take
Fisher’s “On the Mathematical Foundations of Theoretical Statistics” (1922) describes something that sounds a lot like what we’d call “inference” today:
In order to arrive at a distinct formulation of statistical problems, it is necessary to define the task which the statistician sets himself: briefly, and in its most concrete form, the object of statistical methods is the reduction of data. A quantity of data, which usually by its mere bulk is incapable of entering the mind, is to be replaced by relatively few quantities which shall adequately represent the whole, or which, in other words, shall contain as much as possible, ideally the whole, of the relevant information contained in the original data.
This object is accomplished by constructing a hypothetical infinite population, of which the actual data are regarded as constituting a random sample. The law of distribution of this hypothetical population is specified by relatively few parameters, which are sufficient to describe it exhaustively in respect of all qualities under discussion. Any information given by the sample, which is of use in estimating the values of these parameters, is relevant information. Since the number of independent facts supplied in the data is usually far greater than the nunmber of facts sought, much of supplied by any actual sample is irrelevant. It is the object of the sta employed in the reduction of data to exclude this irrelevant information the whole of the relevant information contained in the data.
Note the phrase “hypothetical infinite population”. Fisher is clear that we are estimating parameters which describe characteristics of a hypothetical population from which our data were drawn.
4.3.4 Data in a black box
In “Statistical Modeling: The Two Cultures” (2001), Leo Breiman begins with this:
The idea here is that data are produced by some unknown process that we do not have direct access to. We can measure inputs and outputs, but we can’t see how the inputs create the outputs.
In this paper, Breiman distiguishes between the use of “data models” (such as linear regression models) and “algorithmic models” (such as neural nets, random forests, and support vector machines). Breiman was a statistician who advocated for the use of machine learning tools and believed most statisticians focused too heavily on inference, to the detriment of prediction.
4.3.5 This author’s take
I have my own diagram, similar to Kass’s but with more details and a proposal to separate statistical inference into two stages: inference to the model, and inference from the model:
In this diagram, we use data to learn about the underlying process (or “mechanism”) which created our data. (The process is probably very complex.) We create a model of this data generating process, and draw inference to the model using inferential procedures like confidence intervals and hypothesis testing.
Inference from the model combines our statistical results with anything else we think is relevant for making inferential statements about the “true” data generating process.
Note that there is no mention here of “population”. In this diagram, “data generating process” is describing what “population” typically describes.
4.4 Some fun practical examples
4.4.1 “The Birthday Problem”
This is a classic probability problem: how large of a random sample of people do you need in order for there to be a better than 50% chance two will have the same birthday? The answer is surprisingly small: only 23. If you have 23 people, the probability that at least two will have the same birthday is 0.507, or 50.7%. The Wikipedia page explains the math and the intuition behind the answer, if you’re curious.
There is a false assumption made for the mathematical solution given on the Wikipedia page: we assume that all birthdays are equally likely. In other words, the probability distribution for the variable “what is this person’s birthday?” is uniform across the integers 1 through 365 (this problem also leaves out February 29th).
This is empirically false. There are fewer births on major holidays, and fewer births on weekends. There are also more fall births than spring births. Here is a detailed plot, taken from the cover of Gelman et. al’s textbook “Bayesian Data Analysis”:
Since days of the year fall on different days of the week across years, this would only matter if we sampled people the same age. But, what about the fact that, in the USA, there are more fall births than spring births, and substantial declines on major holidays? What effect does violating our mathematical assumption have on the calculated result?
It turns out that the assumption of uniform probability is a “conservative” assumption in that it makes the number of people needed be as large as possible, or equivalently makes the calculated probability be as small as possible. So the true probability of having two or more people out of 23 with the same birthday is actually bigger than 50.7%.
It also turns out that, for this problem, the solution is still 23. The probability of at least two people out of 22 having the same birthday, assuming uniform probability, is 0.476 or 47.6%. And the empirical distribution of birthday probabilities does not differ from uniform by enough to push this value above 50%.
Here are a couple of articles explaining the adjustment for a non-uniform distribution of birthdays:
4.4.2 “No two decks of cards have ever been shuffled the same”
Link to one of many websites presenting this claim
Here is another (similar) probability question: what are the chances that two fair shuffles of a deck of 52 cards will produce the exact same ordering of cards? The answer is:
\[ \begin{split} \frac{1}{\text{The number of different ways to order a set of 52 cards}}& =\\ \frac{1}{52\cdot 51\cdot 50\cdot\ 49\cdot\ 48\cdot\ ...\ \cdot 6\cdot 5 \cdot 4\cdot 3\cdot 2\cdot 1} &=\\ \\ \frac{1}{52!}&=8\cdot 10^{-67} \end{split} \]
That’s a very small number, and human beings haven’t been shuffling cards for even a teeny tiny fraction of the time that would be needed in order to have a reasonable shot at two shuffles being exactly the same.
But, look at what is assumed here. We are assuming that the first card is a random draw from all 52 possible cards. And then, the second card is a random draw from the remaining 51 possible cards. And so on, until we get down to the final card.
Obviously this is not how human beings shuffle cards. But, remember the theme of this chapter: just because a model assumption is false, doesn’t mean it is consequentially false. We just saw, for instance, that the false assumption underlying the solution to the birthday problem did not invalidate this solution. So, does it matter that the “pick one card completely at random from the remaining cards over and over again” model for card shuffling is false?
The answer this time is almost certainly “yes”. There is a lot of research on shuffling methods.
Consider that most people don’t shuffle a deck well enough to approximate “true randomness”. According to some mathematicians who have studied this, 5 to 7 riffle shuffles are needed to achieve this (see, e.g. this article). Then consider that brand new decks of cards come in a set order. And that some games (e.g. bridge) involve placing like cards together before the next round is played. Now we have the combination of:
- Far from perfect shuffling methods
- Identical or similar starting orders from which imperfect shuffling methods are applied
Does this prove that there have, in fact, been at least two decks of cards throughout all of history that were shuffled into the same order? No, but it at least makes that \(8\cdot 10^{-67}\) figure irrelevant to the real-world version of the question.
4.4.3 Election polling
The paper “Disentangling bias and variance in election polling” compares stated margins of error from election polls with observed errors calculated from subsequent election results:
Here is an outline of the paper:
Statistical margins of error quantify estimation error expected from “random chance”. Consider a 95% margin of error. Conditional on some model assumptions, we can say that if we were to take new random samples from the same population over and over again, in 95% of samples the difference between the true population parameter value and its estimate will be less than the 95% margin of error.
There is more to error than statistical error. For example, our sampling method might make it more likely that certain subsets of the population are sampled than others. Or, certain subsets of the population may be more inclined to talk to pollsters than others. Or there may be data quality issues, e.g. some respondents lie or tell the pollster what they think the pollster wants to hear. Or, the state of public opinion on the day of the poll might change by the time the election takes place. These are all sources of error we’d call bias.
Response rates to polls are very low, less than 10%. So, small changes in non-statistical error could have a large impact on polls (e.g. the “convention boost”, almost certainly caused by supporters of the party who is currently having its convention being more motivated to respond to pollsters).
Non-statistical error (i.e. bias) is a concern in most applications, not just in polling. We usually have no way of measuring bias, because we never get to know the true parameter value we are estimating. Election polling is an interesting exception: we do get to find out the outcome of the election and the actual margin of victory for the winner.
So, the authors of this paper looked at a large number of historical polls taken shortly before an election, and compared the poll estimates to the observed election outcomes. The differences between poll estimates and actual outcomes are observed “errors”. The authors obtained a distribution of observed errors across many elections, and calculated the values that enclosed the central 95% of these errors.
The authors found that the observed 95% margins of error were about twice as large as the statistical margins of error. And so, amount of polling error due to “random chance” was comparable to the amount of polling error due to “bias”. Their advice: when you read the results of an election poll, take the stated margin of error and double it!
The authors also found very little systematic bias in polls toward one party or the other, though this may have changed in recent years.
The Broncos are the only team with 5,072 yards↩︎