4 Uso de librerías aceleradas por GPU
La idea aquí es usar funcionalidad disponible en R, que oculte los detalles de la implementación de bajo nivel, confiando en la experiencia de otros para codificar de manera eficiente los cálculos estándar en la GPU.
Vale la pena mencionar que al ser librerías que funcionan sobre hardware “especial”, estas librerías solo pueden ser instaladas si el equipo de cómputo dispone de dicho hardware, y de los requisitos de software asociados con el mismo. Para el caso de GPUs NVIDIA, como las que están disponibles en el nodo compute-0-12, estos requisitos de software son:
- CUDA Toolkit, que es la plataforma de computación paralela desarrollada por NVIDIA para computación general en unidades de procesamiento gráfico (GPU).
- Controladores de GPU, que normalmente se instala en conjunto con el Toolkit.
4.1 Operaciones de álgebra lineal
Comenzaremos con un uso de alto nivel de la GPU simplemente llamando a rutinas de álgebra lineal que usen la GPU. Dada la naturaleza numérica de la mayoría de las aplicaciones R, es natural que existan paquetes desarrollados como interfaz entre R y GPU. Varios paquetes R ocultan los detalles de la implementación de la GPU y permiten realizar operaciones vectoriales y matriciales, incluido el álgebra lineal, utilizando código R estándar. En algunos casos, sobrecargan las funciones R habituales de modo que simplemente puede llamar a una función del mismo nombre que en la base R.
Algunos paquetes en este contexto incluyen: gpuR, gmatrix, gputools. Desafortunadamente, de estas 3 librerías, únicamente gpuR está disponible para la versión más reciente de R, 3.5, liberada en abril de 2018.
gpuR proporciona funciones habilitadas para GPU para objetos R de una manera simple y accesible. Para acceder a estas funciones se proporcionan nuevas clases gpu* y vcl* para envolver objetos R típicos (eg: vector, matriz), tanto en el host como en los espacios del dispositivo, para reflejar la sintaxis R típica sin la necesidad de conocer OpenCL.
A continuación, se hace una prueba simple en la que se compara el rendimiento de la multiplicación de matrices sobre CPU versus GPU.
set.seed(123456) # Por reproductibilidad
orders <- seq(1000,3000,by=500)
t1 <- t2 <- t3 <- sizes <- c()
for(order in orders) {
print(order)
A = matrix(rnorm(order^2), nrow=order)
sizes <- c( sizes, format(object.size(A), units="auto") )
# GPU version, GPU pointer to CPU memory!! (gpuMatrix is simply a pointer)
gpuA = gpuMatrix(A, type="float") #point GPU to matrix
# GPU version, in GPU memory!! (vclMatrix formation is a memory transfer)
vclA = vclMatrix(A, type="float") #push matrix to GPU
print("cpu...")
elapsed1 <- system.time({C = A %*% A})[3] # Operacion regular (ejecutada en la CPU)
print("gpu...")
elapsed2 <- system.time({gpuC = gpuA %*% gpuA})[3] # Operacion acelerada (ejecutada en la GPU)
print("gpu2...")
elapsed3 <- system.time({vclC = vclA %*% vclA})[3] # Operacion acelerada (ejecutada en la GPU)
t1 = c(t1, elapsed1)
t2 = c(t2, elapsed2)
t3 = c(t3, elapsed3)
# Liberar espacio en memoria:
rm(A,C,gpuA,gpuC,vclA,vclC); gc()
}
# Armar un dataframe con los resultados del bucle
df = data.frame(order = rep(orders,3),
label = rep(paste0(orders," (", sizes, ")"), 3),
mode = rep(c("cpu","gpu","gpu-2"),each=length(orders)),
elapsed = c(t1,t2,t3))library(ggplot2)
df <- readRDS(file = "data/gpuMm.rds")
ggplot(df, aes(x=label, y=elapsed, fill=mode)) +
geom_bar(stat="identity", position=position_dodge()) +
xlab("Orden (Mem)") +
ylab("Tiempo de ejecucion (seg)") #+ scale_y_log10() 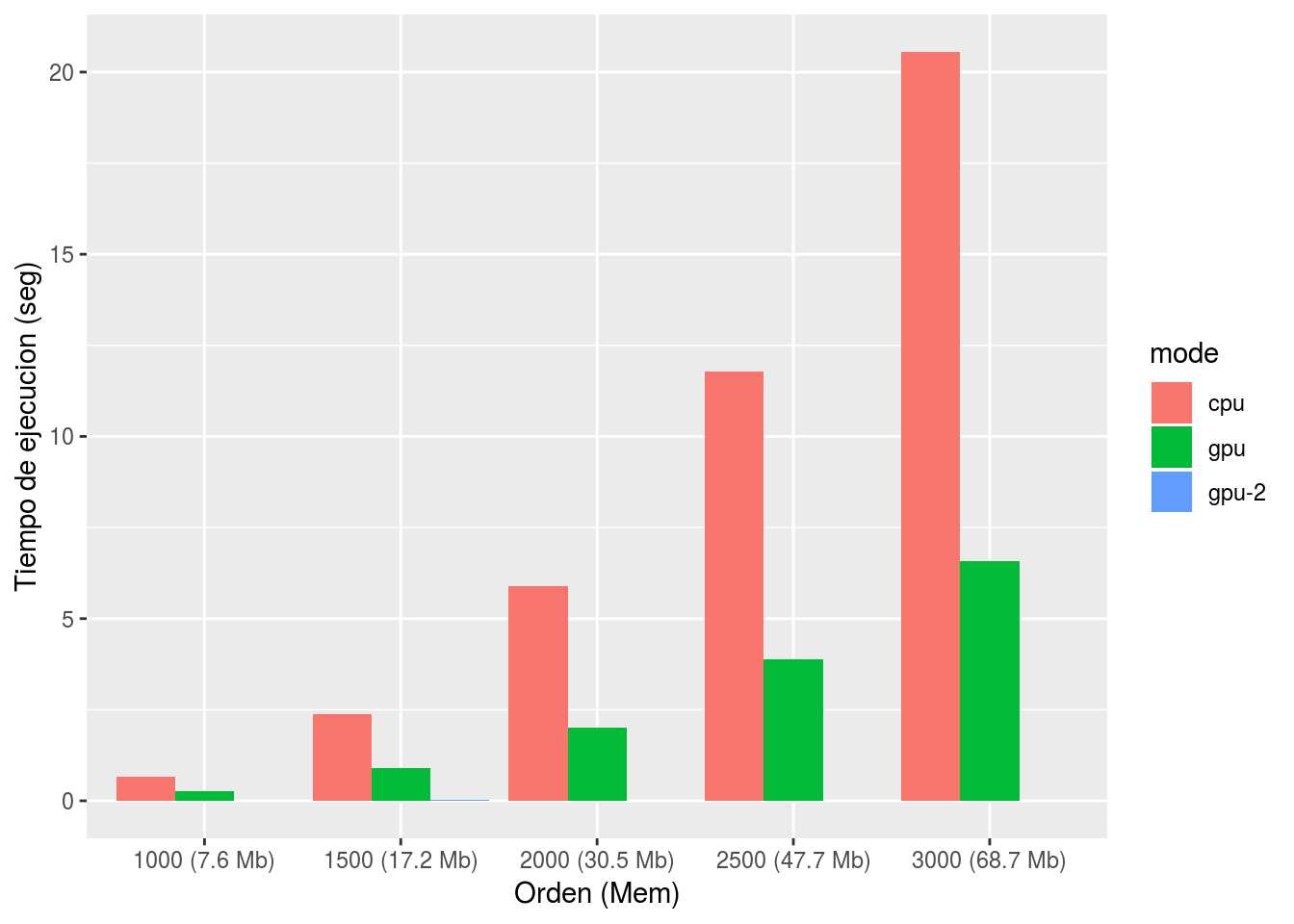
La aceleración evidenciada en este primer ejemplo es una consecuencia de la posibilidad de ejecutar varias tareas paralelas, tal como se muestra en la siguiente figura:
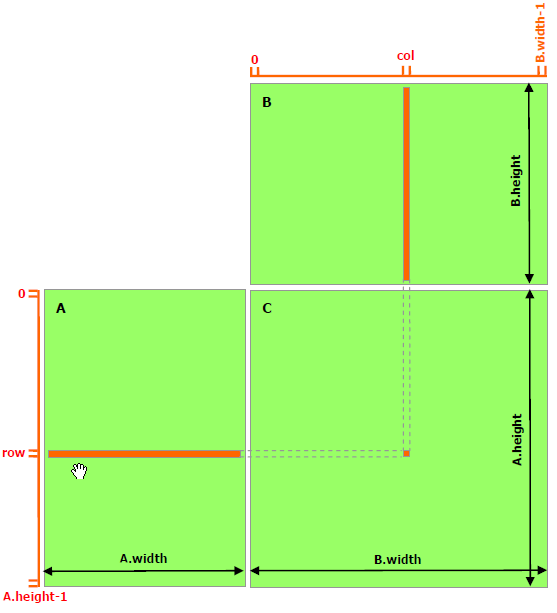
Multiplicación de matrices
4.2 Regresión Linear (OLS, Ordinary Least Squares)
En estadística, los mínimos cuadrados ordinarios es el nombre de un método para encontrar los parámetros poblacionales en un modelo de regresión lineal. Este método minimiza la suma de las distancias verticales entre las respuestas observadas en la muestra y las respuestas del modelo. El parámetro resultante puede expresarse a través de una fórmula sencilla en notación matricial:
\[ y = X \beta + \epsilon \] en donde \(y\) y \(\epsilon\) son vectores, y \(X\) es una matriz de regresores, a la que también se le llama la matriz de diseño.
La estimación de la ecuación anterior, se denota por:
\[ \hat{\beta} = (X'X)^{-1}X'y \] que puede ser re-escrita como: \[ (X'X) \hat{\beta} = X'y \] donde se debe resolver para \(\hat{\beta}\), que en manipulación de matrices, resolver un sistema de ecuaciones es mucho más rápido que invertir una matriz, y frecuentemente evita problemas numéricos presentes alrededor de valores cercanos a cero.
set.seed(123456) # Por reproducibilidad
np <- 300 # número de predictores
nr <- 1e+05 # número de observaciones
X <- cbind(5, 1:nr, matrix(rnorm((np - 1) * nr, 0, 0.01), nrow = nr, ncol = (np - 1)))
beta <- matrix(c(1, 3, runif(np - 1, 0, 0.2)), ncol = 1)
y <- X %*% beta + matrix(rnorm(nr, 0, 1), nrow = nr, ncol = 1)
# Cálculo en la CPU ligeramente optimizado via la utilización de producto cruzado
timeCpu <- system.time({
ms2 <- solve(crossprod(X), crossprod(X, y))
})
# Versión GPU, utilizando clases gpu* que proporcionan punteros de la GPUhacia la memoria de la CPU
library(gpuR)
gpuX = gpuMatrix(X, type = "float") #point GPU to matrix
gpuy = gpuMatrix(y, type = "float")
timeGpu <- system.time({
ms4 <- gpuR::solve(gpuR::crossprod(gpuX), gpuR::crossprod(gpuX, gpuy))
})
# Versión GPU (2), utilizando memoria interna del GPU!! (el llamado a vclMatrix es una transferencia)
vclX = vclMatrix(X, type = "float") #push matrix to GPU
vcly = vclMatrix(y, type = "float")
timeGpu2 <- system.time({
ms5 <- gpuR::solve(gpuR::crossprod(vclX), gpuR::crossprod(vclX, vcly))
})
detach("package:gpuR", unload = TRUE)
# Armar un dataframe con los resultados del bucle
df = data.frame(calculo = c("CPU", "GPU (gpu*)", "GPU (vcl*)"),
tiempo = c(timeCpu[3], timeGpu[3], timeGpu2[3]) )# Plotear los resultados
df <- readRDS(file = "data/gpuOLS.rds")
ggplot(df, aes(x=calculo, y=tiempo, fill=calculo)) +
geom_bar(stat="identity", position=position_dodge()) +
xlab("Tipo de calculo") +
ylab("Tiempo de ejecucion (seg)") #+ scale_y_log10() 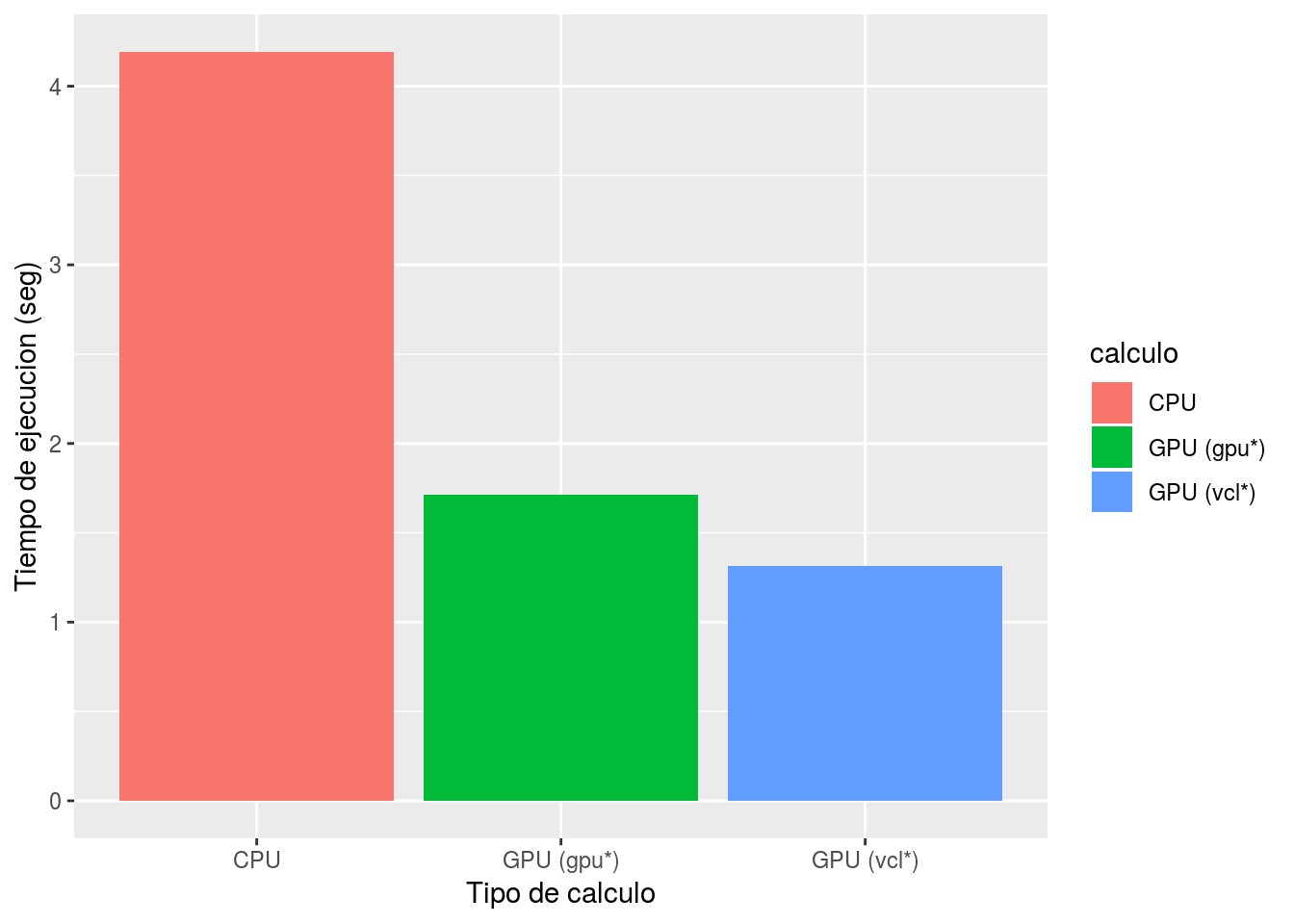
4.3 Ejemplo clásico de reconocimiento de imágenes MNIST
La base de datos MNIST (Modified National Institute of Standards and Technology database; Base de datos modificada del Instituto Nacional de Estándares y Tecnología), es una gran base de datos de dígitos manuscritos que se usa comúnmente para entrenar sistemas de procesamiento de imágenes. La base de datos también se usa ampliamente para entrenamiento y pruebas en el campo del aprendizaje automático (machine learning).

Imágenes de muestra del conjunto de datos de prueba MNIST.
A continuación se incluye el fragmento de un script que haciendo uso de las librerías keras y tensorflow, entrena un modelo de clasificación de imágenes, que hace uso de las capacidades de la GPU. Hay que mencionar que estas librerías funcionan tanto sobre CPUs como GPUs. Para hacer uso de tensorflow con capacidades GPU, es necesario instalar la librería NVIDIA CUDA Deep Neural Network (cuDNN).
library(keras)
use_condaenv("keras")
# install_keras(tensorflow="gpu") # Instalar solo la primera vez
# Preparando los datos
mnist <- dataset_mnist()
x_train <- mnist$train$x
y_train <- mnist$train$y
x_test <- mnist$test$x
y_test <- mnist$test$y
# Re-organizar
x_train <- array_reshape(x_train, c(nrow(x_train), 784))
x_test <- array_reshape(x_test, c(nrow(x_test), 784))
# Re-escalar
x_train <- x_train / 255
x_test <- x_test / 255
y_train <- to_categorical(y_train, 10)
y_test <- to_categorical(y_test, 10)
# Definir el modelo
model <- keras_model_sequential()
model %>%
layer_dense(units = 256, activation = 'relu', input_shape = c(784)) %>%
layer_dropout(rate = 0.4) %>%
layer_dense(units = 128, activation = 'relu') %>%
layer_dropout(rate = 0.3) %>%
layer_dense(units = 10, activation = 'softmax')
summary(model)
model %>% compile(
loss = 'categorical_crossentropy',
optimizer = optimizer_rmsprop(),
metrics = c('accuracy')
)
# Entrenar el modelo
history <- model %>% fit(
x_train, y_train,
epochs = 30, batch_size = 128,
validation_split = 0.2
)
# Evaluar el modelo
model %>% evaluate(x_test, y_test)
# Predecir en datos nuevos
model %>% predict_classes(x_test)A continuación se incluye parte relevante de la salida de los comandos anteriores:
2018-07-07 14:20:40.077703: I tensorflow/core/common_runtime/gpu/gpu_device.cc:1356] Found device 0 with properties:
name: Quadro K1100M major: 3 minor: 0 memoryClockRate(GHz): 0.7055
pciBusID: 0000:01:00.0
totalMemory: 1.95GiB freeMemory: 1.63GiB
2018-07-07 14:20:40.077730: I tensorflow/core/common_runtime/gpu/gpu_device.cc:1406] Ignoring visible gpu device (device: 0, name: Quadro K1100M, pci bus id: 0000:01:00.0, compute capability: 3.0) with Cuda compute capability 3.0. The minimum required Cuda capability is 3.5.
2018-07-07 14:20:40.077740: I tensorflow/core/common_runtime/gpu/gpu_device.cc:923] Device interconnect StreamExecutor with strength 1 edge matrix:
2018-07-07 14:20:40.077745: I tensorflow/core/common_runtime/gpu/gpu_device.cc:929] 0
2018-07-07 14:20:40.077749: I tensorflow/core/common_runtime/gpu/gpu_device.cc:942] 0: N
Train on 48000 samples, validate on 12000 samples
Epoch 1/30
48000/48000 [==============================] - 2s 48us/step - loss: 0.4254 - acc: 0.8707 - val_loss: 0.1649 - val_acc: 0.9525
Epoch 2/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.2029 - acc: 0.9388 - val_loss: 0.1247 - val_acc: 0.9640
Epoch 3/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.1595 - acc: 0.9529 - val_loss: 0.1097 - val_acc: 0.9680
Epoch 4/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.1312 - acc: 0.9613 - val_loss: 0.1035 - val_acc: 0.9712
Epoch 5/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.1158 - acc: 0.9663 - val_loss: 0.0977 - val_acc: 0.9729
Epoch 6/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.1070 - acc: 0.9685 - val_loss: 0.0968 - val_acc: 0.9750
Epoch 7/30
48000/48000 [==============================] - 2s 47us/step - loss: 0.1003 - acc: 0.9714 - val_loss: 0.1028 - val_acc: 0.9728
Epoch 8/30
48000/48000 [==============================] - 2s 48us/step - loss: 0.0922 - acc: 0.9734 - val_loss: 0.0931 - val_acc: 0.9762
Epoch 9/30
48000/48000 [==============================] - 2s 47us/step - loss: 0.0869 - acc: 0.9750 - val_loss: 0.0921 - val_acc: 0.9775
Epoch 10/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.0812 - acc: 0.9762 - val_loss: 0.0991 - val_acc: 0.9752
Epoch 11/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.0803 - acc: 0.9771 - val_loss: 0.0972 - val_acc: 0.9767
Epoch 12/30
48000/48000 [==============================] - 2s 47us/step - loss: 0.0739 - acc: 0.9782 - val_loss: 0.0993 - val_acc: 0.9773
Epoch 13/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.0729 - acc: 0.9785 - val_loss: 0.0883 - val_acc: 0.9798
Epoch 14/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.0728 - acc: 0.9794 - val_loss: 0.0952 - val_acc: 0.9793
Epoch 15/30
48000/48000 [==============================] - 2s 49us/step - loss: 0.0688 - acc: 0.9810 - val_loss: 0.0961 - val_acc: 0.9794
Epoch 16/30
48000/48000 [==============================] - 2s 47us/step - loss: 0.0665 - acc: 0.9811 - val_loss: 0.0963 - val_acc: 0.9782
Epoch 17/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.0631 - acc: 0.9821 - val_loss: 0.0979 - val_acc: 0.9794
Epoch 18/30
48000/48000 [==============================] - 2s 47us/step - loss: 0.0613 - acc: 0.9832 - val_loss: 0.0994 - val_acc: 0.9781
Epoch 19/30
48000/48000 [==============================] - 2s 47us/step - loss: 0.0617 - acc: 0.9832 - val_loss: 0.0989 - val_acc: 0.9797
Epoch 20/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.0605 - acc: 0.9839 - val_loss: 0.1024 - val_acc: 0.9794
Epoch 21/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0601 - acc: 0.9831 - val_loss: 0.1014 - val_acc: 0.9793
Epoch 22/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0583 - acc: 0.9843 - val_loss: 0.0993 - val_acc: 0.9798
Epoch 23/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0572 - acc: 0.9845 - val_loss: 0.1028 - val_acc: 0.9787
Epoch 24/30
48000/48000 [==============================] - 2s 46us/step - loss: 0.0554 - acc: 0.9852 - val_loss: 0.1001 - val_acc: 0.9788
Epoch 25/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0525 - acc: 0.9856 - val_loss: 0.1077 - val_acc: 0.9797
Epoch 26/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0569 - acc: 0.9847 - val_loss: 0.1109 - val_acc: 0.9785
Epoch 27/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0555 - acc: 0.9854 - val_loss: 0.1078 - val_acc: 0.9787
Epoch 28/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0507 - acc: 0.9866 - val_loss: 0.1102 - val_acc: 0.9798
Epoch 29/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0513 - acc: 0.9863 - val_loss: 0.1205 - val_acc: 0.9785
Epoch 30/30
48000/48000 [==============================] - 2s 45us/step - loss: 0.0539 - acc: 0.9854 - val_loss: 0.1169 - val_acc: 0.9789
10000/10000 [==============================] - 0s 25us/step
Mientras se entrena el modelo, se visualiza como varían las métricas de pérdida y precisión (loss and accuracy metrics) en los datasets de test y validación:
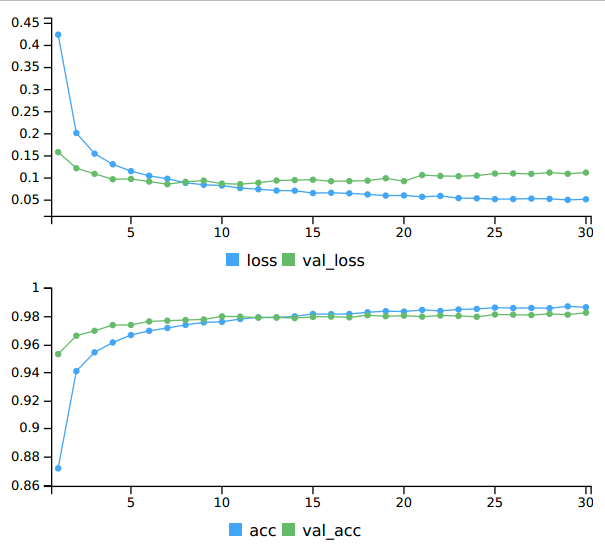
Metricas del modelo