Kapitola 3 Základné nástroje na prieskumnú analýzu údajov
Hlavným cieľom data science je pochopiť mechanizmus, ktorý generuje pozorované údaje. Prvým na to používaným nástrojom je prieskumná analýza údajov (angl. exploratory data analysis), ktorou nazrieme do povahy hromadných javov7 pomocou vlastností skúmaných objektov. Pretože hromadný jav sa skladá z množstva individuálnych javov, tieto vlastnosti nadobúdajú svoje hodnoty náhodne a v štatistike sa nazývajú náhodné premenné (prípadne náhodné veličiny, štatistické znaky, angl. features) a každá hodnota náhodnej premennej môže nastať s určitou pravdepodobnosťou. Náhodnosť premenných je charakterizovaná tzv. rozdelením pravdepodobnosti, či už prostredníctvom pravdepodobnostnej funkcie resp. hustoty rozdelenia, alebo distribučnej funkcie. Napríklad, ak hromadným javom je fyzický stav obyvateľstva, potom náhodnou premennou je napr. výška človeka, ktorá môže nadobudnúť hodnoty od niekoľkých centimetrov až po vyše dvoch metrov (formálne od 0 po nekonečno). Pritom hustota pravdepodobnosti okolo strednej hodnoty je zvyčajne vyššia ako hustota výskytu nízkych či, naopak, vysokých ľudí. Graf hustoty tak má typicky zvonovitý tvar (tzv. Gaussova krivka), zatiaľčo distribučná funkcia (postupná kumulácia pravdepodobností) má tvar písmena S a najviac rastie v miestach okolo strednej hodnoty.
Prieskumná analýza potom pomáha odhaľovať tvar rozdelenia pravdepodobnosti jednotlivých skúmaných veličín aj vzťahy medzi nimi. Cieľom aktuálnej kapitoly je ukázať základné vizuálne nástroje prostredia R používaných na tento účel. Pri jej príprave bola použitá najmä literatúra (Pearson 2018, kap. 3) a (R. Peng 2016, kap. 5 až 7).
3.1 Príprava údajov
Import (read.table) a „krájanie” údajov (subset) sme si predstavili v úvode do jazyka R. Zatiaľ predpokladáme, že naše dáta sú uložené v ideálnej forme, teda premenné (veličiny) v stĺpcoch a pozorovania (namerané hodnoty) v riadkoch.
Prvým pohľadom na tabuľku údajov je identifikácia typu premenných, teda či sú numerické a spojito nadobúdajú hodnoty z nejakého intervalu, alebo sú diskrétne a obsahujú buď číselné alebo znakové hodnoty.
data(mtcars)
head(mtcars,1) # detailný popis datasetu na https://rpubs.com/neros/61800
## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21 6 160 110 3.9 2.62 16.46 0 1 4 4
str(mtcars)
## 'data.frame': 32 obs. of 11 variables:
## $ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
## $ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
## $ disp: num 160 160 108 258 360 ...
## $ hp : num 110 110 93 110 175 105 245 62 95 123 ...
## $ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
## $ wt : num 2.62 2.88 2.32 3.21 3.44 ...
## $ qsec: num 16.5 17 18.6 19.4 17 ...
## $ vs : num 0 0 1 1 0 1 0 1 1 1 ...
## $ am : num 1 1 1 0 0 0 0 0 0 0 ...
## $ gear: num 4 4 4 3 3 3 3 4 4 4 ...
## $ carb: num 4 4 1 1 2 1 4 2 2 4 ...Všetky premenné súboru mtcars nadobúdajú číselné hodnoty, no nie všetky sú v spojitej mierke. Konkrétne počet valcov (t. j. cylindrov, cyl), uloženie valcov (do tvaru písmena V alebo priame, vs), typ prevodovky (automatická alebo manuálna, am), počet rýchlostných stupňov a počet logických karburátorov (carb) sú diskrétne premenné. Niektoré z nich pre lepšiu zrozumiteľnosť prekódujeme z numerických na znakové/slovné, a všetky stĺpce ordinálnych diskrétnych premenných prevedieme na faktory (teda tam, kde záleží na poradí hodnôt).
mtcars$am <- ifelse(mtcars$am == 0,
yes = "automatic",
no = "manual") # vhodné pri malom počte úrovní
mtcars$vs <- sapply(mtcars$vs+1, switch, "Vshaped", "Straight")
# elegantnejšie: car::recode(mtcars$vs, "0='Vshaped'; 1='Straight'")
for (i in c("cyl","gear", "carb")) {
mtcars[[i]] <- factor(mtcars[[i]], levels = sort(unique(mtcars[[i]])), ordered=T)
}
str(mtcars)
## 'data.frame': 32 obs. of 11 variables:
## $ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
## $ cyl : Ord.factor w/ 3 levels "4"<"6"<"8": 2 2 1 2 3 2 3 1 1 2 ...
## $ disp: num 160 160 108 258 360 ...
## $ hp : num 110 110 93 110 175 105 245 62 95 123 ...
## $ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
## $ wt : num 2.62 2.88 2.32 3.21 3.44 ...
## $ qsec: num 16.5 17 18.6 19.4 17 ...
## $ vs : chr "Vshaped" "Vshaped" "Straight" "Straight" ...
## $ am : chr "manual" "manual" "manual" "automatic" ...
## $ gear: Ord.factor w/ 3 levels "3"<"4"<"5": 2 2 2 1 1 1 1 2 2 2 ...
## $ carb: Ord.factor w/ 6 levels "1"<"2"<"3"<"4"<..: 4 4 1 1 2 1 4 2 2 4 ...Interná reprezentácia znakového vektora ako dátový typ factor už nemá taký zmysel (pre úspornejšie uloženie údajov) ako kedysi, no prekódovanie diskrétnych numerických na znakové (či už faktorové alebo nie) má zmysel jednak pri zobrazovaní, jednak pri modelovaní (intuitívne: kvalitatívny rozdiel medzi 4 a 6-valcovými motormi nemusí byť rovnaký ako medzi 6 a 8-valcovými), a to aj pre vylúčenie hodnôt, ktoré sa v praxi nevyskytujú, alebo nie sú zahrnuté do experimentu (napr. 5 valcov).
V rámci prípravy dát by malo zmysel ešte transformovať premenné v imperiálnych jednotkách do metrickej sústavy SI.
Pre lepšiu čitateľnosť zmeníme názvy premenných:
names(mtcars) <- c("reach_mpg", "cylinders", "displacement", "horsepower",
"axle_ratio", "weight", "accel_time", "cyl_config",
"transmission", "gears", "carburetors")3.2 Vyšetrenie jednorozmerného rozdelenia pravdepodobnosti
Druhým krokom exploračnej analýzy je vyšetrenie rozdelenia pravdepodobnosti pre každú premennú jednotlivo:
# extrémy, kvartily a stredná hodnota, alebo tabuľka početnosti, pripadne počet NA
summary(mtcars)
## reach_mpg cylinders displacement horsepower axle_ratio
## Min. :10.40 4:11 Min. : 71.1 Min. : 52.0 Min. :2.760
## 1st Qu.:15.43 6: 7 1st Qu.:120.8 1st Qu.: 96.5 1st Qu.:3.080
## Median :19.20 8:14 Median :196.3 Median :123.0 Median :3.695
## Mean :20.09 Mean :230.7 Mean :146.7 Mean :3.597
## 3rd Qu.:22.80 3rd Qu.:326.0 3rd Qu.:180.0 3rd Qu.:3.920
## Max. :33.90 Max. :472.0 Max. :335.0 Max. :4.930
## weight accel_time cyl_config transmission gears
## Min. :1.513 Min. :14.50 Length:32 Length:32 3:15
## 1st Qu.:2.581 1st Qu.:16.89 Class :character Class :character 4:12
## Median :3.325 Median :17.71 Mode :character Mode :character 5: 5
## Mean :3.217 Mean :17.85
## 3rd Qu.:3.610 3rd Qu.:18.90
## Max. :5.424 Max. :22.90
## carburetors
## 1: 7
## 2:10
## 3: 3
## 4:10
## 6: 1
## 8: 1Príslovie „lepšie raz vidieť ako 100-krát počuť” platí v malej obmene aj pri prieskumnej analýze, a to v tom zmysle, že ľahšie pochopíme chovanie (rozdelenie) náhodnej premennej z vhodného grafu než z množstva číselných reprezentácií.
Vezmime si najprv spojitú kvantitatívnu premennú, napr. výkon motora horsepower. Jedným z najčastejšie používaných grafov na zobrazenie rozdelenia je krabicový graf (box-and-whiskers), ktorý ukazuje 5 súhrnných čísel (Tuckey’s five numbers) z výpisu funkcie summary, avšak iniciatívne oddeľuje odľahlé hodnoty (outliers), ak prekročia vzdialenosť \(1.5(q_{.75}-q_{.25})\) od horného (\(q_{.75}\), 3rd Qu.) a dolného kvartilu (\(q_{.25}\), 1st Qu.).
summary(mtcars$horsepower)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 52.0 96.5 123.0 146.7 180.0 335.0
boxplot(mtcars$horsepower)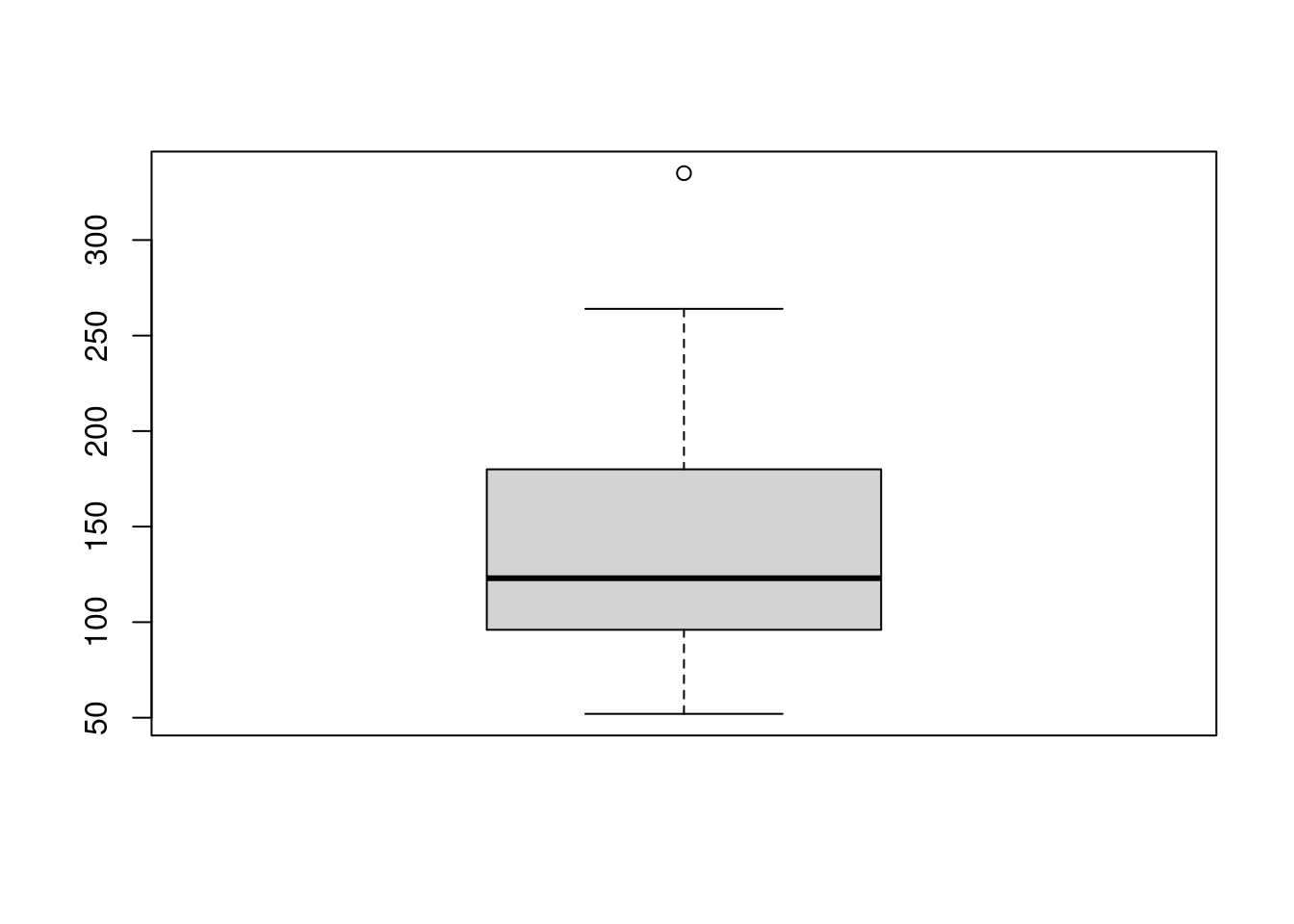
Hrubá čiara predstavuje medián, hranice obdĺžnika sú kvartily, konce fúzov (angl. whiskers) sú vlastné extrémne hodnoty (ešte nepovažované za odľahlé) a nakoniec disktrétne body na grafe zastupujú odľahlé hodnoty, v našom prípade je iba jeden.
Ďalším často používaným grafom (použiteľným aj pre nominálne premenné) je histogram:
table(cut(mtcars$horsepower, breaks = seq(50,350,by=50)))
##
## (50,100] (100,150] (150,200] (200,250] (250,300] (300,350]
## 9 10 6 5 1 1
hist(mtcars$horsepower) # alebo car::truehist(mtcars$horsepower, prob=F)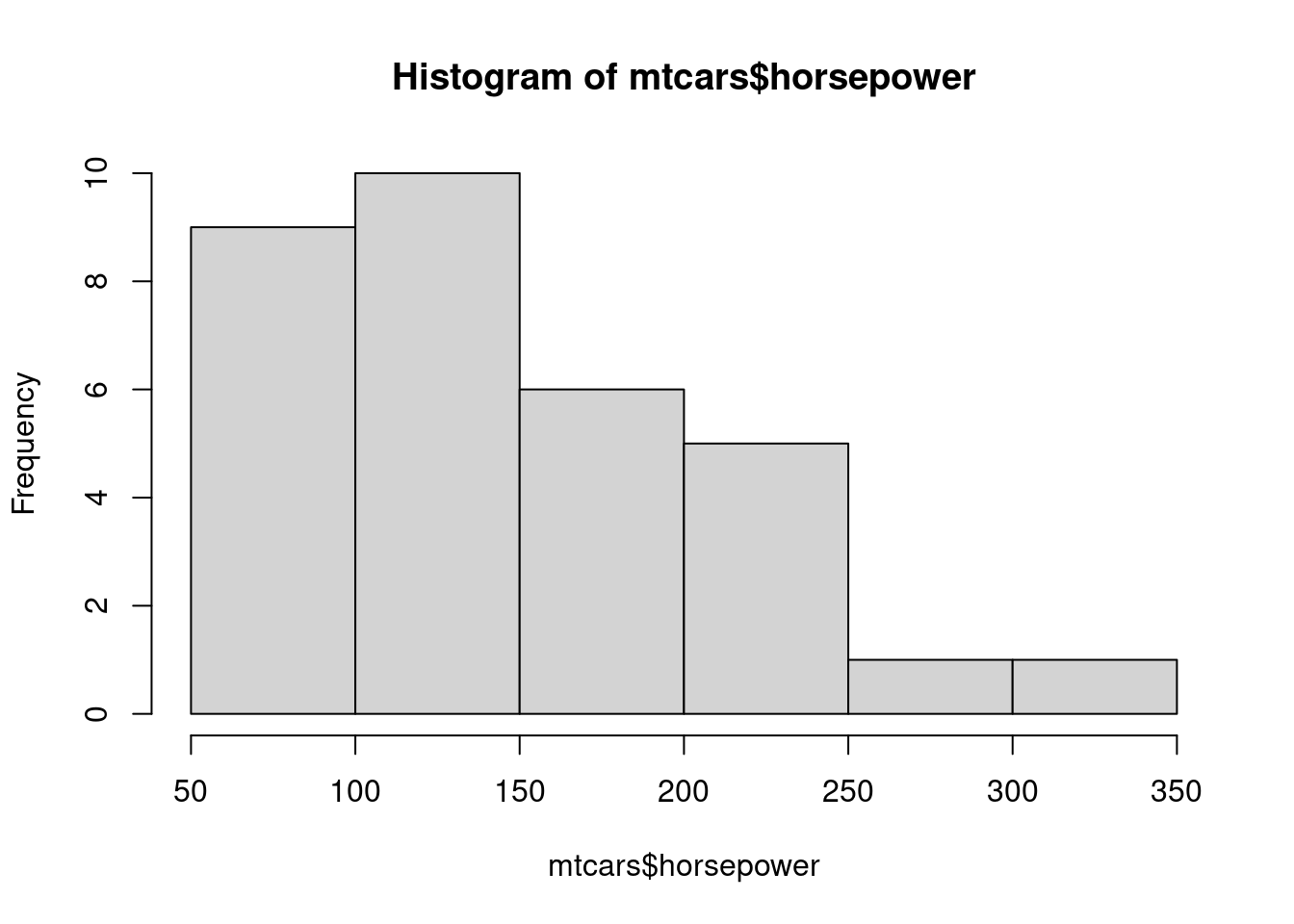
Prakticky je to vizualizácia tabuľky početnosti, výška stĺpcov zodpovedá počtu výskytov (angl. frequency) jednotlivých skupín hodnôt (angl. bins). Vyhladením histogramu dostávame trochu lepší obraz o tzv. hustote rozdelenia spojitých náh.premenných a podobnú službu nám urobí aj zovšeobecnenie krabicového grafu, tzv. husľový (angl. violin) graf, ktorý znázorňuje vyhladenú hustotu empirického rozdelenia (zdvojenú, v symetrickej polohe). Oba sa dajú doplniť tzv. kobercovým (angl. rug) grafom.
old <- par(mfrow=c(1,2)) # rozdelenie zobrazovacej oblasti
hist(mtcars$horsepower, prob=TRUE) # relatívne početnosti
rug(mtcars$horsepower)
lines(density(mtcars$horsepower), lwd=2)
vioplot::vioplot(mtcars$horsepower)
rug(mtcars$horsepower, side=2)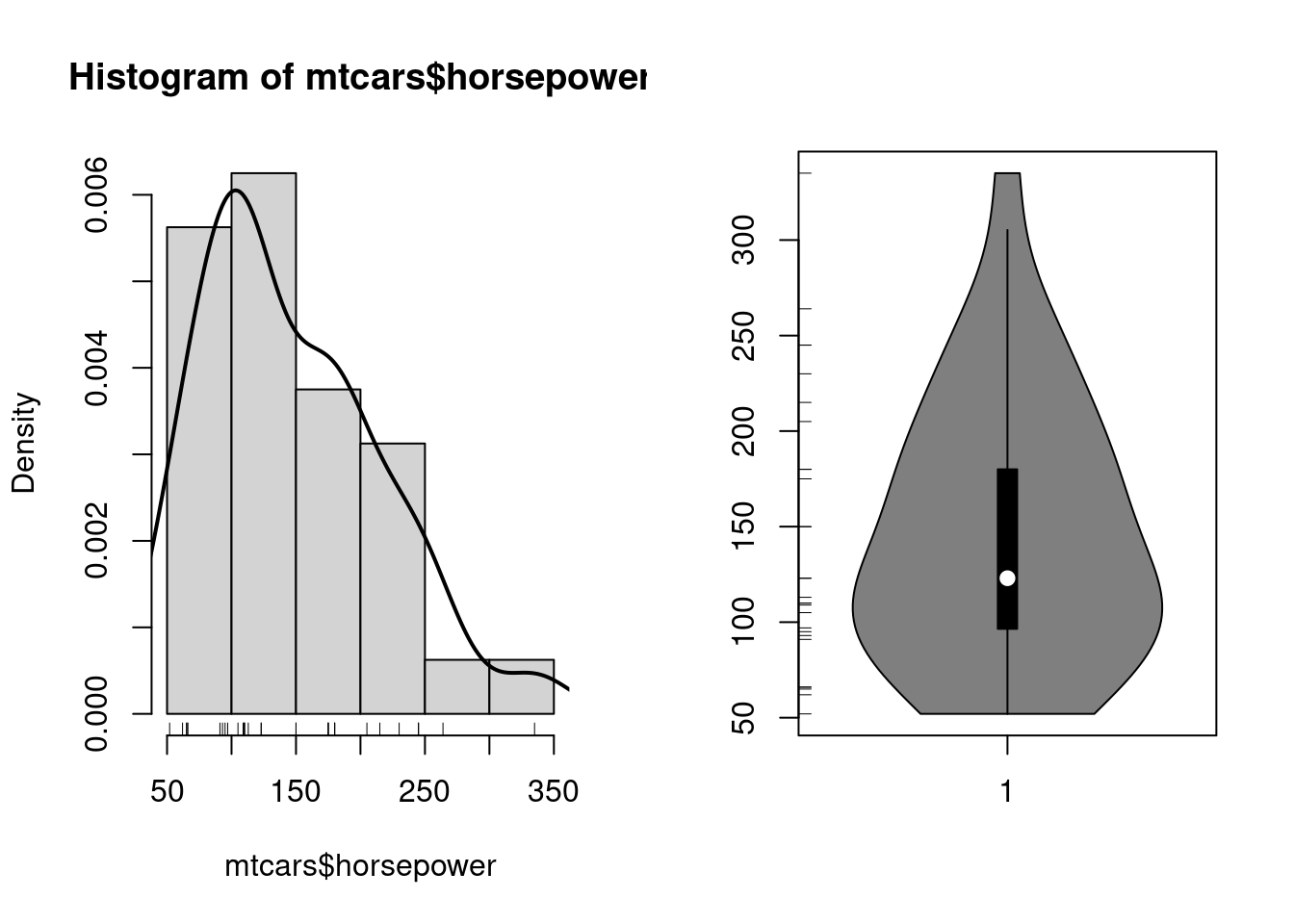
par(old)Na zobrazenie rozdelenia diskrétnej premennej, napr. cylinders, použijeme stĺpcový graf
table(mtcars$cylinders)
##
## 4 6 8
## 11 7 14
barplot(table(mtcars$cylinders))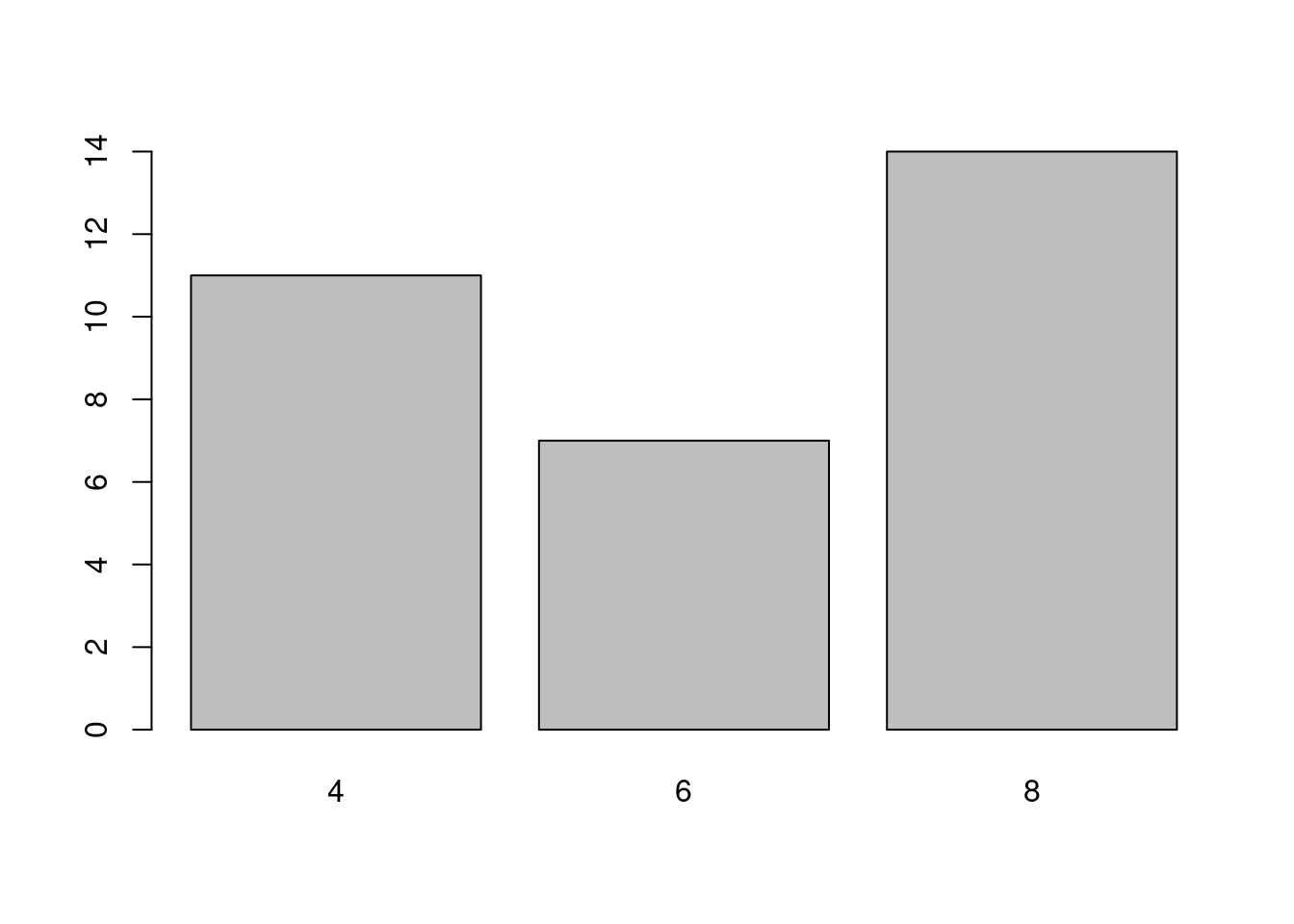
3.3 Vzťahy medzi premennými
Tretím krokom prieskumnej analýzy je hľadanie súvislosti medzi vlastnosťami skúmaných objektov. Najčastejší nástroj pre zobrazenie vzťahu dvoch spojitých náhodných premenných je bodový graf (scatter plot).
plot(horsepower ~ displacement, data = mtcars)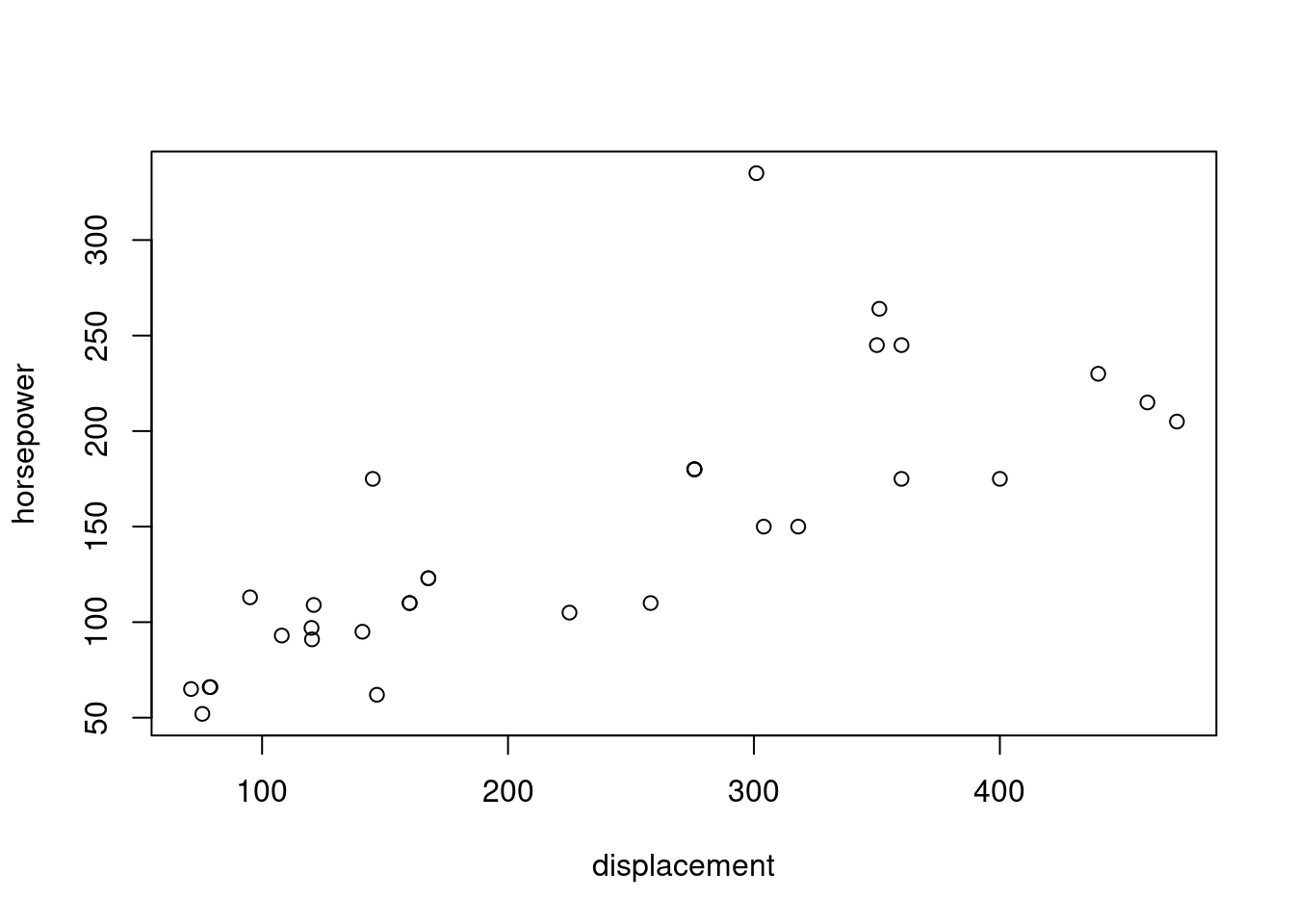
Z grafu vidno, že výkon motora značne súvisí so zdvihovým objemom. Jedno z áut je výrazne efektívne vo využití objemu valcov, žeby to súviselo s počtom valcov? Pozrime, o ktoré auto ide.
mtcars[which.max(mtcars$horsepower),]
## reach_mpg cylinders displacement horsepower axle_ratio weight
## Maserati Bora 15 8 301 335 3.54 3.57
## accel_time cyl_config transmission gears carburetors
## Maserati Bora 14.6 Vshaped manual 5 8Zjavne ide o 8-valec, pozrime teda ešte na ostatné 8-valcové modely a pre lepší prehľad zoraďme podľa výkonu.
tmp <- subset(mtcars, subset = cylinders == "8")
tmp[order(tmp$horsepower, decreasing = T),]
## reach_mpg cylinders displacement horsepower axle_ratio
## Maserati Bora 15.0 8 301.0 335 3.54
## Ford Pantera L 15.8 8 351.0 264 4.22
## Duster 360 14.3 8 360.0 245 3.21
## Camaro Z28 13.3 8 350.0 245 3.73
## Chrysler Imperial 14.7 8 440.0 230 3.23
## Lincoln Continental 10.4 8 460.0 215 3.00
## Cadillac Fleetwood 10.4 8 472.0 205 2.93
## Merc 450SE 16.4 8 275.8 180 3.07
## Merc 450SL 17.3 8 275.8 180 3.07
## Merc 450SLC 15.2 8 275.8 180 3.07
## Hornet Sportabout 18.7 8 360.0 175 3.15
## Pontiac Firebird 19.2 8 400.0 175 3.08
## Dodge Challenger 15.5 8 318.0 150 2.76
## AMC Javelin 15.2 8 304.0 150 3.15
## weight accel_time cyl_config transmission gears carburetors
## Maserati Bora 3.570 14.60 Vshaped manual 5 8
## Ford Pantera L 3.170 14.50 Vshaped manual 5 4
## Duster 360 3.570 15.84 Vshaped automatic 3 4
## Camaro Z28 3.840 15.41 Vshaped automatic 3 4
## Chrysler Imperial 5.345 17.42 Vshaped automatic 3 4
## Lincoln Continental 5.424 17.82 Vshaped automatic 3 4
## Cadillac Fleetwood 5.250 17.98 Vshaped automatic 3 4
## Merc 450SE 4.070 17.40 Vshaped automatic 3 3
## Merc 450SL 3.730 17.60 Vshaped automatic 3 3
## Merc 450SLC 3.780 18.00 Vshaped automatic 3 3
## Hornet Sportabout 3.440 17.02 Vshaped automatic 3 2
## Pontiac Firebird 3.845 17.05 Vshaped automatic 3 2
## Dodge Challenger 3.520 16.87 Vshaped automatic 3 2
## AMC Javelin 3.435 17.30 Vshaped automatic 3 2Spolu s druhým najvýkonnejším má manuálnu prevodovku, 5 rýchlostných stupňov a pomerne nízku hmotnosť. Zobraziť vzťah viac než dvoch premenných priamym pridávaním rozmerov (3D, video?) by bolo neefektívneje, existujú aj lacnejšie triky, napr. pomocou farby, veľkosti a tvaru bodov.
plot(horsepower ~ displacement, data=mtcars,
col = as.integer(mtcars$cylinders),
pch = as.integer(as.factor(mtcars$transmission))
)
legend("topleft", legend = c(4,6,8), pch = 1, col = 1:3, title = "cylinders")
legend("bottomright", legend = sort(unique(mtcars$transmission)), pch = 1:2, title="transmission")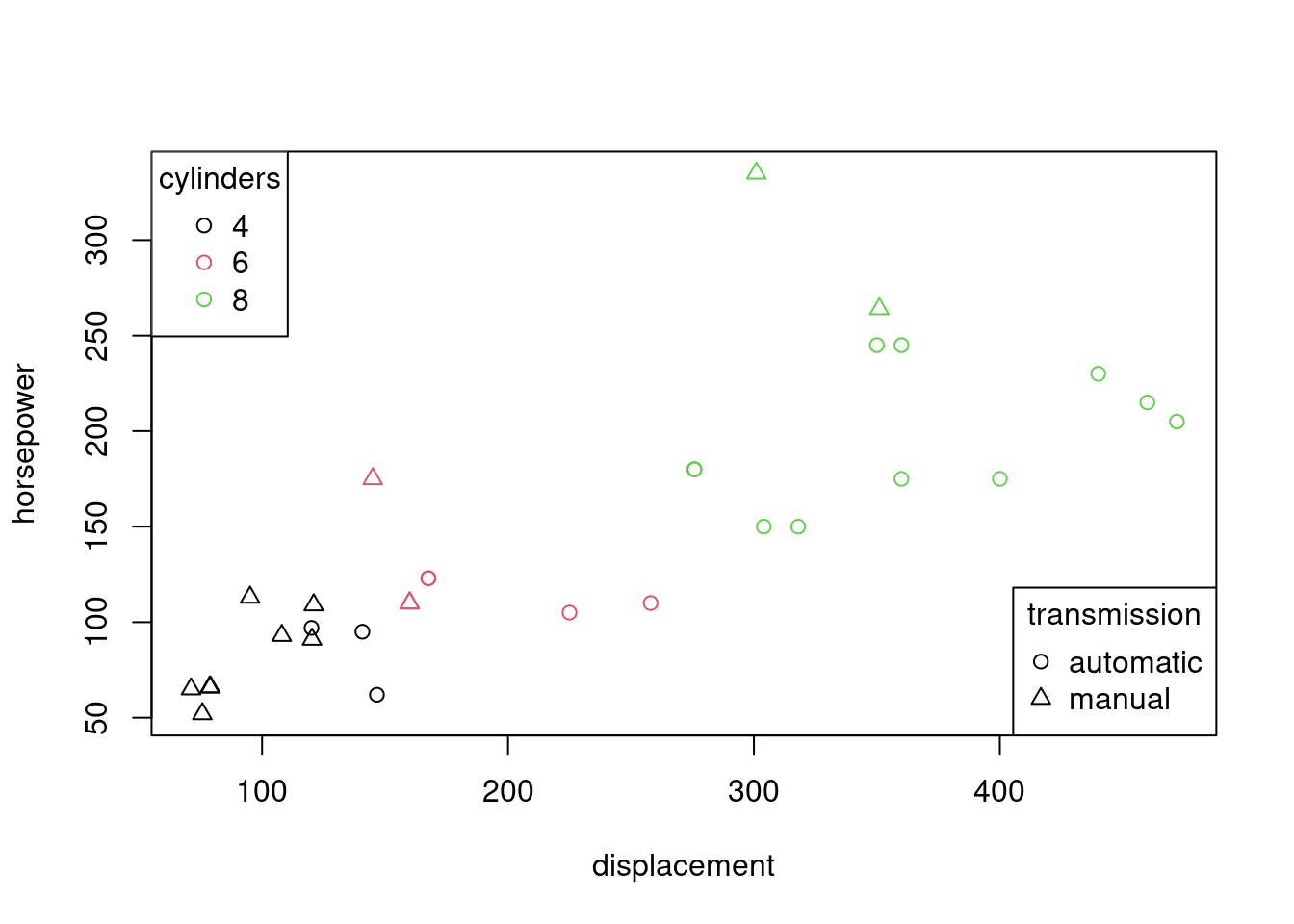
Podobne možno použiť tzv. bublinový graf (bubble plot) na vyjadrenie závislosti napr. medzi výkonom motora a dojazdom v závislosti od počtu valcov a ešte aj doplniť popis
symbols(x = mtcars$horsepower, y = mtcars$reach_mpg,
circles = as.numeric(mtcars$cylinders),
inches = 0.25)
text(x = mtcars$horsepower, y = mtcars$reach_mpg,
mtcars$cylinders)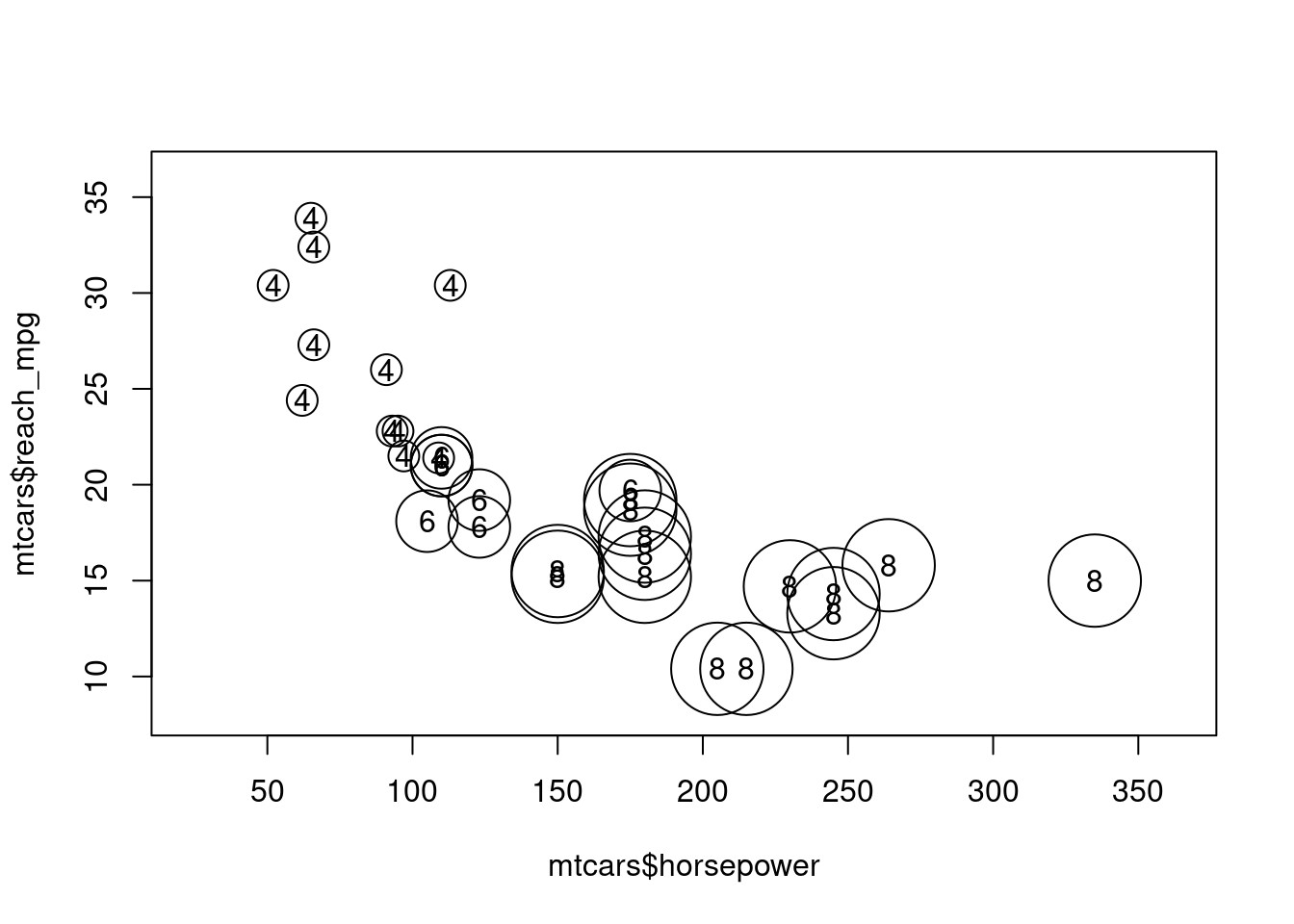
Tento graf je vhodný v prípadoch, keď podmieňujúca premenná (cylinders) je ordinálna (poradová, s daným poradím hodnôt) a body nie sú zobrazené príliš nahusto (čo, zdá sa, nie je tento prípad).
Závislosť diskrétnej a spojitej premennej sa štandardne zobrazuje krabicovými grafmi, pri ktorých šírka môže reflektovať počet pozorovaní. Doplnkovo sa zobrazujú aj jednotlivé pozorovania ako body rozptýlené (angl. jitter) okolo osi každej krabice. Podobnú informáciu sprostredkujú husľové grafy.
sapply(split(mtcars$horsepower, mtcars$cylinders), summary)
## 4 6 8
## Min. 52.00000 105.0000 150.0000
## 1st Qu. 65.50000 110.0000 176.2500
## Median 91.00000 110.0000 192.5000
## Mean 82.63636 122.2857 209.2143
## 3rd Qu. 96.00000 123.0000 241.2500
## Max. 113.00000 175.0000 335.0000boxplot(horsepower ~ cylinders, data = mtcars, varwidth = T, cex = 0)
# ak by cylinders bol vektor typu factor, stačila by generická funkcia plot()
stripchart(horsepower ~ cylinders, data = mtcars,
add = T, vertical = TRUE, method = "jitter", pch = 16)
vioplot::vioplot(horsepower ~ cylinders, data = mtcars)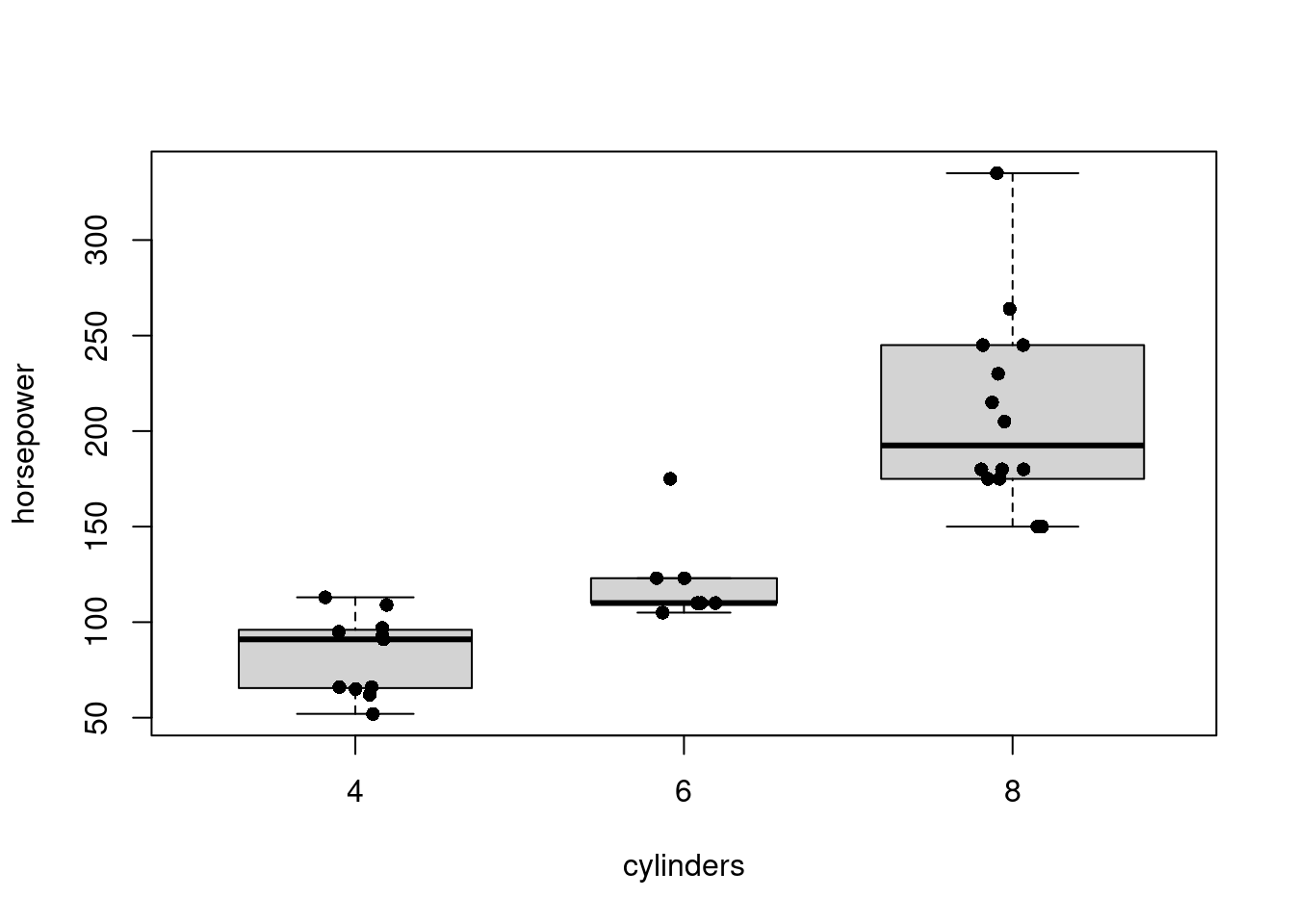
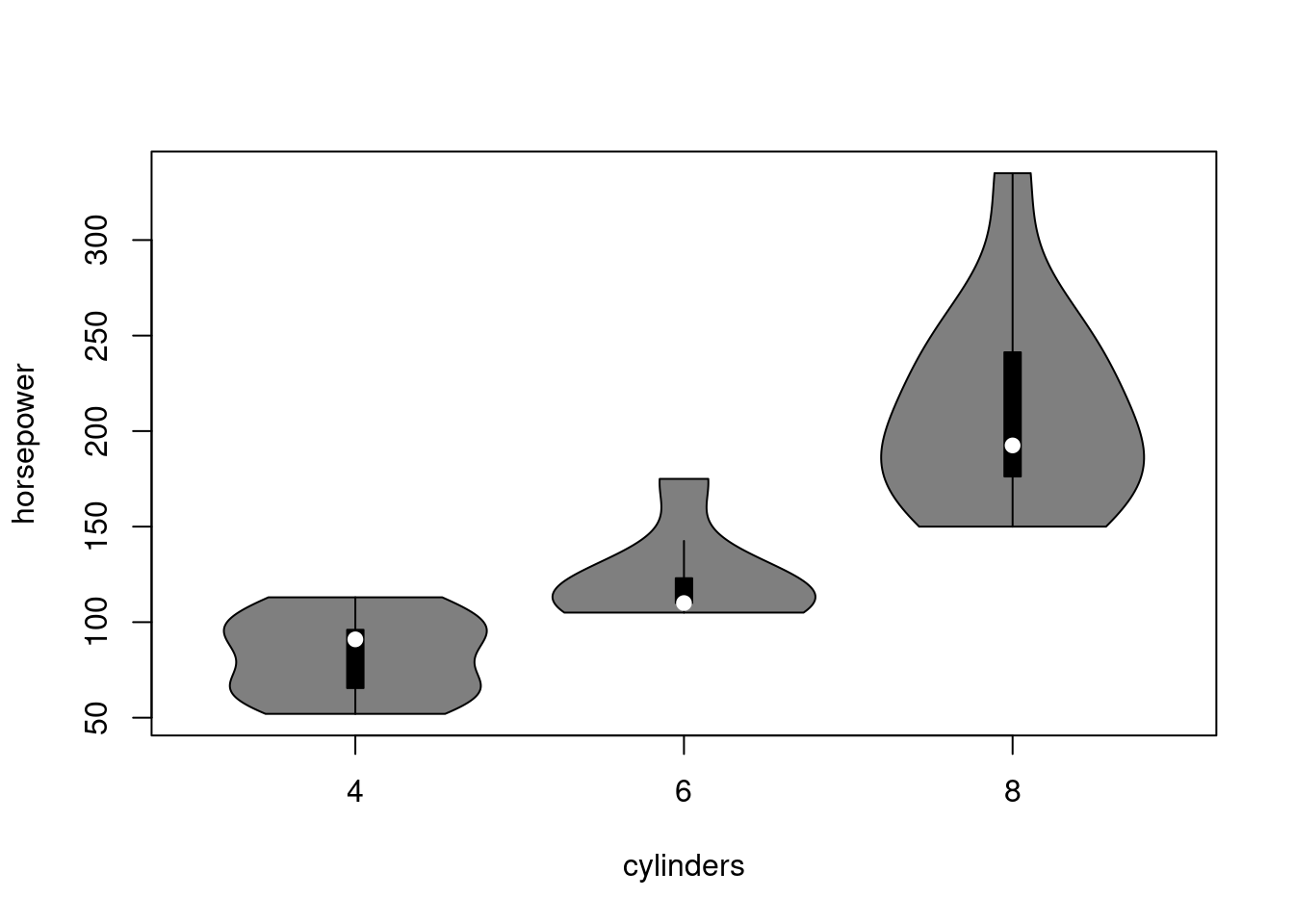
Nárast výkonu pri 6-valcových motoroch nie je taký zásadný ako pri 8-valcových.
Dve diskrétne premenné možno zobraziť mozaikovým grafom, ktorý v plošnej miere vyjadruje početnosti v prienikoch jednotlivých kategórií.
with(mtcars, table(transmission, gears))
## gears
## transmission 3 4 5
## automatic 15 4 0
## manual 0 8 5
mosaicplot(transmission ~ gears, data = mtcars)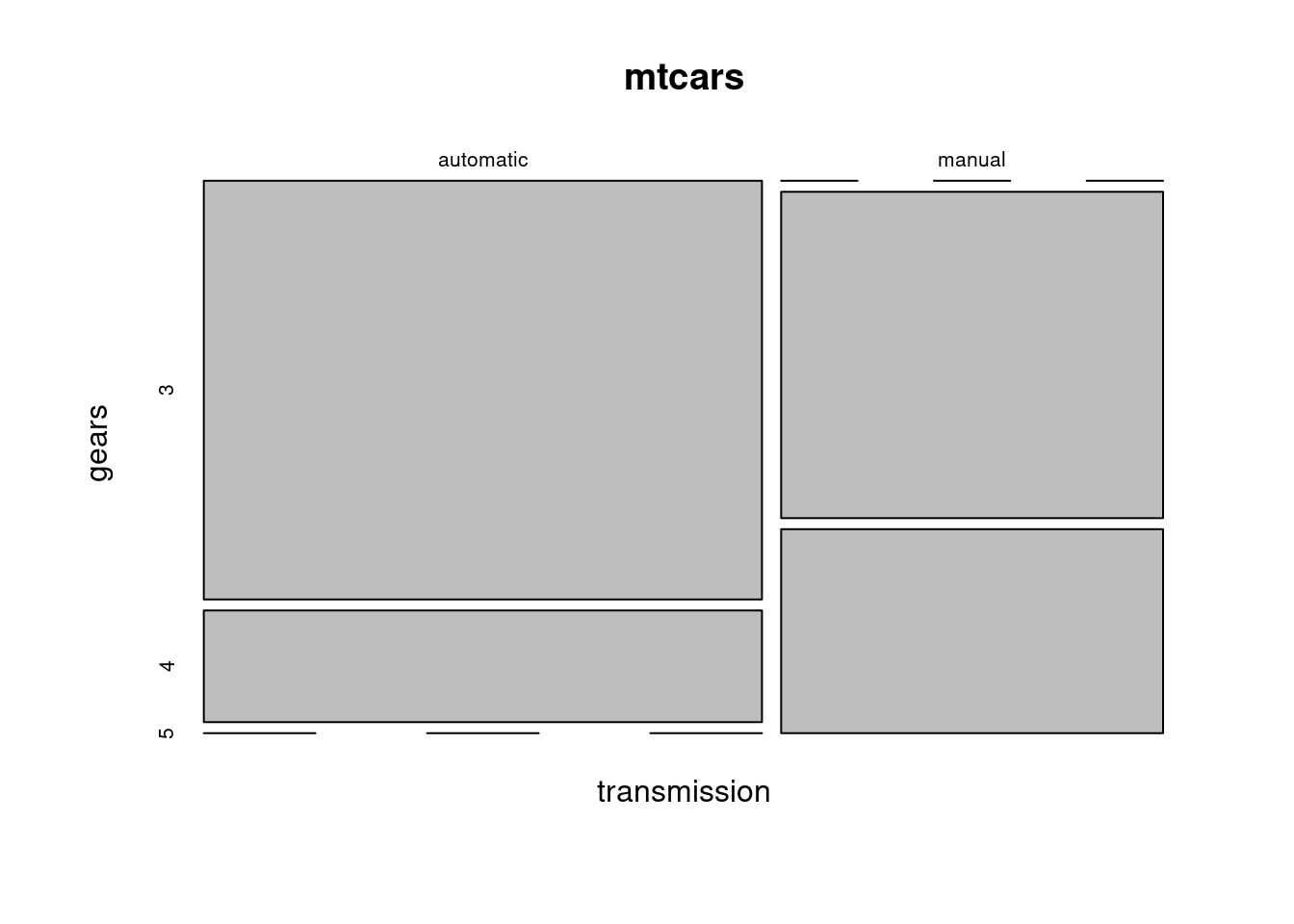
Z toho vidno nielen vyššiu celkovú početnosť automobilov s automatickou prevodovkou, ale hlavne negatívnu závislosť oboch veličín (automaty v sedemdesiatych rokoch ešte nezvládali veľa prevodov).
Rovnaká informácia je alternatívne sprostredkovaná pomocou stĺpcového grafu:
barplot(table(mtcars$transmission, mtcars$gears),
beside = T, # umiestnenie stĺpcov
legend.text = T, args.legend = list(title='transmission'),
xlab = "gears", ylab = "frequency")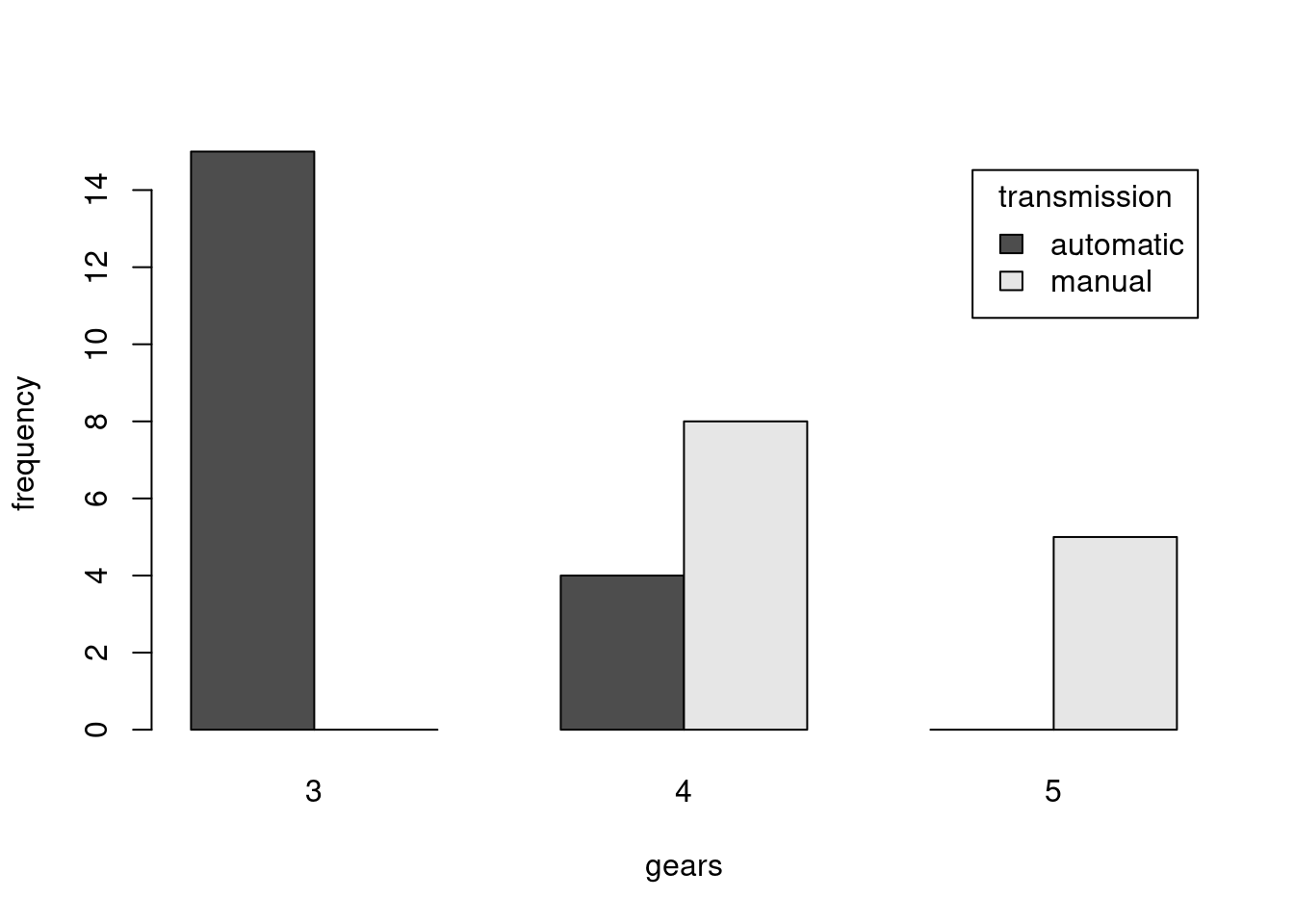
Pridanie ďalších diskrétnych premenných uľahčí napr. balík vcd (Visualizing Categorical Data).
Poznamenajme, že každý zo základných grafov systému R je možné pomocou argumentu subset jednoducho aplikovať iba na podmnožinu pozorovaní. Napríklad z nasledujúceho grafu je tak zjavná prevaha 4-rýchlostných manuálnych prevodoviek v triede ľahších automobilov.
mosaicplot(transmission ~ gears, data=mtcars, subset = weight<3.0)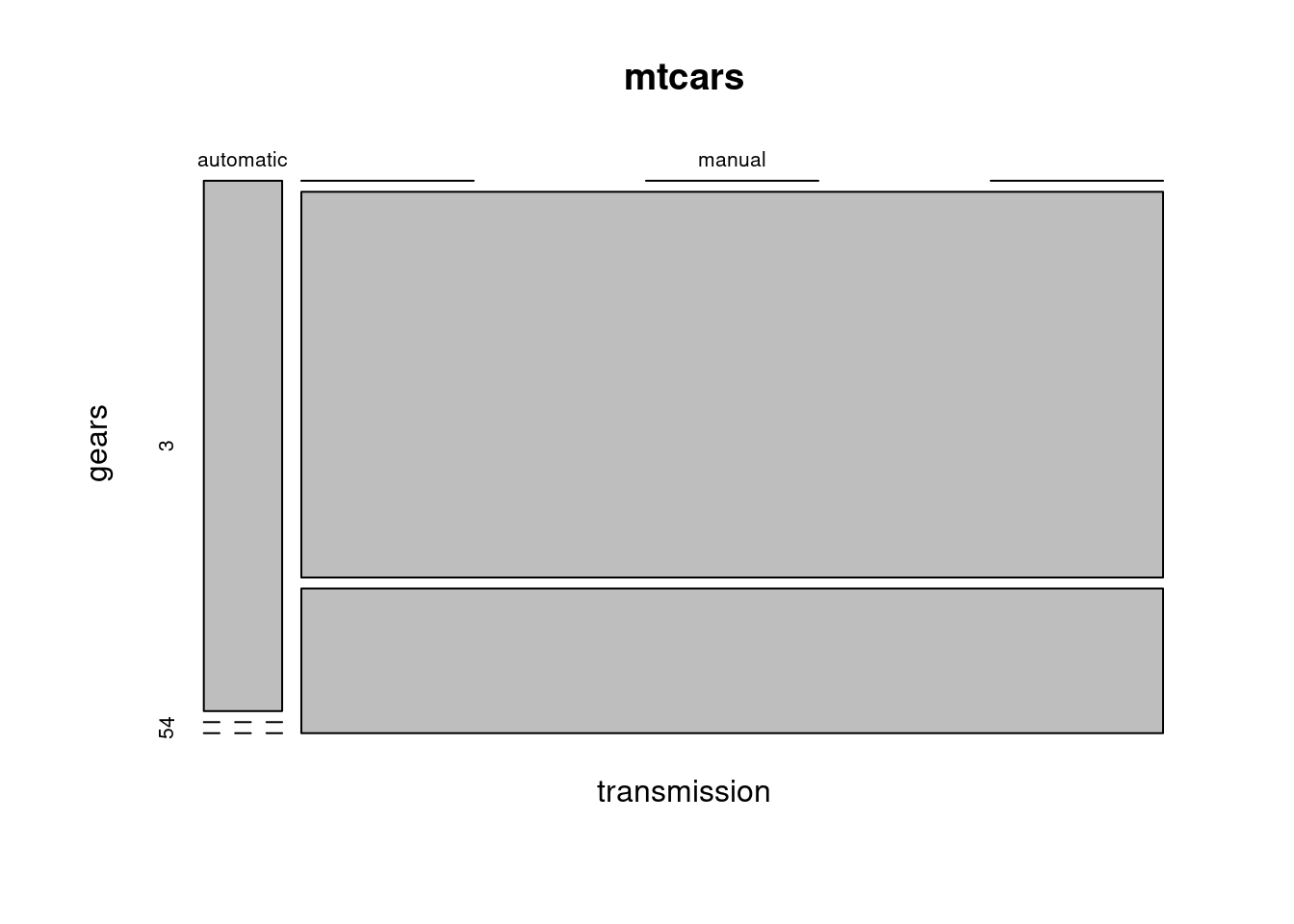
Viac numerických premenných sa tiež dá zobraziť pomocou dvojrozmerného bodového grafu, ale iba po pároch – každá s každou – a opäť je možné farebné odlíšenie podľa jednej diskrétnej premennej.
pairs(~ reach_mpg + displacement + horsepower + weight, data = mtcars,
col = c("red","green3","blue")[mtcars$cylinders],
lower.panel = NULL
)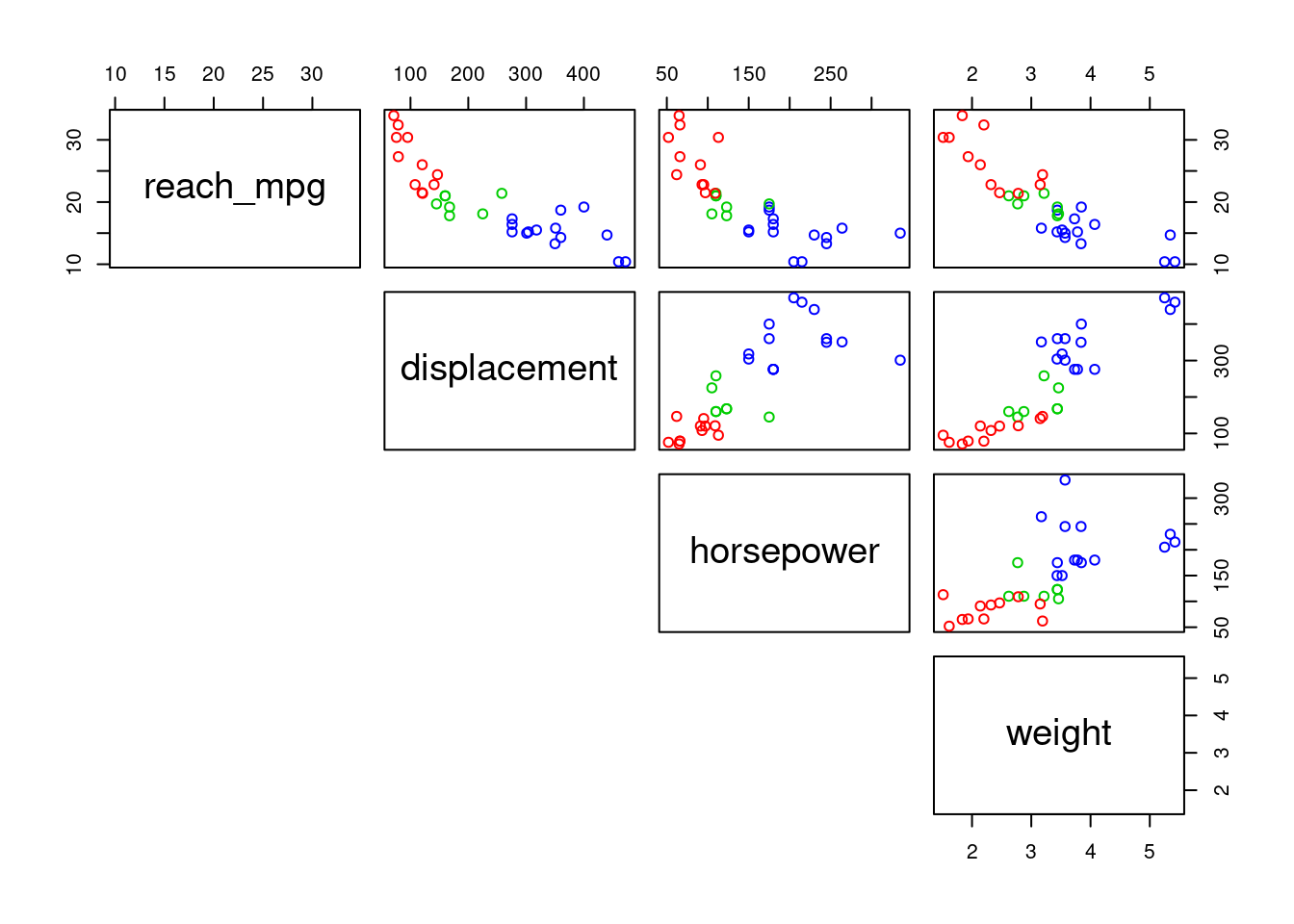
Skupina panelov (rámčeky v hornom či dolnom trojuholníku a na diagonále) sa dá samostatne definovať, no ľahšie je použiť už pripravené funkcie, napr.
psych::pairs.panels(
mtcars[c("reach_mpg", "displacement", "horsepower", "weight")],
ellipses = F, smooth = T, smoother = T, # prepínače pre dolný trojuholník
density = T, rug = T, # diagonálu
cor = T, cex.cor = 0.8, # horný trojuholník
)
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter
## Warning in par(usr): argument 1 does not name a graphical parameter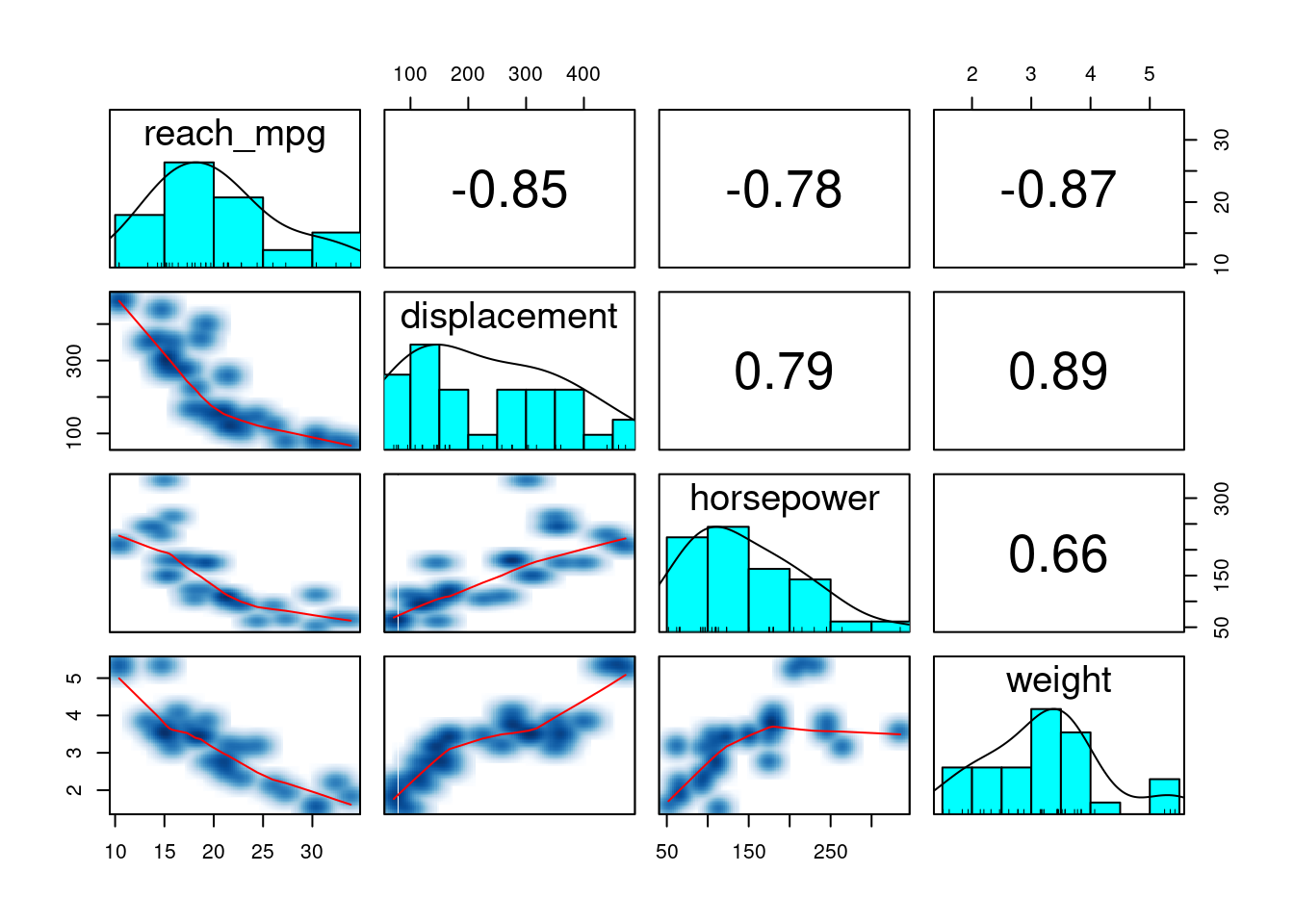
Rozostrenie (smoother) je výhodné pri zobrazení väčšieho množstva údajov, keď by už značky jednotlivých bodov splývali. Vyhladzujúca krivka (smooth) zjednodušuje vývoj závislosti medzi oboma premennými. Číslo v hornom trojuholníku je korelačný koeficient vyjadrujúci na intervale [-1,1] silu závislosti, so špeciálnymi prípadmi: -1 (nepriama úmernosť), 0 (nekorelovanosť), +1 (priama úmernosť). Pre úplnosť, korelačná matica sa vypočíta pomocou
cor( mtcars[c("reach_mpg", "displacement", "horsepower", "weight")] )
## reach_mpg displacement horsepower weight
## reach_mpg 1.0000000 -0.8475514 -0.7761684 -0.8676594
## displacement -0.8475514 1.0000000 0.7909486 0.8879799
## horsepower -0.7761684 0.7909486 1.0000000 0.6587479
## weight -0.8676594 0.8879799 0.6587479 1.00000003.4 Všeobecné zásady
Dobrou zásadou pri konštrukcii grafov je, aby neplytvali miestom, teda neobsahovali príliš málo informácií, ale ani nimi nezahlcovali. Nevhodné je používať efekty, ktoré sťažujú čitateľnosť informácie ako napr. perspektíva v pseudo 3D grafoch (špecialita programu MS Excel) alebo početnosť vyjadrená veľkosťou uhla v koláčovom grafe:
pie(table(mtcars$carburetors), main = "Number of carburetors proportions")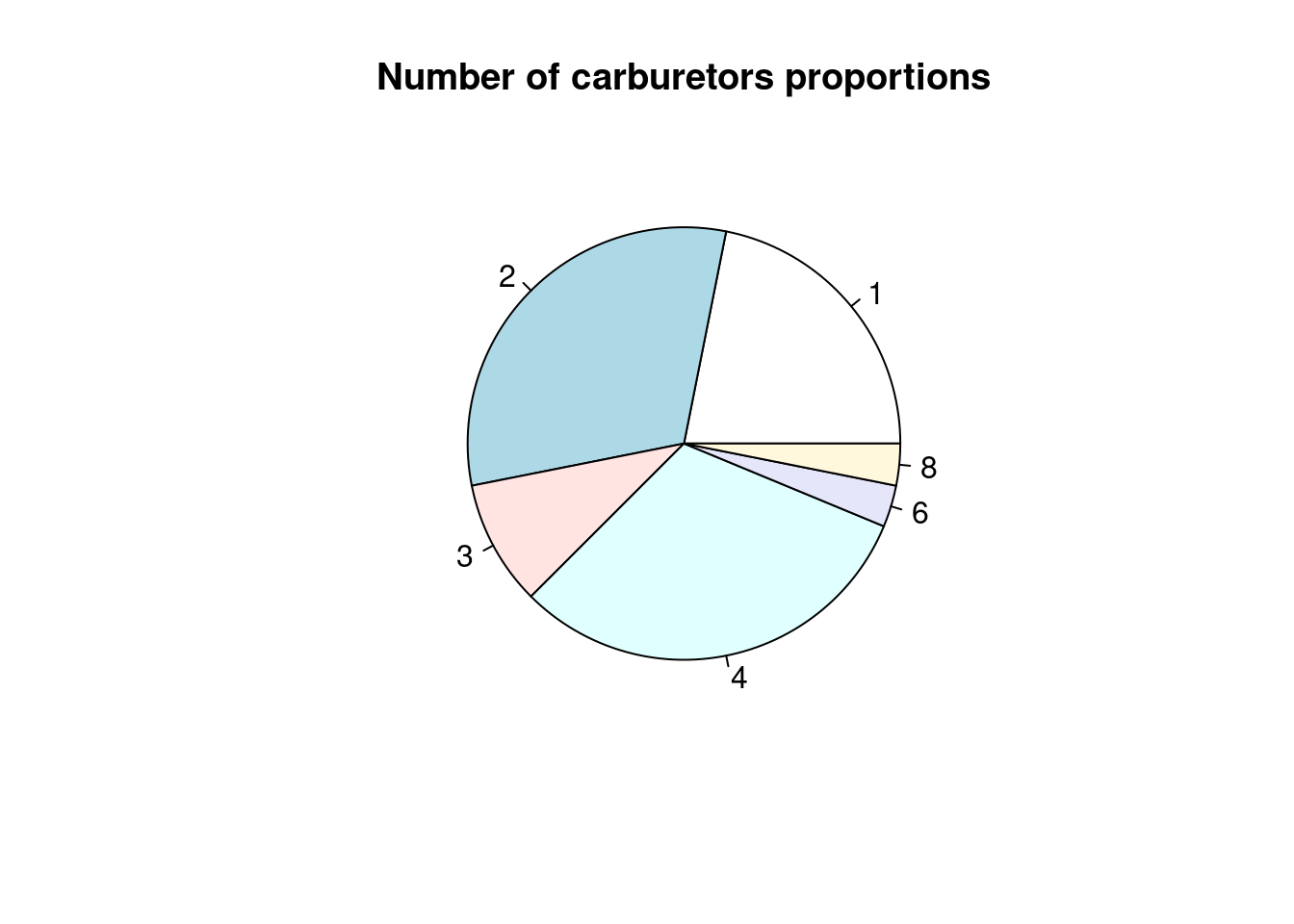
Podobným kontroverzným príkladom je tzv. radarový (alebo pavučinový graf), ktorým sa zvyknú porovnávať viaceré vlastnosti (premenné, stĺpce) vybraných subjektov (riadky). Každá vlastnosť má svoju os, všetky osi sú spojené v strede:
modely <- rownames(mtcars)[c(6, 18,25)]
dat <- subset(mtcars,
subset = rownames(mtcars) %in% modely,
select = c(reach_mpg, displacement, horsepower, weight, accel_time))
fmsb::radarchart(dat,
maxmin = FALSE, # relatívna mierka [0%,100%]
plwd = 2, plty = 1)
legend("topright", legend = modely, col = 1:3, lty = 1 , lwd=2, bty = "n")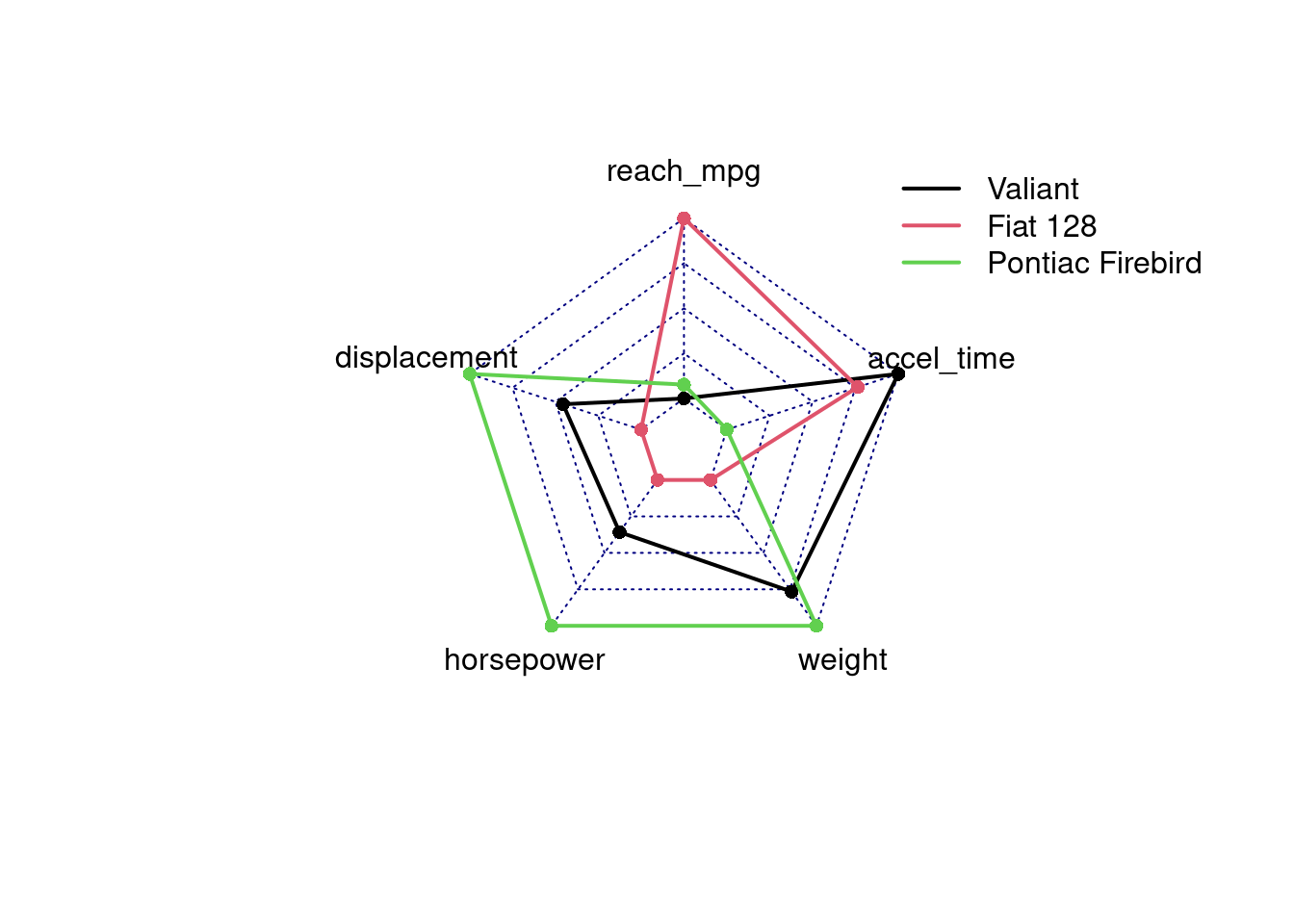
Užitočné zásady, ako nerobiť zlé grafy, sú zhrnuté napr. v (Irizarry a Love 2016, kapitola Exploratory Data Analysis). Ešte komplexnejšie túto problematiku rozoberá kniha (Few 2004).
Pomoc pri zorientovaní sa, aký graf použiť v závislosti od typu a počtu náhodných premenných, poskytne napr. projekt from Data to Viz na stránke https://www.data-to-viz.com/.
3.5 Cvičenie
- Načítajte data frame Cars93 z balíka MASS, zoznámte sa s významom náhodných premenných (stĺpcov), zobrazte si ich číselný súhrn.
- Čo viete na základe vizualizácie povedať o rozdelení pravdepodobnosti ceny amerických vozidiel? Aká je ich priemerná a mediánová cena?
- Zobrazte zastúpenie jednotlivých výrobcov zoradené podľa veľkosti v stĺpcovom grafe (popisy kolmo na os), v koláčovom grafe a Clevelandovom bodovom grafe (dotchart). Veľkosť znakov popisu osí prispôsobte početnosti hodnôt premennej. Ktorý graf je najprehľadnejší?
- Súvisí nejak cena s bezpečnostnou výbavou?
- Ako ovplyvňuje pôvod výrobcu vzťah medzi objemom valcov a výkonom? Odlišnosť v grafe (prostredníctvom farby, znaku alebo iného atribútu) prispôsobte vlastným preferenciám a zobrazte legendu.
- Analyzujte dostupnosť manuálnej prevodovky v jednotlivých veľkostných triedach automobilov. (Je vhodné previesť triedy auta na dátový typ factor s poradím úrovní definovaným manuálne alebo napr. podľa priemernej hmotnosti.)
Literatúra
Hromadný jav je prírodný alebo spoločenský jav, ktorý sa skúma na veľkom počte prípadov.↩︎