9 基礎統計
在本章,我們以Kaggle的「資料科學家的薪資」資料為例,來說明如何用R讀入資料並做基礎的統計分析,包含平均數、變異數、標準差、偏態、峰度等常用的描述統計量。這些統計量有助於我們很快速地瞭解資料的概況,例如平均數可以用來看一組資料的集中趨勢;變異數和標準差可用來看資料分散的程度;偏態和峰度則可以用來看資料分配的形狀。
套件安裝與載入
本章節用到的套件有:moments、e1071、 請以下列程式碼來安裝套件。已安裝過的套件不需再重覆安裝。
install.packages('moment') install.packages('e1071')安裝完套件後,載入套件,以供後續使用。
資料檔
請至kaggle網頁(https://www.kaggle.com/datasets/ruchi798/data-science-job-salaries?datasetId=2268489)下載資料檔ds_salaries.csv。
9.1 資料的讀入
將ds_salaries.csv檔放在R的工作目錄下。接著以R內建的read.table()函數來讀入資料。參數header=TRUE表示要讀入資料的表頭,因.csv檔內的數值是以逗點分隔,故設sep=“,”。
salaryData <- read.table("ds_salaries.csv", header=TRUE, sep=",")執行完上列程式碼後,即可產生名為salaryData的資料框。可以用head(salaryData)在主控台中檢視前六筆資料,或直接在右上角的Environment視窗中,對salaryData按滑鼠左鍵兩下後查看。
head(salaryData)我們可以看到「資料科學家的薪資」資料集蒐集了607位資料科學家的職級與薪資等相關資料,共12種,包含工作年度(work_year)、經驗等級(experience_level)、僱傭類型(employment_type)、職稱(job_title)、薪資(salary)、以美元計價的薪資(salary_in_usd)、遠端工作比率(remote_ratio)、公司規模(company_size)等。下表為僅呈現部份變項的資料表。
| X | work_year | experience_level | employment_type | job_title | salary | salary_currency | salary_in_usd | employee_residence | remote_ratio | company_location | company_size |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2020 | MI | FT | Data Scientist | 70000 | EUR | 79833 | DE | 0 | DE | L |
| 1 | 2020 | SE | FT | Machine Learning Scientist | 260000 | USD | 260000 | JP | 0 | JP | S |
| 2 | 2020 | SE | FT | Big Data Engineer | 85000 | GBP | 109024 | GB | 50 | GB | M |
| 3 | 2020 | MI | FT | Product Data Analyst | 20000 | USD | 20000 | HN | 0 | HN | S |
| 4 | 2020 | SE | FT | Machine Learning Engineer | 150000 | USD | 150000 | US | 50 | US | L |
| 5 | 2020 | EN | FT | Data Analyst | 72000 | USD | 72000 | US | 100 | US | L |
9.2 平均數、變異數和標準差
拿到資料後,我們常會藉由計算平均數、變異數和標準差,來瞭解資料的集中和分散情況。其中,平均數是集中趨勢的指標,可以幫助我們瞭解大多數人的分數集中在哪裡;變異數和標準差則是離散趨勢的指標,可以幫助我們瞭解資料有多分散。
Figure 9.1顯示了兩種不同的資料型態。紅色曲線是平均數為0、標準差為1的常態分配曲線,橫軸為標準化的分數,縱軸則為機率密度函數的數值,可以看到大多數的資料其數值都集中在零附近,愈遠離0的數值愈少,大約有68%的數值會集中在-1到1之間。而當平均數不變,但標準差增加為2時,資料點的數值就愈分散,如藍色曲線所示。
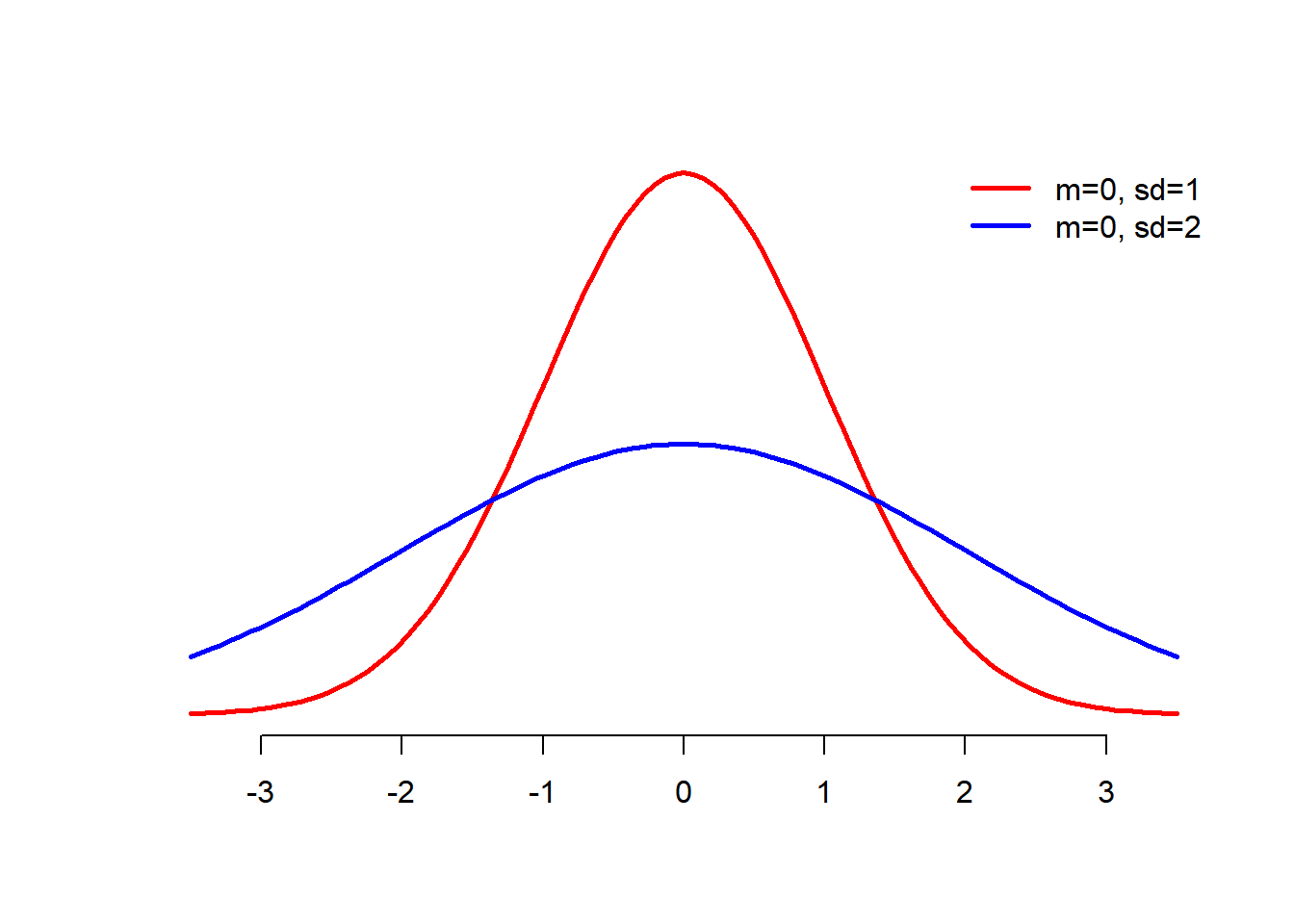
Figure 9.1: 資料的分配。紅色曲線是平均數為0、標準差為1的常態分配曲線。藍色曲線為平均數為0、標準差為2的曲線。
9.2.1 平均數
平均數(mean, \(m\))的計算為將所有資料點的數值(\(x_i\))相加後,除以數值的個數(\(n\)),公式為:
\[ m = \frac {\sum_{i=1}^n x_i} {n} = \frac {x_1 + x_2 + \cdots + x_n}{n} \]
故salary_in_usd的平均數為\(m = (79833 + 260000 + 109024 + \cdots + 200000)/607 = 112297.9\)。在R語言中,我們可以用mean(變數名稱)來計算平均數。以salary_in_usd為例,我們用下列程式碼來計算平均數後,可以得到salary_in_usd的平均數為112297.9,因此,這607位資料科學家的以美元計價後的薪資平均數為112297.9美元,表示大多數的資料科學家薪資在112297.9美元,約三百萬台幣。
mean(salaryData$salary_in_usd)## [1] 112297.9
- 想想看
除了平均數之外,我們也常看資料的中位數,來瞭解資料的集中情形。如何計算salary_in_usd的中位數呢?
9.2.2 變異數和標準差
除了以平均數來瞭解資料的集中趨勢外,我們也常使用變異數和標準差來瞭解資料的分散程度。
變異數旨在瞭解所有資料點和平均數的差異有多大(即多分散),由於有些資料點比平均數要來得小(負值),有些要來得大(正值),這些正和負的數值在相加後互相抵消,以致於看不出差異,因此數學家將這些差異先平方後再加總。變異數即為此加總的平均,也就是平均而言,資料點和平均數的平方差多少。故變異數(var, \(s^2\))即離均差的平方和的平均,即每個資料點的數值 (\(x_i\))減掉平均數(\(\overline x\))後平方再相加,最後再除以資料點的個數-1(\(n-1\)),其公式為:
\[ s^2 = \frac {\sum_{i=1}^n (x_i - \overline x)^2} {n-1} = \frac {(x_1-\overline x)^2 + (x_2-\overline x)^2 + \cdots + (x_n-\overline x)^2}{n-1} \]
以salary_in_usd為例,變異數\(s^2 = ((79833 - 112297.9)^2 + (260000 - 112297.9)^2 + \cdots + (200000 - 112297.9)^2) / 607 = 5034932663\)。若以R語言來計算變異數,可使用var(變數名稱)來計算該變數的變異數。以salary_in_usd為例,計算結果顯示其變異數為5034932663美元。
var(salaryData$salary_in_usd)## [1] 5034932663由於變異數的單位是原單位的平方,在理解上較為不易,因此,我們將變異數(\(s^2\))開根號來計算標準差,使其單位與原測量單位相同。標準差(std, \(s\))的公式為:
\[ s = \sqrt{s^2} = \sqrt{\frac {\sum_{i=1}^n (x_i - \overline x)^2} {n-1}} \]
以salary_in_usd為例,標準差\(s=\sqrt{5034932663}=70957.26\)。在R語言中,可使用sd(變數名稱)來計算變異數。下面的計算結果顯示,salary_in_usd的標準差為70957.26。
sd(salaryData$salary_in_usd)## [1] 70957.26由於標準差與平均數的單位相同,我們可以更快速地由平均數和標準差來理解資料的分配情況。例如,由上述平均數與標準差的計算結果,我們可以知道,若薪資為常態分配,則約有68%的資料科學家其薪資座落於41340.64美元 (即112297.9-70957.26)至183255.16(即112297.9+70957.26)美元之間。
- 想想看
除了變異數和標準差之外,我們也常看資料的最小值、最大值和全距,來瞭解資料的離散情形。如何計算salary_in_usd的最小值、最大值和全距呢?
9.2.3 分組計算平均數、變異數和標準差
在檢視資料的集中與離散趨勢時,我們也常會將資料分為不同組別來加以檢視。以資料科學家的薪資來看,我們可能會想知道,不同經驗等級(如,初階、中階、高階、管理職級)的資料科學家,其薪資狀況如何。
R語言的aggregate()函數,可以幫助我們快速地將資料分組來計算各個統計量。以下我們依照experience_level將資料科學家分為四組:初階職級者(Entry-level/Junior, EN)、中階職級者(Mid-level/Intermediate, MI )、高階職級者(Senior-level/Expert, SE )、以及管理職級者(Executive-level/Director, EX),並依序計算平均數(mean)、變異數(var)與標準差(sd)。
以平均數為例,我們以aggregate(計算變數名稱, by=list(組別名稱=分組變項名稱), mean)來分組計算平均數。在此例中,我們想要依experience_level來分組計算salary_in_usd的平均數,故計算變數名稱為salary_in_usd,分組變項名稱為experience_level,組別名稱為experience(讀者可自訂組別名稱,也可以省略,若省略則R會自動設定組別名稱為Group.1),故程式碼為:
結果顯示,初階職級者(EN)的平均薪資為61643.32美元;中階職級者(MI)為87996.06美元;高階職級者(SE)為138617.29美元,管理職級者(EX)則為199392.04美元。隨著職級愈高階,平均薪資也愈高。
## experience x
## 1 EN 61643.32
## 2 EX 199392.04
## 3 MI 87996.06
## 4 SE 138617.29若要計算四個經驗職級的資料科學家其薪資的變異數與標準差,只要將上式中的mean分別替換為var和std即可。
## experience x
## 1 EN 1970964072
## 2 EX 13705678910
## 3 MI 4083345147
## 4 SE 3328364364變異數的計算結果顯示,初階職級者(EN)薪資的變異數為1970964072美元;中階職級者(MI)為4083345147美元;高階職級者(SE)為3328364364美元,管理職級者(EX)則為13705678910美元。
## experience x
## 1 EN 44395.54
## 2 EX 117071.26
## 3 MI 63901.06
## 4 SE 57691.98標準差的計算結果則顯示,初階職級者(EN)薪資的變異數為44395.54美元;中階職級者(MI)為63901.06美元;高階職級者(SE)為57691.98美元,管理職級者(EX)則為117071.26美元。管理職級者的薪資分散程度較大,表示薪資差異較大。
- 想想看
如何計算salary_in_usd的中位數、最大值、最小值和全距呢?
小技巧:遺漏值的處理
當資料有遺漏值(NA)時,使用上述程式計算時會得到NA。 此時可加上na.rm=TRUE,排除遺漏值來計算平均數、標準差等統計量。
下面以平均數的計算來說明。算先,先製造一個有遺漏值的資料框。 我們可以複製salaryData資料框,將之另存為一個名為salaryData2的資料框。 接著將salaryData2的第一筆資料的salary_in_usd改為NA。
salaryData2 <- salaryData salaryData2$salary_in_usd[1] <- NA成功更改salaryData2的資料後,若我們依上述方法,以mean()函數計算salaryData2的salary_in_usd的平均數時,因為數值中有NA,故計算平均數會得到NA。
mean(salaryData2$salary_in_usd)## [1] NA要避免這個狀況,可以加入參數na.rm=TRUE,排除NA來計算salaryData2的salary_in_use的平均數,得到平均數為112351.4。
mean(salaryData2$salary_in_usd,na.rm=TRUE)## [1] 112351.4分組計算平均數時亦同,可加入na.rm=TRUE來計算平均數。同樣以不同職級資料科學家的薪資為例,我們可以用下列程式碼來分別計算四種不同職級資料科學家的薪資平均數。
aggregate(salaryData2$salary_in_usd, by=list(experience=salaryData2$experience_level), mean, na.rm=TRUE)## experience x ## 1 EN 61643.32 ## 2 EX 199392.04 ## 3 MI 88034.56 ## 4 SE 138617.29
- 想想看
- 如何計算salaryData2這個資料框的salary_in_usd這個變數的變異數和標準差?
- 如何依據experience_level來分組,計算salaryData2這個資料框的salary_in_usd這個變數的變異數和標準差?
9.3 偏態與峰度
除了平均數、變異數和標準差之外,偏態和峰度也是常用的描述統計量,可以用來看資料的分布型態是否為常態或偏離常態。若偏離常態,在後續做統計檢定時可能會違反其假設,需要注意。
下面同樣以salaryData資料中的salary_in_usd來計算偏態和峰度。計算偏態和峰度時,常用的套件有moments和e1071。請注意,計算結果會因不同套件使用的公式不同而有所不同。
9.3.1 偏態
偏態是一個用來衡量資料分配是否為對稱的統計量。一般我們看到的常態分配為一左右對稱的分配。若左右不對稱,則為偏態。偏態又可分為正偏態(positive skew)和負偏態(negative skew)。正偏態為分配的右側較多偏離值,即機率密度函數在右側延伸得較長,資料集中在左側,如Figure 9.2的藍色曲線所示。負偏態則為分配的左側較多偏離值,即機率密度函數在左側延伸得較長,大多數的資料集中在右側,如Figure 9.2的紅色曲線所示。
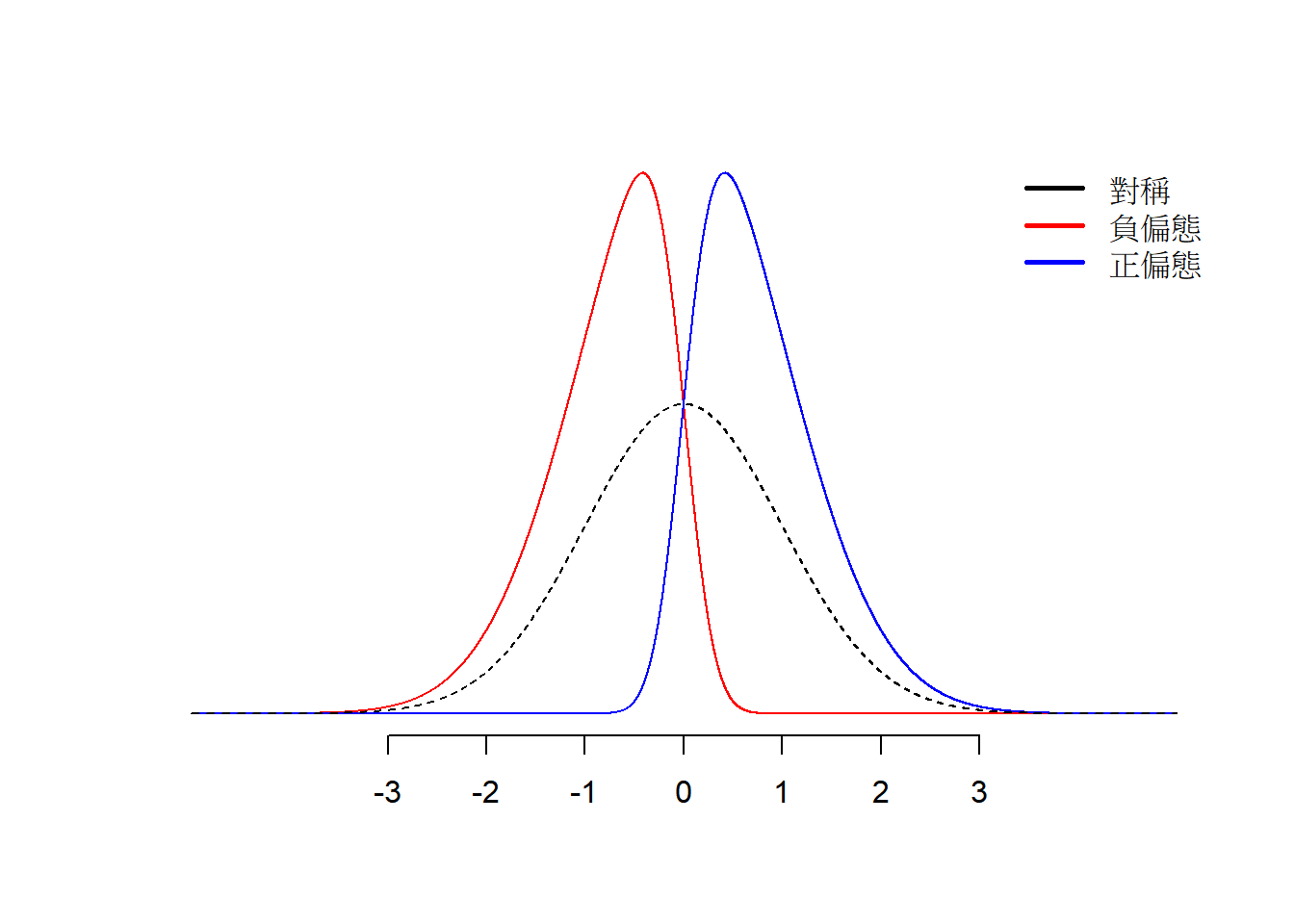
Figure 9.2: 不同偏態的資料型態。黑色曲線是常態分配曲線;紅色曲線為負偏態;藍色曲線為正偏態。
偏態的公式為:
\[ g1 = \frac {\sum_{i=1}^n (x_i - \overline x)^3 / n} {s^3} \]
若g1 = 0,資料為對稱;g1 > 0為正偏態;g1 < 0則為負偏態。
我們以salary_in_usd為例來計算其偏態。我們先用moments這個套件下的skewness()函數來計算偏態。若要計算偏態並做檢定,則可以用agostino.test()函數。
moments::skewness(salaryData$salary_in_usd)## [1] 1.663421
moments::agostino.test(salaryData$salary_in_usd)##
## D'Agostino skewness test
##
## data: salaryData$salary_in_usd
## skew = 1.6634, z = 12.2209, p-value < 2.2e-16
## alternative hypothesis: data have a skewness由上面的結果可知,偏態為1.66,p-value < .001,達顯著,拒絕虛無假設,即薪資有偏態,且因偏態 > 0,可知為正偏(positive skew),即有極少數的資料科學家有非常高的薪水。這樣的結果也可以從第X章8圖XX??的直方圖可以看出來。
需要注意的是,雖然偏態的一般性定義為如上所示,但SAS和SPSS對上述公式做了些校正,其使用的計算公式為:
\[ G1 = \frac {\sqrt{n(n-1)}} {n-2} \times \frac {\sum_{i=1}^n (x_i - \overline x)^3 / n} {s^3} \]
若要得到與SAS或SPSS一樣的結果,可以用e1071套件的skewness()函數來計算偏態。此套件的skewness()函數可以透過type參數來指定用哪一種公式來計算偏態:type=1為舊版本教科書的一般性定義,與moments套件的計算結果相同;type=2則計算結果與SAS與SPSS相同;type=3則計算結果與MINITAB與BMDM相同。套件的參數預設值為3。故我們將type設為2來計算。
e1071::skewness(salaryData$salary_in_usd, type=2)## [1] 1.667545計算結果顯示,偏態為1.67,為正偏態。
小技巧:選擇使用的套件
R有很多免費的套件可以使用,而不同的套件可能有同樣名稱的函數來做類似的運算,因此,要特別注意現在使用的函數是哪個套件下的函數。
以偏態的計算為例,因為e1071與moments這兩個套件用來計算偏態的函數都是skewness(),在兩個套件都載入時,其中一個套件會阻斷另一個套件的運作。為了讓R知道我們想要用哪一個套件的函數來運算,可以用「套件名稱::函數名稱」的方式來使用函數,如同上面的作法;另一種作者則是以detach()來缷載其中一個套件,讓R不會使用該函數的套件來運算。以上面的例子為例,用
detach("package:moments")來卸載moments套件後,在僅載入套件e1071的情況下,便可直接用skewness(iris$Sepal.Length, type=2)來計算偏態。
9.3.2 峰度
峰度是一個用來衡量資料分配存在偏離值(outliers)程度的統計量。若資料的分配相較於常態分配,有著更多的偏離值,尾端拉得更長,稱為高狹峰,如Figure 9.3的紅色曲線所示。反之,若資料的分配比常態分配有著更少的偏離值,分布更為均勻,尾端更不明顯,則稱為低濶峰,如Figure 9.3的藍色曲線所示。
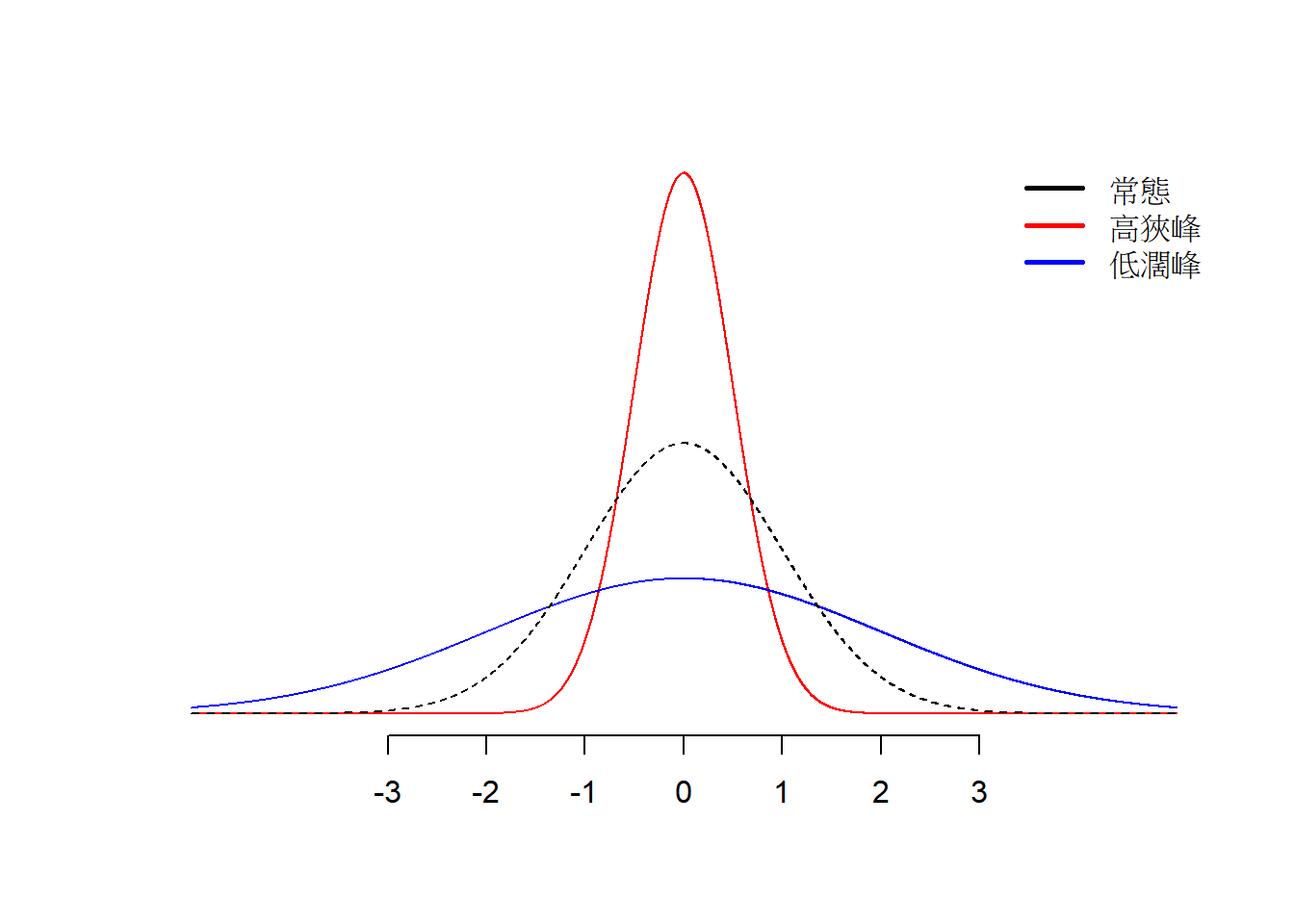
Figure 9.3: 不同峰度的資料型態。黑色曲線是常態分配曲線;紅色曲線為高狹峰;藍色曲線為低闊峰。
峰度的公式為:
\[ g2 = \frac {\sum_{i=1}^n (x_i - \overline x)^4 / n} {s^4} - 3 \]
常態分配的峰度統計量為零。若峰度值大於零為高狹峰,峰度值小於零則為低濶峰。
在R語言中,可以用moments套件的kurtosis()函數來計算峰度。如果要計算峰度並加以檢定,可以用anscombe.test()。需注意的是,moments套件所計算出的峰度值並沒有減去3,可自行減去。
moments::kurtosis(salaryData$salary_in_usd)## [1] 9.291709
moments::anscombe.test(salaryData$salary_in_usd)##
## Anscombe-Glynn kurtosis test
##
## data: salaryData$salary_in_usd
## kurt = 9.2917, z = 9.3882, p-value < 2.2e-16
## alternative hypothesis: kurtosis is not equal to 3計算結果顯示,salary_in_usd的峰度為9.29,減去3後為6.29,p < 0.001,達到統計顯著,故拒絕虛無假設,salary_in_usd的資料並非常態峰。因峰度值>3,可知為高狹峰。
同樣地,SAS和SPSS也對峰度的數值做了一些校正,公式如下:
\[ G2 = ((n+1) \times \frac {\sum_{i=1}^n (x_i - \overline x)^4 / n} {s^4} + 3) \times \frac {(n-1)} {(n-2)(n-3)} \]
若想要得到與SAS或SPSS相同的結果,可以用e1071套件的kurtosis()函數來計算峰度。需注意的是,e1071套件的計算結果是已減去3之後的數值,故常態峰為0。同樣地,此套件的skewness()函數可以透過type參數來指定用哪一種公式來計算偏態。type=1採用舊版本教科書的一般定義,計算結果與moments套件相同;type=2的計算結果與SAS與SPSS相同;type=3的計算結果與MINITAB與BMDM相同。套件的參數預設值為type=3。我們可以將type設為2來計算salary_in_usd的峰度值。
e1071::kurtosis(salaryData$salary_in_usd, type=2)## [1] 6.353795計算結果顯示,峰度為6.35,可知為高狹峰的資料型態。
9.4 多個變項的描述統計量
在上面的例子中,我們一次計算一個變項的一個描述統計量。若要一次做多個變項的多個統計量,R也提供了相關的函數,讓我們可以輕而易舉地完成此任務。
我們以上述的salaryData資料為例,一次計算salary_in_usd和remote_ratio的多個統計量。
第一個方法是用R內建的summary()函數來計算,summary()函數可以計算一資料框所有變項的描述統計量,包含平均數、中位數、最小值、最大值、第一四分位數、和第三四分位數。以salaryData這個資料框為例,我們用summary(salaryData[,c(8,10)])將第8個變項salary_in_usd與第10個變項remote_ratio提取出來,放進summary()函數裡做分析。
## salary_in_usd remote_ratio
## Min. : 2859 Min. : 0.00
## 1st Qu.: 62726 1st Qu.: 50.00
## Median :101570 Median :100.00
## Mean :112298 Mean : 70.92
## 3rd Qu.:150000 3rd Qu.:100.00
## Max. :600000 Max. :100.00計算結果顯示,salary_in_use的平均數為112298,中位數為101570,最小值為2859,最大值是600000,第一四分位數為62726,第三四分位數為150000;remote_ratio的平均數為70.92,中位數為100,最小值為0,最大值是100,第一四分位數為50,第三四分位數為100。
除了R內建的summary()函數外,我們也可以用psych套件的describe()函數來做分析。describe()函數可得到更多常用的描述統計量,如平均數、標準差、偏態、峰度等。其中,偏態與峰度的計算和e1071套件一樣,有三種不同的方法可選擇,type=2時與SPSS的結果一樣。
## vars n mean sd median trimmed mad min max
## salary_in_usd 1 607 112297.87 70957.26 101570 106157.63 62906.72 2859 6e+05
## remote_ratio 2 607 70.92 40.71 100 76.08 0.00 0 1e+02
## range skew kurtosis se
## salary_in_usd 597141 1.67 6.35 2880.07
## remote_ratio 100 -0.90 -0.89 1.65計算結果顯示,salary_in_usd的平均數為112297.87、標準差(sd)為70957.26,中位數為101570,偏態為1.67,峰度為6.35;remote_ratio的平均數(mean)為70.92、標準差(sd)為40.71,中位數(median)為100,偏態(skew)為-0.9,峰度(kurtosis)為-0.89。
9.5 分組計算多個變項的描述統計量
在一些情況下,我們會想要將資料分組後計算各組別的描述統計量。例如,男女生身高的平均數、標準差;各地區的平均壽命等。
以下我們將salaryData的資料依experience_level來分組,計算salary_in_usd和remote_ratio兩變項的描述統計量。
同樣地,我們可以用aggregate()函數來將多個變項分組,計算其描述統計量,語法與章節9.2.3 相同,僅需將使用的函數從特定的統計量函數改為summary即可,即aggregate(計算變數名稱, by=list(組別名稱=分組變項名稱), summary)。
以salaryData為例,我們要依experience_level來分組計算salary_in_usd和remote_ratio兩個變項的描述統計量,故計算變數名稱可給定salaryData[,c(8,10)],組別名稱一樣可設為position,分數變項設為experience_level,程式與執行結果如下。
## position salary_in_usd.Min. salary_in_usd.1st Qu. salary_in_usd.Median
## 1 EN 4000.00 27505.00 56500.00
## 2 EX 69741.00 130006.50 171437.50
## 3 MI 2859.00 48000.00 76940.00
## 4 SE 18907.00 100000.00 135500.00
## salary_in_usd.Mean salary_in_usd.3rd Qu. salary_in_usd.Max. remote_ratio.Min.
## 1 61643.32 85425.75 250000.00 0.00000
## 2 199392.04 233750.00 600000.00 0.00000
## 3 87996.06 112000.00 450000.00 0.00000
## 4 138617.29 170000.00 412000.00 0.00000
## remote_ratio.1st Qu. remote_ratio.Median remote_ratio.Mean
## 1 50.00000 100.00000 69.88636
## 2 50.00000 100.00000 78.84615
## 3 0.00000 100.00000 63.84977
## 4 50.00000 100.00000 75.89286
## remote_ratio.3rd Qu. remote_ratio.Max.
## 1 100.00000 100.00000
## 2 100.00000 100.00000
## 3 100.00000 100.00000
## 4 100.00000 100.00000以salary_in_usd的平均數(salary_in_usd.Mean)來看,分析結果顯示,初階職級者(EN)的平均薪資為61643.32美元;中階職級者(MI)為87996.06美元;高階職級者(SE)為138617.29美元,管理級職者(EX)則為199392.04美元,與章節9.2.3相同。
然而,我們可以看到,用R內建的summary()函數搭配aggregate()函數分組計算多個變項的描述統計量時,結果呈現較為凌亂,不易閱讀,因此,建議可以用psych套件的describeBy()函數來做分析。
describeBy()函數的用法為describeBy(計算變數, list(組別名稱=分組變項名稱)),同樣地可以加入type=2來得到與SAS或SPSS相同的結果。以describeBy()函數來依experience_level分組計算salary_in_usd和remote_ratio兩個變項的描述統計量的程式碼與結果如下。
describeBy(salaryData[,c(8,10)], list(position=salaryData$experience_level),type=2)##
## Descriptive statistics by group
## position: EN
## vars n mean sd median trimmed mad min max
## salary_in_usd 1 88 61643.32 44395.54 56500 57087.85 43516.53 4000 250000
## remote_ratio 2 88 69.89 37.55 100 74.31 0.00 0 100
## range skew kurtosis se
## salary_in_usd 246000 1.50 4.11 4732.58
## remote_ratio 100 -0.81 -0.76 4.00
## ------------------------------------------------------------
## position: EX
## vars n mean sd median trimmed mad min
## salary_in_usd 1 26 199392.04 117071.26 171437.5 182700.59 82886.98 69741
## remote_ratio 2 26 78.85 35.14 100.0 84.09 0.00 0
## max range skew kurtosis se
## salary_in_usd 6e+05 530259 1.86 4.60 22959.56
## remote_ratio 1e+02 100 -1.42 0.71 6.89
## ------------------------------------------------------------
## position: MI
## vars n mean sd median trimmed mad min max
## salary_in_usd 1 213 87996.06 63901.06 76940 80341.38 46227.47 2859 450000
## remote_ratio 2 213 63.85 42.71 100 67.25 0.00 0 100
## range skew kurtosis se
## salary_in_usd 447141 2.65 11.79 4378.43
## remote_ratio 100 -0.57 -1.40 2.93
## ------------------------------------------------------------
## position: SE
## vars n mean sd median trimmed mad min
## salary_in_usd 1 280 138617.29 57691.98 135500 136030.95 52039.26 18907
## remote_ratio 2 280 75.89 39.93 100 82.37 0.00 0
## max range skew kurtosis se
## salary_in_usd 412000 393093 1.00 3.26 3447.76
## remote_ratio 100 100 -1.21 -0.34 2.39由上表可見,以describeBy()對experience_level分組做描述統計時,四個組別EN、EX、MI、SE的分析結果會分別呈現在四個表中,更容易閱讀。
- 想想看
如何依據employment_type來分組,分別計算全職(Full-time, FT)、兼職(Part-time, PT)、合約(Contract, CT)、自由職業(Freelance, FL)者的描述統計量,如平均數、標準差、偏態、峰度等?