1 Circle

1.1 Basics

AB is a diameter of circle $O$ , $PA$ is a tangent line of the circle. $C$ is ther intersect point of $PO$ and the circle. $\angle P=40^o$ . What’s $\angle B$ ？

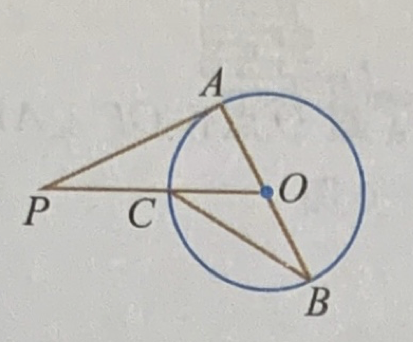
Figure 1.1: Circle 1

The two legs of a right $\triangle ABC$ is tagent with a circle $O$ whose center $O$ is the mid point of the hypotenuse of $\triangle ABC$ . D and E are the tagent points on $AB$ and $AC$ . $BC = 2\sqrt 2$ . What’s the length of arc ${DE}$ ?

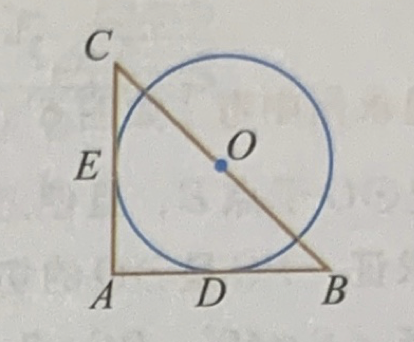
Figure 1.2: Circle 2

A circle $O$ has radius 10, AB and CD are two chords of the circle. $AB \parallel BC$ , $AB = 12$ , $CD=16$ , what’s the distance between AB and CD?
Triangle $ABC$ , $AB=AC$ , $\angle ABC = 30^o$ . $BD$ is a diameter of $\triangle ABC$ ’s circumsribe circle, $CD=\frac{4\sqrt 3}{3}$ , AD=?
$AB$ is a chord of circle $O$ . $E$ is the midpoint of $AB$ . $EC\perp OA$ , BD is a tangent line of Circle $O$ . $AB=12$ , $BD=5$ . What is the radius of the circle?

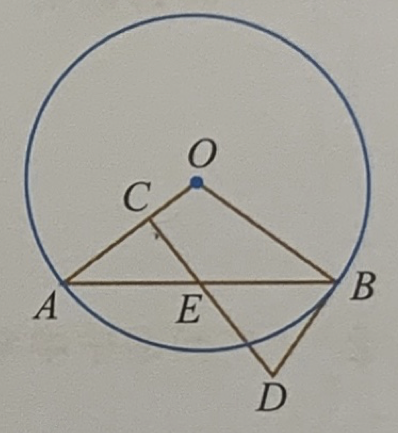
Figure 1.3: Circle 5

BC is the diameter of circle O with radius 3. Circle O interset with AC at point E. EF is a tangent line of Circle O and $EF \perp AB$ at point F. EF is extended and intersect with CB’s extended line at G, $\angle ABG=2\angle C$ , $\sin \angle EGC = \frac{3}{5}$ . AF=?

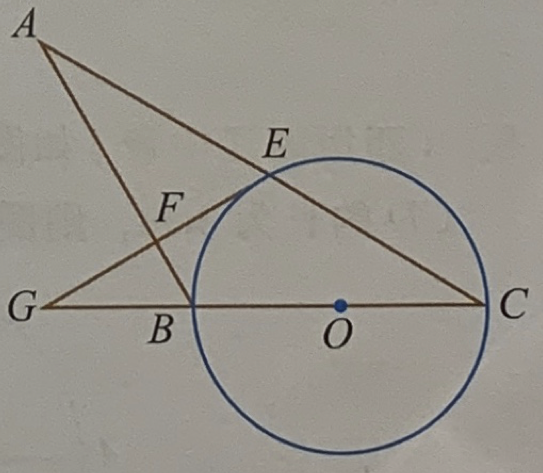
Figure 1.4: Circle 6