1 Supervised and unsupervised learning

1.1 Introduction

The methods in machine learning can be broadly divided into supervised and unsupervised learning methods.

In supervised learning, we have an outcome variable $Y$ (also called output, response, dependent variable) and a set of predictors $\mathbf{X}$ (also called features, dependent variables, covariates). The objective is to estimate the function $f(\mathbf{X})$ that connects $Y$ and $\mathbf{X}$. For example,

$$Y = f(\mathbf{X}) + \varepsilon$$

(if $Y$ is categorical we generally consider the association of $\mathbf{X}$ and the $Pr(Y=k)$)

Having a dataset with observations of $Y$ and $X$ (called training set), we can use these data to find an estimate $\hat f(\mathbf{X})$ according to some optimisation principle.

If we specify a functional for $f(\mathbf{X})$, such as the linear regression model:$f(\mathbf{X}) = \beta_0 + \beta_1X_1 + ... + \beta_p X_p$, we say that we are using a parametric method. If instead we allow the data to estimate the functional form of $f(\mathbf{X})$, such as k-nearest neighbourhood regression, we call the method non-parametric.

In unsupervised learning , the goal is to model the underlying structure or distribution in the data without having the outcome $Y$. In other words, we want to analyse how the features $\mathbf{X}$ are clustered or associated. Examples of these methods are principle components analysis and k-means clustering.

1.2 Readings

Read the following chapters of An introduction to statistical learning:

• 2.1 What is statistical learning?

If you are using R for the first time, I encourage you to complete the section

• 2.3 Introduction to R

1.3 R review

Task 1 - Read a dataset and create a new variable

Read the bmd.csv dataset in R. You can download and read the data or use the path https://www.dropbox.com/s/7wjsfdaf0wt2kg2/bmd.csv?dl=1

bmd.data <- read.csv("https://www.dropbox.com/s/7wjsfdaf0wt2kg2/bmd.csv?dl=1")

If you have downloaded the file, you need to substitute the url above by the path to file in your computer, e.g., “c:\my files\bmd.csv”

The variable id is the identification of the subjects in the dataset, and the variable age is their age. What is the age of the subject id=197?

bmd.data$age is the vector with the ages of all the subjects. Within that vector we need to find the one where bmd.data$id == 197. Notice that double equal sign “==” is a logic statement.

If we write bmd.data$id = 197 we are assigning the value 197 to the variable id and every subject in the dataset gets a new value 197 for that variable.

bmd.data$age[bmd.data$id == 197]

## [1] 69.72845

#or equivalent
bmd.data[bmd.data$id == 197, "age"]

## [1] 69.72845

#or 
bmd.data[bmd.data$id == 197, 2]  #age is the second variable

## [1] 69.72845

Let’s now create a new variable age.months which is age in months (the original is in years).

# we just need to multiply the original by 12
bmd.data$age.months <- bmd.data$age * 12

# we can use = instead of <- 
bmd.data$age.months = bmd.data$age * 12

Finally, let’s recode the variable age into age categories <=50, (50,60], (60,70] and >60.

# we can use the function cut() to 
#create the categories
bmd.data$age.cat <- cut(bmd.data$age, 
                        c(0,50,60,70, 100))

# alternative 
bmd.data$age.cat2[bmd.data$age<50]                    <- 1
bmd.data$age.cat2[bmd.data$age>=50 & bmd.data$age<60] <- 2
bmd.data$age.cat2[bmd.data$age>=60 & bmd.data$age<70] <- 3
bmd.data$age.cat2[bmd.data$age>=70]                   <- 4

#frequencies of the categories
table(bmd.data$age.cat)

## 
##   (0,50]  (50,60]  (60,70] (70,100] 
##       24       45       48       52

TRY IT YOURSELF:

1. Get the ages for all the male subjects, i.e., bmd.data$sex == "M".

See the solution code

bmd.data$age[bmd.data$sex == "M"]  

2. What is the length of the vector above? Or, in other words, how many subjects are male?

See the solution code

length(bmd.data$age[bmd.data$sex == "M"])

#or
table(bmd.data$sex)

3. Using the variables weight_kg and height_cm, compute the body mass index? $\frac{\text{weight in Kg}}{(\text{heigh in m})^2}$

See the solution code

bmd.data$bmi <- bmd.data$weight_kg /(bmd.data$height_cm/100)**2

Task 2 - Histogram

There are several packages specific to graphs ggplot2, lattice, plotly, highcharter, sunburstR, dygraphs, rgl,… The R Graph Gallery is an excellent learning resource for complex plots and visualisation

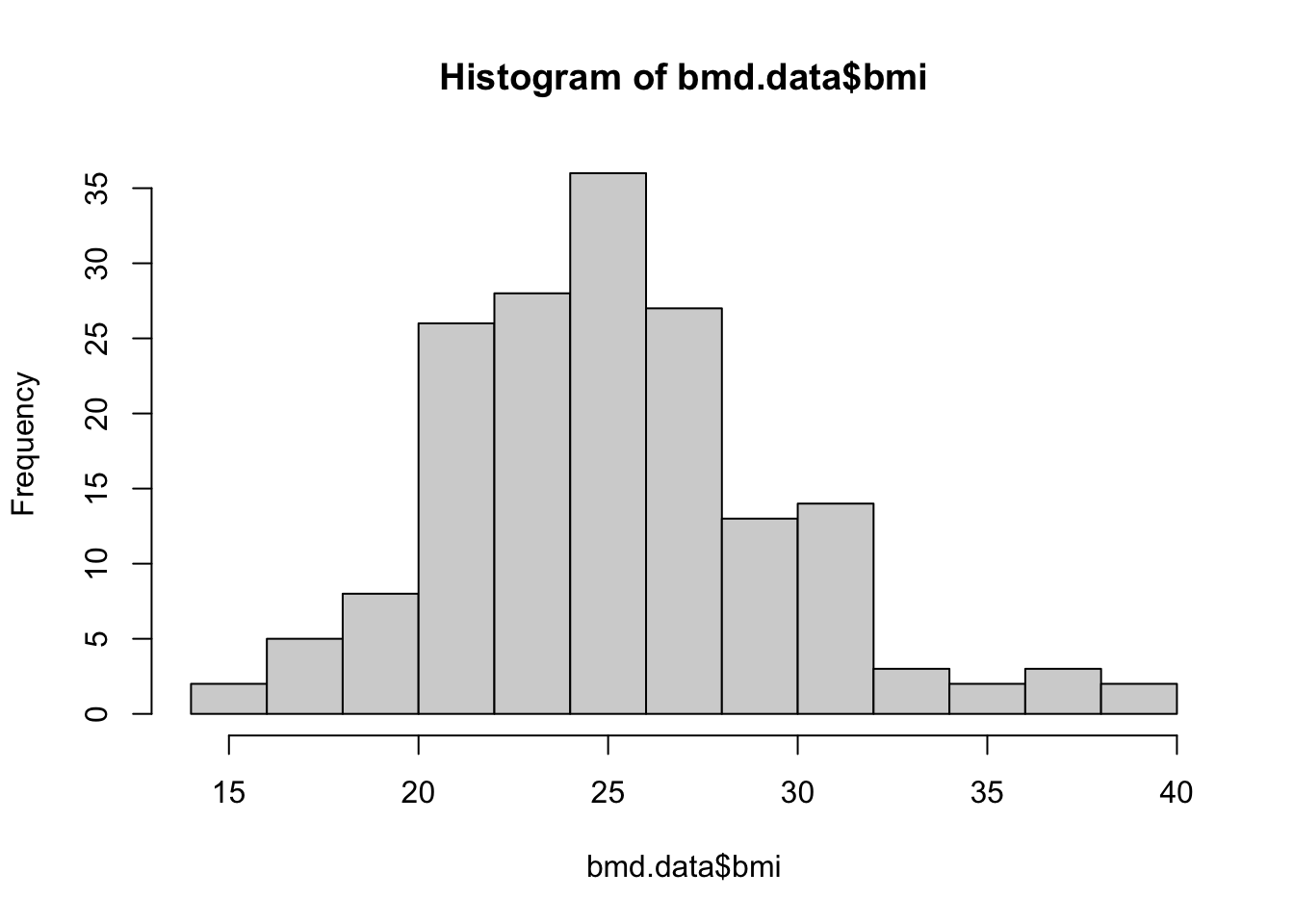
We will start with basic functions. Let’s produce the histogram of the variable bmi created in task 1

hist(bmd.data$bmi)

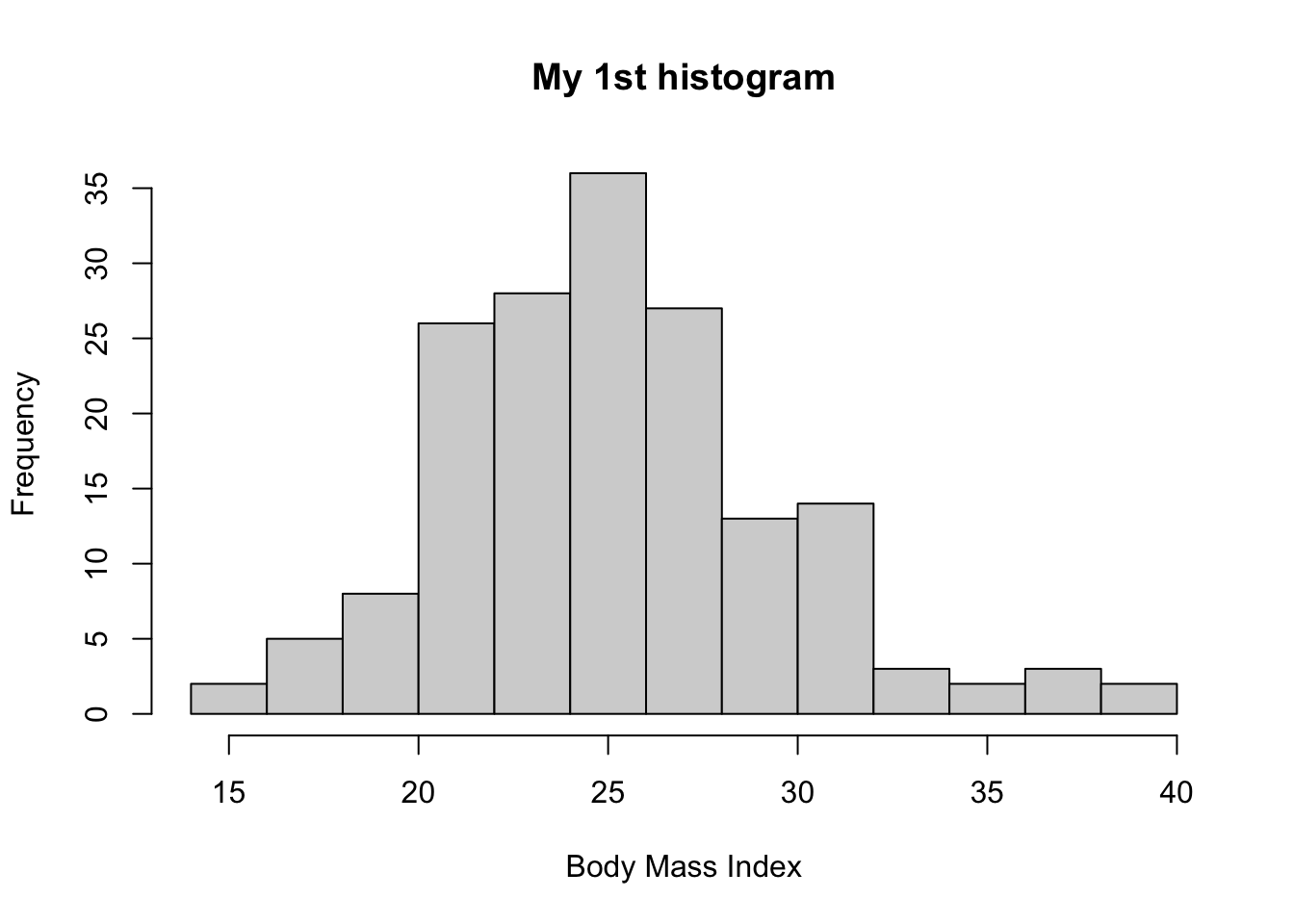
Let’s edit the title and x-axis label

    hist(bmd.data$bmi, 
         main = "My 1st histogram",     
         xlab = "Body Mass Index")

And we can also plot the distribution for males and females, separately

#histogram for males
hist(bmd.data$bmi[bmd.data$sex=="M" ],
     breaks = 10,                  # number of cutoff for the bars
     main= "My 1st histogram",  
     xlab= "Body Mass Index",
     col=rgb(0,0,1,.5))           # color of the bars

#histogram for females
hist(bmd.data$bmi[bmd.data$sex=="F" ],
      breaks = 10,
     main= "My 1st histogram",
     xlab= "Body Mass Index", 
     col=rgb(1,0,0,.5),
     add=T)                      # superimposes the histograms

# Add legend
legend("topright",  
       legend=c("Males","Females"), 
       col=c(rgb(0,0,1,0.5),  rgb(1,0,0,0.5)), 
       pt.cex=2, pch=15 )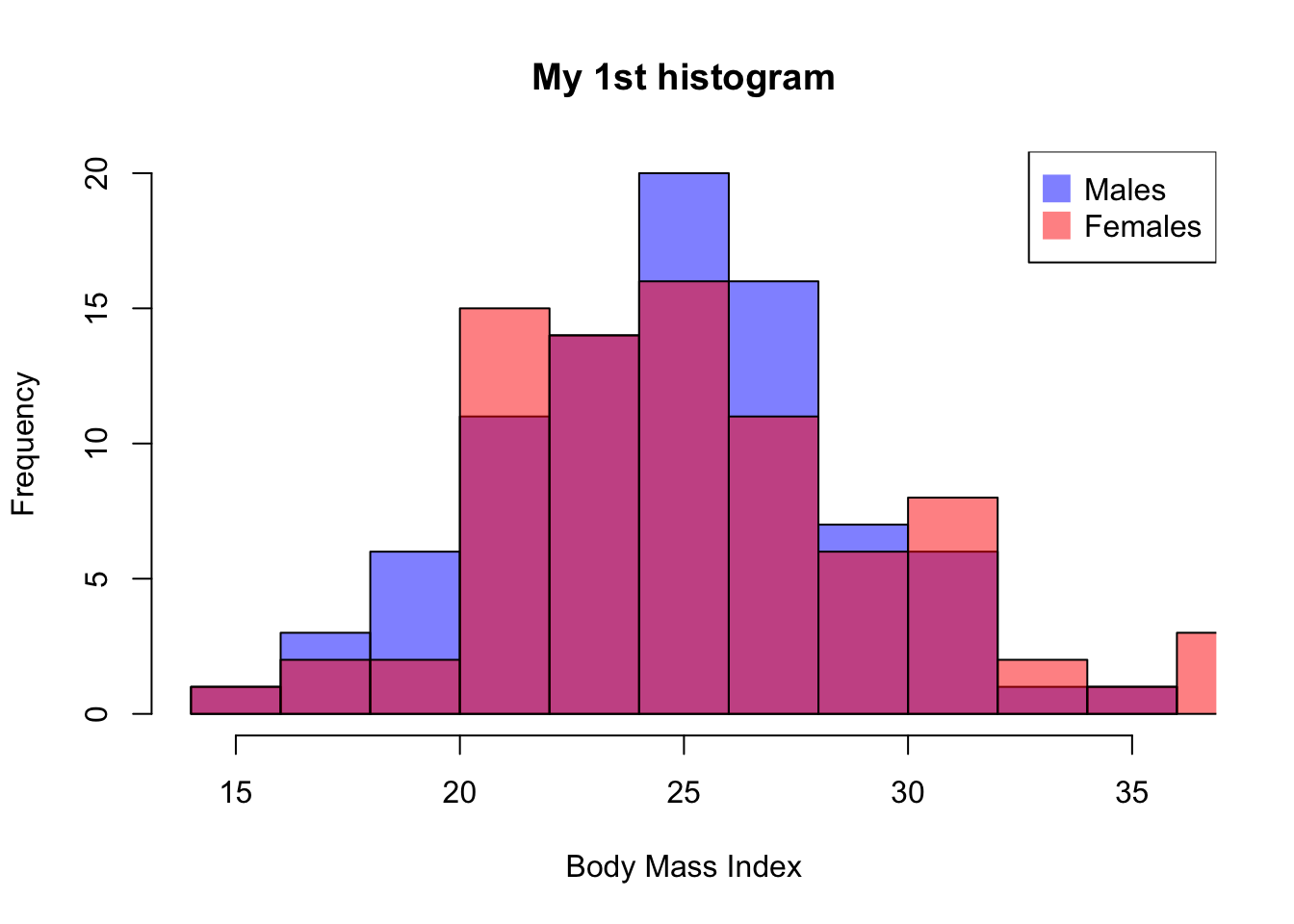

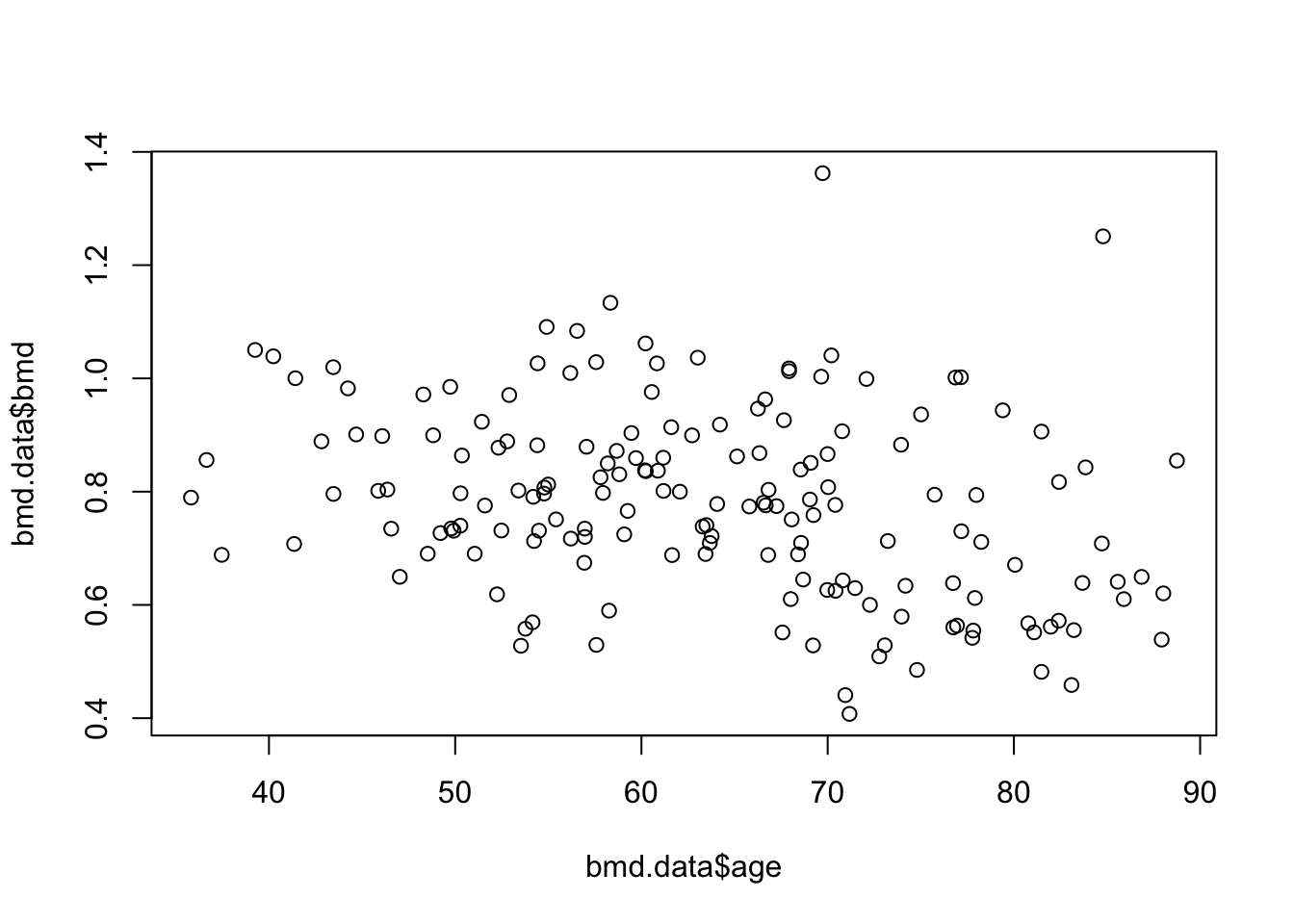
Task 3 - Scatter and boxplot

To see the relation between bone mineral density (BMD) and age we can produce a scatter plot:

# BMD 
plot(bmd.data$age,bmd.data$bmd)

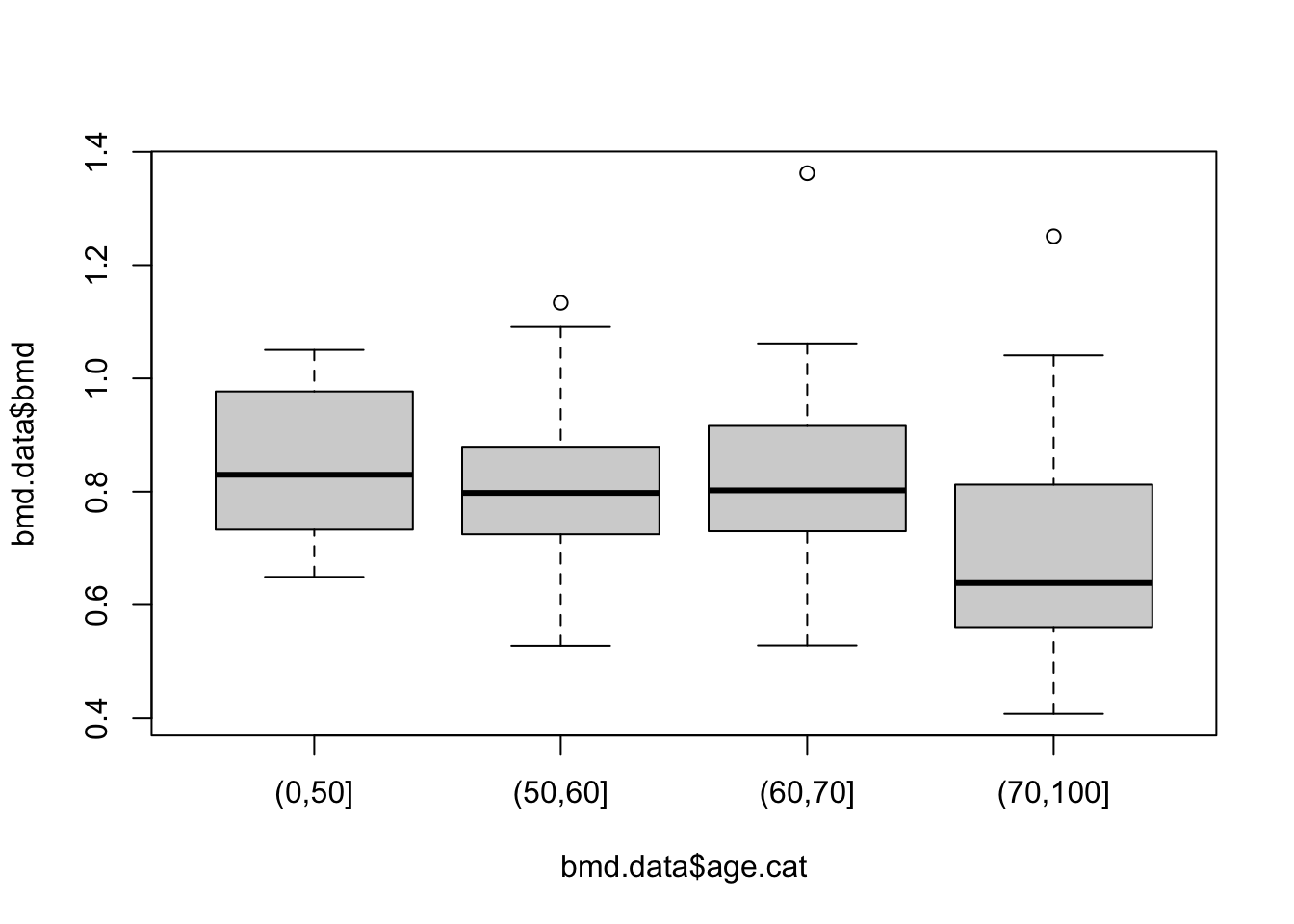
Or a boxplot between bone mineral density (BMD) by categories of age created in task 1

# BMD 
boxplot(bmd.data$bmd ~ bmd.data$age.cat)

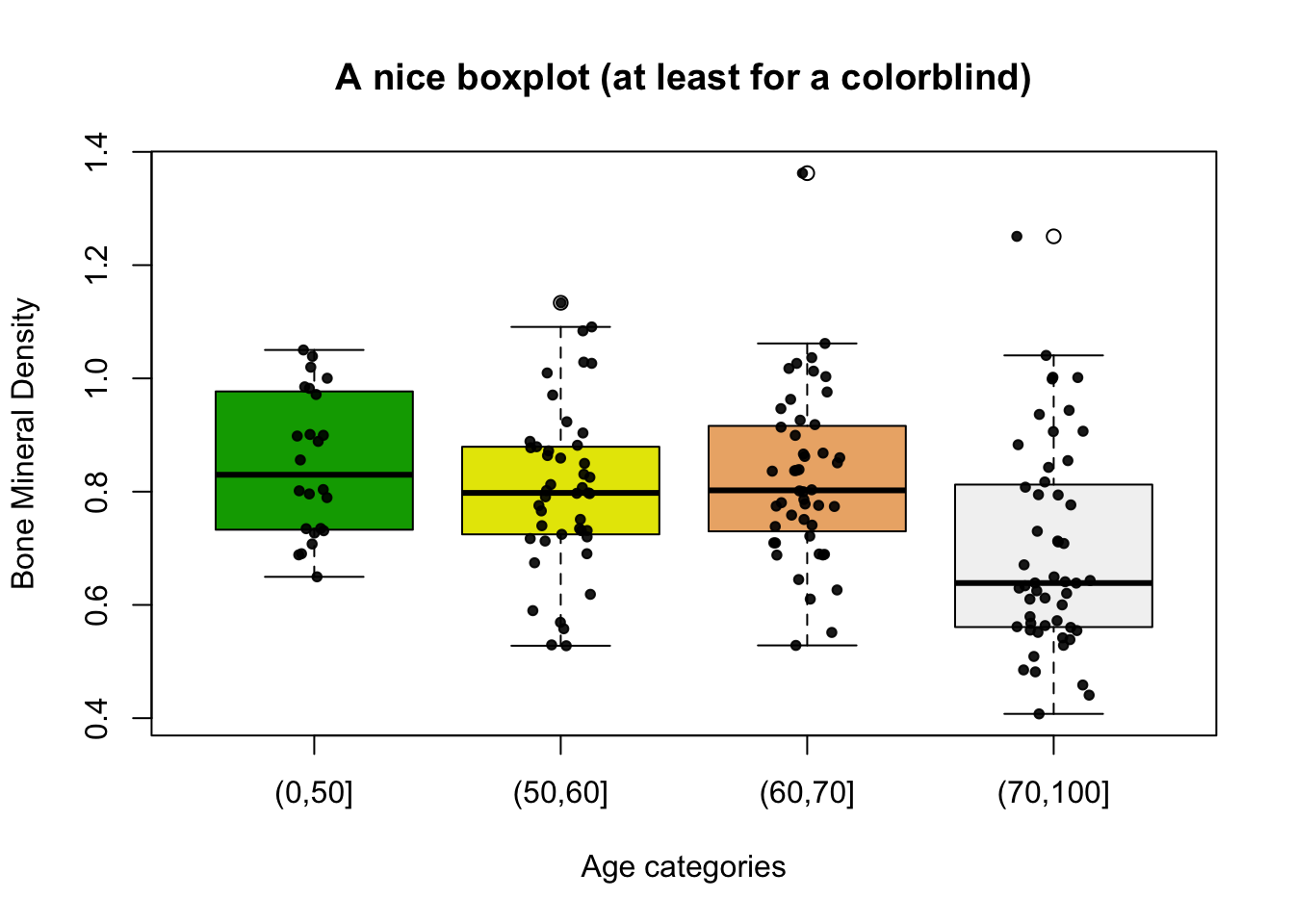
And with a bit more work:

# BMD 
boxplot(bmd.data$bmd ~ bmd.data$age.cat, 
        main = "A nice boxplot (at least for a colorblind)",
        xlab = "Age categories",
        ylab = "Bone Mineral Density",
        col  = terrain.colors(4) ) 

# Add data points
mylevels         <- levels(bmd.data$age.cat) 
levelProportions <- summary(bmd.data$age.cat)/nrow(bmd.data) 

for(i in 1:length(mylevels)){ 
  thislevel  <- mylevels[i] 
  thisvalues <- bmd.data[bmd.data$age.cat == thislevel, "bmd"] 
  #take the x-axis indices and add a jitter, 
  #proportional to the N in each level 
  myjitter   <- jitter(rep(i, length(thisvalues)),              
                       amount=levelProportions[i]/2) 
  points(myjitter, thisvalues, 
    pch=20, col=rgb(0,0,0,.9)) 
}

TRY IT YOURSELF:

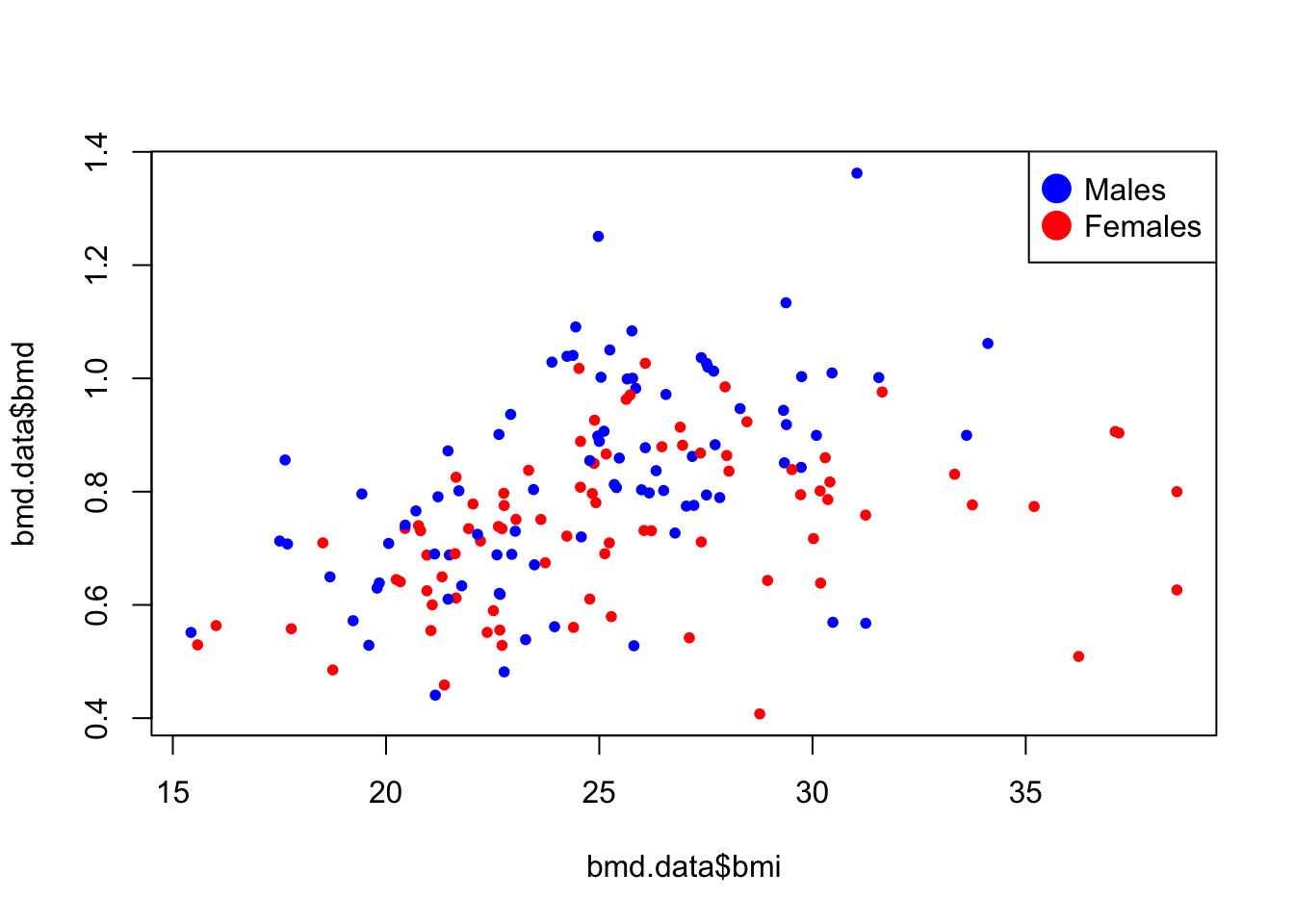
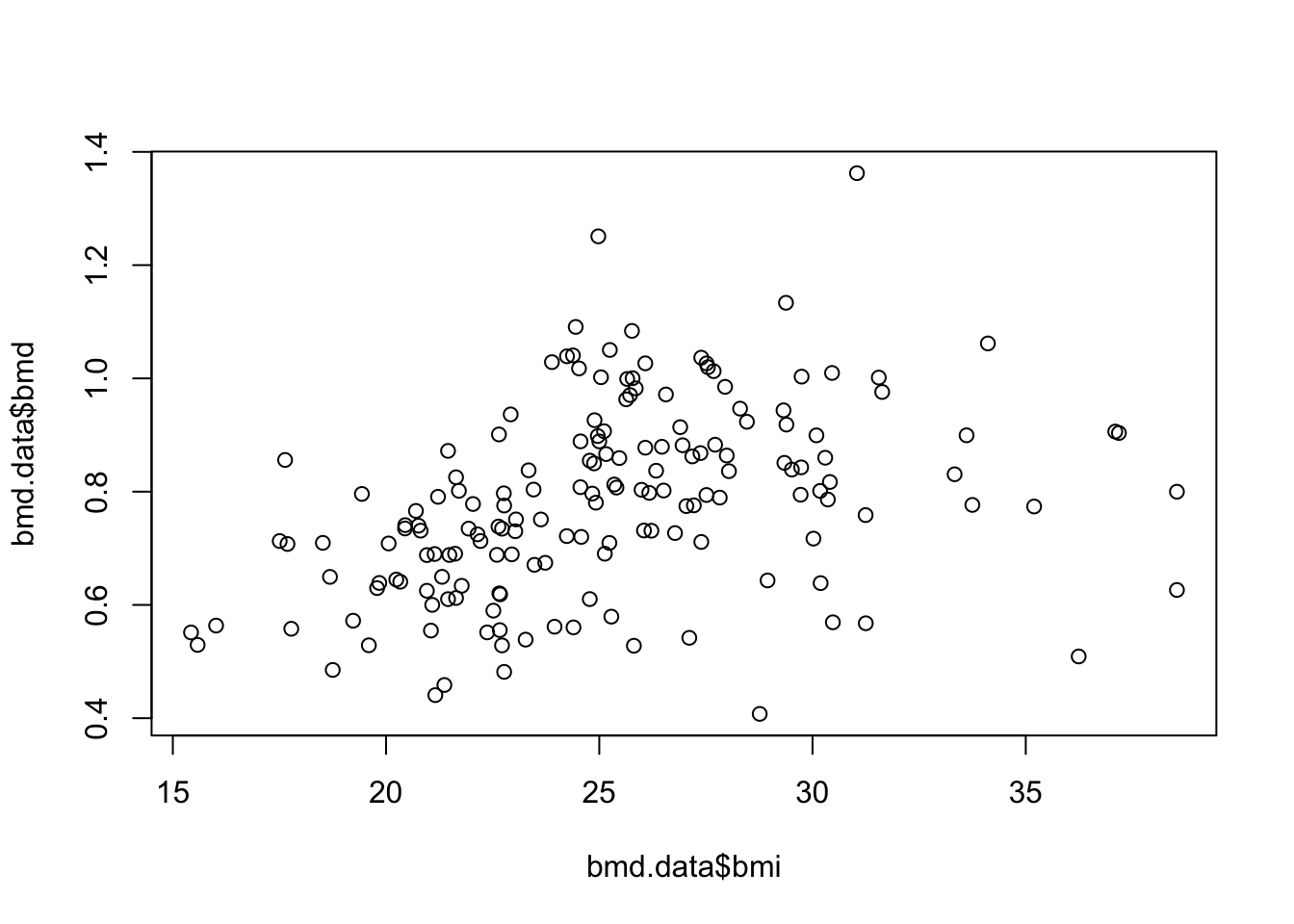
1. Plot a scatter for the relation of bmi and bmd.

See the solution code

plot(bmd.data$bmi,bmd.data$bmd)

2. Plot a scatter for the relation of bmi and bmd with the dots painted by the variable sex.

See the solution code

plot(bmd.data$bmi,bmd.data$bmd, 
     pch=20,
     col= ifelse(bmd.data$sex=="M",  #blue for males
                 "blue",             #red for females
                 "red")
     )

# Add legend
legend("topright",  
       legend=c("Males","Females"), 
       col=c("blue",  "red"), 
       pt.cex=3, pch=20 )