3 Random Forests
3.1 Introduction
We have seen that bagging pools together the results of different trees based on bootstrap samples. These trees will tend to be highly correlated. Random forests use a the same principle of bagged trees but with a difference in the construction of each tree. When growing a tree from one bootstrap sample, instead of evaluating all the predictors when deciding to split a node, Random forests only use a subset of the predictors randomly selected.
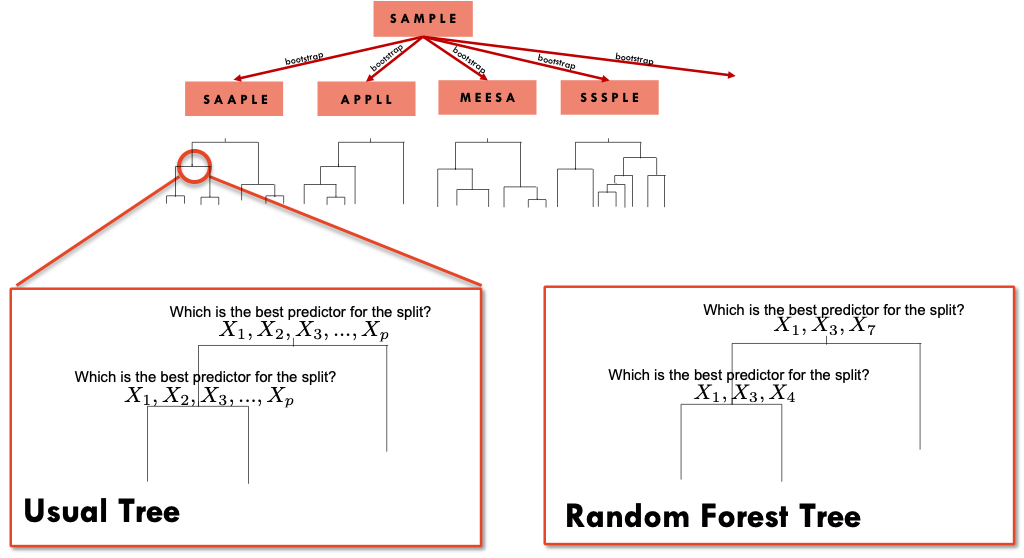
So, let’s say that we have \(p\) predictors and rather than evaluating all the predictors at each knot, we select, for example 3 random predictors at each knot. Notice that the next knot will evaluate 3 different random predictors ( unless, we get the same 3 by chance). This will uncorrelated the trees and produce better predictions.
We can choose not only the number of trees but also the number of variables that will be considered at each node. A recommended option is to select \(\sqrt(p)\) variables from the \(p\) predictors in a classification problem, and \(p/3\) in a regression problem.
3.2 Readings
Read the following chapters of An introduction to statistical learning:
- 8.2.2 Random Forests
3.3 Practice session
Task 1 - Build a Random Forest model
The SBI.csv dataset contains the information of more than 2300 children that attended the emergency services with fever and were tested for serious bacterial infection. The variable sbi has 4 categories: Not Applicable(no infection) / UTI / Pneum / Bact
Create a new variable sbi.bin that identifies if a child was diagnosed or not with serious bacterial infection.
## X id fever_hours age sex wcc prevAB sbi pct crp
## Min. : 1.0 Min. : 495 Min. : 0.00 Min. :0.010 Length:2348 Min. : 0.2368 Length:2348 Length:2348 Min. : 0.00865 Min. : 0.00
## 1st Qu.: 587.8 1st Qu.:133039 1st Qu.: 24.00 1st Qu.:0.760 Class :character 1st Qu.: 7.9000 Class :character Class :character 1st Qu.: 0.16000 1st Qu.: 11.83
## Median :1174.5 Median :160016 Median : 48.00 Median :1.525 Mode :character Median :11.6000 Mode :character Mode :character Median : 0.76000 Median : 30.97
## Mean :1174.5 Mean :153698 Mean : 80.06 Mean :1.836 Mean :12.6431 Mean : 3.74354 Mean : 48.41
## 3rd Qu.:1761.2 3rd Qu.:196030 3rd Qu.: 78.00 3rd Qu.:2.752 3rd Qu.:16.1000 3rd Qu.: 4.61995 3rd Qu.: 66.20
## Max. :2348.0 Max. :229986 Max. :3360.00 Max. :4.990 Max. :58.7000 Max. :156.47000 Max. :429.90# Create a binary variable based on "sbi"
sbi.data$sbi.bin <- as.factor(ifelse(sbi.data$sbi == "NotApplicable", "NOSBI", "SBI"))
table(sbi.data$sbi, sbi.data$sbi.bin)##
## NOSBI SBI
## Bact 0 34
## NotApplicable 1752 0
## Pneu 0 251
## UTI 0 311Now, let’s using a Random Forest to predict if a child has serious bacterial infection with the predictors fever_hours, wcc, age, prevAB, pct, and crp.
However, we will leave 200 observations out to test the model. We will
use the randomForest() function from the randomForest package and fit
100 trees with 2 predictors at each node (\(\sqrt(7)=2.6\))
library(caret)
library(randomForest) #includes the randomForest function
library(rpart)
library(psych) # for the kappa statistics
set.seed(1999)
rf.sbi <- randomForest(sbi.bin ~ fever_hours+age+sex+wcc+prevAB+pct+crp,
data = sbi.data[-c(500:700),], #not using rows 500 to 700
ntree=100, mtry=2)We will also fit one single tree to use as a comparison.
sbi.tree <- rpart(sbi.bin ~ fever_hours+age+sex+wcc+prevAB+pct+crp,
data = sbi.data[-c(500:700),], method="class",
control = rpart.control(cp=.001))
printcp(sbi.tree)##
## Classification tree:
## rpart(formula = sbi.bin ~ fever_hours + age + sex + wcc + prevAB +
## pct + crp, data = sbi.data[-c(500:700), ], method = "class",
## control = rpart.control(cp = 0.001))
##
## Variables actually used in tree construction:
## [1] age crp fever_hours pct prevAB sex wcc
##
## Root node error: 499/2147 = 0.23242
##
## n= 2147
##
## CP nsplit rel error xerror xstd
## 1 0.021042 0 1.00000 1.0000 0.039220
## 2 0.018036 2 0.95792 1.0040 0.039275
## 3 0.015030 3 0.93988 1.0100 0.039357
## 4 0.010020 5 0.90982 1.0020 0.039248
## 5 0.008016 7 0.88978 1.0100 0.039357
## 6 0.007014 10 0.86573 1.0120 0.039384
## 7 0.006012 14 0.83166 1.0060 0.039302
## 8 0.004509 17 0.81363 1.0140 0.039411
## 9 0.004008 21 0.79559 1.0261 0.039571
## 10 0.003340 22 0.79158 1.0220 0.039518
## 11 0.003006 27 0.77355 1.0261 0.039571
## 12 0.002672 31 0.76152 1.0301 0.039624
## 13 0.002004 39 0.73747 1.0501 0.039885
## 14 0.001002 54 0.70741 1.1303 0.040866
## 15 0.001000 56 0.70541 1.1703 0.041321We can now compute the confusion matrix for both approaches, using the 200 cases left out from the model fitting.
sbi.test.data <- sbi.data[c(500:700),]
#confusion matrix for 1 tree
table(sbi.test.data$sbi.bin,
predict(sbi.tree, sbi.test.data, type="class"))##
## NOSBI SBI
## NOSBI 94 10
## SBI 88 9## Call: cohen.kappa1(x = x, w = w, n.obs = n.obs, alpha = alpha, levels = levels)
##
## Cohen Kappa and Weighted Kappa correlation coefficients and confidence boundaries
## lower estimate upper
## unweighted kappa -0.087 -0.0035 0.08
## weighted kappa -0.087 -0.0035 0.08
##
## Number of subjects = 201##
## NOSBI SBI
## NOSBI 98 6
## SBI 84 13## Call: cohen.kappa1(x = x, w = w, n.obs = n.obs, alpha = alpha, levels = levels)
##
## Cohen Kappa and Weighted Kappa correlation coefficients and confidence boundaries
## lower estimate upper
## unweighted kappa -0.0054 0.078 0.16
## weighted kappa -0.0054 0.078 0.16
##
## Number of subjects = 201The random forest has a better prediction ability.
TRY IT YOURSELF:
- Use the
caretpackage to fit the model above. You can use the entire dataset and compute the cross-validated AUC-ROC and confusion matrix
See the solution code
set.seed(1777)
library(caret)
trctrl <- trainControl(method = "repeatedcv",
number = 10,
repeats = 5,
classProbs = TRUE,
summaryFunction = twoClassSummary)
sbi.rf <- train(sbi.bin ~ fever_hours+age+sex+wcc+prevAB+pct+crp,
data = sbi.data,
method = "rf",
trControl = trctrl,
ntree = 100,
tuneGrid = expand.grid(mtry = sqrt(7)),
metric="ROC")
sbi.rf
confusionMatrix(sbi.rf)
Task 2 - Compute the variables importance
Let’s compute the variable importance based on the rf.sbi random forest model.
pred.imp <- varImp(rf.sbi)
pred.imp
#You can also plot the results
barplot(pred.imp$Overall,
names.arg = row.names(pred.imp))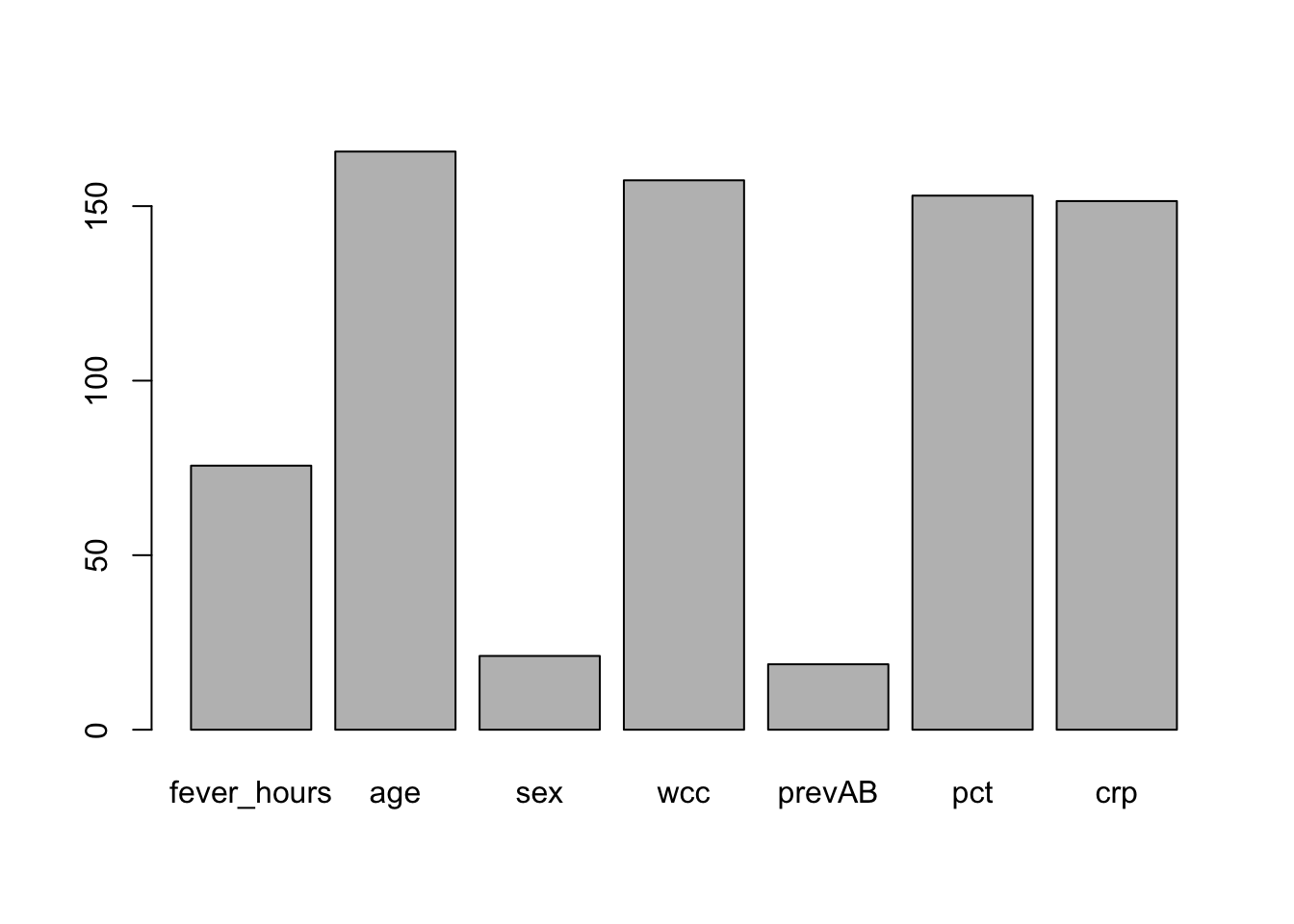
#If you use the caret package
#to fit the model, you can use the vip() function
#from the vip package to creat the plot
library(vip)
vip(sbi.rf) #notice that sbi.rf was created in caret above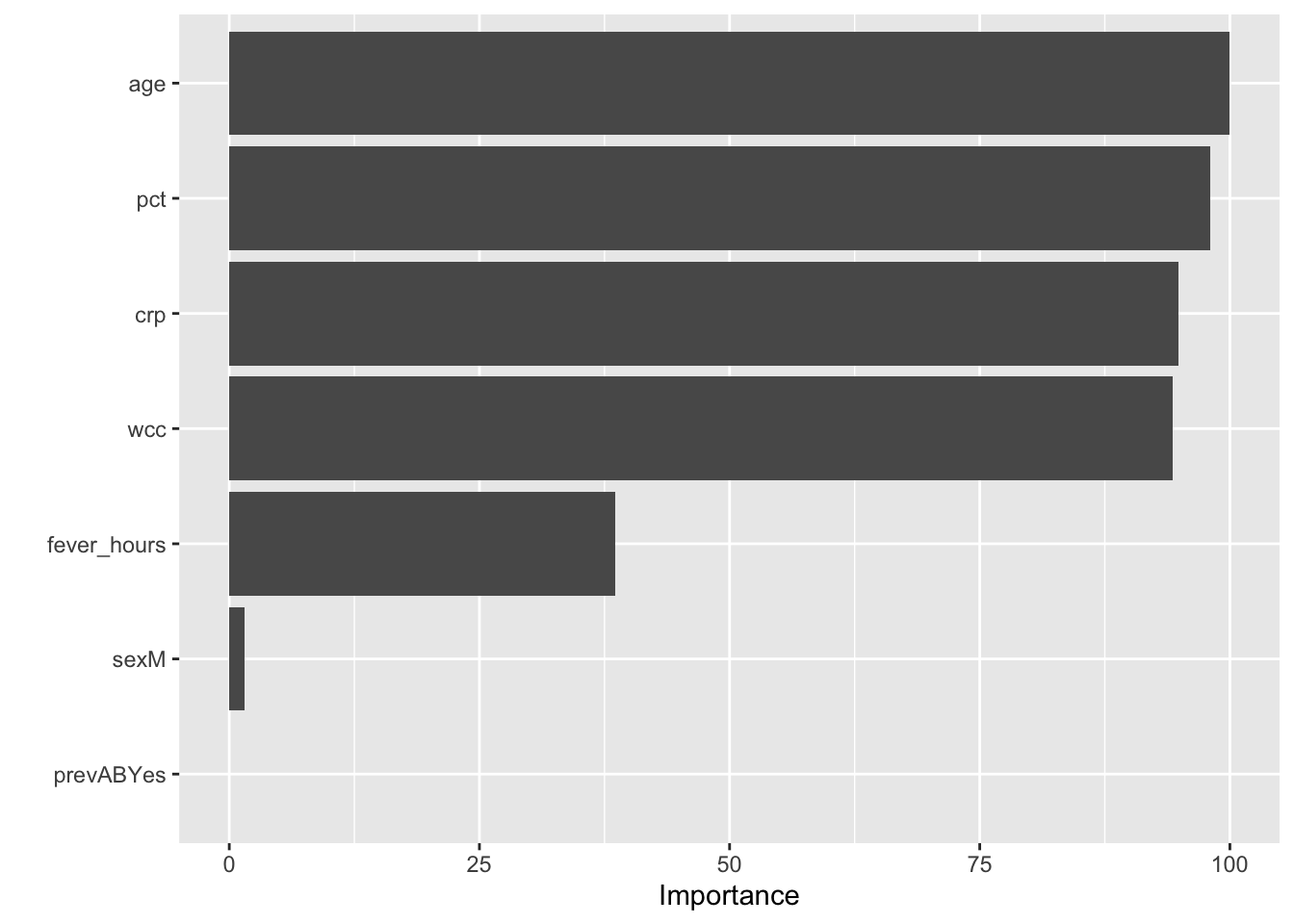
3.4 Exercises
Solve the following exercises:
- The dataset SA_heart.csv contains on coronary heart disease status (variable chd) and several risk factors including the cumulative tobacco consumption tobacco, systolic sbp, and age
Build a predictive model using a random forest with 100 trees to classify chd using tobacco,sbp and age
Find the cross-validated AUC ROC and confusion matrix for the model above and compare them with ones obtained from logistic regression and bagging.
Which is the most important predictor?
What is the predicted probability of coronary heart disease for someone with no tobacco consumption, sbp=132 and 45 years old?
- The dataset fev.csv contains the measurements of forced expiratory volume (FEV) tests, evaluating the pulmonary capacity in 654 children and young adults.
Fit a model based on random forest with 200 tree to predict fev using age, height and sex.
Plot the variables importance.
Compare the MSE of the model above with a GAM model for fev with sex and smoothing splines for height and age.