2 Deep Dive into Linear Algebra
2.1 Definition of Vector Space
Definition: A vector space consists of a set V along with 2 operations “+” (addition) and “*” (scalar multiplication) subject to 10 properties
Example: $L = $ Show L forms a vector under the operations vector addition and vector scalar multiplication.
(i) let \(\vec{a}, \vec{b} \epsilon L\)
\[\therefore \vec{a} = \begin{bmatrix} x_{1} \\ y_{1} \end{bmatrix} = \begin{bmatrix} x_{1} \\ 5y_{1} \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}x_{1} \]
\[\vec{b} = \begin{bmatrix} x_{2} \\ y_{2} \end{bmatrix} = \begin{bmatrix} x_{2} \\ 5y_{2} \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}x_{2}\]
\[\Rightarrow \vec{a} + \vec{b} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}x_{1} + \begin{bmatrix} 1 \\ 5 \end{bmatrix}x_{2} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}(x_{1}+x_{2}) \epsilon L\]
(ii) commutative: \[\vec{a}+\vec{b} = \vec{b}+\vec{a}\]
(iii) let \(\vec{c} \epsilon L\) \[\therefore(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})\] by associativity of vector (+)
(iv) zero vector: let \(x=y=0\) \[\therefore \begin{bmatrix} 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 5 * 0 \end{bmatrix}\]
(v) additive inverse: let \[\vec{d} = \begin{bmatrix} -x_{1} \\ -5x_{1} \end{bmatrix} \epsilon L\]
\[\therefore \vec{a} + \vec{d} = \begin{bmatrix} x_{1} \\ 5x_{1} \end{bmatrix} + \begin{bmatrix} -x_{1} \\ -5x_{1} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\]
\[\therefore\] the additive inverse of \[\vec{a}\] is in L
(vi) let \(c \epsilon \mathbb{R}\); \[c \vec{a} = c\begin{bmatrix} x_{1} \\ 5x_{1} \end{bmatrix} = cx_{1}\begin{bmatrix} 1 \\ 5 \end{bmatrix} \epsilon L\]
\[\therefore\] closed under scalar multiplication
(vii) \[(c_{1}+c_{2})\vec{a} = c_{1}\vec{a} + c_{2}\vec{a}\] by distributive property of scalar multiplication
(viii) \[c_{1}(\vec{a}+\vec{b}) = c_{1}\vec{a} + c_{1}\vec{b}\] by distributive property of vector (+)
(ix) \[(c_{1}c_{2})\vec{a} = c_{1}(c_{2}\vec{a})\] by associativity of scalar multiplication
(x) \[1\vec{a} = \vec{a}\]
Extend to \(\mathbb{R^{n}}\)
I. \(\mathbb{R^{2}}\) (entire space)
II. Any line through origin
III. \(\vec{0}\) (trivial space)
Other kinds of vector spaces:
Example: let \(P_{2} = \begin{Bmatrix}a_{0}+a_{1}x+a_{2}x^{2} | a_{0},a_{1},a_{2} \epsilon \mathbb{R^{2}}\end{Bmatrix}\) Show \(P_{2}\) is a vector space under the operations for addition and multiplication by a constant.
All axioms are easy to check. I’ll show a few.
Closure under addition:
let \(f(x), g(x) \epsilon P_{2} \therefore\) \[f = a_{0}+a_{1}x+a_{2}x^{2}\]
\[g = b_{0}+b_{1}x+b_{2}x^{2}\]
\[\Rightarrow f+g= (a_{0}+b_{0})+(a_{1}+b_{1})x+ (a_{2}+b_{2})x^{2} \epsilon P_{2}\]
therefore closed under addition
Closure under scalar multiplication:
let \(c \epsilon \mathbb{R}\) \[\Rightarrow cf = c(a_{0}+a_{1}x+a_{2}x^{2})\]
\[= ca_{0}+ca_{1}x+ca_{2}x^{2} \epsilon P_{2}\] therefore closed under scalar multiplication
Zero element:
let \(a_{0}=a_{1}=a_{2}=0 \therefore h(x)=0 \epsilon P_{2}\) and \(0 + f(x) = f(x)\)
Subspaces
General polynomial space \[P_{n}=\begin{Bmatrix}a_{0}+a_{1}x+a_{n}x^{n} | n \epsilon \mathbb{N}, a \epsilon \mathbb{R^{2}}\end{Bmatrix}\]
\(P_{k}\) is a subspace of \(P_{n}\) for \(0 \leq k \leq n\)
Example: let \(f(x) = 3x^{2}+2x+1\)
\(f(x) \epsilon P_{n}\) for \(n \geq 2\), \(f(x)\) does not span \(P_{1}\)
Calculus Operations:
Example: \(V=\begin{Bmatrix}y^{'} + y | y^{'} + y = 0\end{Bmatrix}\) homogeneous ODE
Closure under addition: let \(f,g \epsilon V\)
\[\therefore f^{'}+f=0, g^{'}+g=0\] by definition
\[\frac{d}{dx}[f+g]+f+g\]
\[=\frac{df}{dx} + \frac{dg}{dx} + f + g\]
\[=(\frac{df}{dx} + f) + (\frac{dg}{dx} + g)\]
\[= 0 + 0\]
\[ = 0 \therefore f+g \epsilon V\]
Closure under scalar multiplication: let \(c \epsilon \mathbb{R}\)
\[\frac{d}{dx}[cf] + cf\]
\[=c\frac{df}{dx} + cf\]
\[=c(\frac{df}{dx} + f)\]
\[=c * 0\]
\[=0 \therefore cf \epsilon V\]
Zero element: let \(h=0\)
\[\therefore \frac{dh}{dx} + h = 0+0=0 \therefore \vec{0} \epsilon V\]
Yes, this forms a vector space
Examples of Vector Space Rules:
Closure under Addition:
\[ let\ A, B \in V \therefore A= \left[ \begin{array}{cc} a_1 & 0 \\ 0 & a_2 \end{array} \right], \ \ B= \left[ \begin{array}{cc} b_1 & 0 \\ 0 & b_2 \end{array} \right] \]
\[ \Rightarrow A + B = \left[ \begin{array}{cc} a_1+b_1 & 0+0 \\ 0+0 & a_2+b_2 \end{array} \right] = \left[ \begin{array}{cc} a_1+b_1 & 0 \\ 0 & a_2+b_2 \end{array} \right] \in V \]
Closure under Scalar Multiplication:
\[ let\ c \in \mathbb{R} \therefore cA= c\left[ \begin{array}{cc} a_1 & 0 \\ 0 & a_2 \end{array} \right] = \left[ \begin{array}{cc} ca_1 & c\times0 \\ c\times0 & ca_2 \end{array} \right] = \left[ \begin{array}{cc} ca_1 & 0 \\ 0 & ca_2 \end{array} \right] \in V \]
Zero Element:
\[ let\ A=B=0\therefore \left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right] \in V \]
Example: V=set of singular matrices. Is it a vector space? NO
\[ let\ A= \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right],\ B= \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right] \]
\[A,B\in V\ by\ def^{(n)};\ but, A+B=\left[\begin{array}{cc}1 & 0 \\0 & 1\end{array}\right] \notin V\]
therefore not closed, therefore not a vector space
Complex Numbers
Example: \(V=\Bigg\{\left[\begin{array}{cc}1 & 0 \\0 & 1\end{array}\right]\Bigg|\ a,b\in \mathbb{C},\ a+b=0\Bigg\}\)
Is this a Vector Space? YES
Closure under Addition:
\[let\ A, B \in V \therefore A= \left[\begin{array}{cc}0 & a_1 \\a_2 & 0\end{array}\right], \ \ B= \left[\begin{array}{cc}0 & b_1 \\b_2 & 0\end{array}\right]\]
\[a_1 + a_2=0,\ \ b_1 + b_2=0,\ \ \therefore \ a_1 + a_2 + b_1 + b_2=0\]
\[\Rightarrow A + B = \left[\begin{array}{cc}0+0 & a_1+b_1 \\a_2+b_2 & 0+0\end{array}\right] = \left[\begin{array}{cc}0 & a_1+b_1 \\a_2+b_2 & 0\end{array}\right]\in V\]
Closure under Scalar Multiplication:
\[let\ c \in \mathbb{C} \therefore c=c_1 + c_2i\ where\ i=\sqrt{-1}\]
\[\therefore cA= (c_1+c_2i)\left[\begin{array}{cc}a_1 & 0 \\0 & a_2\end{array}\right]\]
\[=c_1\left[\begin{array}{cc}0 & a_1 \\a_2 & 0\end{array}\right] +c_2i\left[\begin{array}{cc}0 & a_1 \\a_2 & 0\end{array}\right]\]
\[=\left[\begin{array}{cc}0 & c_1a_1 \\c_1a_2 & 0\end{array}\right] +\left[\begin{array}{cc}0 & c_2ia_1 \\c_2ia_2 & 0\end{array}\right]\]
\[=\left[\begin{array}{cc}0 & ca_1 \\ca_2 & 0\end{array}\right]\in V\]
Zero Element: \[ let\ A=B=0\therefore \left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right] \in V \]
Subspaces & Spanning Sets
Subspaces of \(\mathbb{R}^{3}\):
- point(\(\overrightarrow{0}\))
- line through origin
- plane through origin
- \(\mathbb{R}^{3}\)
Subspace:
A subspace W of a vector space V is another vector space contained within V; W must be closed under linear combinations
Span:
Let S = \(\{\overrightarrow{s_1},\overrightarrow{s_2},...,\overrightarrow{s_n}\}\); the span of S, denoted span\(\{\)S\(\}\) is the set of all linear combinations.
\(\therefore\) span\(\{\)S\(\}\) = \(\{c_1\overrightarrow{s_1}+...+c_n\overrightarrow{s_n}|c_i\in \mathbb{R},\overrightarrow{s_i}\in S\}\)
Example: \(let\ \hat{i}=\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\ \hat{j}=\left[\begin{array}{c}0 \\1 \\0\end{array}\right],S=\{\hat{i},\hat{j}\}\)
\(\therefore span(S)=\{c_1\hat{i}+c_2\hat{j}|c_i,c_2\in \mathbb{R}\}\)
\(\Rightarrow xy-plane, z=0\)
Example: span\(\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\left[\begin{array}{c}0 \\1 \\0\end{array}\right],\left[\begin{array}{c}0 \\0 \\1\end{array}\right]\Bigg\}\)=\(\mathbb{R}^{3}\)
Example: span\(\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\left[\begin{array}{c}2 \\0 \\0\end{array}\right],\left[\begin{array}{c}3 \\0 \\0\end{array}\right],\left[\begin{array}{c}4 \\0 \\0\end{array}\right]\Bigg\}\)=\(\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right]c\ \Bigg|\ c\in \mathbb{R}\Bigg\}\) = x-axis (line)
Example: span\(\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\left[\begin{array}{c}0 \\0 \\1\end{array}\right],\left[\begin{array}{c}5 \\0 \\5\end{array}\right]\Bigg\}\)=\(\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right]c_1+\left[\begin{array}{c}0 \\0 \\1\end{array}\right]c_2+\left[\begin{array}{c}5 \\0 \\5\end{array}\right]c_3\ \Bigg|\ c_1, c_2, c_3\in \mathbb{R}\Bigg\}\)
\(5\left[\begin{array}{c}1 \\0 \\0\end{array}\right]+5\left[\begin{array}{c}0 \\0 \\1\end{array}\right]=\left[\begin{array}{c}5 \\0 \\5\end{array}\right]\), \(\therefore \Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right]c_1+\left[\begin{array}{c}0 \\0 \\1\end{array}\right]c_2\ \Bigg|\ c_1, c_2\in \mathbb{R}\Bigg\}\) = xz-plane
Solutions to Assorted Problems:
1.17(p. 92-93)
- \(f(x)=0\)
- \(\left[\begin{array}{cccc}0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\end{array}\right]\)
1.22(p. 93)
- let \(\overrightarrow{a}\), \(\overrightarrow{b} \in\) S
\(\therefore \overrightarrow{a}=\left[\begin{array}{c}x_1 \\y_1 \\z_1\end{array}\right]\) so that \(x_1+y_1+z_1=1\) \(\overrightarrow{b}=\left[\begin{array}{c}x_2 \\y_2 \\z_2\end{array}\right]\) so that \(x_2+y_2+z_2=1\\\)But, \(\overrightarrow{a}+\overrightarrow{b}=\left[\begin{array}{c}x_1+x_2 \\y_1+y_2 \\z_1+z_2\end{array}\right]\) and\(\\(x_1+x_2)+(y_1+y_2)+(z_1+z_2)=(x_1+y_1+z_1)+(x_2+y_2+z_2)=1+1=2\not= 1\), \(\therefore \overrightarrow{a}+\overrightarrow{b}\notin\) S, \(\therefore\) Not Closed, \(\therefore\) Not Vector Space
1.23
S\(=\{a+bi|a,b\in \mathbb{R}\}\)
2.2 Linear Independence, Basis, Dimension
Linear Independence
Definition: A set of vectors \(\{ \vec{v_1}, ... ,\vec{v_n} \}\) is linearly independent if none of its elements is a linear combinations of the other elements in the set. Otherwise, the set is linearly dependent
Example 1: \[{ \Biggl\{ \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}}, {\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}}, {\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}}, {\begin{bmatrix} -2 \\ 3 \\ 5 \end{bmatrix} \Biggl\} }\]
Note: \[{ -2 \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}} + 3 {\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}} + 5 {\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}} = {\begin{bmatrix} -2 \\ 3 \\ 5 \end{bmatrix} }\]
\(\therefore \vec{v_4}\) is a linear combination of \(\vec{v_1},\vec{v_2},\vec{v_3}\) , and we say S is linearly dependent
Example 2: \[{ \biggl\{ \begin{bmatrix} 1 \\ 0 \end{bmatrix}}, {\begin{bmatrix} 0 \\ 3\end{bmatrix} \biggl\} }\]
\(\because c_1\vec{v_1} \neq \vec{v_2}\) for any \(c \in R\), the set is linearly independent
Theorem: \(\{ \vec{v_1}, ... ,\vec{v_n} \}\) is linearly independent if and only if \(c_1\vec{v_1} + ... + c_n\vec{v_n} = \vec{0}\) only when \(c_1 = c_2 = ... = c_n = 0\)
- This provides a way to test for linear independence
Example 3: Use the previous theorem to show \({ \biggl\{ \begin{bmatrix} 40 \\ 15 \end{bmatrix}}, {\begin{bmatrix} -50 \\ 25 \end{bmatrix} \biggl\} }\) are linearly independent.
\[ c_1\begin{bmatrix} 40 \\ 15 \end{bmatrix} + c_2\begin{bmatrix} -50 \\ 25 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\]
\(\therefore\) I. \(40c_1 - 50c_2 = 0\)
- \(15c_1 + 25c_2 = 0\) \[c_1 = c_2 = 0\]
Basis
Example 1: \[{ \biggl\{ \begin{bmatrix} 2 \\ 3 \end{bmatrix}}, {\begin{bmatrix} -1 \\ 2\end{bmatrix}, \begin{bmatrix} 0 \\ 5\end{bmatrix} \biggl\} }\]
Since this set has 3 vectors in \(\mathbb{R^{2}}\), the set is linearly dependent.
Example 2: \[{ \{ \begin{bmatrix} 2 \\ 3 \\ 7 \end{bmatrix}}, {\begin{bmatrix} -1 \\ 2 \\10 \end{bmatrix}, \begin{bmatrix} 0 \\ 5 \\ -3\end{bmatrix} \} }\]
Since this set has 3 vectors in \(\mathbb{R^{3}}\),need to test for linear independence.
\[{ c_1 \begin{bmatrix} 2 \\ 3 \\ 7 \end{bmatrix} + c_2 \begin{bmatrix} -1 \\ 2 \\10 \end{bmatrix} + c_3 \begin{bmatrix} 0 \\ 5 \\ -3\end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}}\]
\[ \left[ \begin{array}{rrr|r} 2 & -1 & 0 & 0 \\ 3 & 2 & 5 & 0 \\ 7 & 10 & -3 & 0 \end{array} \right] \longrightarrow \left[ \begin{array}{rrr|r} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right] \]
This matrix is in RREF form, \(\therefore\) the only solution is \(c_1=c_2=c_3=0\), \(\therefore\) the vectors are linearly independent.
Example 3: \[{ \{ 8+3x+3x^2, x+2x^2,2+2x+2x^2,8-2x+5^2 \} }\] Is this set a basis of \(P_{2}\)
\[\begin{bmatrix} 8 & 0 & 2 & 8 \\ 3 & 1 & 2 &-2 \\ 3& 2 & 2 & 5 \end{bmatrix}\]
\(\therefore\) No, since any basis of \(P_2\) requires exactly 3 functions, and we have 4.
Dimension
Defintion: The minimum number of elements required to span a given vector space V.
- Notation: \(dim(V)\) “dimension of V
Let \(V\) be a vector space. \(V\) is called finite-dimensional if \(dim(V) = n < \infty\)
Examples:
\[dim(\mathbb R^{6}) = 6\]
\[dim(M_{2\times2}) = 4\]
\[dim(P_2) = 3\]
Let \(V = {\begin{bmatrix} a & c \\ b & d \end{bmatrix}| a,b,c,d \in \mathbb C }\)
Assume entries are complex-valued and scalars are real-valued, \(\therefore dim(V) = 8\)
Theorem: In any finite dimensional vector space, any 2 bases have the same # of elements.
Note: Some vector spaces are infinite dimensional
Example: Let \(V\) be the set of all functions of 1 variable
\(\therefore V = \{ f(x) | x \in \mathbb R \}\) , \(\therefore dim(V) = \infty\)
Examples from III.2: 2.17 \(V = \Biggl\{ \begin{bmatrix} x \\ y \\ z \\w \end{bmatrix} \Biggl| \space x-w+z = 0 \Biggl\}\)
Basis: \(x + z = w\), \(\therefore x,z\) are free; y is also free since it is unrestricted
\[\therefore V = \Biggl\{ \begin{bmatrix} 1\\0\\0\\1\end{bmatrix}x+ \begin{bmatrix} 0\\1\\0\\0\end{bmatrix}y + \begin{bmatrix} 0\\0\\1\\1\end{bmatrix}z \space \Biggl| \space x,y,z \in \mathbb R \Biggl\} \longrightarrow V = span \Biggl\{ \begin{bmatrix} 1\\0\\0\\1\end{bmatrix}, \begin{bmatrix} 0\\1\\0\\0\end{bmatrix}, \begin{bmatrix} 0\\0\\1\\1\end{bmatrix} \Biggl\}\] Thus, \(\Biggl\{ \begin{bmatrix} 1\\0\\0\\1\end{bmatrix}, \begin{bmatrix} 0\\1\\0\\0\end{bmatrix}, \begin{bmatrix} 0\\0\\1\\1\end{bmatrix} \Biggl\}\) is a basis of V, which means that V is a 3D subspace of \(\mathbb R^4\), and \(dim(V) = 3\) as it has 3 elements in basis
Fundamental Subspaces
Let \(A\) be \(n\times m\). There are 4 associated vector spaces with A.
I. Column space: span of the columns of A
Row space: span of the rows of A
Null space (will learn in later topics)
Left Null Space (will learn in later topics)
Row space:
The row space of a matrix is the span of the rows in the matrix; the dimension of row space is called the row rank
- Notation: rowspace\((A)\)
Example: Let \(A = \begin{bmatrix} 2&3\\4&6 \end{bmatrix}\). What is the \(rowspace\)? \[rowspace(A) = \{ c_1\begin{bmatrix} 2&3 \end{bmatrix} + c_2 \begin{bmatrix} 4&6 \end{bmatrix}| \space c_1,c_2 \in \mathbb R \} = span\{\begin{bmatrix} 2&3 \end{bmatrix}, \begin{bmatrix} 4&6 \end{bmatrix} \}\] \[ = span\{\begin{bmatrix} 2&3 \end{bmatrix}\}, \space \because \space 2\begin{bmatrix} 2&3 \end{bmatrix} = \begin{bmatrix} 4&6 \end{bmatrix} \] \[ \because \space dim(rowspace(A)) = 1 \longrightarrow \space \therefore rank(A) = 1 \]
Column space:
The column space of a matrix is the span of the columns in the matrix; the dimension of column space is called the column rank
- Notation: colspace\((A)\)
Example: \[colspace(A) = \biggl\{ c_1\begin{bmatrix} 2\\4 \end{bmatrix} + c_2 \begin{bmatrix} 3\\6 \end{bmatrix}|c_1,c_2 \in \mathbb R \biggl\} = span \biggl\{\begin{bmatrix} 2\\4 \end{bmatrix}, \begin{bmatrix} 3\\6 \end{bmatrix} \biggl\}\]
\[= span \biggl\{\begin{bmatrix} 2\\4 \end{bmatrix} \biggl\}, \space \because \space \frac{3}{2} \begin{bmatrix} 2\\4 \end{bmatrix} = \begin{bmatrix} 3\\6 \end{bmatrix}\] \[\because \space dim(colspace(A)) = 1 \longrightarrow \space \therefore rank(A) = 1 \]
Theorem: In any \(n\times m\) matrix the row rank and column rank are equal.
- Comment - the rank of a matrix is its row rank or column rank
Example: \[B = \begin{bmatrix} 1&3&7\\2&4&12 \end{bmatrix} \space \therefore B^T = \begin{bmatrix} 1&2\\3&4\\7&12 \end{bmatrix} \]
- Comments:
- \((A^T)^T = A\)
- \((A^T)^T = A\)
- \(rowspace(A) = colspace(A^T)\)
- \(rowspace(A) = colspace(A^T)\)
Example: Let \(A = \begin{bmatrix} 1&3&7\\2&3&8\\0&1&2\\4&0&4\end{bmatrix}\). Determine a basis for \(colspace(A)\)
\[\therefore A^T = \begin{bmatrix} 1&2&0&4\\3&3&1&0\\7&8&2&4 \end{bmatrix}\underset{\overset{-7I +III}{\longrightarrow}}{\overset{-3I+II}{\longrightarrow}} \begin{bmatrix} 1&2&0&4\\0&-3&1&-12\\0&-6&2&-24 \end{bmatrix} \underset{-2II +III}{\longrightarrow} \begin{bmatrix} 1&2&0&4\\0&-3&1&-12\\0&0&0&0 \end{bmatrix} = RREF(A^T)\]
Theorem: Let A be \(n\times m\), \(RREF(A^T) = RREF(A)^T\)
Thus, \(RREF(A) = \begin{bmatrix} 1&0&0 \\2&-3&0\\0&1&0\\4&-12&0 \end{bmatrix}, \space \therefore basis(colspace(A)) = \Biggl\{ \begin{bmatrix} 1 \\2\\0\\4 \end{bmatrix}, \begin{bmatrix} 0 \\-3\\1\\-12 \end{bmatrix} \Biggl\}\)
Theorem(3.13): For any linear system with n unknowns, m equations, and matrix of coefficiencts A, then:
- rank(A) = r
- the vector space of solutions has dimensions \(n-r\)
are equivalent statements.
Corollary(3.14): Let A be \(n\times n\). Then:
- (i) rank(A) = n
- (ii) A is non-singular
- (iii) rows of A are linearly independent
- (iv) columns of A are linearly independent
- (v) associated linear system has 1 solution
are equivalent statements.
Solutions to Assorted Problems:
2.21(a): Let \(V = \{ f(x) = a_0+a_1x+a_2x^2+a_3x^3 | a_i \in \mathbb R, f(7) = 0 \}\)
\[f(7) = 0, \therefore a_0+7a_1+7^{2}a_2+7^{3}a_3 = 0 \longrightarrow a_0=-7a_1-7^{2}a_2-7^{3}a_3\]
\(\therefore\) there are 3 free variables, and \(dim(V)=3\)
2.21(d): \(V = \{ f(x) = a_0+a_1x+a_2x^2+a_3x^3 | a_i \in \mathbb R, f(7) = 0, f(5) = 0, f(3) = 0, f(1) = 0 \}\)
\[a_0+7a_1+7^{2}a_2+7^{3}a_3 = 0\]
\[a_0+5a_1+5^{2}a_2+5^{3}a_3 = 0\]
\[a_0+3a_1+3^{2}a_2+3^{3}a_3 = 0\]
\[a_0+1a_1+1a_2+1a_3 = 0\]
\(\therefore\) there are 0 free variables because of 4 pivots, \(\therefore dim(V)=0\)
2.22: \(V = span \{ cos^2\theta,sin^2\theta,cos2\theta,sin2\theta \}\) | \(dim(V) = ?\) \[cos^2\theta+sin^2\theta=1 \longrightarrow sin^2\theta=1-cos^2\theta\] \[cos2\theta = 2cos^2\theta-1\] \[sin2\theta = 2sin\theta cos\theta\] \[\therefore span\{ cos^2\theta,1-cos^2\theta, 2cos^2\theta-1, sin2\theta \}\] \(\therefore\) The basis of the span of the space can be written as \(\{ cos^2\theta,1, sin2\theta \}\), and \(dim(V)=3\)
More Examples - 1
\(span \{ 1,x,x^2 \} = P_2\) and \(\{1,x,x^2 \}\) is a basis of \(P_2\)
More Examples - 2
\[M_{2\times2} = \biggl\{ \begin{bmatrix} a&c\\b&d \end{bmatrix} \biggl| \space a,b,c,d \in \mathbb R \biggl\}\]
\(dim(M_{2\times2}) = 4\), since basis\((M_{2\times2}) = \biggl\{ \begin{bmatrix} 1&0\\0&0 \end{bmatrix},\begin{bmatrix} 0&1\\0&0 \end{bmatrix},\begin{bmatrix} 0&0\\1&0 \end{bmatrix},\begin{bmatrix} 0&0\\0&1 \end{bmatrix} \biggl\}\)
More Examples - 3 \[V = \biggl\{ \begin{bmatrix} a&c\\b&d \end{bmatrix} \biggl| \space a,b,c,d \in \mathbb C \biggl\}\] \(dim(V) = 4\), since basis\((V) = \biggl\{ \begin{bmatrix} 1&0\\0&0 \end{bmatrix},\begin{bmatrix} 0&1\\0&0 \end{bmatrix},\begin{bmatrix} 0&0\\1&0 \end{bmatrix},\begin{bmatrix} 0&0\\0&1 \end{bmatrix},\begin{bmatrix} i&0\\0&0 \end{bmatrix},\begin{bmatrix} 0&i\\0&0 \end{bmatrix},\begin{bmatrix} 0&0\\i&0 \end{bmatrix},\begin{bmatrix} 0&0\\0&i \end{bmatrix} \biggl\}\)
2.3 Orthogonal Matrices, Change of Basis
Orthogonal Vector
Definition: Two vectors \(\vec{x}\) and \(\vec{y}\) are orthogonal if \(\vec{x} \cdot \vec{y} = 0\) Note: This is equivalent to \(\vec{x}\) perpendicular to \(\vec{y}\)
For example: Let \(S = {\vec{v}_{1}, ...., \vec{v}_{n}}\) we say the set S is an orthogonal set is \(\vec{x}_{i} \cdot \vec{x}_{j} = 0, i \neq j\)
Example: \(S = {\hat{i}, \hat{j}, \hat{k}}\)
\(\hat{i} = \begin{bmatrix} 1\\ 0\\ 0 \\ \end{bmatrix}\) \(\hat{j} = \begin{bmatrix} 0\\ 1\\ 0 \\ \end{bmatrix}\) \(\hat{k} = \begin{bmatrix} 0\\ 0\\ 1 \\ \end{bmatrix}\)
\(\hat{i} \cdot \hat{j} = 0\) \(\hat{j} \cdot \hat{k} = 0\) \(\hat{i} \cdot \hat{k} = 0\)
So Set S is an orthogonal set of vectors
Orthogonal Vector
Definition: An orthogonal set of vectors that each vector is a unit vector.
Example: \(\hat{u}\) = \(\frac{1}{5} \begin{bmatrix} 3\\ 4\\ \end{bmatrix}\) = \(\begin{bmatrix} \frac{3}{5}\\ \frac{4}{5}\\ \end{bmatrix}\) \(||\hat{u}|| = \sqrt{\frac{3}{5}^{2} + \frac{4}{5}^{2}} = 1\)
Orthogonal Matrix
Let \(\hat{q}_{1}, ..., \hat{q}_{n}\) be an orthonormal set, if (i) \(\hat{q}_{i} \cdot \hat{q}_{j}, i \neq j\) (ii) \(||\hat{q}_{i}|| = 1\)
Then \(Q = \begin{bmatrix} \\\ \hat{q}_{1} && \hat{q}_{2} && \hat{q}_{3} .... \hat{q}_{n}\\\\\end{bmatrix}\) is an orthogonal matrix.
Example: \(\hat{u} = \begin{bmatrix} cos\theta && -sin\theta\\ sin\theta && cos\theta\\ \end{bmatrix}\), show Q is an orthogonal matrix:
\(\hat{q}_{1} \cdot \hat{q}_{2} = cos\theta(sin\theta) = sin\theta(cos\theta) = 0\) \(||\hat{q}_{1}|| \cdot ||\hat{q}_{2}|| = \sqrt{cos^{2}\theta + sin^{2}\theta} = 1\)
Orthonormal Basis
Theorem: Let S = {\(\hat{v}_{1}, ... , \hat{v}_{n}\)} is an orthonormal basis Then for each \(\hat{x} \epsilon V\), \(\hat{x} = (\hat{x} \cdot \hat{v}_{1}) \hat{v}_{1} + ... + (\hat{x} \cdot \hat{v}_{n}) \hat{v}_{n}\)
Example: If S = {\(\hat{v}_{1}, ... , \hat{v}_{n}\)}, \(\hat{v}_{1} = \begin{bmatrix} 0\\ 1\\0 \end{bmatrix}\), \(\hat{v}_{2} = \begin{bmatrix} -\frac{4}{5}\\ 0\\ \frac{3}{5} \end{bmatrix}\), \(\hat{v}_{3} = \begin{bmatrix} \frac{3}{5}\\ 0\\\frac{4}{5} \end{bmatrix}\)
Show that S is an orthogonal basis.
Steps:
1. Check if S is a basis
\[A = \begin{bmatrix} 0 & -\frac{4}{5} & \frac{3}{5} \\ 1 & 0 & 0 \\ 0 & \frac{3}{5} & \frac{4}{5} \\ \end{bmatrix}\rightarrow \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{bmatrix}\]
There are three pivots, so S is a basis
2. Check if it is an orthogonal matrix
\[\hat{v}_{1} \cdot \hat{v}_{2} = 0\]
\[\hat{v}_{1} \cdot \hat{v}_{3} = 0\]
\[\hat{v}_{2} \cdot \hat{v}_{3} = 0\]
It is an orthogonal set of matrix
3. Check if it is normal (magnitude = 1)
\[||\hat{v}_{1}|| = \sqrt{0^{2} + 1^{2} + 0^{2}} = 1\]
\[||\hat{v}_{2}|| = \sqrt{(-\frac{4}{5})^{2} + \frac{3}{5}^{2}} = 1\]
\[||\hat{v}_{3}|| = \sqrt{\frac{3}{5}^{2} + \frac{4}{5}^{2}} = 1\]
2.4 Projection and Change of Basis
How to construct orthonormal or orthonormal basis:
Projection:
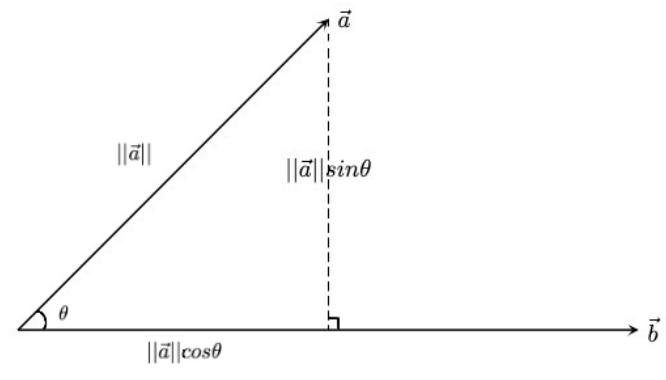
orthogonal projection of \(\overrightarrow{a}\) onto \(\overrightarrow{b}\) (\(proj_{\overrightarrow{b}}\overrightarrow{a}\))
Magnitude of projection vector (component of projection)
\(||proj_{\overrightarrow{b}}\overrightarrow{a}|| = ||\overrightarrow{a}||cos\theta\)
In addition, realize that \(\overrightarrow{a}\cdot\overrightarrow{b} = ||\overrightarrow{a}||||\overrightarrow{b}||cos\theta\)
\(\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||} = ||\overrightarrow{a}||cos\theta\)
\(||proj_{\overrightarrow{b}}\overrightarrow{a}|| = \frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||}\)
Projection vector (unit vector in direction of \(\overrightarrow{b}\) scaled by component)
\(proj_{\overrightarrow{b}}\overrightarrow{a} = (\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||}) \frac{\overrightarrow{b}}{||\overrightarrow{b}||} = (\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||^2})\overrightarrow{b}\)
Projection into Subspaces:
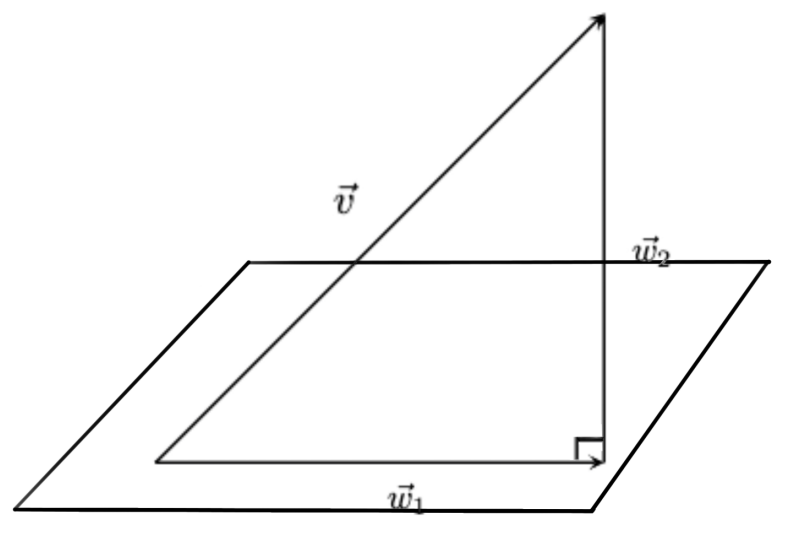
Let V be a vector space with subspace w, \(\overrightarrow{w}, \overrightarrow{v}\in \overrightarrow{v}\)
Theroem: If V is a vector space and W is a subspace of V then for each \(\overrightarrow{v} \in V\)
\(\overrightarrow{v} =\overrightarrow{w}_1 + \overrightarrow{w}_2\) where \(\overrightarrow{w}_1\in W\) and \(\overrightarrow{w}_2\perp W\)
How to determine \(\overrightarrow{w}_1\) and \(\overrightarrow{w}_2\)?
Theorem: Let W be a finite dimensional subspace of a vector space V. If {\(\overrightarrow{u}_1\),…, \(\overrightarrow{u}_n\)} is an orthonormal basis of W and \(\overrightarrow{x} \in V\) then \(proj_{W}\overrightarrow{x} = \frac{\overrightarrow{x} \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1 + ...+ \frac{\overrightarrow{x} \cdot \overrightarrow{v}_n}{||\overrightarrow{v}_n||^2}\overrightarrow{v}_n\)
Example:
Let \(V = \mathbb{R}^3\) and \(W =\) span{\(\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}\), \(\begin{bmatrix} -\frac{4}{5} \\ 0 \\ \frac{3}{5} \\ \end{bmatrix}\)}. Compute \(proj_{W}\overrightarrow{x}\) where \(\overrightarrow{x} = <1,1,1>\)
\(\therefore proj_{W}\overrightarrow{x} = (<1,1,1>\cdot <0,1,0>) \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} + (<1,1,1> \cdot <-\frac{4}{5},0,\frac{3}{5}>)\begin{bmatrix} -\frac4{5} \\ 0 \\ \frac{3}{5} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} + \begin{bmatrix} \frac{4}{25} \\ 0 \\ -\frac{3}{25} \\ \end{bmatrix} = \begin{bmatrix} \frac{4}{25} \\ 1 \\ -\frac{3}{25} \\ \end{bmatrix}\)
\(proj_{W}\overrightarrow{x} = \overrightarrow{w}_1\)
\(\therefore \overrightarrow{w}_2 = \overrightarrow{x} - proj_{W}\overrightarrow{x} = \begin{bmatrix} \frac{21}{25} \\ 0 \\ \frac{28}{25} \\ \end{bmatrix}\)
Key Result
Theorem: Every finite dimensional vector space has an orthonormal basis.
Proof: We will proceed by constructing an algorithmic solution:
The Gram-Schmidt Process:
*Goal: Given a basis of a vector space construct an orthonormal basis.
Let {\(\overrightarrow{u}_1\),…, \(\overrightarrow{u}_n\)} be any basis and {\(\overrightarrow{v}_1\),…, \(\overrightarrow{v}_n\)} be the desired orthonormal basis.
\(\overrightarrow{v}_1 = \overrightarrow{u}_1\)
Let \(\overrightarrow{w}_1 =\) span{\(\overrightarrow{v}_1\)}
\(\therefore \overrightarrow{v}_2 = \overrightarrow{u}_2 - proj_{w_1}\overrightarrow{u}_2\)
\(\therefore \overrightarrow{v}_2 = \overrightarrow{u}_2 - \frac{\overrightarrow{u}_2 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1\)
Let \(\overrightarrow{w}_2 =\) span{\(\overrightarrow{v}_1\), \(\overrightarrow{v}_2\)}
\(\therefore \overrightarrow{v}_3 = \overrightarrow{u}_3 - proj_{w_2}\overrightarrow{u}_3\)
\(\therefore \overrightarrow{v}_3 = \overrightarrow{u}_3 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_2}{||\overrightarrow{v}_2||^2}\overrightarrow{v}_2\)
…
Continue in this fashion up to \(\overrightarrow{v}_n\)
Example:
Use the Gram-Schmidt process to transform the basis \(\overrightarrow{u}_1 = <1,1,1>\), \(\overrightarrow{u}_2 = <0,1,1>\), \(\overrightarrow{u}_3 = <0,0,1>\)
\(\overrightarrow{v}_1 = \overrightarrow{u}_1 = <1,1,1>\)
\(\overrightarrow{v}_2 = \overrightarrow{u}_2 - proj_{\overrightarrow{w_1}}\overrightarrow{u}_2\)
\(\overrightarrow{v}_2 = <0,1,1> - \frac{\overrightarrow{u}_2 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1\)
\(\overrightarrow{v}_2 = <0,1,1> - \frac{2}{3}<1,1,1>\)
\(\overrightarrow{v}_2 = <0,1,1> - <\frac{2}{3},\frac{2}{3},\frac{2}{3}>\)
\(\overrightarrow{v}_2 = <-\frac{2}{3},\frac{1}{3},\frac{1}{3}>\)
\(\overrightarrow{v}_3 = \overrightarrow{u}_3 - proj_{w_2}\overrightarrow{u}_3\)
\(\overrightarrow{v}_3 = \overrightarrow{u}_3 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_2}{||\overrightarrow{v}_2||^2}\overrightarrow{v}_2\)
\(\overrightarrow{v}_3 = <0,0,1> - \frac{1}{3}<1,1,1> - \frac{1}{2}<-\frac{2}{3},\frac{1}{3},\frac{1}{3}>\)
\(\overrightarrow{v}_3 = <0,-\frac{1}{2},\frac{1}{2}>\)
\(\therefore \overrightarrow{v}_1, \overrightarrow{v}_2, \overrightarrow{v}_3\) orthogonal (not orthonormal)
Normalize => unit vectors
\(\overrightarrow{v}_1\) => \(\frac{1}{||\overrightarrow{v}_1||}\overrightarrow{v}_1 = <\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}>\) Repeat for \(\overrightarrow{v}_2\),\(\overrightarrow{v}_3\)