2 Fundamentals of Isabelle

Let’s start by creating a file Playground.thy with the following contents

theory Playground
imports Main
begin
(* here we will write our code*)
end

We can use (* *) as comments. Those are ignored by Isabelle.

2.1 Inductive data types

The set of natural numbers nat is defined inductively as

hide_type nat (* use this line to avoid conflicst with Main library *)

datatype nat = Zero | Suc nat

(This is not actual definition of nat)

We can represent 0 as Zero, number 1 as Suc Zero, number 2 as Suc (Suc Zero) and so on. This is widely known as Peano arithmetic.

2.2 Functions

Functions can be defined usig primrec. For example addition can be introduced as the follows

primrec plus :: "nat ⇒ nat ⇒ nat" where
"plus Zero y = y" |
"plus (Suc x) y = Suc (plus x y)"

Isabelle uses ⇒ (written as => in ASCII) to denote the type of functions. If x and y are types then x ⇒ y is a function type (⇒ has left associativity). Such mathematical expressions must be enclosed in double quotes " ". After the type comes where keyword which marks the beginning of function specification (this is not function definition! You’ll see later). Our function has two cases separated by |. The first case applies when the first argument is Zero. You can test it with the value command, for example 0+2 is

value "plus Zero (Suc (Suc Zero))"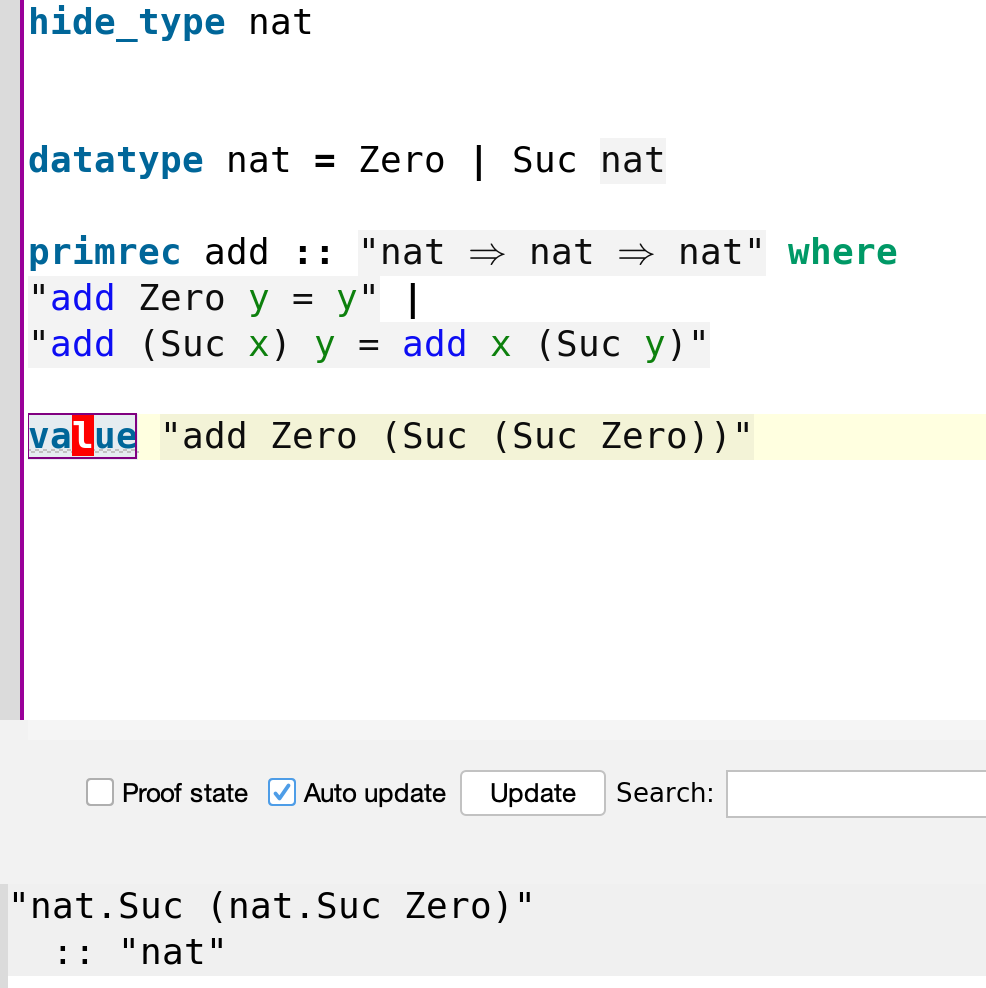

evaluation output

The second case applies when the first argument is a successor Suc x of some number x. For example 1+2 outputs 3 as follows

value "plus (Suc Zero) (Suc (Suc Zero))" (* this prints "nat.Suc (nat.Suc (nat.Suc Zero))" *)

The functions Zero and Suc are called constructors. Their types are natand nat ⇒ nat which you can check using value

value "Suc" (* this prints "nat ⇒ nat" *)
value "Zero" (* and this prints "nat" *)

All inductive types (datatype) have some size. The size tells us how deep the recursion is. For example

value "size Zero"  (* prints "0" *)
value "size (Suc Zero)" (* prints "1" *)
value "size (Suc (Suc Zero))" (* prints "2" *)

A constructor can take more than one argument

datatype x = X1 | X2 x | X3 x x

value "size X1" (* prints "0" *)
value "size (X2 X1)" (* prints "1" *)
value "size (X3 X1 X1)" (* still prints "1" *)
value "size (X3 X1 (X2 X1))" (* now prints "2" *)

The value of size is always a finite number, which brings us to primitive recursion.

2.3 Primitive recursion

In Isabelle all functions must terminate. For example the following is illegal

primrec f :: "nat ⇒ nat" where
"f x = f x"

because the evaluation of f would never end. The reason why we don’t want that is because it would allow us to prove any statement about f to be true (proofs by induction will be shown soon).

To avoid such problems primrec must be a primitive recursive function. Those functions must be of the form

datatype x = X1 a | X2 b | ... Xn c
primrec f :: "x ⇒ y" where
"f (X1 a) = ... f a ..." |
"f (X2 b) = ... f b ..." |
... |
"f (Xn c) = ... f c ..." 

which means that they consider all cases (X1 a, X1 b, … Xn c) of some inductive type x and can only perform recursion (e.g. f a) on constructor parameters but not on the original input (e.g. f (X1 a) not allowed on the right side). This means that the size of first argument always decreases and because it is finite and non-negative it must eventually reach 0 and end.

Primitive recursive functions are very limiting and not Turing-complete, therefore, if primrec is not enough, we can use fun but we may have to provide our own proof that the recursion always ends (fun will be shown later).

2.4 Theorems and proofs

To write proofs we can use theorem keyword. For example let’s write proof that addition is associative, that is, x+(y+z)=(x+y)+z for all natural numers x,y,z

theorem add_associativity : "plus x (plus y z) = plus (plus x y) z" 

If you place your cursor below the theorem and toggle the “Proof state” button you will see the state of your proof

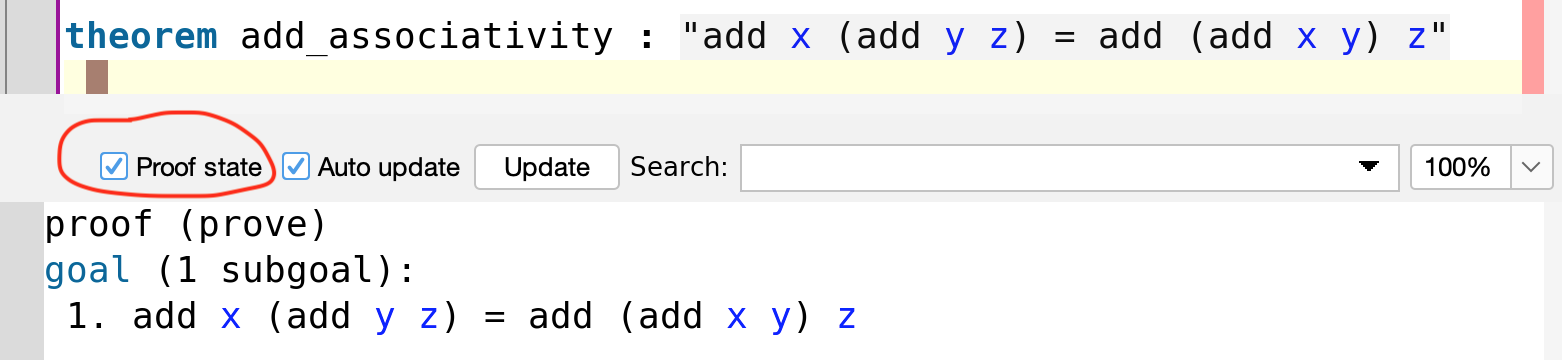
proof state

When dealing with inductive types a good idea is to prove theorems by induction. This is done with apply(induct_tac x) tactic.

theorem add_associativity : "plus x (plus y z) = plus (plus x y) z" 
  apply(induct_tac x)

Now the state of the proof becomes

proof (prove)
goal (2 subgoals):
 1. plus Zero (plus y z) = plus (plus Zero y) z
 2. ⋀x. plus x (plus y z) = plus (plus x y) z ⟹
         plus (Suc x) (plus y z) = plus (plus (Suc x) y) z

We have two subgoals. First one is to prove that initial condition for Zero, second is to prove recursive case while having access to inductive hypothesis plus x (plus y z) = plus (plus x y) z. The long double arrow ⟹ (written ==> in ASCII) is the logical implication. Symbol ⋀ is the universal quantifier “for all x”. The goals we have now could be simplified. Isabelle can do a lot of the leg work automatically by using apply(auto) tactic.

theorem add_associativity : "plus x (plus y z) = plus (plus x y) z" 
  apply(induct_tac x)
   apply(auto)
  done

Now all the goals are proved

proof (prove)
goal:
No subgoals!

and we can add done to finish the theorem.

2.4.1 Querying and using proofs

If you ever forget what the theorem states, you can use command thm to look it up

thm add_associativity

which prints

plus ?x (plus ?y ?z) = plus (plus ?x ?y) ?z

Isabelle has added ? to all variables, which means that from now on you can substitute those variables for an arbitrary expression like this

theorem zero_plus_one_plus_z: "plus Zero (plus (Suc Zero)  z) = plus (plus Zero (Suc Zero)) z"
  apply(subst add_associativity)
  apply(rule refl)
  done

The subst command will look for any pattern that looks like plus ?x (plus ?y ?z) and substitute it for plus (plus ?x ?y) ?z. In this case ?x matches with Zero, ?y matches Suc Zero and ?z matches z.

If you are curious what refl does you can look it up in the same way

thm refl

which prints

?t = ?t

You can hold Ctrl (or Cmd on OSX) and click on any term to go to its definition. Click on refl and you will be redirected to a file from Isabelle’s Main library, to the exact line that defines refl

subsubsection ‹Axioms and basic definitions›

axiomatization where
  refl: "t = (t::'a)" and 
  subst: "s = t ⟹ P s ⟹ P t" and
  ext: "(⋀x::'a. (f x ::'b) = g x) ⟹ (λx. f x) = (λx. g x)"
    ― ‹Extensionality is built into the meta-logic, and this rule expresses
         a related property.  It is an eta-expanded version of the traditional
         rule, and similar to the ABS rule of HOL› and

  the_eq_trivial: "(THE x. x = a) = (a::'a)"

The proof of zero_plus_one_plus_z could be written more compactly as

theorem t: "plus Zero (plus (Suc Zero)  z) = plus (plus Zero (Suc Zero)) z"
  apply(rule add_associativity)
  done

Here, instead of substituting left side for the right side and then applying equality rule refl, we apply the add_associativity directly. If both left and right sides of equation match then it is obvious that they are equal and the proof is done.

These examples show how we can use previous theorems to prove new ones. The Main library contains a galore of theorems to choose from. You can search for proofs by name

or by pattern involving wildcards _

search

or by pattern involving ?-prefixed variables

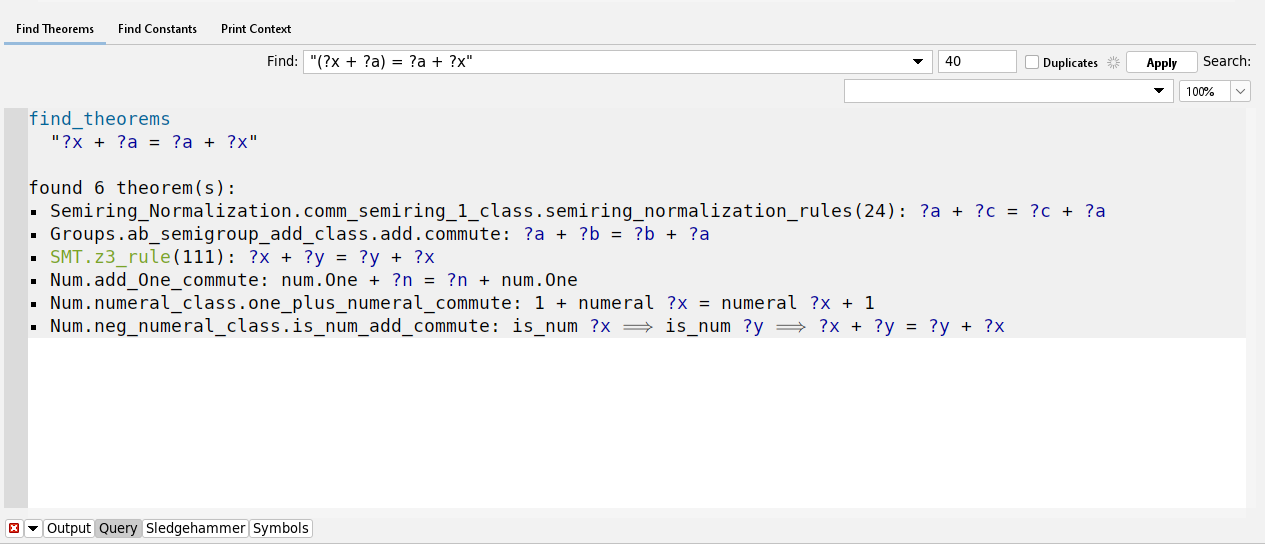
search

2.4.2 More complex proofs

Here are a few more examples of easy theorems

theorem add_suc_rev : " plus x (Suc y) = plus (Suc x) y" 
  by(induct_tac x, auto)
  
theorem add_suc_out : "plus (Suc x) y = Suc (plus x y)" 
  by(induct_tac x, auto)
  
theorem add_zero : "plus x Zero = x" 
  by(induct_tac x, auto)

The by keyword is a shorthand one-line notation for simple proofs and is equivalent to the multi-line proof we did before. Let’s try a more complex theorem.

theorem add_commutativity : "plus x y = plus y x" 
  apply(induct_tac x)
    apply(simp)

We start with induction and simplification but it only gets us so far

proof (prove)
goal (2 subgoals):
 1. y = plus y Zero
 2. ⋀x. plus x y = plus y x ⟹ Suc (plus y x) = plus y (Suc x)

We have already proved the first subgoal in form of add_zero theorem. We can tell Isabelle to use it by using simp add: add_zero.

theorem add_commutativity : "plus x y = plus y x" 
  apply(induct_tac x)
   apply(simp add:add_zero)

This solves the first subgoal

proof (prove)
goal (1 subgoal):
 1. ⋀x. plus x y = plus y x ⟹ plus (Suc x) y = plus y (Suc x)

The tactic simp is similar to auto but it only applies to a single subgoal and can be extended in many ways (like with add:) that auto cannot. auto uses more heuristics and can solve more problems out-of-the-box. simp gives more control to us. Now, to solve the remaining subgoal, not even simp is detailed enough. We will have to tell Isabelle which substitution rules to use exactly (simp and auto do this behind the scenes). We want to apply apply(subst add_suc_rev)

proof (prove)
goal (1 subgoal):
 1. ⋀x. plus x y = plus y x ⟹ plus (Suc x) y = plus (Suc y) x

and then apply(subst add_suc_out)

proof (prove)
goal (1 subgoal):
 1. ⋀x. plus x y = plus y x ⟹ Suc (plus x y) = plus (Suc y) x

and again apply(subst add_suc_out)

proof (prove)
goal (1 subgoal):
 1. ⋀x. plus x y = plus y x ⟹ Suc (plus x y) = Suc (plus y x)

then we finish off with apply(simp). The full proof looks as follows

theorem add_commutativity : "plus x y = plus y x" 
  apply(induct_tac x)
   apply(simp add:add_zero)
  apply(subst add_suc_rev)
  apply(subst add_suc_out)
  apply(subst add_suc_out)
  apply(simp)
  done

2.4.3 The thinking process

You might be wondering how I arrived at this proof. In fact, I started from the end. My initial goal was to prove add_commutativity but I couldn’t. Whenever you’re stuck in Isabelle, it’s always a good idea to backtrack and try to prove something simpler first. I tried proving all the smaller auxiliary theorems like add_suc_out first. Even those were difficult because initially my definition of plus looked like this

primrec plus :: "nat ⇒ nat ⇒ nat" where
"plus Zero y = y" |
"plus (Suc x) y = plus x (Suc y)" (* Suc applied to y! *)

Only after changing the definition to Suc (plus x y) all of the theorems became much easier to prove. This is something you will see often when working with Isabelle or any other proof assistant. There are many equivalent definitions but some are more elegant than others.

2.5 Inductive predicates

Data types are limited to representing finite entities. For example we can use lists to store a finite number of even numbers

value "[0::Nat.nat,2,4,6]"
(* it prints
"[0, 2, 4, 6]"
  :: "Nat.nat list"  <- notice Nat.nat comes from the imported Main. It's not our own definition.
*)

In many programming languages we can also use hash-maps to do something like

# This is Python code
is_even = {
 0 : True,
 1 : False,
 2 : True,
 3 : False,
 4 : True
}

The problem with data types is that they cannot store infinite sets. We could turn the hash-map is_even into a function instead

datatype nat = Zero | Suc nat 

fun is_even :: "nat ⇒ bool" where 
"is_even Zero = True" |
"is_even (Suc Zero) = False" |
"is_even (Suc(Suc n)) = is_even n"

Now calling is_even (Suc (Suc Zero)) is equivalent to looking up a hash-map in Python is_even[2] but we are no longer limited to finite sets. Notice that we had to use fun because primrec does not allow nested patterns is_even (Suc(Suc n)) on the left. We will investigate fun in depth later.

If functions are like infinite hash-maps then inductive predicates

inductive Even :: "nat ⇒ bool" where
zero: "Even Zero"
| double: "Even (Suc (Suc n))" if "Even n" for n

are like infinite linked lists.

While is_even returns True on numbers that are even and False on those that aren’t, the inductive predicate Even can be proved to hold for even numbers but cannot be proved to hold for anything else. By analogy a list only contains elements that belong to it whereas a hash-map must also hold odd numbers and mark them as False. Note one interesting difference between finite and infinite data structures. If you try to iterate over an entire linked-list or hash-map you will eventually reach the end. By exploiting this fact, you don’t need to store False entries in a hash-map but this cannot be done with infinite structures. For this reason mathematicians refer to finite structures as effective.

To prove that 4 is even we can proceed as follows

theorem "Even (Suc (Suc (Suc (Suc Zero))))"
  apply(rule double)
  apply(rule double)
  apply(rule zero)
  done

We can also prove that is_even x is true only when Even x holds

theorem "Even m ⟹ is_even m" 
  apply(induction rule: Even.induct)
  by(simp_all)

The long arrow ⟹ is logical implication (written ==> in ASCII).

The tactic apply(induction rule: Even.induct) says that we want to prove the theorem by induction and yields the following two subgoals.

 1. is_even Zero
 2. ⋀n. Even n ⟹ is_even n ⟹ is_even (nat.Suc (nat.Suc n))

Those are then easy to prove using apply(rule double) and apply(rule zero) so we just let Isabelle do the rest automatically by calling by(simp_all).

2.5.1 When to use inductive over recursive

If you need to prove statements about the negative cases (here those would be odd numbers) then working with recursive functions is easier. On the other hand if you do not care about negative cases and only want to prove statements about positive ones (even numbers) then inductive definitions often yield simpler proofs.

In some cases it is impossible to give recursive definitions. In particular those are problems that are not decidable. Then our only option is to use inductive definitions (which is related to semi-decidability).

2.6 Type declarations and axiomatization

2.6.1 Sets

We can declare a new type without providing any definition. This is done with typedecl keyword. Of course such types are not very useful on their own so they are typically combined with some axiomatization. For example the following is how Isabelle defines sets

typedecl 'a set

axiomatization Collect :: "('a ⇒ bool) ⇒ 'a set" ― ‹comprehension›
  and member :: "'a ⇒ 'a set ⇒ bool" ― ‹membership›
  where mem_Collect_eq [iff, code_unfold]: "member a (Collect P) = P a"
    and Collect_mem_eq [simp]: "Collect (λx. member x A) = A"

The apostrophe in front of 'a is a special notation that indicates that a is not any specific type. Instead 'a can be substituted for any other concrete type. It works like a wildcard or like generic types in many programming languages.

We do not know anything about 'a set other than that it can be created with function Collect and that its members can be queried with member. We know that those two functions are “inverse” of each other which more precisely expressed by axioms mem_Collect_eq and Collect_mem_eq. We can use those two facts like we would use any other theorem. Axioms are theorems that we assume to be true without giving any proofs. We also do not need to provide definitions for Collect and member. They are like “interface” functions in some programming languages.

We introduce notation

notation
  member  ("'(∈')") and
  member  ("(_/ ∈ _)" [51, 51] 50)

so that we can write x ∈ X instead of member x X. There is also nice syntax for set comprehension

syntax
  "_Coll" :: "pttrn ⇒ bool ⇒ 'a set"    ("(1{_./ _})")
translations
  "{x. P}" ⇌ "CONST Collect (λx. P)"

so that we can write {x . P x} instead of Collect P for some predicate P. We will investigate syntax and notation later. Their only purpose is to make things more readable.

2.6.2 Natural numbers

The previous definition of natural numbers nat was simplified. The one actually provided by Isabelle is more complicated. Before we can see it we have to first declare ind but instead of definining it, we only state its axioms

typedecl ind

axiomatization Zero_Rep :: ind and Suc_Rep :: "ind ⇒ ind"
  ― ‹The axiom of infinity in 2 parts:›
  where Suc_Rep_inject: "Suc_Rep x = Suc_Rep y ⟹ x = y"
    and Suc_Rep_not_Zero_Rep: "Suc_Rep x ≠ Zero_Rep"

Notice that ind behaves just like nat but unlike Suc, the Suc_Rep_inject might be applied infinitely. It is possible to use ind to express infinity ∞ (this is what codatatype is for) but nat could never do that (due to size).

Nonetheless, most of the time we want to work with finite numbers. For this purpose we define predicate Nat that includes only finite elements of ind

inductive Nat :: "ind ⇒ bool"
  where
    Zero_RepI: "Nat Zero_Rep"
  | Suc_RepI: "Nat i ⟹ Nat (Suc_Rep i)"

Now the real definition of nat is a subset of ind set that consists of only finite numbers Nat.

typedef nat = "{n. Nat n}"
  morphisms Rep_Nat Abs_Nat
  using Nat.Zero_RepI by auto

Infinite numbers, known as ordinals, will be covered later. The meaning of morphisms will be explained soon but it’s not important at this point.

2.6.3 All types are inhabited

Another important example of an axiom is

axiomatization undefined :: 'a

Other proof assistants such as Coq, Agda, Lean, etc. are based on constructive logic and in particular homotopy type theory. In those logics it is possible for a type to be empty. It is usually known as False or Void and it used to express negation.

Isabelle is based on higher-order-logic. It can use law of excluded middle and negation out-of-the-box. As empty types are not needed anymore, Isabelle is free to assume axioms such as undefined. It states that every type 'a has some inhabitant. Note that ' is used to indicate a type variable, which we can substitue for any concrete type like undefined::nat.

This axiom allows us to prove things like

datatype bool = True | False

lemma "undefined = True ∨ undefined = False" 
  apply(case_tac "undefined::bool") 
  apply(rule disjI1)
  apply(simp)
  apply(rule disjI2)
  apply(simp)
  done

The tactic apply(case_tac "undefined::bool") tries to consider all possible cases in which something of type bool could be defined. undefined must be either undefined = bool.True or undefined = bool.False, and in both of those cases the theorem should hold. Hence, we have two subgoals

 1. undefined = bool.True ⟹
    undefined = bool.True ∨ undefined = bool.False
 2. undefined = bool.False ⟹
    undefined = bool.True ∨ undefined = bool.False

The tactic apply(rule disjI1) is the first (1) introduction (I) rule for disjunction (dist). It says that if P is true then P ∨ Q is true. Analogically apply(rule disjI2) says that if Q is true then P ∨ Q is true. After applying apply(rule disjI1) we arrive at

 1. undefined = bool.True ⟹ undefined = bool.True
 2. undefined = bool.False ⟹
    undefined = bool.True ∨ undefined = bool.False

The equality in first subgoal is trivial so we can just use apply(simp) to automatically simplify it. We then proceed analogically with the second subgoal.

The undefined axiom has some major implications which will manifest themselves later. Here is more on this topic as well.

Most importantly, you should be aware that ∀𝑥. 𝑃 𝑥 → ∃𝑥. 𝑃 𝑥 is a valid first-order logic sentence. This is known as ontological commitment and is also explained here. Isabelle is based on first-order logic (actually higher-order logic) and commits to this law, therefore, it is sound to assume such an axiom as undefined.

2.7 Meta logic

2.7.1 Meta universal quantifier

Isabelle has a meta language. You could have seen it before in form of the ⋀ symbol (written \And in ASCII) which works like ∀ (written \forall in ASCII). The difference is that ∀ is a constructed function that we imported from Isabelle’s Main library

definition All :: "('a ⇒ bool) ⇒ bool"  (binder "∀" 10)
  where "All P ≡ (P = (λx. True))"

whereas ⋀ does not have any definition and is fundamental part Isabelle proof assistant itself. For example when proving something that involves ∀ weh have to use allI rule

theorem t: "∀ x. P x"
  apply(rule allI)

which produces a goal

1. ⋀x. P x

You should understand it as follows. In order to prove that P holds for all ∀x, Isabelle fixes an arbitrary ⋀x. If you can prove P x for an arbitrary x then P must hold for all x. You can use tacticts such as induct_tac x on variables bound by ⋀. For example

theorem t: "∀ x::nat. P x"
  apply(rule allI)
  apply(induct_tac x)

yields 2 subgoalds

 1. ⋀x. P 0
 2. ⋀x n. P n ⟹ P (Suc n)

However, if you tried to use induct_tac x directly when x is bound to ∀ you will get an error

theorem t: "∀ x::nat. P x"
  apply(induct_tac x) (*Error:  No such variable in subgoal: "x" *)

2.7.2 Meta implication

There is a similar difference between logical implication ⟶ (written as -->) and meta-logic implication ⟹ (==>). For example

theorem t: "P x ⟶ Q x"
  apply(rule impI)

yields subgoal

1. P x ⟹ Q x

and now we can use P x as an assumption when proving Q x. For instance to prove that P x ⟶ P x we can write

theorem t: "P x ⟶ P x"
  apply(rule impI)
  apply(assumption)
  done

2.7.3 Meta equality

Lastly there is logical equality = and meta-equality ≡ (==). You can use using [[simp_trace]] to see a detailed trace of what simp is doing behind the scenes

theorem t: "x = y ⟹ y = x"
  using [[simp_trace]]
  apply(simp)

and you can see that the automatic simplifier tries to explore different possible assignments ≡ of variables (I added my comments after #)

[1]SIMPLIFIER INVOKED ON THE FOLLOWING TERM:
x = y ⟹ y = x 
[1]Adding rewrite rule "??.unknown":
x ≡ y 
[1]Applying instance of rewrite rule "??.unknown":
x ≡ y 
[1]Rewriting:
x ≡ y 
[1]Applying instance of rewrite rule "HOL.simp_thms_6":
?x1 = ?x1 ≡ True 
[1]Rewriting:
y = y ≡ True 
[1]Applying instance of rewrite rule "HOL.implies_True_equals":
(PROP ?P ⟹ True) ≡ True 
[1]Rewriting:
(x = y ⟹ True) ≡ True

Meta equality is also used for term substitution and rewriting.

2.8 Abstraction and representation

Recall that when defining nat here

typedef nat = "{n. Nat n}"
  morphisms Rep_Nat Abs_Nat
  using Nat.Zero_RepI by auto

we used typedef and morphisms. This is a fundamental mechanism for introducing new types. In fact, Isabelle’s internal implementation of datatype command uses typedef behind the scene.

You could imagine that every type in Isabelle is a set. Don’t confuse it with the 'a set type but instead think of each type as a “meta-logic set”. Then typedef allows you to take any 'a set (in this case {n. Nat n}) and produce a new meta-logic set (in this case nat). typedef also gives you two new functions - one called “representation” (Rep_Nat) and the other called “abstraction” (Abs_Nat). You can use abstraction to transform any element of 'a set into an element of the meta-set (type of Abs_Nat is {n. Nat n} => nat and type of Rep_Nat is nat => {n. Nat n}). The two functions are inverse of one another and typedef will also automaticaly generate several theorems that we can use. For example

theorem "Abs_Nat (Rep_Nat x) = x"
  apply(rule Rep_Nat_inverse)
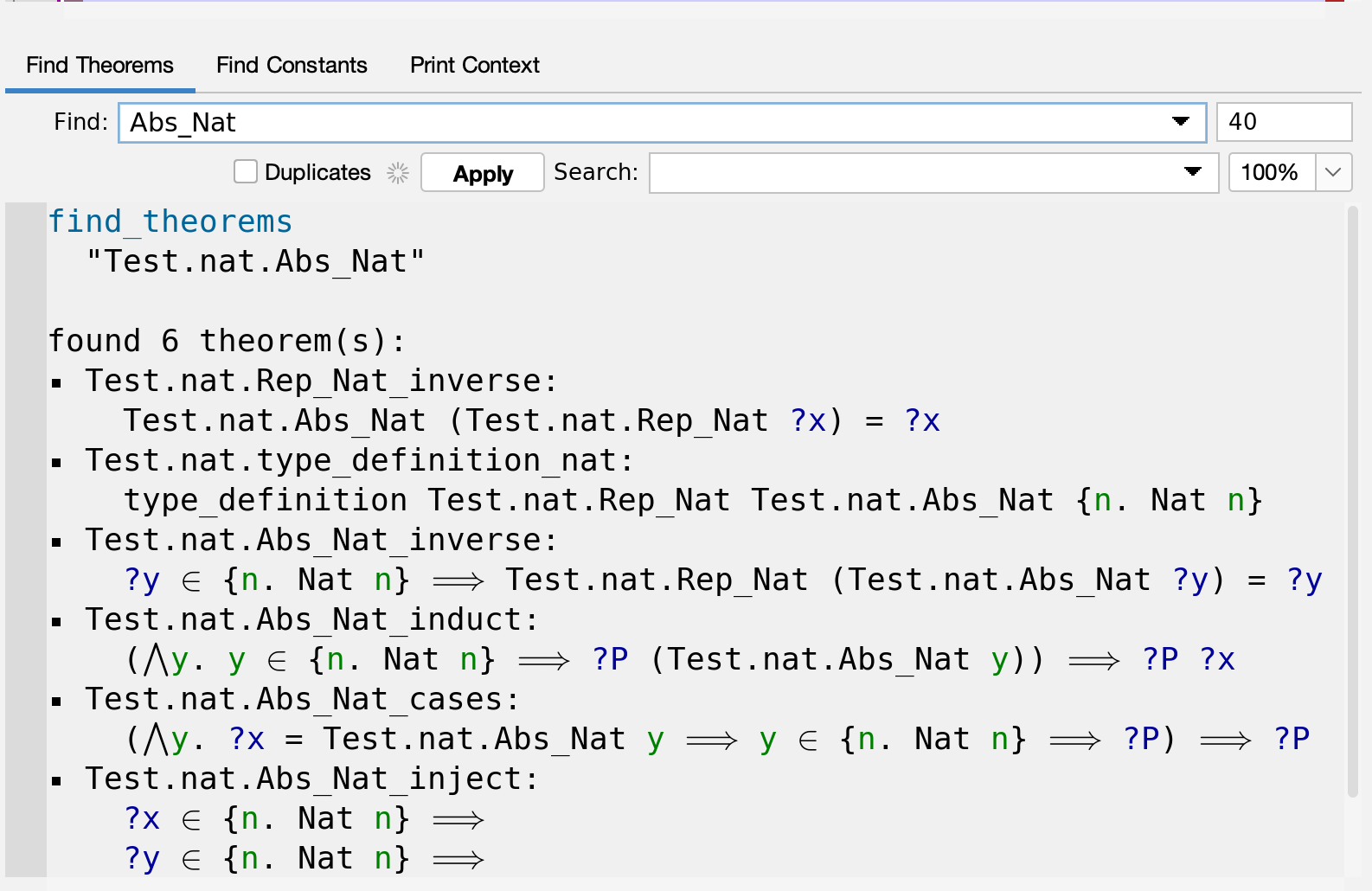
  done

The axiom Rep_Nat_inverse is auto-generated by typedef. You can find others by using search tab and typing in Rep_Nat or Abs_Nat

query

Lastly, every typedef must be finished with a proof of being inhabited. In this case the goal is

 1. ∃x. x ∈ {n. Nat n}

and is easily proved by using Nat.Zero_RepI by auto. The using keyword instructs auto to use a specific fact. There are millions of theorems and auto does not consider all of them because it would take too long. We have to explicitly allow it to use Nat.Zero_RepI.

If you want to better understand what using Nat.Zero_RepI by auto does, consider this more explicit proof

typedef nat = "{n. Nat n}"
  morphisms Rep_Nat Abs_Nat
  (* goal: ∃x. x ∈ {n. Nat n} *)
  apply(rule exI)  
  (* goal: ?x ∈ {n. Nat n} *)
  apply(subst Set.mem_Collect_eq)
  (* goal: Nat ?x *)
  apply(rule Nat.Zero_RepI)
  done

which shows that nat is inhabited because zero (Nat.Zero_RepI) belongs to it.

Recall that we have to prove that all types are inhabited because of the undefined axiom we discussed previously.

2.8.1 Morphisms can be omitted

The keyword morphisms is optional. We could have written

typedef nat = "{n. Nat n}"
  using Nat.Zero_RepI by auto

theorem "Abs_nat (Rep_nat x) = x"
  apply(rule Rep_nat_inverse)
  done

If we do not provide the names of abstraction and representation functions ourselves, typedef will auto-generate them for us. Their default names are dictated by the naming convention like on the example.

2.9 Syntactic sugars and Lists

Isabelle defines lists as follows.

(* use no_notation to avoid conflicts with list already defined in Main library *)
no_notation Nil ("[]") and Cons (infixr "#" 65) and append (infixr "@" 65)

datatype 'a list =
    Nil  ("[]")
  | Cons 'a "'a list"  (infixr "#" 65)

The ("[]") introduces a pretty notation for the empty list Nil and (infixr "#" 65) is a syntactic sugar for appending to a list. For example

value " x # y # z # []" (* is of type "'a list *)

is equivalent to writing

value "Cons x (Cons y (Cons z Nil))"

The keyword infixr specifies associativity of the operation. Compare

value " x # (y # (z # []))" (* is of type "'a list *)

value "((x # y) # z) # []" (* is of type "'a list list list *)

with the alternative definition that uses infixl instead

datatype 'a list =
    Nil  ("[]")
  | Cons 'a "'a list"  (infixl "#" 65)
  
value " x # y # z # []" (* is of type  "'a list list list" *)

value " x # (y # (z # []))" (* is of type "'a list" *)

Also see what happens if we now switch the order of arguments of Cons

datatype 'a list =
    Nil  ("[]")
  | Cons "'a list" 'a (infixl "#" 65)
  
value "[] # x # y # z" (* is of type  "'a list" *)

value "[] # (x # (y # z))" (* is of type "'a list list list" *)

From now on, let’s stick to our first definition, that is Cons 'a "'a list" (infixr "#" 65). We can make our notation even more readable by introducing a custom bracket notation

syntax
  "_list" :: "args => 'a list"    ("[(_)]")

translations
  "[x, xs]" == "x#[xs]"
  "[x]" == "x#[]"

We can now write [x,y,z] instead of x # y #z # []. The transaltions will be used to automatically turn

value "x # y # z # []"

into brackets and print the following output

"[x, y, z]"
  :: "'a Test.list"

as equivalent We can define list concatenation as follows.

primrec append :: "'a list ⇒ 'a list ⇒ 'a list" (infixr "@" 65) where
append_Nil: "[] @ ys = ys" |
append_Cons: "(x#xs) @ ys = x # xs @ ys"

The way syntax and translations work can be easily deduced from the example. The (_) that appears in ("[(_)]") is a wildcard that matches whatever we write between [ and ]. Then translations further work on that string and rewrite it into # and [] notation.

The infix operators can be defined for any function, not only constructors. For example

primrec append :: "'a list ⇒ 'a list ⇒ 'a list" (infixr "@" 65) where
append_Nil: "[] @ ys = ys" |
append_Cons: "(x#xs) @ ys = x # xs @ ys"

allows us to concatenate two lists using x @ y instead of having to write append x y

value "[x,y] @ [z,w]"
(* prints 
"[x, y, z, w]"
  :: "'a list"
*)

2.10 Type classes and semigroups

2.10.1 List and nat are semigroups

Very often different mathematical objects share common properties. For example compare append for list with plus for nat

no_notation Nil ("[]") and Cons (infixr "#" 65) and append (infixr "@" 65) and plus (infixl "+" 65) and Groups.zero_class.zero ("0")

datatype nat = Zero ("0") | Suc nat

primrec plus :: "nat ⇒ nat ⇒ nat" (infixl "+" 65) where
"0 + y = y" |
"(Suc x) + y = Suc (x + y)"

datatype 'a list =
    Nil  ("[]")
    | Cons 'a "'a list"  (infixr "#" 65)

primrec append :: "'a list ⇒ 'a list ⇒ 'a list" (infixr "@" 65) where
append_Nil: "[] @ ys = ys" |
append_Cons: "(x#xs) @ ys = x # xs @ ys"

It holds for both that

theorem app_assoc : "x @ (y @ z) = (x @ y) @ z"
  by (induct_tac x) auto

theorem add_assoc : "x + (y + z) = (x + y) + z"
  by (induct_tac x) auto

In mathematics, structures like this are called semigroups. There are infinitely many other entities that satisfy associativity law. Many theorems about those objects can be proved in the exact same way, without referring to the details of their definitions. We can use type classes to save ourselves work and write general proofs that will be reused for all semigroups. A programmer might know type classes under Let’s work through an example to better understand this.

2.10.2 Instantiating natural numbers

Let’s erase our previous code and start fresh. We start by defining class of all structures that can be added together using plus function.

class plus =
  fixes plus :: "'a ⇒ 'a ⇒ 'a"  (infixl "+" 65)

Next we have to specify that nat can be added and belongs to the class plus. This is done using instantiation command.

instantiation nat :: plus
begin
  
primrec plus_nat :: "nat ⇒ nat ⇒ nat" where
"plus_nat 0 y = y" |
"plus_nat (Suc x) y = Suc (plus_nat x y)"

instance ..
end

The naming convention requires us to call the function plus_nat instead of just plus. If you place your cursor right after begin you will see output

instantiation
  nat :: plus
  plus_nat == plus_class.plus :: nat ⇒ nat ⇒ nat

telling you that nat is an subtype of type plus. The second line says that you have to define function named plus_nat which will correspond to the fixes plus required by the class. Once we finished defining plus_nat we use instance .. to provide all necessary proofs. In this case our class does not need any proofs so we just type ...

2.10.3 Instantiating lists

We proceed analogically for list

datatype 'a list =
    Nil  ("[]")
    | Cons 'a "'a list"  (infixr "#" 65)

instantiation  list :: (type) plus
begin
  
primrec plus_list :: "'a list ⇒ 'a list ⇒ 'a list" where
"plus_list []  ys = ys" |
"plus_list (x#xs) ys = x # (plus_list xs ys)"

instance ..
end

Notice an important detail here. The type list takes a type argument 'a. We are not allowed to write

instantiation  "'a list" :: plus

Instead the type parameter becomes a parameter of plus.

2.10.4 Restricting type parameters

The (type) in the snippet above means that we can accept any type in place of 'a. It is possible to restrict the scope of 'a to only those types that belong some class. For example consider definining plus for pairs as follows

(a, b) + (c, d) = (a + c, b + d)

This requires that a and c can be added together. Same goes for b and d. To express this in Isabelle we can use pairs (also known as tuples to programmers or Cartesian product to mathematicians)

value "(x, y) :: nat × nat" (* with pretty syntax *)
value "(Pair x y) :: (nat, nat) prod" (* without pretty syntax *)

We can define + for pairs 'a × 'b but we have to assume 'a and 'b are restricted to class plus too. This can be done with prod :: (plus, plus) notation as follows

instantiation  prod :: (plus, plus) plus
begin
  
fun plus_prod :: "'a × 'b ⇒ 'a × 'b ⇒ 'a × 'b" where
"plus_prod (a, b) (c, d) = (a + c, b + d)"

instance ..
end

We can now use + on tuples like we would on any other mathematical object

value "(x, y)+(z, w):: nat × nat"
(* this prints
"(x + z, y + w)"
  :: "nat × nat"
*)

2.10.5 Type classes with axioms

Type classes are more than just collections of functions. They can also assume certain axioms that those functions must satisfy. For example semigroups require associativity law a+(b+c)=(a+b)+c. This is how Isabelle defines semigroups

class semigroup_add = plus +
  assumes add_assoc: "(a + b) + c = a + (b + c)"
begin

It is a class that is a subset of plus class (if types are “meta sets”, then type classes are super-sets containing types and other type classes) such that plus satisfies add_assoc axiom. The instantiation of semigroup_add will now require instance proof block which contains proofs of the necessary axioms and ends with qed.

instantiation nat :: semigroup_add
begin
instance proof
  fix a b c :: nat
  show "(a + b) + c = a + (b + c)"
  apply(induct_tac a)
   apply(auto)
    done
qed
end

If you place your cursor at the end of begin you will see the following proof state

 1. ⋀a b c. a + b + c = a + (b + c)

We have already proved this before using induct_tac. The problem now is that you can’t use induct_tac a because a is not fixed yet. We use the command fix a b c :: nat in order to make those variables usable in our proofs. Next we have to decide which goal we want to prove by using the show command. In this case there is only one class axiom to prove but in other cases there might be multiple theorems that need to be proved. After show we are finally able to write the proof.

2.10.6 Proofs that use class axioms

You might be wondering why we’ve been using the word “axiom” even though we clearly had to provide its proof. Aren’t axioms suppose to be theorems that have no proofs? That was the case for axioms stated with axiomatization command. Here we are working with class axioms instead. The reason why we call add_assoc an axiom is because we can use it in proofs like this

theorem assoc_left:
fixes x y z :: "'a::semigroup_add"
shows "x + (y + z) = (x + y) + z"
using add_assoc by (rule sym)

The theorem assoc_left shows x + (y + z) = (x + y) + z but it assumes (fixes) that x, y and z are of any type 'a thet belongs to semigroup_add. We can now use add_assoc as if it was an axiom. We never made any reference to the type nat. It might as well be a list or something else. We don’t know and it doesn’t matter for the proof. The only information about 'a that the proof is allowed to use are its class axioms.

2.11 Quotient types

2.11.1 Integer numbers in mathematics

(If you’re well-versed in mathematics and know how integers are represented, feel free to skip straight to next section.)

Sometimes we want to treat certain set elements as if they were one and the same entity. For example so far we’ve been only dealing with natural numbers 0, 1, 2... and we defined the + operation. The - operation cannot be defined on nat because 2-3=-1 is not a nat. In order to define 2-3 we have to imagine existence of some element x such that x+3=2. It is clear that x is not in nat. We can do the same trick as mathematicians did for complex numbers. We can use pairs of natural numbers and pretend that the second one is negative. Here are some examples

(0, 0) stands for 0-0=0
(1, 0) stands for 1-0=1
(2, 0) stands for 2-0=2
(0, 1) stands for 0-1=-1
(0, 2) stands for 0-1=-2

We can define addition + just like we defined it for pairs before. Adding two positive numbers works as expected.

1+2 stands for (1,0)+(2,0)=(1+2,0+0)=(3,0) stands for 3

Instead of “stands for” let us write ≅ (\cong). Mathematicians call this congruence. Adding negative numbers works as well.

-1+(-2) ≅ (0,1)+(0,2)=(0+0,1+2)=(0,3) ≅ -3

The trouble begins when we try to add positive and negative numbers together. It turns out that -1 can also be written as

2-3≅(2,0)+(0,3)=(2,3)
3-4≅(3,0)+(0,4)=(3,4)
... and so on

The type nat × natcontains many different elements that are all congruent to the same integer. In order to define typedef int we need an abstraction function Abs_int :: nat × nat => int that works like this

Abs_int (0,1) = -1
Abs_int (1,2) = -1
Abs_int (2,3) = -1
...

But we already said that abstraction and representation functions are inverse of one another. So the Rep_int :: int => nat × nat function is in fact not a function at all because it maps one int to infinitely many possible nat × nat pairs. This cannot be done with typedef! Instead we need to take advantage of equivalence classes.

2.11.2 Equivalence classes

A relation R :: 'a => 'a => bool is called equivalence relation if it satisfies 3 (“class”) axioms

1. symmetry: ∀x y. R x y ⟶ R y x

definition symp :: "('a ⇒ 'a ⇒ bool) ⇒ bool"
  where "symp R ⟷ (∀x y. R x y ⟶ R y x)"

This definition states that R is symmetric (symp r) if and only if (⟷) when x is in relation with y then y is in relation with x. (Example: If John is friends with Pete then Pete is friends with John. Anti-example: If John owes money to Pete then it doesn’t necessarily mean that Pete owes money to John)

2. reflexivity: ∀x. R x x

definition reflp :: "('a ⇒ 'a ⇒ bool) ⇒ bool"
  where "reflp R ⟷ (∀x. R x x)"

3. transitivity: ∀x y. x=y

definition transp :: "('a ⇒ 'a ⇒ bool) ⇒ bool"
  where "transp R ⟷ (∀x y z. R x y ⟶ R y z ⟶ R x z)"

If some R satisfies all of those properties then R is an equivalence relation. This is how Isabelle defines a lemma (synonym for theorem) that states equivp R. (Don’t pay too much attention to the proof. It relies on many other lemmas you can find in Main. If you copy it, it won’t work for you unless you prove them too.)

lemma equivpI: "reflp R ⟹ symp R ⟹ transp R ⟹ equivp R"
  by (auto elim: reflpE sympE transpE simp add: equivp_def)

When R :: 'a => 'a => bool is an equivalence relation then we can perform partial application of some x :: 'a to R and obtain a predicate R x :: 'a => bool. This predicate defines an equivalence class. If you collect R x into a set { y . (R x) y } you will obtain a subset of 'a. The characteristic property of equivalence classes is that those sets are either equal ({ y . (R x1) y } = { y . (R x2) y } whenever R x1 x2) or disjoint but they cannot intersect. Therefore, Isabelle defines equivp R as follows.

definition equivp :: "('a ⇒ 'a ⇒ bool) ⇒ bool"
  where "equivp R ⟷ (∀x y. R x y = (R x = R y))"

It states that predicate R x y holds if and only if (=) the equivalence classes are equal (R x = R y).

2.11.3 Integer numbers in Isabelle

Recall that an integer x :: int is represented by pair of natural numbers (a,b) :: nat × nat such that x=a-b. It is possible to check whether two integers x = xa - xb and y=ya - yb are equal without using - operation. This is done as follows

xa - xb = x = y = ya - yb \ to both sides add + xb + yb
xa + yb = ya + xb

Therefore, we define equivalence relation intrel

fun intrel :: "(nat × nat) ⇒ (nat × nat) ⇒ bool"
  where "intrel (xa, xb) (ya, yb) = (xa + yb = ya + xb)"

Now we can finally define int as follows

quotient_type int = "nat × nat" / "intrel"
  morphisms Rep_Integ Abs_Integ
proof (rule equivpI)
  show "reflp intrel"
    by (auto simp: reflp_def)
  show "symp intrel" 
    by (auto simp: symp_def)
  show "transp intrel"
    by (auto simp: transp_def)
qed

The command quotient_type is similar to typedef but this time we divide nat × nat into equivalence classes of relation intrel and each class is treated as an element of the new set int. The set int looks something like this

int = { ..., -2, -1, 0, 1, 2, ... }

where each number is a subset of nat × nat

-1 = {..., (0, 1), (1, 2), (2, 3), (3, 4), (4, 5), ...}
0 = {..., (0, 0), (1, 1), (2, 2), (3, 3), (4, 4), ...}
1 = {..., (1, 0), (2, 1), (3, 2), (4, 3), (5, 4), ...}

We cannot use any relation. We have to prove that intrel is indeed an equivalence relation. This is done using proof (rule equivpI) which requires us to prove 3 goals

 1. reflp intrel
 2. symp intrel
 3. transp intrel

You can apply unfold tactic like this

quotient_type int = "nat × nat" / "intrel"
  morphisms Rep_Integ Abs_Integ
proof (rule equivpI)
  show "reflp intrel"
    apply(unfold reflp_def)
    by (auto simp: reflp_def)
  show "symp intrel" 
    apply(unfold symp_def)
    by (auto simp: symp_def)
  show "transp intrel"
    apply(unfold transp_def)
    by (auto simp: transp_def)
qed

and place cursor at the end of each unfold to see the full statement that needs to proved

1. ∀x. intrel x x
2. ∀x y. intrel x y ⟶ intrel y x
3. ∀x y z. intrel x y ⟶ intrel y z ⟶ intrel x z

Important remark: The reason why we need to prove that intrel is an equivalence relation is because this ensures that no representation (a,b) stands for two different integers. Otherwise an ambiguity would arise and nothing could be proved about int later on.

2.11.4 Lifting

TODO: describe lifting

lift_definition plus_int :: "int ⇒ int ⇒ int"
  is "λ(x, y) (u, v). (x + u, y + v)"
  by clarsimp

2.12 Main library

In this section we review many components of Isabelle’s Main library that are ubiquitous everywhere else. Learning this will make you familiar with basic concepts from abstract algebra and set theory. Feel free to skip this section and come back to individual subsections as necessary.

2.12.1 Order

2.12.1.1 Motivation of order axioms

We take it for granted that numbers are ordered. For example we know that no matter which two numbers we pick, one of them must be greater or equal to the other. For all x and y, either x ≤ y or y ≤ x. For Isabelle this is not so obvious. What does ≤ even mean? For example we could intuitively agree that the empty set {} is smaller than {1}, which in turn is “obviously” smaller than {1,2}. The set {2} is also greater than {} and {1,2}. In Isabelle we can write is as

value "{1} ≤ ({1,2}::nat set)" (* prints "True" *)
value "{2} ≤ ({1,2}::nat set)" (* prints "True" *)
value "{} ≤ ({1}::nat set)" (* prints "True" *)
value "{} ≤ ({2}::nat set)" (* prints "True" *)

What about comparing {1} with {2}?

value "{1} ≤ ({2}::nat set)" (* prints "False" *)
value "{2} ≤ ({1}::nat set)" (* prints "False" *)

This violates the rule that so “obviously” held for numbers

linear: "x ≤ y ∨ y ≤ x"

We also intuitively know that if x ≤ y and y ≤ x then x=y.

order_antisym : "x ≤ y ⟹ y ≤ x ⟹ x = y"

There are certain mathematical objects that violate order_antisym too. For example consider any ranking board where players are ordered by the number of points they scored. Two players may have equal score but that doesn’t mean they are the same person.

2.12.1.2 Order type classes

Isabelle defines an entire hierarchy of type classes that correspond to different orders. The first one is ord which only defines two predicates less_eq and less but does not assume any axioms. The sole purpose of this class is to introduce syntactic sugar.

(* Use this line to avoid conflicts with Main*)
no_notation less_eq  ("'(≤')") and less_eq  ("(_/ ≤ _)"  [51, 51] 50) and  less  ("'(<')") and  less  ("(_/ < _)"  [51, 51] 50) and greater_eq (infix "≥" 50) and greater  (infix ">" 50)

class ord =
  fixes less_eq :: "'a ⇒ 'a ⇒ bool"
    and less :: "'a ⇒ 'a ⇒ bool"
begin

notation
  less_eq  ("'(≤')") and
  less_eq  ("(_/ ≤ _)"  [51, 51] 50) and
  less  ("'(<')") and
  less  ("(_/ < _)"  [51, 51] 50)

abbreviation (input)
  greater_eq  (infix "≥" 50)
  where "x ≥ y ≡ y ≤ x"

abbreviation (input)
  greater  (infix ">" 50)
  where "x > y ≡ y < x"

notation (ASCII)
  less_eq  ("'(<=')") and
  less_eq  ("(_/ <= _)" [51, 51] 50)

notation (input)
  greater_eq  (infix ">=" 50)

end

The command abbreviation defines a new notation for an arbitrary expression. A programmer might call this a “macro”. The input and ASCII in brackets specify Isabelle mode (many unicode symbols have their ASCII counterparts that are easier to type).

A more interesting class is preorder which assumes reflexivity and transitivity

class preorder = ord +
  assumes less_le_not_le: "x < y ⟷ x ≤ y ∧ ¬ (y ≤ x)"
  and order_refl [iff]: "x ≤ x"
  and order_trans: "x ≤ y ⟹ y ≤ z ⟹ x ≤ z"
begin
 (* Here is a bunch of properties that follow from axioms *)
end

The axiom less_le_not_le is necessary because it specifies how less_eq and less predicates are related to one another. Preorder is the most general notion of order that encompasses all of the examples before. We can already use it to prove many simple but useful properties. I have omitted them to keep the definition concise. You can find them in Orderings.thy in Main (using Query or Ctrl+Click 2.4.1).

Now we finally reach partial order.

class order = preorder +
  assumes order_antisym: "x ≤ y ⟹ y ≤ x ⟹ x = y"
begin
    (* lots of theorems *)
end

It includes the law of anti-symmetry. It means that we will never encounter such paradoxes where two different elements have been assigned the same “spot” in the ordering. A notable example of partially ordered object is 'a set.

The final class is total order which additionally states that all elements can be compared. Types such as nat and int are totally ordered.

class linorder = order +
  assumes linear: "x ≤ y ∨ y ≤ x"
begin
    (* lots of theorems *)
end

Mathematicians usually refer to ≤ as (total/partial) order and to < as strict (total/partial) order. The axioms of strict order are derived from axioms of order by applying less_le_not_le axiom. The following lemma is a statement to that

lemma order_strictI:
  fixes less (infix "<" 50)
    and less_eq (infix "≤" 50)
  assumes "⋀a b. a ≤ b ⟷ a < b ∨ a = b"  (*axiom serving same purpose as less_le_not_le *)
  assumes "⋀a b. a < b ⟹ ¬ b < a" (* assymetry instead of anti-symmetry*)
  assumes "⋀a. ¬ a < a" (* irreflexivity instead of reflexivity *)
  assumes "⋀a b c. a < b ⟹ b < c ⟹ a < c" (*transitivity*)
  shows "class.order less_eq less" (* This is order where predicates less_eq and less switched places *)
  by (rule ordering_orderI) (rule ordering_strictI, (fact assms)+)

If you place your cursor at the end of shows "class.order less_eq less" you will see the following goal

1. class.order (≤) (<)

After apply(unfold class.order_def) it becomes

1. class.preorder (≤) (<) ∧ class.order_axioms (≤)

After apply(unfold class.preorder_def) and apply(unfold class.order_axioms_def) we arrive at this convoluted expression

1. ((∀x y. (x < y) = (x ≤ y ∧ ¬ y ≤ x)) ∧ (∀x. x ≤ x) ∧ (∀x y z. x ≤ y ⟶ y ≤ z ⟶ x ≤ z)) ∧
    (∀x y. x ≤ y ⟶ y ≤ x ⟶ x = y)

If we simplify it using apply(auto) we see more clearly the axioms.

 1. ⋀x y. x < y ⟹ x ≤ y
 2. ⋀x y. x < y ⟹ y ≤ x ⟹ False
 3. ⋀x y. x ≤ y ⟹ ¬ y ≤ x ⟹ x < y
 4. ⋀x. x ≤ x
 5. ⋀x y z. x ≤ y ⟹ y ≤ z ⟹ x ≤ z
 6. ⋀x y. x ≤ y ⟹ y ≤ x ⟹ x = y

We can therefore tell that class.order is itself a function that takes two predicates and produces a set of axioms. What order_strictI shows is that if you swap those two predicates you transform those axioms into different but equivalent ones that correspond to strict order.

Having defined order we can now introduce two functions min and max. They are so simple that we do not need to use primrec nor fun because there is no need for recursion at all. In such cases we can use definition.

definition (in ord) min :: "'a ⇒ 'a ⇒ 'a" where
  "min a b = (if a ≤ b then a else b)"

definition (in ord) max :: "'a ⇒ 'a ⇒ 'a" where
  "max a b = (if a ≤ b then b else a)"

The notation (in ord) means that those functions are only available for types 'a that instantiate ord.

Click to see an equivalent code example

The notation (in ord) is equivalent to writing the following

class ord =
  fixes less_eq :: "'a ⇒ 'a ⇒ bool"
    and less :: "'a ⇒ 'a ⇒ bool"
begin
  (* ... lemmas ... *)
  definition min :: "'a ⇒ 'a ⇒ 'a" where
    "min a b = (if a ≤ b then a else b)"

  definition  max :: "'a ⇒ 'a ⇒ 'a" where
    "max a b = (if a ≤ b then b else a)"
end

2.12.1.3 Instantiating fun

Functions are partially ordered. For example f(x)=2*x is “obviously” greater than g(x)=x because g(x) ≤ f(x)for all x. This is proved as follows.

(* an auxiliary lemma similar to Nat.nat_mult_1:"1 * x = x" *)
lemma mul_1_I : "(x::nat) = 1 * x" by (rule sym, rule Nat.nat_mult_1)

theorem "(λ x::nat . x) ≤ (λ x::nat . 2*x)"
  apply(rule le_funI) (* goal: "⋀x. x ≤ 2 * x" *)
  apply(subst mul_1_I) (* goal: "⋀x. 1 * x ≤ 2 * x" *)
  apply(rule mult_le_mono1) (* goal: "⋀x. 1 ≤ 2", mult_le_mono1: "i ≤ j ⟹ i*k ≤ j*k" *)
  apply(simp)
  done

The instantiation of ord for function type 'a ⇒ 'b (also denoted by 'a 'b fun) is as follows

instantiation "fun" :: (type, ord) ord
begin

definition
  le_fun_def: "f ≤ g ⟷ (∀x. f x ≤ g x)"

definition
  "(f::'a ⇒ 'b) < g ⟷ f ≤ g ∧ ¬ (g ≤ f)"

instance ..

end

The preorder and order do not introduce and new operations so instantiating them only requires proofs of a few axioms. This can be done as follows.

instance "fun" :: (type, preorder) preorder proof
qed (auto simp add: le_fun_def less_fun_def
  intro: order_trans order.antisym)

instance "fun" :: (type, order) order proof
qed (auto simp add: le_fun_def intro: order.antisym)

2.12.2 Lattices

2.12.2.1 Motivation of Lattices

Lattices play major role in Boolean algebra, which in turn is a basis that we will need to work with topology, measure theory and later on probability, real analysis and so on.

We mentioned that 'a set is not totally ordered and instead only follows partial order class order.If we attempted to draw a graph of all elements that are less or equal some set {x,y,z}, we would see the following.

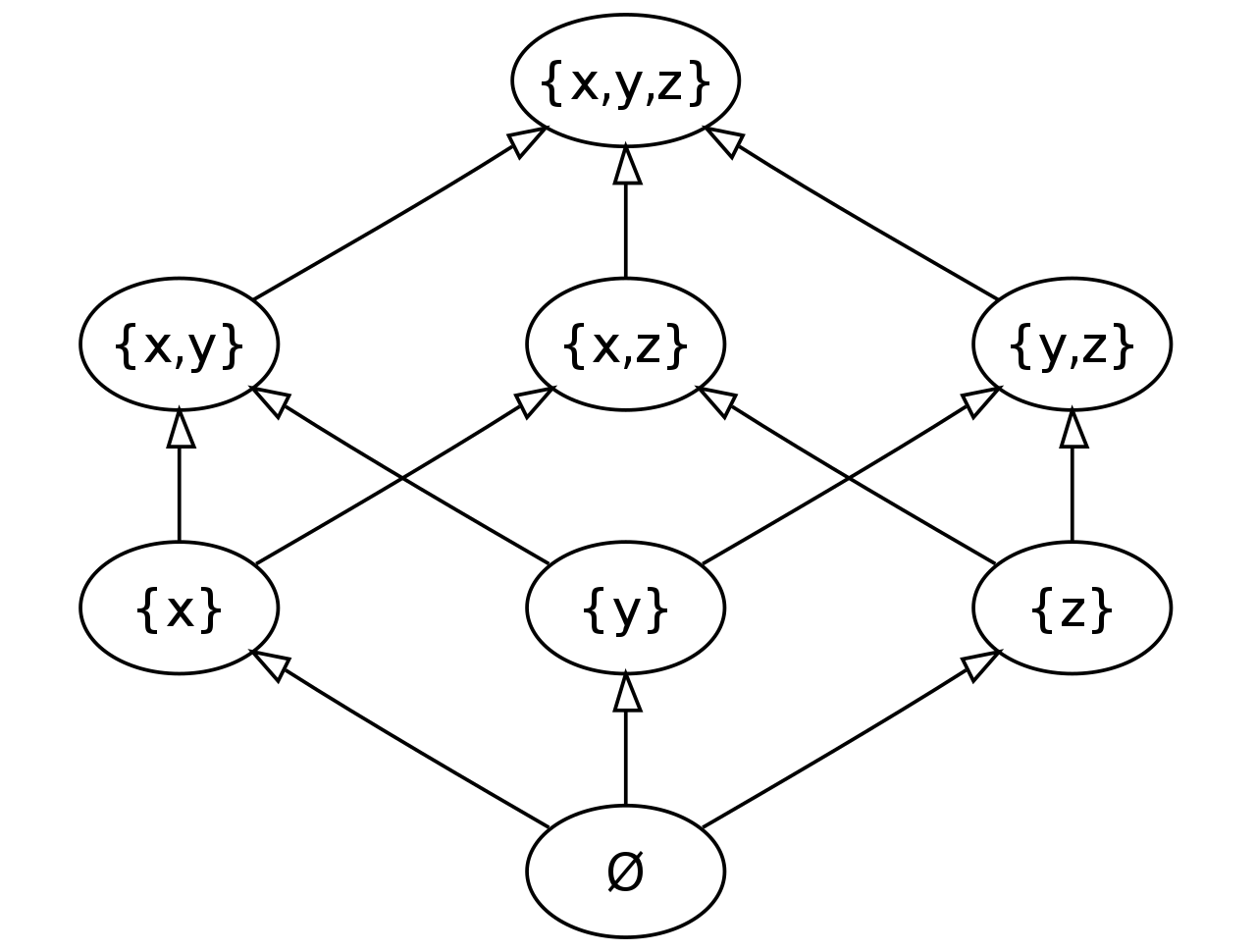
lattice

The empty set is the least element. Every other set is greater than it. Similarly the set {x,y,z} is the greatest element.

By taking the intersection of two sets we can find their greatest common ancestor in the graph. The union of two sets gives us their least common descendant. For example {x,y} ∩ {x,z} = {x} and {z} ∪ {x} = {x,z} (∩ is written \u, ∪ is \i).

A similar pattern applies to totally ordered set of nat numbers. The minimum of two nat’s yields their greatest lower bound. Maximum yields least upper bound. For example max 3 5 = 5 and min 3 5 = 3.

Lattices allow us to generalize this pattern by introducing two operations called meet ∧ (/\ in ASCII) and join ∨ (\/). In the case of nat, minimum is meet and maximum is join. Notice that ∧ and ∨ are also logical conjunction and disjunction, then

theorem "max x (y::nat) = z ⟹ z ≥ x ∧ z ≥ y"
  by auto

theorem "max x (y::nat) = z ⟹ z ≤ x ∨ z ≤ y"
  by auto
  
theorem "min x (y::nat) = z ⟹ z ≥ x ∨ z ≥ y"
  by auto
  
theorem "min x (y::nat) = z ⟹ z ≤ x ∧ z ≤ y"
  by auto

In the case of 'a set, intersection ∩ is meet ∧ and union ∪ is join ∨.

theorem "x ∪ y = {z. z ∈ x ∨ z ∈ y}"
  by auto

theorem "x ∩ y = {z. z ∈ x ∧ z ∈ y}"
  by auto

Therefore, nat is a lattice, 'a set is a lattice and Boolean logic is also a lattice.

In order to avoid confusing meet and join with conjunction and disjunction, there is also an alternative notation. Meet can be written as ⊓, join as ⊔. Meet and join are names of the algebraic operations, just like plus is the name of +. However, the values produced by using these operations are called infimum (for meet) and supremum (for join), just like the result of x+y is called a sum. Infimum and supremum are shorter synonyms for greatest lower bound and least upper bound.

Isabelle uses ⊓ and ⊔ notation instead of ∧ and ∨.

2.12.2.2 Semilattices in Isabelle

The definition of lattices in Isabelle follows a similar philosophy as orders. First we introduce type classes which define the operations of infimum and supremum but don’t provide any axioms.

class inf =
  fixes inf :: "'a ⇒ 'a ⇒ 'a" (infixl "⊓" 70)

class sup =
  fixes sup :: "'a ⇒ 'a ⇒ 'a" (infixl "⊔" 65)

Next we define two “halves” of a lattice (called semilattice)

class semilattice_inf = order + inf +
  assumes inf_le1 [simp]: "x ⊓ y ≤ x"
  and inf_le2 [simp]: "x ⊓ y ≤ y"
  and inf_greatest: "x ≤ y ⟹ x ≤ z ⟹ x ≤ y ⊓ z"

class semilattice_sup = order + sup +
  assumes sup_ge1 [simp]: "x ≤ x ⊔ y"
  and sup_ge2 [simp]: "y ≤ x ⊔ y"
  and sup_least: "y ≤ x ⟹ z ≤ x ⟹ y ⊔ z ≤ x"
begin
(* You might get an error here if you copy-paste this code. Explanation under "Watch out!!" button below. *)
lemma dual_semilattice: "class.semilattice_inf sup greater_eq greater"
  by (rule class.semilattice_inf.intro, rule dual_order)
    (unfold_locales, simp_all add: sup_least)

end

It is a partially ordered (order) type equipped with only one of the two operations. The axioms inf_le1 and inf_le2 (sup_ge1 and sup_ge2) ensure that the element x ⊓ y (x ⊔ y) is lesser (greater) than any of the elements x and y. Axiom inf_greatest (sup_least) says that there is no fourth element that is in-between all three.

The lemma dual_semilattice is the most interesting. To find out what it means, let us unfold the definitions

lemma dual_semilattice: "class.semilattice_inf sup greater_eq greater"
  apply(unfold class.semilattice_inf_def)
  apply(unfold class.semilattice_inf_axioms_def)
  apply(rule conjI) defer (* defer switches order of subgoals *)
  apply(rule conjI) defer
  apply(rule conjI)

which yields 4 goals

 1. ∀x y. y ≤ sup x y
 2. ∀x y z. y ≤ x ⟶ z ≤ x ⟶ sup y z ≤ x
 3. class.order (λx y. y ≤ x) (λx y. y < x)
 4. ∀x y. x ≤ sup x y

Also by searching for name: semilattice_inf_def (and name: semilattice_sup_def) in Query > Find Theorem tab we get

Lattices.class.semilattice_inf_def:
    Lattices.class.semilattice_inf ?inf ?less_eq ?less ≡
    class.order ?less_eq ?less ∧ Lattices.class.semilattice_inf_axioms ?inf ?less_eq
Lattices.class.semilattice_sup_def:
    Lattices.class.semilattice_sup ?sup ?less_eq ?less ≡
    class.order ?less_eq ?less ∧ Lattices.class.semilattice_sup_axioms ?sup ?less_eq

Watch out!!

If you’re trying to copy this code and experiment on your own you might come across this error

Type unification failed: No type arity bool :: sup

Failed to meet type constraint:

Term:  (⊔) :: ??'a ⇒ ??'a ⇒ ??'a
Type:  bool ⇒ bool ⇒ bool

This is because Isabelle might swap the order of arguments.

Playground.class.semilattice_inf_def:
    Playground.class.semilattice_inf ?less_eq ?less ?inf ≡
    class.order ?less_eq ?less ∧ Playground.class.semilattice_inf_axioms ?less_eq ?inf

The fix is to make sure that the order matches again.

lemma dual_semilattice: "class.semilattice_inf greater_eq greater sup"

Therefore, the lemma dual_semilattice states that if we apply to sup greater_eq greater to Lattices.class.semilattice_inf ?inf ?less_eq ?less we obtain a valid lattice. Visually it means that we flip the lattice upside-down. Top element becomes bottom one and vice-versa. Meet becomes join. Less than becomes greater than. Such flipped lattice is called dual.

2.12.2.3 Lattices in Isabelle

Infimum semilattice allows us to find “minimum” of two elements but we have no means of finding the “maximum” one. Supremum semilattice has the opposite problem. Therefore, let us define lattice

class lattice = semilattice_inf + semilattice_sup

as an object equipped with both meet and join. A similar duality holds here as well.

context lattice
begin

lemma dual_lattice: "class.lattice sup (≥) (>) inf"
  by (rule class.lattice.intro,
      rule dual_semilattice,
      rule class.semilattice_sup.intro,
      rule dual_order)
    (unfold_locales, auto)
    
end

Notice that dual_semilattice was proved in a begin and end scope that followed directly after definition of semilattice_sup type class. This time, dual_lattice is defined within context lattice. The two notations are equivalent.

Example

class semilattice_sup = order + sup +
  assumes sup_ge1 [simp]: "x ≤ x ⊔ y"
  and sup_ge2 [simp]: "y ≤ x ⊔ y"
  and sup_least: "y ≤ x ⟹ z ≤ x ⟹ y ⊔ z ≤ x"

(* you can put some code in between or you could even move dual_semilattice to a different file *)

context semilattice_sup
begin

lemma dual_semilattice: "class.semilattice_inf greater_eq greater sup"
  by (rule class.semilattice_inf.intro, rule dual_order)
    (unfold_locales, simp_all add: sup_least)

end

We are going to now state several important algebraic properties of lattices but we will omit the proofs. They are left as an exercise or can be found in Main library.

lemma dual_lattice: "class.lattice sup (≥) (>) inf"

lemma inf_sup_absorb [simp]: "x ⊓ (x ⊔ y) = x"

lemma sup_inf_absorb [simp]: "x ⊔ (x ⊓ y) = x"

lemma distrib_sup_le: "x ⊔ (y ⊓ z) ≤ (x ⊔ y) ⊓ (x ⊔ z)"

lemma distrib_inf_le: "(x ⊓ y) ⊔ (x ⊓ z) ≤ x ⊓ (y ⊔ z)"

lemma distrib_imp1:
  assumes distrib: "⋀x y z. x ⊓ (y ⊔ z) = (x ⊓ y) ⊔ (x ⊓ z)"
  shows "x ⊔ (y ⊓ z) = (x ⊔ y) ⊓ (x ⊔ z)"

lemma distrib_imp2:
  assumes distrib: "⋀x y z. x ⊔ (y ⊓ z) = (x ⊔ y) ⊓ (x ⊔ z)"
  shows "x ⊓ (y ⊔ z) = (x ⊓ y) ⊔ (x ⊓ z)"

The last two of them work only if you assume distrib (distributivity). It is such an important case that it deserved its own type class

class distrib_lattice = lattice +
  assumes sup_inf_distrib1: "x ⊔ (y ⊓ z) = (x ⊔ y) ⊓ (x ⊔ z)"

2.12.3 Top and bottom

2.12.3.1 Type classes

Bottom is an element ⊥ such that every other a is greater or equal ⊥.

class bot =
  fixes bot :: 'a ("⊥")

class order_bot = order + bot +
  assumes bot_least: "⊥ ≤ a"

For example nat has 0 as bottom

value "bot::nat"
(* prints "0" *)

and set has {} as bottom

value "bot::nat set"
(* prints "{}" *)

Remark: if all types are inhabited how can we have empty set?

We mentioned before (2.6.3) that all types in Isabelle are inhabited and therefore we have the undefined axiom. So you might be wondering how is it possible that we have an empty set? The answer is simple. Empty set is an element of type set. Only types must be inhabited. Empty set {} is the proof that 'a set is inhabited for all types 'a.

Analogically the top element ⊤ is the greatest one.

class top =
  fixes top :: 'a ("⊤")

class order_top = order + top +
  assumes top_greatest: "a ≤ ⊤"

A lattice endowed with top or bottom element is defined as bounded lattice

class bounded_lattice_top = lattice + order_top

class bounded_lattice_bot = lattice + order_bot

class bounded_lattice = lattice + order_bot + order_top

Key properties of top and bottom are

lemma inf_bot_left [simp]: "⊥ ⊓ x = ⊥"

lemma inf_bot_right [simp]: "x ⊓ ⊥ = ⊥"

lemma sup_top_left [simp]: "⊤ ⊔ x = ⊤"

lemma sup_top_right [simp]: "x ⊔ ⊤ = ⊤"

2.12.3.2 Instantiating fun

Let us use function type as an the example again (2.12.1.3). The bottom function is a constant function that returns the bottom element of its domain. Analogically for top.

instantiation "fun" :: (type, bot) bot
begin

definition
  "⊥ = (λx. ⊥)" (* recall that λ (written `\l`) is an anonymous function (also known as lambda expression) *)

instance ..

end

instantiation "fun" :: (type, order_bot) order_bot
begin

lemma bot_apply [simp, code]:
  "⊥ x = ⊥"
  by (simp add: bot_fun_def)

instance proof
qed (simp add: le_fun_def)

end

instantiation "fun" :: (type, top) top
begin

definition
  [no_atp]: "⊤ = (λx. ⊤)" 

instance ..

end

instantiation "fun" :: (type, order_top) order_top
begin

lemma top_apply [simp, code]:
  "⊤ x = ⊤"
  by (simp add: top_fun_def)

instance proof
qed (simp add: le_fun_def)

end

If the code above throws parsing errors, it might be because symbols ⊥ and ⊤ are not available in your context. The simplest fix is to replace them with bot and top.

2.12.4 Boolean algebra

Everything we’ve discussed so far comes together in form of Boolean algebra.

class boolean_algebra = distrib_lattice + bounded_lattice + minus + uminus +
  assumes inf_compl_bot: ‹x ⊓ - x = ⊥›
    and sup_compl_top: ‹x ⊔ - x = ⊤›
  assumes diff_eq: ‹x - y = x ⊓ - y›

It is a bounded lattice with distributivity property x ⊔ (y ⊓ z) = (x ⊔ y) ⊓ (x ⊔ z) which additionally also contains negation operation called minus

class minus =
  fixes minus :: "'a ⇒ 'a ⇒ 'a"  (infixl "-" 65)
  
(* uminus is just unary version of minus *)
class uminus =
  fixes uminus :: "'a ⇒ 'a"  ("- _" [81] 80)

There are two famous examples of Boolean algebra.

2.12.4.1 Instantiating bool

The set of numbers {0,1}, also known as bool type.

value "bot::bool" (* "False" *)
value "top::bool" (* "True" *)
value "-True" (* "False" *)
value "¬True" (* "False", symbol ¬ is written as ~ in ASCII *)
value "True ∧ False" (* "False" *)
value "inf True False" (* "False" *)
value "True ∨ False" (* "True" *)
value "sup True False" (* "False" *)

The instantiation looks as follows.

instantiation bool :: boolean_algebra
begin

definition bool_Compl_def [simp]: "uminus = Not"

definition bool_diff_def [simp]: "A - B ⟷ A ∧ ¬ B"

definition [simp]: "P ⊓ Q ⟷ P ∧ Q"

definition [simp]: "P ⊔ Q ⟷ P ∨ Q"

instance by standard auto

end

We won’t go into detail because that would require better understanding of bool.

What is bool in Isabelle? Disgression on intuitionistic logic and Coq.

In Isabelle bool is axiomatized as follows

typedecl bool

axiomatization implies :: "[bool, bool] ⇒ bool"  (infixr "⟶" 25)
  and eq :: "['a, 'a] ⇒ bool"
  and The :: "('a ⇒ bool) ⇒ 'a"

This means that everything is defined in terms of implication ⟶. Understanding it would require us to diverge to lambda calculus and intuitionistic logic. In particular False is defined as principle of explosion

definition False :: bool
  where "False ≡ (∀P. P)"

It says that everything (all predicates P) is true. So once you prove False, anything can follow. Negation ¬ P is defined as an implication from which False follows.

definition Not :: "bool ⇒ bool"  ("¬ _" [40] 40)
  where not_def: "¬ P ≡ P ⟶ False"

In Coq, which is based on intuitionistic (constructive) logic, False is a type that has no inhabitant. If False it is impossible to construct and P ⟶ False" says that given P you can construct False, then clearly P must be impossible to construct too. In Coq, types are propositions (theorems), so False is a theorem that cannot be proved. In Isabelle theorems are logical expressions in which bool plays a crucial role. In Coq proofs are algorithms that construct inhabitants of theorems. In Isabelle theorems are not constructive and are instead proved by natural deduction and term rewriting (application of rules and substituions). Many definitions in Isabelle have no computational meaning and can’t be executed. What value command does, is term rewriting, not “algorithm evaluation” like in Coq.

value "{x::bool . True}" (* prints "{True, False}" *)
value "{x::bool . x=False}" (* prints "{False}" *)
value "{x::nat . x=2}" (* Error! *)

The third expression has no algorithmic meaning because nat is infinite.

value  "{1,2} ∪ {3::nat}" (* prints "{1,2,3}" *)
value  "{1,x} ∪ {3::nat}" (* prints "fold insert (List.insert 1 [x]) {3}" *)

The evaluation of second expression gets stuck because term rewriting couldn’t decide whether x=3 or not (if x=3 then outputs would be {1,3}, otherwise it’s {1,3,x}).

2.12.4.2 Instantiating set

The second example, which we will study in greater detail, is set.

Its instantiation is long and complex. Before we present it, let’s first review a few facts about Isabelle’s type classes that we have omitted before (2.10). Consider this (dummy) example.

class a =
  fixes f :: "'a ⇒ 'a"

class b = a +
  assumes "f (f x) = x"

datatype nat = Suc nat | O

instantiation nat :: a
begin
definition f_nat :: "nat ⇒ nat"
  where "f_nat x = x"
instance ..
end

instantiation nat :: b
begin
instance proof
  fix x::nat
  show "f (f x) = x"
    apply(subst f_nat_def)
    apply(rule f_nat_def)
    done
  qed
end

If we have just two type classes a and b, it is not a problem to call instantiation twice. In the case of boolean_algebra the type class hierarchy is considerably richer. We can make our code more compact as follows.

class a =
  fixes f :: "'a ⇒ 'a"

class b = a +
  assumes "f (f x) = x"

datatype nat = Suc nat | O

instantiation nat :: b
begin
definition f_nat :: "nat ⇒ nat"
  where  "f_nat x = x" 
instance proof
  fix x::nat
  show "f (f x) = x"
    by (subst f_nat_def, rule f_nat_def)
  qed
end

Both code snippets are equivalent. Notice that fixes f :: "'a ⇒ 'a" uses “generic” types 'a but later we state that f_nat :: "nat ⇒ nat". Isabelle performs type unification and concludes that 'a=nat. This is how you can specialize types in instantiation.

Now let us recall (2.6.1) the definition of set

typedecl 'a set

axiomatization Collect :: "('a ⇒ bool) ⇒ 'a set"
  and member :: "'a ⇒ 'a set ⇒ bool" 
  where mem_Collect_eq [iff, code_unfold]: "member a (Collect P) = P a"
    and Collect_mem_eq [simp]: "Collect (λx. member x A) = A"

and let’s prove two auxiliary lemmas

lemma set_eqI:
  assumes "⋀x. member x A ⟷ member x B"
  shows "A = B"
proof -
  from assms have "Collect (λ x. member x A) = Collect (λ x. member x B)"
    by simp
  then show ?thesis by simp
qed

lemma set_eq_iff: "A = B ⟷ (∀x. member x A ⟷ member x B)"
  by (auto intro:set_eqI)

which we will now use in the instantiation of boolean_algebra on set

instantiation set :: (type) boolean_algebra
begin

definition less_eq_set
  where "A ≤ B ⟷ (λx. member x A) ≤ (λx. member x B)"

definition less_set
  where "A < B ⟷ (λx. member x A) < (λx. member x B)"

definition inf_set
  where "inf A B = Collect (inf (λx. member x A) (λx. member x B))"

definition sup_set
  where "sup A B = Collect (sup (λx. member x A) (λx. member x B))"

definition bot_set (* appreciate this beauty*)
  where "bot = Collect bot" (* bot on the left is empty set, bot on the right is False *)

definition top_set
  where "top = Collect top"

definition uminus_set
  where "- A = Collect (- (λx. member x A))"

definition minus_set
  where "A - B = Collect ((λx. member x A) - (λx. member x B))"

instance 
  by standard
    (simp_all add: less_eq_set_def less_set_def inf_set_def sup_set_def
      bot_set_def top_set_def uminus_set_def minus_set_def
      less_le_not_le sup_inf_distrib1 diff_eq set_eqI fun_eq_iff
      del: inf_apply sup_apply bot_apply top_apply minus_apply uminus_apply)
end

There is a lot to learn from these code snippets (feel free to copy-paste and investigate them).

First, we notice that proof and qed notation used in proof of set_eqI. It shows that proof/qed can be used anywhere. (Previously we only used it right after instance command, which might make you falsely believe that proof…qed are somehow special to type classes.) We can also see the new notation from … then inside proof of set_eqI. It is one of advantages of proof…qed. We can use it to break up long proofs into smaller “subproofs”. The notation from X have Y by Z says Z is a proof of Y under assumptions X. The keyword assms means that we are using the same assumptions assumes as in the main theorem (in this case assms is "⋀x. member x A ⟷ member x B"). Analogically ?thesis stands for the main goal stated under shows. After then we can use the proved “subtheorem” to prove other things (?thesis in this case). Tactic simp will automatically use it.

Second, if you replace instance by standard with instance proof and your cursor there you will see a total of 16 subgoals to be proved. That’s a lot and most of them are simple. If we used fix and show notation we would have to write 16 times show XXX by simp. The standard by allows us save time and only write simp once (albeit a very large one). Recall (2.4.2) that add after simp means that we instruct automatic theorem prover to use specific theorems in the process, whereas del removes unnecessary theorems (which may cause simp to get stuck and fail) that were previously marked with [simp].

Third, many definitions seem to compare lambda functions, e.g. (λx. member x A) ≤ (λx. member x B). Does it mean that functions are lattices? This leads us to the next example.

2.12.4.3 Instanting fun

The meet of two functions is defined as meet of the values they return. Same for join and minus. If the function domain is a lattice then clearly the function itself must also be a lattice.

instantiation "fun" :: (type, semilattice_sup) semilattice_sup
begin

definition "f ⊔ g = (λx. f x ⊔ g x)"

lemma sup_apply [simp, code]: "(f ⊔ g) x = f x ⊔ g x"
  by (simp add: sup_fun_def)

instance
  by standard (simp_all add: le_fun_def)

end

instantiation "fun" :: (type, semilattice_inf) semilattice_inf
begin

definition "f ⊓ g = (λx. f x ⊓ g x)"

lemma inf_apply [simp, code]: "(f ⊓ g) x = f x ⊓ g x"
  by (simp add: inf_fun_def)

instance by standard (simp_all add: le_fun_def)

end

instance "fun" :: (type, lattice) lattice ..

instance "fun" :: (type, distrib_lattice) distrib_lattice
  by standard (rule ext, simp add: sup_inf_distrib1)

instance "fun" :: (type, bounded_lattice) bounded_lattice ..

instantiation "fun" :: (type, uminus) uminus
begin

definition fun_Compl_def: "- A = (λx. - A x)"

lemma uminus_apply [simp, code]: "(- A) x = - (A x)"
  by (simp add: fun_Compl_def)

instance ..

end

instantiation "fun" :: (type, minus) minus
begin

definition fun_diff_def: "A - B = (λx. A x - B x)"

lemma minus_apply [simp, code]: "(A - B) x = A x - B x"
  by (simp add: fun_diff_def)

instance ..

end

2.12.5 Sets

2.12.5.1 Basic properties

We are going to gloss over some important properties of set which we will frequently use in next chapters.

The empty set {} is syntactic sugar for bot.

abbreviation empty :: "'a set" ("{}")
  where "{} ≡ bot"

Empty set together with insert allows us to define any finite set (can you think of inductive definition?)

definition insert :: "'a ⇒ 'a set ⇒ 'a set"
  where insert_compr: "insert a B = {x. x = a ∨ x ∈ B}"

The subset ⊂ operation is syntactic sugar for lattice’s partial order.

abbreviation subset :: "'a set ⇒ 'a set ⇒ bool"
  where "subset ≡ less"

abbreviation subset_eq :: "'a set ⇒ 'a set ⇒ bool"
  where "subset_eq ≡ less_eq"

notation
  subset  ("'(⊂')") and
  subset  ("(_/ ⊂ _)" [51, 51] 50) and
  subset_eq  ("'(⊆')") and
  subset_eq  ("(_/ ⊆ _)" [51, 51] 50)

Here are some crucial properties useful for proofs.

lemma subsetI [intro!]: "(⋀x. x ∈ A ⟹ x ∈ B) ⟹ A ⊆ B"
  by (simp add: less_eq_set_def le_fun_def)

lemma subsetD [elim, intro?]: "A ⊆ B ⟹ c ∈ A ⟹ c ∈ B"
  by (simp add: less_eq_set_def le_fun_def)

lemma subset_eq: "A ⊆ B ⟷ (∀x∈A. x ∈ B)"
  by blast

lemma contra_subsetD [no_atp]: "A ⊆ B ⟹ c ∉ B ⟹ c ∉ A"
  by blast

Most of them are proved by blast which is similar to auto but more powerful some situations.

Very often we might want to use bounded universal ∀x∈X.P x and existential ∃x∈X.P x quantifiers, whose domain restricted to a certain set X. This is done using Ball and Bex

definition Ball :: "'a set ⇒ ('a ⇒ bool) ⇒ bool"
  where "Ball A P ⟷ (∀x. x ∈ A ⟶ P x)"   ― ‹bounded universal quantifiers›

definition Bex :: "'a set ⇒ ('a ⇒ bool) ⇒ bool"
  where "Bex A P ⟷ (∃x. x ∈ A ∧ P x)"   ― ‹bounded existential quantifiers›

along with several introduction and elimination rules (essential for many proofs)

lemma ballI [intro!]: "(⋀x. x ∈ A ⟹ P x) ⟹ ∀x∈A. P x"
  by (simp add: Ball_def)

lemma bspec [dest?]: "∀x∈A. P x ⟹ x ∈ A ⟹ P x"
  by (simp add: Ball_def)

lemma ballE [elim]: "∀x∈A. P x ⟹ (P x ⟹ Q) ⟹ (x ∉ A ⟹ Q) ⟹ Q"
  unfolding Ball_def by blast

lemma bexI [intro]: "P x ⟹ x ∈ A ⟹ ∃x∈A. P x"
  unfolding Bex_def by blast

lemma bexCI: "(∀x∈A. ¬ P x ⟹ P a) ⟹ a ∈ A ⟹ ∃x∈A. P x"
  unfolding Bex_def by blast

lemma bexE [elim!]: "∃x∈A. P x ⟹ (⋀x. x ∈ A ⟹ P x ⟹ Q) ⟹ Q"
  unfolding Bex_def by blast

lemma ball_conj_distrib: "(∀x∈A. P x ∧ Q x) ⟷ (∀x∈A. P x) ∧ (∀x∈A. Q x)"
  by blast

lemma bex_disj_distrib: "(∃x∈A. P x ∨ Q x) ⟷ (∃x∈A. P x) ∨ (∃x∈A. Q x)"
  by blast

When working with Isabelle you will notice that nearly every operation comes with several congruence rules. Their purpose is to prove that some objects are equal if their “contents” are equal. The earlier theorems set_eq_iff and set_eqI might also be considered
congruence rules but most often mathematicians call it the rule of extensionality. Below are congruence rules for Bex and Ball

lemma ball_cong:
  "⟦ A = B;  ⋀x. x ∈ B ⟹ P x ⟷ Q x ⟧ ⟹
    (∀x∈A. P x) ⟷ (∀x∈B. Q x)"
by (simp add: Ball_def)


lemma bex_cong:
  "⟦ A = B;  ⋀x. x ∈ B ⟹ P x ⟷ Q x ⟧ ⟹
    (∃x∈A. P x) ⟷ (∃x∈B. Q x)"
by (simp add: Bex_def cong: conj_cong)

The notation ⟦ P ; Q ⟧ ⟹ R is a syntactic sugar for P⟹Q⟹R.

There are dozens other smaller lemmas, but you should be able to easily find them in the search tab as necessary.

A very frequently used notation for set containing all elements (top)

abbreviation UNIV :: "'a set"
  where "UNIV ≡ top"

lemma UNIV_def: "UNIV = {x. True}"
  by (simp add: top_set_def top_fun_def)

lemma UNIV_I [simp]: "x ∈ UNIV"
  by (simp add: UNIV_def)

The advantage of using {} and UNIV over bot and top is that the former are unambiguously sets, whereas the interpretation of latter depends on the context.

2.12.5.2 Operations on sets

We already discussed that unions and intersections are the operations join and meet defined for any lattice. The boolean_algebra introduces a new - operation, which in the context of sets corresponds to set complement.
It’s most important properties (introduction and elimination rules) are the following.

lemma Compl_iff [simp]: "c ∈ - A ⟷ c ∉ A"
  by (simp add: fun_Compl_def uminus_set_def)

lemma ComplI [intro!]: "(c ∈ A ⟹ False) ⟹ c ∈ - A"
  by (simp add: fun_Compl_def uminus_set_def) blast

lemma ComplD [dest!]: "c ∈ - A ⟹ c ∉ A"
  by simp

lemma Compl_eq: "- A = {x. ¬ x ∈ A}"
  by blast

For intersection we have

lemma IntI [intro!]: "c ∈ A ⟹ c ∈ B ⟹ c ∈ A ∩ B"
  by simp
  
lemma IntD1: "c ∈ A ∩ B ⟹ c ∈ A"
  by simp

lemma IntD2: "c ∈ A ∩ B ⟹ c ∈ B"
  by simp

and for union there is

lemma UnI1 [elim?]: "c ∈ A ⟹ c ∈ A ∪ B"
  by simp

lemma UnI2 [elim?]: "c ∈ B ⟹ c ∈ A ∪ B"
  by simp

lemma UnE [elim!]: "c ∈ A ∪ B ⟹ (c ∈ A ⟹ P) ⟹ (c ∈ B ⟹ P) ⟹ P"
  unfolding Un_def by blast

There is the power set operation, which is specific to set type only (not part of boolean_algebra).

definition Pow :: "'a set ⇒ 'a set set"
  where Pow_def: "Pow A = {B. B ⊆ A}"

We can apply all elements of some set to a function. This operation is called function image.

definition image :: "('a ⇒ 'b) ⇒ 'a set ⇒ 'b set"    (infixr "`" 90)
  where "f ` A = {y. ∃x∈A. y = f x}"

lemma image_eqI [simp, intro]: "b = f x ⟹ x ∈ A ⟹ b ∈ f ` A"
  unfolding image_def by blast

lemma imageI: "x ∈ A ⟹ f x ∈ f ` A"
  by (rule image_eqI) (rule refl)

An image taken over the full set UNIV is called function’s range

abbreviation range :: "('a ⇒ 'b) ⇒ 'b set"  ― ‹of function›
  where "range f ≡ f ` UNIV"

These are some notable introduction and elimination rules useful for proofs

lemma range_eqI: "b = f x ⟹ b ∈ range f"
  by simp

lemma rangeI: "f x ∈ range f"
  by simp

lemma rangeE [elim?]: "b ∈ range (λx. f x) ⟹ (⋀x. b = f x ⟹ P) ⟹ P"
  by (rule imageE)

lemma range_subsetD: "range f ⊆ B ⟹ f i ∈ B"
  by blast

2.12.5.3 Injection, surjection, bijection

We defined function images and ranges (2.12.5.2). Now we can use those definitions to introduce injective, surjective and bijective functions.

definition inj_on :: "('a ⇒ 'b) ⇒ 'a set ⇒ bool"  ― ‹injective›
  where "inj_on f A ⟷ (∀x∈A. ∀y∈A. f x = f y ⟶ x = y)"

The definition inj_on states that some function f :: 'a ⇒ 'b with domain A::'a set is injective if and only if (⟷) the outputs f x and f y are equal only when inputs x and y are equal (or more intuitively - every element x∈A is mapped to a different output f x). Actually f’s domain is the whole set 'a but inj_on only considers injectivity f when domain is restricted to the subset A. For example

value "inj_on (λ x::bool . True) {True}" (* yields "True" *)
value "inj_on (λ x::bool . True) {False}" (* yields "True" *) 
value "inj_on (λ x::bool . True) {False, True}" (* yields "False" *)

Surjectivity is expressed as f ` A = B, which means that every element y∈B has some corresponding input x∈A that produces it (f x = y). Recall (2.12.5.2) that this is in fact the definition of image.

definition image :: "('a ⇒ 'b) ⇒ 'a set ⇒ 'b set"    (infixr "`" 90)
  where "f ` A = {y. ∃x∈A. y = f x}"

Two functions are bijective if they are both injective and surjective at the same time

definition bij_betw :: "('a ⇒ 'b) ⇒ 'a set ⇒ 'b set ⇒ bool"  ― ‹bijective›
  where "bij_betw f A B ⟷ inj_on f A ∧ f ` A = B"

Very commonly we are interested in studying these properties on the entire set 'a rather than some subset A. Therefore Isabelle defines abbreviations.

abbreviation inj :: "('a ⇒ 'b) ⇒ bool"
  where "inj f ≡ inj_on f UNIV"

abbreviation surj :: "('a ⇒ 'b) ⇒ bool"
  where "surj f ≡ range f = UNIV"

abbreviation bij :: "('a ⇒ 'b) ⇒ bool"
  where "bij f ≡ bij_betw f UNIV UNIV"

Bijectivity means that there is one-to-one correspondence between elements of A and B. This is captured by this lemma.

lemma bij_pointE:
  assumes "bij f"
  obtains x where "y = f x" and "⋀x'. y = f x' ⟹ x' = x"
proof -
  from assms have "inj f" by (rule bij_is_inj)
  moreover from assms have "surj f" by (rule bij_is_surj)
  then have "y ∈ range f" by simp
  ultimately have "∃!x. y = f x" by (simp add: range_ex1_eq)
  with that show thesis by blast
qed

This proof uses Isar syntax and relies on several other lemmas defined in Main. We won’t go through them as it is not necessary to memorize entirety of Main (good skills in using search tab are enough). The keyword obtains means that we can always find an x that fulfills some requirements where. In this case for every y there exists some x that yields y = f x
and there is no other x' is produces y. You may observe that obtains corresponds to existential quantifier, while fixes corresponds to universal.

In topology especially important is the concept of inverse images which are sets of all inputs x that yield output in some set B

definition vimage :: "('a ⇒ 'b) ⇒ 'b set ⇒ 'a set"  (infixr "-`" 90)
  where "f -` B ≡ {x. f x ∈ B}"

In Isabelle inverse function is defined using Hilbert’s epsilon operator SOME

definition inv_into :: "'a set ⇒ ('a ⇒ 'b) ⇒ ('b ⇒ 'a)" where
"inv_into A f = (λx. SOME y. y ∈ A ∧ f y = x)"

lemma inv_into_def2: "inv_into A f x = (SOME y. y ∈ A ∧ f y = x)"
by(simp add: inv_into_def)

abbreviation inv :: "('a ⇒ 'b) ⇒ ('b ⇒ 'a)" where
"inv ≡ inv_into UNIV"

This means that for every function f :: 'a ⇒ 'b we can produce its inverse function inv f :: 'b ⇒ 'a by arbitrarily choosing SOME element y::'a that maps f y = x. Once we choose y for a specific x then we have to stay consistent. We can’t choose different y each time we use (inv f) x. Moreover if there does not exist any y that fulfills property y ∈ A ∧ f y = x then an arbitrary y::'a will be chosen (which must exist because all types are inhabited 2.6.3). There may be many different ways to choose y and therefore there may be many different candidate functions for an inverse inv f. We don’t know which one of them will be picked by Isabelle (in fact Isabelle doesn’t “physically” pick any). Proofs of any theorem involving inv f must work for all possible choices of inv f. Due to this it is generally difficult to reason about inv f. Mathematicians don’t like it and they would typically say that inverse functions don’t exist unless f is bijective. Then inv f is unique. For each x there is only one y that can be chosen by SOME y.

Hilbert epsilon operator axiomatization

The Hilbert choice is axiomatized in Hilbert_Choice.thy theory

axiomatization Eps :: "('a ⇒ bool) ⇒ 'a"
  where someI: "P x ⟹ P (Eps P)"

syntax (epsilon)
  "_Eps" :: "pttrn ⇒ bool ⇒ 'a"  ("(3ϵ_./ _)" [0, 10] 10)
syntax (input)
  "_Eps" :: "pttrn ⇒ bool ⇒ 'a"  ("(3@ _./ _)" [0, 10] 10)
syntax
  "_Eps" :: "pttrn ⇒ bool ⇒ 'a"  ("(3SOME _./ _)" [0, 10] 10)
translations
  "SOME x. P" ⇌ "CONST Eps (λx. P)"

Bijections have the following special properties. Inverse of inverse is the identity function.

lemma inv_inv_eq: "bij f ⟹ inv (inv f) = f"
  by (rule inv_equality) (auto simp add: bij_def surj_f_inv_f)

The inverse image of f is equal to the image of inverse inf v.

lemma bij_vimage_eq_inv_image:
  assumes "bij f"
  shows "f -` A = inv f ` A"
proof
  show "f -` A ⊆ inv f ` A"
    using assms by (blast intro: bij_is_inj [THEN inv_into_f_f, symmetric])
  show "inv f ` A ⊆ f -` A"
    using assms by (auto simp add: bij_is_surj [THEN surj_f_inv_f])
qed

2.13 Function sets

Function type 'a => 'b is built into Isabelle, on par with meta-logic operations 2.7. All functions in Isabelle are total \(\ref{primrec-functions}\) and therefore 'a => 'b assigns some 'b to every 'b. Sometimes we would like to work with functions as if they were sets.

We can use restrict f A

definition "restrict" :: "('a ⇒ 'b) ⇒ 'a set ⇒ 'a ⇒ 'b"
  where "restrict f A = (λx. if x ∈ A then f x else undefined)"

in order to restrict f’s domain from 'a to only a subset A::'a set. Such restricted function would then be partial (there would be no output assigned to inputs not in A) but that would violate Isabelle’s assumption of all functions being total. Therefore, we cannot actually create partial functions and must instead resort to returning undefined if input is not in A. For most purposes this is enough and if it is not, then we can use relations ('a × 'b) set or 'a ⇒ 'b ⇒ bool as in Relation.thy theory (in Main) or 2.11.2.

Define extensional A as the set of all partial functions from 'a to 'b that are restricted to subset A::'a set.

definition extensional :: "'a set ⇒ ('a ⇒ 'b) set"
  where "extensional A = {f. ∀x. x ∉ A ⟶ f x = undefined}"

Define set A → B of all functions from A to B as

abbreviation funcset :: "'a set ⇒ 'b set ⇒ ('a ⇒ 'b) set"  (infixr "→" 60)
  where "A → B ≡ Pi A (λ_. B)"

which is a special case of Pi function

definition Pi :: "'a set ⇒ ('a ⇒ 'b set) ⇒ ('a ⇒ 'b) set"
  where "Pi A F = {f. ∀x. x ∈ A ⟶ f x ∈ F x}"

Usually we use symbol Π to denote Pi

syntax
  "_Pi" :: "pttrn ⇒ 'a set ⇒ 'b set ⇒ ('a ⇒ 'b) set"  ("(3Π _∈_./ _)"   10)
  "_lam" :: "pttrn ⇒ 'a set ⇒ ('a ⇒ 'b) ⇒ ('a ⇒ 'b)"  ("(3λ_∈_./ _)" [0,0,3] 3)
translations
  "Π x∈A. B" ⇌ "CONST Pi A (λx. B)"
  "λx∈A. f" ⇌ "CONST restrict (λx. f) A"

Note that λx∈A. f belongs to the set extensional A.

The Π plays a major role in dependent type theory. Its definition x ∈ A ⟶ f x ∈ F x says that A is the domain of f but the range is not F. Instead f x can only take values from the set F x which itself depends on x. In the special case A → B the range is defined as a constant F = (λ_. B), which equivalently could have been defined as

abbreviation funcset :: "'a set ⇒ 'b set ⇒ ('a ⇒ 'b) set"  (infixr "→" 60)
  where "A → B ≡ {f. ∀x. x ∈ A ⟶ f x ∈ B}"

The definition of A → B does not tell us anything about f when x ∉ A. For this purpose there is an analogical notion of partial Pi functions

definition PiE :: "'a set ⇒ ('a ⇒ 'b set) ⇒ ('a ⇒ 'b) set"
  where "PiE S T = Pi S T ∩ extensional S"

abbreviation "Pi⇩E A B ≡ PiE A B"

Symbol ⇩ stands for subscript notation

This symbol is written as \<^sub> (or simply \sub) and it allows us to write in subscript. Any letter you type afterwards is printed in subscript in jEdit. It’s very similar to the \b for bold font 2.14.1.

together with a very similar function notation A →⇩E B which has E is subscript

abbreviation extensional_funcset :: "'a set ⇒ 'b set ⇒ ('a ⇒ 'b) set" (infixr "→⇩E" 60)
  where "A →⇩E B ≡ (Π⇩E i∈A. B)"

Notice that in Π⇩E i∈A. B the variable i is not necessary and B is constant. Therefore, writing A →⇩E B is the equivalent to (A → B) ∩ extensional A.

The subscript E stands for extensional functions which means that in order to check whether two partial extensional functions x ∈ k →⇩E s and y ∈ k →⇩E s are equal, it suffices to show that x i = y i only within the domain i ∈ k. We know that outside the domain k the functions are undefined, therefore x i = undefined = y i for i ∉ k.

lemma PiE_ext: "⟦x ∈ PiE k s; y ∈ PiE k s; ⋀i. i ∈ k ⟹ x i = y i⟧ ⟹ x = y"
  by (metis ext PiE_E)

This would not be possible if x and y belonged to k → s, because then x and y might be different outside k. This is why defining restrict as above is so important.

Function composition is defined as

definition "compose" :: "'a set ⇒ ('b ⇒ 'c) ⇒ ('a ⇒ 'b) ⇒ ('a ⇒ 'c)"
  where "compose A g f = (λx∈A. g (f x))"

It respects partial domains as expected

lemma funcset_compose: "f ∈ A → B ⟹ g ∈ B → C ⟹ compose A g f ∈ A → C"
  by (simp add: Pi_def compose_def restrict_def)

and has a few

other obvious properties.

lemma compose_assoc:
  assumes "f ∈ A → B"
  shows "compose A h (compose A g f) = compose A (compose B h g) f"
  using assms by (simp add: fun_eq_iff Pi_def compose_def restrict_def)

lemma compose_eq: "x ∈ A ⟹ compose A g f x = g (f x)"
  by (simp add: compose_def restrict_def)

lemma surj_compose: "f ` A = B ⟹ g ` B = C ⟹ compose A g f ` A = C"
  by (auto simp add: image_def compose_eq)

An important concept from type theory is covariance and contravariance and they are defined as follows. The Pi functions are covariant in their second argument

lemma Pi_mono: "(⋀x. x ∈ A ⟹ B x ⊆ C x) ⟹ Pi A B ⊆ Pi A C"
  by auto

and contravariant in their first argument

lemma Pi_anti_mono: "A' ⊆ A ⟹ Pi A B ⊆ Pi A' B"
  by auto

2.14 Locales

So far we’ve been using type classes to define all concepts. This allowed us to abstract many mathematical objects into one common interface. As useful as they are, type classes have a certain limitation. We can only instantiate a type class once on each type. There are many cases when we would like to change the type class definition depending on the context. For example we could define order as lexicographic order or length-lexicographic order or reverse-lexicographic order and so on. We could define norm on real vectors as ℓ¹ or ℓ² norm. In order to have more flexibility, we can use locales. They are the primary tool that facilitates working with abstract algebra. It will also allow us to better understand type classes which are a special case of locales.

I recommend a great tutorial written by one of the professors who supervised development of locales in Isabelle.

2.14.1 Semigroups

The simplest possible algebraic structure are semigroups

locale semigroup =
  fixes f :: "'a ⇒ 'a ⇒ 'a"  (infixl "❙*" 70)
  assumes assoc [ac_simps]: "a ❙* b ❙* c = a ❙* (b ❙* c)"

What are the vertical bars?

The strangely looking bars are Isabelles way of marking bold symbols. If you type it in jEdit it will look much better.

You need to type \<^bold> (usually just typing \b is enough for autosuggestion to pop up). This will give you the bar ❙. Any symbol you place after the bar will become bold

.

The typical example of a semigroup are strings together with string concatenation. While Isabelle has a dedicated string type

type_synonym string = "char list" (* can store ASCII/Unicode *)

this is not what I mean by strings. To a mathematician strings are exactly the type 'a list where 'a is typically called an alphabet.

The semigroup locale is a predicate. If you search for semigroup in the Find Theorem tab you will see the following definitions

semigroup.assoc: semigroup ?f ⟹ ?f (?f ?a ?b) ?c = ?f ?a (?f ?b ?c)
semigroup_def: semigroup ?f ≡ ∀a b c. ?f (?f a b) c = ?f a (?f b c)
semigroup.intro: (⋀a b c. ?f (?f a b) c = ?f a (?f b c)) ⟹ semigroup ?f

The semigroup_def says that semigroup f holds if and only if f (f a b) c = f a (f b c) holds for all a, b and c. Therefore, the type of semigroup is ('a ⇒ 'a ⇒ 'a) ⇒ bool. If we use fixes multiple times to introduce more constants/functions, the locale will take all of them as arguments. If

locale x =
   fixes a :: "'a"
   fixes b :: "'b"
   fixes c :: "'c"

then x :: 'a ⇒ 'b ⇒ 'c ⇒ bool.

We can interpretation to tell Isabelle which functions f satisfy the predicate semigroup.

(* use this to avoid notation conflicts with Main library*)
no_notation append (infixr "@" 65) and Nil ("[]") and Cons (infixr "#" 65)

datatype 'a list =  Nil  ("[]")  | Cons (hd: 'a) (tl: "'a list")  (infixr "#" 65)

primrec append :: "'a list ⇒ 'a list ⇒ 'a list" (infixr "@" 65) where
append_Nil: "[] @ ys = ys" |
append_Cons: "(x#xs) @ ys = x # xs @ ys"

interpretation append: semigroup append
proof
  fix xs ys zs :: "'a list"
  show "(xs @ ys) @ zs = xs @ (ys @ zs)"
    by (induct xs) simp_all
qed 

In this example we define append (concatenation of lists 2.9) and show that it is an associative operation on lists.

2.14.2 Monoids

Monoids are semigroups that have a special member, called neutral element, which works the same way as 1 works in multiplication, that is 1 * x = x and x * 1 = x.

locale monoid = semigroup +
  fixes z :: 'a ("❙1")
  assumes left_neutral [simp]: "❙1 ❙* a = a"
  assumes right_neutral [simp]: "a ❙* ❙1 = a"

Again we can lookup the type of monoid to see how locale composition + stacks the fixes on top of each other.

monoid.axioms(1): monoid TYPE(?'c) ?f ⟹ semigroup ?f
monoid.axioms(2): monoid TYPE(?'c) ?f ⟹ monoid_axioms TYPE(?'c)
monoid_def: monoid TYPE(?'c) ?f ≡ semigroup ?f ∧ monoid_axioms TYPE(?'c)
monoid.left_neutral: monoid TYPE(?'c) ?f ⟹ 1 * ?a = ?a
monoid.right_neutral: monoid TYPE(?'c) ?f ⟹ ?a * 1 = ?a
monoid.intro: semigroup ?f ⟹ monoid_axioms TYPE(?'c) ⟹ monoid TYPE(?'c) ?f

We can add interpretation for both semigroup and monoid in one go. For example lists are monoids too.

datatype 'a list =  Nil  ("[]")  | Cons (hd: 'a) (tl: "'a list")  (infixr "#" 65)

primrec append :: "'a list ⇒ 'a list ⇒ 'a list" (infixr "@" 65) where
append_Nil: "[] @ ys = ys" |
append_Cons: "(x#xs) @ ys = x # xs @ ys"

interpretation append: monoid append Nil
proof
  fix xs ys zs :: "'a list"
  show "(xs @ ys) @ zs = xs @ (ys @ zs)"
    by (induct xs) simp_all
  show "xs @ [] = xs"
    by (induct xs) simp_all
qed simp

Note that every semigroup can be extended to become a monoid. Hence, all examples of semigroups are also (or could become) examples of monoids and vice-versa.

Monoids and semigroups play a crucial role in formal languages and automata theory. We won’t be going into those now.

2.14.3 Groups

Groups are the next step after monoids. They specify that every element has an inverse

locale group = semigroup +
  fixes z :: 'a ("❙1")
  fixes inverse :: "'a ⇒ 'a"
  assumes group_left_neutral: "❙1 ❙* a = a"
  assumes left_inverse [simp]:  "inverse a ❙* a = ❙1"

For example int is a group if we use plus as the operation ❙* and 0 as the neutral element ❙1. For every number x there exists the negated number inverse x = -x. Then "inverse a ❙* a = ❙1" becomes "-a + a = 0"

A negative example is nat. Natural numbers are not a group because -x does not exist in nat.

Similarly strings are not a group because we would need to have “negative strings” inverse x such that x concatenated with inverse x yields the empty string x @ (inverse x) = []. Interestingly, mathematicians were not discouraged by this and they invented “negative strings” anyway. They don’t call them strings but instead refer to them as words. The group in which concatenating “negative strings” is possible is called the free group.

2.14.4 Group properties

Groups allow us to cancel equal elements on both sides of an equation.

context group begin

lemma left_cancel: "a ❙* b = a ❙* c ⟷ b = c"
proof
  assume "a ❙* b = a ❙* c"
  then have "inverse a ❙* (a ❙* b) = inverse a ❙* (a ❙* c)" by simp
  then have "(inverse a ❙* a) ❙* b = (inverse a ❙* a) ❙* c"
    by (simp only: assoc)
  then show "b = c" by (simp add: group_left_neutral)
qed simp

end

Let us appreciate how readable Isabelle proofs are. We could paraphrase it very intuitively as

\[ a b = a c \] \[ \frac{1}{a} (a b) = \frac{1}{a} (a c) \] \[ (\frac{1}{a} a) b = (\frac{1}{a} a) c \] \[ 1 b = 1 c \] \[ b = c \]

Analogically for the right side

lemma right_cancel: "b ❙* a = c ❙* a ⟷ b = c"
proof
  assume "b ❙* a = c ❙* a"
  then have "b ❙* a ❙* inverse a= c ❙* a ❙* inverse a"
    by simp
  then show "b = c"
    by (simp add: assoc)
qed simp

Every group is a monoid. This is expressed using sublocale command.

context group begin

sublocale monoid
proof
  fix a
  have "inverse a ❙* a = ❙1" by simp
  then have "inverse a ❙* (a ❙* ❙1) = inverse a ❙* a"
    by (simp add: group_left_neutral assoc [symmetric])
  with left_cancel show "a ❙* ❙1 = a"
    by (simp only: left_cancel)
qed (fact group_left_neutral)

end

The inverse element is unique

lemma inverse_unique:
  assumes "a ❙* b = ❙1"
  shows "inverse a = b"
proof -
  from assms have "inverse a ❙* (a ❙* b) = inverse a"
    by simp
  then show ?thesis
    by (simp add: assoc [symmetric])
qed

We omitted specifying that the context is group but if you are going to copy-paste this code and try it yourself, make sure to put it in the right context.

The inverse of neutral element is itself

lemma inverse_neutral [simp]: "inverse ❙1 = ❙1"
  by (rule inverse_unique) simp


lemma inverse_inverse [simp]: "inverse (inverse a) = a"
  by (rule inverse_unique) simp

The inverse can also be multiplied on the right side.

lemma right_inverse [simp]: "a ❙* inverse a = ❙1"
proof -
  have "a ❙* inverse a = inverse (inverse a) ❙* inverse a"
    by simp
  also have "… = ❙1"
    by (rule left_inverse)
  then show ?thesis by simp
qed

Inversion can be distributed over group operation ❙* (usually this operation is called group multiplication).

lemma inverse_distrib_swap: "inverse (a ❙* b) = inverse b ❙* inverse a"
proof (rule inverse_unique)
  have "a ❙* b ❙* (inverse b ❙* inverse a) =
    a ❙* (b ❙* inverse b) ❙* inverse a"
    by (simp only: assoc)
  also have "… = ❙1"
    by simp
  finally show "a ❙* b ❙* (inverse b ❙* inverse a) = ❙1" .
qed

2.14.5 Abelian

When semigroup, monoid or group satisfies the property that a ❙* b = b ❙* c then we call it abelian semigroup, abelian monoid or abelian group.

Here is how abelian semigroups are defined

locale abel_semigroup = semigroup +
  assumes commute [ac_simps]: "a ❙* b = b ❙* a"
begin

lemma left_commute [ac_simps]: "b ❙* (a ❙* c) = a ❙* (b ❙* c)"
proof -
  have "(b ❙* a) ❙* c = (a ❙* b) ❙* c"
    by (simp only: commute)
  then show ?thesis
    by (simp only: assoc)
qed

end

It is a semigroup that additionally satisfies "a ❙* b = b ❙* a" which mathematicians call the commutativity property.

Abelian monoid is defined as

locale comm_monoid = abel_semigroup +
  fixes z :: 'a ("❙1")
  assumes comm_neutral: "a ❙* ❙1 = a"
begin

sublocale monoid
  by standard (simp_all add: commute comm_neutral)

end

2.14.6 Type classes with sublocales

It is possible to first define a locale and prove its various properties and then include it in a type class. This has been done in the case of semigroups as follows.

class plus =
  fixes plus :: "'a ⇒ 'a ⇒ 'a"  (infixl "+" 65)

class semigroup_add = plus +
  assumes add_assoc [algebra_simps, algebra_split_simps, field_simps, field_split_simps]:
    "(a + b) + c = a + (b + c)"
begin

sublocale add: semigroup plus
  by standard (fact add_assoc)

end

There are analogical type classes for monoids and groups. All of the reamining concepts are defined using type classes instead of locales. HOL-Algebra library uses locales and introduces far more advanced objects than Main. We should still be familiar with the type classes because they are later necessary to introduce vector spaces and other objects useful mathematical analysis.

2.15 Archive of formal proofs

However, the right way to formalise advanced algebra is not obvious. During the formal development the user has to decide how mathematical structures should be best organized in the proof assistant so that they can be used mechanically in an efficient way. It is well-known in the Isabelle community that the main algebra library needs to be rebuilt from scratch. In fact, there are many libraries for algebra in Isabelle: HOL-Algebra6 from the previous millennium (1999), the more recent HOL- Computational_Algebra7, and moreover some entries in the Archive of Formal Proofs8 like Groups, Rings and Modules [18] and Vector Spaces [21] among others. As a result, there is a lot of overlapping material, which makes the status of algebra confusing and unclear for the newcomer in the Isabelle world

-- Citation from Simple Type Theory is not too Simple

There is no point in studying legacy code. Instead we will import more modern formalizations from archive of formal proofs. Download the newest version and then follow the installation instructions here.

We are going to use it in subsequent chapters. In order to import any theory from APF, go to the directory where you unzipped afp-current.tar.gz. Inside it there should be thys subdirectory containing many packages. For example you might see there Jacobson_Basic_Algebra and inside it there is Group_Theory.thy. In order to import it use the following code

theory YourTheoryName
  imports "Jacobson_Basic_Algebra.Group_Theory"
begin
  
end