Pertemuan 1 Pendahuluan

1.1 Mengapa Analisis Data Kategorik?

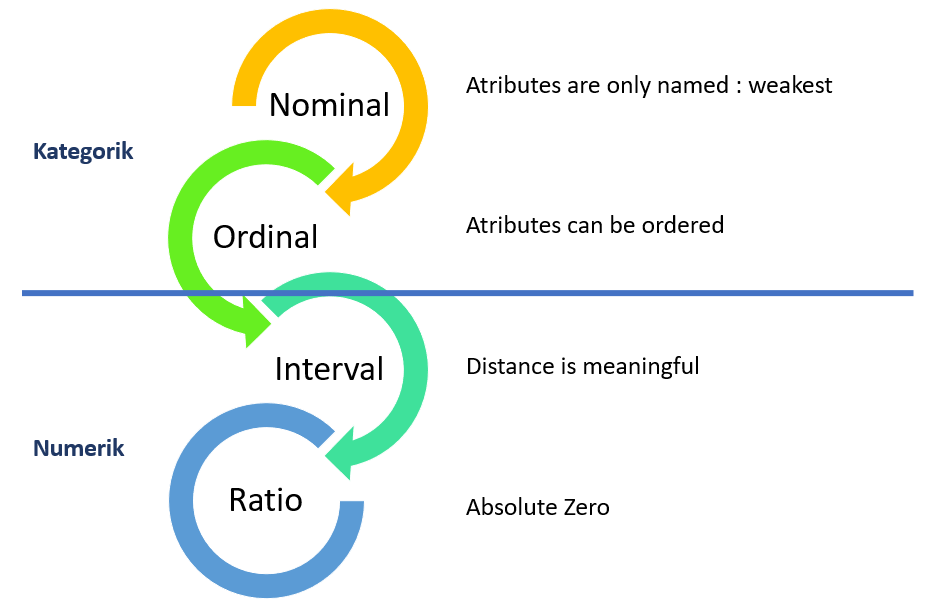
Figure 1.1: Mengapa Analisis Data Kategorik?

Alasan utama kenapa digunakan Analisis Data Kategorik untuk melakukan analisis data pada data dengan tipe nominal dan ordinal adalah tiap skala memiliki karakternya sendiri-sendiri. Penanganan data memerlukan pemahaman karakter data, teknik yang digunakan menyesuaikan karakter data dan informasi yang ingin didapatkan dari data tersebut.

1.2 Penyajian Data Kategorik melalui Tabel

Dalam analisis data kategorik, analisis yang menarik dilakukan adalah analisis tabulasi silang/tabel kontingensi. Dalam software R tabulasi silang bisa disusun dari data raw (data individu) atau bisa diinput secara langsung tabulasi silang tersebut.

Cara pertama yaitu membentuk tabulasi silang dari data raw yang diilustrasikan dengan file responden sebagai berikut:

Import Data ke R

Pada proses ini, data sudah berformat .csv, sehingga bisa dimasukkan ke R dengan fungsi read.csv. Anda bisa download terlebih dahulu file responden.csv

responden <- read.csv("data/responden.csv",
                      sep=",",
                      header=TRUE)

Jika ingin mengetahui summary atau ringkasan dari data tersebut, bisa digunakan fungsi summary

summary(responden)

##    Responden       J.Kelamin     T.Pendidikan   T.Pendapatan
##  Min.   : 1.00   Min.   :0.00   Min.   :1.00   Min.   :1.0  
##  1st Qu.:13.25   1st Qu.:1.00   1st Qu.:1.25   1st Qu.:3.0  
##  Median :25.50   Median :1.00   Median :2.00   Median :4.0  
##  Mean   :25.50   Mean   :0.82   Mean   :2.48   Mean   :3.6  
##  3rd Qu.:37.75   3rd Qu.:1.00   3rd Qu.:4.00   3rd Qu.:5.0  
##  Max.   :50.00   Max.   :1.00   Max.   :4.00   Max.   :6.0

Jika ingin mengetahui, beberapa data dari objek responden, bisa menggunakan fungsi head, secara default akan dikeluarkan 6 baris teratas.

head(responden)

##   Responden J.Kelamin T.Pendidikan T.Pendapatan
## 1         1         1            1            4
## 2         2         1            3            6
## 3         3         1            2            4
## 4         4         1            2            5
## 5         5         1            4            4
## 6         6         1            4            1

Jika ingin melihat 5 baris teratas saja, maka bisa menggunakan opsi n, sebagai berikut

head(responden,
     n=5)

##   Responden J.Kelamin T.Pendidikan T.Pendapatan
## 1         1         1            1            4
## 2         2         1            3            6
## 3         3         1            2            4
## 4         4         1            2            5
## 5         5         1            4            4

1.2.1 Membuat Tabel Kontingensi dari Data

Untuk membuat Tabel Kontingensi dari Data responden, digunakan fungsi table

tabel1<-table(responden$J.Kelamin,
              responden$T.Pendidikan)

Adapun isi dari tabel1 tersebut adalah tabel kontingensi dengan row/baris adalah J.Kelamin dan column/kolom adalah T.Pendidikan

tabel1

##    
##      1  2  3  4
##   0  0  3  0  6
##   1 13 11  9  8

Anda bisa menggunakan fungsi rowSums, untuk melihat penjumlahan barisnya (dalam kasus ini per J.Kelamin)

rowSums(tabel1)

##  0  1 
##  9 41

Sementara itu, Anda bisa menggunakan fungsi colSums, untuk meliihat penjumlahan kolomnya.

colSums(tabel1)

##  1  2  3  4 
## 13 14  9 14

1.2.2 Membuat Tabel Proporsi dari Data

Pada proses pembuatan tabel proporsi, Anda bisa membuatnya dari tabel1 di atas.

tabel2_1<-prop.table(tabel1)
tabel2_1

##    
##        1    2    3    4
##   0 0.00 0.06 0.00 0.12
##   1 0.26 0.22 0.18 0.16

Atau Anda bisa menggunakan sintaks berikut ini.

tabel2_2<-prop.table(table(responden$J.Kelamin,
                           responden$T.Pendidikan))
tabel2_2

##    
##        1    2    3    4
##   0 0.00 0.06 0.00 0.12
##   1 0.26 0.22 0.18 0.16

1.2.3 Membuat Tabel 3 dimensi atau lebih

Untuk membuat tabel 3 dimensi atau lebih, bisa digunakan fungsi ftable

tabel3<-ftable(responden$J.Kelamin,
               responden$T.Pendidikan,
               responden$T.Pendapatan)
tabel3

##      1 2 3 4 5 6
##                 
## 0 1  0 0 0 0 0 0
##   2  0 1 1 0 1 0
##   3  0 0 0 0 0 0
##   4  1 0 3 1 1 0
## 1 1  2 1 1 2 3 4
##   2  0 1 4 4 2 0
##   3  1 2 3 1 1 1
##   4  2 1 0 2 2 1

1.3 Penyajian Data Kategorik melalui grafik

Input Data secara Langsung ke R

Deskripsi Data :

Suatu survei dilakukan terhadap pengguna dan bukan pengguna jasa keuangan. Berikut ini tersaji tabulasi silang antara pekerjaan responden dengan skor tingkat kemampuannya dalam pengelolaan keuangan. Bagaimanakah hubungan antar kedua peubah ini?

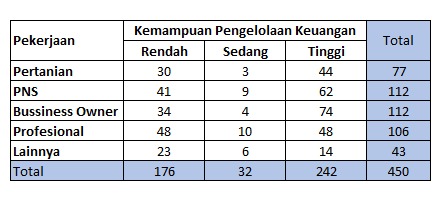
Figure 1.2: Tabel Kontingentsi

survei<-matrix(data=c(30,41,34,48,23,3,9,4,10,6,44,62,74,48,14),
               ncol=3,
               nrow=5,
               byrow=FALSE,
               dimnames=list(c("Pertanian","PNS","Business owner","Profesional","Lainnya"),
                             c("Rendah","Sedang","Tinggi"))
               )

Data yang telah diinput di atas, akan tampak seperti berikut ini :

survei

##                Rendah Sedang Tinggi
## Pertanian          30      3     44
## PNS                41      9     62
## Business owner     34      4     74
## Profesional        48     10     48
## Lainnya            23      6     14

Tabulasi silang/tabel kontingensi yang telah diinput di atas, dapat disajikan dalam bentuk grafik.

1.3.1 Grouped Dot Chart

Dot chart merupakan grafik titik yang menunjukkan nilai frekuensi atau proporsi dari suatu kriteria kategorik dari tabulasi silang atau tabel kontingensi.

Dalam membuat Dot Chart harus ditentukan kriteria/peubah apa yang menjadi dasar pengelompokan dan apakah disajikan dalam bentuk nilai frekuensi atau proporsi. Berikut disajikan beberapa alternatif penyajian Dot Chart dengan menggunakan data Survei yang merupakan tabel dua arah antara peubah jenis pekerjaan dan kemampuan pengelolaan keuangan:

Pengelompokkan berdasarkan Kolom

Pengelompokan berdasarkan Kolom pada data survei ini, adalah dikelompokkan berdasarkan Kemampuan pengelolaan Keuangan.

dotchart(survei,xlab="Frequency",xlim=c(0,100))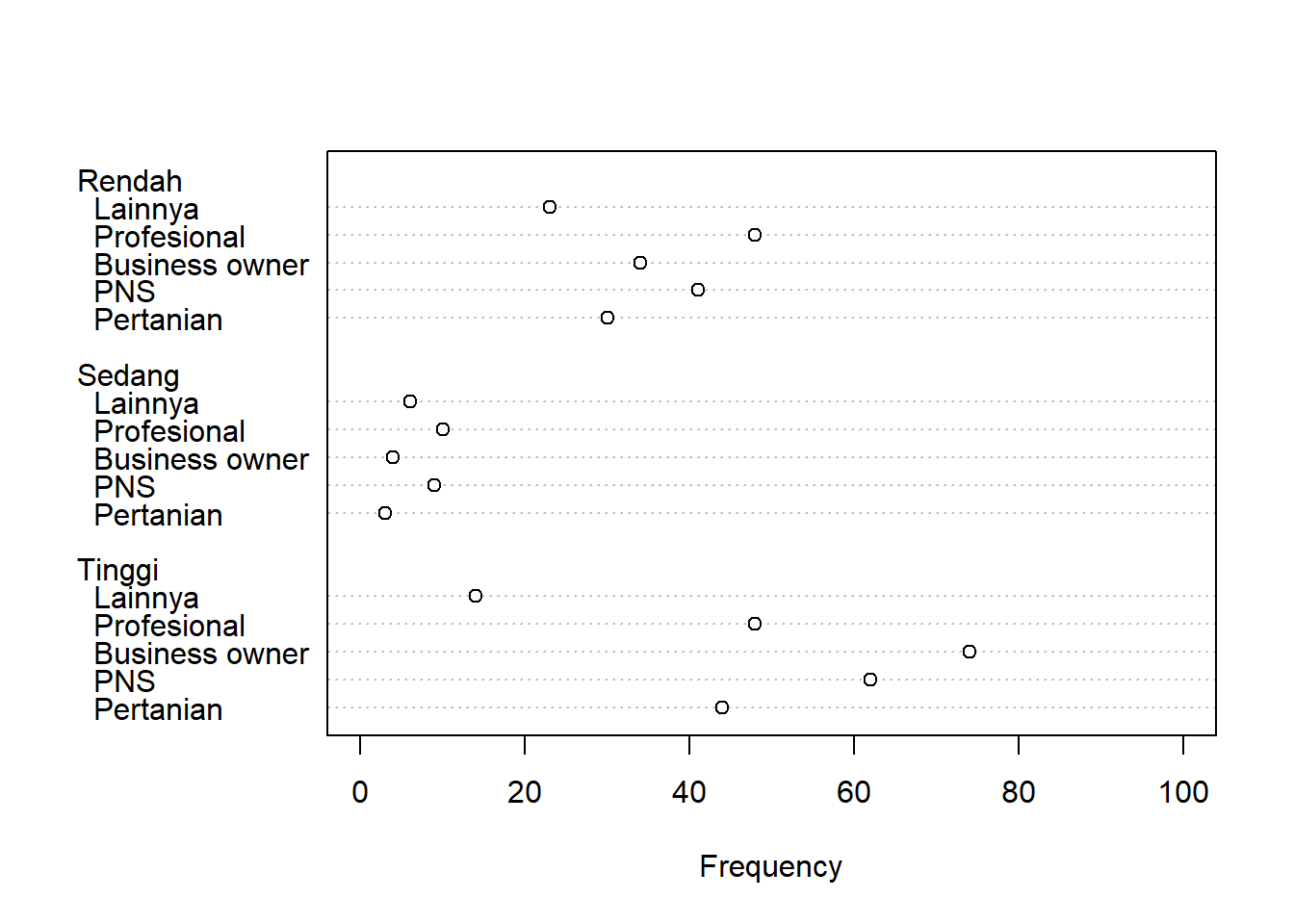

Pengelompokkan berdasarkan Baris

Pengelompokan berdasarkan Baris pada data survei ini, adalah dikelompokkan berdasarkan Pekerjaan.

#pengelompokkan berdasarkan kemampuan pengelolaan keuangan
dotchart(t(survei),xlab="Frequency",xlim=c(0,100))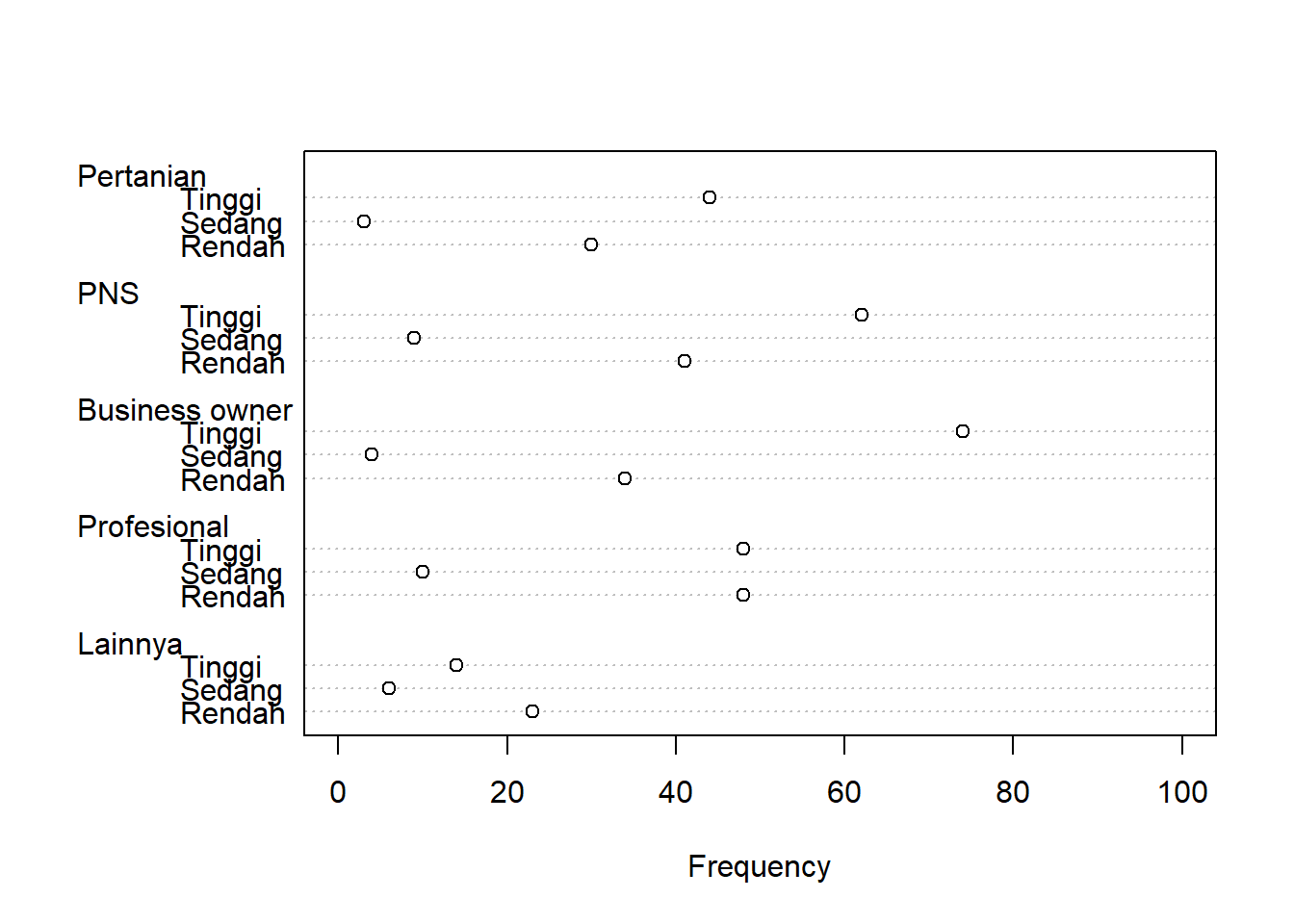

Dot Chart Proporsi

Untuk menggunakan Dot Chart Proporsi, maka objek survei perlu dibagi dengan total nilai datanya yaitu sejumlah 450. Dalam sintaks R tersebut, diwakili dengan n.

n<-sum(survei)
propsurvei<-survei/n
dotchart(t(propsurvei),xlab="Relative Frequency", xlim=c(0,0.3))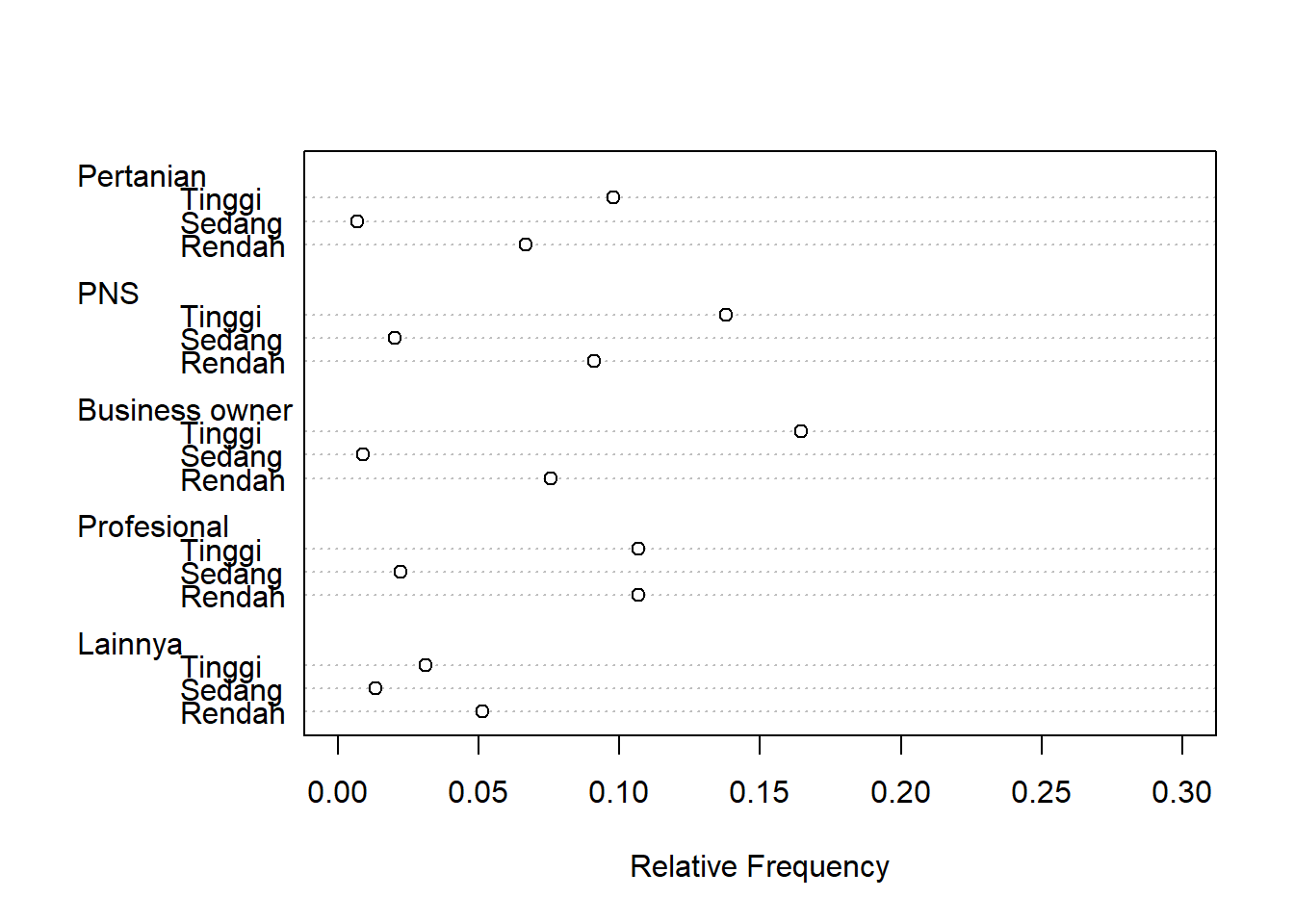

Dot Chart proporsi per jenis pekerjaan

Untuk membuat Dot Chart per jenis pekerjaan, data survei, dibagi dengan total dari colSums nya. Objek jumkerja, diulangi sebanyak 5 kali, sesuai dengan jumlah variasi pekerjaan yang ada, yaitu 5 macam.

jumkerja <-colSums(survei)
proppekerjaan <-survei/rbind(jumkerja,jumkerja,jumkerja,jumkerja,jumkerja)
dotchart(t(proppekerjaan),xlab="Conditional Relative Frequency",xlim=c(0,0.4))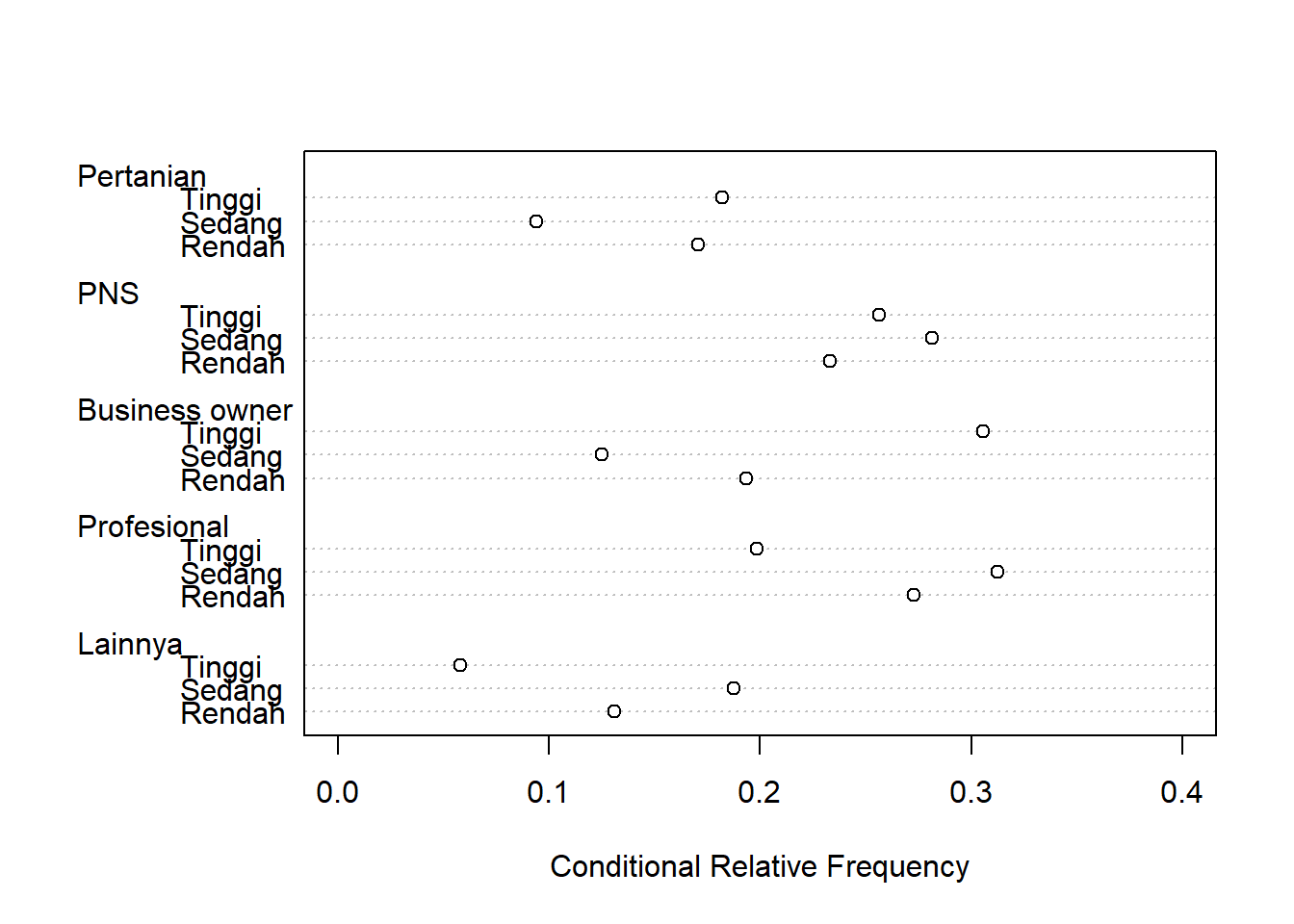

1.3.2 Grouped Dot Whisker Chart

Grouped Dot Whisker Chart merupakan pengembangan dari Group Dot Chart dengan nilai proporsi dari data tabulasi silang. Pada Grouped Dot Whisker Chart data proporsi ditambahkan dengan informasi selang kepercayaan dari proporsi yaitu nilai proporsi ditambahkan dengan informasi margin of error. Dimana margin of error merupakan perkalian antara standar deviasi dari proporsi dengan rumus $\sigma^2 = \frac{PQ}{n}$ (Standard Deviation ($\sigma$) merupakan akar dari $\sigma^2$) dengan nilai $Z_{\frac{\alpha}{2}}$ dimana $\alpha$ ditentukan 5 persen sehingga $Z_{\frac{\alpha}{2}}$ sama dengan $Z_{0.025}$.

Rumus Selang Kepercayaan

\[P ± Margin of Error\]

\[P ± \sigma Z_{0.025} \]

survei<-t(survei)
survei

##        Pertanian PNS Business owner Profesional Lainnya
## Rendah        30  41             34          48      23
## Sedang         3   9              4          10       6
## Tinggi        44  62             74          48      14

n<-sum(survei)
propsurvei<-survei/n
dotchart(propsurvei,xlab="Proportion",lcolor="white",xlim=c(0,0.3))
sd<-sqrt((1.-propsurvei)*propsurvei/n)
sd<-sd*qnorm(0.975)
hlo<-propsurvei-sd
hhi<-propsurvei+sd
titik<-c(propsurvei[,5],propsurvei[,4],propsurvei[,3],propsurvei[,2],propsurvei[,1])
kiri <-c(hlo[,5],hlo[,4],hlo[,3],hlo[,2],hlo[,1])
kanan<-c(hhi[,5],hhi[,4],hhi[,3],hhi[,2],hhi[,1])
dlx<-cbind(kiri,titik,kanan)
ys<-c(1:3,6:8,11:13,16:18,21:23)
dly<-cbind(ys,ys,ys)
ldl<-length(survei)
for (i in 1:ldl) lines(dlx[i,],dly[i,])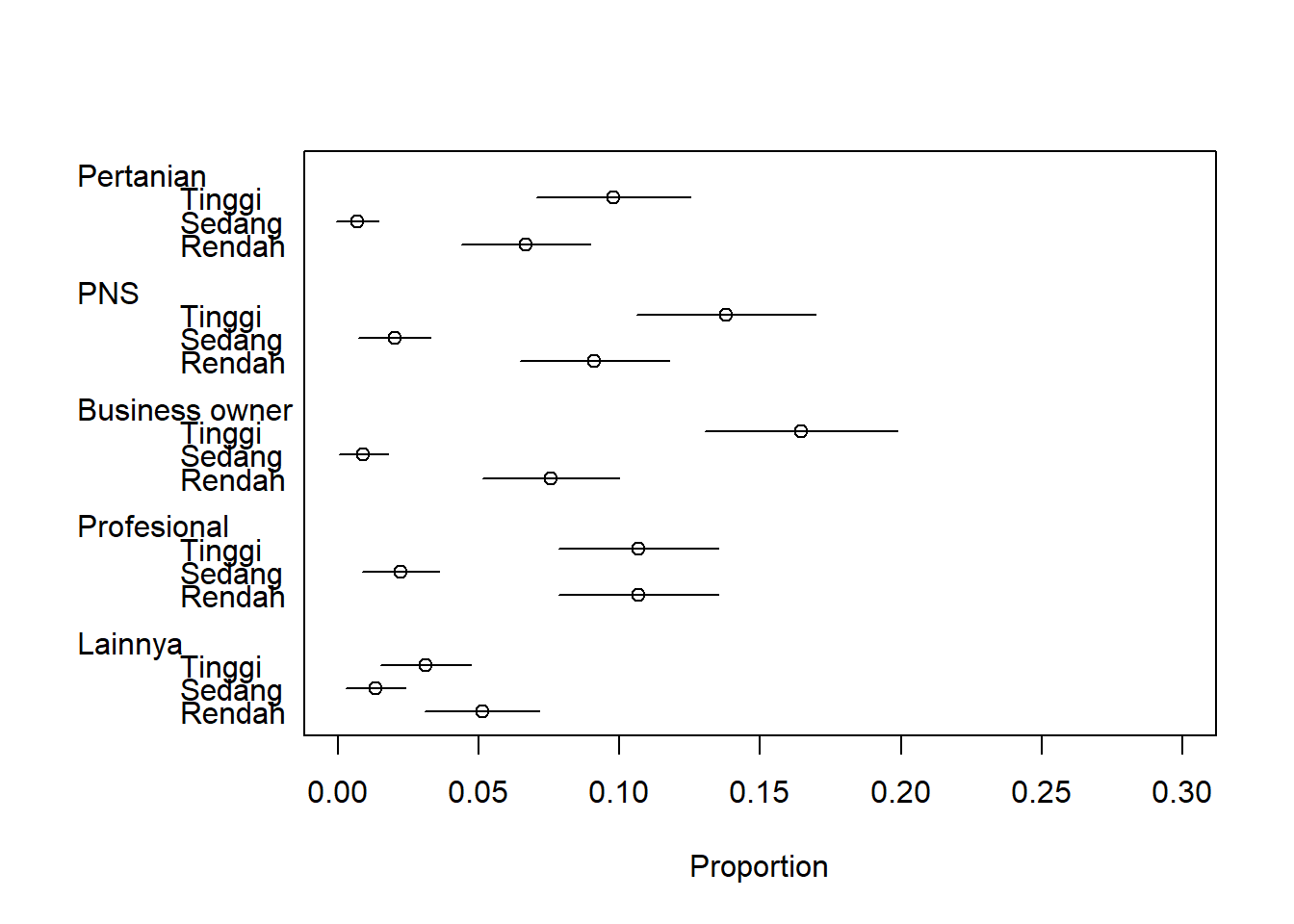

1.3.3 Two Way Dot Chart

Penyajian Bersarang

library(lattice)
dotplot(survei,
        xlab="Frequency",
        ylab="Kemampuan Pengelolaan Keuangan",
        as.table=TRUE,
        groups=FALSE,
        stack=FALSE,
        layout=c(1,5),
        scales=list(alternating=3))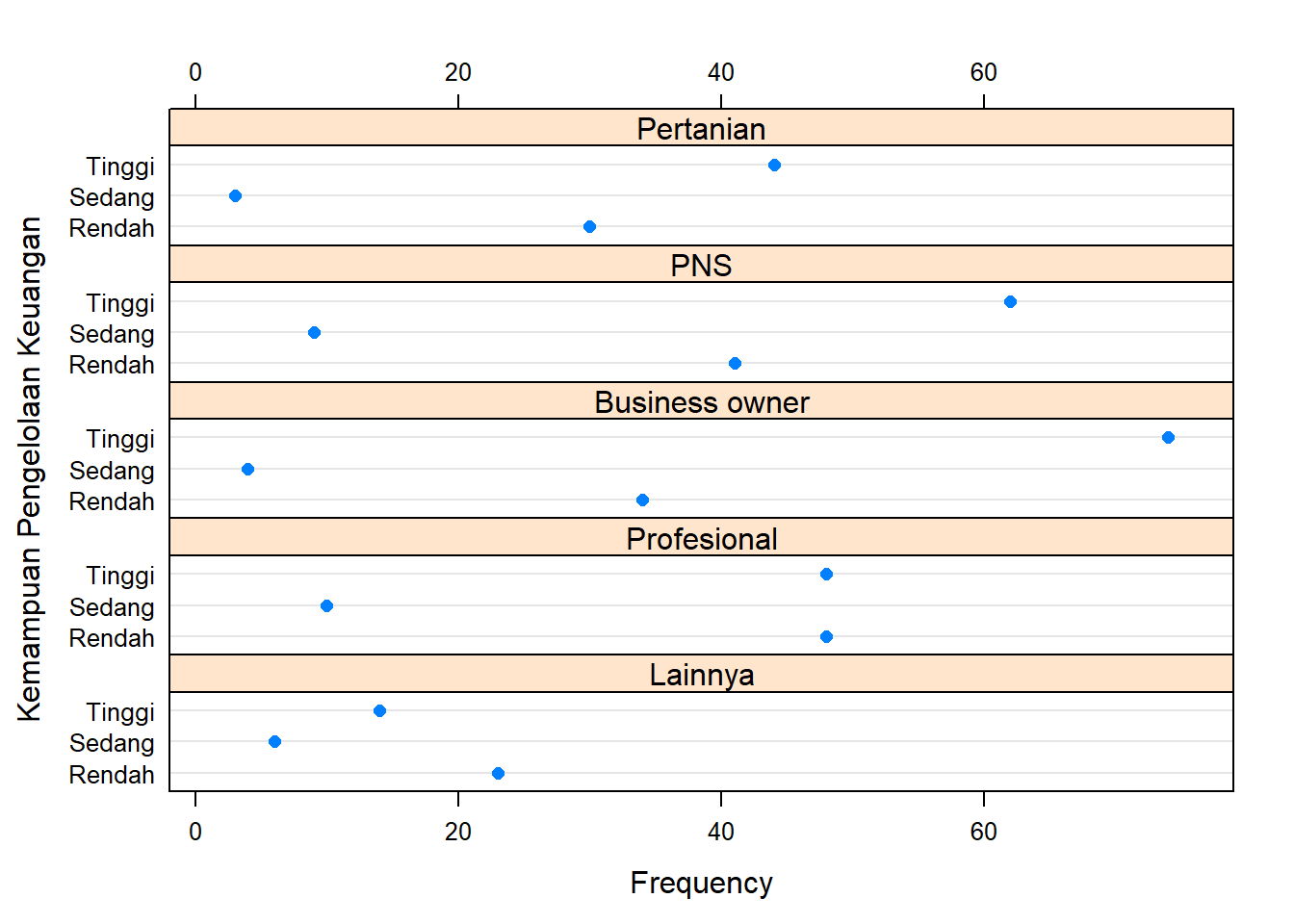

Penyajian Bersilang

dotplot(survei,
        xlab="Frequency",
        ylab="Kemampuan Pengelolaan Keuangan",
        as.table=TRUE,
        groups=FALSE,
        stack=FALSE,
        layout=c(5,1),
        scales=list(alternating=3))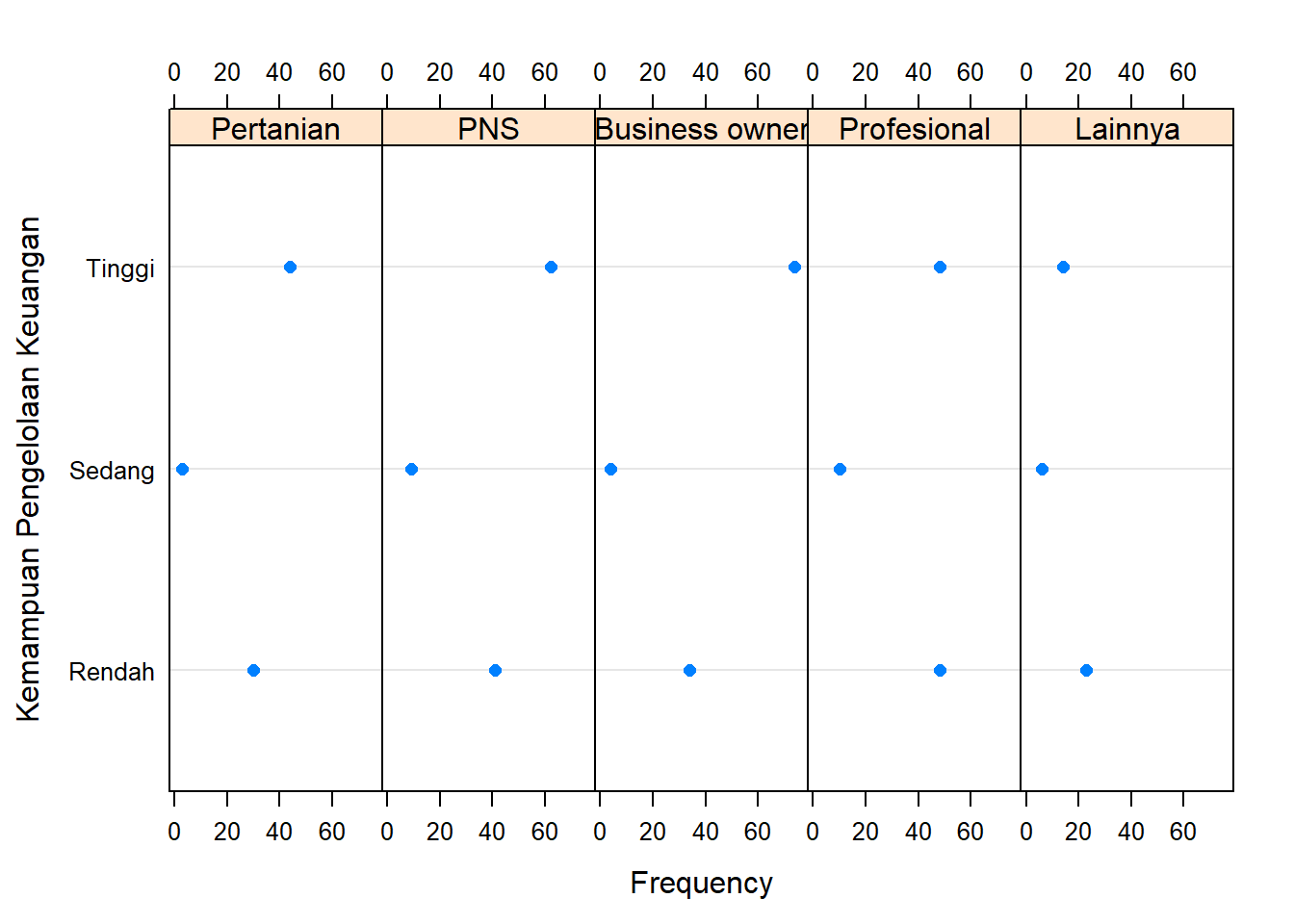

1.3.4 Side by side Bar Chart

Side by side bar chart merupakan grafik batang yang menunjukkan nilai frekuensi untuk kriteria tertentu dalam tabulasi silang atau tabel kontingensi. Kategori tersebut disajikan dalam grafik batang dengan penggolongan kriteria suatu peubah ke samping.

Barplot Frekuensi

barplot(survei,
        horiz=TRUE,
        xlab="Frequency",
        ylab="Pekerjaan",
        beside=TRUE,
        cex.names=0.6,
        xlim=c(0,100),
        col=c(6,7,4))
legend("topright",
       legend= rownames(survei),
       fill=c(6,7,4),
       ncol = 2,
       cex = 0.5)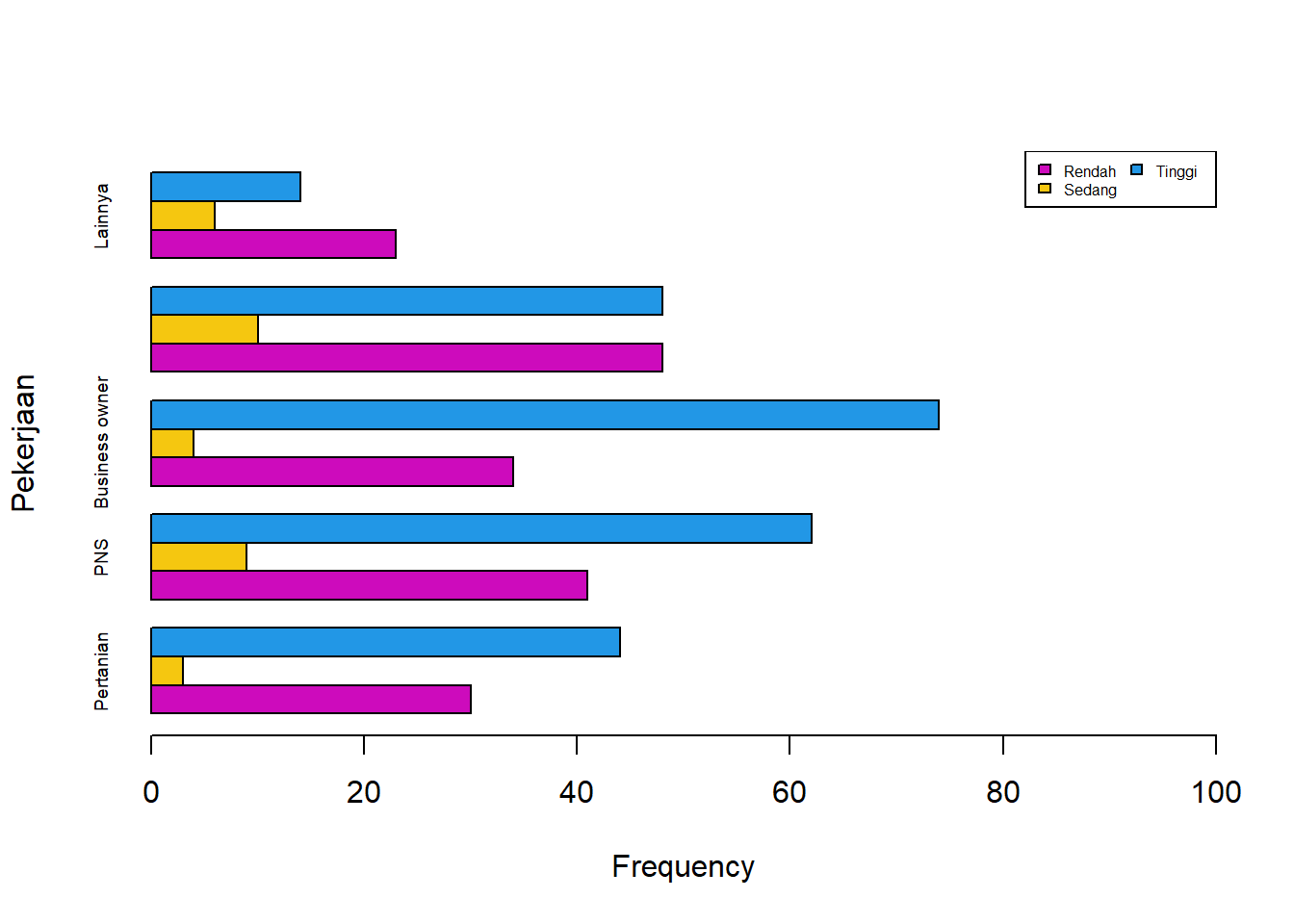

*Barplot Proporsi

barplot(propsurvei,
        horiz=TRUE,
        xlab="Relative Frequency",
        ylab="Pekerjaan",
        beside=TRUE,
        cex.names=0.6,
        xlim=c(0,0.3),
        col=c(5,10,15))
legend("topright",
       legend= rownames(propsurvei),
       fill=c(5,10,15),
       ncol = 2,
       cex = 0.5)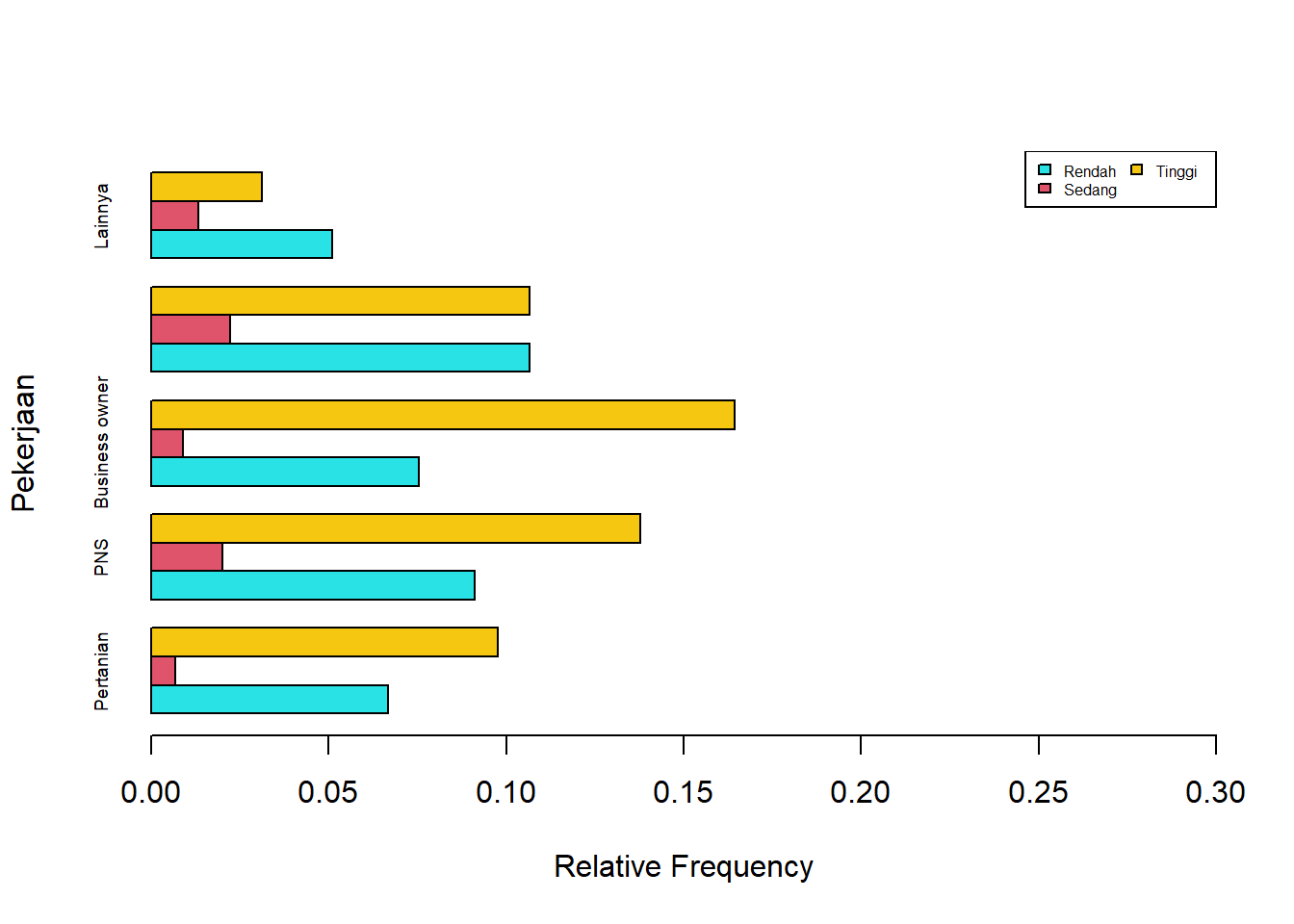

1.3.5 Side by side Stacked Bar Chart

Side by side stacked bar chart merupakan salah satu bentuk penyajian data kategorik tabulasi silang atau tabel kontingensi. Sejalan dengan grafik batang pada no 4 namun kriteria kategori disajikan bertumpuk (stacked).

barplot(survei,
        horiz=TRUE,
        xlab="Frequency",
        ylab="Pekerjaan",
        beside=FALSE,
        cex.names=0.6,
        xlim=c(0,150),
        col=c(3,4,6))
legend("topright", 
       legend= rownames(survei),
       fill=c(3,4,6),
       ncol = 2,
       cex = 0.5)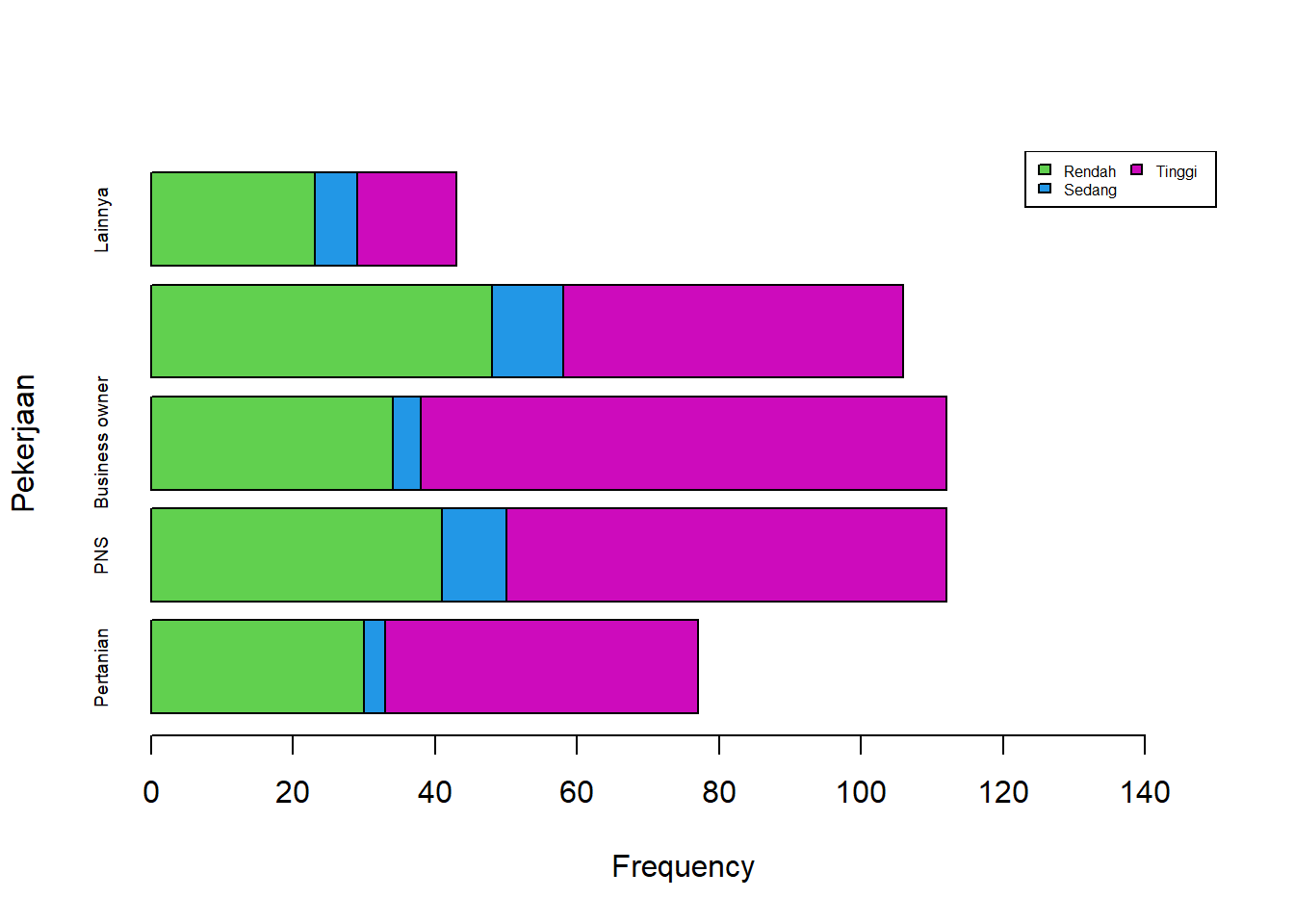

1.3.6 Mosaic Chart

Mosaic chart merupakan grafik untuk menampilkan data kategorik dalam tabulasi silang/tabel kontingensi yang sejenis dengan side by side stacked bar chart. Perbedaan antara side by side stacked bar chart dengan mosaic chart adalah jika pada stacked bar chart total frekuensi jika mosaic chart totalnya adalah 100 persen. Atau mosaic chart merupakan stacked bar chart untuk proporsi terhadap total kategori suatu peubah. Misal pada contoh adalah proporsi terhadap total jenis pekerjaan.

mosaicplot(t(survei),
           main="Mosaic Chart",
           las=1,
           cex=0.75,
           color=c(2,4,7))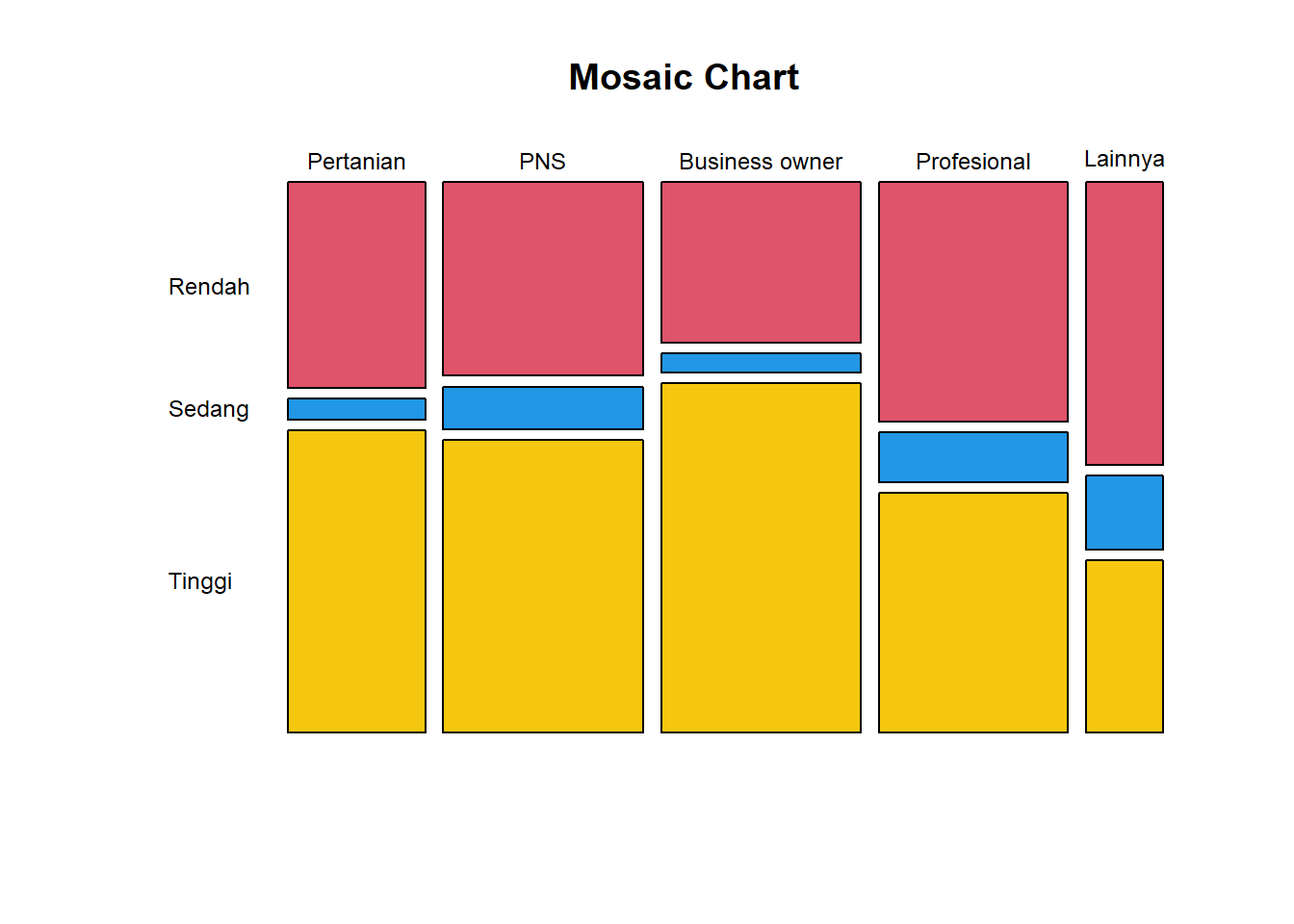

1.4 Konsep Peubah Acak

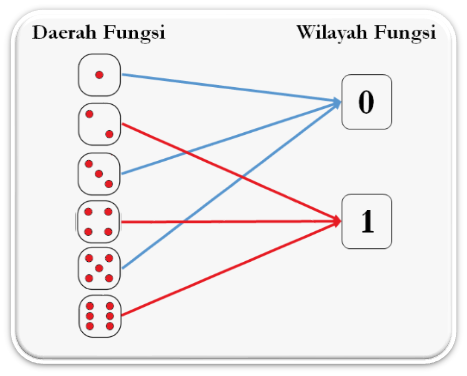
Peubah acak merupakan suatu fungsi yang memetakan ruang kejadian (daerah fungsi) ke ruang bilangan riil (wilayah fungsi). Fungsi Peubah Acak merupakan suatu langkah dalam statistika untuk mengkuantifikasikan kejadian-kejadian alam. Pendefinisian fungsi peubah acak harus mampu memetakan SETIAP KEJADIAN DALAM RUANG CONTOH dengan TEPAT ke SATU BILANGAN bilangan riil.

1.5 Beberapa Jenis Peubah Acak

Diskrit (Kategorik)
- Bernoulli
- Binom
- Poisson
- Geometrik, …
Kontinu
- Normal
- t
- $X^2$
- F
- Gamma, …

1.5.1 Sebaran Bernoulli

Merupakan fenomena dengan dua kemungkinan hasil.

Sukses -> $X = 1$
Gagal -> $X = 0 $

Peluang Sukses dilambangkan dengan p

Karena Bernoulli merupakan kasus khusus dari Binomial dengan besarnya percobaan hanya satu (n=1). Pada R, Bernoulli bisa menggunakan fungsi rbinom(n, size, prob) dari library stats, dengan size = 1. Berikut akan dibangkitkan 100 kejadian Bernoulli dengan prob = 0.2

rbinom(n = 100,
       size = 1,
       prob = 0.2)

Maka, hasilnya adalah kumpulan kejadian Sukses (1) atau Gagal (0), sebagai berikut :

##   [1] 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 1 1 0 1 0 0 1 0 0 0 0 0 0 1 0 1
##  [38] 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0
##  [75] 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1

Misal, kita ingin melihat barplot dari 100 kejadian bernoulli, maka sintaksnya adalah sebagai berikut :

p = 0.2

x <- rbinom(n = 100,
            size = 1,
            prob = 0.2)
barplot(table(x))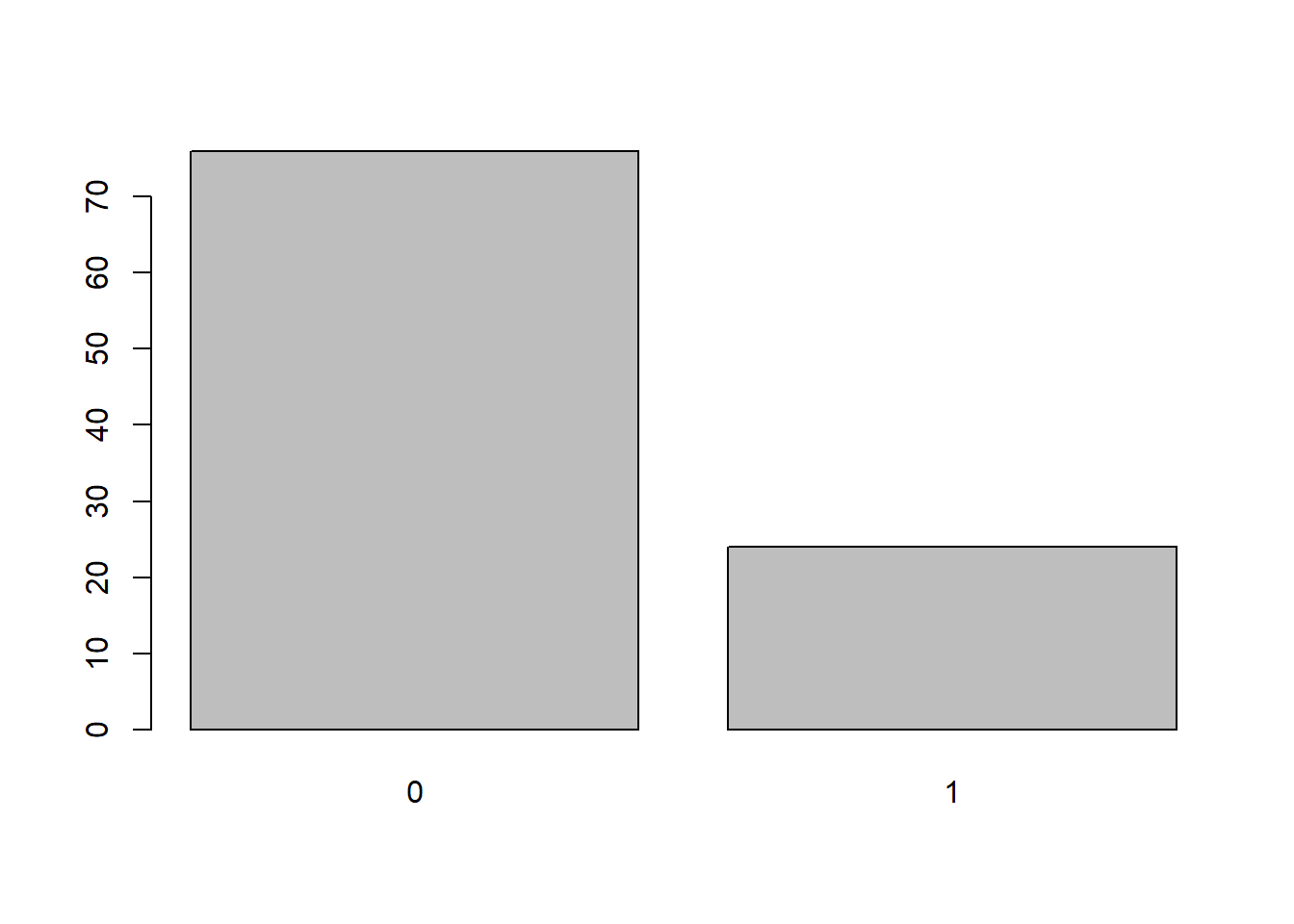

p = 0.5

y <- rbinom(n = 100,
            size = 1,
            prob = 0.5)
barplot(table(y))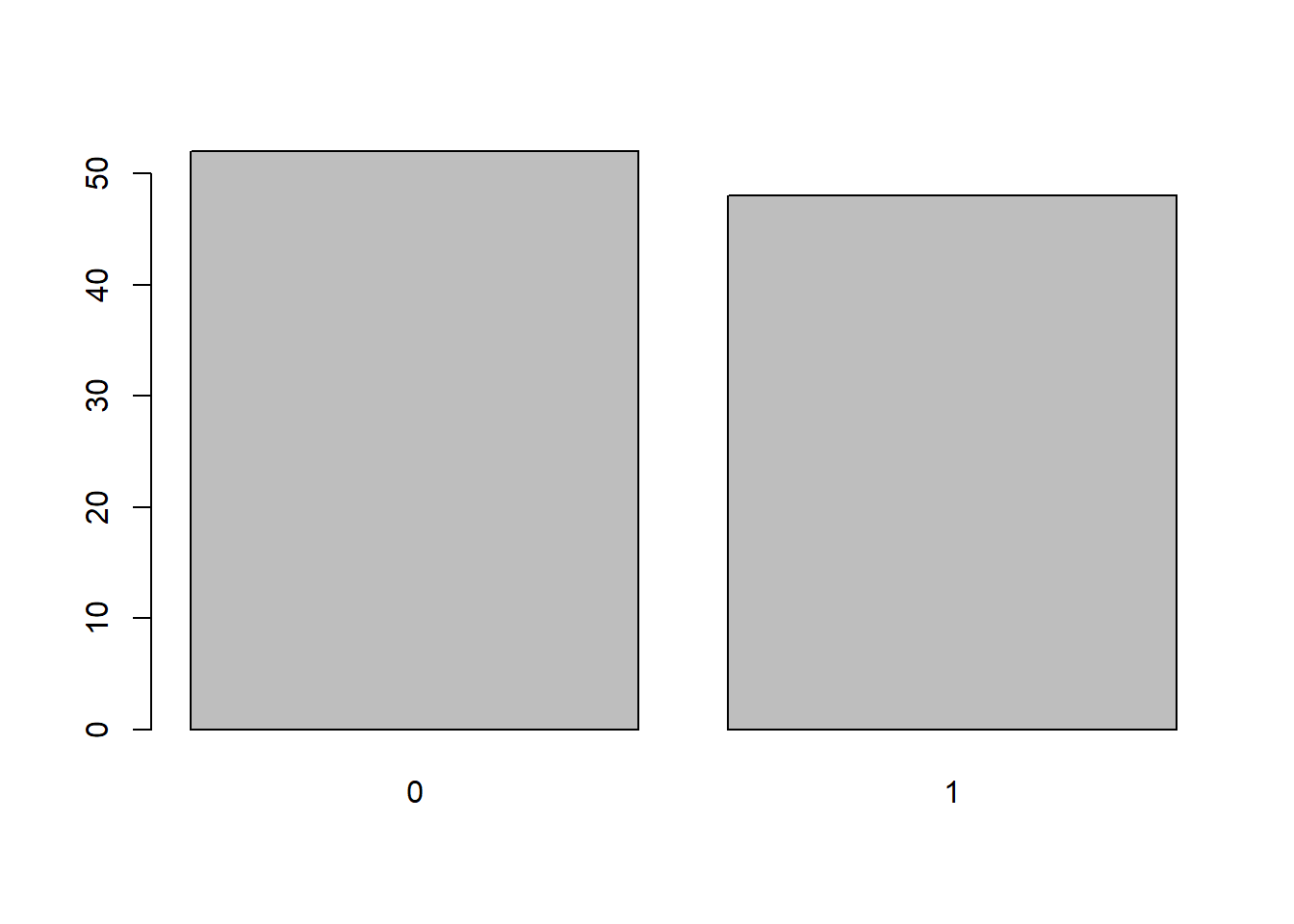

Terlihat bahwa data bangkitan antara P=0.2 dan P=0.5 terlihat berbeda dan pada P=0.5 cenderung seimbang antara y=1 dan y=0. Nilai P pada sebaran Bernoulli merupakan parameter dari sebaran tersebut yang menentukan sebaran dari data.

1.5.2 Sebaran Binomial

Sebaran Binomial merupakan sebaran dari beberapa kejadian Bernoulli yang saling bebas. Adapun karakteristik dari Sebaran Binomial adalah sebagai berikut:

Terdiri dari beberapa percobaan sejenis
Tiap percobaan terdiri dari dua kemungkinan hasil: sukses dan gagal
Tiap percobaan saling bebas
Peluang sukses (P) sama untuk semua percobaan
Peubah acak y, merupakan jumlah suksed dari beberapa percobaan yang mengikuti sebaran Binomial dengan parameter n dan p
y dapat bernilai y=0,1,…,n

Berikut merupakan sintaks untuk membangkitkan data sebanyak 100 kali dari sebaran Binomial, dengan size = 8 dan prob = 0.5:

x <- rbinom(n = 100,
            size = 8,
            prob = 0.5)
barplot(table(x))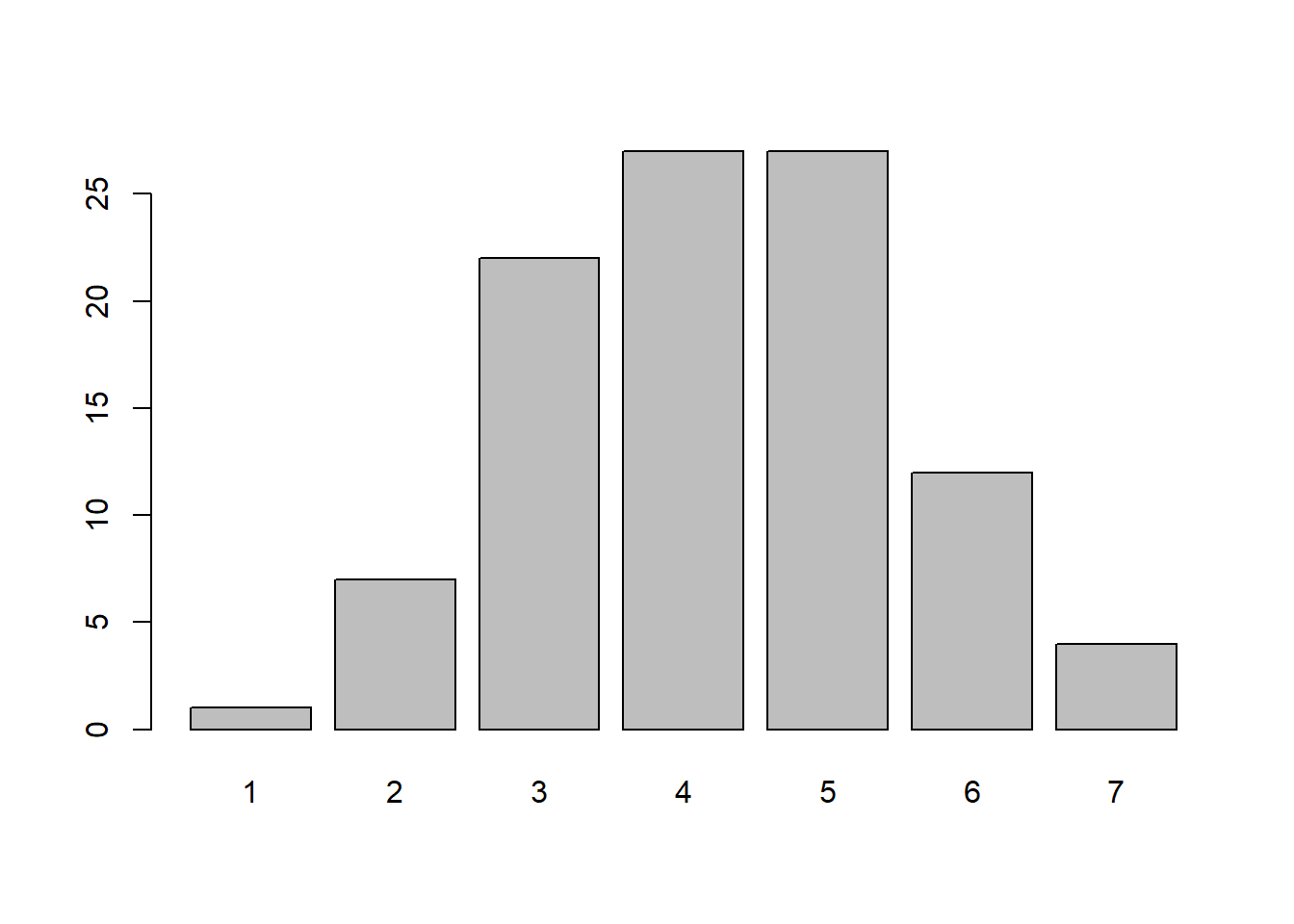

Contoh lain, dengan paramater yang sama dengan sebelumnya, namun kali ini dengan n = 1000

x <- rbinom(n = 1000,
            size = 8,
            prob = 0.5)
barplot(table(x))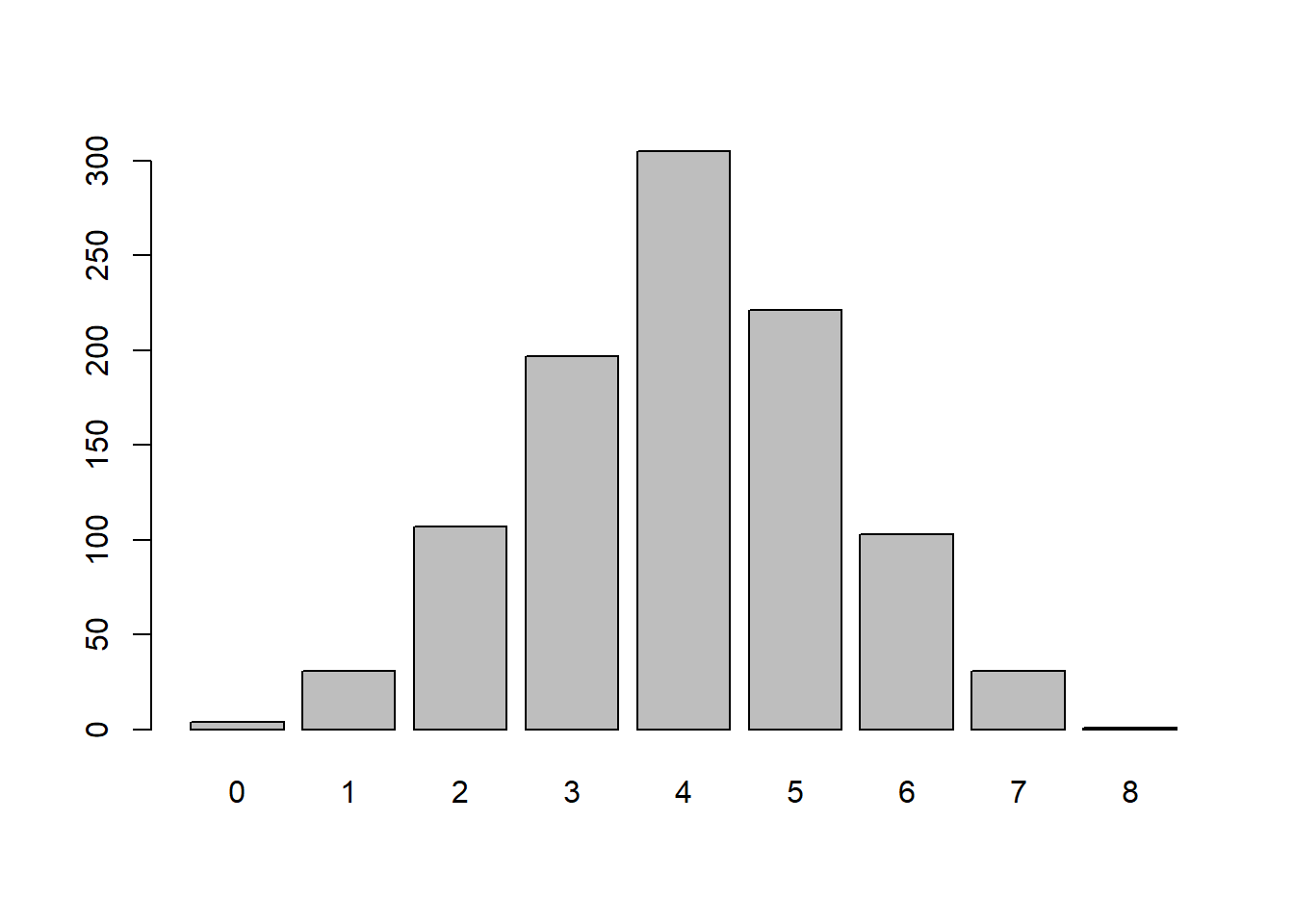

Berdasarkan diagram garis di atas diperoleh informasi bahwa semakin besar jumlah data yang dibangkitkan maka akan cenderung membentuk grafik yang simetris (cenderung membentuk bentuk lonceng/ kurva normal)

Contoh Kasus Binomial

Misalkan terdapat 12 nasabah asuransi di suatu tempat. Diketahui bahwa proporsi nasabah telat bayar polis ialah 1/6. Jika antar nasabah saling bebas tentukanlah peluang bahwa terdapat 7 sampai 9 nasabah yang telat bayar polis!

Diketahui bahwa

X ~ banyaknya nasabah asuransi yang telat membayar X ~ binomial(size = 12, prob = 1/6) $7 ≤ q ≤ 9$ \[P(7≤X≤9) = P(X≤9) - P(X≤9) \]

pbinom (q = 9,
        size = 12,
        prob = 1/6) - pbinom(q = 6,
                             size = 12,
                             prob = 1/6)

## [1] 0.001291758

1.5.3 Sebaran Poisson

Sebaran Poisson merupakan sebaran yang menggambarkan karakteristik data pada kejadian yang jarang terjadi pada suatu waktu tertentu atau suatu tempat tertentu. Contohnya jumlah kesalahan ketik pada suatu halaman, kedatangan bus jurusan kota A pada waktu tertentu.

Berikut merupakan sintaks untuk membangkitkan 1000 data dari sebaran Poisson dengan parameter tertentu ( $\lambda = 1,3,6$ ):

$\lambda = 1$

x <- rpois(n = 1000,
           lambda = 1)
barplot(table(x))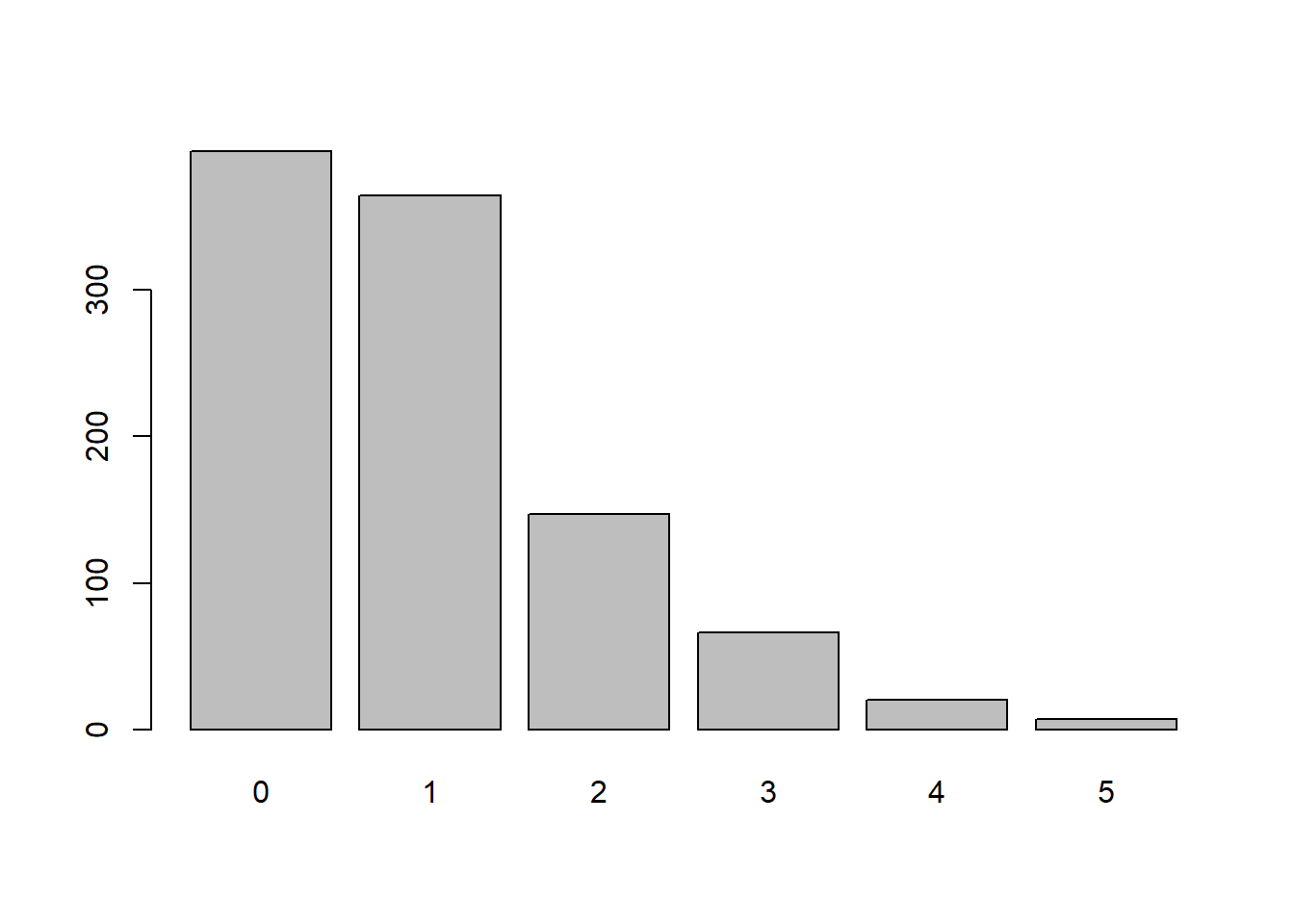

$\lambda = 3$

x <- rpois(n = 1000,
           lambda = 3)
barplot(table(x))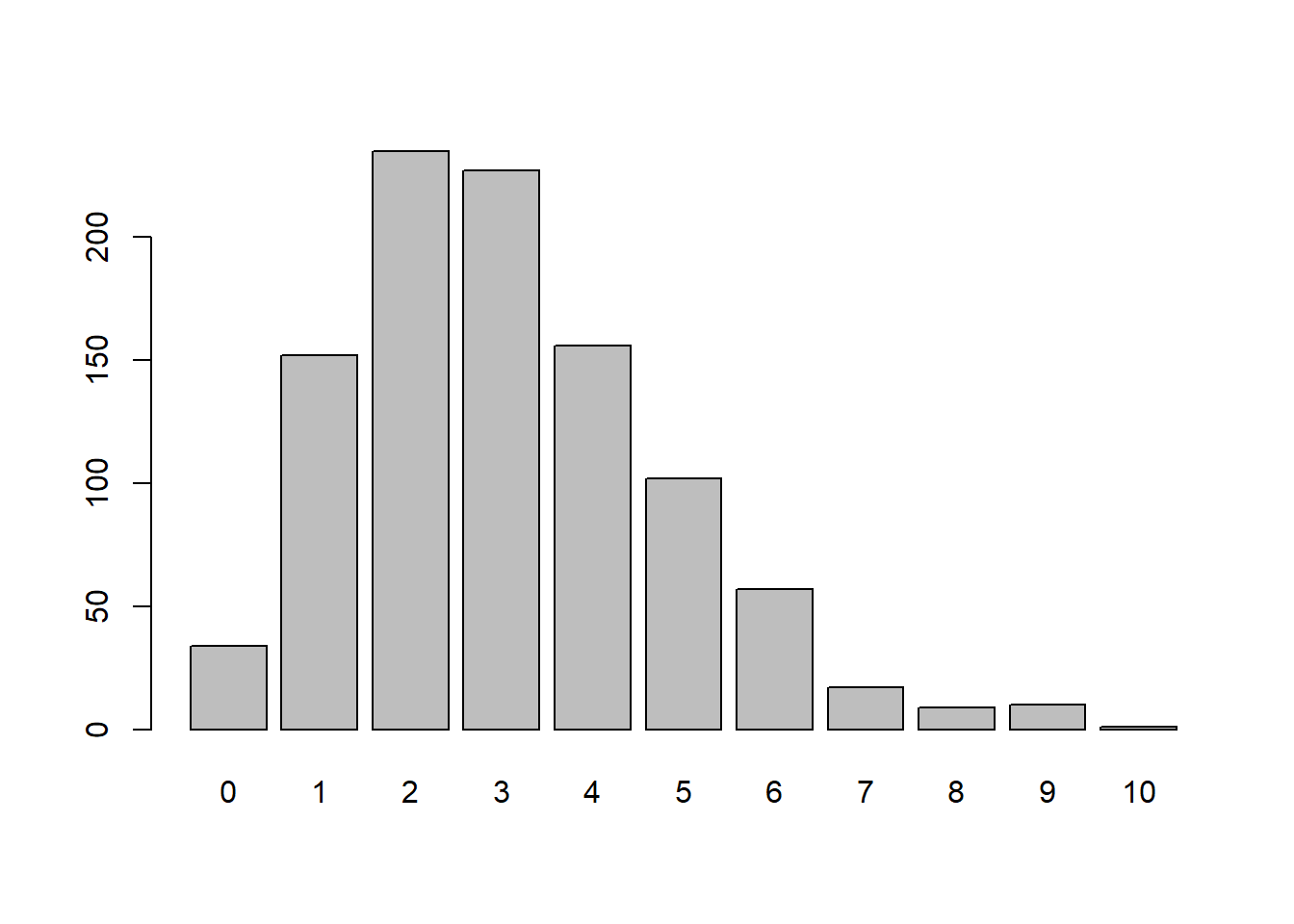

$\lambda = 6$

x <- rpois(n = 1000,
           lambda = 6)
barplot(table(x))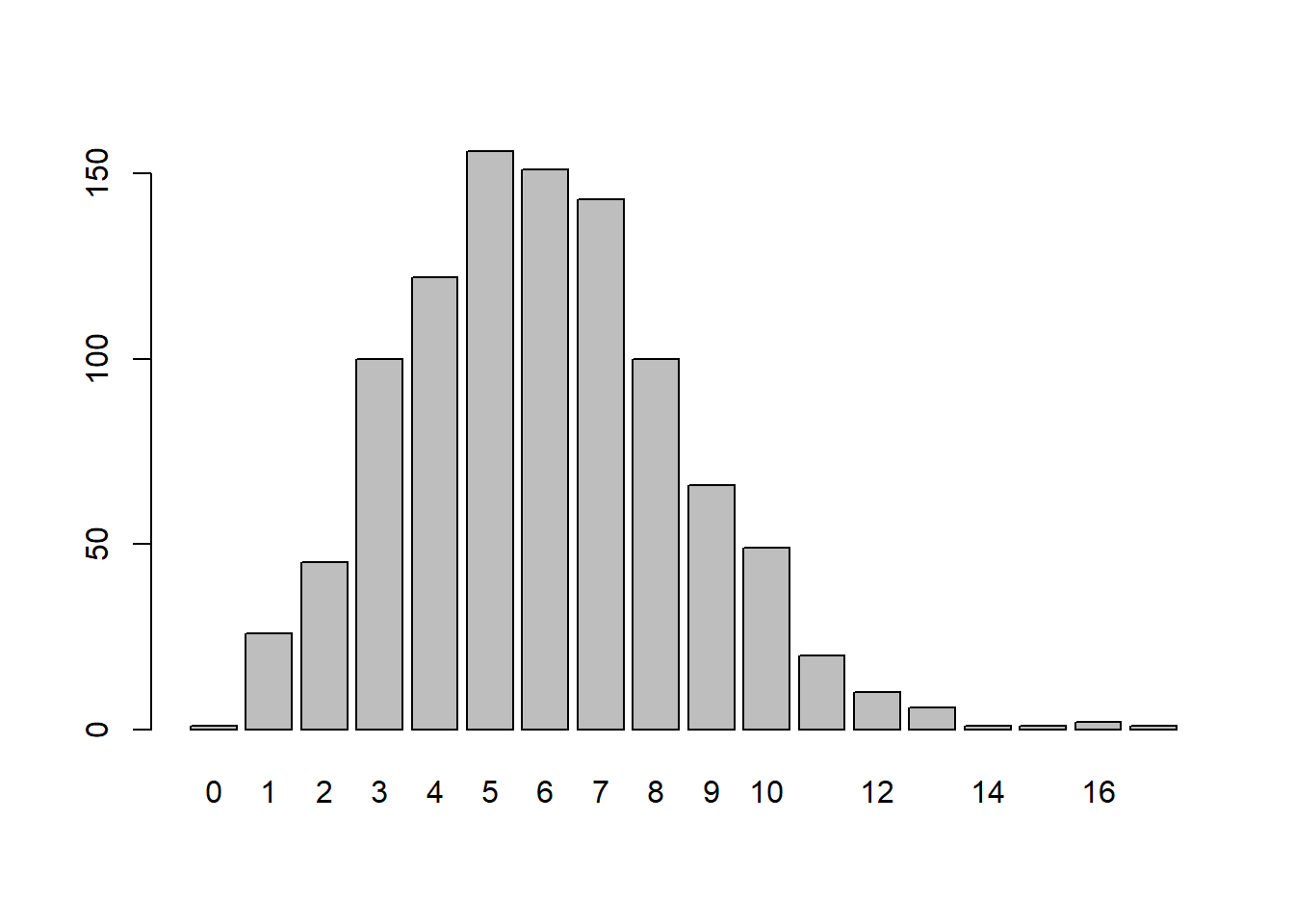

Besaran parameter Lamda menentukan kemencengan dari grafik data. Semakin kecil lamda maka akan semakin menceng ke kanan.

Contoh Kasus Poisson

Misalkan di suatu kota secara rata rata terdapat 2 mesin ATM yang rusak dalam 1 tahun:

Berapakah peluang tidak mesin ATM rusak dalam 1 tahun ke depan
Berapakah peluang terdapat 2 mesin ATM rusak dalam 2 tahun ke depan

Solusi :

a.X adalah banyaknya mesin ATM yang rusak pada waktu 1 tahun, maka $X ~ poisson(\lambda = 1)$

$P(X=0)$

ppois(q = 0,
      lambda=1)

## [1] 0.3678794

Misal Y banyaknya mesin ATM yang rusak dalam waktu 2 tahun maka $X ~ poisson(\lambda = 2)$, peluang terdapat 2 mesin ATM yang rusak dalam 2 tahun ke depan adalah

diff(ppois(q = c(1,2),
           lambda=2))

## [1] 0.2706706

1.5.4 Sebaran Geometrik

Sebaran geometrik merupakan percobaan Bernoulli yang diperlukan hingga muncul Sukses pertama (P(S)=p)

Berikut sintaks untuk membangkitkan data dari populasi yang mengikuti sebaran geometrik dengan parameter P tertentu.

prob = 0.2

x <- rgeom(n = 1000,
           prob = 0.2)
barplot(table(x))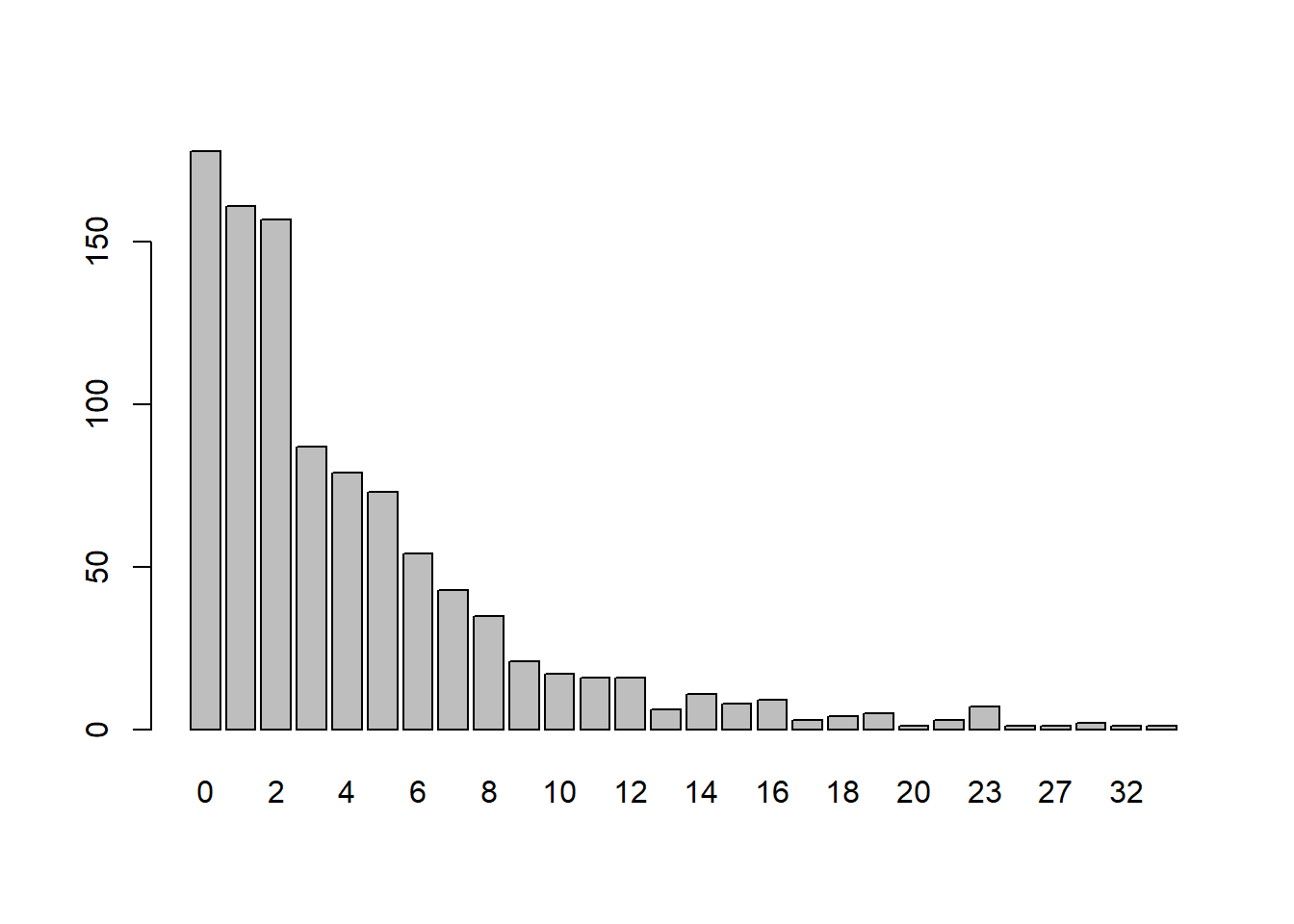

prob = 0.5

x <- rgeom(n = 1000,
           prob = 0.5)
barplot(table(x))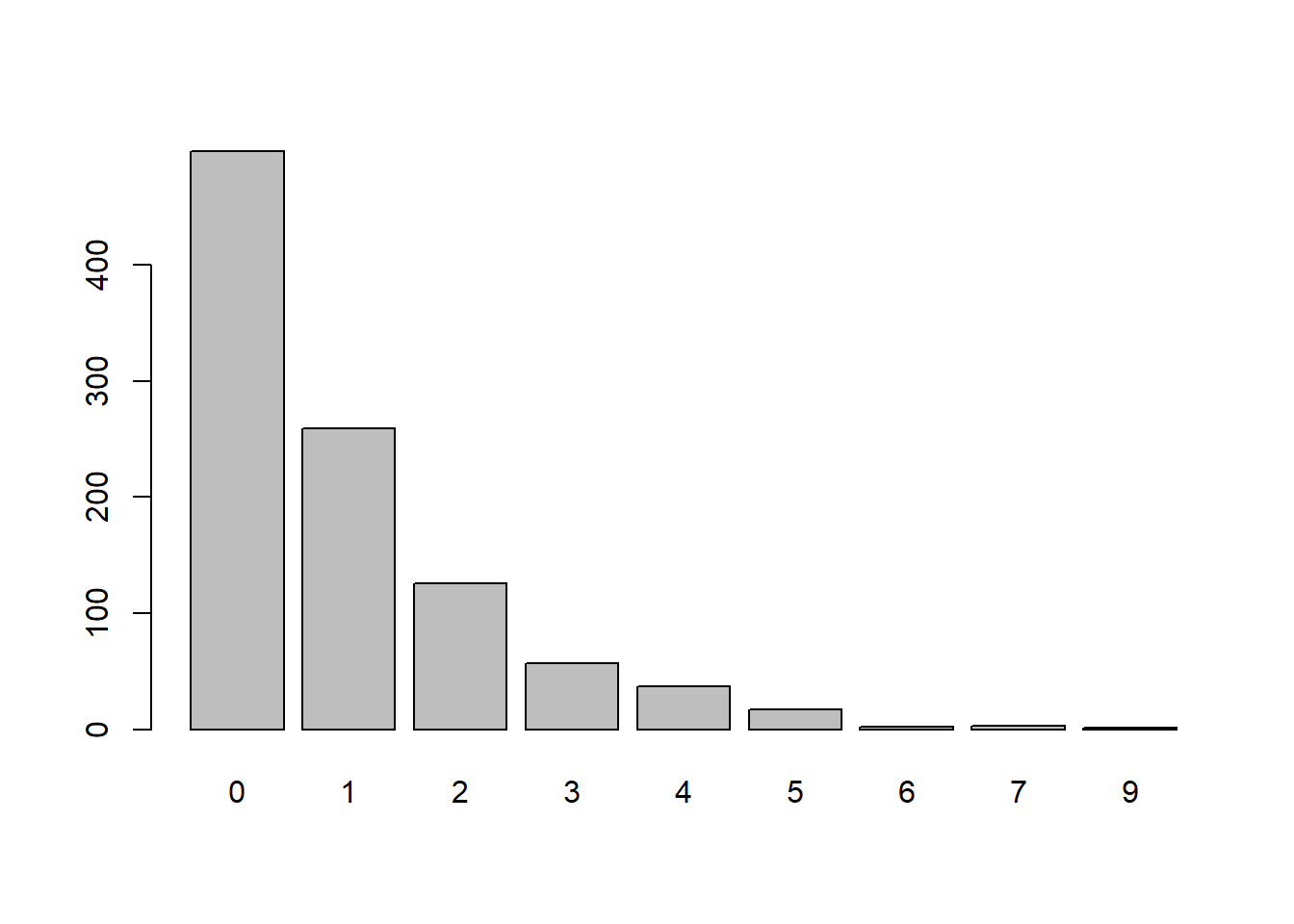

prob = 0.8

x <- rgeom(n = 1000,
           prob = 0.8)
barplot(table(x))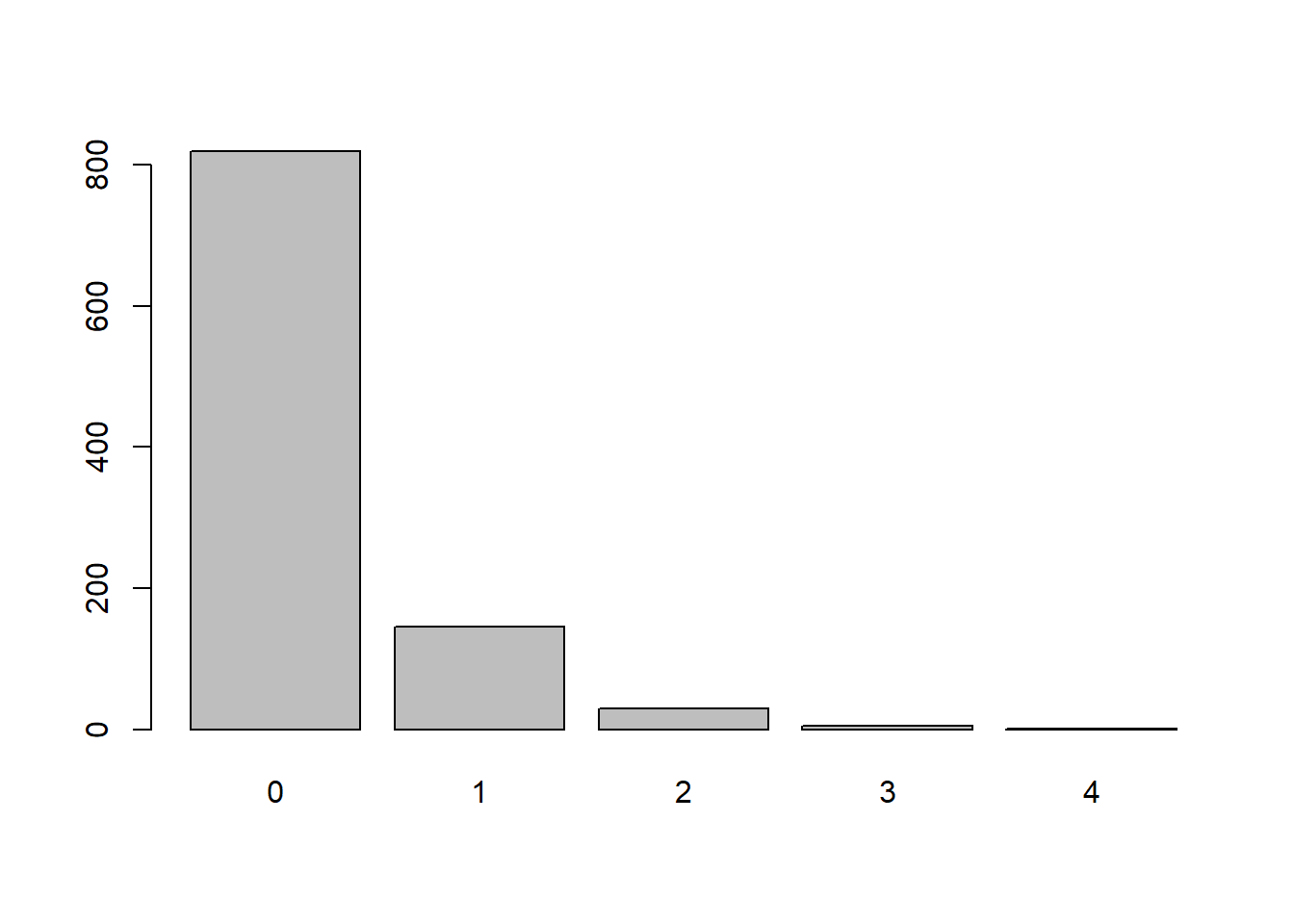

Perbedaan pada nilai parameter dari sebaran geometrik berpengaruh pada lebar nilai x yang keluar. Semakin besar nilai P maka nilai x akan semakin sempit atau semakin sedikit nilai x yang muncul. Namun secara grafik terlihat bahwa bangkitan data dari sebaran geometrik selalu menceng ke kanan.

Contoh Kasus Geometrik

Misalkan X banyaknya bulan yang dilalui sampai Pak Yus menang undian, dengan peluang memang sebesar 0.45

Berapakah Peluang Pak Yus menang di Bulan ke-3?
Berapakah Peluang Pak Yus menang setelah bulan ke-4?

Solusi :

$P(X=3)$

diff(pgeom(q = c(2,3),
           prob=0.45))

## [1] 0.07486875

b $P(X>4)$

pgeom(q = 4,
      prob=0.45,
      lower.tail = FALSE)

## [1] 0.05032844

1.5.5 Sebaran Hipergeometrik

Jika pada sebaran Binomial, nilai P setiap pengulangan diasumsikan sama. Pada sebaran Hipergeometrik nilai P tidak sama dan biasa terjadi pada percontohan tanpa pengembalian (sampling without replacement) dari populasi terhingga (finite).

Berikut adalah sintaks untuk membangkitkan data dari populasi yang berdistribusi hipergeometrik dengan parameter m, n, dan k. Parameter m merupakan banyaknya karakteristik A, n banyaknya karakteristik B, dan k banyaknya yang diambil.

m = 50, n = 50, k = 10

x <- rhyper(nn = 1000,
            m = 50,
            n = 50,
            k = 10)
barplot(table(x))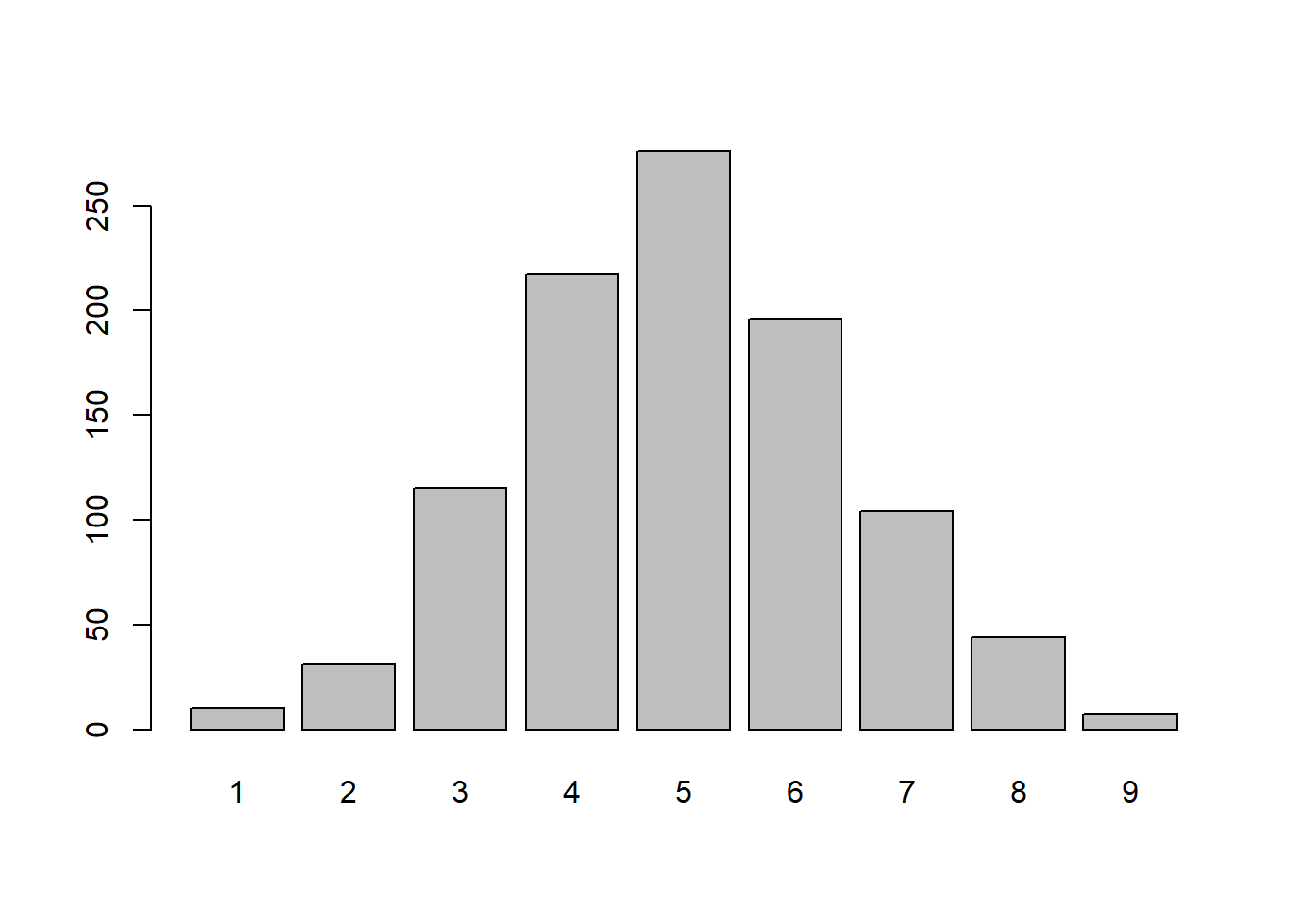

m = 20, n = 80, k = 10

x <- rhyper(nn = 1000,
            m = 20,
            n = 580,
            k = 10)
barplot(table(x))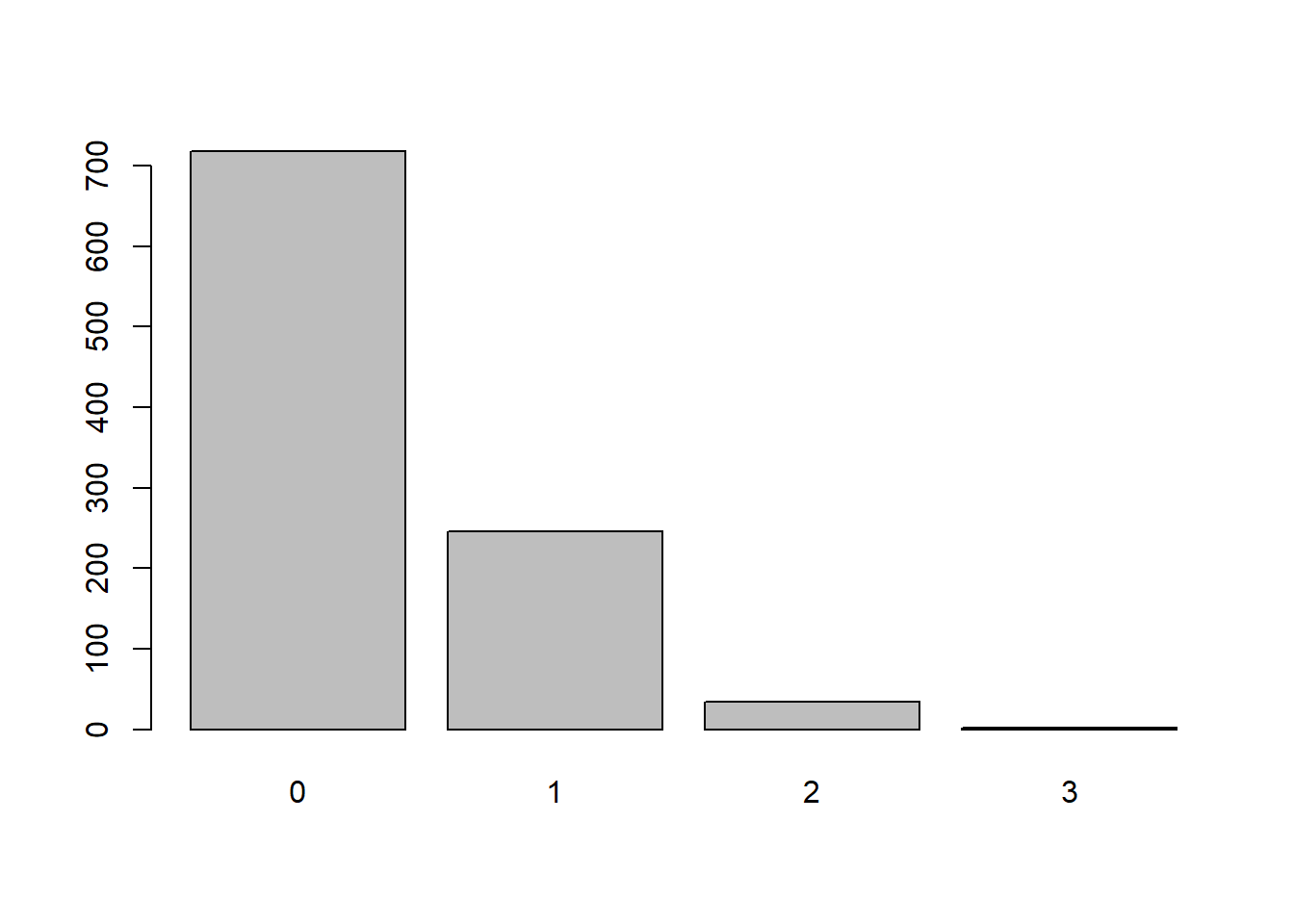

Besaran parameter menentukan sebaran dari data bangkitan, semakin besar m dan n akan menentukan kemencengan dari data bangkitan. Jika nilai m dan n cenderung seimbang maka data dari bangkitan cenderung simetris.

1.6 Dari Contoh ke Populasi (Inferensia)

You can label chapter and section titles using {#label} after them, e.g., we can reference Chapter 1. If you do not manually label them, there will be automatic labels anyway, e.g., Chapter ??.

Figures and tables with captions will be placed in figure and table environments, respectively.

par(mar = c(4, 4, .1, .1))
plot(pressure, type = 'b', pch = 19)

Figure 1.3: Here is a nice figure!

Reference a figure by its code chunk label with the fig: prefix, e.g., see Figure 2.1. Similarly, you can reference tables generated from knitr::kable(), e.g., see Table 2.1.

knitr::kable(
  head(iris, 20), caption = 'Here is a nice table!',
  booktabs = TRUE
)

Table 1.1: Here is a nice table!
Sepal.Length	Sepal.Width	Petal.Length	Petal.Width	Species
5.1	3.5	1.4	0.2	setosa
4.9	3.0	1.4	0.2	setosa
4.7	3.2	1.3	0.2	setosa
4.6	3.1	1.5	0.2	setosa
5.0	3.6	1.4	0.2	setosa
5.4	3.9	1.7	0.4	setosa
4.6	3.4	1.4	0.3	setosa
5.0	3.4	1.5	0.2	setosa
4.4	2.9	1.4	0.2	setosa
4.9	3.1	1.5	0.1	setosa
5.4	3.7	1.5	0.2	setosa
4.8	3.4	1.6	0.2	setosa
4.8	3.0	1.4	0.1	setosa
4.3	3.0	1.1	0.1	setosa
5.8	4.0	1.2	0.2	setosa
5.7	4.4	1.5	0.4	setosa
5.4	3.9	1.3	0.4	setosa
5.1	3.5	1.4	0.3	setosa
5.7	3.8	1.7	0.3	setosa
5.1	3.8	1.5	0.3	setosa

You can write citations, too. For example, we are using the bookdown package (Xie 2021) in this sample book, which was built on top of R Markdown and knitr (Xie 2015).

References

Xie, Yihui. 2015. Dynamic Documents with R and Knitr. 2nd ed. Boca Raton, Florida: Chapman; Hall/CRC. http://yihui.org/knitr/.

———. 2021. Bookdown: Authoring Books and Technical Documents with r Markdown. https://CRAN.R-project.org/package=bookdown.