3 Descriptive Statistics (Review)

Descriptive statistics is a branch of statistics that deals with the collection, organization, analysis, interpretation, and presentation of data. It involves summarizing and organizing data in a way that helps to make sense of it, and to communicate the findings effectively to others. In this chapter, we will review the key concepts and techniques of descriptive statistics, including measures of central tendency, measures of dispersion, and graphical representation of data. Whether you are a student, a researcher, or a professional working with data, understanding and applying these concepts and techniques will enable you to better understand and make sense of the data you are working with.

Definition 3.1 Descriptive statistics described the main features of a collection of data quantitatively.

1. Summarizes a dataset quantitatively without employing a probabilistic formulation.
2. It is the starting point of any statistical analysis.

In statistical analysis, it is important to understand the difference between a population and a sample. A population is the entire group of individuals or objects that we want to study or make inferences about. A sample is a subset of the population that we actually collect data from and use to represent the population. The goal of statistical analysis is to use the information from the sample to make inferences about the population. In order to make valid inferences, it is important to carefully select a representative sample from the population, and to use appropriate statistical techniques to analyze the data. In the following sections, we will provide formal definitions of population and sample, and discuss the importance of sampling in statistical analysis.

• Population: Complete set of all items of interest for an investigator. The population size, commonly denoted by the capital letter N, can be very large. Even going all the way to infinity in some cases.

• Sample: An observed subset of a population. The sample size, commonly denoted by the lower case letter n, is much smaller and often limited to the data available to the investigator.

Based on these definitions we can formally state the objective and goals of statistics.

“The goal of Statistics is to make a stament based on a sample of data that have general validity for the population at large.”

In principle, we would like to analyze the entire population to make those statements. However, doing so is often costly or even unfeasible. Therefore, we limit our analysis to a smaller sample that is representative of the population. Hence, a primary concern of any statistician should be deriving representative samples of a population of interest given the available information (i.e., data). To do so, there are many techniques that have been developed over the history of Statistics.

• Random Sampling: A procedure through which we select a sample of n objects from a population in such a way that each member of the population can be chosen strictly by chance. The randomization step ensures that the selection of a member does not influence the selection of any other member, and each member of the population is equally likely to be chosen for each observation. Formally, this particular selection mechanism is called a random draw with replacement (because the probabilities of selecting other members does not change after selecting an arbitrary element of the set of possible members).

The last two pieces of jargon we will need for this course are simple yet tend to prove confusing to students taking their first steps in the field: Parameter and Statistic. A parameter is a characteristic of a population that we want to estimate or infer from a sample. A statistic is a characteristic of a sample that we use to estimate or infer the value of a population parameter. In other words, a parameter is a property of the entire population, while a statistic is a property of the sample that we use to make inferences about the population. It is important to distinguish between parameters and statistics, because the techniques we use to estimate population parameters from sample statistics depend on the specific properties of the sample and the population.

• Parameter: A numerical measure that describes a specific characteristic of a population.

• Statistic: A numerical measure that describes a specific characteristic of a sample.

In this course, we will focus on data that is both quantitative and numerical. In contrast to qualitative and categorical data. Here is a brief article elucidating the differences between each data type for the curious reader.

• Numerical variables: A numerical or continuous variable (attribute) is one that may take on any value within a finite or infinite interval (e.g., height, weight, temperature, blood glucose, …). There are two types of numerical variables, discrete and continuous.

1. Discrete numerical variables: A measurable variable that may take a finite or infinite (and countable) number of values defined in the space of real numbers \(\mathbb{R}\).

2. Continuous numerical variables: A measurable variable that may take an infinite number of values within a range (i.e., interval) of values defined in the space of real numbers \(\mathbb{R}\).

3.1 Frequency Distribution Tables

A frequency table is a tool that is commonly used to organize and summarize data for discrete numerical variables. It is a table that displays the number of times (or frequency) each unique value of a variable appears in the data. For example, if we have a dataset containing the ages of a group of people, we can use a frequency table to count the number of people in each age group. Frequency tables are useful for understanding the distribution of a discrete numerical variable, and for identifying patterns and trends in the data. They are also a useful starting point for more advanced statistical analyses, such as calculating measures of central tendency and dispersion. In the following section, we will provide a formal definition of a frequency table, and discuss how to create and interpret them. First, a few definitions.

• Frequency distribution: A table to organize and summarize discrete data. All frequency distribution tables are composed of two columns:

  1. Left column: Contains all possible values of the variable being studied.
  2. Right column: Contains the frequencies (i.e., number of observations) in the sample data for each numerical value in the left column.

A frequency table can be represented with only the following four elements:

1. X := A generic characteristic of the population being analyzed. Also called Statistical variable.

2. x_i := A specific observed numerical value of characteristic X.

3. i = 1,2,…,k; where k denotes the number of values the statistical variable X can take in the sample.

4. n(x_i) := The number of observations associated with value x_i in the sample. Also called the Absolute Frequency. It follows that the sum of the absolute frequency of each value x_i in the sample equals the total number of observations, n, in the sample (i.e., the sample size). Mathematically,

\[\begin{equation*} \sum_{i=1}^k n(x_i) = n \end{equation*}\]

Armed with these elements we present our first example of a frequency distribution table.

Code

x_i <- c("x_1", "x_2", "x_3", ".", "x_k")
nx_i <- c("n(x_1)", "n(x_2)", "n(x_3)", ".", "n(x_k)")

freq_table <- data.frame(x_i, nx_i)

# Use the kable() function to create the table
knitr::kable(freq_table, caption = "Frequency distribution table")

Table 3.1: Frequency distribution table

x_i	nx_i
x_1	n(x_1)
x_2	n(x_2)
x_3	n(x_3)
.	.
x_k	n(x_k)

3.2 Relative Frequency Distribution

It follows from our assumption of random selection with replacement that the probability of each observed numerical value \(x_i\), denoted \(p(x_i)\), is simply the ratio \(\frac{n(x_i)}{n}\). Formally,

• Relative frequency of x_i: \(p(x_i) = p_i = \frac{n(x_i)}{n}\), which since it is a probability we immediately know the following must be true \(\sum_i^k p(x_i) = 1\).

Similarly to absolute frequencies, we can construct a relative frequency distribution table to study the probabilities of each numerical observation.

Code

x_i <- c("x_1", "x_2", "x_3", ".", "x_k")
px_i <- c("p(x_1)", "p(x_2)", "p(x_3)", ".", "p(x_k)")

rel_freq_table <- data.frame(x_i, px_i)

# Use the kable() function to create the table
knitr::kable(rel_freq_table, caption = "Relative frequency distribution table")

Table 3.2: Relative frequency distribution table

x_i	px_i
x_1	p(x_1)
x_2	p(x_2)
x_3	p(x_3)
.	.
x_k	p(x_k)

It follows that for a quantitative variable \(X\), the frequency operator \(Fr(X \in B), B \in \mathbb{R}\) defines the relative frequency with which \(X\) takes values included in \(B\). Also, if \(X\) is discrete we have \(Fr(X \in B) = \sum_{i:x_i \in B} p(x_i)\).

Having define a function to compute the frequency of individual observations it is natural to proceed by defining the cumulative frequency function \(F\) for each data type.

3.2.1 Discrete numerical variables

\[\begin{equation*} F: \mathbb{R} \rightarrow [0, 1] \text{ defined as } F(x) = Fr(X \leq x) = Fr(X \in (-\inf, x]) \end{equation*}\]

In the specific case of a discrete variable,

\[\begin{equation*} F(x) = \sum_{i:x_i \leq x} p(x_i), x \in (-\inf, \inf) \end{equation*}\]

Properties:

• \(F\) always starts from 0 (on the left of \(x_1\)) and always reaches 1 (on the right of \(x_k\)).
• \(F\) is always positive.
• \(F\) is monotonic and non-decreasing.
• \(F\) is a step function.
• \(F\) is continuous from the right, also at its discontinuity points \(( \{x_i\}_{i=1}^k )\).
• \(F\) has discontinuity points \(( \{x_i\}_{i=1}^k )\).
• \(F\) is bounded from above and from below.
• \(F\) The height at each step is equal to a relative frequency.
• There exists a one-to-one correspondence between a discrete variable and its cumulative frequency distribution function.

Example 3.1 \[( \{x_i\}_{i=1}^k ), ( \{p_i\}_{i=1}^k )\]

\[\begin{equation} F(x)= \begin{cases} 0 & x < x_1\\ p_1 & x_1 \leq x < x_2\\ p_1 + p_2 & x_2 \leq x < x_3\\ . & .\\ . & .\\ 1 & x \geq x_k\\ \end{cases} \end{equation}\]

Code

# Create a dataframe with the variable values and their frequencies
set.seed(1234)
df <- data.frame(height = round(rnorm(100, mean=50, sd=10)))

cfd_disc <- ggplot(df, aes(height)) + 
  geom_step(stat = "ecdf") +
  ggtitle("Cumulative Frequency Distribution Plot (discrete)") +
  xlab("x") +
  ylab("Frequency ( F(x) )")

cfd_disc # gives errors with plotly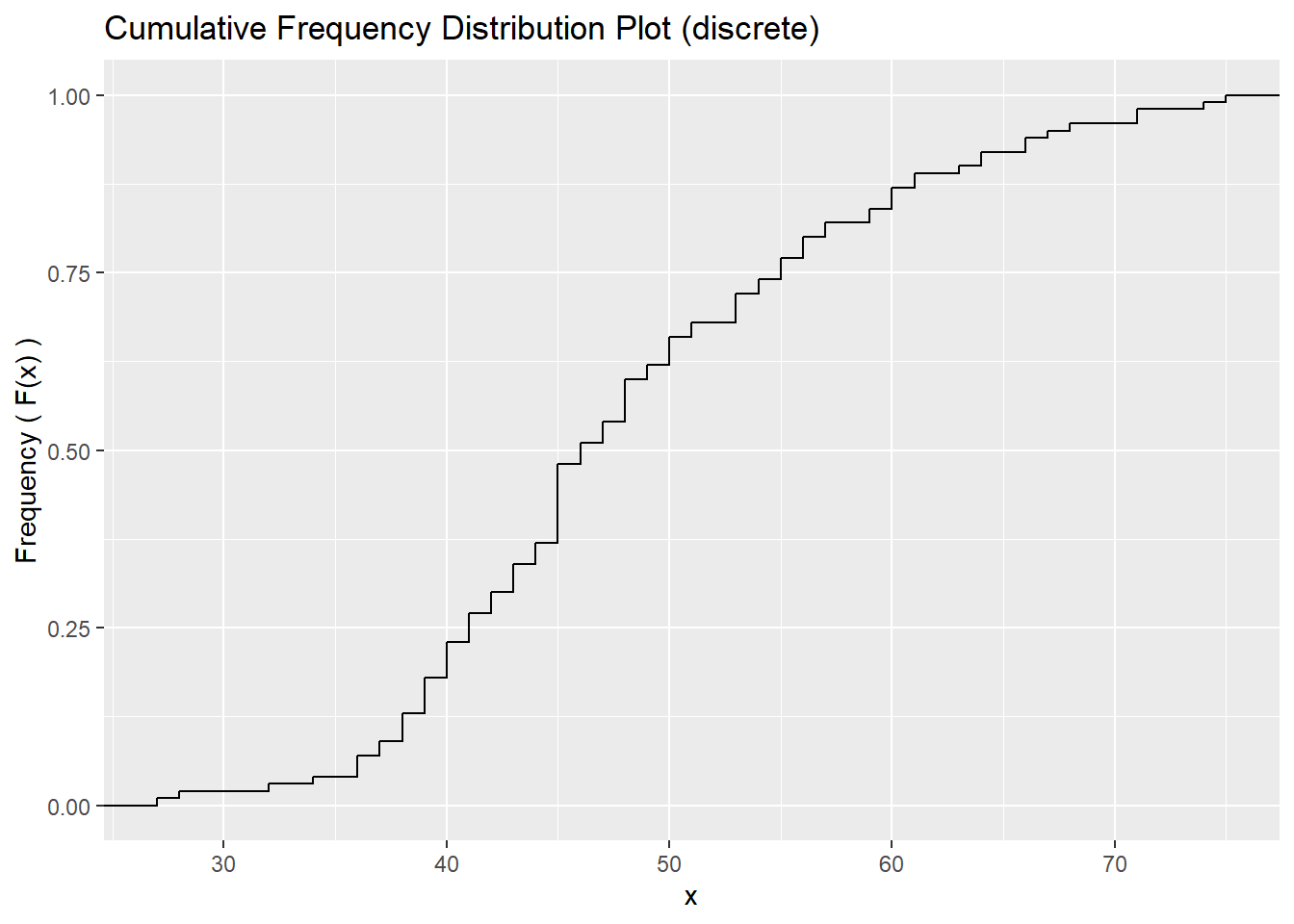

3.2.2 Continuous numerical variables

A frequency distribution by intervals table is a statistical tool used to organize and summarize a set of continuous data by dividing it into intervals or bins. It is used to visualize the distribution of the data and identify patterns or trends. The table consists of a list of intervals or bins (denote intervals), along with the number of observations or the frequency of observations (denoted p_i) within each interval. The intervals can be of equal size or unequal size, depending on the needs of the analysis. Moreover, we often include the interval length (denoted delta_i), and the densities (denoted density_i). Frequency distribution by intervals tables are often used in conjunction with histograms, which are graphical representations of the data that show the frequency distribution visually.

Code

intervals <- c("[x_1; x_2)", "[x_2; x_3)", ".", ".", "[x_k; x_k+1]")
p_i <- c("p_1", "p_2", ".", ".", "p_k")
delta_i <- c("x_2 - x_1", "x_3 - x_2", ".", ".", "x_k+1 - x_k")
density_i <- c("p_1 / delta_1", "p_2 / delta_2", ".", ".", "p_k / delta_k")

freq_table_intervals <- data.frame(intervals, p_i, delta_i, density_i)

knitr::kable(freq_table_intervals, caption = "Frequency distribution by intervals table")

Table 3.3: Frequency distribution by intervals table

intervals	p_i	delta_i	density_i
[x_1; x_2)	p_1	x_2 - x_1	p_1 / delta_1
[x_2; x_3)	p_2	x_3 - x_2	p_2 / delta_2
.	.	.	.
.	.	.	.
[x_k; x_k+1]	p_k	x_k+1 - x_k	p_k / delta_k

A density function is a mathematical function that describes the probability distribution of a continuous variable. It is analogous to the frequency function for discrete variables and it is used to describe the probability of a given value or range of values occurring in the data. The density function is defined as a function of the statistical variable and has the property that the total area under the curve of the function is equal to 1. This property ensures that the function is a valid probability distribution, as the sum of all probabilities must be equal to 1. Density functions are often used in statistical analysis to describe the distribution of continuous data and to make predictions about future observations. They are also used to calculate statistical measures such as the mean, variance, and standard deviation of the data.

The density function, denoted \(f(x)\), is defined in a piecewise manner as follows:

\[\begin{equation} f(x)= \begin{cases} density_1 & x_1 \leq x < x_2\\ density_2 & x_2 \leq x < x_3\\ density_3 & x_3 \leq x < x_4\\ . & .\\ . & .\\ density_k & x_k \leq x \leq x_{k+1}\\ 0 & otherwise \end{cases} \end{equation}\]

Properties:

• \(f(x) \geq 0 \forall x\)
• \(\int_{-\inf}^\inf f(x) dx = 1\)
• \(\forall x_{a,b} s.t. -\inf \leq x_a \leq x_b \leq \inf, \\ Fr(x_a \leq X \leq x_b) = \int_{x_a}^{x_b} f(x) dx\)

Note: \(Fr(X = x_a) = \int_{x_a}^{x_b} f(x) dx = 0\), which means that the probability of our statistical variable of interest \(X\) takes a specific value \(x_a\) is always 0.

In a similar fashion as for the discrete case we can use this density function to compute the cumulative frequency distribution function, denoted F(x), of a continuous random variable.

\[\begin{equation} F(x)= \begin{cases} 0 & x_1 \leq x \leq x_1\\ (x - x_1) \cdot density_1 & x_1 \leq x \leq x_2\\ p_1 + (x - x_2) \cdot density_2 & x_2 \leq x \leq x_3\\ p_1 + p_2 + (x - x_3) \cdot density_3 & x_3 \leq x \leq x_4 \\ . & .\\ . & .\\ 1 & x \geq x_{k+1} \end{cases} \end{equation}\]

Properties:

• \(F\) is monotonic and non-decreasing
• \(F\)is continuous
• \(\lim_{x \to -\infty} F(x) = 0\), and \(\lim_{x \to +\infty} F(x) = 1\)
• \(F'(x) = f(x), \forall x \in \{x_1, x_2,...,x_{k+1}\} \\ \implies Fr(x_a \leq X \leq x_b) = \int_{x_a}^{x_b} f(x) dx = [F(x)]_{x_a}^{x_b} = F(x_b) - F(x_a)\)

Code

# Create a dataframe with x values
df <- data.frame(x = c(-5, 5))

# Plot the cumulative frequency distribution
p <- ggplot(df, aes(x)) +
  stat_function(fun = pnorm, args = list(mean = 0, sd = 0.5), geom = "line") +
  ggtitle("Cumulative Frequency Distribution (continuous)") +
  xlab("c") +
  ylab("Frequency ( F(x) )") +
  theme(plot.title = element_text(face = "bold"),
        plot.subtitle = element_text(face = "italic"))

ggplotly(p)

3.3 Generalized Mean of Order r

The general mean of order r, also known as the power mean, is a type of statistical measure that represents the central tendency of a set of data. It is defined as the \(n_{th}\) root of the sum of the \(r_{th}\) powers of the data values, where \(n\) is the number of data values and \(r\) is a positive real number. The general mean of order \(r\) is a generalization of the arithmetic mean, which is the special case where \(r = 1\), and the geometric mean, which is the special case where \(r = 0\). The general mean of order \(r\) is useful for comparing data sets with different scales or for emphasizing different aspects of the data. For example, the geometric mean is often used to compare data sets with skewed distributions, as it is less sensitive to outliers than the arithmetic mean.

I \(X\) is a discrete variable, then for \(X>0\), \(\{x_i\}_{i=1}^k, \{p_i\}_{i=1}^k\) the generalized mean of order \(r\) of \(X\) is

\[\mu_r(x) = (\sum_{i=1}^k x_i^r \cdot p_i)^{\frac{1}{r}} \]

NOTE: Some generalized means can also be defined when \(X<0\)

Example 3.2

1. $ r=1 1(x) = ({i=1}^k x_i^1 p_i)^1$, commonly called Arithmethic mean.
2. $ r=-1 {-1}(x) = ({i=1}^k x_i^{-1} p_i)^{-1}$, commonly called Harmonic mean.
3. $ r=2 {2}(x) = ({i=1}^k x_i^{2} p_i)^{}$, commonly called the Quadratic mean.

3.3.1 Geometric mean

If \(X\) is a discrete variable, and \(X>0\), then the geometric mean of \(X\) is defined as

\[ r=0 \implies \mu_0(x) = e^{\sum_{i=1}^k log(x_i) \cdot p_i} = \prod_{i=1}^k x_i^{p_i}\]

Theorem 3.1 If \(X>0\) is a discrete variable, then \(\forall r < s,\) where \(r,s \in \mathbb{R}, \mu_r(x) \leq \mu_s(x)\) and \(\lim_{r \rightarrow 0} \mu_r(x) = \mu_0(x)\)

3.3.2 Arithmethic mean

If \(X\) is a discrete variable, then the arithmethic mean of \(X\) is defined as

\[ \mu(x) = M(x) = \sum_{i=1}^k x_i \cdot p_i = \mu\]

Properties:

• \(M(a + bX) = a + b \cdot M(X), \forall a,b \in \mathbb{R}\) (the mean is a linear operator)
• \(M(X - \mu) = 0\)
• \(a^* = \mu\) is the minimizer of \(M[(X-a)^2]\) (that is, \(M[(X-a)^2] \geq M[(X-\mu)^2], \forall a \in \mathbb{R}\))
• The \(r^{th}\) moment of \(X\) is defined using the arithmetich mean as \(M(X^r), r \in \mathbb{N}\).

3.3.3 Generalized mean from “raw” data

Suppose we have a sample of data \(\{X_j\}_{j=1}^n\), where \(X_j > 0 \forall j\), for which we can obtain a frequency distribution table \(\{x_i\}_{i=1}^k, \{p_i\}_{i=1}^k\). Then,

\[ \mu_r(X) = (\sum_{i=1}^k x_i^r \cdot p_i)^{\frac{1}{r}} = (\frac{1}{n} \sum_{j=1}^n X_j^r)^{\frac{1}{r}}\]

Also, \(\mu_0(X) = \prod_{i=1}^k x_i^{p_i} = \prod_{j=1}^n X_j^{\frac{1}{n}}\)

3.3.4 Weighted generalized mean

Suppose we have a sample of data \(\{X_j\}_{j=1}^n\), where \(X_j > 0 \forall j\), for which we can obtain a frequency distribution table \(\{x_i\}_{i=1}^k, \{p_i\}_{i=1}^k\) and weights \(\{w_j\}_{j=1}^n, w_j \geq 0 \forall j\). Then,

\[ \mu_r^w(X) = ( {\frac{ \sum_{j=1}^n w_j \cdot X_j^r }{ \sum_{j=1}^n w_j }} )^{\frac{1}{r}}\]

and \[ \mu_o(X) = \prod_{j=1}^n X_j^{ \frac{ w_j }{ \sum_{j=1}^n w_j } }\]

Properties of generalized means and geometric mean:

We define \(m(y_1,...,y_n)\) as the mean calculated on “raw” data \(\{y_j\}_{j=1}^n\). Then \(m\) it must satisfy

1. Consistency: \(m(a,a,...,a) = a, \forall a \in \mathbb{R}\)

2. Internality: \(min(\{y_j\}_{j=1}^n) \leq m(\{y_j\}_{j=1}^n) \leq max(\{y_j\}_{j=1}^n)\). Furthermore, \[ \lim_{r \rightarrow -\infty} \mu_r(Y) = min(\{y_j\}_{j=1}^n) \\ \lim_{r \rightarrow \infty } \mu_r(Y) = max(\{y_j\}_{j=1}^n)\]

3. Monotonicity: For two datasets of equal length \(\{y_j\}_{j=1}^n\) and \(\{z_j\}_{j=1}^n\) such that \(y_j \leq z_j, \forall j\). Then,

\[ m(\{y_j\}_{j=1}^n) \leq m(\{z_j\}_{j=1}^n) \]

4. Associativity: If \(\forall s, p \geq 1 \wedge \forall \{y_j\}_{j=1}^s, \{z_j\}_{j=1}^p\), then

\[ m(y_1,...,y_s,z_1,...,z_p) = m(\overline{y_1},...,\overline{y_s},\overline{z_1},...,\overline{z_p})\]

where $ = m({y_j}{j=1}^s)$ and $ = m({z_j}{j=1}^p)$.

3.3.5 Median

The following applies to both discrete and continuous variables \(X\).

\[ Med(X) = \text{m}\] The meadian represents the value (or interval of values) that splits the distribution of \(X\) into equal parts (50% + 50%) in terms of relative frequency. When \(X\) is discrete, the \(\underline{median may not be unique}\). When \(X\) is continuous, the \(\underline{median is always unique}\).

3.3.6 Quantiles

These are values that split the distribution of a statistical variable into a given number of equal parts in terms of relative frequency.

Example 3.3 Quartiles split the distribution into four equal parts,

• \(q_1 = 1^{st}\) quartile.\[ Fr(X \leq q_1) \geq 0.25 \wedge Fr(X \geq q_1) \geq 0.75\]
• \(q_2 = 2^{nd}\) quartile = median
• \(q_3 = 3^{rd}\) quartile. \[ Fr(X \leq q_1) \geq 0.75 \wedge Fr(X \geq q_1) \geq 0.25\]

3.3.7 Mode

The mode corresponds to the most frequent value(s) in a dataset. When \(X\) is discrete, the mode is \(\underline{the value(s) with the largest relative frequency}\). When \(X\) is continuous, the mode is \(\underline{the interval(s) with the largest density}\).

3.3.8 Variance

The following applies to both discrete and continuous variables \(X\).

\[ Var(X) = M([X-\mu]^2) \]

Note that if \(X\) is discrete, then \(Var(X) = \sum_{i=1}^k (x_i - \mu)^2 \cdot p_i = \frac{1}{n} \sum_{j=1}^n (X_j - \mu)^2\).

Properties:

• \(Var(X) = M([X-\mu]^2) = M(X^2) - \mu^2\)
• \(Var(X) = 0 \iff X=\mu\) (constant)
• \(Var(X + a) = Vas(X), \forall a \in \mathbb{R}\)
• \(Var(bX) = b^2 \cdot Var(X), \forall b \in \mathbb{R} \\ \implies Var(a + bX) = b^2 \cdot Var(X), \forall a,b \in \mathbb{R}\)

3.3.9 Standard deviation {stdev}

\[ \delta(X) = SD(X) = \sqrt{Var(X)} \]

3.3.10 Coefficient of variation

\[ cv(X) = \frac{\delta(X)}{|\mu|} \]

3.3.11 Chebyshev’s inequality

The following applies to both discrete and continuous variables \(X\). If \(M(X)=\mu\) and \(Var(X)=\delta^2\), then

\[ Fr( |X-\mu| \geq \epsilon ) \leq \frac{\delta^2}{\epsilon^2}, \forall \epsilon>0\]

or

\[ Fr(|X - \mu| \leq \epsilon) \geq 1 - \frac{\delta^2}{\epsilon^2}, \forall \epsilon>0\]

Example 3.4 Let \(\mu = 500\) and \(\delta^2 = 25\). Then, we can use this information to compute Chebyshev’s inequality in the following manner

\[ Fr(490 \leq X \leq 510) = Fr(|X - 500| \leq 10) \geq 1 - \frac{25}{100} = 0.75\] Recall that SD = \(\sqrt{Var(X)}\), which is 5 in this case.