Capítulo 1 Aula 06 - Exercícios
1.1 Exercício 1
Conjunto de dados:
dadosCen01 = read_excel("dados/Data_HousePrice_Area.xlsx", sheet = 1)
dadosCen02 = read_excel("dados/Data_HousePrice_Area.xlsx", sheet = 2)Dados do cenário 01
## # A tibble: 10 × 2
## `Square Feet` `House Price`
## <dbl> <dbl>
## 1 1400 245
## 2 1600 312
## 3 1700 279
## 4 1875 308
## 5 1100 199
## 6 1550 219
## 7 2350 405
## 8 2450 324
## 9 1425 319
## 10 1700 255Dados do cenário 02
## # A tibble: 10 × 2
## `Square Feet` `House Price`
## <dbl> <dbl>
## 1 1400 245
## 2 1800 312
## 3 1700 279
## 4 1875 308
## 5 1200 199
## 6 1480 219
## 7 2350 405
## 8 2100 324
## 9 2000 319
## 10 1700 255No gráfico:
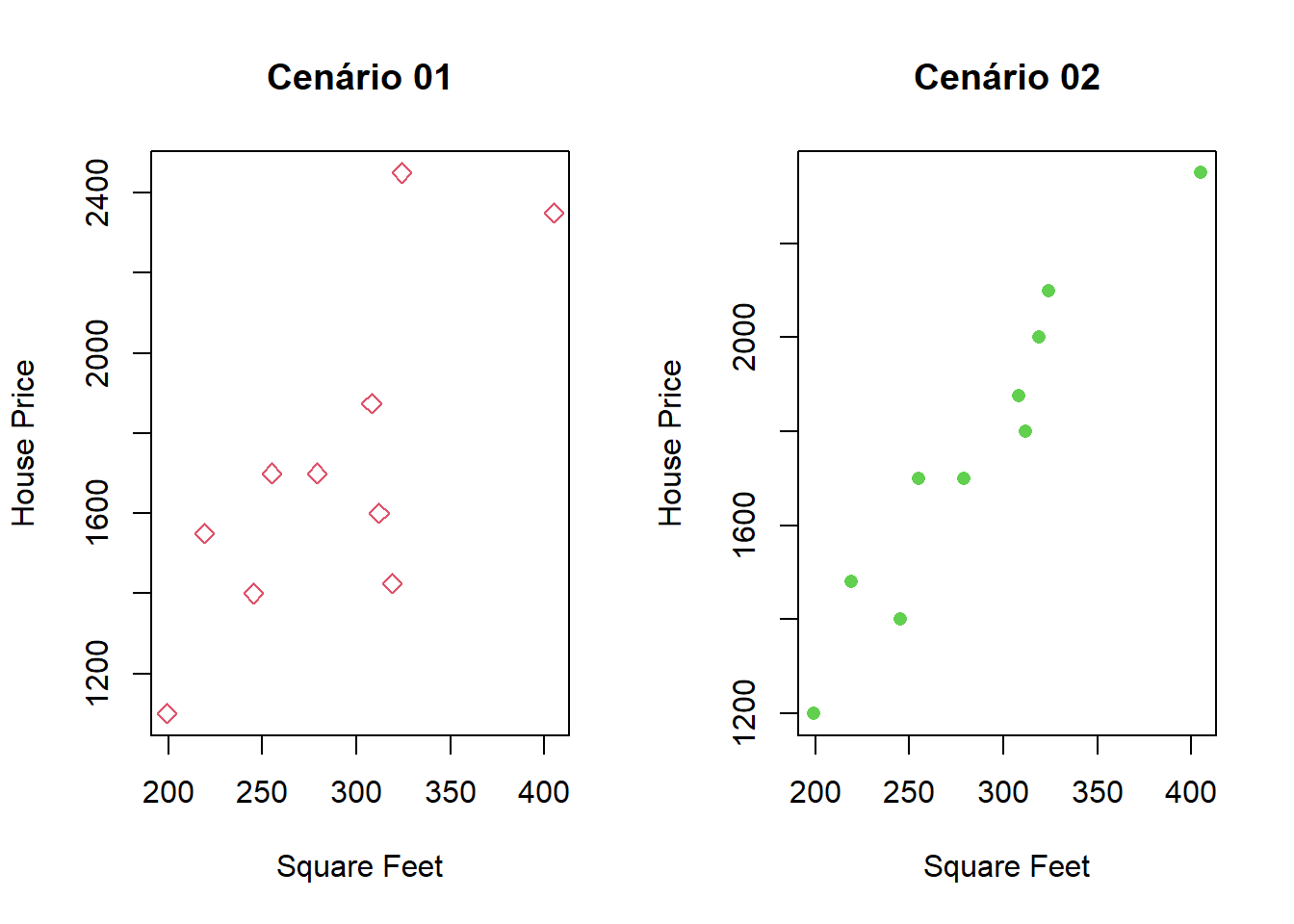
Comparando os dois gráficos, podemos observar:
- O primeiro conjunto é mais esparso
- O segundo cenário os dados estão agrupados de forma linear
1.1.1 Estatísticas descritivas:
Cenário 1
House Price
summary(dadosCen01$`House Price`)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 199.0 247.5 293.5 286.5 317.2 405.0Square Feet
summary(dadosCen01$`Square Feet`)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1100 1456 1650 1715 1831 2450Cenário 2
House Price
summary(dadosCen02$`House Price`)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 199.0 247.5 293.5 286.5 317.2 405.0Square Feet
summary(dadosCen02$`Square Feet`)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1200 1535 1750 1760 1969 2350Vamos agora ajustar um modelo de regressão para ambos os cenários
1.1.2 Ajustes do modelo:
Cenário 01
modelCen01 = lm(dadosCen01$`Square Feet` ~ dadosCen01$`House Price`)
modelCen01##
## Call:
## lm(formula = dadosCen01$`Square Feet` ~ dadosCen01$`House Price`)
##
## Coefficients:
## (Intercept) dadosCen01$`House Price`
## 199.034 5.291\(y = 199.034 + 5.291 x\)
Cálculo do resíduo:
\(y = 199.034 + 5.291 x\) para \(x = 1400\), \(y = valor\). Diferença entre o y dado e o calculado é o resíduo.
resumoMod01 = summary(modelCen01)
resumoMod01##
## Call:
## lm(formula = dadosCen01$`Square Feet` ~ dadosCen01$`House Price`)
##
## Residuals:
## Min 1Q Median 3Q Max
## -461.97 -137.86 16.33 125.32 536.58
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 199.034 464.284 0.429 0.6795
## dadosCen01$`House Price` 5.291 1.589 3.329 0.0104 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 287 on 8 degrees of freedom
## Multiple R-squared: 0.5808, Adjusted R-squared: 0.5284
## F-statistic: 11.08 on 1 and 8 DF, p-value: 0.01039\(R^2\): 0.58
Vamos analisar os resíduos:
plot(modelCen01$residuals ~ dadosCen01$`House Price`)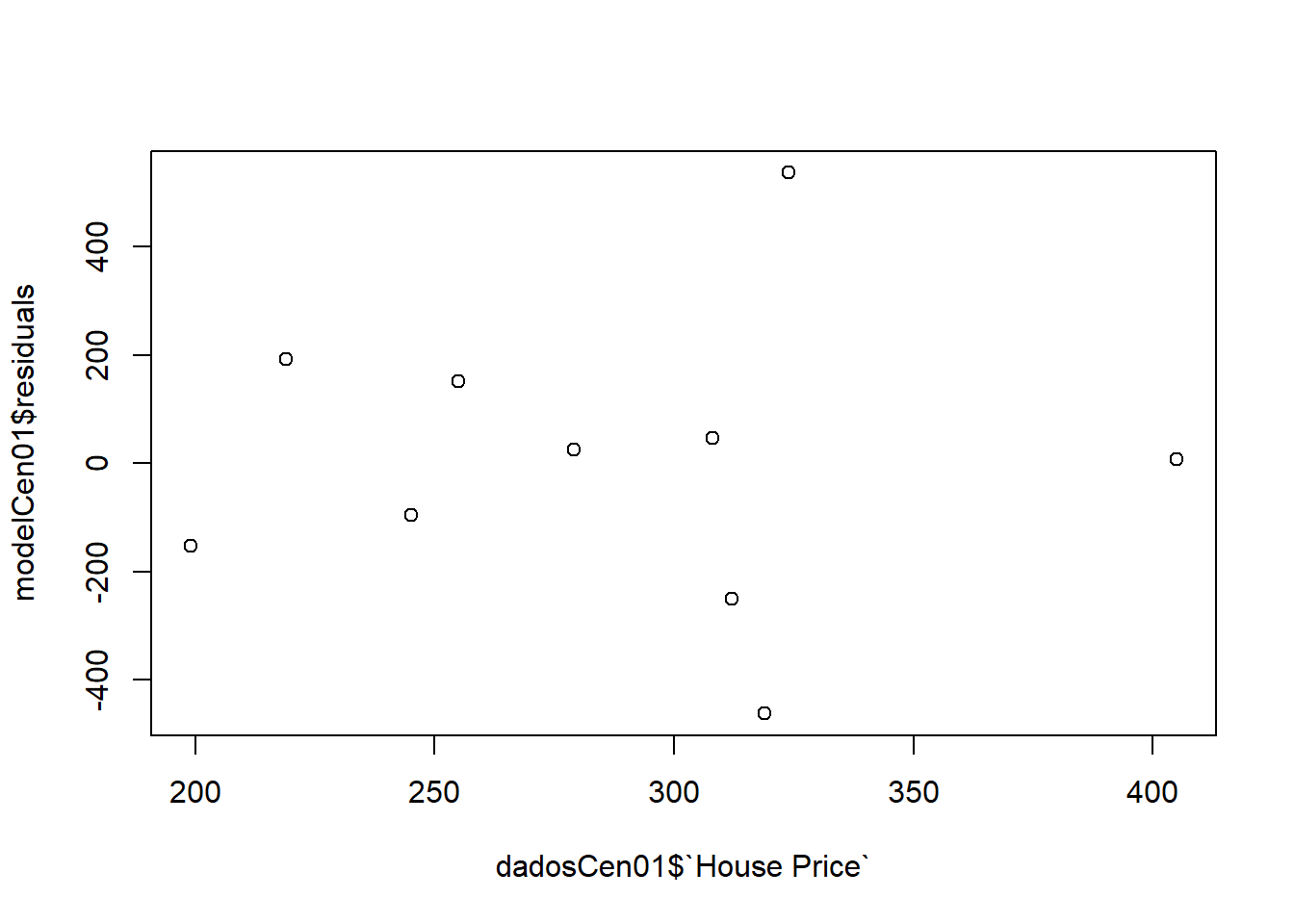
Escreva as observações do gráfico
Cenário 02
modelCen02 = lm(`Square Feet` ~ `House Price`, data = dadosCen02)
modelCen02##
## Call:
## lm(formula = `Square Feet` ~ `House Price`, data = dadosCen02)
##
## Coefficients:
## (Intercept) `House Price`
## 186.202 5.495\(y = 186.202 + 5.495 x\)
Cálculo do resíduo:
\(y = 186.202 + 5.495 x\) para \(x = 1400\), \(y = valor\). Diferença entre o y dado e o calculado é o resíduo.
resumoMod02 = summary(modelCen02)
resumoMod02##
## Call:
## lm(formula = `Square Feet` ~ `House Price`, data = dadosCen02)
##
## Residuals:
## Min 1Q Median 3Q Max
## -132.46 -75.18 -11.46 83.03 133.44
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 186.2023 162.3765 1.147 0.285
## `House Price` 5.4949 0.5558 9.886 9.25e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 100.4 on 8 degrees of freedom
## Multiple R-squared: 0.9243, Adjusted R-squared: 0.9149
## F-statistic: 97.73 on 1 and 8 DF, p-value: 9.246e-06\(R^2\): 0.92
Vamos analisar os resíduos:
plot(modelCen02$residuals ~ dadosCen02$`House Price`)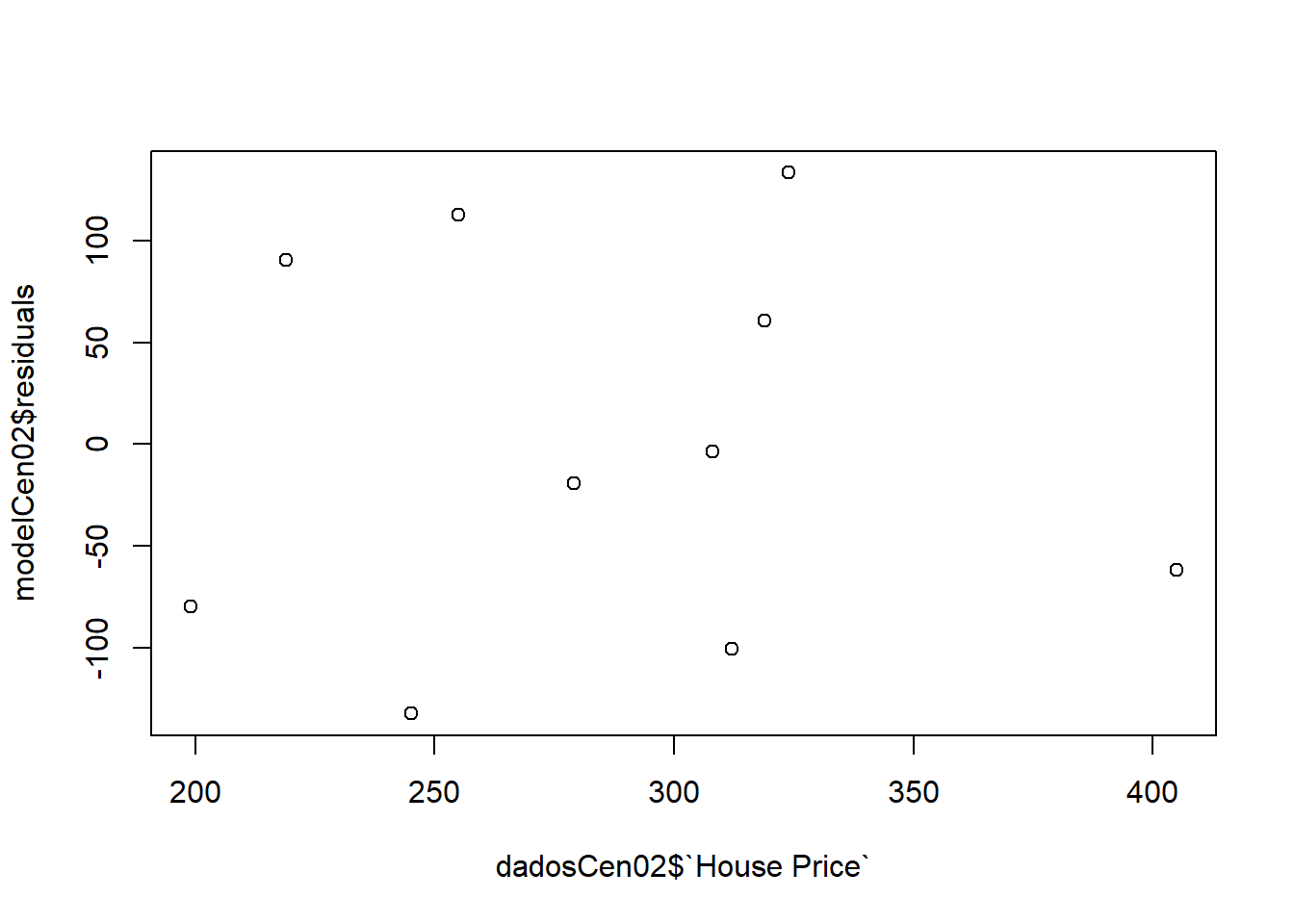
Escreva as observações do gráfico