Chapter 2 Concepts

I shall begin by introducing resouces I find useful.

2.1 The tip of the iceberg

In this section, I draw materials from Harringtong’s book: Games, Strategies and Decision Making. I also consult Felix Munoz-Garcia’s notes for his EconS 424 class.

Here are some basic concepts we need to cover first.

• Strategic interdependence

• Preferences: complete and transitive

• utility: the number assigned to the preference (when complete and transitive)

    - utility function: a list of options and their associated utilities

• Belief:

    - experiential learning: interacting again and again
    - simulated introspection: self-awareness, thinking about thinking

simulating the introspective process of someone else in order to figure out what that individual will do.

2.1.1 Building a game

Two primary forms: extensive and strategic.

A player is rational when she acts in her own best interests. More specifically, given a player’s beliefs as to how other players will behave, the player selects a strategy in order to maximize her payoff.

The rules of a game seek to answer the following questions: (from Felix Munoz-Garcia’s notes)

1. Who is playing? \(\rightarrow\) set of players (I)
2. What are they playing with? \(\rightarrow\) Set of available actions (S)
3. Where each player gets to play? \(\rightarrow\) Order, or time structure of the game.
4. How much players can gain (or lose)? \(\rightarrow\) Payoffs (measured by a utility function \(U_{i}(s_{i},s_{-i})\)

Common knowledge: (about event E)

• I know E.
• I know you know E.
• I know that you know that I know you know E … (ad infinitum).

We assume common knowledge about the rules of the game.

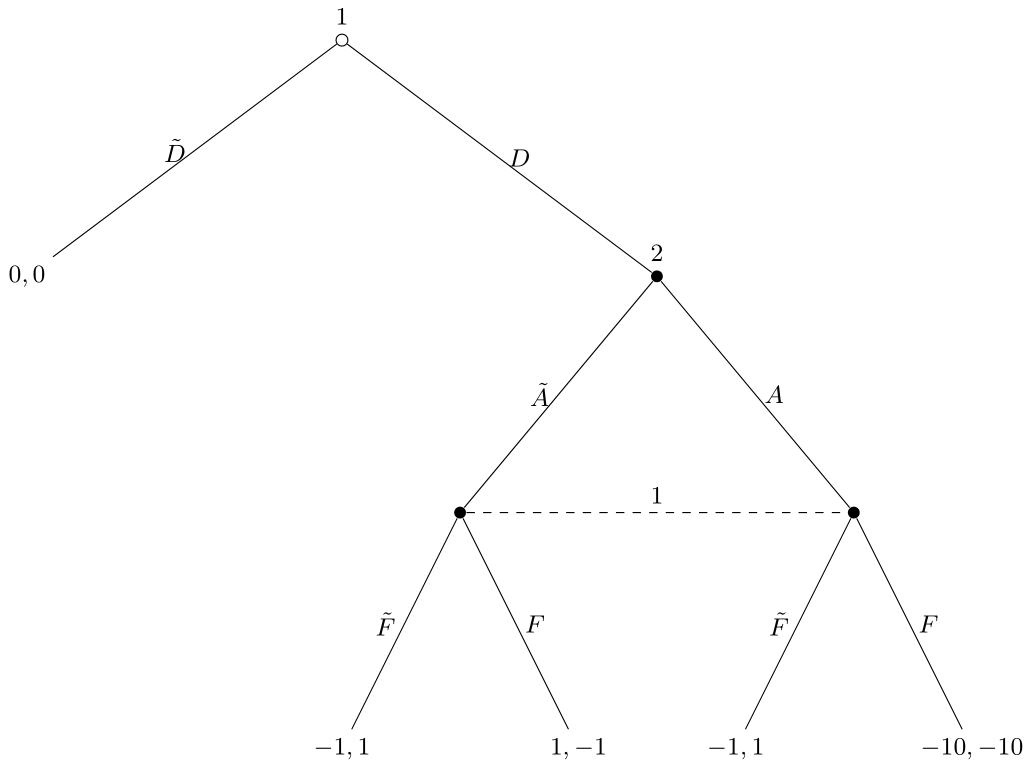
Figure 2.1: Example: Extensive Form Game Tree

• Information set: two or more nodes connected by a dashed line. This represents that the player cannot distinguish which dot she is at, i.e. she does not know what actions the other player(s) has taken.

  • imperfect vs incomplete information. imperfect: one does not know past choice(s) of some player(s). incomplete: some aspect of the game are not common knowledge. (Typical solution, incomplete to imperfect by introducing Nature)
• node: dots, representing a point in the game when a player needs to make a decision
• branch: representing available actions
• payoffs: number at the terminal node, representing utility

• strategy: a fully specified decision rule for how to play a game, a catalog of contingency plans

“a plan so complete that it cannot be upset by enemy action or Nature; for everything that the enemy or Nature may choose to do, together with a set of possible actions for yourself, is just part of a description of the strategy.”

— J. D. Williams

• strategy set (space): a set comprising all possible strategies of a player

  • e.g., \(s_{1}=\{DF, D \widetilde{F}, \widetilde{D}F, \widetilde{D}\widetilde{F}\}\)
  • why do we need to specify future actions after \(\widetilde{D}\)? (potential mistakes, strategic interdependence and backward induction)

• strategy profile: a vector (list) desribing a particular strategy for all players in a game.

  • e.g., \(s=(s_{1},s_{2})\)

2.1.2 Strategic form games

• set of players
• strategy set
• payoff functions

• n-tuple: n of something. e.g., an n-tuple of strategies in a game with n players

• Extensive to normal form: one way; Normal to extensive form: potentially many ways.

		Player 2
		C	D
Player 1	A	1,1	1,1
	B	3,2	2,3

2.2 Solving a game

• A strictly (weakly) dominated (dominant) strategy

• Rational players do not adopt a strictly dominated strategy, hence iterative deletion of strictly dominated strategies (IDSDS).

  • rationality as common knowledge

• ``A strategy is rationalizable if it is consistent with rationality being common knowledge, which means that the strategy is optimal for a player, given beliefs that are themselves consistent with rationality being common knowledge." (from Harrington, check strategy a and c in the following matrix)

			Player 2
		x	y	z
	a	3,1	1,2	1,3
Player 1	b	1,2	0,1	2,0
	c	2,0	3,1	5,0
	d	1,1	4,2	3,3

• Nash equilibrium. All players’ strategies are best replies.
• symmetric game: players have the same strategy sets and if you switch the players’ strategies, their payoffs also switch
• symmetric equilibrium: players use the same strategy

For a symmetric strategy profile in a symmetric game, if one player’s strategy is a best reply, then all players’ strategies are best replies.

“Identifying a criterion that always delivers a unique solution is the “holy grail” of game theory."

• selecting among NE:

  • undominated NE. players don’t use weakly dominated strategies
  • payoff dominant NE (the Pareto criterion).

• mixed strategy vs. pure strategy

  • there is always a NE in mixed strategies
  • “non-degenerate” mixed strategies denotes a set of strategies that a player plays with strictly positive probability.
  • “degenerate” mixed strategy is just a pure strategy (degenerate probability distribution concentrates all its probability weight at a single point)

• maximin vs. minimax

  • Minimax strategy: minimizing one’s own maximum loss
  • Maximin strategy: maximizing one’s own minimum gain

• Strictly competitive games, constant-sum games, zero-sum games.

  • NE
  • before John Nash, Security strategies (Max-Min strategy)
  • not necessarily the same results. the exception is strictly competitive games

2.3 Rules of a tree

Here are some rules of a game tree, taken from Felix’s notes.

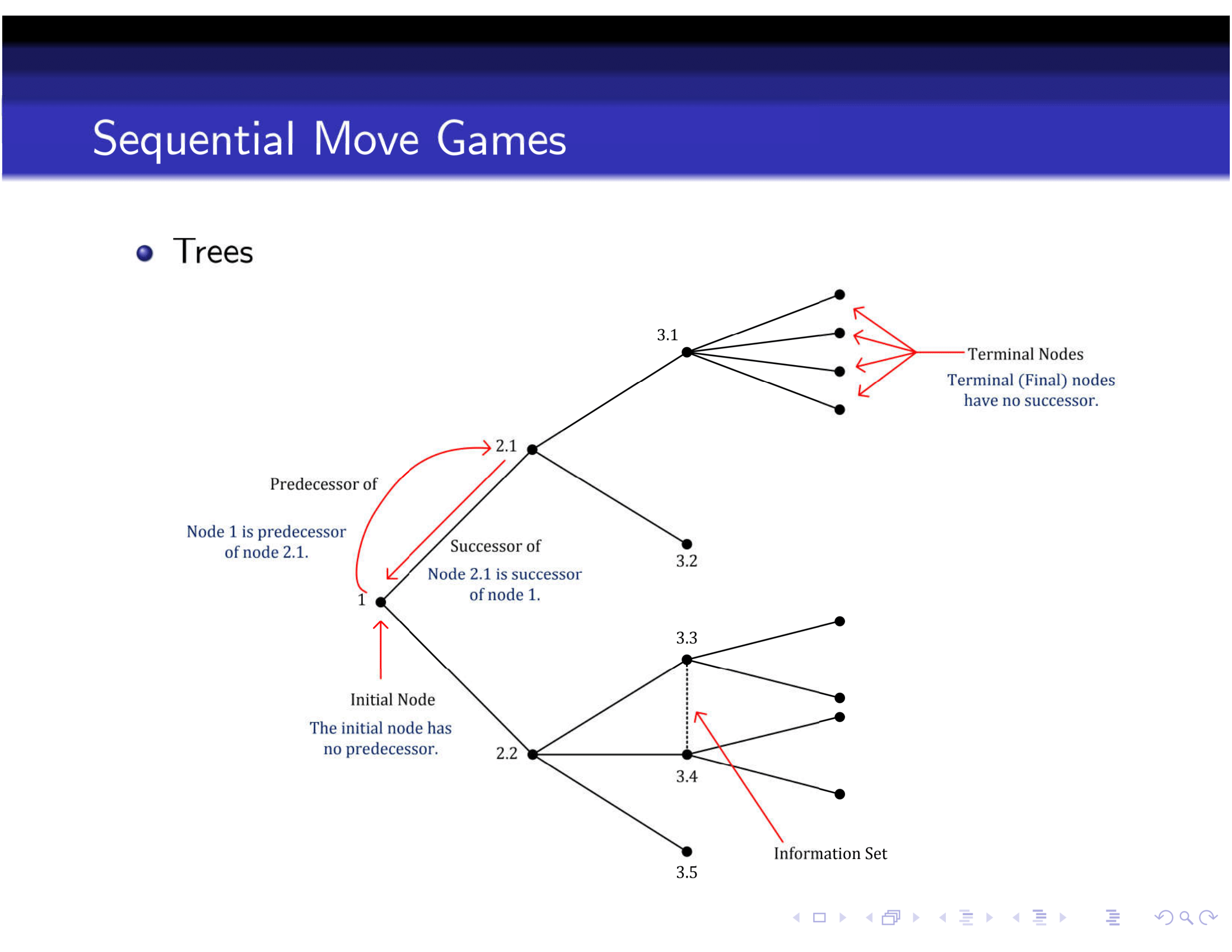
Figure 2.2: Rules of a Game Tree

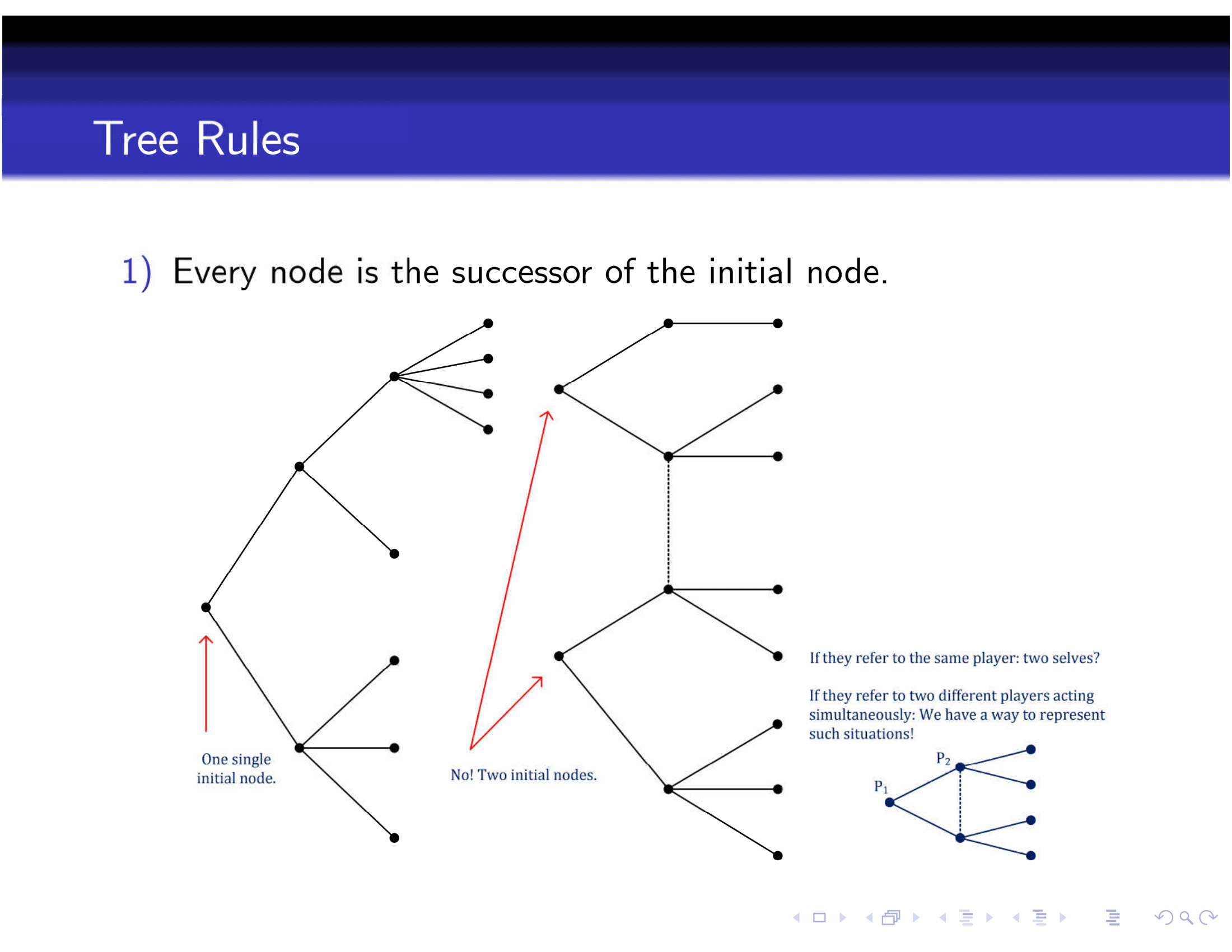
Figure 2.2: Rules of a Game Tree

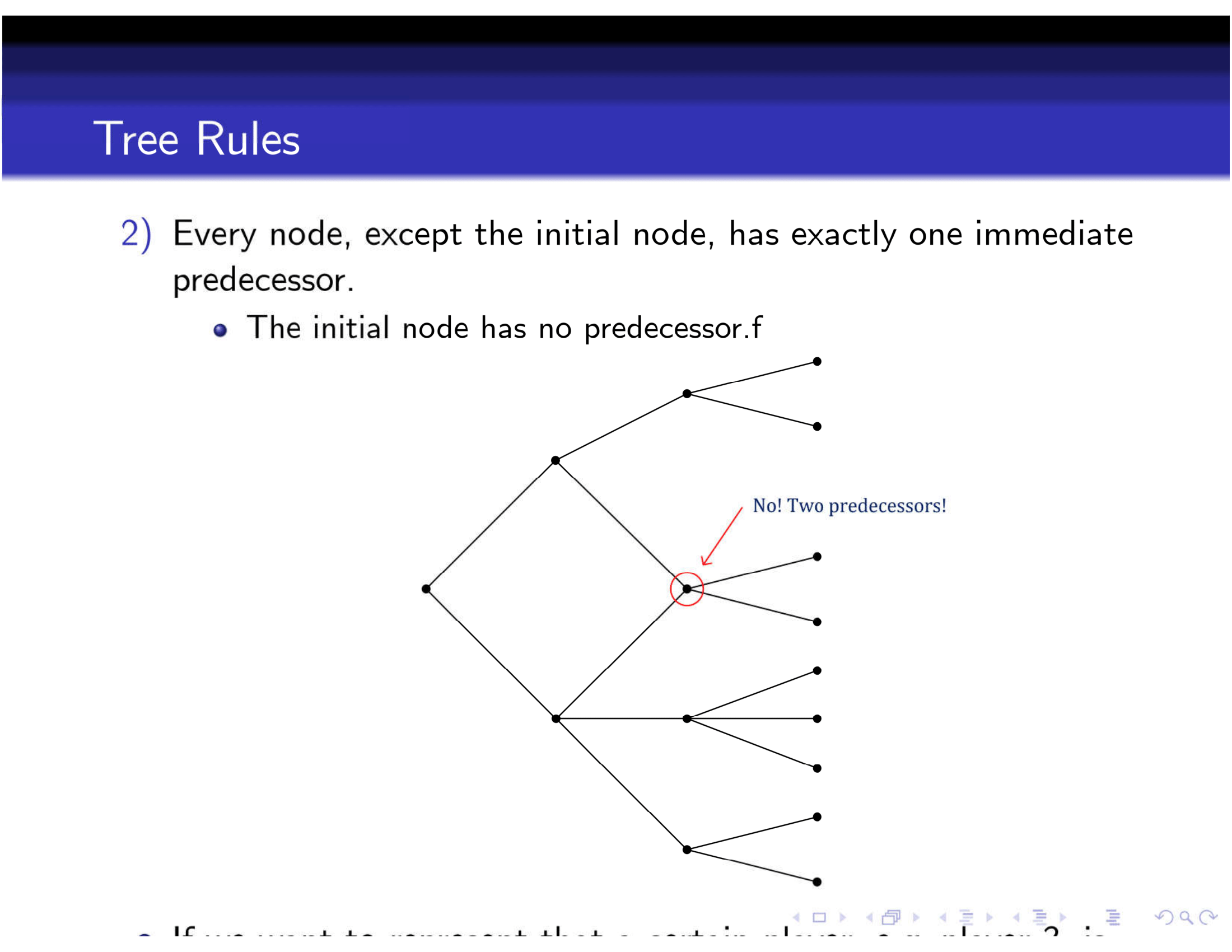
Figure 2.2: Rules of a Game Tree

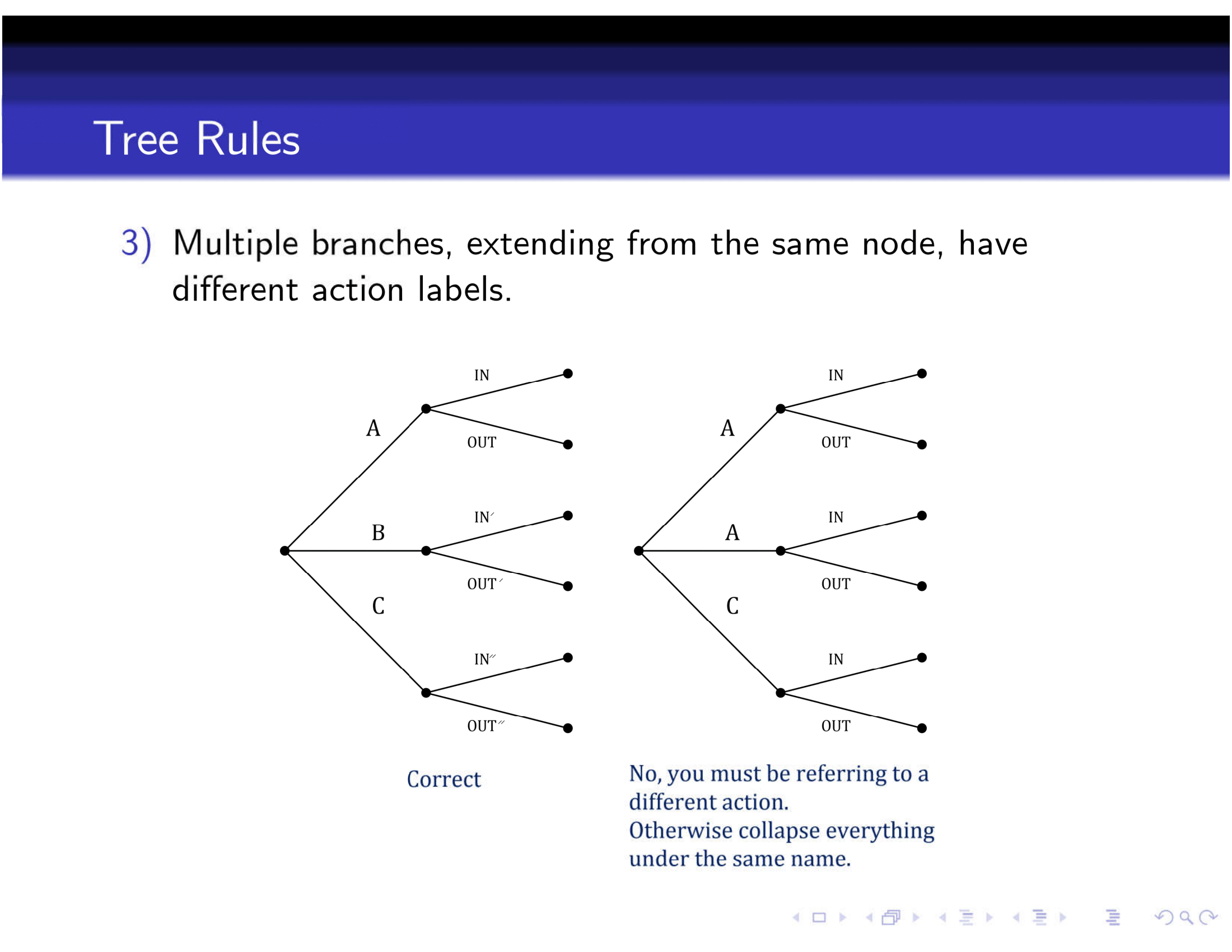
Figure 2.2: Rules of a Game Tree

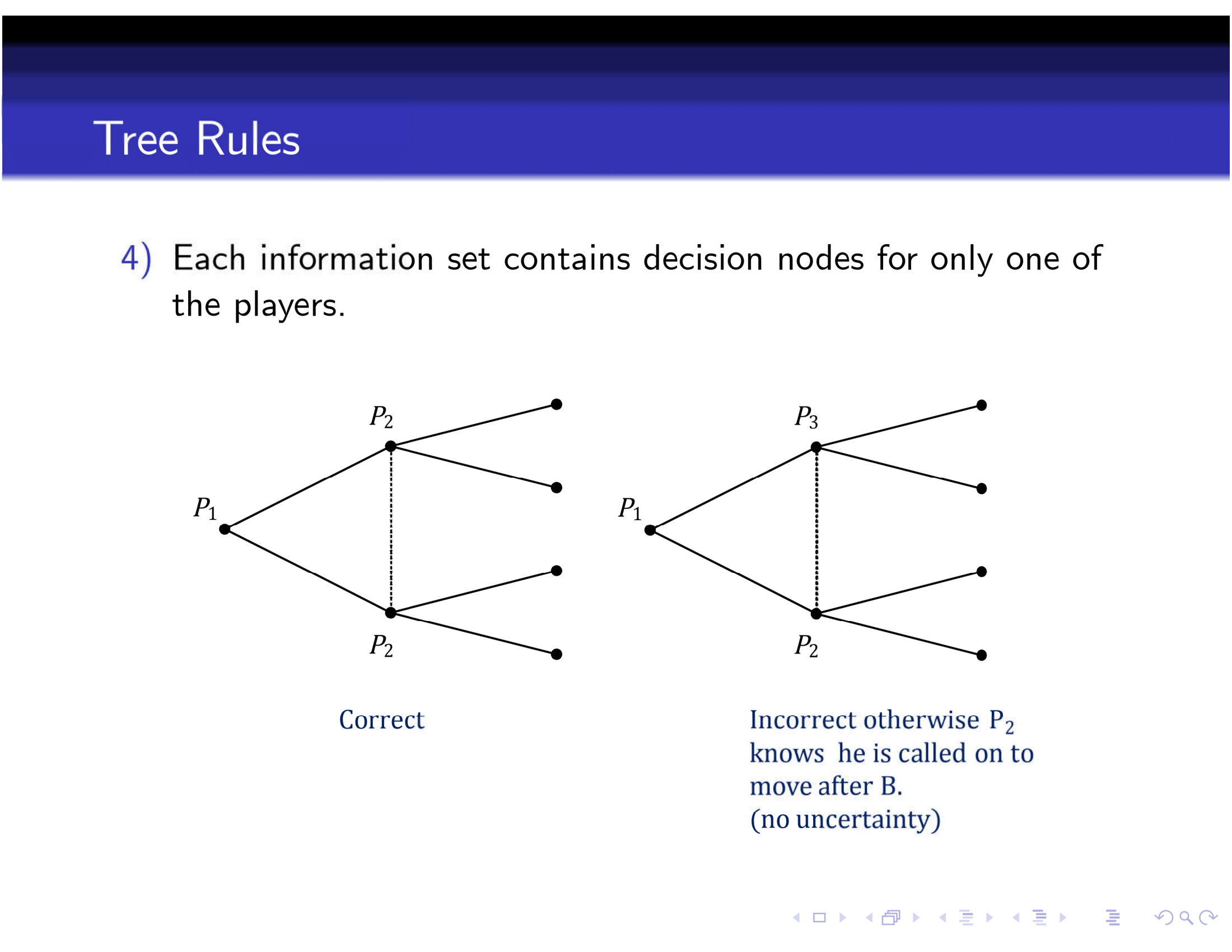
Figure 2.2: Rules of a Game Tree

Figure 2.2: Rules of a Game Tree

Figure 2.2: Rules of a Game Tree

Figure 2.2: Rules of a Game Tree

• subgame perfect Nash equilibrium (SPNE)

  • why a new solution? why not just NE
  • incredible threats

• sequentially rational

Player i’s strategy is sequentially rational if it specifies an optimal action for player i at any node (or information set) of the game where he is called on to move, even those information sets that player i does not believe (ex-ante) that will be reached in the game.

• Backward Induction:

  • starting from every terminal node, every player uses optimal actions at every subgame of the game tree.
  • subgame: a node (and its successors) are not in an information set that contains nodes that are not its successors

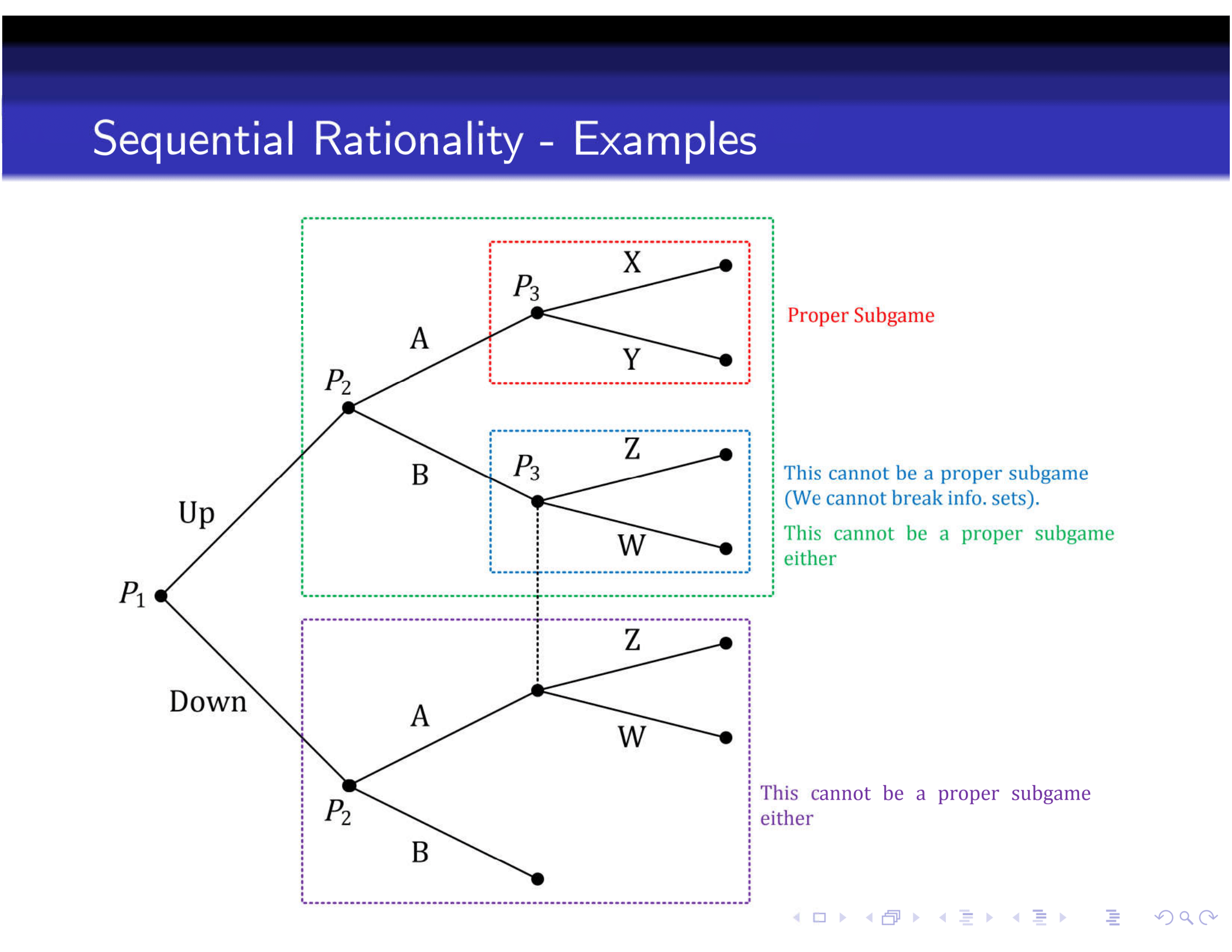
Figure 2.3: A Proper Subgame

• discrepency between SPNE prediction and observations in experiments

  • bounded rationality. last 1-2 stages of a game ok, but at we move further away from the terminal nodes
  • uncertainty
  • logical inconsistency with backward induction

only nonoptimal play could have brought the game to the current point, yet we presume that future play will be optimal. (from Harrington)

2.4 A glimpse into the iceberg

• bargaining games

  • infinite bargaining
  • multilateral bargaining
  • To learn more, Muthoo, Bargaining Theory with Applications

• Sequential games with imperfect information

• commitment: limiting future options

In a game-theoretic context, commitment refers to a decision with some permanency that has an impact on future decision making. (from Harrington)

• Games with private information

  • common knowledge assumption is relaxed. for instance, one player does not know the other’s payoffs
  • incomplete info to imperfect info
    • Nature; type
    • Bayesian game (Nature-augmented) becomes common knowledge since no player knows her type at the start (hence, no private info). common knowledge: Nature will determine players’ types (and the probabilities)
  • Bayes–Nash equilibrium
    • similar to NE: maximize payoff given others’ strategies
    • form accurate beliefs (conjectures) of others’ strategy; given these beliefs, prescribe optimal actions for every possible type

• Signaling games

  • In addition to private information, add sequential moves (which reveals information).
  • perfect Bayes–Nash equilibrium
    • sequential rationality
    • consistent beliefs (Bayes’s rule)
    • types: separating, pooling, semiseparating equilibrium
  • too many PBE?
    • Intuitive criterion; Divinity (\(D_{1}\)) criterion

• Cheap talk games: signaling games with messages

  • message: a costless action; does not affect payoffs
  • babbling equilibrium: a pooling equilibrium in a cheap talk game (no more informative than babble)
  • preplay communication can be useful in games of complete information

• Repeated games

  • model cooperation
  • infinite horizon; indefinite horizon
  • grim-trigger strategy
  • dynamic programming; Bellman equations
  • Partially Optimal Strategy leads to optimal strategy. One-step deviation

A strategy is partially optimal (in the sense of subgame perfect Nash equilibrium) if, for every period and history, the action prescribed by the strategy yields the highest payoff compared with choosing any other current action, while assuming that the player acts according to the strategy in all future periods.

2.5 Bargaining

Here are some of my notes from Muthoo’s non-technical introduction to bargaining theory.

• A bargaining situation is a situation in which two or more players have a common interest to co-operate, but have conflicting interests over exactly how to co-operate.

• A main focus of any theory of bargaining is on the efficiency and distribution properties of the outcome of bargaining.

  • The former property relates to the possibility that the players fail to reach an agreement, or that they reach an agreement after some costly delay. so what is (in)efficient? disagreements and/or costly delayed agreements
  • The distribution property relates to the issue of exactly how the gains from co-operation are divided between the players.

• If the bargaining process is ‘frictionless’—by which I mean that neither player incurs any cost from haggling—then each player may continuously demand that agreement be struck on terms that are most favourable to her.

  • A basic source of a player’s cost from haggling comes from the twin facts that bargaining is time consuming and that time is valuable to the player.
  • Another potential source of friction in the bargaining process comes from the possibility that the negotiations might break down into disagreement because of some exogenous and uncontrollable factors.

• Outside vs. inside options

  • A key principle is that a player’s outside option will increase her bargaining power if and only if the outside option is sufficiently attractive; if it is not attractive enough, then it will have no effect on the bargaining outcome. This is the so-called outside option principle (OOPS).

  • A negotiator’s ‘inside’ option is the payoff that she obtains during the bargaining process—that is, while the parties to the negotiations are in temporary disagreement.