library(Rcpp)
library(rTensor)
warm_gp_initialization <- function(Y, mu_d_logit, g_i, n_topics) {
N <- dim(Y)[1]
D <- dim(Y)[2]
T <- dim(Y)[3]
P <- ncol(g_i)
# Convert Y to logit scale, with smoothing to avoid infinite values
Y_smooth <- (Y * (N * D * T - 1) + 0.5) / (N * D * T)
Y_logit <- log(Y_smooth / (1 - Y_smooth))
# Center Y_logit by subtracting mu_d_logit
Y_centered <- array(0, dim = c(N, D, T))
for (d in 1:D) {
Y_centered[, d, ] <- Y_logit[, d, ] - matrix(mu_d_logit[[d]], nrow = N, ncol = T, byrow = TRUE)
}
# Create a tensor object
Y_tensor <- as.tensor(Y_centered)
# Perform Tucker decomposition
tucker_result <- tucker(Y_tensor, ranks = c(n_topics, D, T))
# Initialize Lambda (N x K x T)
Lambda <- array(0, dim = c(N, n_topics, T))
for (k in 1:n_topics) {
Lambda[, k, ] <- tucker_result$U[[1]][, k] %o% tucker_result$U[[3]][, k]
}
# Initialize Phi (K x D x T)
Phi <- array(0, dim = c(n_topics, D, T))
for (k in 1:n_topics) {
Phi[k, , ] <- tucker_result$U[[2]][, k] %o% tucker_result$U[[3]][, k]
}
# Initialize Gamma using a conservative approach
Gamma <- matrix(rnorm(n_topics * P, mean = 0, sd = 0.1), nrow = n_topics, ncol = P)
# Fixed hyperparameters for length and variance scales
length_scales_lambda <- rep(20, n_topics)
var_scales_lambda <- rep(1, n_topics)
length_scales_phi <- rep(20, n_topics * D)
var_scales_phi <- rep(1, n_topics * D)
return(list(
Lambda = Lambda,
Phi = Phi,
Gamma = Gamma,
length_scales_lambda = length_scales_lambda,
var_scales_lambda = var_scales_lambda,
length_scales_phi = length_scales_phi,
var_scales_phi = var_scales_phi
))
}
cppFunction('
NumericVector fast_logistic(NumericVector x) {
int n = x.size();
NumericVector result(n);
for(int i = 0; i < n; ++i) {
result[i] = 1.0 / (1.0 + exp(-x[i]));
}
return result;
}
')
precompute_K_inv <- function(T, length_scale, var_scale) {
time_diff_matrix <- outer(1:T, 1:T, "-") ^ 2
K <- var_scale * exp(-0.5 * time_diff_matrix / length_scale ^ 2)
K <- K + diag(1e-6, T)
K_inv <- solve(K)
log_det_K <- determinant(K, logarithm = TRUE)$modulus
return(list(K_inv = K_inv, log_det_K = log_det_K))
}
mcmc_sampler_optimized <- function(y,
mu_d_logit,
g_i,
n_iterations,
initial_values,
alpha_lambda,
beta_lambda,
alpha_sigma,
beta_sigma,
alpha_phi,
beta_phi,
alpha_sigma_phi,
beta_sigma_phi,
alpha_Gamma,
beta_Gamma) {
current_state <- initial_values
n_individuals <- dim(current_state$Lambda)[1]
n_topics <- dim(current_state$Lambda)[2]
T <- dim(current_state$Lambda)[3]
n_diseases <- dim(current_state$Phi)[2]
# Initialize adaptive proposal standard deviations
adapt_sd <- list(
Lambda = array(0.01, dim = dim(current_state$Lambda)),
Phi = array(0.01, dim = dim(current_state$Phi)),
Gamma = matrix(
0.01,
nrow = nrow(current_state$Gamma),
ncol = ncol(current_state$Gamma)
)
)
# Initialize storage for samples
samples <- list(
Lambda = array(0, dim = c(
n_iterations, dim(current_state$Lambda)
)),
Phi = array(0, dim = c(n_iterations, dim(
current_state$Phi
))),
Gamma = array(0, dim = c(
n_iterations, dim(current_state$Gamma)
))
)
# Precompute constant matrices
# In your main function, before the MCMC loop:
K_inv_lambda <- lapply(1:n_topics, function(k)
precompute_K_inv(
T,
current_state$length_scales_lambda[k],
current_state$var_scales_lambda[k]
))
K_inv_phi <- lapply(1:(n_topics * n_diseases), function(idx)
precompute_K_inv(
T,
current_state$length_scales_phi[idx],
current_state$var_scales_phi[idx]
))
for (iter in 1:n_iterations) {
# Update Lambda
proposed_Lambda <- current_state$Lambda + array(rnorm(prod(dim(
current_state$Lambda
)), 0, adapt_sd$Lambda),
dim = dim(current_state$Lambda))
current_log_lik <- log_likelihood_vec(y, current_state$Lambda, current_state$Phi, mu_d_logit)
proposed_log_lik <- log_likelihood_vec(y, proposed_Lambda, current_state$Phi, mu_d_logit)
lambda_mean <- g_i %*% t(current_state$Gamma)
current_log_prior <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean[i, k],
K_inv_lambda[[k]]$K_inv,
K_inv_lambda[[k]]$log_det_K
)
})
}))
proposed_log_prior <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
proposed_Lambda[i, k, ],
lambda_mean[i, k],
K_inv_lambda[[k]]$K_inv,
K_inv_lambda[[k]]$log_det_K
)
})
}))
log_accept_ratio <- (proposed_log_lik + proposed_log_prior) - (current_log_lik + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$Lambda <- proposed_Lambda
adapt_sd$Lambda <- adapt_sd$Lambda * 1.01
} else {
adapt_sd$Lambda <- adapt_sd$Lambda * 0.99
}
# Update Phi (similar structure to Lambda update)
proposed_Phi <- current_state$Phi + array(rnorm(prod(dim(
current_state$Phi
)), 0, adapt_sd$Phi), dim = dim(current_state$Phi))
current_log_lik <- log_likelihood_vec(y, current_state$Lambda, current_state$Phi, mu_d_logit)
proposed_log_lik <- log_likelihood_vec(y, current_state$Lambda, proposed_Phi, mu_d_logit)
current_log_prior <- sum(sapply(1:n_topics, function(k) {
sapply(1:n_diseases, function(d) {
idx <- (k - 1) * n_diseases + d
log_gp_prior_vec(current_state$Phi[k, d, ],
0,
K_inv_lambda[[k]]$K_inv,
K_inv_lambda[[k]]$log_det_K)
})
}))
proposed_log_prior <- sum(sapply(1:n_topics, function(k) {
sapply(1:n_diseases, function(d) {
idx <- (k - 1) * n_diseases + d
log_gp_prior_vec(proposed_Phi[k, d, ],
0,
K_inv_lambda[[k]]$K_inv,
K_inv_lambda[[k]]$log_det_K)
})
}))
log_accept_ratio <- (proposed_log_lik + proposed_log_prior) - (current_log_lik + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$Phi <- proposed_Phi
adapt_sd$Phi <- adapt_sd$Phi * 1.01
} else {
adapt_sd$Phi <- adapt_sd$Phi * 0.99
}
# Update Gamma (similar structure to original)
proposed_Gamma <- current_state$Gamma + matrix(rnorm(prod(dim(
current_state$Gamma
)), 0, adapt_sd$Gamma),
nrow = nrow(current_state$Gamma))
current_log_prior <- sum(dnorm(
current_state$Gamma,
0,
sqrt(alpha_Gamma / beta_Gamma),
log = TRUE
))
proposed_log_prior <- sum(dnorm(proposed_Gamma, 0, sqrt(alpha_Gamma / beta_Gamma), log = TRUE))
lambda_mean_current <- g_i %*% t(current_state$Gamma)
lambda_mean_proposed <- g_i %*% t(proposed_Gamma)
current_log_likelihood <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean_current[i, k],
K_inv_lambda[[k]]$K_inv,
K_inv_lambda[[k]]$log_det_K
)
})
}))
proposed_log_likelihood <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean_proposed[i, k],
K_inv_lambda[[k]]$K_inv,
K_inv_lambda[[k]]$log_det_K
)
})
}))
log_accept_ratio <- (proposed_log_likelihood + proposed_log_prior) - (current_log_likelihood + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$Gamma <- proposed_Gamma
adapt_sd$Gamma <- adapt_sd$Gamma * 1.01
} else {
adapt_sd$Gamma <- adapt_sd$Gamma * 0.99
}
# Store samples
samples$Lambda[iter, , , ] <- current_state$Lambda
samples$Phi[iter, , , ] <- current_state$Phi
samples$Gamma[iter, , ] <- current_state$Gamma
if (iter %% 100 == 0)
cat("Iteration", iter, "\n")
}
return(samples)
}
# Updated log_likelihood_vec function
log_likelihood_vec <- function(y, Lambda, Phi, mu_d_logit) {
n_individuals <- dim(Lambda)[1]
n_topics <- dim(Lambda)[2]
T <- dim(Lambda)[3]
n_diseases <- dim(Phi)[2]
logit_pi <- array(0, dim = c(n_individuals, n_diseases, T))
for (k in 1:n_topics) {
for (t in 1:T) {
logit_pi[, , t] <- logit_pi[, , t] + Lambda[, k, t] %*% t(Phi[k, , t])
}
}
for (d in 1:n_diseases) {
logit_pi[, d, ] <- logit_pi[, d, ] + matrix(mu_d_logit[[d]],
nrow = n_individuals,
ncol = T,
byrow = TRUE)
}
# Apply logistic function element-wise
pi <- array(fast_logistic(as.vector(logit_pi)), dim = dim(logit_pi))
log_lik <- 0
for (i in 1:n_individuals) {
for (d in 1:n_diseases) {
at_risk <- which(cumsum(y[i, d, ]) == 0)
if (length(at_risk) > 0) {
event_time <- max(at_risk) + 1
if (event_time <= T) {
log_lik <- log_lik + log(pi[i, d, event_time])
}
log_lik <- log_lik + sum(log(1 - pi[i, d, at_risk]))
} else {
log_lik <- log_lik + log(pi[i, d, 1])
}
}
}
return(log_lik)
}
log_gp_prior_vec <- function(x, mean, K_inv, log_det_K) {
T <- length(x)
centered_x <- x - mean
quad_form <- sum(centered_x * (K_inv %*% centered_x))
return(-0.5 * (log_det_K + quad_form + T * log(2 * pi)))
}otpimized
Quarto
Quarto enables you to weave together content and executable code into a finished document. To learn more about Quarto see
You can add options to executable code like this
source("~/Dropbox (Personal)/bern_sim.R")
Attaching package: 'dplyr'The following object is masked from 'package:MASS':
selectThe following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionShape of mu_d_matrix: 12 56
Shape of mean_lambda: 10 2
Shape of mu_i: 10 56 initial_values <- warm_gp_initialization(y, mu_d_logit, g_i, n_topics)
|
| | 0%
|
|=== | 4%
|
|====== | 8%
|
|======================================================================| 100%print(dim(y))[1] 10 12 56print(dim(initial_values$Lambda))[1] 10 2 56print(dim(initial_values$Phi))[1] 2 12 56print(length(mu_d_logit))[1] 12print(length(mu_d_logit[[1]]))[1] 56# Define hyperparameters
alpha_lambda <- 2
beta_lambda <- 0.1
alpha_sigma <- 2
beta_sigma <- 2
alpha_phi <- 2
beta_phi <- 0.1
alpha_sigma_phi <- 2
beta_sigma_phi <- 2
alpha_Gamma <- 2
beta_Gamma <- 2
# Run MCMC
start=proc.time()
mcmc_results <- mcmc_sampler_optimized(y, mu_d_logit, g_i, n_iterations = 5000, initial_values,
alpha_lambda, beta_lambda, alpha_sigma, beta_sigma,
alpha_phi, beta_phi, alpha_sigma_phi, beta_sigma_phi,
alpha_Gamma, beta_Gamma)Iteration 100
Iteration 200
Iteration 300
Iteration 400
Iteration 500
Iteration 600
Iteration 700
Iteration 800
Iteration 900
Iteration 1000
Iteration 1100
Iteration 1200
Iteration 1300
Iteration 1400
Iteration 1500
Iteration 1600
Iteration 1700
Iteration 1800
Iteration 1900
Iteration 2000
Iteration 2100
Iteration 2200
Iteration 2300
Iteration 2400
Iteration 2500
Iteration 2600
Iteration 2700
Iteration 2800
Iteration 2900
Iteration 3000
Iteration 3100
Iteration 3200
Iteration 3300
Iteration 3400
Iteration 3500
Iteration 3600
Iteration 3700
Iteration 3800
Iteration 3900
Iteration 4000
Iteration 4100
Iteration 4200
Iteration 4300
Iteration 4400
Iteration 4500
Iteration 4600
Iteration 4700
Iteration 4800
Iteration 4900
Iteration 5000 stop=proc.time()
stop-start user system elapsed
25.858 0.899 27.073 a=readRDS("~/Dropbox (Personal)/UKB_topic_app/disease_array_incidence.rds")
prs_subset=na.omit(readRDS("~/Dropbox (Personal)/pheno_dir/prs_subset.rds"))
mu_d_list=readRDS("~/Dropbox (Personal)/massivemudlist.rds")
names=readRDS("~/Desktop/namesofphenos.rds")
names(mu_d_list)=names$phenotype
colnames(a)=names$phenotype
top=names(sapply(mu_d_list,sum)[order(sapply(mu_d_list,sum),decreasing = T)][1:20])
## make sure everything matches
mu_d_l=mu_d_list[top]
f=sample(intersect(rownames(a[,1,]),rownames(prs_subset)),1000)
y2=a[f,top,]
g_i=prs_subset[f,-c(10,16,18,36,37)]
all.equal(colnames(y2),names(mu_d_l))[1] TRUE# Ensure dimensions are correct
n_individuals <- length(f)
n_diseases <- length(mu_d_l)
T <- dim(y2)[3]
n_topics <- 3 # You can adjust this as needed
n_genetic_factors <- ncol(g_i)
# Ensure y2 is in the correct format (should be binary)
y <- as.array(y2)
Y=y
N <- dim(Y)[1]
D <- dim(Y)[2]
T <- dim(Y)[3]
P <- ncol(g_i)
# Convert Y to logit scale, with smoothing to avoid infinite values
Y_smooth <- (Y * (N * D * T - 1) + 0.5) / (N * D * T)
Y_logit <- log(Y_smooth / (1 - Y_smooth))
m=apply(Y_logit,c(2,3),mean)
mu_d_list=list();for(i in 1:nrow(m)){
mu_d_list[[i]]=m[i,]}
mu_d_logit <- mu_d_list
# Ensure g_i is a matrix
g_i <- as.matrix(g_i)
print(dim(y))[1] 1000 20 51print(dim(g_i))[1] 1000 32print(length(mu_d_logit))[1] 20initial_values <- warm_gp_initialization(y, mu_d_logit, g_i, n_topics)
|
| | 0%
|
|=== | 4%
|
|====== | 8%
|
|======================================================================| 100%alpha_lambda <- beta_lambda <- 1
alpha_sigma <- beta_sigma <- 1
alpha_phi <- beta_phi <- 1
alpha_sigma_phi <- beta_sigma_phi <- 1
alpha_Gamma <- beta_Gamma <- 1
# Run MCMC
start=proc.time()
mcmc_results <- mcmc_sampler_optimized(y, mu_d_logit, g_i, n_iterations = 5000, initial_values,
alpha_lambda, beta_lambda, alpha_sigma, beta_sigma,
alpha_phi, beta_phi, alpha_sigma_phi, beta_sigma_phi,
alpha_Gamma, beta_Gamma)Iteration 100
Iteration 200
Iteration 300
Iteration 400
Iteration 500
Iteration 600
Iteration 700
Iteration 800
Iteration 900
Iteration 1000
Iteration 1100
Iteration 1200
Iteration 1300
Iteration 1400
Iteration 1500
Iteration 1600
Iteration 1700
Iteration 1800
Iteration 1900
Iteration 2000
Iteration 2100
Iteration 2200
Iteration 2300
Iteration 2400
Iteration 2500
Iteration 2600
Iteration 2700
Iteration 2800
Iteration 2900
Iteration 3000
Iteration 3100
Iteration 3200
Iteration 3300
Iteration 3400
Iteration 3500
Iteration 3600
Iteration 3700
Iteration 3800
Iteration 3900
Iteration 4000
Iteration 4100
Iteration 4200
Iteration 4300
Iteration 4400
Iteration 4500
Iteration 4600
Iteration 4700
Iteration 4800
Iteration 4900
Iteration 5000 stop=proc.time()
stop-start user system elapsed
3004.475 192.465 3207.969 saveRDS(mcmc_results,"~/Dropbox (Personal)/mcmc_results_827_fast.rds")library(coda)
analyze_results <- function(mcmc_results, parameter) {
# Extract the parameter samples
samples <- mcmc_results[[parameter]]
# Get dimensions
dim_samples <- dim(samples)
n_iterations <- dim_samples[1]
if (length(dim_samples) == 4) { # For 3D parameters like Phi and Lambda
n_topics <- dim_samples[2]
n_diseases_or_individuals <- dim_samples[3]
T <- dim_samples[4]
# Choose a few representative slices to plot
slices <- list(
c(1, 1, T %/% 2), # First topic, first disease/individual, middle time point
c(n_topics, n_diseases_or_individuals, T %/% 2), # Last topic, last disease/individual, middle time point
c(n_topics %/% 2, n_diseases_or_individuals %/% 2, T) # Middle topic, middle disease/individual, last time point
)
for (slice in slices) {
chain <- mcmc(samples[, slice[1], slice[2], slice[3]])
# Plot trace
plot(chain, main=paste(parameter, "- Topic", slice[1], "Disease/Individual", slice[2], "Time", slice[3]))
# Print summary
print(summary(chain))
# Effective sample size
print(effectiveSize(chain))
}
} else if (length(dim_samples) == 3) { # For 2D parameters like Gamma
n_topics <- dim_samples[2]
n_columns <- dim_samples[3]
# Choose a few representative slices to plot
slices <- list(
c(1, 1), # First topic, first column
c(n_topics, n_columns), # Last topic, last column
c(n_topics %/% 2, n_columns %/% 2) # Middle topic, middle column
)
for (slice in slices) {
chain <- mcmc(samples[, slice[1], slice[2]])
# Plot trace
plot(chain, main=paste(parameter, "- Topic", slice[1], "Column", slice[2]))
# Print summary
print(summary(chain))
# Effective sample size
print(effectiveSize(chain))
}
} else { # For 1D parameters like length scales and var scales
chain <- mcmc(samples)
# Plot trace
plot(chain, main=parameter)
# Print summary
print(summary(chain))
# Effective sample size
print(effectiveSize(chain))
}
# Calculate overall acceptance rates
acceptance_rates <- mean(diff(as.vector(samples)) != 0)
print(paste("Overall acceptance rate:", round(acceptance_rates, 3)))
}
# Usage
analyze_results(mcmc_results, "Phi")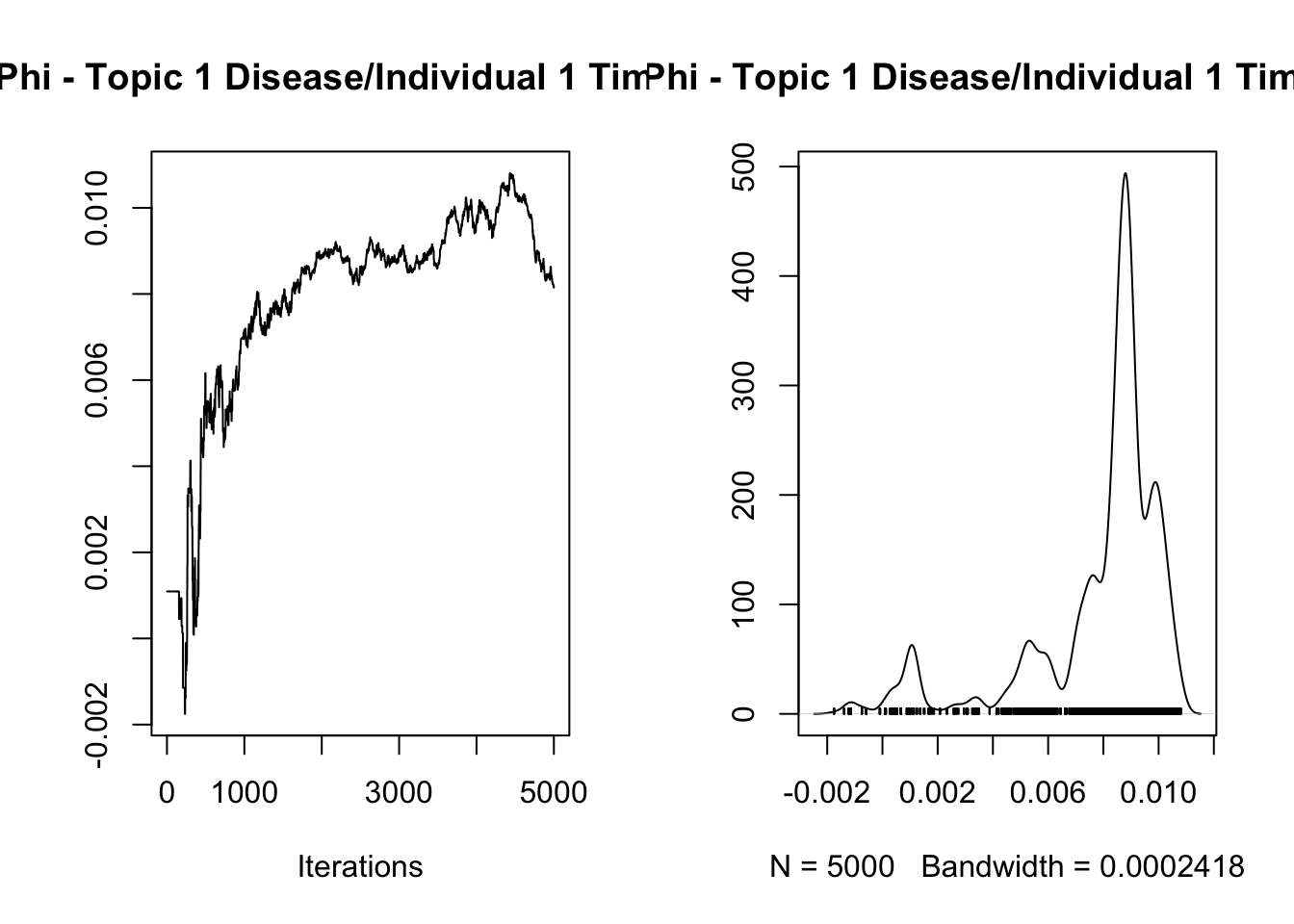
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
0.0078556 0.0024820 0.0000351 0.0013699
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
0.0005296 0.0074772 0.0087052 0.0091564 0.0104729
var1
3.282832 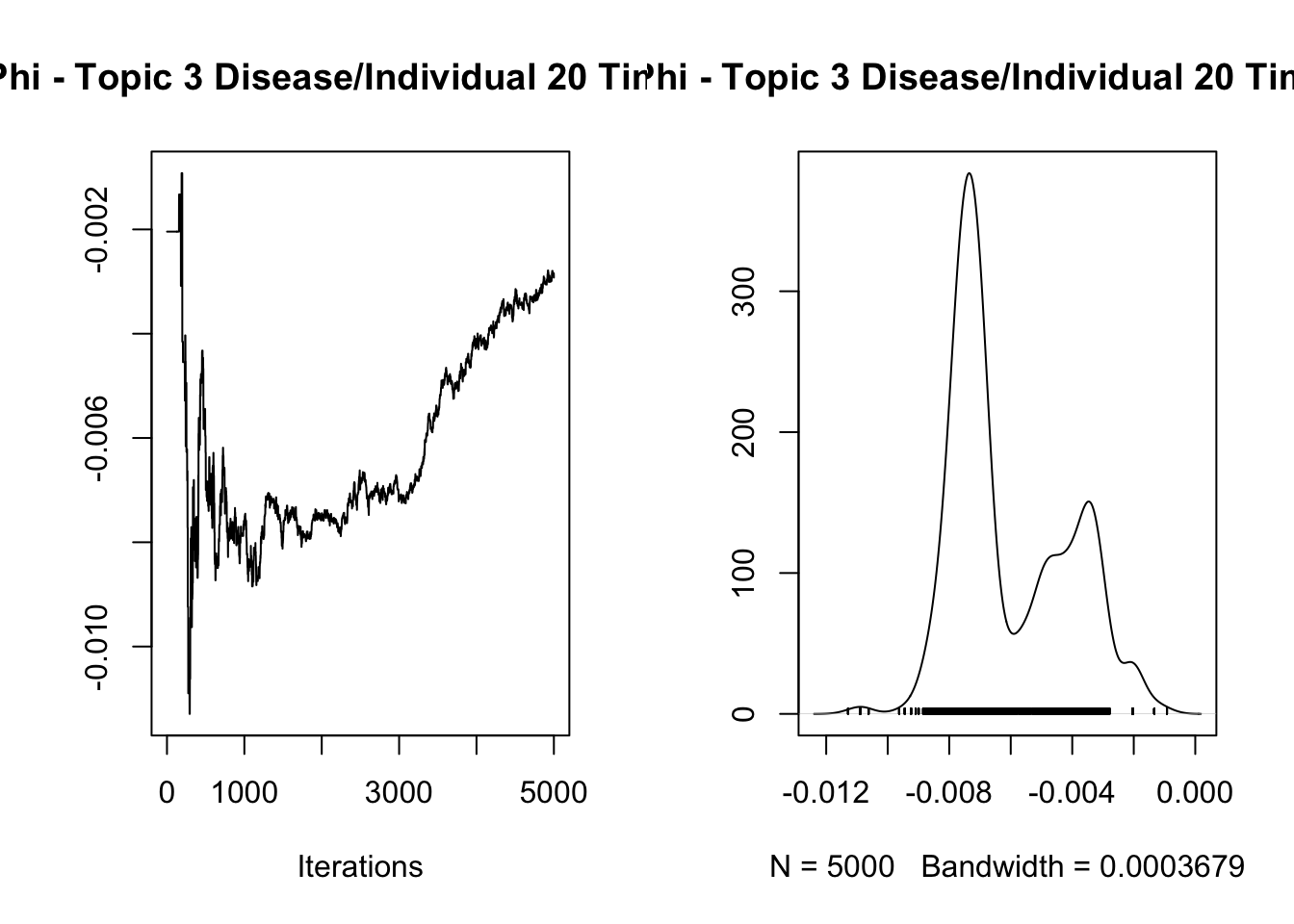
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
-6.064e-03 1.906e-03 2.696e-05 6.926e-04
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-0.008570 -0.007524 -0.006969 -0.004265 -0.002042
var1
7.576806 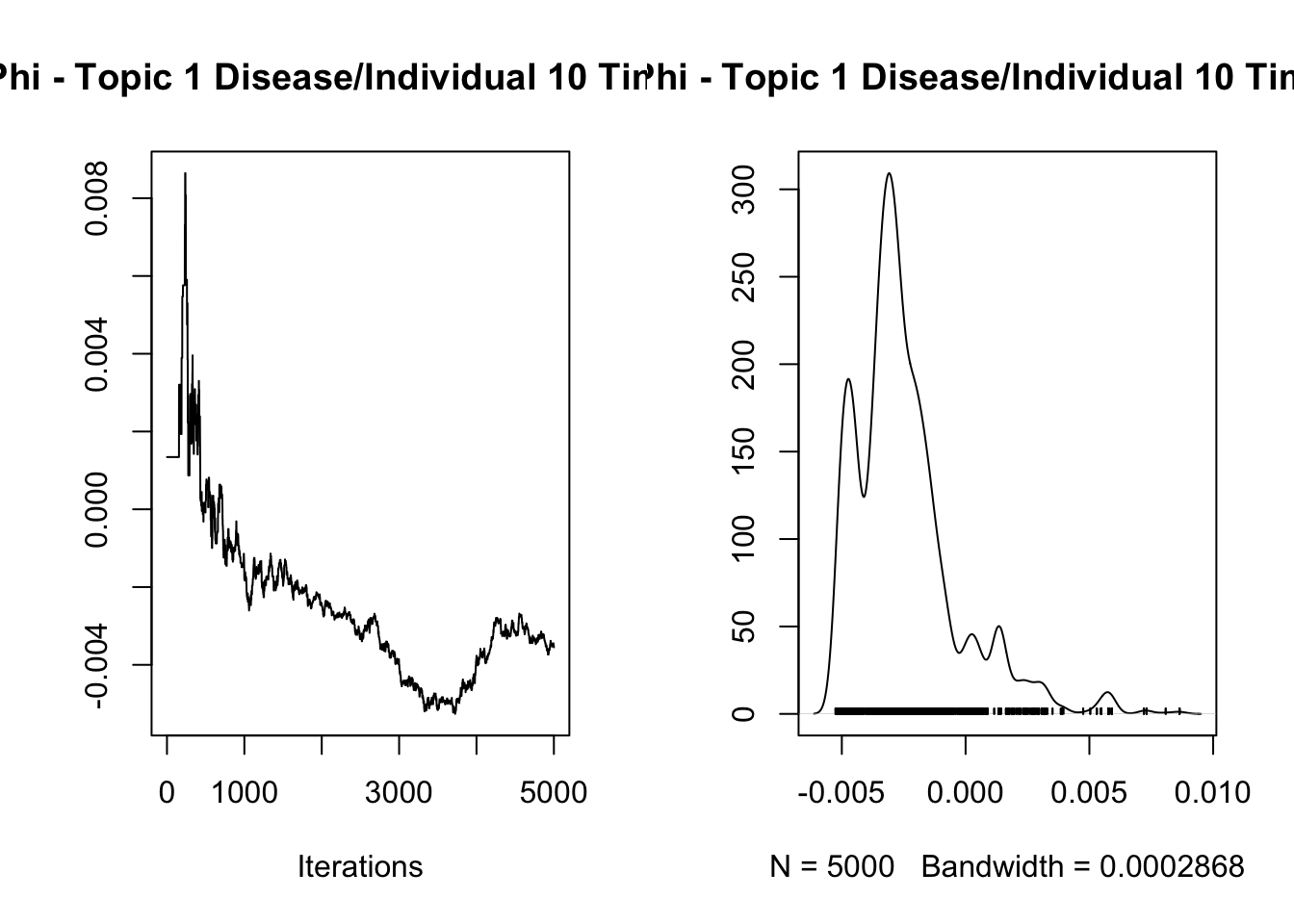
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
-2.430e-03 2.085e-03 2.949e-05 9.388e-04
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-0.005029 -0.003687 -0.002847 -0.001695 0.002967
var1
4.934092
[1] "Overall acceptance rate: 0.446"analyze_results(mcmc_results, "Lambda")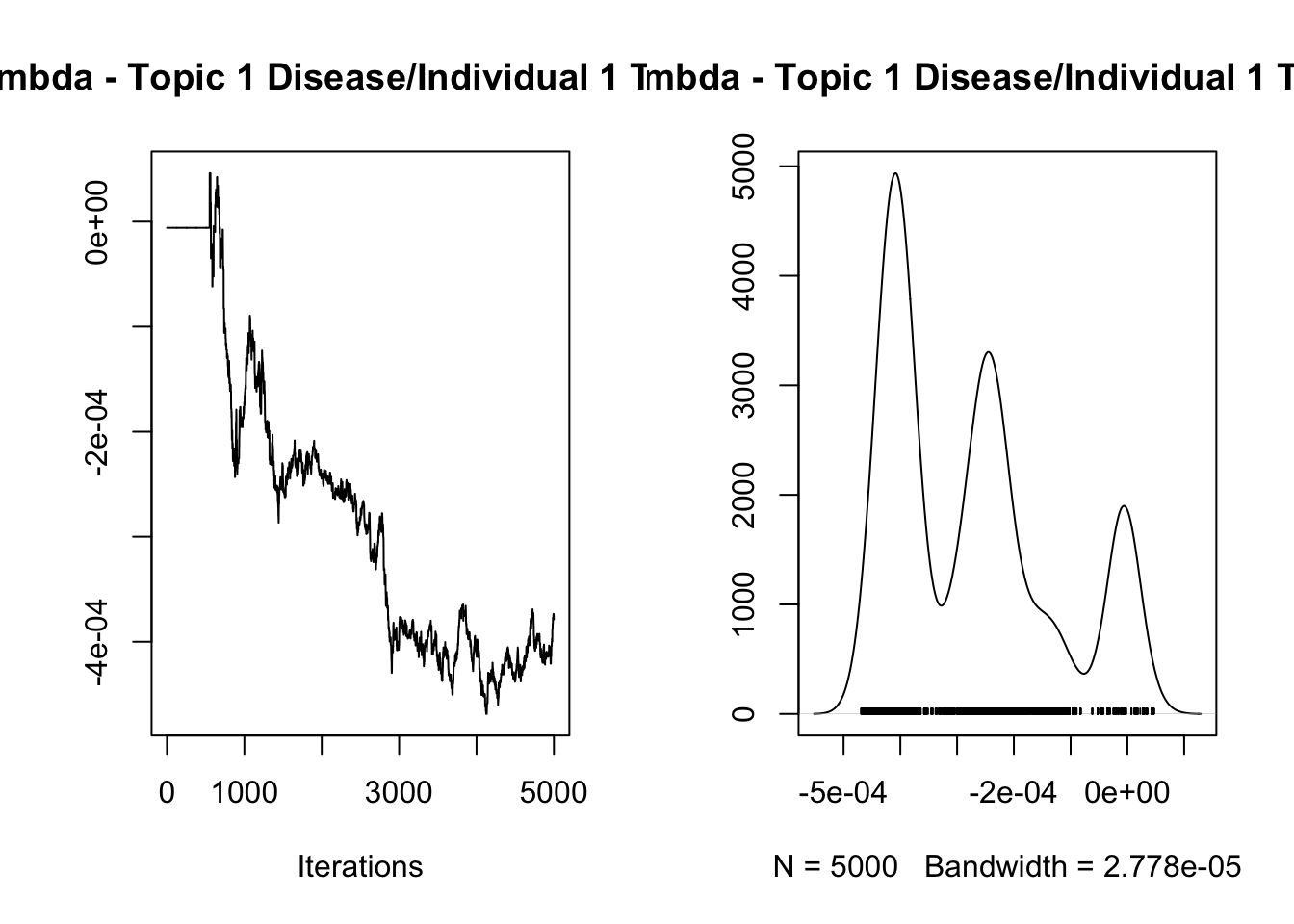
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
-2.753e-04 1.439e-04 2.035e-06 1.096e-04
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-4.435e-04 -4.048e-04 -2.801e-04 -2.103e-04 -5.875e-06
var1
1.723856 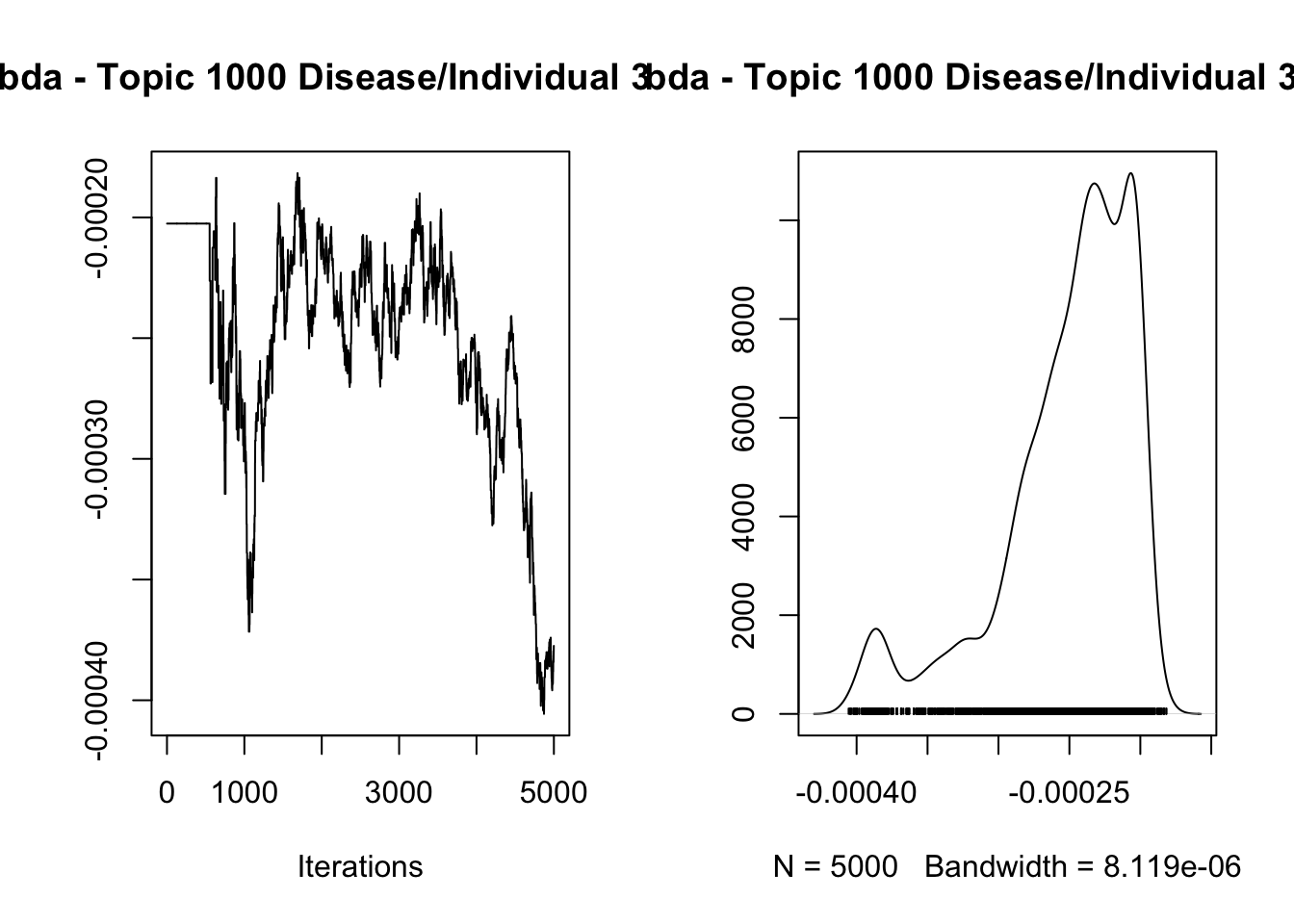
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
-2.516e-04 4.756e-05 6.726e-07 1.639e-05
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-0.0003860 -0.0002726 -0.0002396 -0.0002162 -0.0001992
var1
8.422534 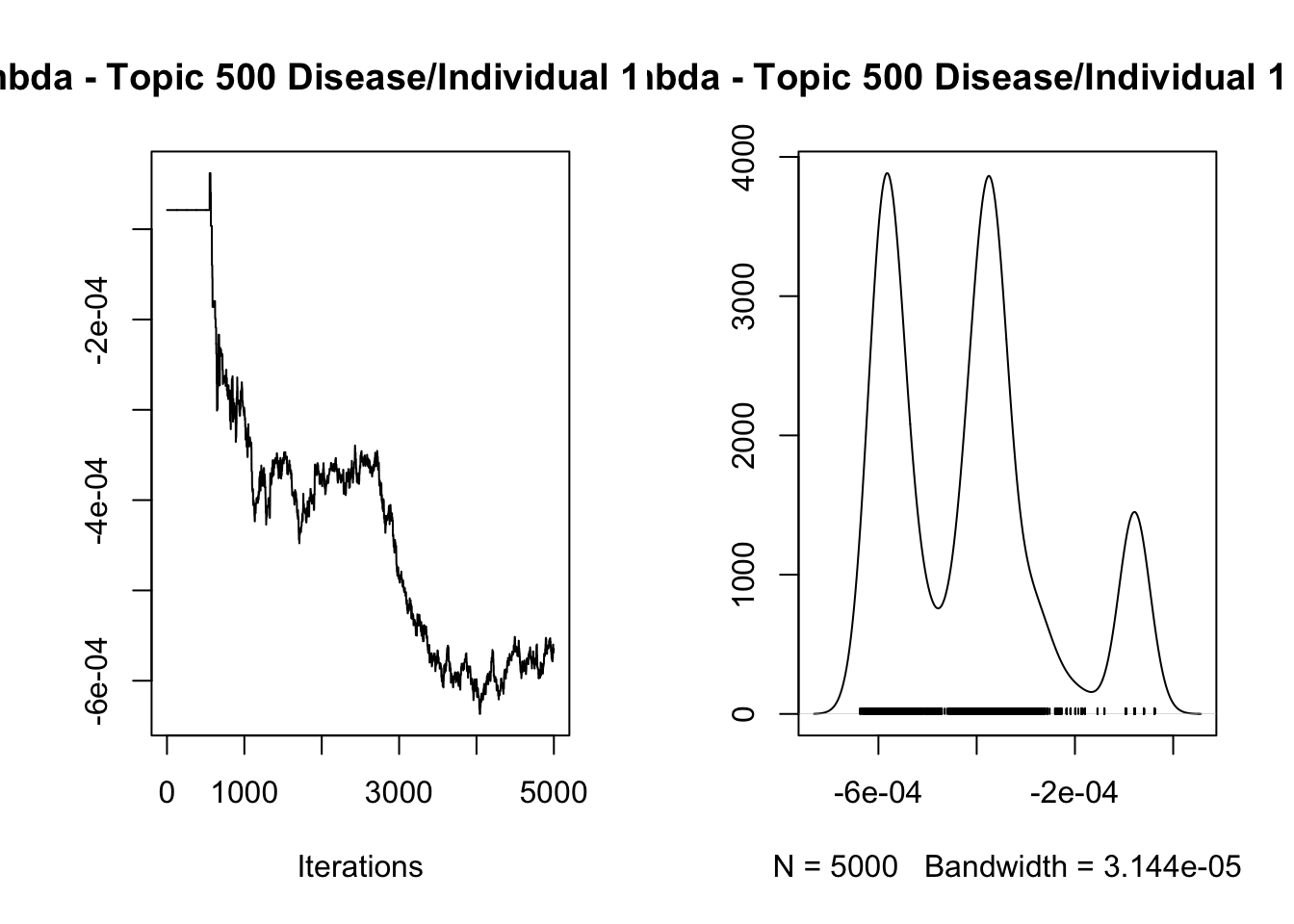
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
-4.144e-04 1.629e-04 2.304e-06 1.206e-04
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-6.115e-04 -5.740e-04 -4.003e-04 -3.549e-04 -7.879e-05
var1
1.825832
[1] "Overall acceptance rate: 0.423"analyze_results(mcmc_results, "Gamma")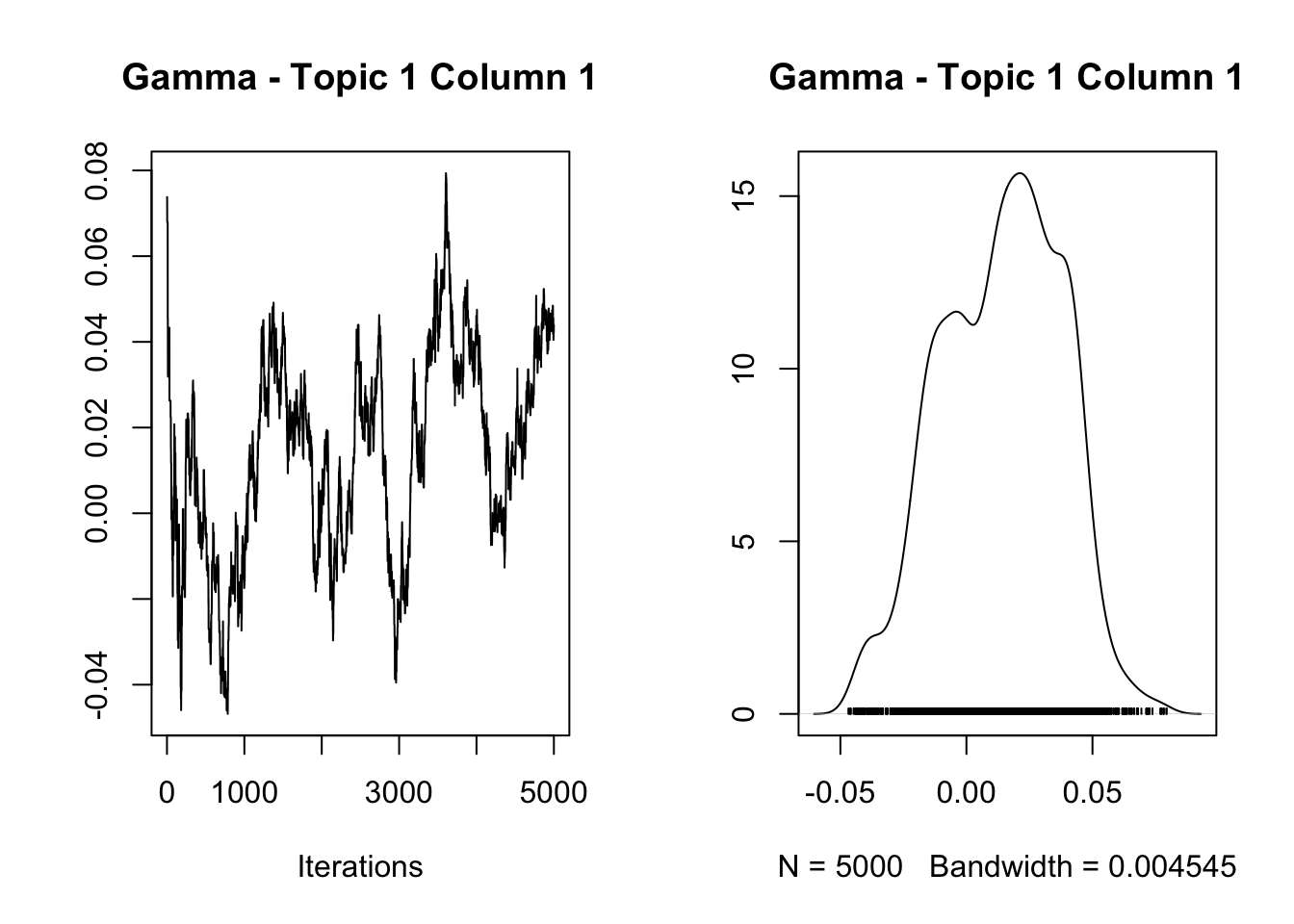
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
0.0139171 0.0235509 0.0003331 0.0067270
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-0.035195 -0.004133 0.015798 0.031889 0.054173
var1
12.25678 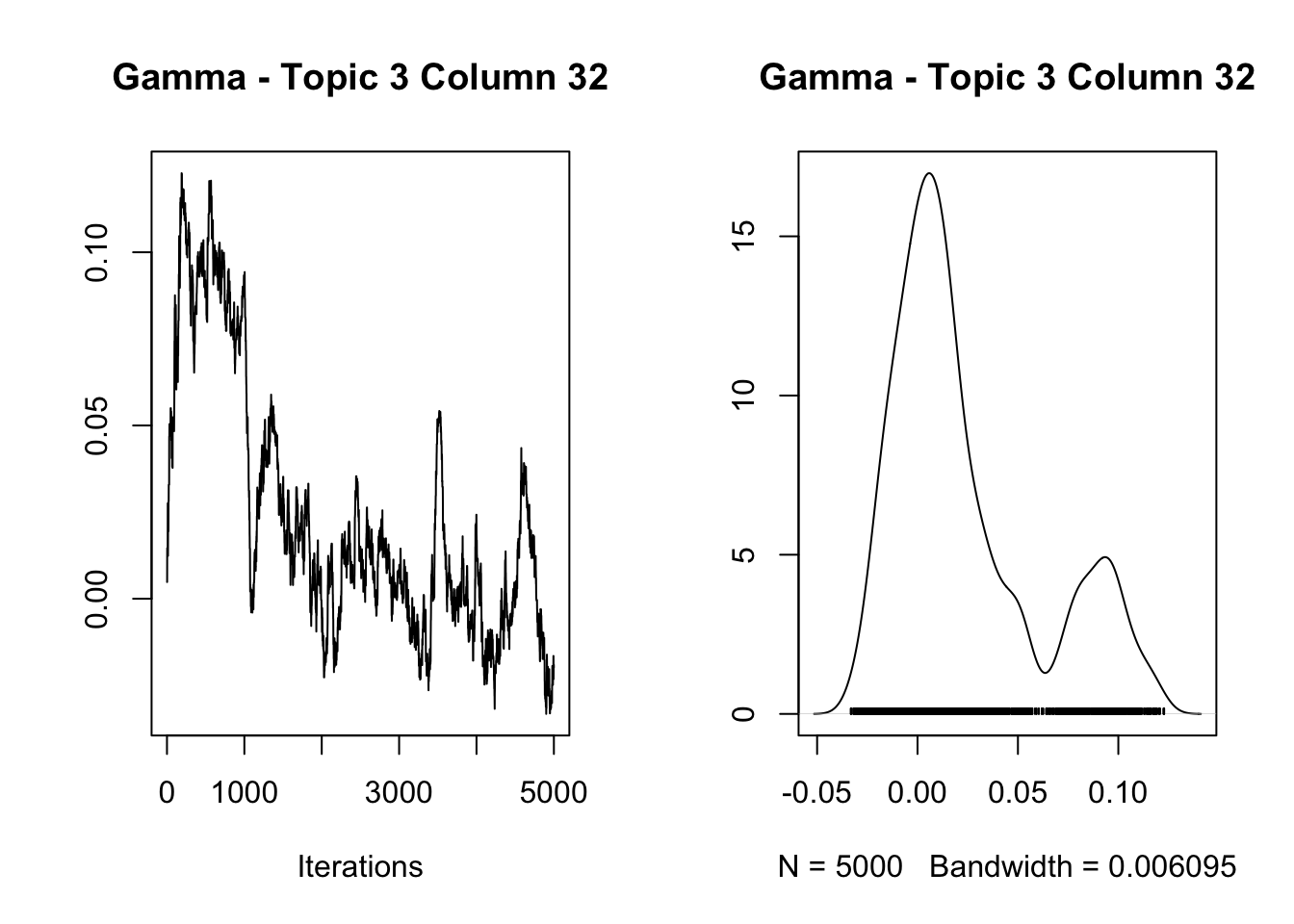
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
0.0237617 0.0372435 0.0005267 0.0170315
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-0.022648 -0.002359 0.011943 0.039964 0.107077
var1
4.781855 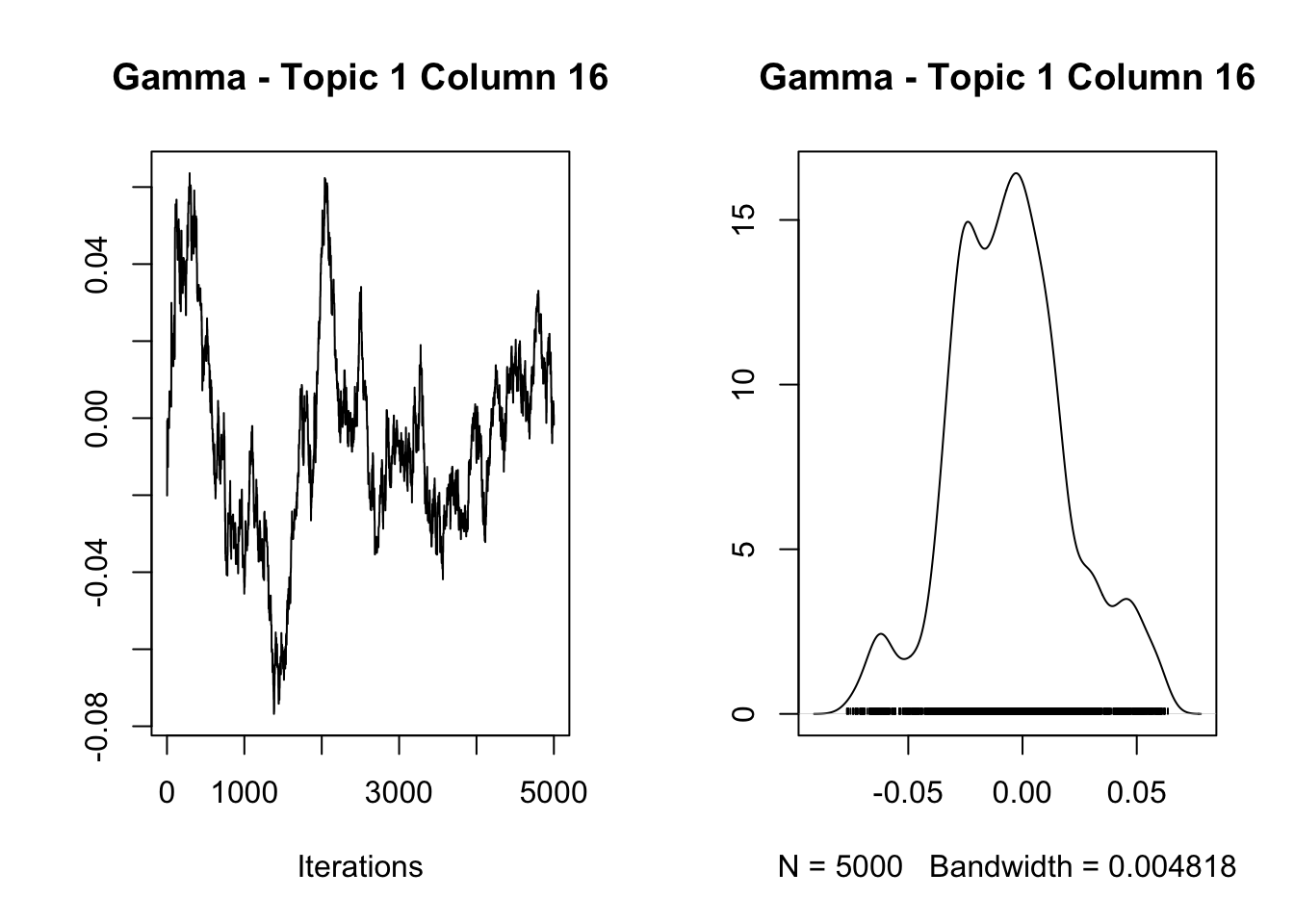
Iterations = 1:5000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
-0.0053648 0.0260095 0.0003678 0.0098597
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
-0.060991 -0.023716 -0.006285 0.009739 0.051094
var1
6.958786
[1] "Overall acceptance rate: 0.49"if we want to update the vari scale:
# Updated log_gp_prior_vec function
log_gp_prior_vec <- function(x, mean, length_scale, var_scale, time_diff_matrix) {
T <- length(x)
K <- var_scale * exp(-0.5 * time_diff_matrix / length_scale^2)
K <- K + diag(1e-6, T)
centered_x <- x - mean
log_det_K <- sum(log(eigen(K, symmetric = TRUE, only.values = TRUE)$values))
L <- chol(K)
quad_form <- sum(backsolve(L, centered_x, transpose = TRUE)^2)
return(-0.5 * (log_det_K + quad_form + T * log(2 * base::pi)))
}
mcmc_sampler_optimized <- function(y,
mu_d_logit,
g_i,
n_iterations,
initial_values,
alpha_lambda,
beta_lambda,
alpha_sigma,
beta_sigma,
alpha_phi,
beta_phi,
alpha_sigma_phi,
beta_sigma_phi,
alpha_Gamma,
beta_Gamma) {
current_state <- initial_values
n_individuals <- dim(current_state$Lambda)[1]
n_topics <- dim(current_state$Lambda)[2]
T <- dim(current_state$Lambda)[3]
n_diseases <- dim(current_state$Phi)[2]
# Initialize adaptive proposal standard deviations
adapt_sd <- list(
Lambda = array(0.01, dim = dim(current_state$Lambda)),
Phi = array(0.01, dim = dim(current_state$Phi)),
Gamma = matrix(
0.01,
nrow = nrow(current_state$Gamma),
ncol = ncol(current_state$Gamma)
),
var_scales_lambda = rep(0.1, n_topics),
var_scales_phi = rep(0.1, n_topics * n_diseases)
)
# Initialize storage for samples
samples <- list(
Lambda = array(0, dim = c(
n_iterations, dim(current_state$Lambda)
)),
Phi = array(0, dim = c(n_iterations, dim(
current_state$Phi
))),
Gamma = array(0, dim = c(
n_iterations, dim(current_state$Gamma)
)),
var_scales_lambda = matrix(0, nrow = n_iterations, ncol = n_topics),
var_scales_phi = matrix(0, nrow = n_iterations, ncol = n_topics * n_diseases)
)
# Precompute time difference matrix and exp terms
T <- dim(current_state$Lambda)[3]
time_diff_matrix <- outer(1:T, 1:T, "-") ^ 2
exp_term_lambda <- lapply(current_state$length_scales_lambda, function(l)
exp(-0.5 * time_diff_matrix / l ^ 2))
exp_term_phi <- lapply(current_state$length_scales_phi, function(l)
exp(-0.5 * time_diff_matrix / l ^ 2))
for (iter in 1:n_iterations) {
# Update Lambda
proposed_Lambda <- current_state$Lambda + array(rnorm(prod(dim(
current_state$Lambda
)), 0, adapt_sd$Lambda),
dim = dim(current_state$Lambda))
current_log_lik <- log_likelihood_vec(y, current_state$Lambda, current_state$Phi, mu_d_logit)
proposed_log_lik <- log_likelihood_vec(y, proposed_Lambda, current_state$Phi, mu_d_logit)
lambda_mean <- g_i %*% t(current_state$Gamma)
current_log_prior <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean[i, k],
K_inv_lambda[[k]]$K_inv, K_inv_lambda[[k]]$log_det_K)
)
})
}))
proposed_log_prior <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
proposed_Lambda[i, k, ],
lambda_mean[i, k],
K_inv_lambda[[k]]$K_inv, K_inv_lambda[[k]]$log_det_K
)
})
}))
log_accept_ratio <- (proposed_log_lik + proposed_log_prior) - (current_log_lik + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$Lambda <- proposed_Lambda
adapt_sd$Lambda <- adapt_sd$Lambda * 1.01
} else {
adapt_sd$Lambda <- adapt_sd$Lambda * 0.99
}
# Update Phi (similar structure to Lambda update)
proposed_Phi <- current_state$Phi + array(rnorm(prod(dim(
current_state$Phi
)), 0, adapt_sd$Phi), dim = dim(current_state$Phi))
current_log_lik <- log_likelihood_vec(y, current_state$Lambda, current_state$Phi, mu_d_logit)
proposed_log_lik <- log_likelihood_vec(y, current_state$Lambda, proposed_Phi, mu_d_logit)
current_log_prior <- sum(sapply(1:n_topics, function(k) {
sapply(1:n_diseases, function(d) {
idx <- (k - 1) * n_diseases + d
log_gp_prior_vec(
current_state$Phi[k, d, ],
0,
current_state$length_scales_phi[idx],
current_state$var_scales_phi[idx],
time_diff_matrix
)
})
}))
proposed_log_prior <- sum(sapply(1:n_topics, function(k) {
sapply(1:n_diseases, function(d) {
idx <- (k - 1) * n_diseases + d
log_gp_prior_vec(
proposed_Phi[k, d, ],
0,
K_inv_lambda[[k]]$K_inv, K_inv_lambda[[k]]$log_det_K
)
})
}))
log_accept_ratio <- (proposed_log_lik + proposed_log_prior) - (current_log_lik + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$Phi <- proposed_Phi
adapt_sd$Phi <- adapt_sd$Phi * 1.01
} else {
adapt_sd$Phi <- adapt_sd$Phi * 0.99
}
# Update Gamma (similar structure to original)
proposed_Gamma <- current_state$Gamma + matrix(rnorm(prod(dim(
current_state$Gamma
)), 0, adapt_sd$Gamma),
nrow = nrow(current_state$Gamma))
current_log_prior <- sum(dnorm(
current_state$Gamma,
0,
sqrt(alpha_Gamma / beta_Gamma),
log = TRUE
))
proposed_log_prior <- sum(dnorm(proposed_Gamma, 0, sqrt(alpha_Gamma / beta_Gamma), log = TRUE))
lambda_mean_current <- g_i %*% t(current_state$Gamma)
lambda_mean_proposed <- g_i %*% t(proposed_Gamma)
current_log_likelihood <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean_current[i, k],
K_inv_lambda[[k]]$K_inv, K_inv_lambda[[k]]$log_det_K
)
})
}))
proposed_log_likelihood <- sum(sapply(1:n_individuals, function(i) {
sapply(1:n_topics, function(k) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean_proposed[i, k],
K_inv_lambda[[k]]$K_inv, K_inv_lambda[[k]]$log_det_K
)
})
}))
log_accept_ratio <- (proposed_log_likelihood + proposed_log_prior) - (current_log_likelihood + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$Gamma <- proposed_Gamma
adapt_sd$Gamma <- adapt_sd$Gamma * 1.01
} else {
adapt_sd$Gamma <- adapt_sd$Gamma * 0.99
}
# Update var_scales_lambda
for (k in 1:n_topics) {
proposed_var_scale <- exp(
log(current_state$var_scales_lambda[k]) + rnorm(1, 0, adapt_sd$var_scales_lambda[k])
)
current_log_prior <- dgamma(
current_state$var_scales_lambda[k],
shape = alpha_sigma,
rate = beta_sigma,
log = TRUE
)
proposed_log_prior <- dgamma(
proposed_var_scale,
shape = alpha_sigma,
rate = beta_sigma,
log = TRUE
)
current_log_likelihood <- sum(sapply(1:n_individuals, function(i) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean[i, k],
K_inv_lambda[[k]]$K_inv, K_inv_lambda[[k]]$log_det_K
)
}))
proposed_log_likelihood <- sum(sapply(1:n_individuals, function(i) {
log_gp_prior_vec(
current_state$Lambda[i, k, ],
lambda_mean[i, k],
K_inv_lambda[[k]]$K_inv, K_inv_lambda[[k]]$log_det_K
)
}))
log_accept_ratio <- (proposed_log_likelihood + proposed_log_prior) -
(current_log_likelihood + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$var_scales_lambda[k] <- proposed_var_scale
adapt_sd$var_scales_lambda[k] <- adapt_sd$var_scales_lambda[k] * 1.01
} else {
adapt_sd$var_scales_lambda[k] <- adapt_sd$var_scales_lambda[k] * 0.99
}
}
# Update var_scales_phi
for (idx in 1:(n_topics * n_diseases)) {
proposed_var_scale <- exp(log(current_state$var_scales_phi[idx]) + rnorm(1, 0, adapt_sd$var_scales_phi[idx]))
current_log_prior <- dgamma(
current_state$var_scales_phi[idx],
shape = alpha_sigma_phi,
rate = beta_sigma_phi,
log = TRUE
)
proposed_log_prior <- dgamma(
proposed_var_scale,
shape = alpha_sigma_phi,
rate = beta_sigma_phi,
log = TRUE
)
k <- (idx - 1) %/% n_diseases + 1
d <- (idx - 1) %% n_diseases + 1
current_log_likelihood <- log_gp_prior_vec(
current_state$Phi[k, d, ],
0,
current_state$length_scales_phi[idx],
current_state$var_scales_phi[idx],
exp_term_phi[[idx]]
)
proposed_log_likelihood <- log_gp_prior_vec(
current_state$Phi[k, d, ],
0,
current_state$length_scales_phi[idx],
proposed_var_scale,
exp_term_phi[[idx]]
)
log_accept_ratio <- (proposed_log_likelihood + proposed_log_prior) -
(current_log_likelihood + current_log_prior)
if (log(runif(1)) < log_accept_ratio) {
current_state$var_scales_phi[idx] <- proposed_var_scale
adapt_sd$var_scales_phi[idx] <- adapt_sd$var_scales_phi[idx] * 1.01
} else {
adapt_sd$var_scales_phi[idx] <- adapt_sd$var_scales_phi[idx] * 0.99
}
}
# Store samples
samples$Lambda[iter, , , ] <- current_state$Lambda
samples$Phi[iter, , , ] <- current_state$Phi
samples$Gamma[iter, , ] <- current_state$Gamma
samples$var_scales_lambda[iter, ] <- current_state$var_scales_lambda
samples$var_scales_phi[iter, ] <- current_state$var_scales_phi
#
# # Store samples
# samples$Lambda[iter, , , ] <- current_state$Lambda
# samples$Phi[iter, , , ] <- current_state$Phi
# samples$Gamma[iter, , ] <- current_state$Gamma
if (iter %% 100 == 0)
cat("Iteration", iter, "\n")
}
return(samples)
}