Chapter 8 Spatial Models - Geographically Weighted Regression

8.1 Introduction

This practical extends the regression models that you constructed in Week 2 to the spatial (special?) case, and particularly considers approaches for handling spatial autocorrelation (SA) in the input data. Recall that SA describes the covariation of measurements made at nearby locations, and if data are spatially autocorrelated, and / or variables are correlated with each other1, then this can reduce model reliability and precision (unstable parameter estimates, inflated standard errors, inferential biases etc - Dormann et al. (2013)). As a result, model extrapolation may be erroneous and there may be problems in separating variable effects on the process of interest (Meloun et al. 2002). The key point is that the failure to specify the correct model when SA and / or collinearity is present can result in a loss of precision and power in the coefficient estimates, resulting in poor inference and process understanding.

This practical introduces two approach for handling spatially autocorrelated data: Geographically Weighted Regression (GWR - Brunsdon, Fotheringham, and Charlton (1996), Fotheringham, Brunsdon, and Charlton (2003)). However, recent thinking has around Geographically Weighted models has advanced and as has been argued by many authors Multi-scale GWR (MGWR) Fotheringham, Yang, and Kang (2017) is now considered as the default GWR (Comber et al. 2022).

This session will again use the Georgia data that was used in Week 2 and will again construct a regression model of median income as before in order to compare with the the GWR and MGWR model outputs

You will need the following packages

library(sf)
library(tidyverse)
library(GWmodel)    # to undertake the GWR
library(tmap)       # for mapping

And you will need to load the georgia data as in Week 2 which contains census data for the counties in Georgia, USA.

download.file("https://github.com/gwverse/gw/blob/main/data/georgia.rda?raw=True",
              "./georgia.RData", mode = "wb")
load("georgia.RData")

You should examine this in the usual way - you may want to practice your EDA and spatial EDA outside of the practical - and recall that this data has a number of County level variables :

  • Rural % (PctRural)
  • % with college degree (PctBach)
  • % elderly (PctEld)
  • % foreign born (PctFB)
  • % classed as being in poverty (PctPov)
  • % that are black (PctBlack)
  • median income of the county (MedInc in dollars)

Recall that the classic OLS regression has the basic form of:

\[ y_i = \beta_{0} + \sum_{k=1}^{m}\beta_{k}x_{ik} + \epsilon_i \]

where for observations indexed by \(i=1 \dots n\), \(y_i\) is the response variable, \(x_{ik}\) is the value of the \(k^{th}\) predictor variable, \(m\) is the number of predictor variables, \(\beta_0\) is the intercept term, \(\beta_k\) is the regression coefficient for the \(k_{th}\) predictor variable and \(\epsilon_i\) is the random error term that is independently normally distributed with zero mean and common variance \(\sigma^2\). OLS is commonly used for model estimation in linear regression models.

And that this is specified using the function lm (linear model). The model we constructed in Week 5 is recreated here with the response variable \(y\) is median income (MedInc), and the 6 (i.e. \(k\)) socio-economic variables are PctRural, PctBach, PctEld, PctFB, PctPov, PctBlack are the different predictor variables, the \(k\) different \(x\)’s:

df = st_drop_geometry(georgia)
m = lm(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, data = df) 
summary(m)
## 
## Call:
## lm(formula = MedInc ~ PctRural + PctBach + PctEld + PctFB + PctPov + 
##     PctBlack, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -12420.3  -2989.7   -616.3   2209.5  25820.1 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 52598.95    3108.93  16.919  < 2e-16 ***
## PctRural       73.77      20.43   3.611 0.000414 ***
## PctBach       697.26     112.21   6.214 4.73e-09 ***
## PctEld       -788.62     179.79  -4.386 2.14e-05 ***
## PctFB       -1290.30     473.88  -2.723 0.007229 ** 
## PctPov       -954.00     104.59  -9.121 4.19e-16 ***
## PctBlack       33.13      37.17   0.891 0.374140    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5155 on 152 degrees of freedom
## Multiple R-squared:  0.7685, Adjusted R-squared:  0.7593 
## F-statistic: 84.09 on 6 and 152 DF,  p-value: < 2.2e-16

Recall also from Week 2 that we are interested in the following regression model properties:

  • Significance indicated by the p-value in the column \(Pr(>|t|)\) as a measure of how statistically surprising the relationship is;
  • The Coefficient Estimates (the \(\beta_{k}\) values) that describe how change in the \(x_k\) are related (linearly) to changes in \(y\);
  • And the Model fit given by the \(R^2\) value, that tells us how well the model predicts \(y\).

Finally we could inspect the model outliers (observations where the model is over- or under-predicting Median Income) through the studentised residual and even undertake a Moran’s I test of them, etc.

# determine studentised residuals and attach to georgia
s.resids <- rstudent(m)
georgia$s.resids = s.resids
# map the spatial distribution of outliers
tm_shape(georgia) + 
  tm_polygons('s.resids', breaks = c(min(s.resids), -1.5, 1.5, max(s.resids)), 
              palette = c("indianred1","antiquewhite2","powderblue"), 
              title = "Residuals") +
tm_layout(legend.format= list(digits = 1), frame = F) 
# moran test
library(spdep)
geor.nb <- poly2nb(georgia) 
geor.lw = nb2listw(geor.nb)
moran.test(georgia$s.resids, geor.lw)

In this case the residuals are only marginally spatially autocorrelated (clustered).

All well and good. However the implicit assumptions in linear regression that the relationships between the various \(x\) terms and \(y\) are linear, that the error terms have identical and independent normal distributions and that the relationships between the \(x_k\)’s and \(y\) are the same everywhere, are quite often a consequence of wishful thinking, rather than a rigorously derived conclusion. To take a step closer to reality, it is a good idea to look beyond these assumptions to obtain more reliable predictions, or gain a better theoretical understanding of the process being considered.

Regression models (and most other models) are aspatial and because they consider all of the data in the study area in one universal model, they are referred to as Global models. For example, the coefficient estimates of the model Median Income in Georgia assume that the contributions made by the different variables in predicting MedInc are the same across the study area. In reality this assumption of spatial invariance is violated in many instances when geographic phenomena are considered.

For example, the association between PctBach and MedInc, might be different in different places. This is a core concept for geographical data analysis, that of process spatial heterogeneity. That is, how and where processes, relationships, and other phenomena vary spatially, as introduced in Week 1 and reinforced in the lecture this week.

In this session you will explore two approaches for handling the impacts of the spatial dependence of the error terms and process spatial heterogeneity using:

  1. Geographically Weighted Regression
  2. Multiscale GWR

These both require some sort measure of distance and recall that a degree has different dimensions depending on where you are on the earth2. For this reason, the georgia data needs to be transformed to a geographic reference system, in this case the EPSG 102003 USA Contiguous Albers Equal Area Conic.

georgia = st_transform(georgia, "ESRI:102003")

8.2 Geographically Weighted Regression

8.2.1 Description

In overview, geographically weighted (GW) approaches use a moving window or kernel that passes through the study area. At each location being considered, data under the window are used to make a local calculation of some kind, such as a regression. The data are weighted by their distance to the kernel centre and in this way GW approaches construct a series of models at discrete locations in the study area rather than a single one for whole study area.

There are a number of options for the shape of the kernel - see page 6 in Gollini et al. (2013) - and the default is to use a bi-square kernel. This generates higher weights at locations very near to the kernel centre relative to those towards the edge.

The size or bandwidth of the kernel is critical as it determines the degree of smoothing and the scale over which the GWR operates. This can and should be optimally determined rather than just picking a bandwidth. An optimal bandwidth for GWR can be found by minimising a model fit diagnostic. Options include a leave-one-out cross-validation (CV) score which optimises model prediction accuracy and the Akaike Information Criterion (AIC) which optimises model parsimony - that is it trades off prediction accuracy with model complexity (number of variables used). Note also that the kernel can be defined as a fixed value (i.e. a distance), or in an adaptive way (i.e. with a specific number of nearby data points). Gollini et al. (2013) provide a description of this.

The standard GWR model the same as an OLS regression (Equation 1 above), except that now location included and a value for each regression coefficient is assigned to a location \((u,v)\) in space (e.g. \(u\) is an easting and \(v\) a northing), so that we denote it \(\beta_k(u,v)\).

This is a Geographically weighted regression that examines how that relationships between \(y\) and \(x\) vary spatially:

\[ y = \beta_{0_(u_i, v_i)} + \sum_{m}^{k=1}\beta_{k}x_{ik_{(u_i, v_i)}} + \epsilon_{(u_i, v_i)} \]

Thus there are 2 basic steps to any GW approach:

  1. Determine the optimal kernel bandwidth (i.e. how many data points to include in each local model or the kernel / window size);
  2. Fit the GW model.

8.2.2 Undertaking a GWR

These steps are undertaken in the code block below with an adaptive bandwidth, noting that georgia needs to be converted to an sp format data (the GWmodel package has not been updated to take sf format objects).

The bandwidth - the kernel size - is critical: it how many data points / observations are included in each local model. However, determining the optimal bandwidth requires different potential bandwidths to be evaluated, which in turn requires some measure of model fit to be applied. There are 2 options for this in a GWR (as indicated above):

  • leave-one-out Cross Validation (CV). This essentially removes each observation one at a time for a potential bandwidth, and provides a measure of how well the local model with that bandwidth predicts the value of each removed data point;
  • Akaike’s Information Criterion (AIC or corrected AIC, AICc). This provides a measure of model parsimony, a kind of balance between model accuracy and model complexity. A parsimonious model is one that has a explanatory power but is as simple as possible.

In determining the optimal GWR bandwidth, AIC is preferred to CV because it reflects model parsimony and its use tends to avoid over-fitting GWR models (thus AIC bandwidths tend to be larger than bandwidths found using CV).

The GWmodel package (Lu et al. 2014) has tools for determining the optimal GWR bandwidth, but requires the data to be transformed to sp format from sf:

# convert to sp
georgia.sp = as(georgia, "Spatial")
# determine the kernel bandwidth
bw <- bw.gwr(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack,
             approach = "AIC",
             adaptive = T,
             data=georgia.sp) 
## Adaptive bandwidth (number of nearest neighbours): 105 AICc value: 3161.766 
## Adaptive bandwidth (number of nearest neighbours): 73 AICc value: 3160.592 
## Adaptive bandwidth (number of nearest neighbours): 51 AICc value: 3166.921 
## Adaptive bandwidth (number of nearest neighbours): 84 AICc value: 3160.866 
## Adaptive bandwidth (number of nearest neighbours): 63 AICc value: 3161.106 
## Adaptive bandwidth (number of nearest neighbours): 76 AICc value: 3160.435 
## Adaptive bandwidth (number of nearest neighbours): 81 AICc value: 3160.339 
## Adaptive bandwidth (number of nearest neighbours): 81 AICc value: 3160.339

You should have a look at the bandwidth: it is an adaptive bandwidth (kernel size) indicating that its size varies but the nearest 81 observations will be used to compute each local weighted regression. Here it, has a value of 81 indicating that 51% of the county data will be used in each local calculation (there are 159 records in the data):

bw
## [1] 81

Try running the below to see the fixed distance bandwidth

# determine the kernel bandwidth
bw2 <- bw.gwr(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack,
             approach = "AIC",
             adaptive = F,
             data=georgia.sp) 
## Fixed bandwidth: 348973.8 AICc value: 3167.445 
## Fixed bandwidth: 215720.8 AICc value: 3164.119 
## Fixed bandwidth: 133365.9 AICc value: 3195.926 
## Fixed bandwidth: 266618.9 AICc value: 3165.536 
## Fixed bandwidth: 184264.1 AICc value: 3166.21 
## Fixed bandwidth: 235162.2 AICc value: 3164.468 
## Fixed bandwidth: 203705.4 AICc value: 3164.278 
## Fixed bandwidth: 223146.8 AICc value: 3164.226 
## Fixed bandwidth: 211131.3 AICc value: 3164.118 
## Fixed bandwidth: 208294.9 AICc value: 3164.153 
## Fixed bandwidth: 212884.4 AICc value: 3164.112 
## Fixed bandwidth: 213967.8 AICc value: 3164.112 
## Fixed bandwidth: 212214.8 AICc value: 3164.113 
## Fixed bandwidth: 213298.2 AICc value: 3164.111 
## Fixed bandwidth: 213554 AICc value: 3164.111
bw2
## [1] 213298.2

This indicates a fixed bandwidth of ~213km. For comparison the distances between the counties is summarised below:

summary(as.vector(st_distance(georgia)))
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##       0   85620  156531  166238  237457  517837

You should now create the GWR model with adaptive bandwidth stored in bw, and have a look at the outputs:

# fit the GWR model
m.gwr <- gwr.basic(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, 
                adaptive = T,
                data = georgia.sp,
                bw = bw)  
## Warning in proj4string(data): CRS object has comment, which is lost in output; in tests, see
## https://cran.r-project.org/web/packages/sp/vignettes/CRS_warnings.html
m.gwr
##    ***********************************************************************
##    *                       Package   GWmodel                             *
##    ***********************************************************************
##    Program starts at: 2022-11-17 16:18:55 
##    Call:
##    gwr.basic(formula = MedInc ~ PctRural + PctBach + PctEld + PctFB + 
##     PctPov + PctBlack, data = georgia.sp, bw = bw, adaptive = T)
## 
##    Dependent (y) variable:  MedInc
##    Independent variables:  PctRural PctBach PctEld PctFB PctPov PctBlack
##    Number of data points: 159
##    ***********************************************************************
##    *                    Results of Global Regression                     *
##    ***********************************************************************
## 
##    Call:
##     lm(formula = formula, data = data)
## 
##    Residuals:
##      Min       1Q   Median       3Q      Max 
## -12420.3  -2989.7   -616.3   2209.5  25820.1 
## 
##    Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
##    (Intercept) 52598.95    3108.93  16.919  < 2e-16 ***
##    PctRural       73.77      20.43   3.611 0.000414 ***
##    PctBach       697.26     112.21   6.214 4.73e-09 ***
##    PctEld       -788.62     179.79  -4.386 2.14e-05 ***
##    PctFB       -1290.30     473.88  -2.723 0.007229 ** 
##    PctPov       -954.00     104.59  -9.121 4.19e-16 ***
##    PctBlack       33.13      37.17   0.891 0.374140    
## 
##    ---Significance stars
##    Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
##    Residual standard error: 5155 on 152 degrees of freedom
##    Multiple R-squared: 0.7685
##    Adjusted R-squared: 0.7593 
##    F-statistic: 84.09 on 6 and 152 DF,  p-value: < 2.2e-16 
##    ***Extra Diagnostic information
##    Residual sum of squares: 4039148010
##    Sigma(hat): 5072.185
##    AIC:  3178.235
##    AICc:  3179.195
##    BIC:  3084.338
##    ***********************************************************************
##    *          Results of Geographically Weighted Regression              *
##    ***********************************************************************
## 
##    *********************Model calibration information*********************
##    Kernel function: bisquare 
##    Adaptive bandwidth: 81 (number of nearest neighbours)
##    Regression points: the same locations as observations are used.
##    Distance metric: Euclidean distance metric is used.
## 
##    ****************Summary of GWR coefficient estimates:******************
##                   Min.   1st Qu.    Median   3rd Qu.     Max.
##    Intercept 43440.948 48665.142 52741.146 57087.412 63591.03
##    PctRural     17.365    48.016    70.557   113.294   159.32
##    PctBach     241.782   545.409   649.463   875.683  1289.66
##    PctEld    -1241.607  -997.115  -858.012  -784.066  -612.84
##    PctFB     -3262.616 -2229.952 -1378.769  -640.259  1054.16
##    PctPov    -1751.745 -1279.423  -861.680  -511.577  -396.18
##    PctBlack   -220.872   -51.320    31.407    80.502   190.92
##    ************************Diagnostic information*************************
##    Number of data points: 159 
##    Effective number of parameters (2trace(S) - trace(S'S)): 38.0215 
##    Effective degrees of freedom (n-2trace(S) + trace(S'S)): 120.9785 
##    AICc (GWR book, Fotheringham, et al. 2002, p. 61, eq 2.33): 3160.339 
##    AIC (GWR book, Fotheringham, et al. 2002,GWR p. 96, eq. 4.22): 3113.561 
##    BIC (GWR book, Fotheringham, et al. 2002,GWR p. 61, eq. 2.34): 3074.997 
##    Residual sum of squares: 2468829871 
##    R-square value:  0.8584923 
##    Adjusted R-square value:  0.8136482 
## 
##    ***********************************************************************
##    Program stops at: 2022-11-17 16:18:56

The printout gives quite a lot of information: the standard OLS regression model, a summary of the GWR coefficients and a whole range of fit measures (\(R^2\), AIC, BIC).

8.2.3 Evaluating the results

The code above prints out the whole model summary. You should compare the summary of the local (i.e. spatially varying) GWR coefficient estimates with the global (i.e. fixed) outputs of the ordinary regression coefficient estimates. Note the first line of code below. The output of the GWR model has lots of information including a slot called SDF or spatial data frame and this is an sp format object.

# GWR outouts
names(m.gwr)
## [1] "GW.arguments"  "GW.diagnostic" "lm"            "SDF"          
## [5] "timings"       "this.call"     "Ftests"

To access the data table in the SDF slot @data is added to this.

tab.gwr <- rbind(apply(m.gwr$SDF@data[, 1:7], 2, summary), coef(m))
rownames(tab.gwr)[7] <- "Global"
tab.gwr <- round(tab.gwr, 1)

And you can inspect this table - note that the t() function transposes the table:

t(tab.gwr)
Table 8.1: A comparison of the GWR and OLS regression coefficient estimates.
Min. 1st Qu. Median Mean 3rd Qu. Max. Global
Intercept 43440.9 48665.1 52741.1 53030.3 57087.4 63591.0 52598.9
PctRural 17.4 48.0 70.6 79.0 113.3 159.3 73.8
PctBach 241.8 545.4 649.5 700.6 875.7 1289.7 697.3
PctEld -1241.6 -997.1 -858.0 -887.9 -784.1 -612.8 -788.6
PctFB -3262.6 -2230.0 -1378.8 -1423.2 -640.3 1054.2 -1290.3
PctPov -1751.7 -1279.4 -861.7 -938.3 -511.6 -396.2 -954.0
PctBlack -220.9 -51.3 31.4 16.5 80.5 190.9 33.1

You could write this out to a csv file for inclusion in a report or similar:

write.csv(t(tab.gwr), file = "coef_tab.csv")

So the Global coefficient estimates are similar to the Mean and Median values of the GWR output. But you can see the variation in the association between median income (MedInc) and the different coefficient estimates.

So for example, for PctPov (poverty) :

  • the global coefficient estimate is -954.
  • the local coefficient estimate varies from -1279.4 to -511.6 between the 1st and 3rd quartiles.

8.2.4 Mapping GWR outputs

The variation in the GWR coefficient estimates can be mapped to show how different factors are varying associated with Median Income in different parts of Georgia. These data are held in the SDF of the GWmodel output which is converted to sf format in the code below and examined:

gwr_sf = st_as_sf(m.gwr$SDF)
gwr_sf

There are lots of information in the GWR output, but here we are interested in are the coefficient estimates and the t-values whose names are the same as the inputs (and the t-values with _TV).

The code below creates maps where large variation in the relationship between the predictor variable and median income was found as in Figure 8.1:

tm_shape(gwr_sf) +
  tm_fill(c("PctBach", "PctPov"), palette = "viridis", style = "kmeans") +
  tm_layout(legend.position = c("right","top"), frame = F)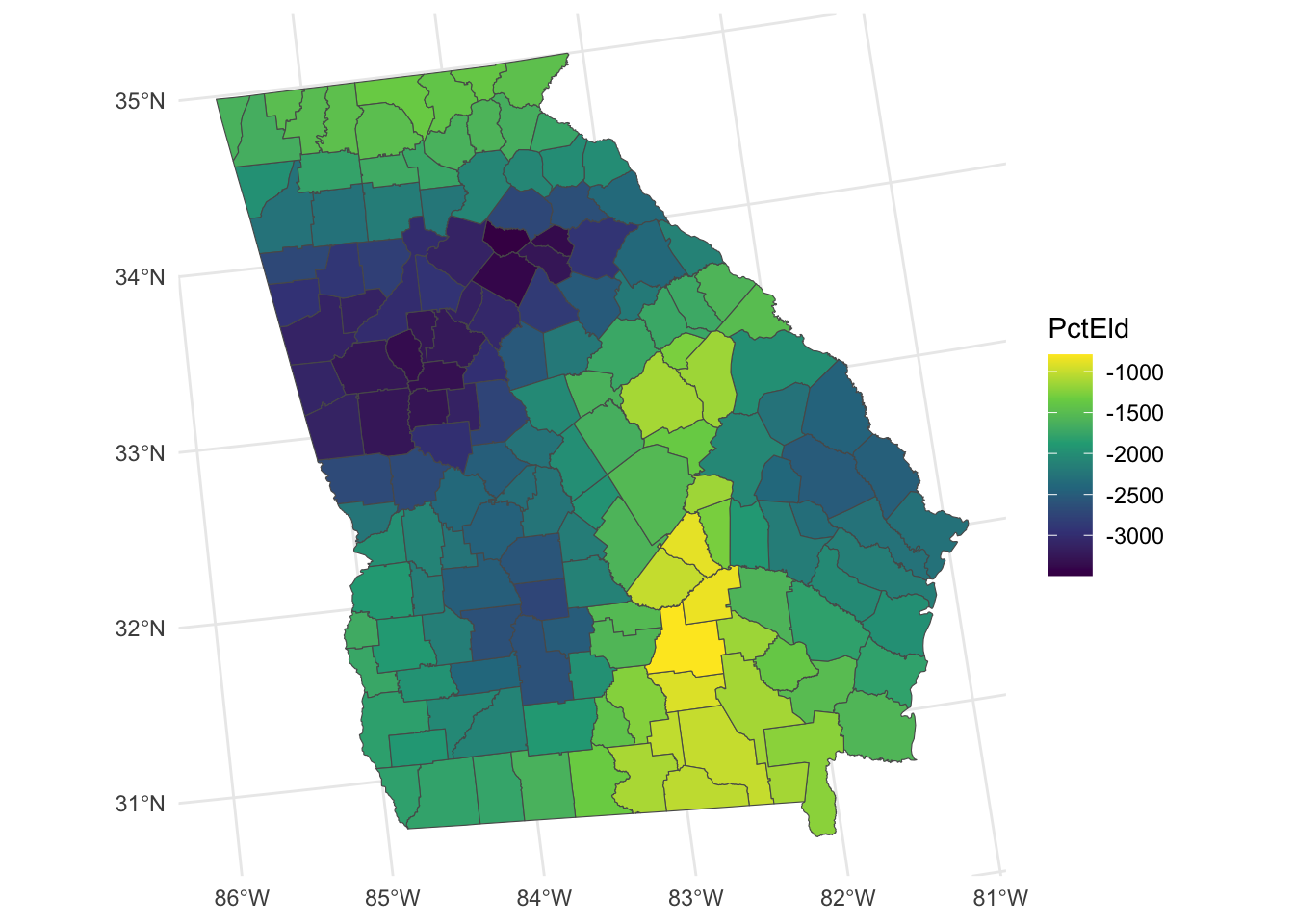
Maps of the GWR coefficient estimates.

Figure 8.1: Maps of the GWR coefficient estimates.

It is also possible to create maps showing coefficients whose values flip from positive to negative in different parts of the state, as in Figure 8.2.

tm_shape(gwr_sf) +
  tm_fill(c("PctFB", "PctBlack"),midpoint = 0, style = "kmeans") +
  tm_style("col_blind")+
  tm_layout(legend.position = c("right","top"), frame = F)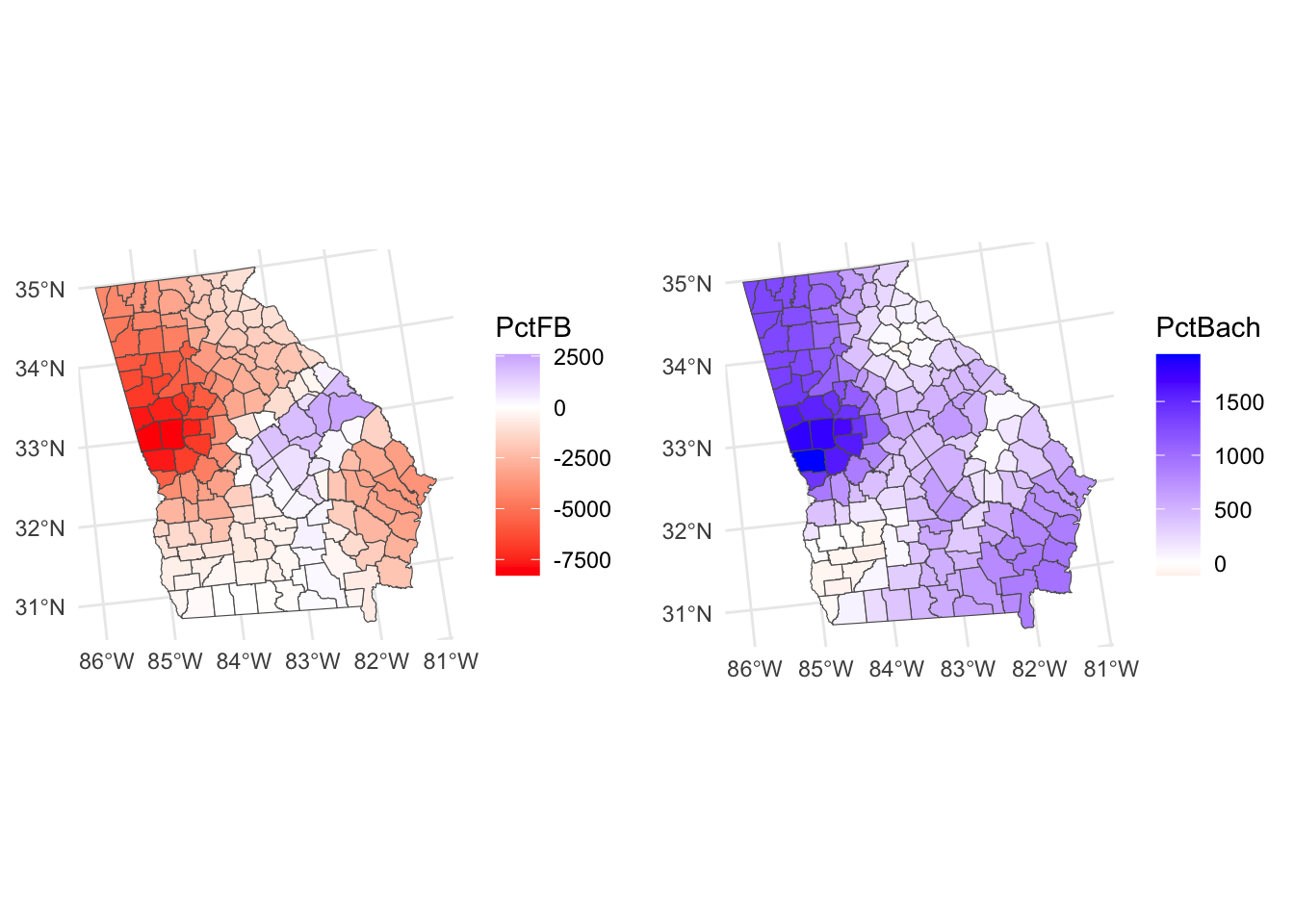
Maps of GWR coefficient estimates, whose values flip from positive to negative.

Figure 8.2: Maps of GWR coefficient estimates, whose values flip from positive to negative.

So what we see here are the local variations in the degree to which changes in different variables are associated with changes in Median Income. The maps above are not maps of the predictor variables (PctBach, PctPov and PctBlack). Rather, they show how the relationships between the inputs and Median Income vary spatially - the spatially vary strength of the relationships,

Now a critical aspect is that coefficient significance through the p-value is now local rather than a global statistic. Here we need to go into the t-values from which p-values are derived3. Significant coefficient estimates are those whose t-values are less than -1.96 or greater than +1.96. It possible to identify and map these locations from the GWR outputs which have the t-values (_TV) for each input variable.

The code below recreates one of the maps above maps but highlights areas where PctBlack is a significant predictor of MedInc (Figure 8.3. It shows that coefficients are highly localized.

# determine which are significant
tval = gwr_sf %>%dplyr::select(all_of("PctBlack_TV")) %>% st_drop_geometry()
signif = tval < -1.96 | tval > 1.96
# map the counties
tm_shape(gwr_sf) +
  tm_fill("PctBlack",midpoint = 0) + tm_style("col_blind")+
  tm_layout(legend.position = c("right","top"))+
  # now add the tvalues layer
  tm_shape(gwr_sf[signif,]) + tm_borders()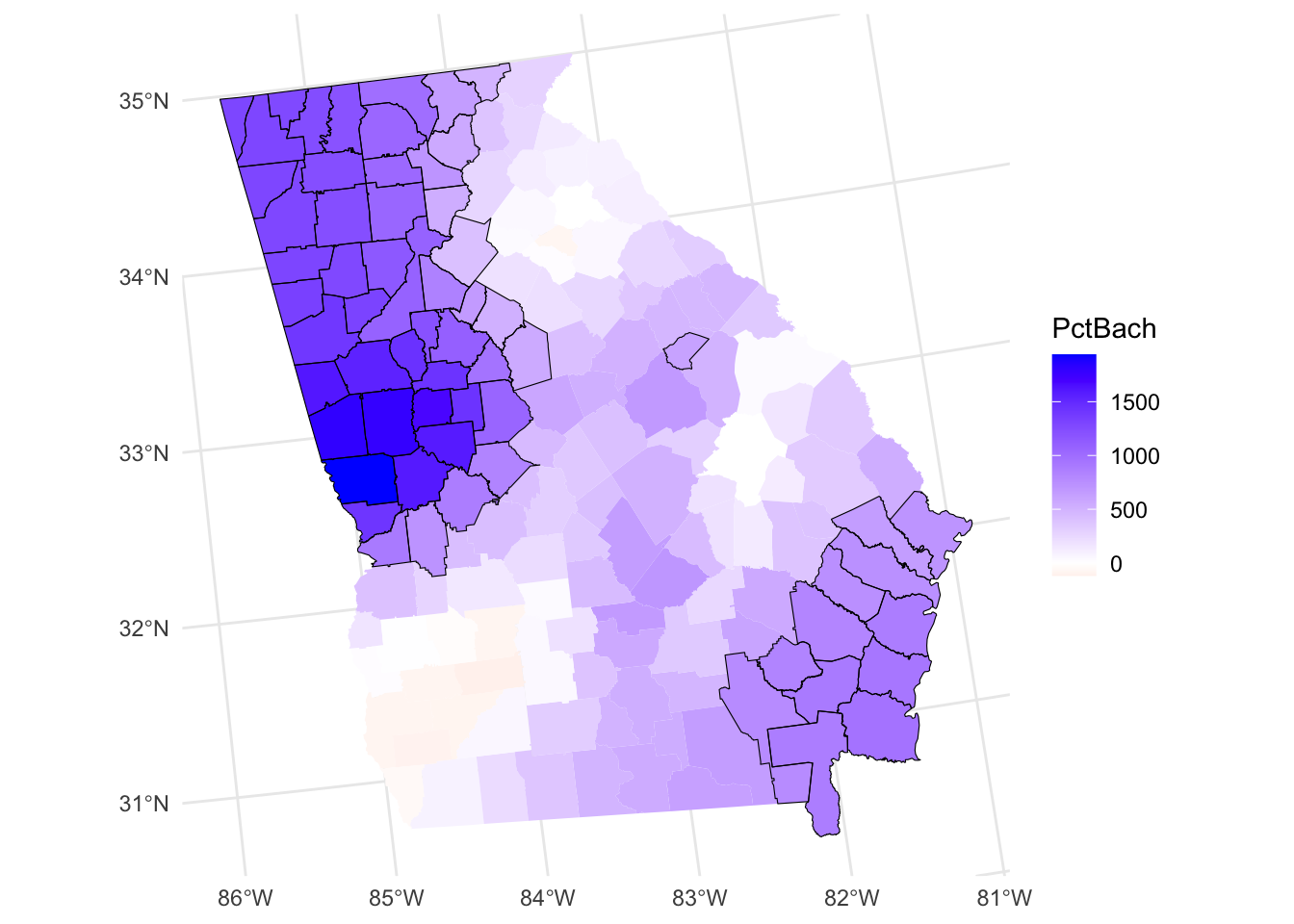
A map of the spatial variation of the PCTBlack coefficient estimate, with significant areas highlighted.

Figure 8.3: A map of the spatial variation of the PCTBlack coefficient estimate, with significant areas highlighted.

8.2.5 GWR Summary

GWR investigates if and how relationships between response and predictor variables vary geographically. It is underpinned by the idea that whole map (constant coefficient) regressions such as those estimated by ordinary least squares may make unreasonable assumptions about the stationarity of the regression coefficients under investigation. Such approaches may wrongly assume that regression relationships (between predictor and target variables) are the same throughout the study area.

GWR outputs provides measures of process heterogeneity – geographical variation in data relationships – through the generation of mappable and varying regression coefficients, and associated statistical inference. It has been extensively applied in a wide variety of scientific and socio-scientific disciplines.

There are a number of things to note about GWR:

  1. It reflects a desire to shift away from global, whole map (Openshaw 1996) and one-size-fits-all statistics, towards approaches that capture local process heterogeneity. This was articulated by Goodchild’s (2004) who proposed a 2nd law of geography: the principle of spatial heterogeneity or non-stationarity, noting the lack of a concept of an average place on the Earth’s surface comparable, for example, to the concept of an average human (Goodchild 2004).

  2. There have been a number of criticisms of GWR (see Section 7.6 in Gollini et al. (2013)).

  3. There have been a number of advances to standard GWR notably Multi-Scale which is now considered to be the default GWR. These have all been summarised in a GWR Route map paper (Comber et al. 2022).

Consideration of developments and limitations will be useful for your assignment write up.

Task 1

Create a function for creating a tmap of coefficients held in an sf polygon object, whose values flip, highlighting significant observations. Note that functions are defined in the following way:

my_function_name = function(parameter1, paramter2) { # note the  curly brackets 
  # code to do stuff
  # value to return
}

A very simple example is below. This simply takes variable name from an sf object, creates a vector of values and returns the median and the mean:

median_mean_from_sf = function(x, var_name) {
  # do stuff
  x = x %>% dplyr::select(all_of(var_name)) %>% st_drop_geometry() %>% unlist()
  mean_x = mean(x, na.rm = T)
  median_x = median(x, na.rm = T)
  # values to return
  c(mean_x, median_x)
}
# test it
median_mean_from_sf(x = georgia, var_name = "MedInc")
## [1] 37147.09 34307.00

You should be able to use the code that was used to generate the plot above for the do stuff bit:

# determine which are significant
tval = gwr_sf %>% dplyr::select(all_of("PctBlack_TV")) %>% st_drop_geometry()
signif = tval < -1.96 | tval > 1.96
# map the counties
tm_shape(gwr_sf) +
  tm_fill("PctBlack",midpoint = 0) + tm_style("col_blind")+
  tm_layout(legend.position = c("right","top"))+
  # now add the tvalues layer
  tm_shape(gwr_sf[signif,]) + tm_borders()

NB You are advised to attempt the tasks after the timetabled practical session. Worked answers are provided in the last section of the worksheet.

8.3 Multi-scale GWR

8.3.1 Description

In a standard GWR only a single bandwidth is determined and applied to each predictor variable. In reality some relationships in spatially heterogeneous processes may operate over larger scales than others>f this is the case the best-on-average scale of relationship non-stationarity determined by a standard GWR may under- or over-estimate the scale of individual predictor-to-response relationships.

To address this, Multi-scale GWR (MGWR) can be used (Yang 2014; Fotheringham, Yang, and Kang 2017; Oshan et al. 2019). It determines a bandwidth for each predictor variable individually, thereby allowing individual response-to-predictor variable relationships to vary. The individual bandwidths provide insight into the scales of relationships between response and predictor variables, allowing for local to global bandwidths. Recent work has suggested that MGWR should be the default GWR (Comber et al. 2022), with a standard GWR only being used in specific circumstances.

8.3.2 Undertaking a MGWR

The code below undertakes a search for the optimal bandwidths, and then having found them will generate a MSGWR model - it will generate a lot of text to your screen!

gw.ms <- gwr.multiscale(MedInc~ PctRural + PctBach + PctEld + PctFB + PctPov + PctBlack, 
                        data = as(georgia, "Spatial"),
                        adaptive = T, max.iterations = 1000,
                        criterion="CVR",
                        kernel = "bisquare",
                        bws0=c(100,100,100,100,100,100),
                        verbose = F, predictor.centered=rep(T, 6))

8.3.3 Evaluating the results

We can examine the bandwidths for the individual predictor variables:

bws = gw.ms$GW.arguments$bws
bws
## [1]  32 157 157 157  36  23  82

And how the coefficient estimates vary:

coefs_msgwr = apply(gw.ms$SDF@data[, 1:7], 2, summary)
round(coefs_msgwr,1)
##         Intercept PctRural PctBach PctEld   PctFB  PctPov PctBlack
## Min.      38804.1     63.0   758.5 -866.4 -4489.0 -2068.0   -129.0
## 1st Qu.   44196.3     67.0   775.6 -853.2 -3378.9 -1415.9    -82.0
## Median    48749.2     73.5   788.9 -842.5 -1672.4  -657.4    -18.5
## Mean      51870.4     71.0   787.4 -820.0 -1798.6  -916.5      3.4
## 3rd Qu.   60835.2     74.5   799.7 -779.3  -490.2  -469.1     96.7
## Max.      73454.1     76.3   808.3 -752.9  1166.1  -277.5    156.4

Finally these can be assembled into a table:

tab.mgwr = data.frame(Bandwidth = bws, 
                 t(round(coefs_msgwr,1)))
names(tab.mgwr)[c(3,6)] = c("Q1", "Q3")
tab.mgwr
Table 8.2: The MSGWR variable specific bandwidths and coefficient estimates.
Bandwidth Min. Q1 Median Mean Q3 Max.
Intercept 32 38804.1 44196.3 48749.2 51870.4 60835.2 73454.1
PctRural 157 63.0 67.0 73.5 71.0 74.5 76.3
PctBach 157 758.5 775.6 788.9 787.4 799.7 808.3
PctEld 157 -866.4 -853.2 -842.5 -820.0 -779.3 -752.9
PctFB 36 -4489.0 -3378.9 -1672.4 -1798.6 -490.2 1166.1
PctPov 23 -2068.0 -1415.9 -657.4 -916.5 -469.1 -277.5
PctBlack 82 -129.0 -82.0 -18.5 3.4 96.7 156.4

You should examine these, particularly the degree to which the coefficient estimates vary in relation to their bandwidths. Notice that smaller bandwidths (a smaller moving window) results in greater variation and this reduces as the bandwidths tend towards the global (recall that there are \(n = 159\) observations in the georgia data). So some of the bandwidths indicate highly local relationships with the target variable, while other are highly global, with bandwidths approaching \(n = all\).

Notice the coefficients and the degree to whcih vary, alongside the bandwidths - high bandwidths of course reult in less variation in the coefficient estimates.

These tell us something about the local-ness of the interactions of different covariates with the target variable MedInc: PctFB, PctPov and PctBlack have small, highly local bandwidths, using few data points in each local regression. Whilst PctRural, PctBach and PctEld have a global relationship with MedInc and nearly all of their values are used in each local regression model.

In the standard GWR PctBlack and PctFB flipped and they do so here potentially because of the more localised bandwidths (recall that the standard GWR model had a bandwidth of 81).

You could write this out to a csv file for inclusion in a report or similar as in the GWR coefficient example above. And the coefficients can be mapped. To a degree there is no point in mapping the coefficients whose bandwidths tend towards the global (i.e. are close to \(n\)), but the others are potentially interesting.

Again these are held in the SDF of the GWmodel output which is converted to sf format in the code below and examined:

mgwr_sf = st_as_sf(gw.ms$SDF)
mgwr_sf

8.3.4 Mapping MGWR outputs

The code below creates the maps for the local covariates:

p1 = tm_shape(mgwr_sf) +
  tm_fill(c("Intercept", "PctPov"), palette = "viridis", style = "kmeans") +
  tm_layout(legend.position = c("right","top"), frame = F)
# coefficients whose values flip 
p2 = tm_shape(mgwr_sf) +
  tm_fill(c("PctFB", "PctBlack"),midpoint = 0, style = "kmeans") +
  tm_style("col_blind")+
  tm_layout(legend.position = c("right","top"), frame = F) 
tmap_arrange(p1, p2, nrow = 2)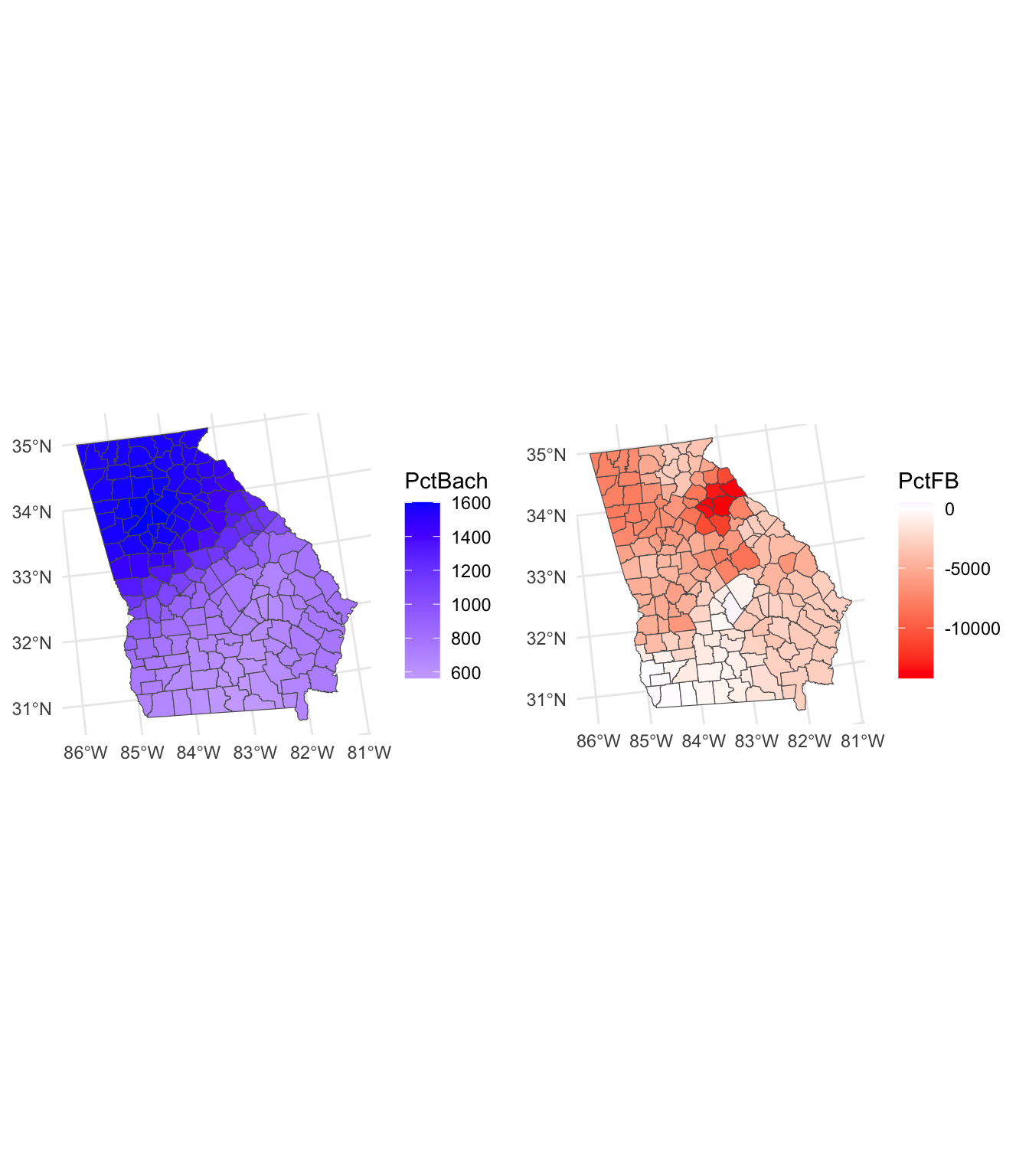
Maps of the MGWR coefficient estimates.

Figure 8.4: Maps of the MGWR coefficient estimates.

You may have noticed that t-values are also included in the outputs and gain significant areas can be identified and highlighted. This suggests a different spatial extent to that indicated by a standard GWR.

# determine which are significant
tval = mgwr_sf$PctBlack_TV
signif = tval < -1.96 | tval > 1.96
# map the counties
tm_shape(mgwr_sf) +
  tm_fill("PctBlack",midpoint = 0) + tm_style("col_blind")+
  tm_layout(legend.position = c("right","top"))+
  # now add the tvalues layer
  tm_shape(mgwr_sf[signif,]) + tm_borders()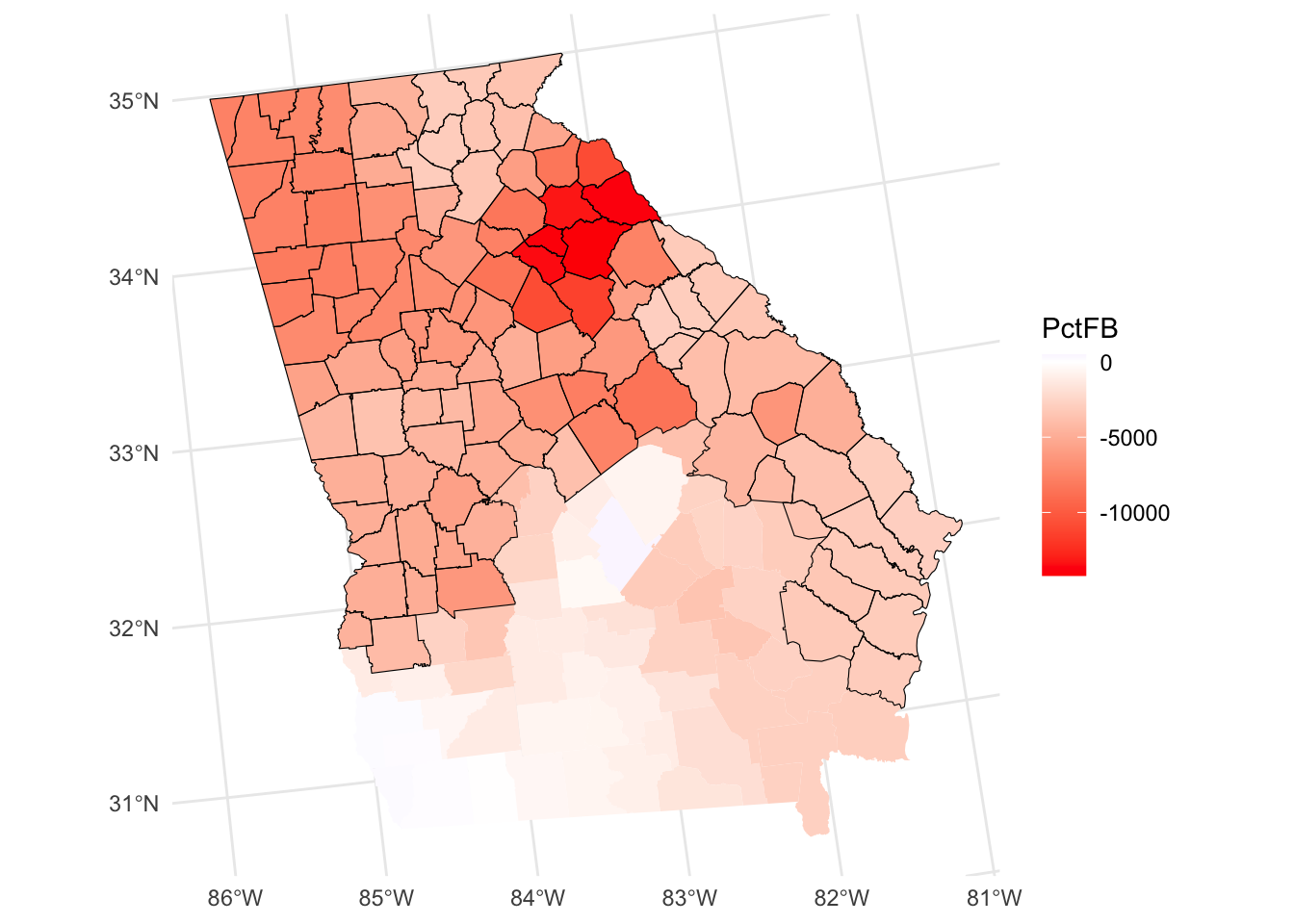
A map of the spatial variation of the PCTBlack coefficient estimate arising from a MGWR, with significant areas highlighted.

Figure 8.5: A map of the spatial variation of the PCTBlack coefficient estimate arising from a MGWR, with significant areas highlighted.

8.3.5 Comapring GWR and MGWR

It is instructive to compare the GWR and MGR outputs, both in terms of the numeric distributions and the spatial ones. The inter-quartile ranges of the numeric distributions give as idea about the different spreads and we can examine these with respect to the global coefficient estimates from the OLS model and the MGWR bandwidths:

gwr.iqr <- t(tab.gwr[c(2,5,7),])
mgwr.iqr <- tab.mgwr[, c(1,3,6)]
cbind(gwr.iqr, mgwr.iqr)
##           1st Qu. 3rd Qu.  Global Bandwidth      Q1      Q3
## Intercept 48665.1 57087.4 52598.9        32 44196.3 60835.2
## PctRural     48.0   113.3    73.8       157    67.0    74.5
## PctBach     545.4   875.7   697.3       157   775.6   799.7
## PctEld     -997.1  -784.1  -788.6       157  -853.2  -779.3
## PctFB     -2230.0  -640.3 -1290.3        36 -3378.9  -490.2
## PctPov    -1279.4  -511.6  -954.0        23 -1415.9  -469.1
## PctBlack    -51.3    80.5    33.1        82   -82.0    96.7

The maps similarly may show large differences in both the value of the coefficient estimates (see Figure 8.6) in different places but also the significant areas (see Figure 8.7).

# gwr
p1 = tm_shape(gwr_sf) +
  tm_fill(c("Intercept", "PctPov"), palette = "viridis", style = "kmeans") +
  tm_layout(legend.position = c("right","top"), frame = F)
# mgwr
p2 = tm_shape(mgwr_sf) +
  tm_fill(c("Intercept", "PctPov"), palette = "viridis", style = "kmeans") +
  tm_layout(legend.position = c("right","top"), frame = F)
tmap_arrange(p1, p2, nrow = 2)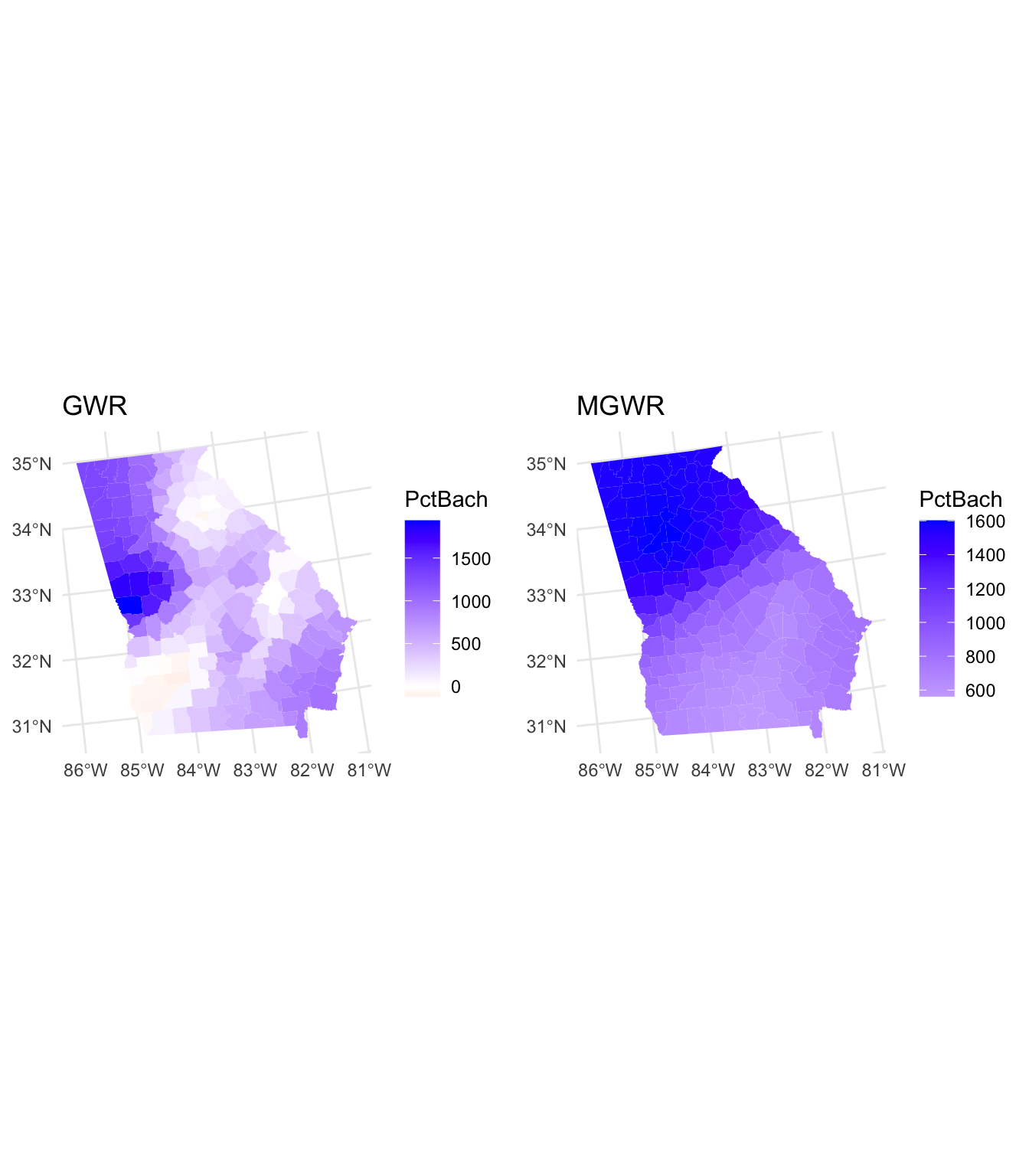
Maps of the coefficients arising from a GWR (top) and MGWR (bottom).

Figure 8.6: Maps of the coefficients arising from a GWR (top) and MGWR (bottom). 

# gwr
tval = gwr_sf$PctFB_TV
signif = tval < -1.96 | tval > 1.96
# map the counties
p1 = tm_shape(gwr_sf) +
  tm_fill("PctFB",midpoint = 0) + tm_style("col_blind")+
  tm_layout(legend.position = c("right","top"))+
  # now add the tvalues layer
  tm_shape(mgwr_sf[signif,]) + tm_borders()
# mgwr
tval = mgwr_sf$PctFB_TV
signif = tval < -1.96 | tval > 1.96
# map the counties
p2 = tm_shape(mgwr_sf) +
  tm_fill("PctFB",midpoint = 0) + tm_style("col_blind")+
  tm_layout(legend.position = c("right","top"))+
  # now add the tvalues layer
  tm_shape(mgwr_sf[signif,]) + tm_borders()
tmap_arrange(p1, p2, nrow = 1)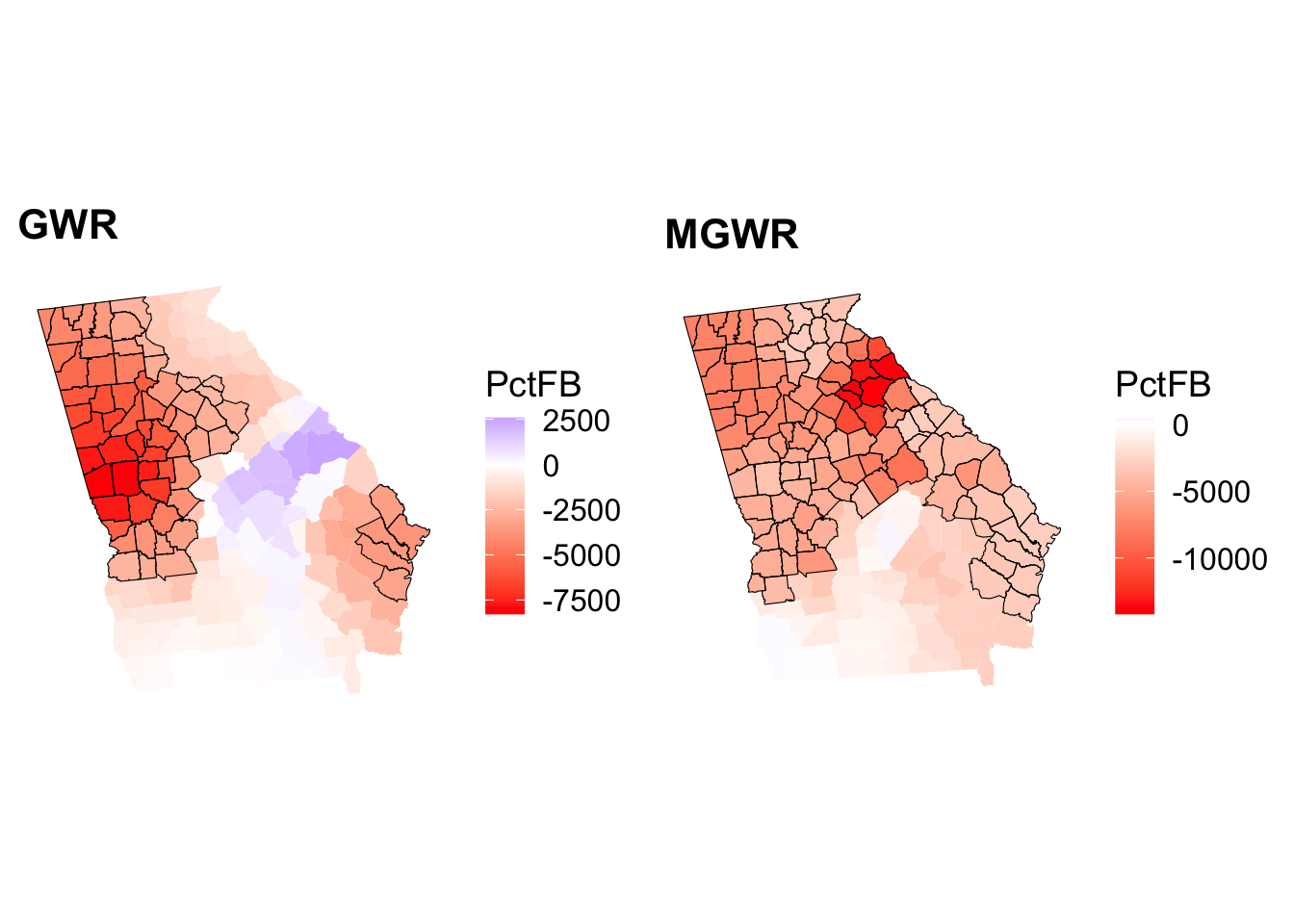
Maps of the signiticant coefficients arising from a GWR (left) and MGWR (right).

Figure 8.7: Maps of the signiticant coefficients arising from a GWR (left) and MGWR (right).

8.3.6 MGWR Summary

A single bandwidth is used in standard GWR under the assumption that the response-to-predictor relationships operate over the same scales for all of the variables contained in the model. This may be unrealistic because some relationships can operate at larger scales and others at smaller ones. A standard GWR will nullify these differences and find a best-on-average scale of relationship non-stationarity (geographical variation), as described through the bandwidth.

MSGWR was proposed to allow for a mix of relationships between predictor and response variables: from highly local to global. In MGWR, the bandwidth for each relationship is determined separately, allowing the scale of individual response-to-predictor relationships to vary.

For these reasons, the MGWR has been recommended as the default GWR. MGWR plus an OLS regression provides solid basis for making a decision to use a GWR and for determining the variation predictor variable to response variable relationships: the MGWR bandwidths indicate their different scales. A standard GWR should only be used in circumstances where all the predictors are found to have the same bandwidth.

8.4 Answers to Tasks

Task 1

Create a function for creating a tmap of coefficients held in an sf polygon object, whose values flip, highlighting significant observations.

The function below takes three inputs:

  • x an sf object
  • var_name the name of a variable in the GWR output
  • vr_name_TV the name of the t-values for the variable in the GWR output
my_map_signif_coefs_func = function(x, var_name, var_name_TV) {
  # determine which are significant
  tval = x %>% dplyr::select(all_of(var_name_TV)) %>% st_drop_geometry()
  signif = tval < -1.96 | tval > 1.96
  # map the counties
  p_out = tm_shape(x) +
    tm_fill(var_name,midpoint = 0) + tm_style("col_blind")+
    tm_layout(legend.position = c("right","top"))+
    # now add the tvalues layer
    tm_shape(x[signif,]) + tm_borders()
  # return the output
  p_out
}

Test it!

my_map_signif_coefs_func(x = gwr_sf, var_name = "PctBlack", var_name_TV = "PctBlack_TV")

References

Brunsdon, Chris, A Stewart Fotheringham, and Martin E Charlton. 1996. “Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity.” Geographical Analysis 28 (4): 281–98.
Comber, Alexis, Christopher Brunsdon, Martin Charlton, Guanpeng Dong, Richard Harris, Binbin Lu, Yihe Lü, et al. 2022. “A Route Map for Successful Applications of Geographically Weighted Regression.” Geographical Analysis.
Dormann, Carsten F, Jane Elith, Sven Bacher, Carsten Buchmann, Gudrun Carl, Gabriel Carré, Jaime R Garcı́a Marquéz, et al. 2013. “Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance.” Ecography 36 (1): 27–46.
Fotheringham, A Stewart, Chris Brunsdon, and Martin Charlton. 2003. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. John Wiley & Sons.
Fotheringham, A Stewart, Wenbai Yang, and Wei Kang. 2017. “Multiscale Geographically Weighted Regression (MGWR).” Annals of the American Association of Geographers 107 (6): 1247–65.
Gollini, Isabella, Binbin Lu, Martin Charlton, Christopher Brunsdon, and Paul Harris. 2013. “GWmodel: An r Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models.” arXiv Preprint arXiv:1306.0413.
Goodchild, Michael F. 2004. “The Validity and Usefulness of Laws in Geographic Information Science and Geography.” Annals of the Association of American Geographers 94 (2): 300–303.
Lu, Binbin, Paul Harris, Martin Charlton, and Chris Brunsdon. 2014. “The GWmodel r Package: Further Topics for Exploring Spatial Heterogeneity Using Geographically Weighted Models.” Geo-Spatial Information Science 17 (2): 85–101.
Meloun, Milan, Jiřı́ Militkỳ, Martin Hill, and Richard G Brereton. 2002. “Crucial Problems in Regression Modelling and Their Solutions.” Analyst 127 (4): 433–50.
Openshaw, Stan. 1996. “Developing GIS-Relevant Zone-Based Spatial Analysis Methods.” Spatial Analysis: Modelling in a GIS Environment, 55–73.
Oshan, Taylor M, Ziqi Li, Wei Kang, Levi J Wolf, and A Stewart Fotheringham. 2019. “Mgwr: A Python Implementation of Multiscale Geographically Weighted Regression for Investigating Process Spatial Heterogeneity and Scale.” ISPRS International Journal of Geo-Information 8 (6): 269.
Yang, Wenbai. 2014. “An Extension of Geographically Weighted Regression with Flexible Bandwidths.” PhD thesis, University of St Andrews.

  1. collinearity is when pairs of predictor variables have a strong positive or negative relationship with each other and increases as more predictors are introduced.↩︎

  2. see https://www.thoughtco.com/degree-of-latitude-and-longitude-distance-4070616↩︎

  3. There is a nice description here at the start of this webpage - ignore all the MiniTab stuff! https://blog.minitab.com/blog/statistics-and-quality-data-analysis/what-are-t-values-and-p-values-in-statistics↩︎