- 1. Fundamental Interval and Ratio Scales
- 2. Conjoint Measurement Theory
- 3. Rasch’s Example
- 4. Fundamental Measurement and the Rasch Model
- 5. Invariant-Person Comparisons
- 6. Invariant-Item Comparisons
- 7. A Caveat 注意事項
- 8. Funamental Measurement of Persons in More Complex Models (2PL)
- 9. Fundamental Measurement and Scale type
- 10. Evaluating Psychological Data for Fundamental Scalability
- 11. Justifying Scale Level in CTT (1)
- 11. Justifying Scale Level in CTT (2)
- 12. Practical Importance of Scale Level
- 13. My practice (Fig. 6.9)
- Appendix
1. Fundamental Interval and Ratio Scales
- For physical attributes, objects are fundamentally measurable, the properties of order and addition have a physical analogue (類比).
- Order. One rod is observed to be longer than another.
- Addition. Two (equal) rods can be added. If their composite length equals a longer rod, then the length of the longer must be twice the length of the shorter rods.
2. Conjoint Measurement Theory
- The theory of conjoint measurement (Luce & Tuckey, 1964). .font60[(提出 Tukey’s HSD test 的那位 Tukey!)] specifies conditions that can establish the required properties of order and additivity for interval-scale measurement.
- Conjoint measurement is obtained when an outcome variable is an additive function of two other variables, assuming that all three variables may be ordered for magnitude.
[p.141]
3. Rasch’s Example
Conjoint measurement theory may be applied to Rasch’s (1960) favorite example as follows.
Acceleration=ForceMasslog(Acceleration)=log(Force)−log(Mass)
For Rasch’s 1PL model, the item performance scaled as log odds is an additive combination of log trait level, θs, and log item difficulty, βi.
log(Item Odds)=log(Trait Level)−log(Item Difficulty)
[Eq. 6.6-6.8]
wiki The definition of measurement
- In physics and metrology, the standard definition of measurement is the estimation of the ratio between a magnitude of a continuous quantity and a unit magnitude of the same kind (de Boer, 1994/95; Emerson, 2008).
e.g., “The hallway is 4 m long”. - For some other quantities, Invariant are ratios b/w attribute differences. e.g., the Fahrenheit or Celsius scales.
- What are really being measured with such instruments are the magnitudes of temperature differences.
e.g., the unit of the Celsius scale is 1/100th of the difference in temperature between the freezing and boiling points of water at sea level.
wiki Extensive and intensive quantity
- Extensive (外延性). Length, or Mass.
e.g., 60(g) 饅頭剝成兩份 -> 30(g)+30(g) - Intensive (內含性) . Temperature.
e.g., 60(°C) 饅頭剝成兩份 -> 30(°C)+30(°C) ??
(i.e., 溫度不具有可加性) - Psychological attributes?? like temperature, or like length?? The theory of conjoint measurement provides a theoretical means of dealing w/ this.
[See: Theory of conjoint measurement from Wikipedia]
4. Fundamental Measurement and the Rasch Model
Rasch model derived from several conditions for scores.
- the sufficiency of the unweighted total score (Fisher, 1995)
- consistency of ordering persons and items (Roskam & Jansen, 1984)
- additivity (Andrich, 1988)
- the principle of specific objectivity (Rasch, 1977). Comparisons b/w objects must be generalizable beyond the specific conditions under which they were observed.
(See also: Specific objectivity - local and general)
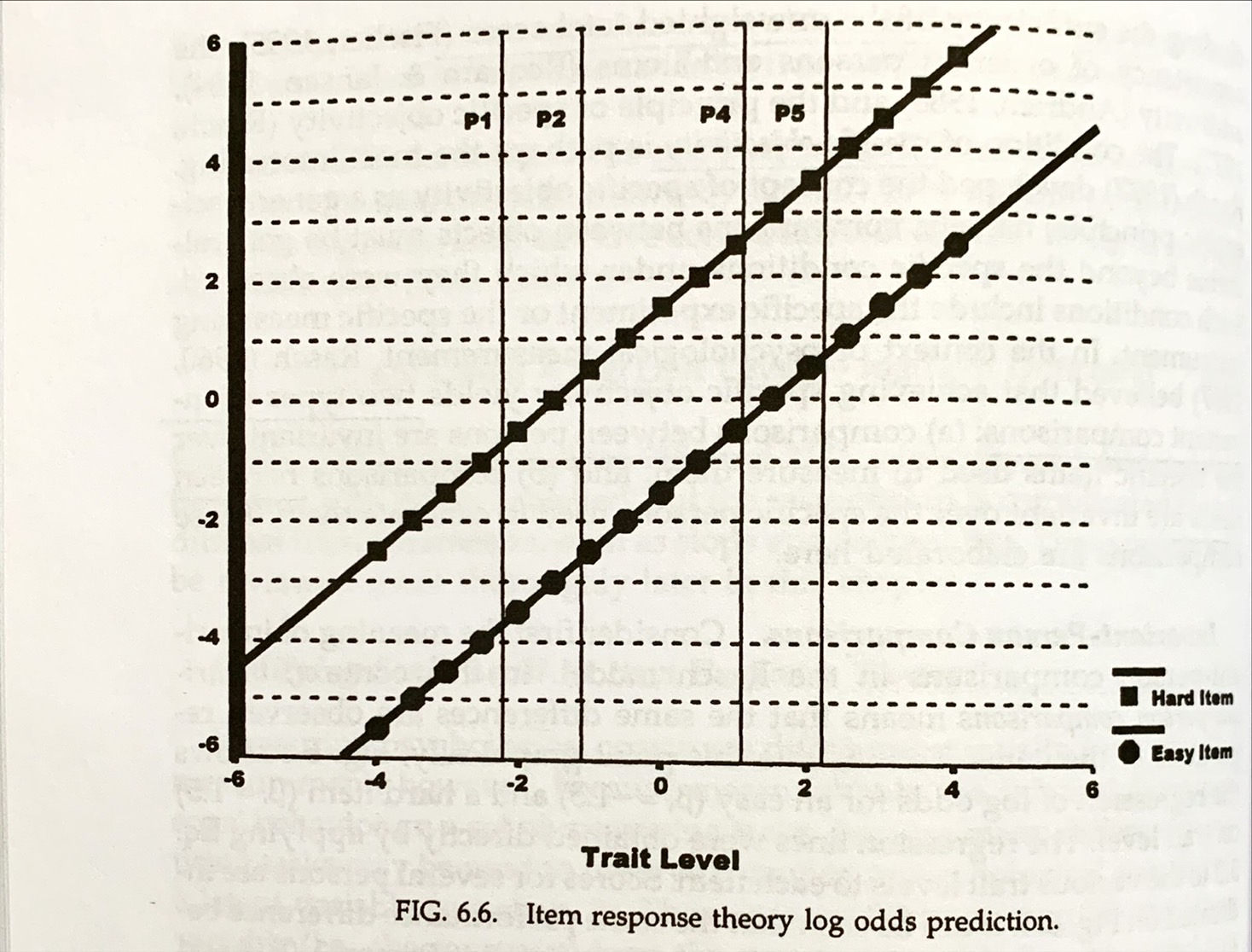
5. Invariant-Person Comparisons
[
 ]
[]
]
[]
Compare persons at the low/high end.
lnP(Xi1)1−P(Xi1)−lnP(Xi2)1−P(Xi2)=(θ1−βi)−(θ2−βi)=θ1−θ2=−2.20−(−1.10)=−1.10
lnP(Xi4)1−P(Xi4)−lnP(Xi5)1−P(Xi5)=(θ4−βi)−(θ5−βi)=θ1−θ2=1.10−2.20=−1.10
[Eq. 6.10-6.11]
6. Invariant-Item Comparisons
- Log odds of item 1 and item 2, for any subjects.
lnP(X1s)1−P(X1s)=θs−β1 lnP(X2s)1−P(X2s)=θs−β2
[Eq. 6.12]
Item comparisons for 1PL/2PL models.
lnP(X1s)1−P(X1s)−lnP(X2s)1−P(X2s)=(θs−β1)−(θs−β2)=−(β1−β2)
For 2PL model, the difference does NOT depend only on item difficulty (i.e. we also need to consider θs, α1, and α2).
lnP(X1s)1−P(X1s)−lnP(X2s)1−P(X2s)=α1(θs−β1)−α2(θs−β2)=θs(α1−α2)−(α1β1−α2β2)
[Eq. 6.13-6.14]
7. A Caveat 注意事項
- (O) equating trait levels across non-overlapping item sets, e.g. adaptive testing.
- (O) item parameters estimates are not much influenced by the trait distribution in the calibration sample. (See Whitely & Dawis, 1974).
- (X) the estimates from test data will have identical properties over either items or over persons.
- e.g., if the item set is easy, a low trait level will be more accurately estimated than a high trait level. (information)
Although estimates can be equated over these conditions, the standard errors are influenced. (See Ch. 7, 8, 9)
8. Funamental Measurement of Persons in More Complex Models (2PL)
[ lnP(Xi1)1−P(Xi1)−lnP(Xi2)1−P(Xi2)=αi(θ1−βi)−αi(θ2−βi)=αi(θ1−θ2)=αi(−2.20−(−1.10))=−1.10αi [Eq. 6.15]]
[]
9. Fundamental Measurement and Scale type
Ratio scale –> interval scale.
The odds that a person passes an item is given by the ratio of trait level to item difficulty. Where ξs=exp(θs),ϵi=exp(βi).
Pi11−Pi1=eθ1eβi=ξ1ϵi;Pi21−Pi2=ξ2ϵi
Consider the Rasch model in the log odds form. lnPi11−Pi1=θs−βi [Eq. 6.16, 6.18]
The odds ratio of person 1 and person 2 at item i as follows.
Pi11−Pi1Pi21−Pi2=ξ1ϵiξ2ϵi=ξ1ξ2
The relative odds b/w that any item is solved for the 2 persons is simply the ratio of their trait levels.
[Eq. 6.17]
10. Evaluating Psychological Data for Fundamental Scalability
Luce and Tukey (1964) outline several conditions that must be obtained to support additivity. (可加性需要幾個條件)
- Solvability and the Archmidean condition. (to ensure continuity) (See also. Theory of conjoint measurement).
- Single cancellation or independence axiom.
- Double cancellation axiom.
Michell (1990) shows how the double canellation condition establishes that two parameters are additivity related to a third variable.
Consider two natural attributes A, and X. It is not known that either A or X is a continuous quantity, or both.
- A: (a, b, c)
- X: (x, y, z)
- P: (a, x), (b, y),…, (c, z)
The quantification of A, X and P depends upon the behaviour of the relation holding upon the levels of P.
[See: Theory of conjoint measurement from Wikipedia]
wiki Single Cancellation Axiom
The theory of conjoint measurement
It can be seen that a > b because (a, x) > (b, x), (a, y) > (b, y) and (a, z) > (b, z).
[See: Theory of conjoint measurement from Wikipedia]
wiki Double Cancellation Axiom
Given that: (a,y)>(b,x) is true if and only if a+y>b+x, and (b,z)>(c,y) is true if and only if b+z>c+y, it follows that: a+y+b+z>b+x+c+y.
Cancelling the common terms results in: (a,z)>(c,x).
[See: Theory of conjoint measurement from Wikipedia]
Double Cancellation Condition (機率值也可以)
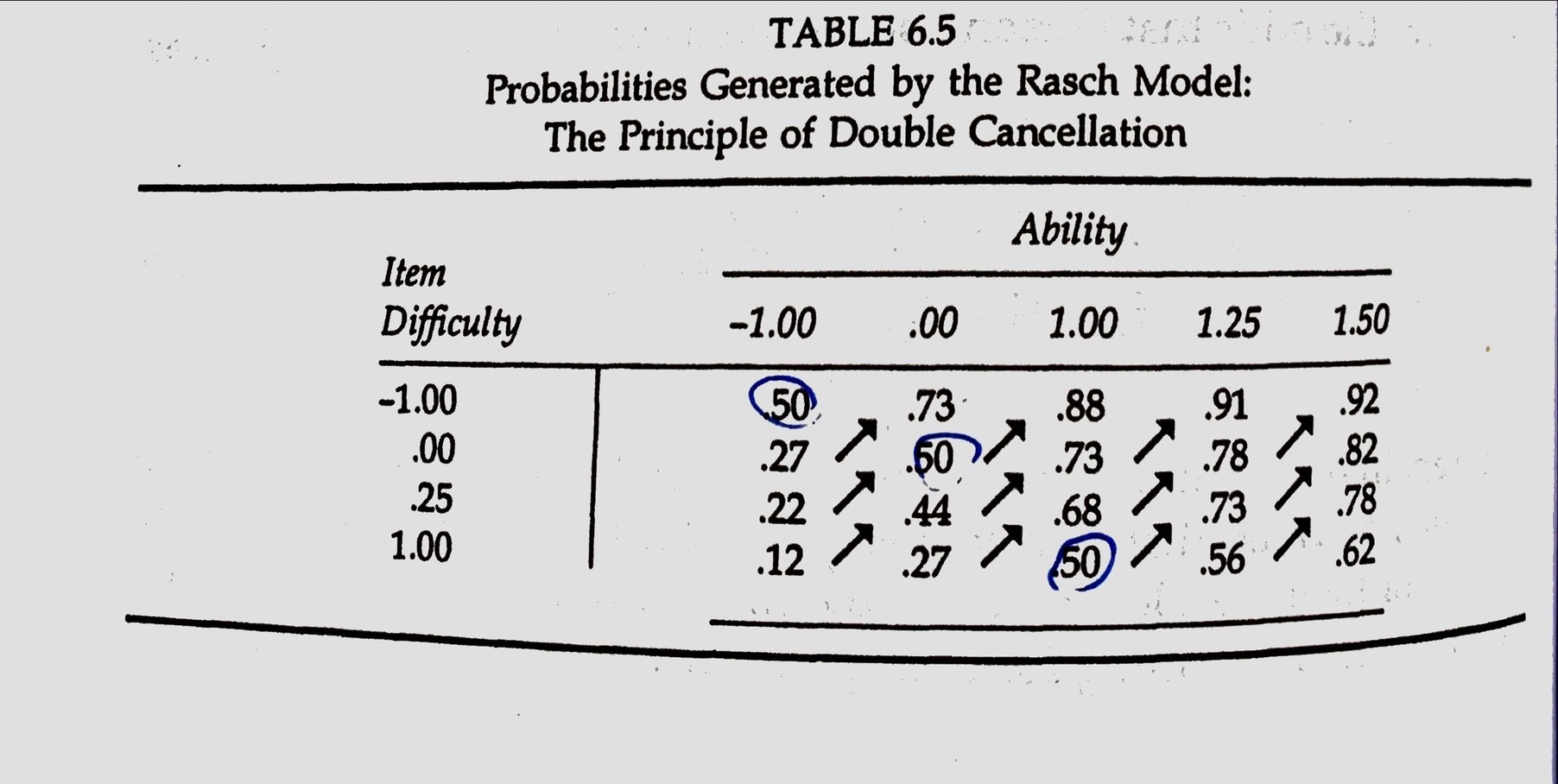
.font90[ - Single cancellation. the relative order of probabilities for any two items is the same, regardless of the ability column. Also, the probabilities for persons is the same. - Double cancellation. the third variable (表格中的機率值) increases as both the other two variables (難度、能力) increase.]
[Table 6.5]
with only minor exceptions, these data generally correspond to the double-cancellation pattern.
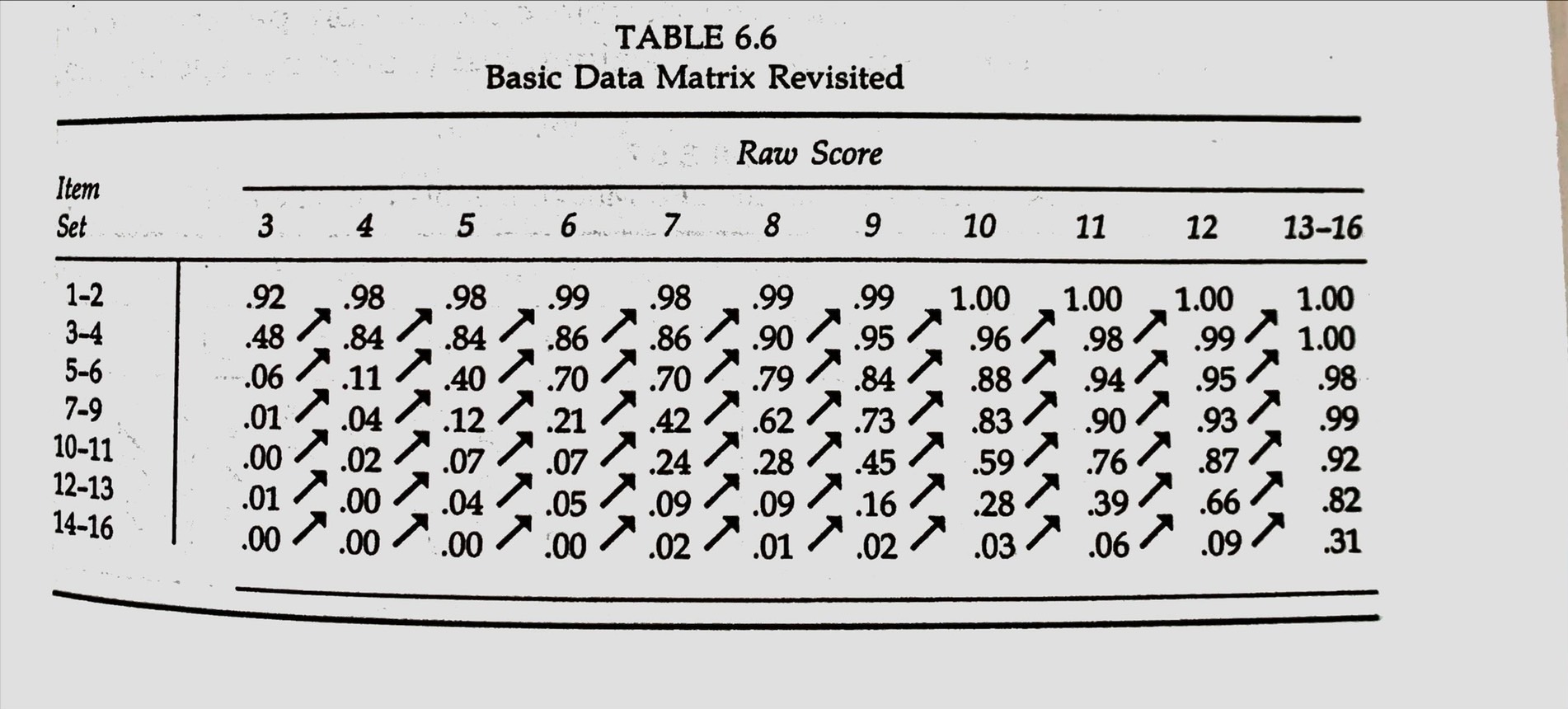
[Table 6.6]
Fig. 3.1 revisited.
[
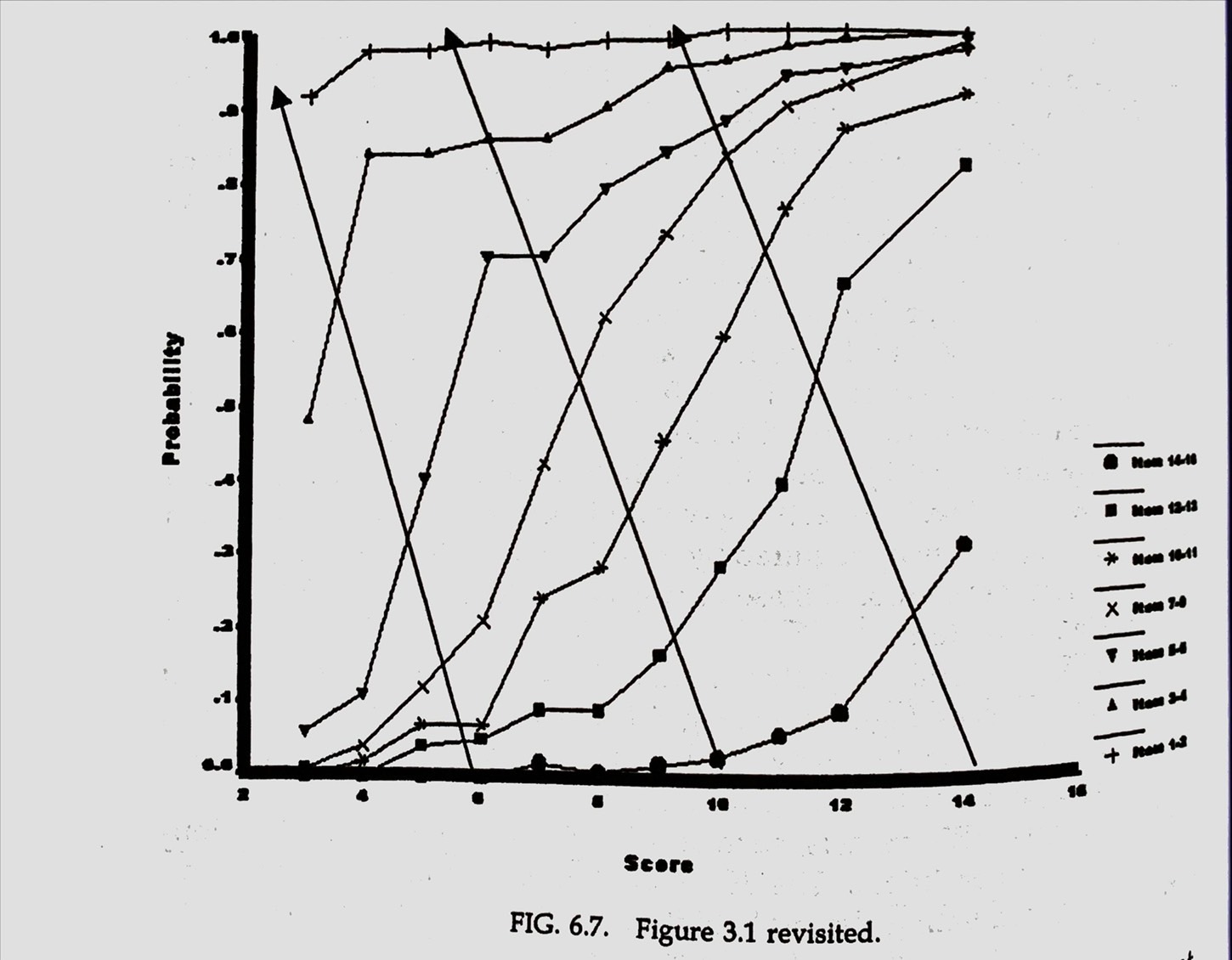 [Fig. 6.7]]
[
- double cancellation is shown by the diagonal arrows.
- double cancellation is equivalent to stating that the ICCs do not cross.]
[Fig. 6.7]]
[
- double cancellation is shown by the diagonal arrows.
- double cancellation is equivalent to stating that the ICCs do not cross.]
- More complex IRT model (2PL) do not meet the double-cancellation conditions. (discrimination)
- Conjoint measurement theory is only one view of scale level. The 2PL model may be more favorably evaluated under other views of scale level.
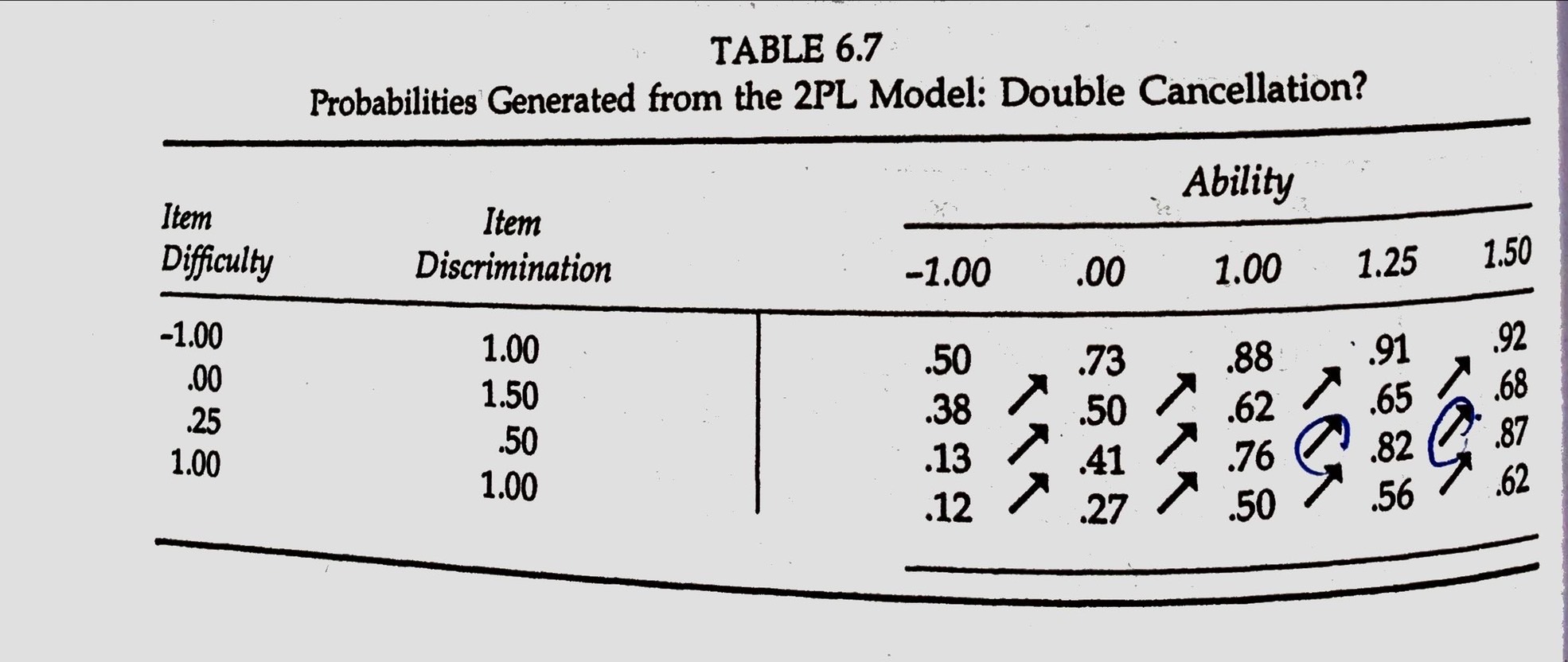
[Table 6.7]
11. Justifying Scale Level in CTT (1)
The meaning of score differences clearly depends on the test and its item properties. Interval-level can be justified in CTT if two conditions hold,
1. the true trait level , measured on an interval scale, is normally distribution. (assumption)
2. observed scores have a normal distribution.
- items can be selected to yield normal distributions by choosing difficulty levels that are appropriate for the norm group. (.40 ~ .60)
- non-normally distributed observed scores can be normalized.
11. Justifying Scale Level in CTT (2)
[
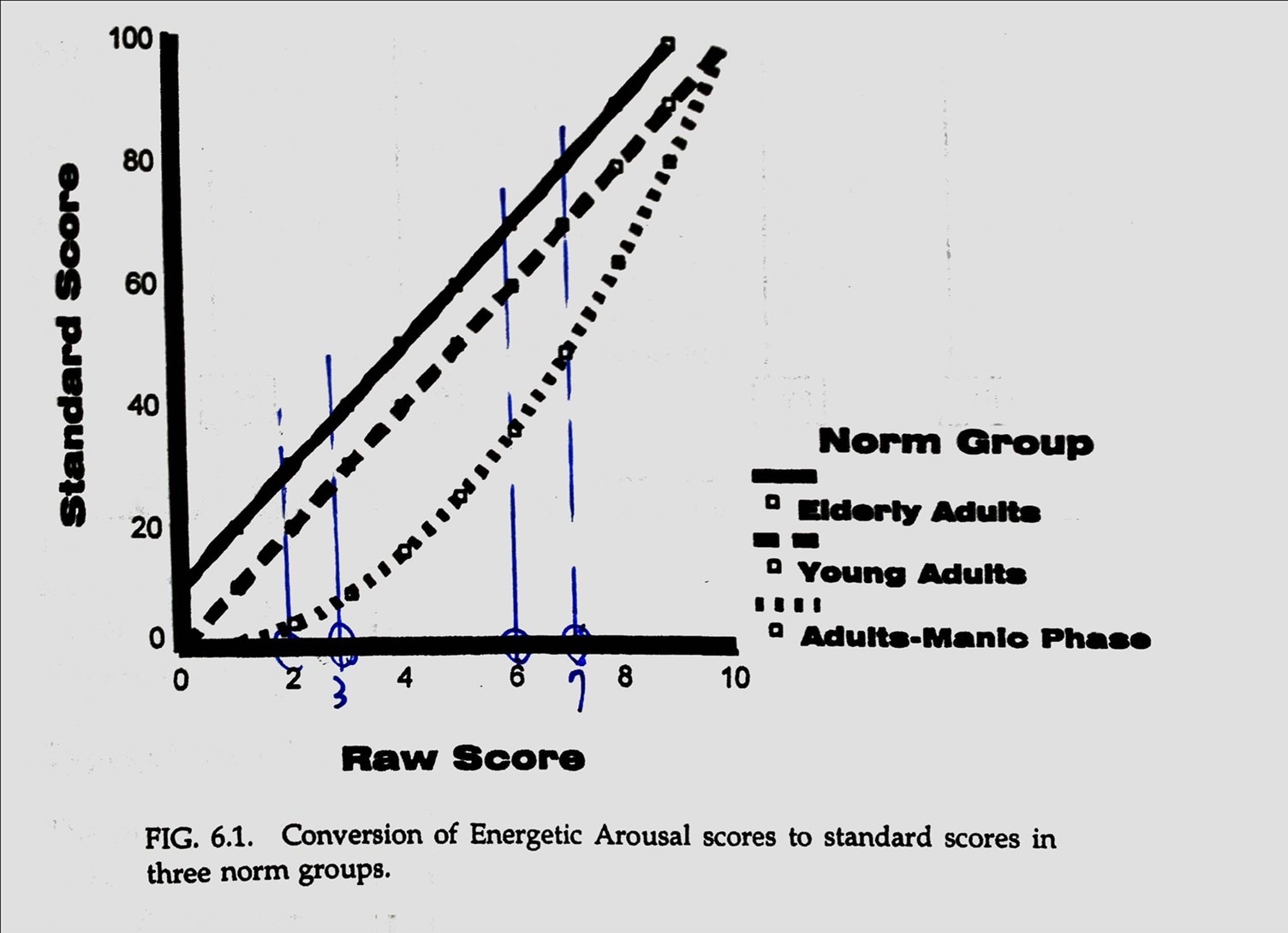 ]
]
[ When multiple norm groups exist, it is difficult to justify scaling level on the basis of achieving a certain distribution of scores. ]
12. Practical Importance of Scale Level
same data can lead different conclusions. CTT/IRT
- Two groups w/ equal true means can differ significantly on observed means if the observed scores are not linearly related to true score. (Maxwell & Delaney, 1985)
- Significant interactions can be observed from raw scores in factorial ANOVA designs (Embretson, 1997).
- Estimates of growth and learning curves, repeated measures comparisons and even regression coefficients have been shown to depend on the scale level reached for observed scores.
Mapping proportion correct to trait level
[
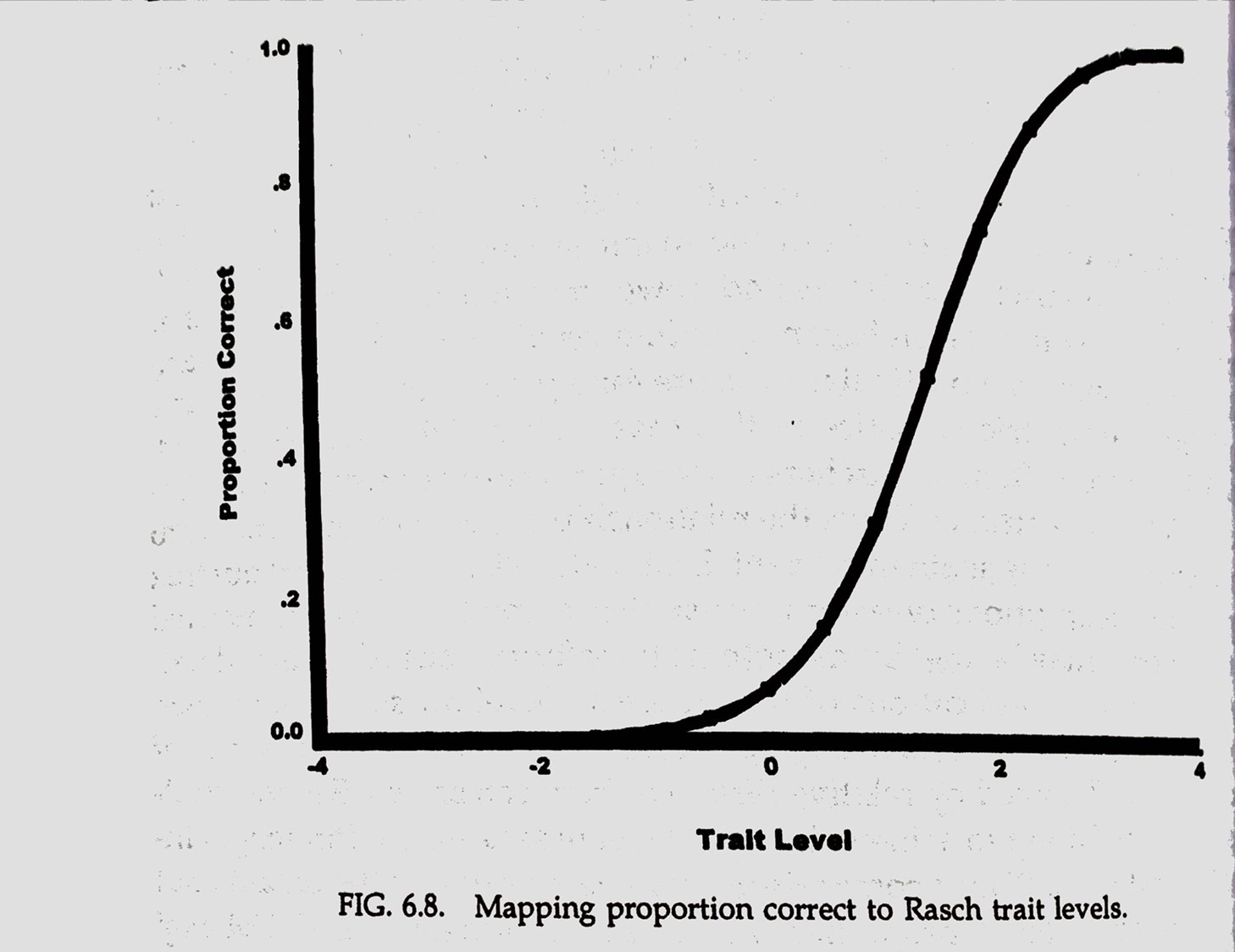 ]
]
[]
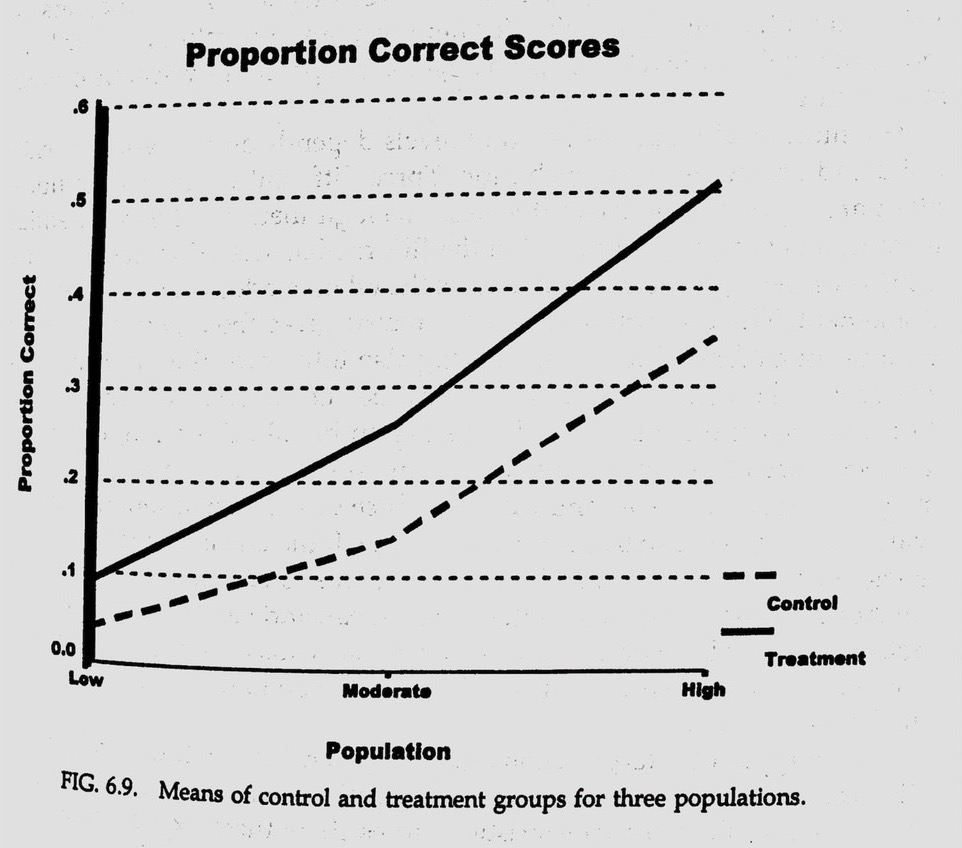
A simulation study of 3x2 factorial ANOVA design
- 300 cases per group
- randomly sampled from a distribution w/ variance =1.0
- means of control group. -1 (low), 0 (moderate), 1 (high).
- means of treatment group. -0.5 (low), 0.5 (moderate), 1.5 (high).
Conclusion. The greatest differences b/w conditions will be found for the population for which the level of test difficulty is most appropriate. (high trait w/ hard item, 1.5)
Means of control and treatment groups for three populations.
[
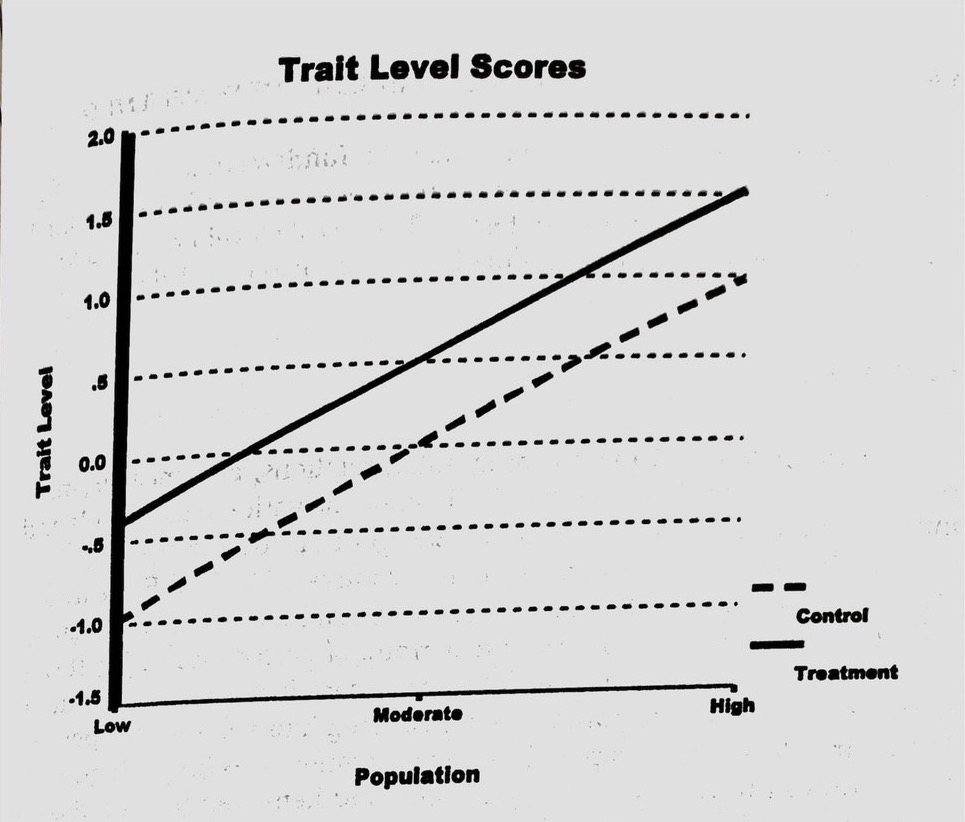 ]
[
]
[
 ]
]
13. My practice (Fig. 6.9)
| trt | grp | m.true | m.trait | Δθ | m.prop. | ΔP | e.prop. |
|---|---|---|---|---|---|---|---|
| cnt | L | -1.0 | -0.987 | - | 0.107 | - | 0.077 |
| cnt | M | 0.0 | 0.013 | 1.000 | 0.223 | 0.116 | 0.184 |
| cnt | H | 1.0 | 1.010 | 0.997 | 0.399 | 0.176 | 0.380 |
| trt | L | -0.5 | -0.487 | - | 0.157 | - | 0.121 |
| trt | M | 0.5 | 0.513 | 1.000 | 0.304 | 0.147 | 0.272 |
| trt | H | 1.5 | 1.510 | 0.997 | 0.501 | 0.197 | 0.502 |
.font80[
Note. (1) set.seed(1234),
(2)m.true=mean of true. (3)m.trait=mean of trait level. (4)m.prop=mean of proportion correct. (5)e.prop= em.trait−1.5/(1+em.trait−1.5)
]
ANOVA tables
## Analysis of Variance Table
##
## Response: prp
## Df Sum Sq Mean Sq F value Pr(>F)
## grp 2 30.590 15.2949 536.7894 < 2e-16 ***
## trt 1 2.731 2.7306 95.8334 < 2e-16 ***
## grp:trt 2 0.208 0.1042 3.6575 0.02599 *
## Residuals 1794 51.117 0.0285
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Analysis of Variance Table
##
## Response: tht
## Df Sum Sq Mean Sq F value Pr(>F)
## grp 2 1200.0 600.00 594.86 <2e-16 ***
## trt 1 112.5 112.50 111.54 <2e-16 ***
## grp:trt 2 0.0 0.00 0.00 1
## Residuals 1794 1809.5 1.01
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1小疑問
- 如果改成用前述條件模擬1筆作答資料(例如 10 題的二元計分資料),卻會發現 IRT 或 CTT 都沒有交互作用?也無法很好的復原回 true score?? (不知道是模擬資料的問題或是??)
- 模擬 6 組不同分配的資料,跑同一個 IRT 模型是否會有一些問題??(分開跑每組的 θ 平均會是 0)
Appendix
sim_dat4 <- \(sim_m, sim_t, sim_g) {
N <- 300
set.seed(1234)
tht <- rnorm(N, mean=sim_m, sd=1)
tht <- as.data.frame(tht)
tht$grp <- sim_g
tht$trt <- sim_t
return(tht)
}p_fun <- \(x){
exp(x-1.5)/(1+exp(x-1.5))
}
th_fun <- \(p){
log(p/(1-p)) + 1.5
}
prp_calc <- \(dat) {
prp <- c()
for (i in 1:nrow(dat) ) {
prp[i] <- p_fun( dat$tht[i] )
}
dat$prp <- prp
return(dat)
}# simulate data
dat_tl <- sim_dat4(sim_m=-0.5, sim_t='trt', sim_g='L')
dat_tm <- sim_dat4(sim_m=0.5, sim_t='trt', sim_g='M')
dat_th <- sim_dat4(sim_m=1.5, sim_t='trt', sim_g='H')
dat_cl <- sim_dat4(sim_m=-1, sim_t='cnt', sim_g='L')
dat_cm <- sim_dat4(sim_m=0, sim_t='cnt', sim_g='M')
dat_ch <- sim_dat4(sim_m=1, sim_t='cnt', sim_g='H')
dat <- rbind(dat_tl, dat_tm, dat_th, dat_cl, dat_cm, dat_ch)
dat$id <- seq(1:nrow(dat))
dat$id <- as.factor(dat$id)
dat$grp <- as.factor(dat$grp)
dat$trt <- as.factor(dat$trt)
dat <- prp_calc(dat)
anova( lm(prp ~ grp*trt, data = dat) )
anova( lm(tht ~ grp*trt, data = dat) )