Chapter 13 Time Series Visualization & Analysis
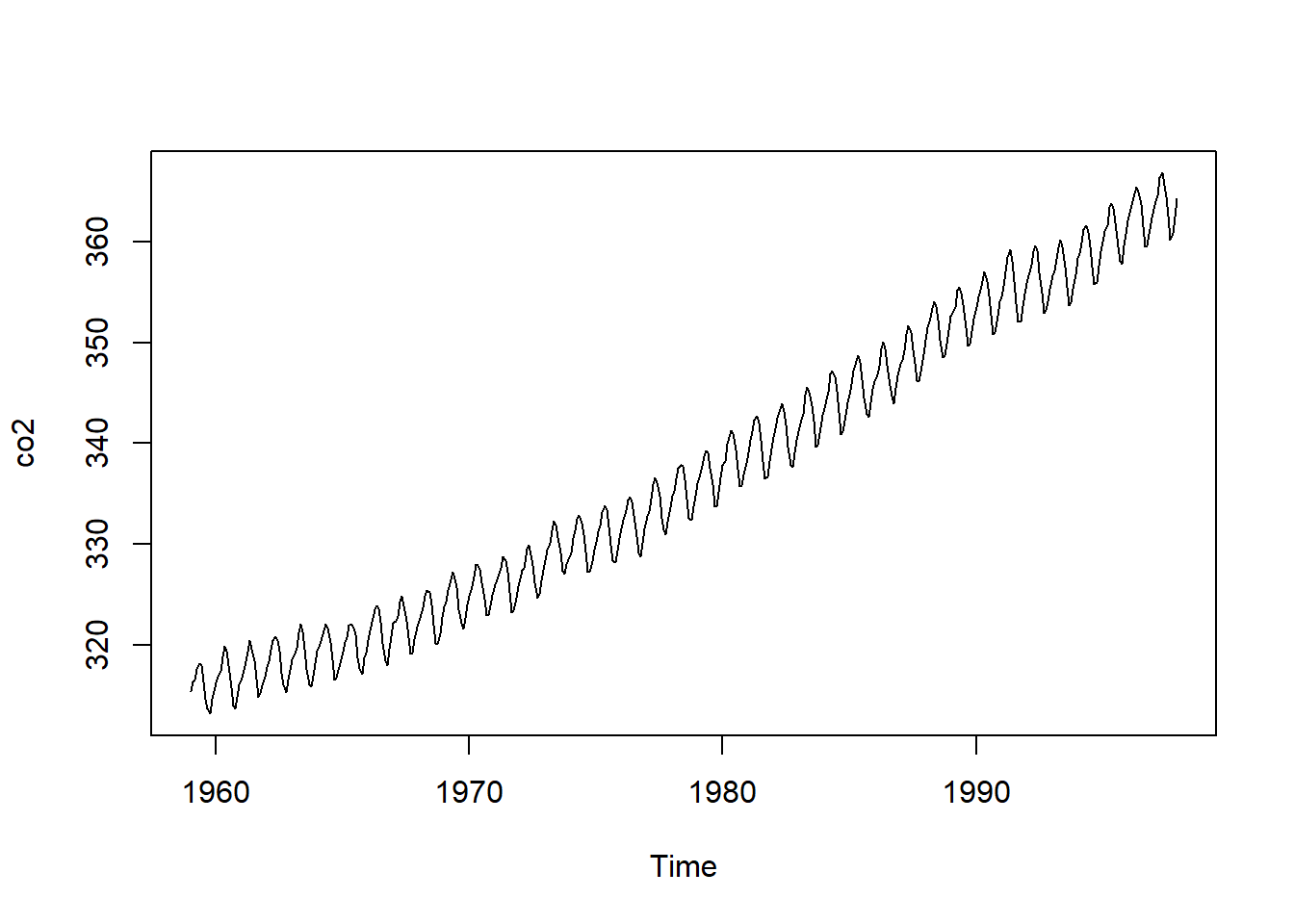
We’ve been spending a lot of time in the spatial domain in this book, but environmental data clearly also exists in the time domain, such as what’s been collected about CO2 on Mauna Loa, Hawai’i, since the late 1950s (shown above). Environmental conditions change over time; and we can sample and measure air, water, soil, geologic and biotic systems to investigate explanatory and response variables that change over time. And just as we’ve looked at multiple geographic scales, we can look at multiple temporal scales, such as the long-term Mauna Loa CO2 data above, or much finer-scale data from data loggers such as eddy covariance flux towers (Figures 13.1 and 13.2).

FIGURE 13.1: Red Clover Valley eddy covariance flux tower installation
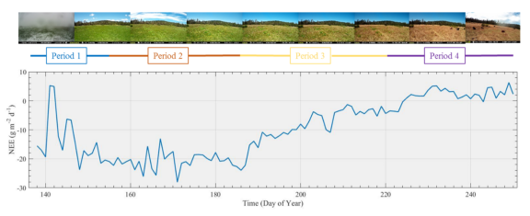
FIGURE 13.2: Loney Meadow net ecosystem exchange (NEE) results
(Blackburn, Oliphant, and Davis 2021)
In this chapter, we’ll look at a variety of methods for working with data over time. Many of these methods have been developed in the financial sector, but have many applications in environmental data science. The time series data type has been used in R for some time, and in fact a lot of the built-in data sets are time series, like the Mauna Loa CO2 data or the flow of the Nile (Figure 13.3).
plot(Nile)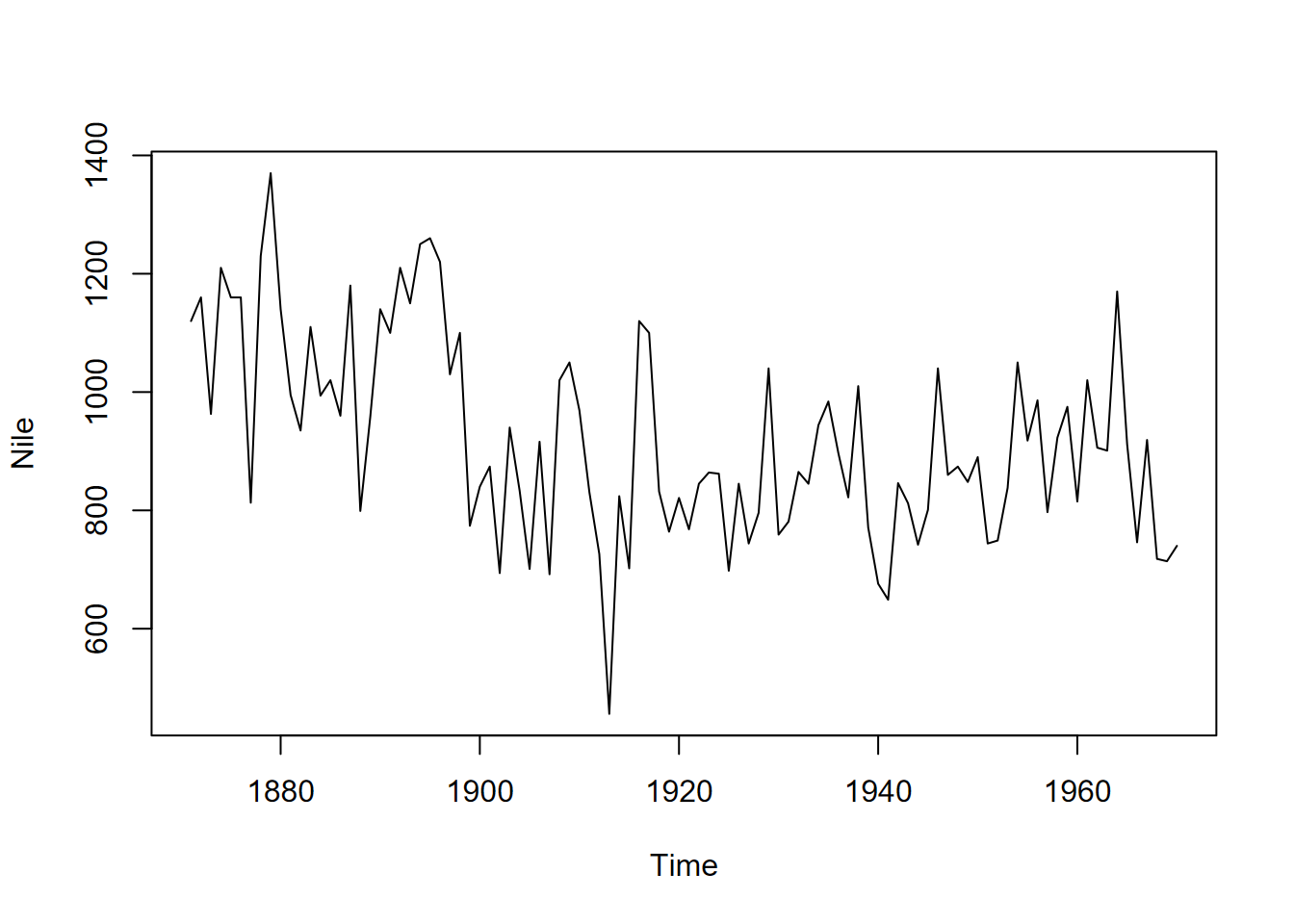
FIGURE 13.3: Time series of Nile River flows
So what’s the benefit of a time series data object? Why not just use a data frame with time stamps as a variable?
You could just work with these data as data frames, and often this is all you need. In this chapter, for instance, we won’t work exclusively with time series data objects; our data will just include variation over time. However there are advantages in R understanding how to deal with actual time series in a temporal dimension, including knowing what time unit they’re in especially if there are periodic fluctuations over that time period. This is similar to spatial data where it’s useful to maintain the geometry of our data and coordinate system they’re in. So we should learn how time series objects work and how they’re built, just as we did with spatial data.
13.1 Unit, frequency, seasonality and trend of time series
A time series can be assumed to have a time unit which we’ll create by assigning a frequency parameter, and from there comes the concept of “seasonality” where we want to consider values changing over the period of that time unit, like seasons of the year or “seasons” of the day or week or other time unit. There may also be a trend over time that we may be interested in knowing. Decomposing the time series will display all of these things, if the time series is set up right.
A good place to see the effect of seasonality is to look at the Mauna Loa CO2 data, which shows regular annual cycles, yet with a regularly increasing trend over the years. One time-series graphic, a decomposition, shows the original observations, followed by a trend line that removes the seasonal and local (short-term) random irregularities, a detrended seasonal picture which removes that trend to just show the seasonal cycles, followed by the random irregularities (Figure 13.4).
plot(decompose(co2))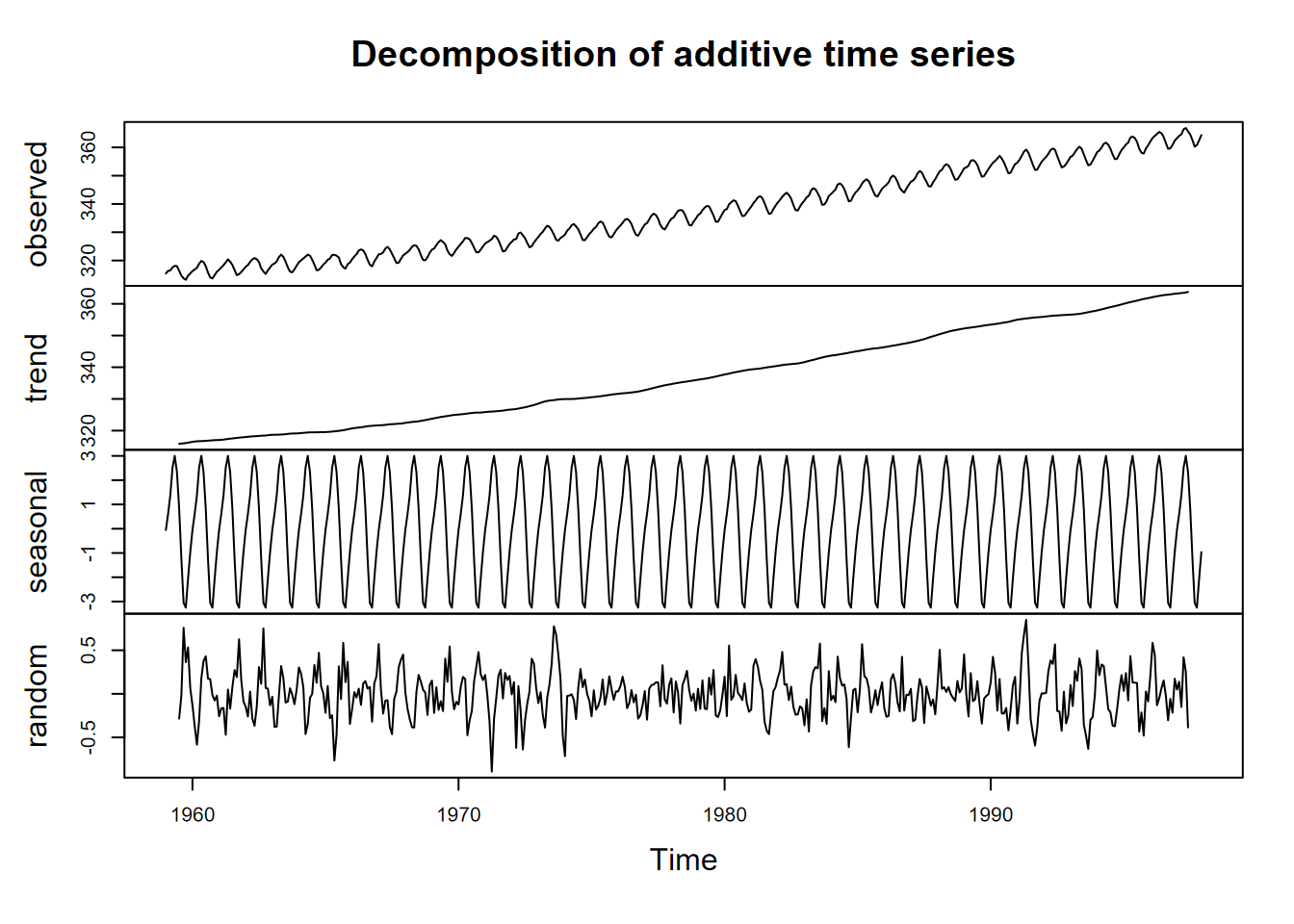
FIGURE 13.4: Decomposition of Mauna Loa CO2 data
In reading this graph, note the vertical scale: the units are all the same – parts per million – so the actual amplitude of the seasonal cycle should be the same as the annual amplitude of the observations. It’s just scaled to the chart height, which tends to exaggerate the seasonal cycles and random irregularities.
13.2 Creation of time series (ts) data
A time series (ts) can be created with the ts() function.
- the time unit can be anything
- observations must be a regularly spaced series
- time values are not normally included as a variable in the ts
We’ll build a simple time series with monthly high and low temperatures in San Francisco I just pulled off a Google search. We’ll start with just building a data frame, first converting the temperatures from Fahrenheit to Celsius (Figure 13.5).
library(tidyverse)
SFhighF <- c(58,61,62,63,64,67,67,68,71,70,64,58)
SFlowF <- c(47,48,49,50,51,53,54,55,56,55,51,47)
SFhighC <- (SFhighF-32)*5/9
SFlowC <- (SFlowF-32)*5/9
SFtempC <- bind_cols(high=SFhighC,low=SFlowC)
plot(ts(SFtempC), main="SF temperature, monthly time unit")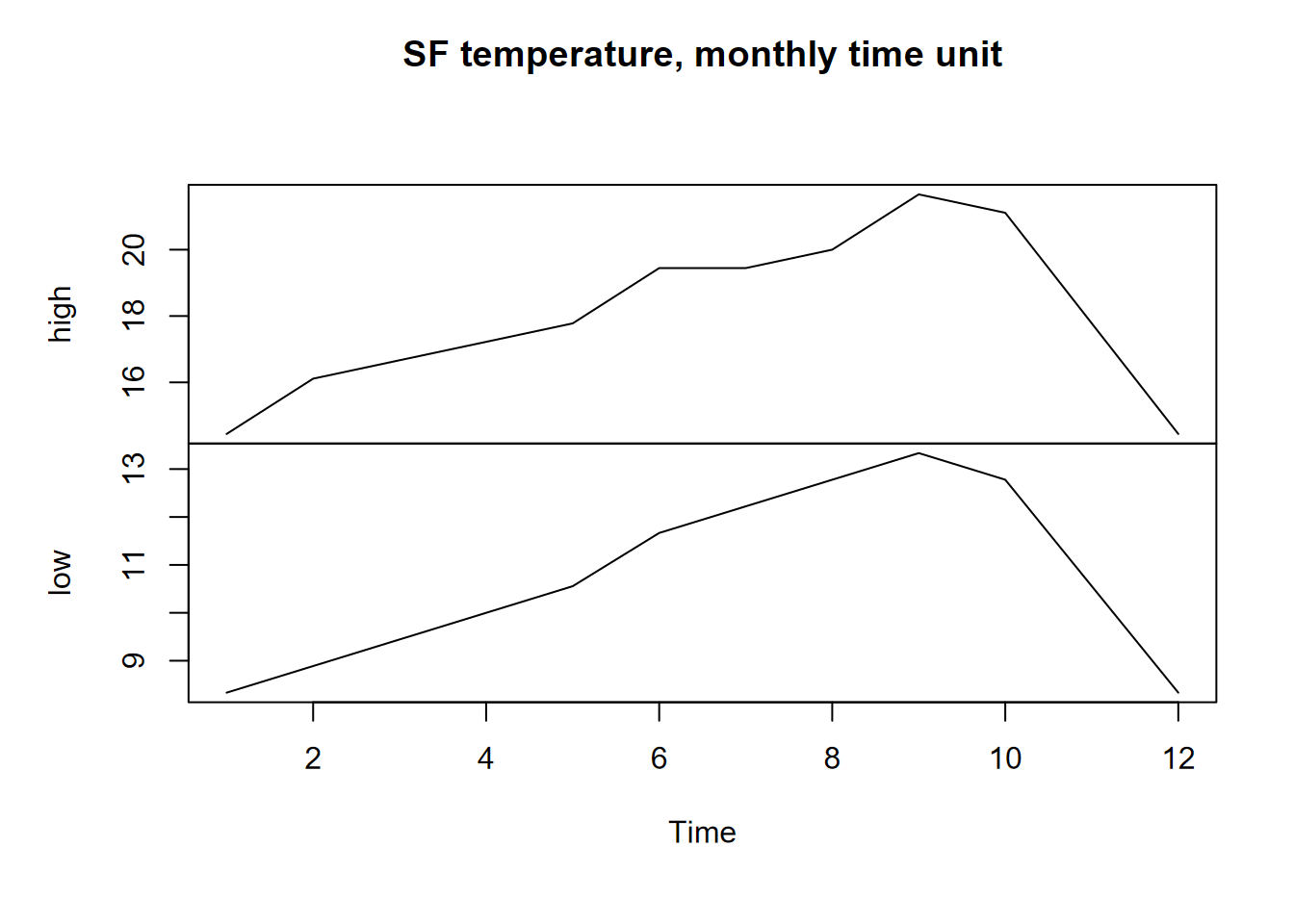
FIGURE 13.5: San Francisco monthly highs and lows as time series
13.2.1 Frequency, start and end parameters for ts()
To convert this data frame into a time series, we’ll need to provide at least a frequency setting (the default frequency=1 was applied above), which sets how many observations per time unit. The ts() function doesn’t seem to care what the time unit is in reality, however some functions figure it out, at least for an annual time unit, e.g. that 1-12 means months when there’s a frequency of 12 (Figure 13.6).
plot(ts(SFtempC, frequency=12), main="yearly time unit")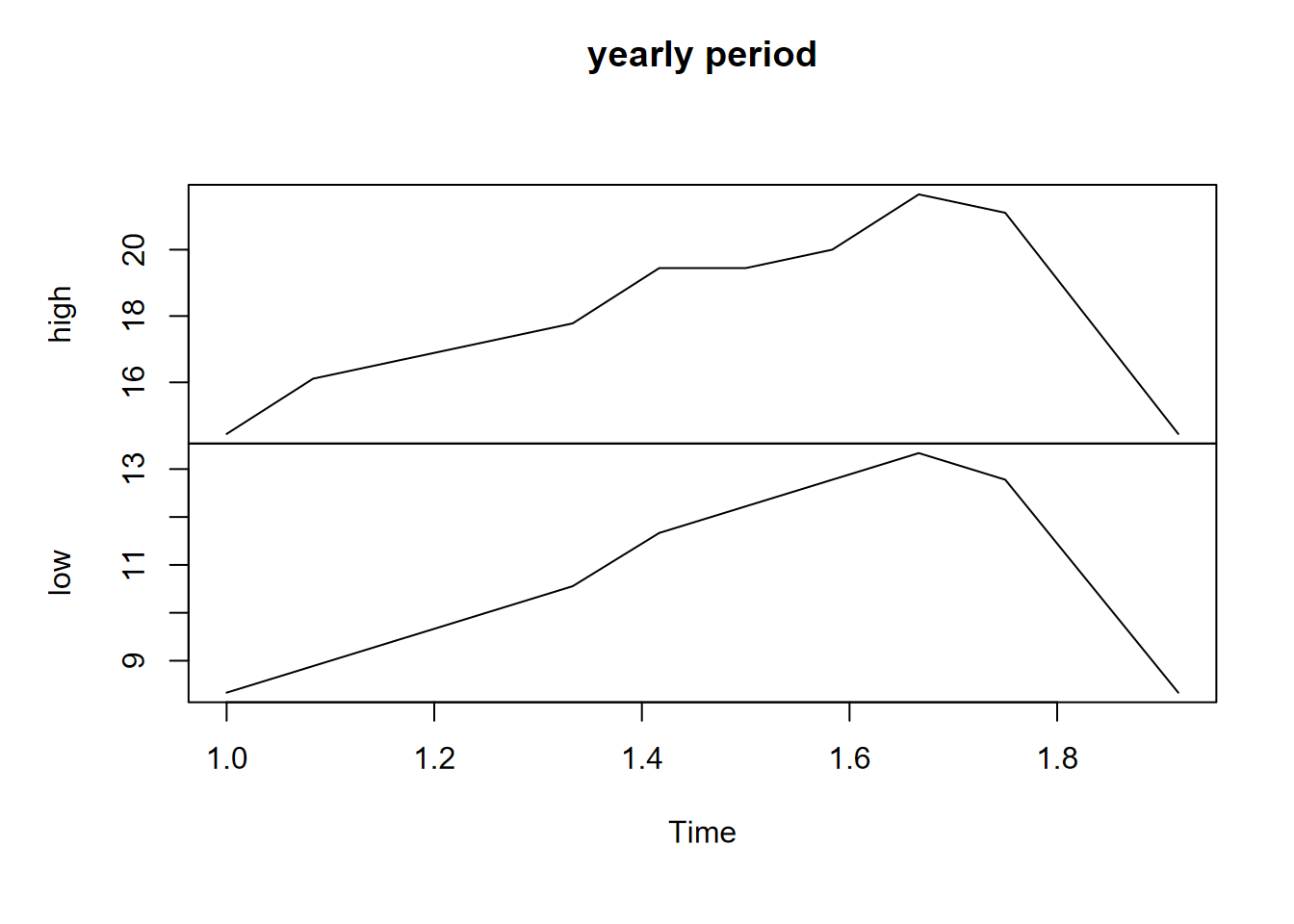
FIGURE 13.6: SF data with yearly time unit
frequency < 1
You can have a frequency less than 1. For instance, for greenhouse gases (CO2, CH4, N2O) captured from ice cores in Antarctica (Law Dome Ice Core, just south of Cape Poinsett, Antarctica (Irizarry (2019))), there are values for every 20 years, so if we want year to be the time unit, the frequency would need to be to be 1/20 years = 0.05 (Figure 13.7).
library(dslabs)
data("greenhouse_gases")
GHGwide <- pivot_wider(greenhouse_gases, names_from = gas,
values_from = concentration)
GHG <- ts(GHGwide, frequency=0.05, start=20)
plot(GHG)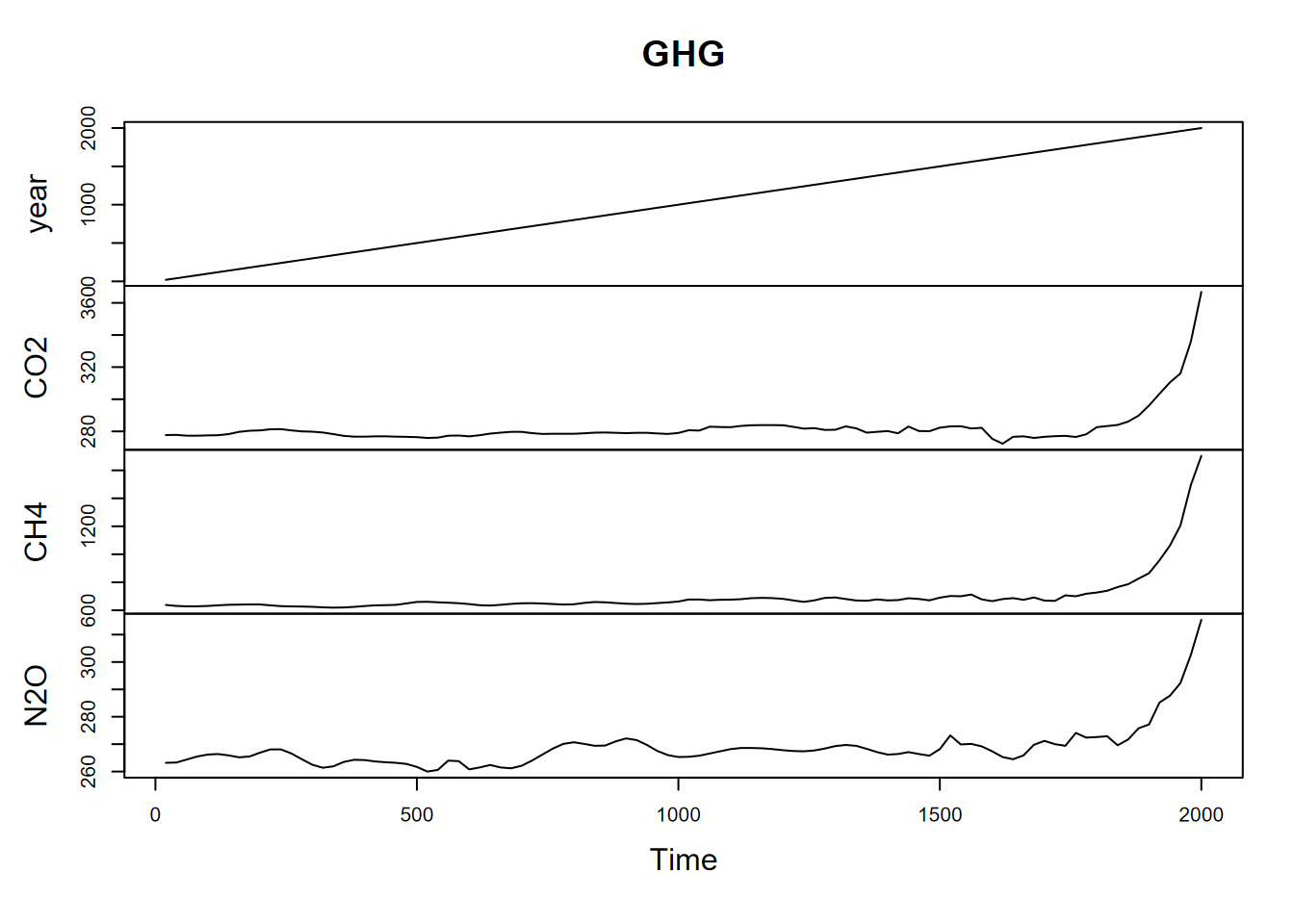
FIGURE 13.7: Greenhouse gases with 20 year observations, so 0.05 annual frequency
13.3 Associating times with time series
In the greenhouse gas data above, we not only specified frequency to define the time unit, we also provided a start value of 20 to provide an actual year to start the data with. Time series don’t normally include time stamps, so we need to specify start and end parameters. This can either a single number (if it’s the first reading during the time unit) or a vector of two numbers (the second of which is an integer), which specify a natural time unit and a number of samples into the time unit (e.g. which month during the year, or which hour, minute or second during that day, etc.)
Example with year as the time unit and monthly data, starting July 2019 and ending June 2020:
frequency=12, start=c(2019,7), end=c(2020,6)
13.3.1 Subsetting time series by times
Time series can be queried for their frequency, start, and end properties, and we’ll look at these for a built-in time series data set, sunspot.month, which has monthly values of sunspot activity from 1749 to 2013 (Figure 13.8).
plot(sunspot.month)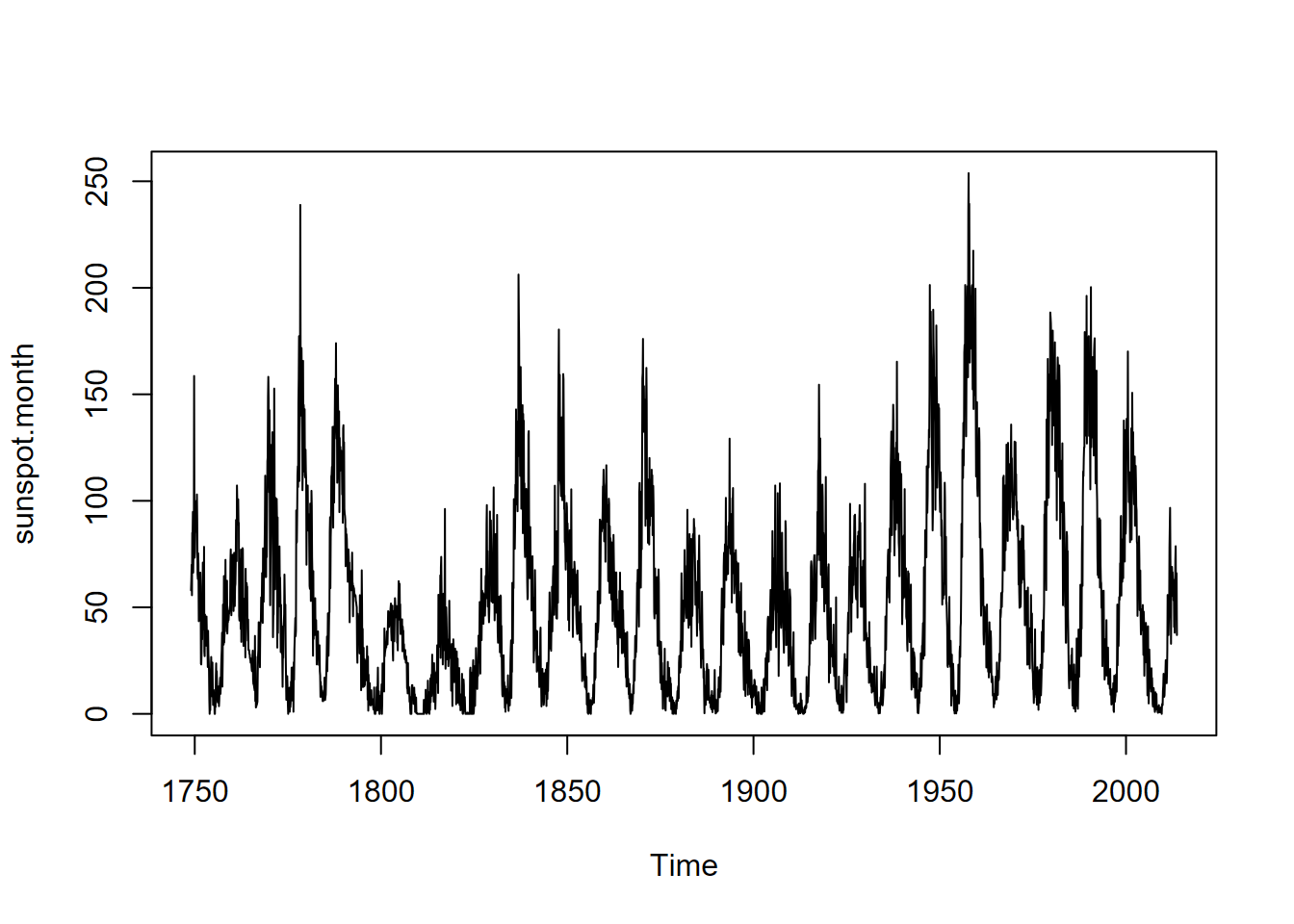
FIGURE 13.8: Monthly sunspot activity from 1749 to 2013
frequency(sunspot.month)## [1] 12start(sunspot.month)## [1] 1749 1What are the two values?
end(sunspot.month)## [1] 2013 9To subset a section of a time series, we can use the window function (Figure 13.9).
plot(window(sunspot.month, start = 1940, end = 1970))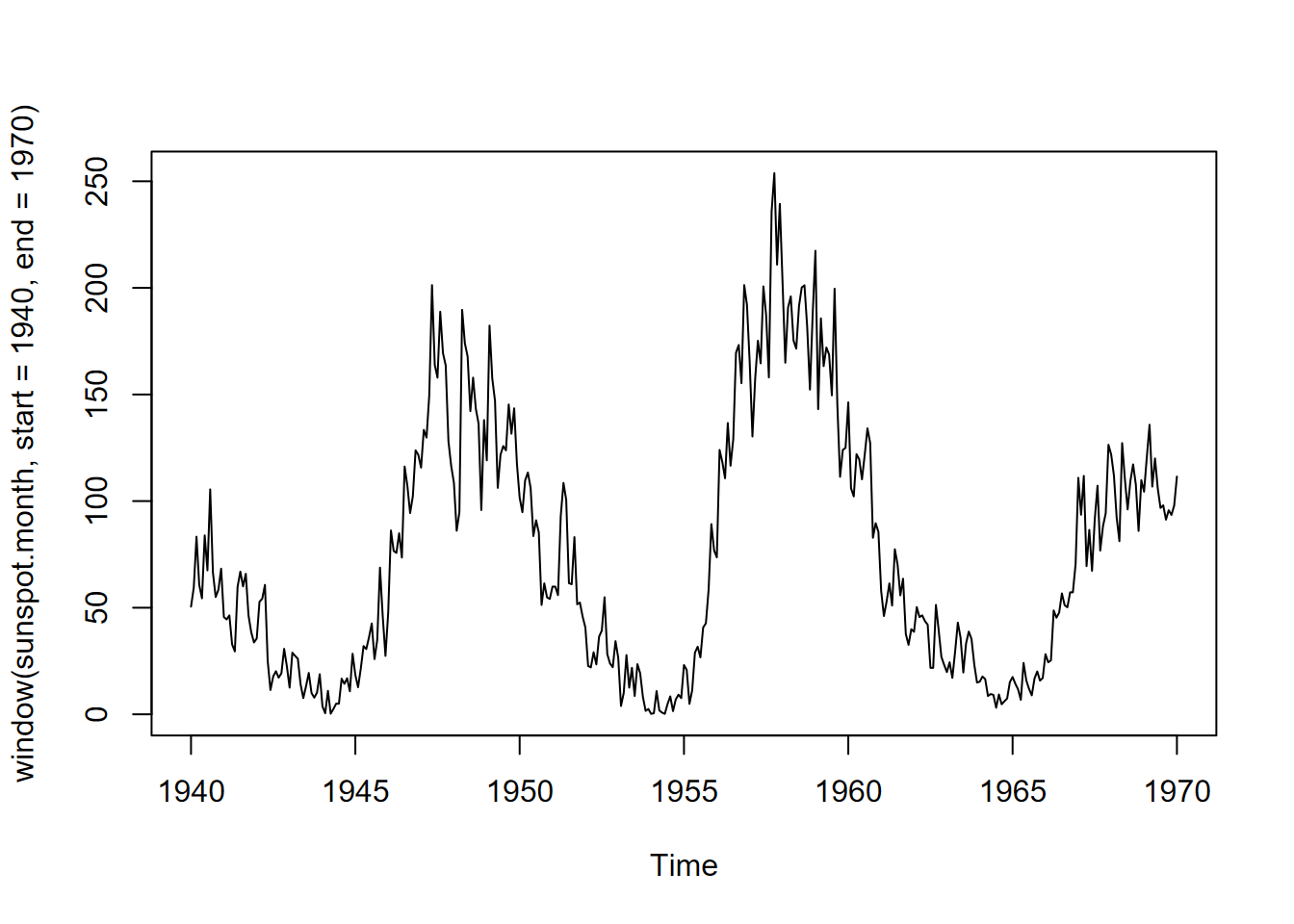
FIGURE 13.9: Monthly sunspot activity from 1940 to 1970
13.3.2 Changing the frequency to use a different period
We commonly use periods of days or years, but other options are possible. During the COVID-19 pandemic, weekly cycles of cases were commonly reported due to the weekly work cycle and weekend activities. Lunar tidal cycles are another.
Sunspot activity is known to fluctuate over about a 11 year cycle, and other than the well-known effects on radio transmission is also part of short-term climate fluctuations (so must be considered when looking at climate change). We can see the 11-year cycle in the above graphs, and we can perhaps see it more clearly in a decomposition where we set the period to the 11 year cycle.
To do this, we need to change the frequency. This is pretty easy to do, but to understand the process, first realize that we can take the original time series and create an identical copy to see how we can set the same parameters that already exist:
sunspot <- ts(sunspot.month, frequency=12, start=c(1749,1))To create one with an 11-year sunspot cycle would then require just setting an appropriate frequency:
sunspotCycles <- ts(sunspot.month, frequency=11*12, start=c(1749,1))But we might want to figure out when to start, so let’s window it for the first 20 years (Figure 13.10).
plot(window(sunspot.month, end=c(1769,12)))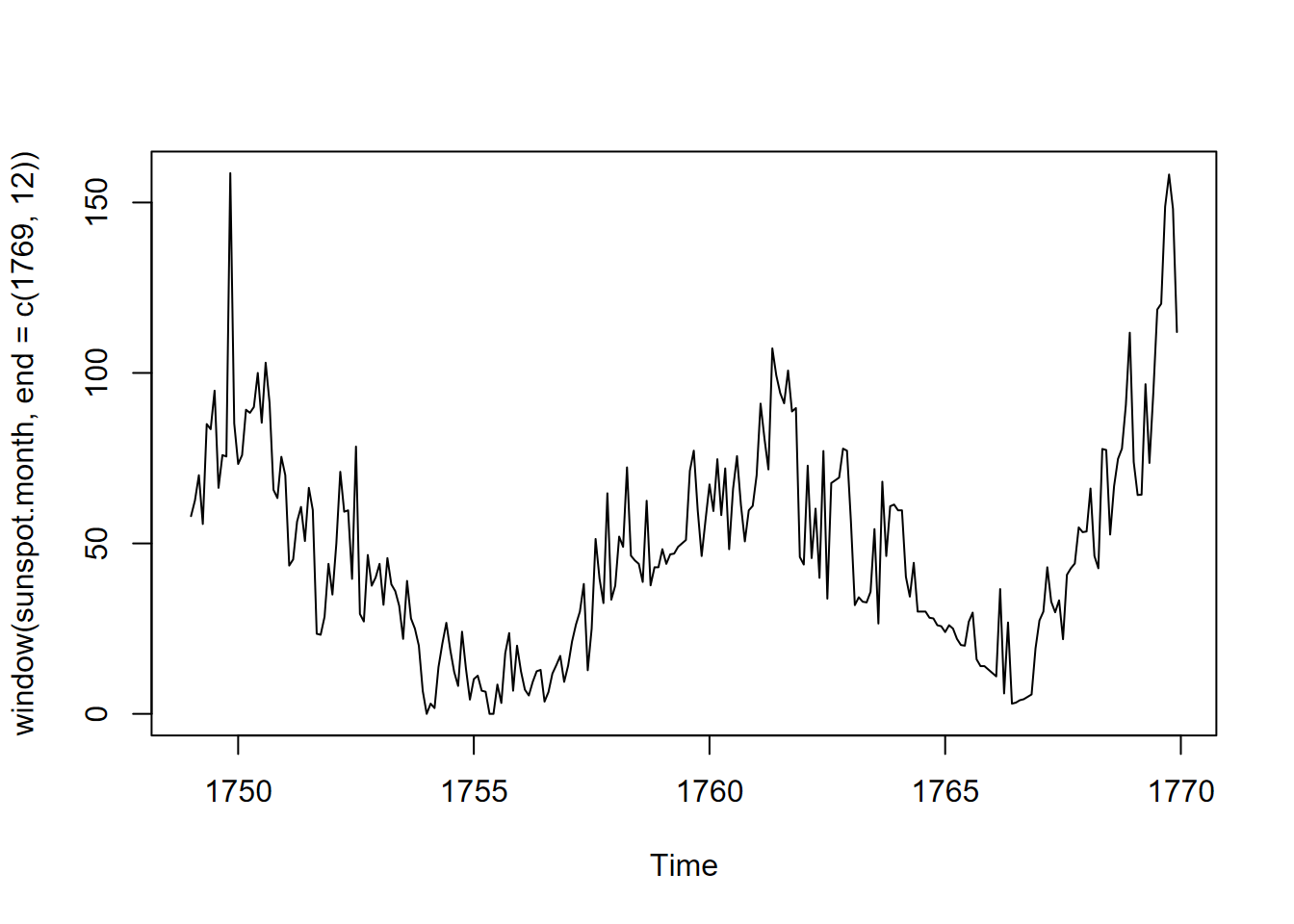
FIGURE 13.10: Sunspots of the first 20 years of data
Looks like a low point about 1755, so let’s start there:
sunspotCycles <- ts(window(sunspot.month, start=1755), frequency=11*12, start=1755)Now this is assuming that the sunspot cycle is exactly 11 years, which is probably not right, but a look at the decomposition might be useful (Figure 13.11).
plot(decompose(sunspotCycles))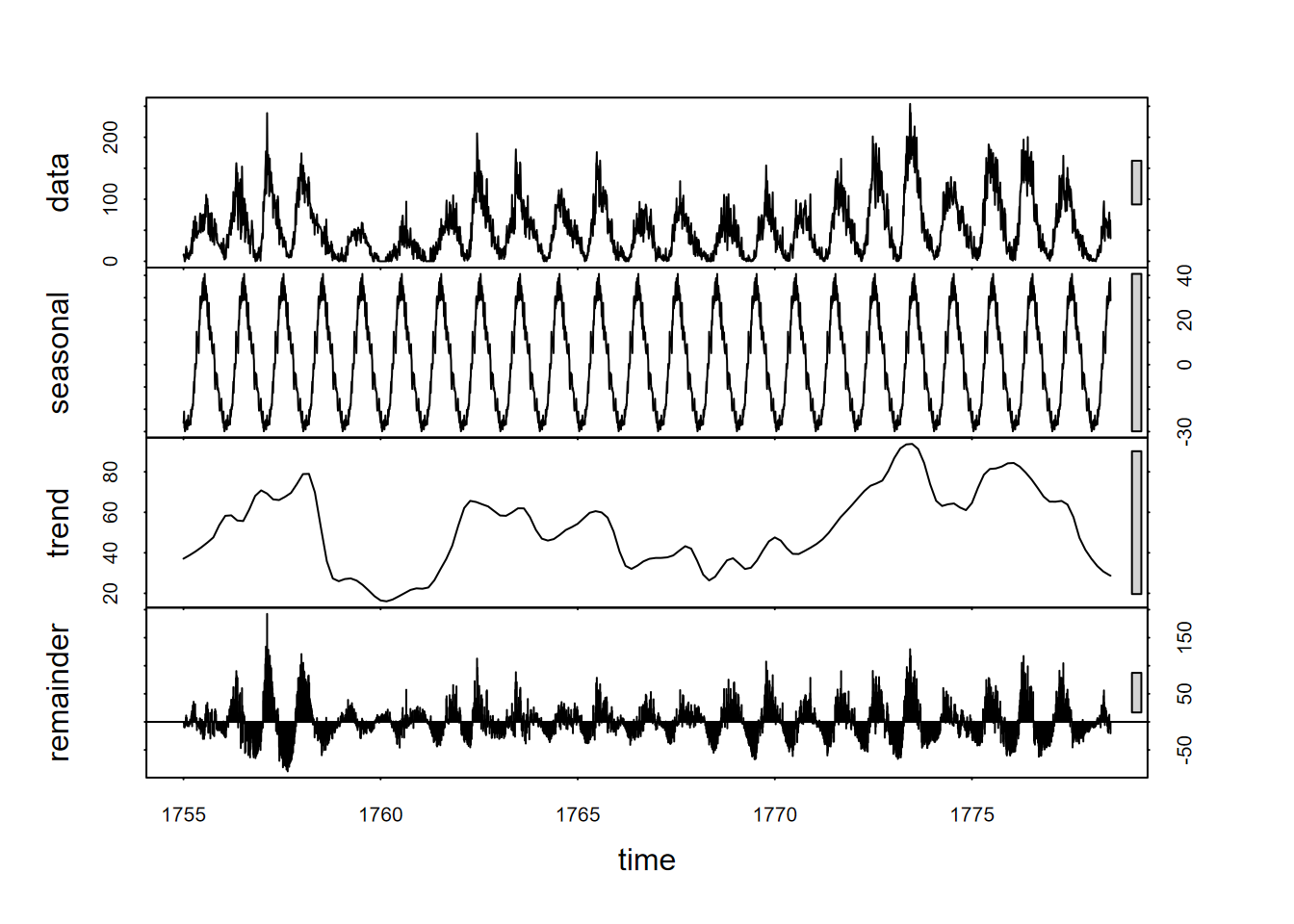
FIGURE 13.11: 11-year sunspot cycle decomposition
The seasonal picture makes things look simple, but it’s deceptive. The sunspot cycle varies significantly, and since we can see the random variation is much greater than the seasonal, this suggests that we might not be able to use this periodicity reliably. But it was worth a try, and a good demonstration of an unconventional type of period.
13.3.3 Time stamps and extensible time series
What we’ve been looking at so far are data in regularly spaced series where we just provide the date and time as when the series starts and ends. The data don’t include what we’d call time stamps as a variable, and these aren’t really needed if our data set is regularly spaced. However, there are situations where there may be missing data or imperfectly spaced data. Missing data for regularly spaced data can simply be entered as NA, but imperfectly spaced data may need a time stamp. One way is with extensible time series which we’ll look at below, but first let’s look at a couple of lubridate functions for working with days of the year and Julian dates, which can help with time stamps.
13.3.3.1 Lubridate and Julian Dates
As we saw earlier, the lubridate package makes dealing with dates a lot easier, with many routines for reading and manipulating dates in variables. If you didn’t really get a good understanding of using dates and times with lubridate, you may want to review that section earlier in the book. Dates and times can be difficult to work with, so you’ll need to make sure you know the best tools, and lubridate has the best tools.
One variation on dates it handles well are Julian dates, the number of days since some start date
- The origin (Julian date 0) can be arbitrary
- The default for julian() is 1970-01-01
For climatological work where the year is very important, we usually want the number of days of any given year.
- lubridate’s
yday()gives you this. - same thing as setting the origin for
julian()as the 12-31 of the previous year. - Useful in time series when the year is the time unit and observations are by days of the year (e.g. for climate data)
library(lubridate)
julian(ymd("2020-01-01"))## [1] 18262
## attr(,"origin")
## [1] "1970-01-01"julian(ymd("1970-01-01"))## [1] 0
## attr(,"origin")
## [1] "1970-01-01"yday(ymd("2020-01-01"))## [1] 1julian(ymd("2020-01-01"), origin=ymd("2019-12-31"))## [1] 1
## attr(,"origin")
## [1] "2019-12-31"To create a decimal yday including fractional days, here’s a function which simply uses the number of hours in a day, minutes in a day, and seconds in a day.
ydayDec <- function(d) {
yday(d)-1 + hour(d)/24 + minute(d)/1440 + second(d)/86400}
datetime <- now()
print(datetime)## [1] "2022-08-20 13:01:27 PDT"print(ydayDec(datetime), digits=12)## [1] 231.54267884113.3.3.2 Extensible time series (xts)
We’ll look at an example where we need to provide time stamps. Weekly water quality data (E. coli, total coliform, and Enterococcus bacterial counts) were downloaded from San Mateo County Health Department for San Pedro Creek, collected weekly since 2012, usually on Monday but sometimes on Tuesday, but with the date recorded in the variable SAMPLE_DATE.
First, we’ll just look at this with the data frame, and plot by SAMPLE_DATE:
library(igisci)
library(tidyverse)
SanPedroCounts <- read_csv(ex("SanPedro/SanPedroCreekBacterialCounts.csv")) %>%
filter(!is.na(`Total Coliform`)) %>%
rename(Total_Coliform = `Total Coliform`, Ecoli = `E. Coli`) %>%
dplyr::select(SAMPLE_DATE,Total_Coliform,Ecoli)To create a time series from the San Pedro Creek E. coli data, we need to use a package xts (Extensible Time Series), using SAMPLE_DATE to order the data (Figure 13.12).
library(xts); library(forecast)
Ecoli <- xts(SanPedroCounts$Ecoli, order.by = SanPedroCounts$SAMPLE_DATE)
attr(Ecoli, 'frequency') <- 52
plot(as.ts(Ecoli))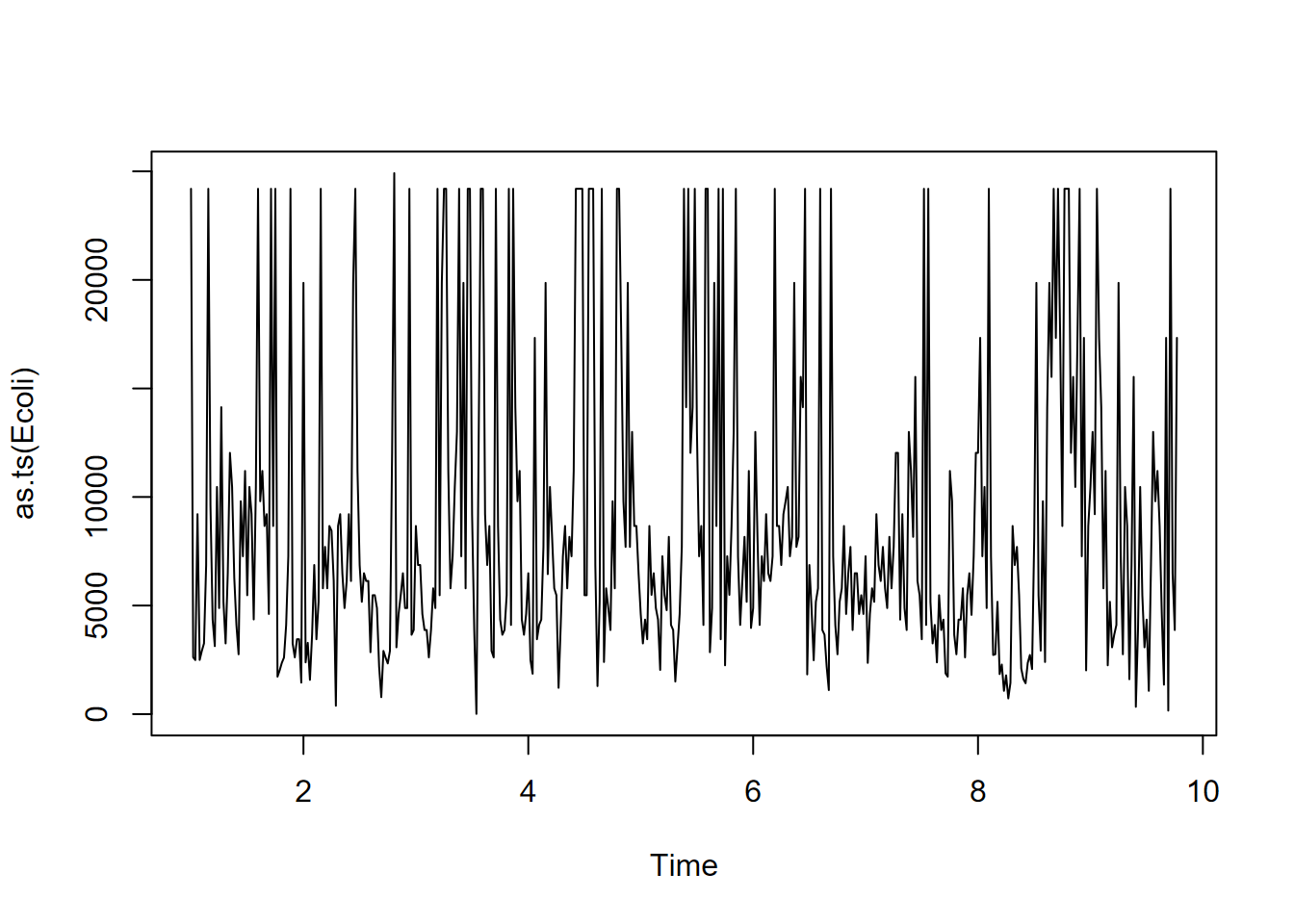
FIGURE 13.12: San Pedro Creek E. coli time series
Then a decomposition can be produced of the E. coli data (Figure 13.13). Note the use of as.ts to produce a normal time series.
plot(decompose(as.ts(Ecoli)))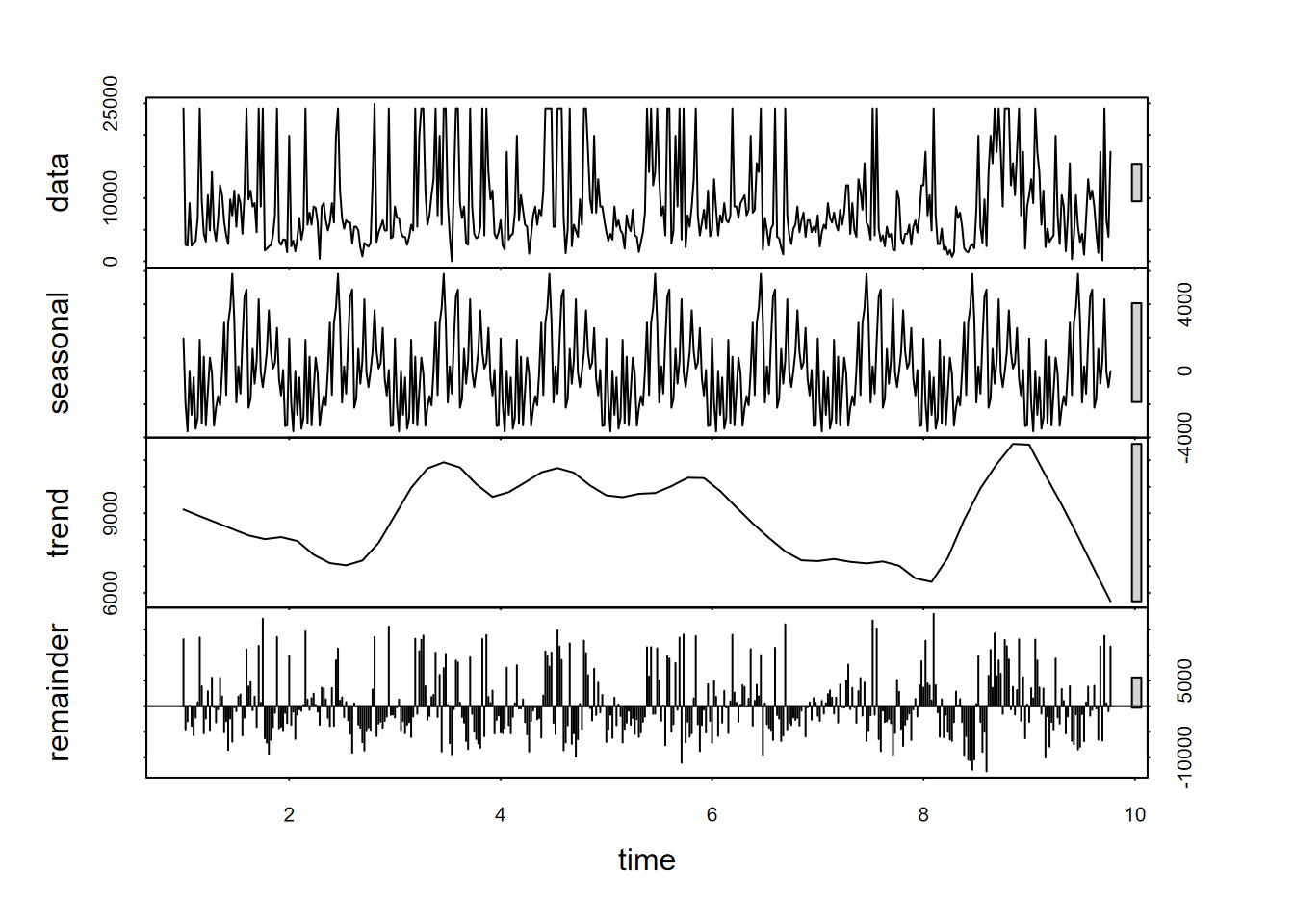
FIGURE 13.13: Decomposition of weekly E. coli data, annual period (frequency 52)
What we can see from the above decomposition is no real signal from the annual cycle (52 weeks), since while there is some tendency for peak levels (“first-flush” events) happening late in the calendar year, the timing of those first heavy rains varies significantly from year to year.
13.4 Data smoothing: moving average (ma)
The great amount of fluctuation in bacterial counts we see above makes it difficult to interpret the significant patterns. A moving average is a simple way to generalize data, using an order parameter to define the size of the moving window, which should be an odd number.
To see how it works, let’s apply a ma() to the SF data we created a few steps back. This isn’t data we need to smooth, but we can see how the function works by comparing the original and averaged data.
library(forecast)
ts(SFtempC, frequency=12)## high low
## Jan 1 14.44444 8.333333
## Feb 1 16.11111 8.888889
## Mar 1 16.66667 9.444444
## Apr 1 17.22222 10.000000
## May 1 17.77778 10.555556
## Jun 1 19.44444 11.666667
## Jul 1 19.44444 12.222222
## Aug 1 20.00000 12.777778
## Sep 1 21.66667 13.333333
## Oct 1 21.11111 12.777778
## Nov 1 17.77778 10.555556
## Dec 1 14.44444 8.333333ma(ts(SFtempC,frequency=12),order=3)## [,1] [,2]
## Jan 1 NA NA
## Feb 1 15.74074 8.888889
## Mar 1 16.66667 9.444444
## Apr 1 17.22222 10.000000
## May 1 18.14815 10.740741
## Jun 1 18.88889 11.481481
## Jul 1 19.62963 12.222222
## Aug 1 20.37037 12.777778
## Sep 1 20.92593 12.962963
## Oct 1 20.18519 12.222222
## Nov 1 17.77778 10.555556
## Dec 1 NA NAA moving average can also be applied to a vector or a variable in a data frame – doesn’t have to be a time series. For the water quality data, we’ll use a large order (15) to best clarify the significant pattern of E. coli counts (Figure 13.14).
ggplot(data=SanPedroCounts) + geom_line(aes(x=SAMPLE_DATE, y=ma(Ecoli, order=15)))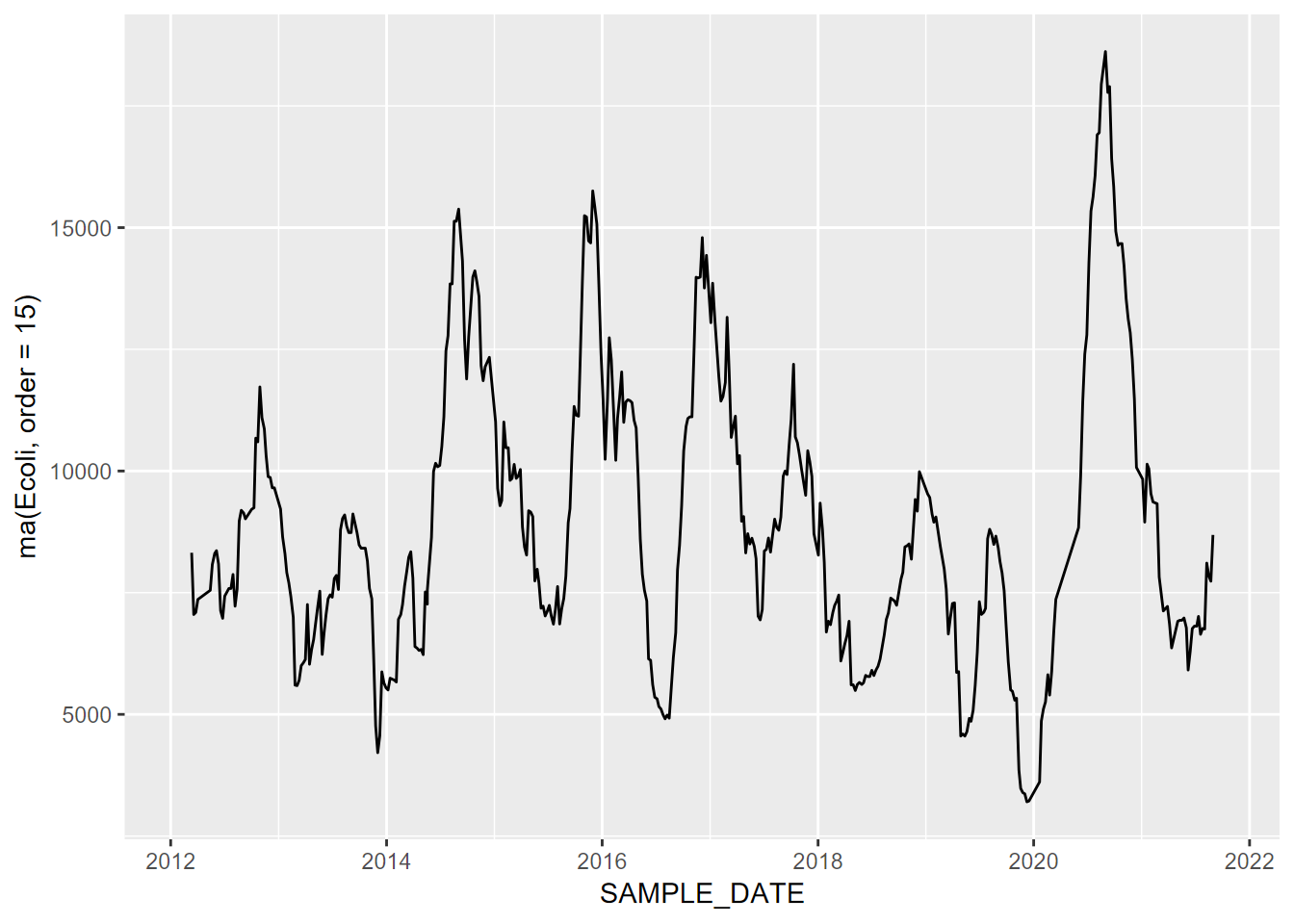
FIGURE 13.14: Moving average (order=15) of E. coli data
Moving average of CO2 data
We’ll look at another application of a moving average looking at CO2 data from Antarctic ice cores (Irizarry (2019)), first the time series itself (Figure 13.15)…
library(dslabs)
data("greenhouse_gases")
GHGwide <- pivot_wider(greenhouse_gases,
names_from = gas,
values_from = concentration)
CO2 <- ts(GHGwide$CO2,
frequency = 0.05)
plot(CO2)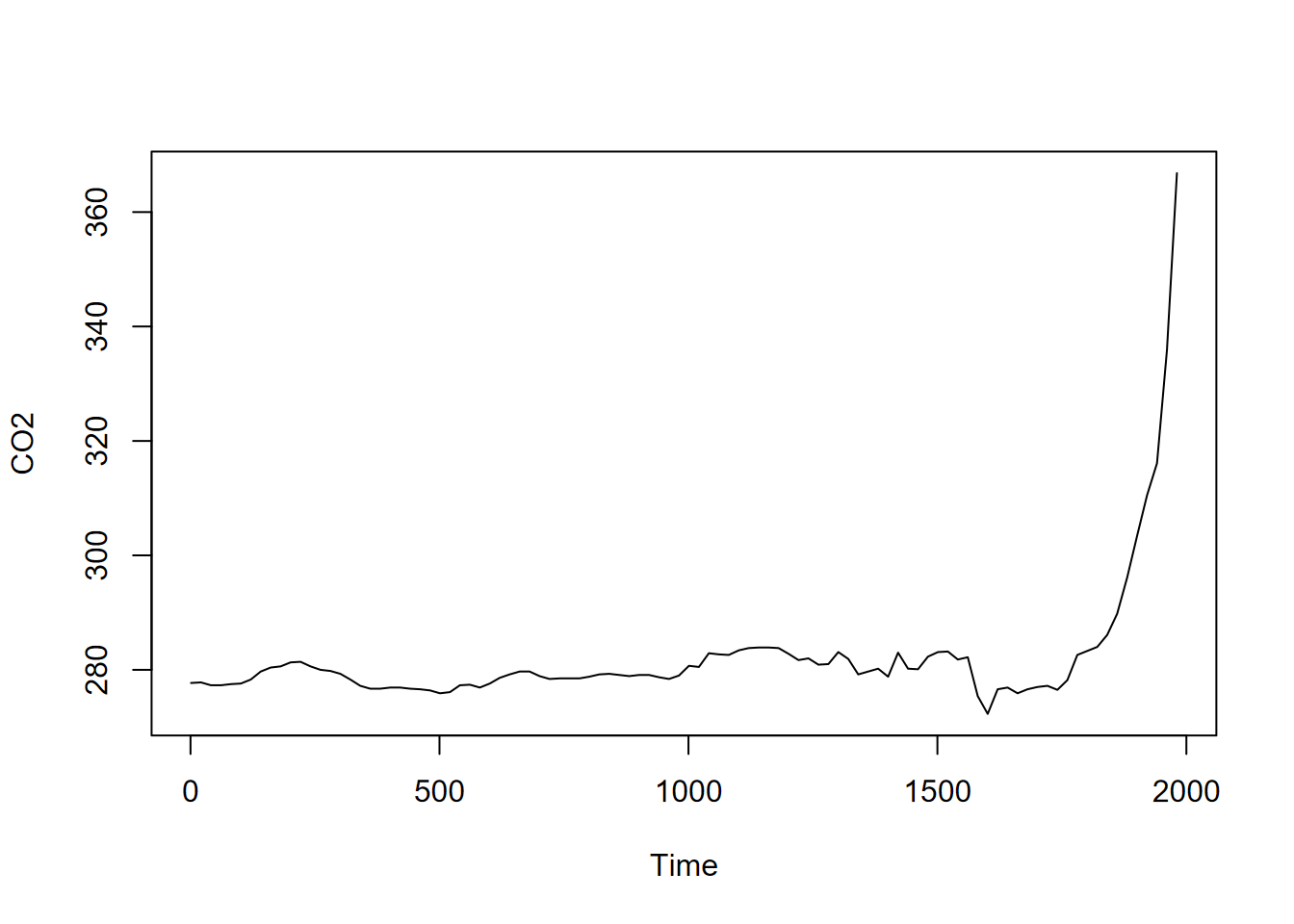
FIGURE 13.15: GHG CO2 time series
… and then the moving average with an order of 7 (Figure 13.16).
library(forecast)
CO2ma <- ma(CO2, order=7)
plot(CO2ma)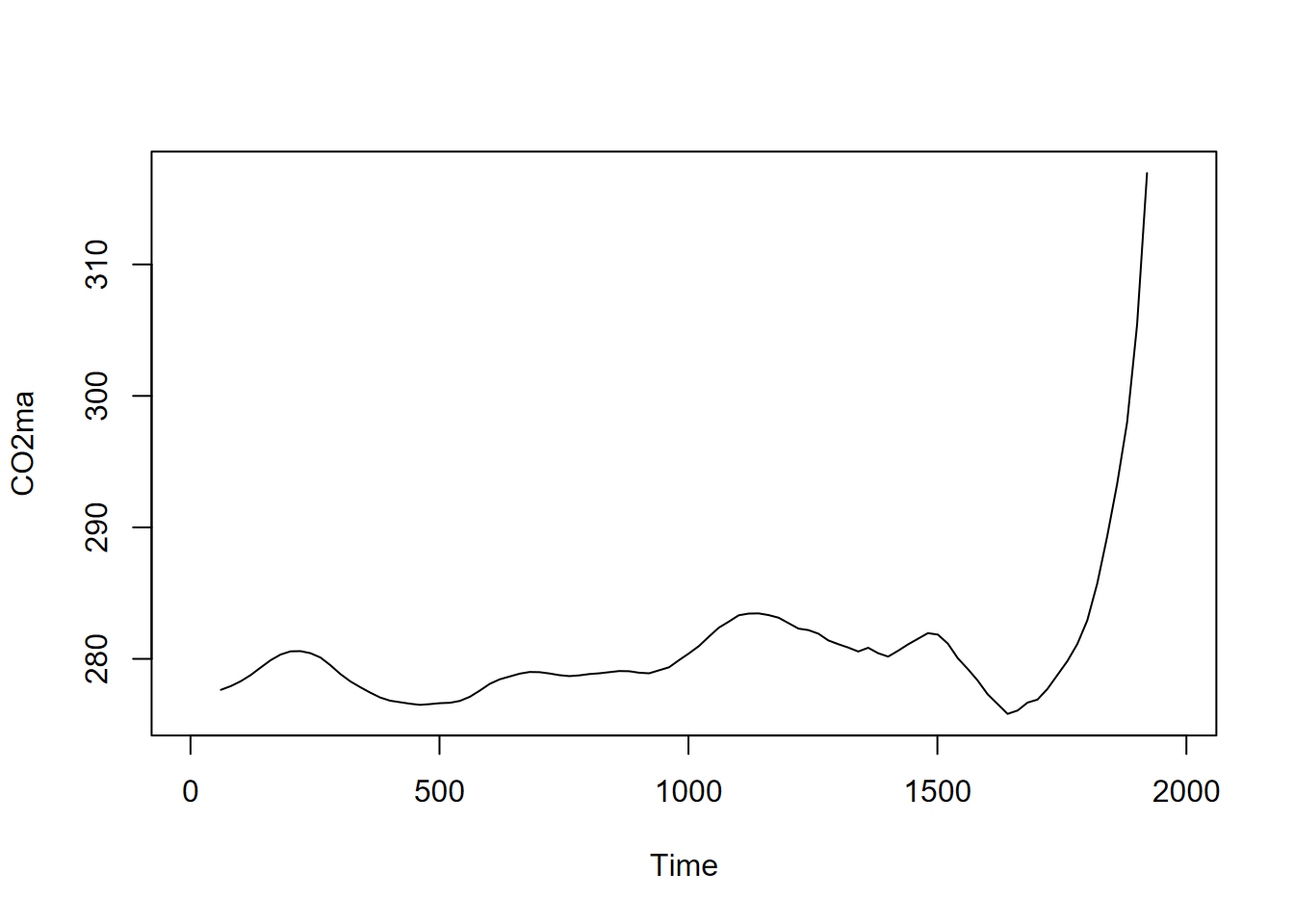
FIGURE 13.16: Moving average (order=7) of CO2 time series
For periodic data we can decompose time series into seasonal and trend signals, with the remainder left as random variation. But even for non-periodic data, we can consider random variation by simply subtracting the major signal of the moving average from the original data (Figure 13.17).
plot(CO2-CO2ma)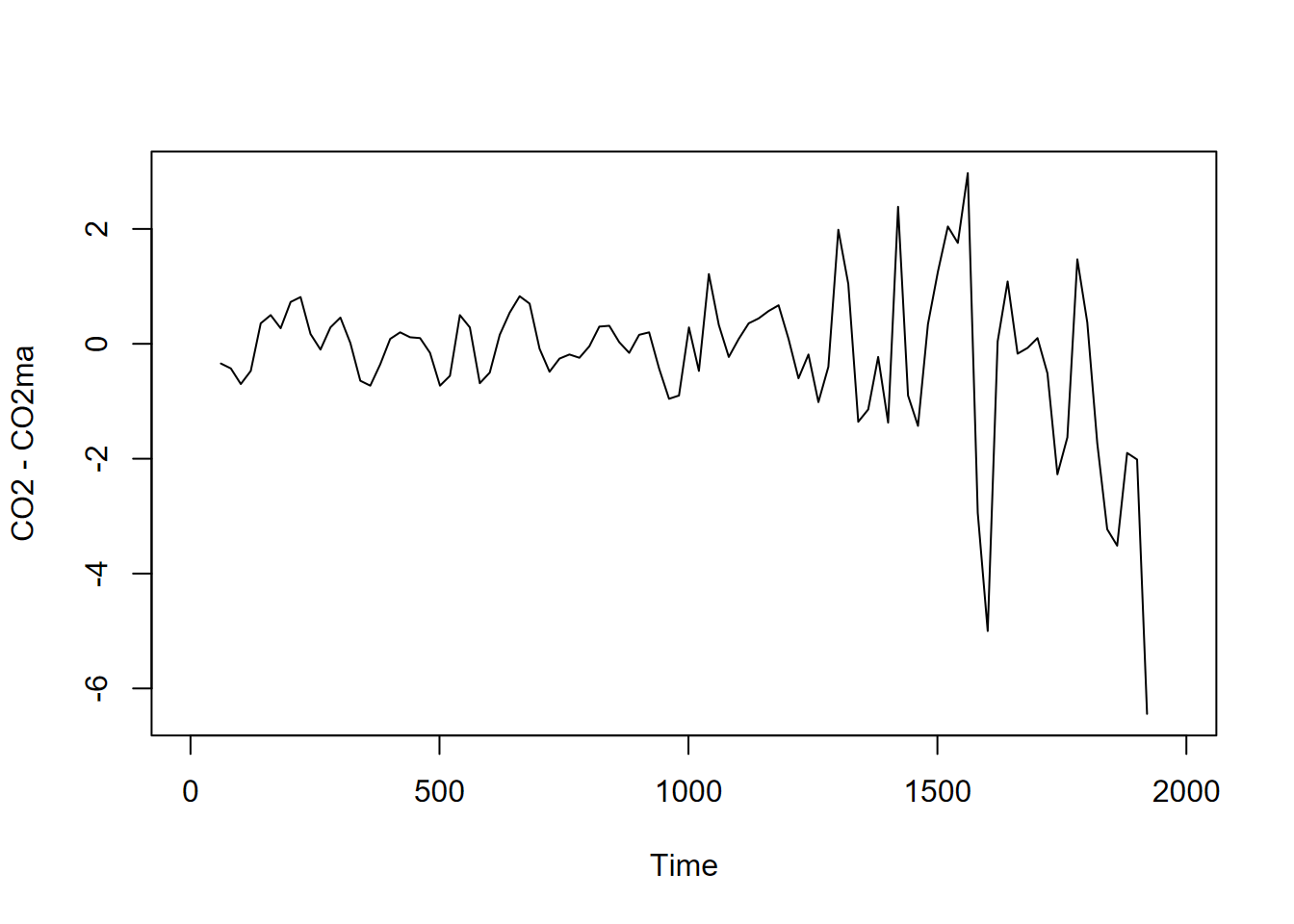
FIGURE 13.17: Random variation seen by subtracting moving average
13.5 Seasonal decomposition of Time series with Loess stl
Another type of decomposition involves local regression or “loess” by using the tool stl (seasonal decomposition of time series using loess) If s.window = "periodic" the mean is used for smoothing: the seasonal values are removed and the remainder smoothed to find the trend (Figure 13.18).
plot(stl(co2, s.window="periodic"))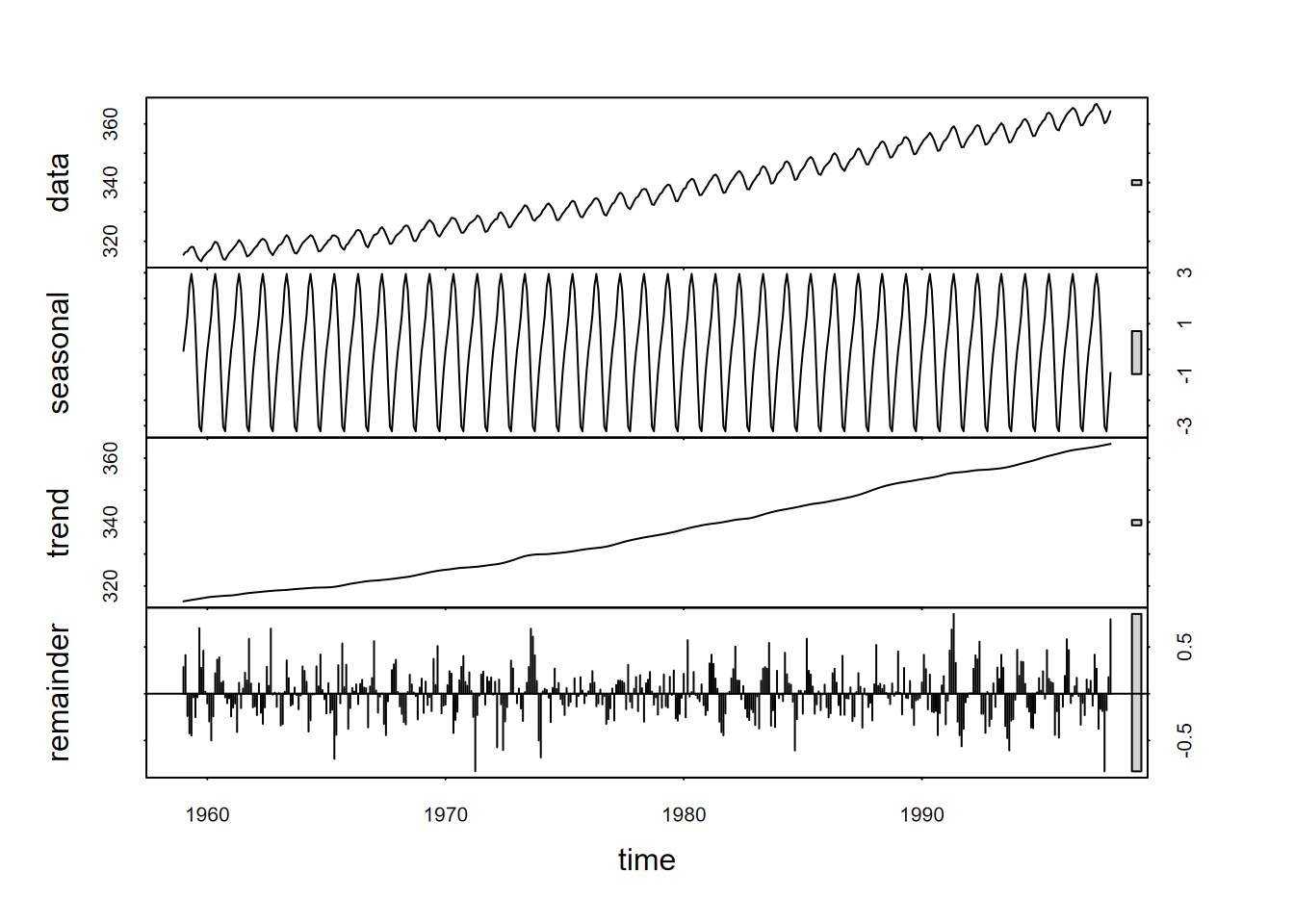
FIGURE 13.18: Seasonal deomposition of time series using loess (stl) applied to co2
As we saw above with the decomposition, the E. coli data doesn’t have a clear annual cycle; the same is apparent with the stl result here. The trend may however be telling us something about the general trend of bacterial counts over time (Figure 13.19).
plot(stl(Ecoli, s.window="periodic"))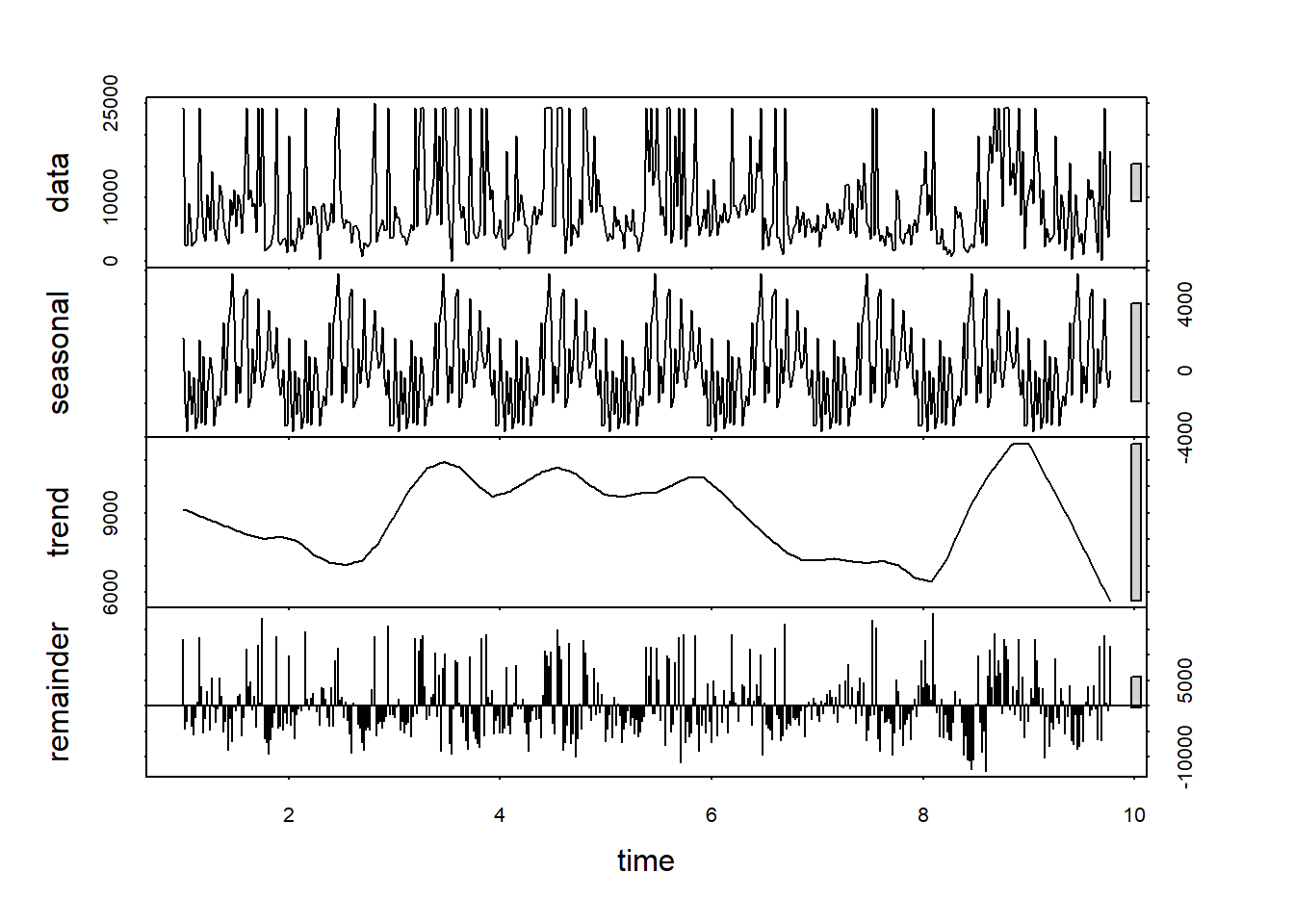
FIGURE 13.19: stl of E. coli data, with noisy annual signal
Maybe we can use a moving average to try to see a clearer pattern? We’ll need to use tseries::na.remove to remove the NA at the beginning and end of the data, and I’d probably recommend making sure we’re not creating any time errors doing this (Figure 13.20).
ecoli15 <- tseries::na.remove(as.ts(ma(Ecoli, order=15)))
plot(stl(ecoli15, s.window="periodic"))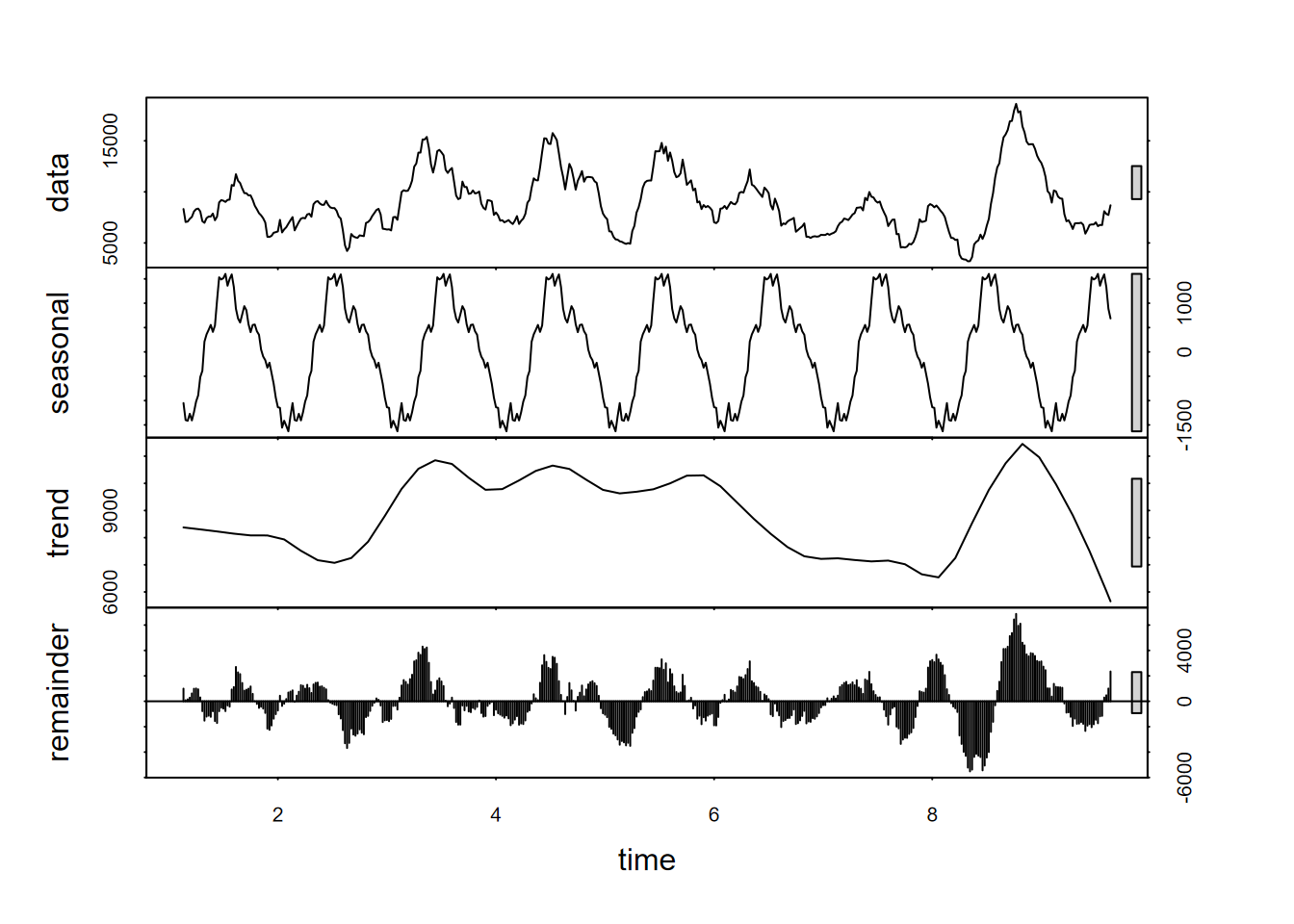
FIGURE 13.20: Decomposition using stl of a 15th-order moving average of E. coli data
For more on loess, see:
https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/loess
Another local fitting method employs a polynomial model. See:
13.6 Decomposition of data logger data: Marble Mountains
Data loggers can create a rich time series data set, with readings repeated at very short time frames (depending on the capabilities of the sensors and data logging system) and extending as far as the instrumentation allows. For a study of chemical water quality and hydrology of a karst system in the Marble Mountains of California, a spring resurgence was instrumented to measure water level, temperature, and specific conductance (a surrogate for total dissolved solids) over a 4-year period (J. D. Davis and Davis 2001) (Figures 13.21 and 13.22). The frequency was quite coarse – one sample every 2 hours – but still provides a useful data set to consider some of the time series methods we’ve been exploring (Figure 13.21).

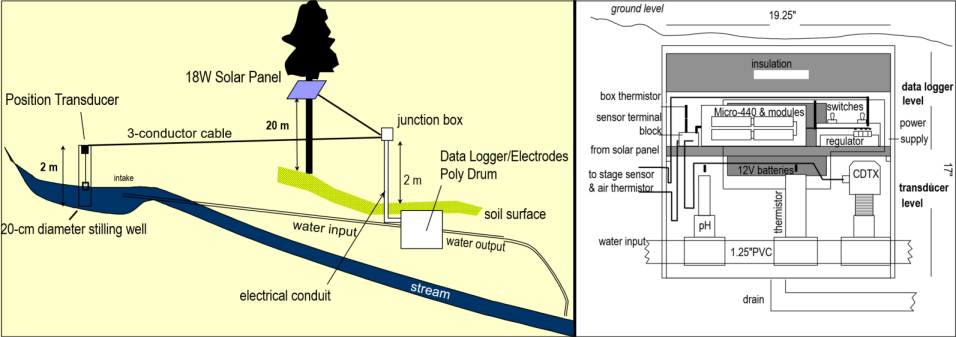
FIGURE 13.21: Marble Mountains resurgence data logger design


FIGURE 13.22: Marble Mountains resurgence data logger equipment
You might want to start by just reading the data, and having a look at it.
read_csv(ex("marbles/resurgenceData.csv"))## # A tibble: 17,537 × 9
## date time wlevelm WTemp ATemp EC InputV BTemp precip_mm
## <chr> <time> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 9/23/1994 14:00 0.325 5.69 24.7 204. 12.5 24.8 NA
## 2 9/23/1994 16:00 0.325 5.69 20.4 207. 12.5 18.7 NA
## 3 9/23/1994 18:00 0.322 5.64 16.6 207. 12.5 16.3 NA
## 4 9/23/1994 20:00 0.324 5.62 16.1 207. 12.5 14.9 NA
## 5 9/23/1994 22:00 0.324 5.65 15.6 207. 12.5 14.0 NA
## 6 9/24/1994 00:00 0.323 5.66 14.4 207. 12.5 13.3 NA
## 7 9/24/1994 02:00 0.323 5.63 13.9 207. 12.5 12.8 NA
## 8 9/24/1994 04:00 0.322 5.65 13.1 207. 12.5 12.3 NA
## 9 9/24/1994 06:00 0.319 5.61 11.8 207. 12.5 11.9 NA
## 10 9/24/1994 08:00 0.321 5.66 13.1 207. 12.4 11.6 NA
## # … with 17,527 more rowsWhat we can see is that the date_time stamps show that measurements are every 2 hours. This will help us set the frequency for an annual period. The start time is 1994-09-23 14:00:00, so we need to provide that information as well. Note the computations used to do this (I first worked out that the yday for 9/23 was 266) (Figure 13.23).
resurg <- read_csv(ex("marbles/resurgenceData.csv")) %>%
mutate(date_time = mdy_hms(paste(date, time))) %>%
dplyr::select(ATemp, BTemp, wlevelm, EC, InputV) # removed date_time,
resurgTS <- ts(resurg, frequency = 12*365, start = c(1994, 266*12+7))
plot(resurgTS)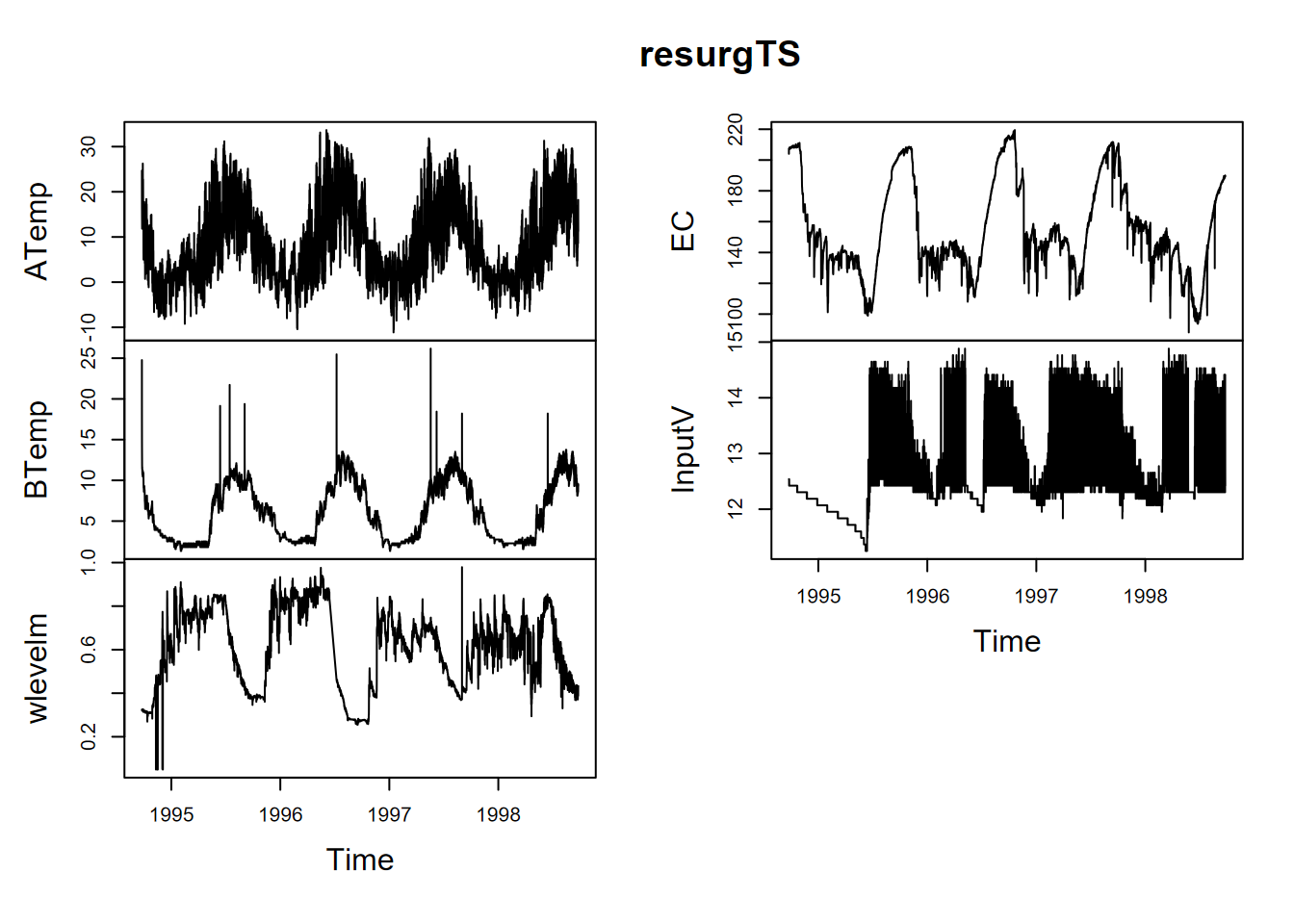
FIGURE 13.23: Data logger data from the Marbles resurgence
In this study, water level water level has an annual seasonality that might be best understood by decomposition (Figure 13.24).
library(tidyverse); library(lubridate)
resurg <- read_csv(ex("marbles/resurgenceData.csv")) %>%
mutate(date_time = mdy_hms(paste(date, time))) %>%
dplyr::select(date_time, ATemp, BTemp, wlevelm, EC, InputV)
wlevelm <- ts(resurg$wlevelm, frequency = 12*365,
start = c(1994, 266*12+7))
fit <- stl(wlevelm, s.window="periodic")
plot(fit)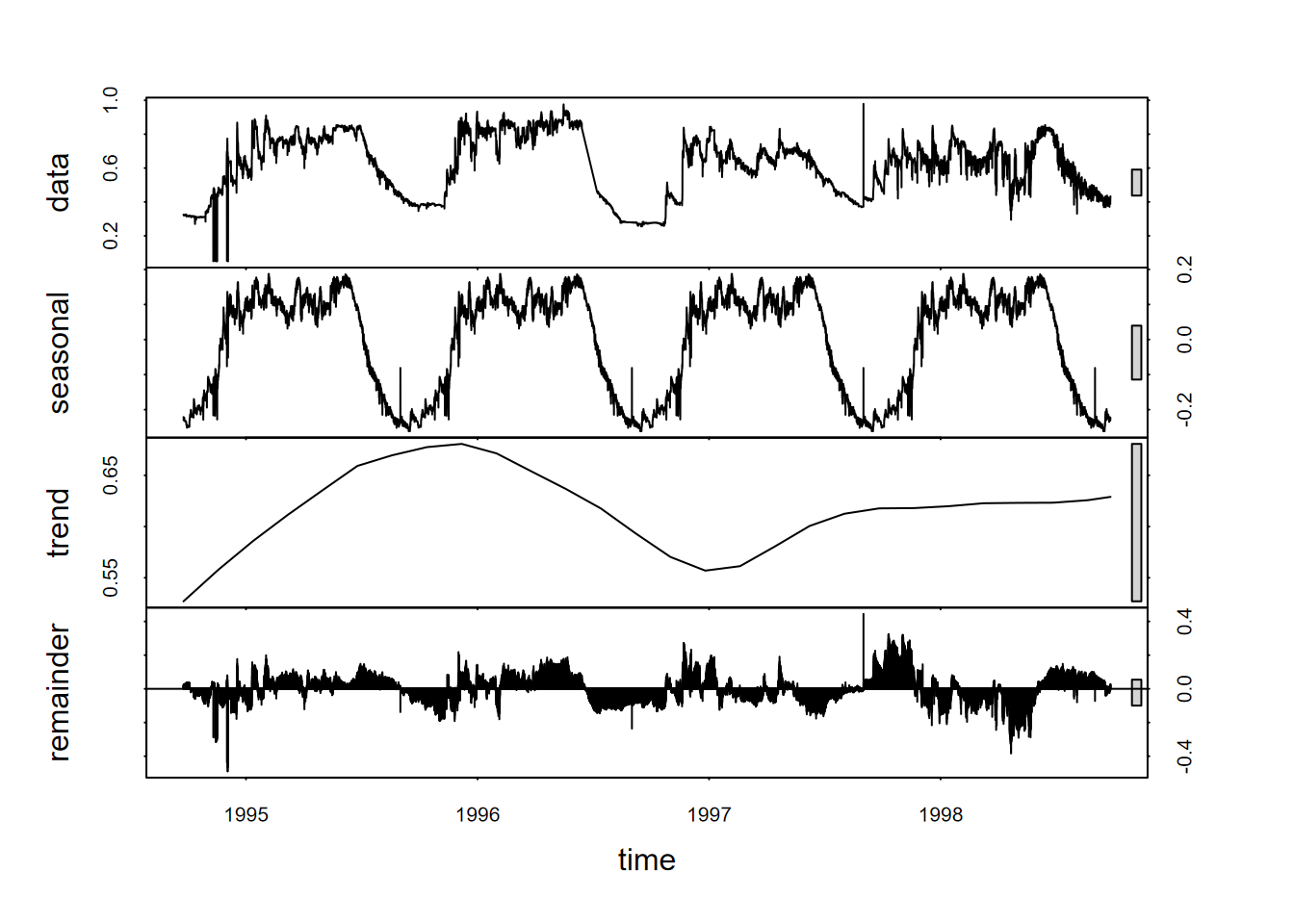
FIGURE 13.24: stl decomposition of Marbles water level time series
13.7 Facet graphs for comparing variables over time
We’ve just been looking at a data set with multiple variables, and often what we’re just needing to do is to create a combination of graphs of these variables over a common timeframe on the x axis. We’ll look at some flux data from Loney Meadow (Figure 13.25).

FIGURE 13.25: Flux tower installed at Loney Meadow, 2016. Photo credit: Darren Blackburn
The flux tower data were collected at a high frequency for eddy covariance processing where 3D wind speed data are used to model the movement of atmospheric gases, including CO2 flux driven by photosynthesis and respiration processes. Note that the sign convention of CO2 flux is that positive flux is release to the atmosphere, which might happen when less photosynthesis is happening but respiration and other CO2 releases continue, while a negative flux might happen when more photosynthesis is capturing more CO2.
A spreadsheet of 30-minute summaries from 17 May to 6 September can be found in the igisci extdata folder as "meadows/LoneyMeadow_30minCO2fluxes_Geog604.xls", and includes data on photosynthetically active radiation (PAR), net radiation (Qnet), air temperature, relative humidity, soil temperature at 2 and 10 cm depth, wind direction, wind speed, rainfall, and soil volumetric water content (VWC). There’s clearly a lot more we can do with these data (see Blackburn, Oliphant, and Davis (2021)), but for now we’ll just create a facet graph from the multiple variables collected.
library(igisci)
library(readxl); library(tidyverse); library(lubridate)
vnames <- read_xls(ex("meadows/LoneyMeadow_30minCO2fluxes_Geog604.xls"),
n_max=0) %>% names()
vunits <- read_xls(ex("meadows/LoneyMeadow_30minCO2fluxes_Geog604.xls"),
n_max=0, skip=1) %>% names()
Loney <- read_xls(ex("meadows/LoneyMeadow_30minCO2fluxes_Geog604.xls"),
skip=2, col_names=vnames) %>%
rename(DecimalDay = `Decimal time`,
YDay = `Day of Year`,
Hour = `Hour of Day`,
CO2flux = `CO2 Flux`,
Tsoil2cm = `Tsoil 2cm`,
Tsoil10cm = `Tsoil 10cm`) %>%
mutate(datetime = as_date(DecimalDay, origin="2015-12-31"))The time unit we’ll want to use for time series is going to be days, and we can also then look at the data over time, and a group_by-summarize process by days will give us a generalized picture of changes over the collection period reflecting phenological changes from first exposure after snowmelt through the maximum growth period and through the major senescence period of late summer. We’ll look at a faceted graph from a pivot_long table (Figure 13.26).
LoneyDaily <- Loney %>%
group_by(YDay) %>%
summarize(CO2flux = mean(CO2flux),
PAR = mean(PAR),
Qnet = mean(Qnet),
Tair = mean(Tair),
RH = mean(RH),
Tsoil2cm = mean(Tsoil2cm),
Tsoil10cm = mean(Tsoil10cm),
wdir = mean(wdir),
wspd = mean(wspd),
Rain = mean(Rain),
VWC = mean(VWC))
LoneyDailyLong <- LoneyDaily %>%
pivot_longer(cols = CO2flux:VWC,
names_to="parameter",
values_to="value") %>%
filter(parameter %in% c("CO2flux", "Qnet", "Tair", "RH", "Tsoil10cm", "VWC"))
p <- ggplot(data = LoneyDailyLong, aes(x=YDay, y=value)) +
geom_line()
p + facet_grid(parameter ~ ., scales = "free_y")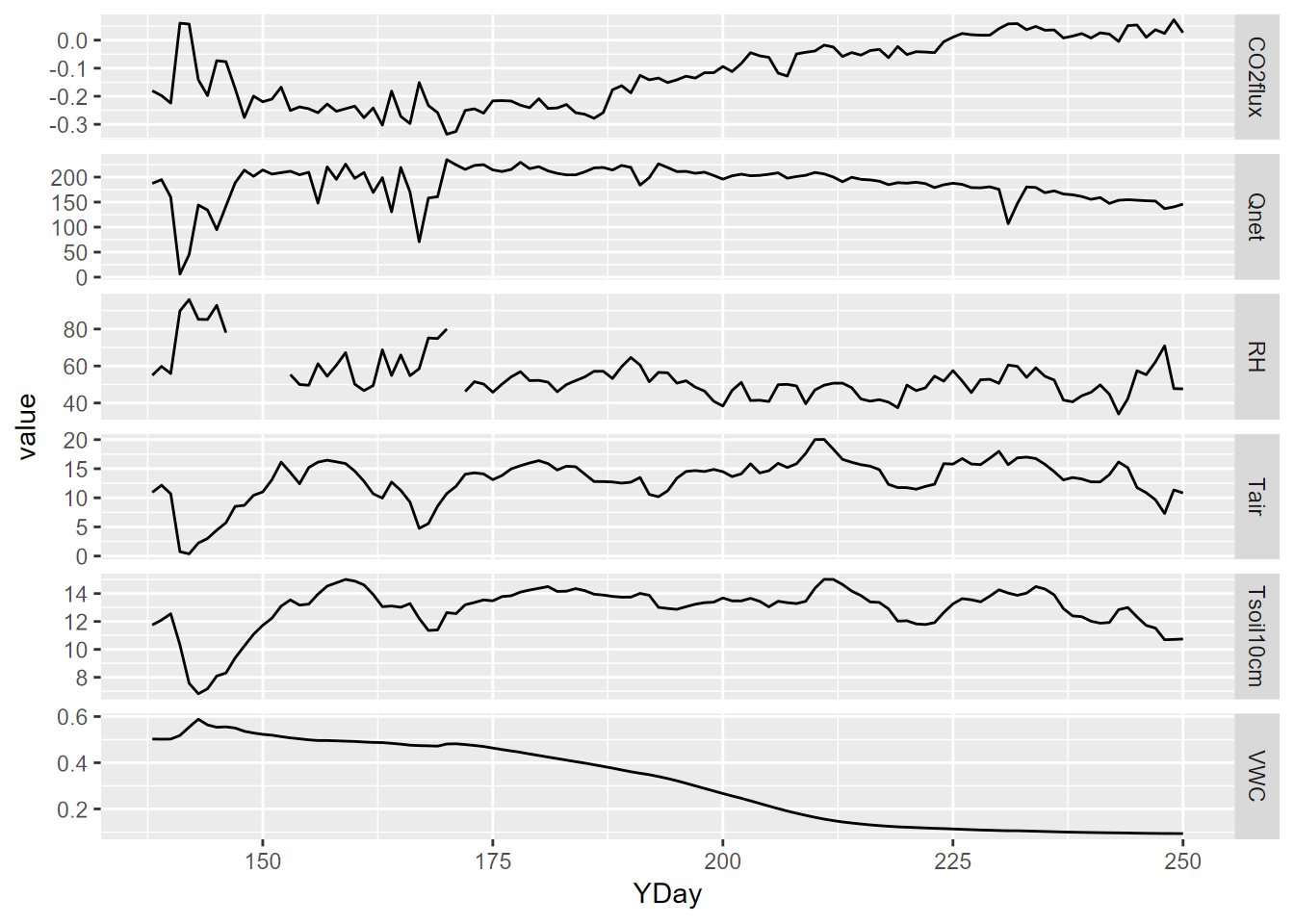
FIGURE 13.26: Facet plot with free y scale of Loney flux tower parameters
13.8 Lag regression
Lag regression is like a normal linear model, but there’s a timing difference, or lag, between the explanatory and response variables. We have used this method to compare changes in snow melt in a Sierra Nevada watershed and changes in reservoir inflows downstream (Powell et al. (2011)).
Another good application of lag regression is comparing solar radiation and temperature. We’ll explore solar radiation and temperature data over an 8-day period for Bugac, Hungary, and Manaus, Brazil, maintained by the European Fluxes Database (European Fluxes Database, n.d.). These data are every half hour, but let’s have a look. You could navigate to the spreadsheet and open it in Excel, and I would recommend it – you should know where the extdata are stored on your computer – since this is the easiest way to see that there are two worksheets. With that worksheet naming knowledge, we can also have a quick look in R:
library(readxl)
read_xls(ex("ts/SolarRad_Temp.xls"), sheet="BugacHungary")## # A tibble: 17,521 × 7
## Year `Day of Yr` Hr SolarRad Tair ...6 ...7
## <chr> <chr> <chr> <chr> <chr> <lgl> <chr>
## 1 YYYY DOY 0-23.5 W m^-2 deg C NA Site details
## 2 2006 1 0.5 0 0.55000001192092896 NA http://www.icos-…
## 3 2006 1 1 0 0.56999999284744263 NA <NA>
## 4 2006 1 1.5 0 0.82999998331069946 NA <NA>
## 5 2006 1 2 0 1.0399999618530273 NA <NA>
## 6 2006 1 2.5 0 1.1699999570846558 NA <NA>
## 7 2006 1 3 0 1.2000000476837158 NA <NA>
## 8 2006 1 3.5 0 1.2300000190734863 NA <NA>
## 9 2006 1 4 0 1.2599999904632568 NA <NA>
## 10 2006 1 4.5 0 1.2599999904632568 NA <NA>
## # … with 17,511 more rowsIndeed the readings are every half hour, so for a daily period, we should use a frequency of 48. We need to remove the second line of data that has the units of the measurements which we’ll do by filtering out based on one of them (Year != "YYYY"). And also there’s some stuff in the columns past Tair that we don’t want, so a dplyr::select is in order (Figure 13.27).
library(readxl); library(tidyverse)
BugacSolstice <- read_xls(ex("ts/SolarRad_Temp.xls"),
sheet="BugacHungary", col_types = "numeric") %>%
filter(Year != "YYYY" & `Day of Yr` < 177 & `Day of Yr` > 168) %>%
dplyr::select(SolarRad, Tair)
BugacSolsticeTS <- ts(BugacSolstice, frequency = 48)
plot(BugacSolstice, main="a simple scatter plot that illustrates hysteresis") 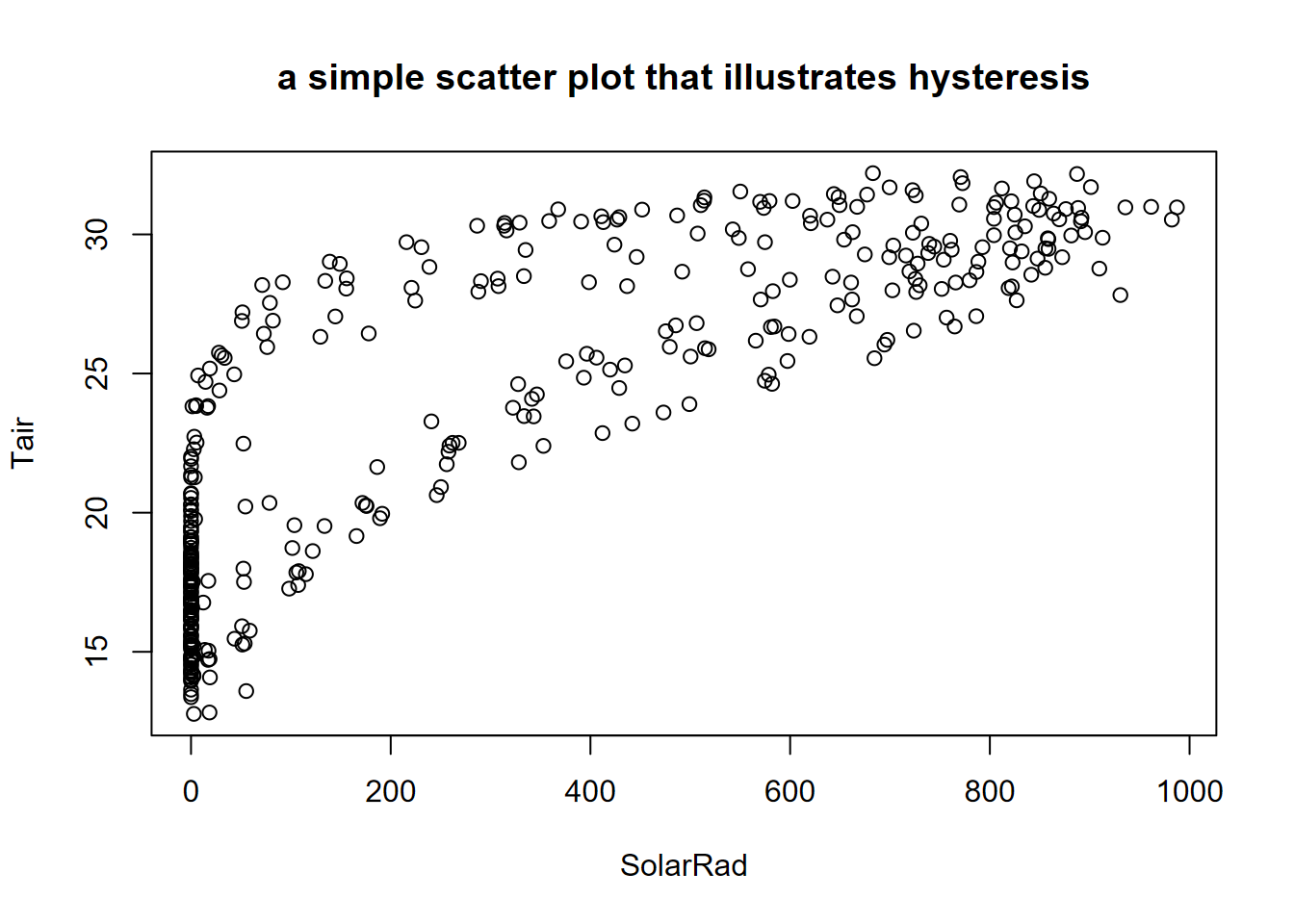
FIGURE 13.27: Scatter plot of Bugac solar radiation and air temperature
Side note: Hysteresis is “the dependence of a state of a system on its history” (“Hysteresis” (n.d.)), and one place this can be seen is in periodic data, when an explanatory variable’s effect on a response variable differs on an increasing limb from what it produces on a decreasing limb. Two classic situations where this occur are in (a) water quality, where the rising limb of the hydrograph will carry more sediment load than a falling limb; and in (b) the daily or seasonal pattern of temperature in response to solar radiation, which we can see in the graph above with two apparent groups of scatterpoints representing the varying impact of solar radiation in spring vs fall, where temperatures lag behind the increase in solar radiation (Figure 13.28).
plot(BugacSolsticeTS)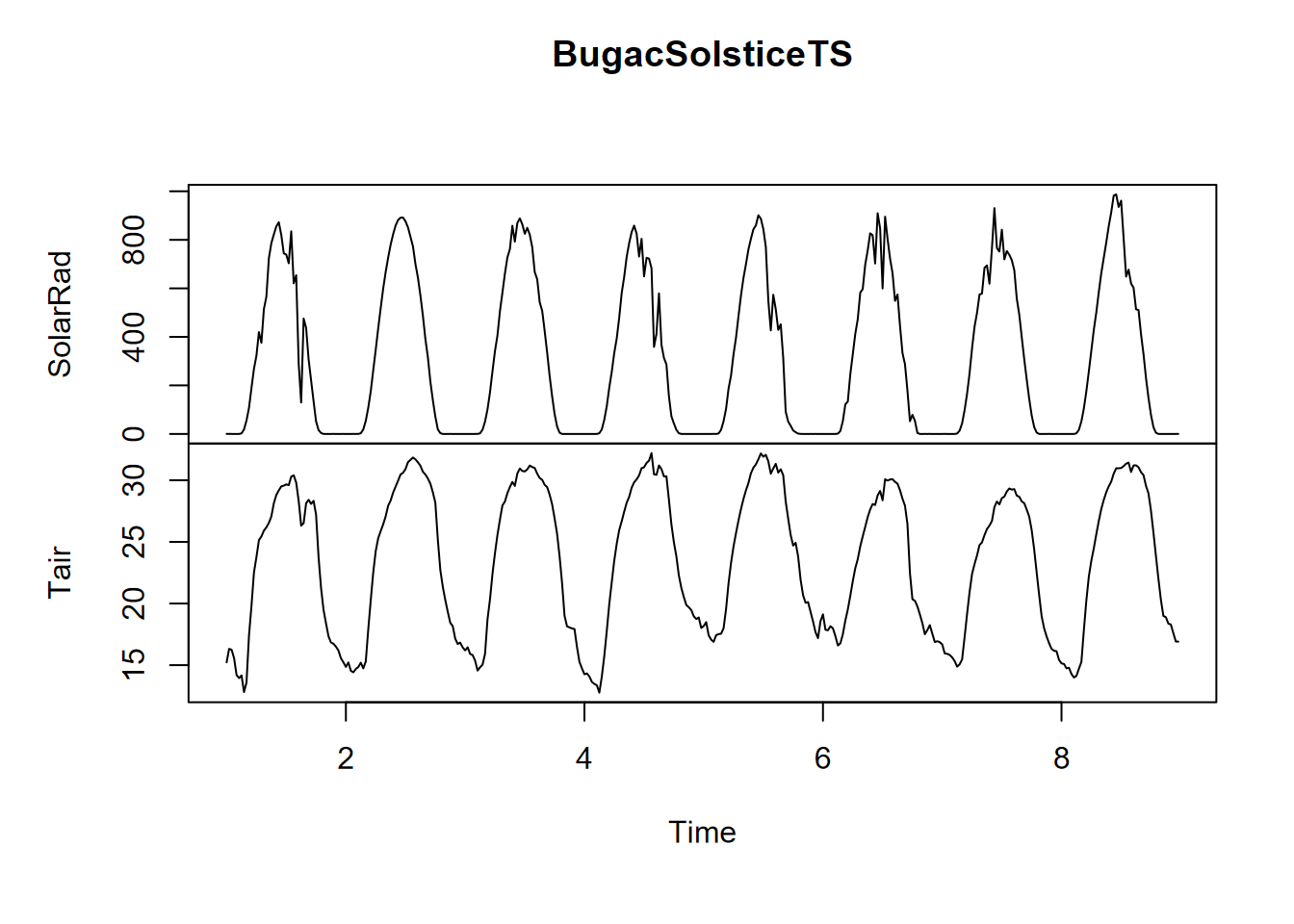
FIGURE 13.28: Solstice 8-day time series of solar radiation and temperature
13.8.1 The lag regression, using a lag function in a linear model
The lag function uses a lag setting of the number of units of observations to model against. so we compare air temperature Tair to a lagged solar radiation SolarRad as lm(Tair~lag(SolarRad,i) where i is the number of units to lag. The following code loops through 6 values (0:5) for i, starting with assigning the RMSE (root mean squared error) for no lag (0), then appending to RMSE for i of 1:5 to hopefully hit the minimum value.
getRMSE <- function(i) {sqrt(sum(lm(Tair~lag(SolarRad,i),
data=BugacSolsticeTS)$resid**2))}
RMSE <- getRMSE(0)
for(i in 1:5){RMSE <- append(RMSE,getRMSE(i))}
lagTable <- bind_cols(lags = 0:5,RMSE = RMSE)
knitr::kable(lagTable)| lags | RMSE |
|---|---|
| 0 | 64.01352 |
| 1 | 55.89803 |
| 2 | 50.49347 |
| 3 | 48.13214 |
| 4 | 49.64892 |
| 5 | 54.36344 |
Minimum RMSE is for a lag of 3, so 1.5 hours. Let’s go ahead and use that minimum RMSE lag and look at the summarized model.
n <- lagTable$lags[which.min(lagTable$RMSE)]
paste("Lag: ",n)## [1] "Lag: 3"summary(lm(Tair~lag(SolarRad,n), data=BugacSolsticeTS))##
## Call:
## lm(formula = Tair ~ lag(SolarRad, n), data = BugacSolsticeTS)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.5820 -1.7083 -0.2266 1.8972 7.9336
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.352006 0.174998 104.87 <2e-16 ***
## lag(SolarRad, n) 0.016398 0.000386 42.48 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.472 on 379 degrees of freedom
## (3 observations deleted due to missingness)
## Multiple R-squared: 0.8265, Adjusted R-squared: 0.826
## F-statistic: 1805 on 1 and 379 DF, p-value: < 2.2e-16So, not surprisingly, air temperature has a significant relationship to solar radiation. Confirmatory statistics should never be surprising, but just give us confidence in our conclusions. What we didn’t know before was just what amount of lag produces the strongest relationship, with the least error (root mean squared error, or RMSE), which turns out to be 3 observations or 1.5 hours. Interestingly, the peak solar radiation and temperature are separated by 5 units, so 2.5 hours, which we can see by looking at the generalized seasonals from decomposition (Figure 13.29). There’s a similar lag for Manaus, though the peak solar radiation and temperatures coincide.
SolarRad_comp <- decompose(ts(BugacSolstice$SolarRad, frequency = 48))
Tair_comp <- decompose(ts(BugacSolstice$Tair, frequency = 48))
seasonals <- bind_cols(Rad = SolarRad_comp$seasonal, Temp = Tair_comp$seasonal)ggplot(seasonals) +
geom_line(aes(x=seq_along(Temp), y=Temp), col="black",size=1.5) +
geom_line(aes(x=seq_along(Rad), y=Rad/50), col="gray", size=1) +
scale_x_continuous(breaks = seq(0,480,12))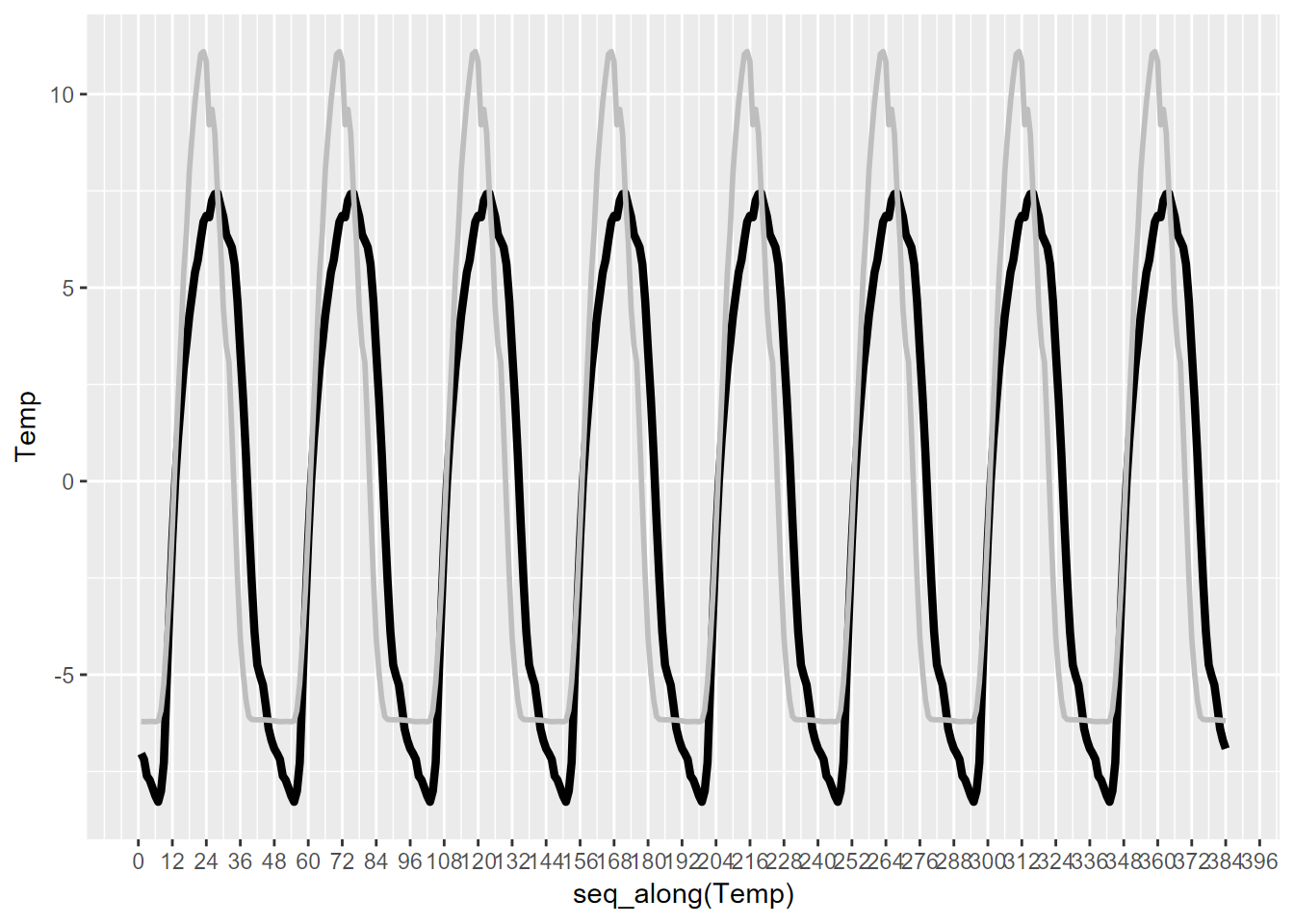
FIGURE 13.29: Bugac solar radiation and temperature
paste(which.max(seasonals$Rad), which.max(seasonals$Temp))## [1] "23 28"13.9 Ensemble summary statistics
For any time series data with meaningful time units like days or years (or even weeks when the data varies by days of the week – this has been the case with COVID-19 data), ensemble averages (along with other summary statistics) are a good way to visualize changes in a variable over that time unit.
As you could see from the decomposition and sequential graphics we created for the Bugac and Manaus solar radiation and temperature data, looking at what happens over one day as an “ensemble” of all of the days – where the mean value is displayed along with error bars based on standard deviations of the distribution – might be a useful figure.
We’ve used group_by-summarize elsewhere in this book and this is yet another use of that handy method. Note that the grouping variable Hr is not categorical, not a factor, but simply a numeric variable of the hour as a decimal number – so 0.0, 0.5, 1.0, etc. – representing half-hourly sampling times, so since these repeat each day so can be used as a grouping variable (Figure 13.30).
library(cowplot)
Manaus <- read_xls(system.file("extdata","ts/SolarRad_Temp.xls",package="igisci"),
sheet="ManausBrazil", col_types = "numeric") %>%
dplyr::select(Year:Tair) %>% filter(Year != "YYYY")
ManausSum <- Manaus %>% group_by(Hr) %>%
summarize(meanRad = mean(SolarRad), meanTemp = mean(Tair),
sdRad = sd(SolarRad), sdTemp = sd(Tair))
px <- ManausSum %>% ggplot(aes(x=Hr)) + scale_x_continuous(breaks=seq(0,24,3))
p1 <- px + geom_line(aes(y=meanRad), col="blue") +
geom_errorbar(aes(ymax = meanRad + sdRad, ymin = meanRad - sdRad)) +
ggtitle("Manaus 2005 ensemble solar radiation")
p2 <- px + geom_line(aes(y=meanTemp),col="red") +
geom_errorbar(aes(ymax=meanTemp+sdTemp, ymin=meanTemp-sdTemp)) +
ggtitle("Manaus 2005 ensemble air temperature")
plot_grid(plotlist=list(p1,p2), ncol=1, align='v') # from cowplot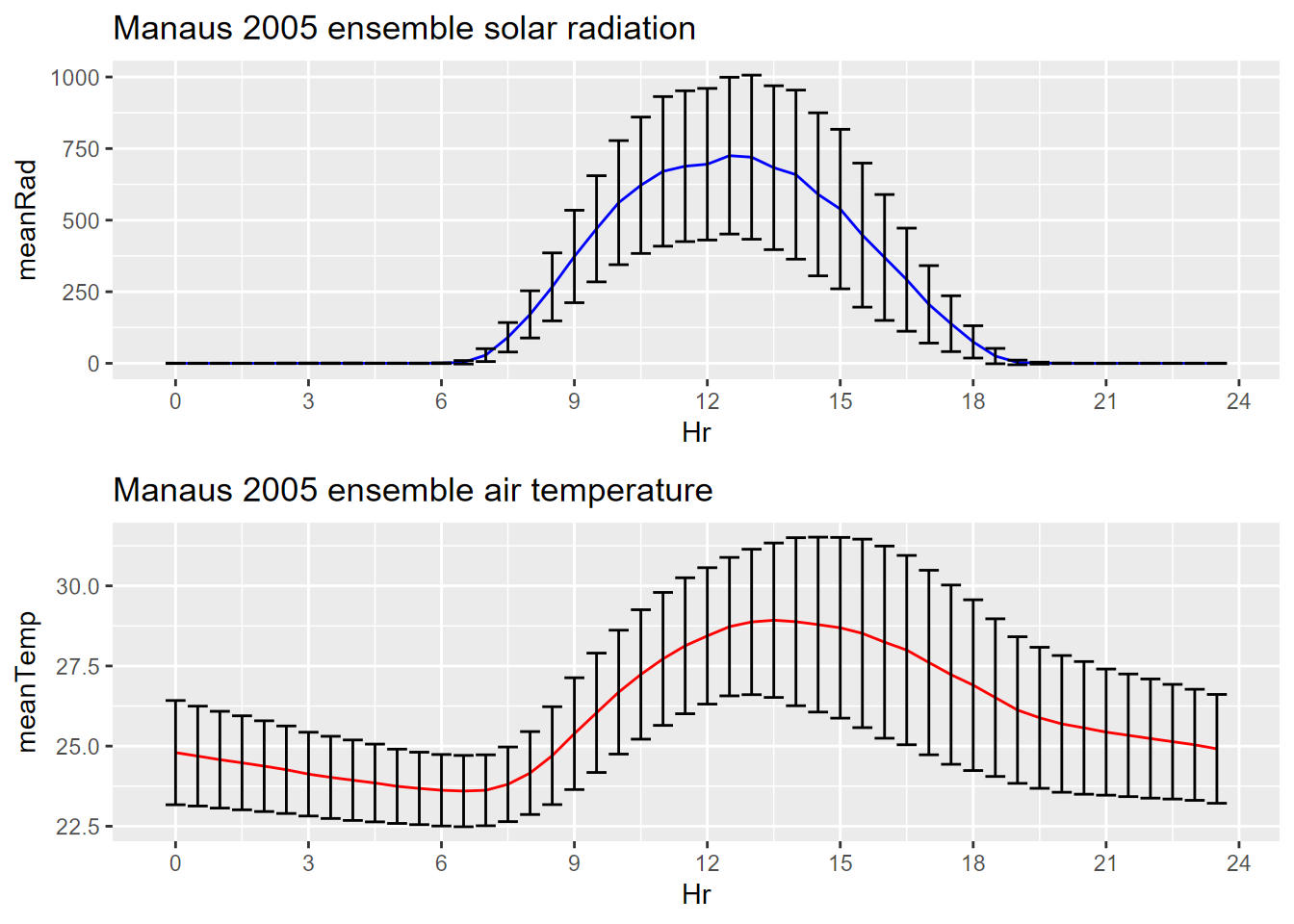
FIGURE 13.30: Manaus ensemble averages with error bars
13.10 Learning more about time series in R
There has been a lot of work on time series in R, especially in the financial sector where time series are important for forecasting models. Some of these methods should have applications in environmental research. Here are some resources for learning more:
- At CRAN: https://cran.r-project.org/web/views/TimeSeries.html
- The time series data library: https://pkg.yangzhuoranyang.com/tsdl/
- https://a-little-book-of-r-for-time-series.readthedocs.io/
Exercises
Exercise 13.1 Create an half-hourly ensemble plot of Bugac, Hungary, similar to the one we created for Manaus, Brazil.
Exercise 13.2 Create a ManausJan tibble for just the January data, then decompose a ts of ManausJan$SolarRad, and plot it. Consider carefully what frequency to use to get a daily time unit. Also, remember that “seasonal” in this case means “diurnal”. Code and plot.
Exercise 13.3 Then do the same for air temperature (Tair) for Manaus in January, providing code and plot. What observations can you make from this on conditions in Manaus in January.
Exercise 13.4 Now do both of the above for Bugac, Hungary, and reflect on what it tells you, and how these places are distinct (other than the obvious).
Exercise 13.5 Now do the same for June. You’ll probably need to use the yday and ymd (or similar) functions from lubridate to find the date range for 2005 or 2006 (neither are leap years, so they should be the same).
Exercise 13.6 Do a lag regression over an 8-day period over the March equinox (about 3/21), when the sun’s rays should be close to vertical since it’s near the Equator, but it’s very likely to be cloudy at the Intertropical Convergence Zone. As we did with the Bugac data, work out the best lag value using the minimum-RMSE model process we used for Bugac, and produce a summary of that model.
Exercise 13.7 Create an ensemble plot of monthly air and box temperature from the Marble Mountains Resurgence data. The air temperature was measured from a thermistor mounted near the ground but outside the box, and the box temperature was measured within the buried box (see the pictures to visualize this.)
Exercise 13.8 How about hourly? The Marbles resurgence data was collected every 2 hours. Interpret what you see here, and what the air vs box temperature patterns might make sense considering where the variance comes from.
Exercise 13.9 Create a facet graph of daily (summarize by Date, after reading it in with mdy(date), air temperature (ATemp), water level (wlevelm), conductance (EC), and input voltage from the solar panel (InputV) from the Marble Mountains resurgence data (Figure 13.31).
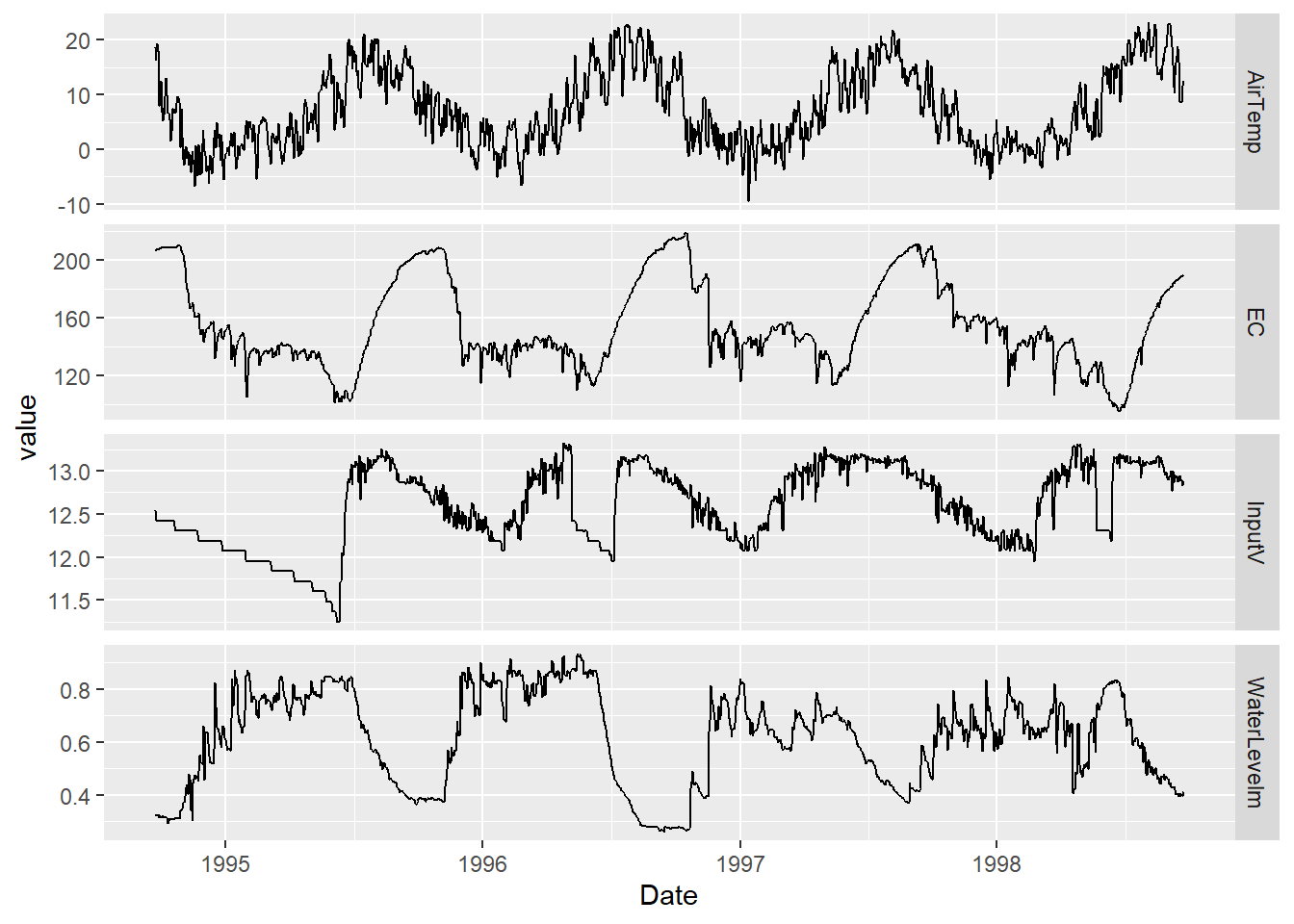
FIGURE 13.31: Facet graph of Marble Mountains resurgence data (goal)
Exercise 13.10 Tree-ring data: Using forecast::ma, find a useful order value for a curve that communicates a pattern of tree rings over the last 8000 years, with high values around -3500 and 0 years. Note: the order may be pretty big, and you might want to loop through a sequence of values to see what works. I found that creating a sequence in a for loop with seq(from=100,to=1000,by100) useful, and any further created some odd effects.
Exercise 13.11 Sunspot activity is known to fluctuate over about a 11 year cycle, and other than the well-known effects on radio transmission is also part of short-term climate fluctuations (so must be considered when looking at climate change). The built-in data set sunspot.month has monthly values of sunspot activity from 1749 to 2014. Use the frequency function to understand its time unit, then create an alternative ts with an 11 year cycle as frequency (how do you define its frequency?) and plot a decomposition and stl.