Chapter 10 Statistical Summaries and Tests
10.1 Goals of statistical analysis
To frame how we might approach statistical analysis and modeling, there are various goals that are commonly involved:
To understand our data
- nature of our data, through summary statistics and various graphics like histograms
- spatial statistical analysis
- time series analysis
To group or classify things based on their properties
- using factors to define groups, and deriving grouped summaries
- comparing observed vs expected counts or probabilities
To understand how variables relate to one another
- or maybe even explain variations in other variables, through correlation analysis
To model behavior and maybe predict it
- various linear models
To confirm our observations from exploration (field/lab/vis)
- inferential statistics e.g. difference of means tests, ANOVA, \(\chi^2\)
To have the confidence to draw conclusions, make informed decisions
To help communicate our work
These goals can be seen in the context of a typical research paper or thesis outline in environmental science:
Introduction
Literature Review
Methodology
Results
- field, lab, geospatial data
Analysis
- statistical analysis
- qualitative analysis
- visualization
Discussion
- making sense of analysis
- possibly recursive, with visualization
Conclusion
- conclusion about what the above shows
- new questions for further research
- possible policy recommendation
The scope and theory of statistical analysis and models is extensive, and there are many good books on the subject that employ the R language. This chapter is a short review of some of these methods and how they apply to environmental data science.
10.2 Summary Statistics
Summary statistics such as mean, standard deviation, variance, minimum, maximum, and range are derived in quite a few R functions, commonly as a parameter or a sub-function (see mutate). An overall simple statistical summary is very easy to do in base R:
summary(tidy_eucoak)## site site # tree Date
## Length:180 Min. :1.000 Length:180 Min. :2006-11-08
## Class :character 1st Qu.:2.000 Class :character 1st Qu.:2006-12-07
## Mode :character Median :4.000 Mode :character Median :2007-01-30
## Mean :4.422 Mean :2007-01-29
## 3rd Qu.:6.000 3rd Qu.:2007-03-22
## Max. :8.000 Max. :2007-05-07
##
## month rain_mm rain_subcanopy slope
## Length:180 Min. : 1.00 Min. : 1.00 Min. : 9.00
## Class :character 1st Qu.:16.00 1st Qu.:16.00 1st Qu.:12.00
## Mode :character Median :28.50 Median :30.00 Median :24.00
## Mean :37.99 Mean :34.84 Mean :20.48
## 3rd Qu.:63.25 3rd Qu.:50.00 3rd Qu.:27.00
## Max. :99.00 Max. :98.00 Max. :32.00
## NA's :36 NA's :4
## aspect runoff_L surface_tension runoff_rainfall_ratio
## Min. :100.0 Min. : 0.000 Min. :28.51 Min. :0.00000
## 1st Qu.:143.0 1st Qu.: 0.000 1st Qu.:37.40 1st Qu.:0.00000
## Median :196.0 Median : 0.825 Median :62.60 Median :0.03347
## Mean :186.6 Mean : 2.244 Mean :55.73 Mean :0.05981
## 3rd Qu.:221.8 3rd Qu.: 3.200 3rd Qu.:72.75 3rd Qu.:0.08474
## Max. :296.0 Max. :16.000 Max. :72.75 Max. :0.42000
## NA's :8 NA's :44 NA's :810.2.1 Summarize by group: stratifying a summary
In the visualization chapter and elsewhere, we’ve seen the value of adding symbolization based on a categorical variable or factor. Summarizing by group has a similar benefit, and provides a tabular output in the form of a data frame, and the tidyverse makes it easy to extract several summary statistics at once. For instance, for the euc/oak study, we can create variables of the mean and maximum runoff, the mean and standard deviation of rainfall, for each of the sites. This table alone provides a useful output, but we can also use it in further analyses.
eucoakrainfallrunoffTDR %>%
group_by(site) %>%
summarize(
rain = mean(rain_mm, na.rm = TRUE),
rainSD = sd(rain_mm, na.rm = TRUE),
runoffL_oak = mean(runoffL_oak, na.rm = TRUE),
runoffL_euc = mean(runoffL_euc, na.rm = TRUE),
runoffL_oakMax = max(runoffL_oak, na.rm = TRUE),
runoffL_eucMax = max(runoffL_euc, na.rm = TRUE),
)## # A tibble: 8 × 7
## site rain rainSD runoffL_oak runoffL_euc runoffL_oakMax runoffL_eucMax
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 AB1 48.4 28.2 6.80 6.03 6.80 6.03
## 2 AB2 34.1 27.9 4.91 3.65 4.91 3.65
## 3 KM1 48 32.0 1.94 0.592 1.94 0.592
## 4 PR1 56.5 19.1 0.459 2.31 0.459 2.31
## 5 TP1 38.4 29.5 0.877 1.66 0.877 1.66
## 6 TP2 34.3 29.2 0.0955 1.53 0.0955 1.53
## 7 TP3 32.1 28.4 0.381 0.815 0.381 0.815
## 8 TP4 32.5 28.2 0.231 2.83 0.231 2.8310.2.2 Boxplot for visualizing distributions by group
We’ve looked at this already in the visualization chapter, but a Tukey boxplot is a good way to visualize distributions by group. In this soil CO2 study of the Marble Mountains (J. D. Davis, Amato, and Kiefer 2001) (Figure 10.1), some sites had much greater variance, and some sites tended to be low vs high (Figure 10.2).
soilCO2_97$SITE <- factor(soilCO2_97$SITE)
ggplot(data = soilCO2_97, mapping = aes(x = SITE, y = CO2pct)) +
geom_boxplot()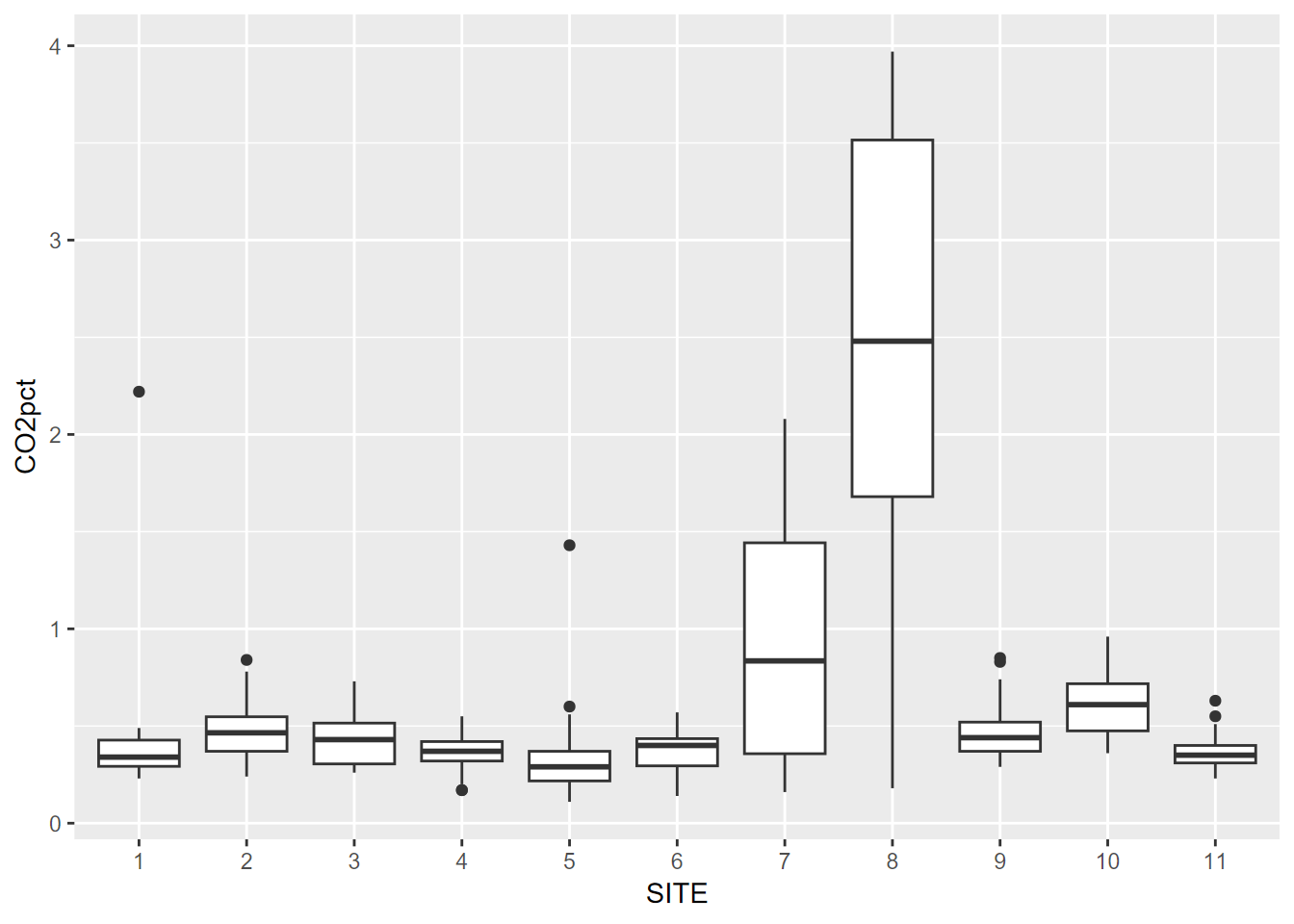
FIGURE 10.1: Tukey boxplot by group
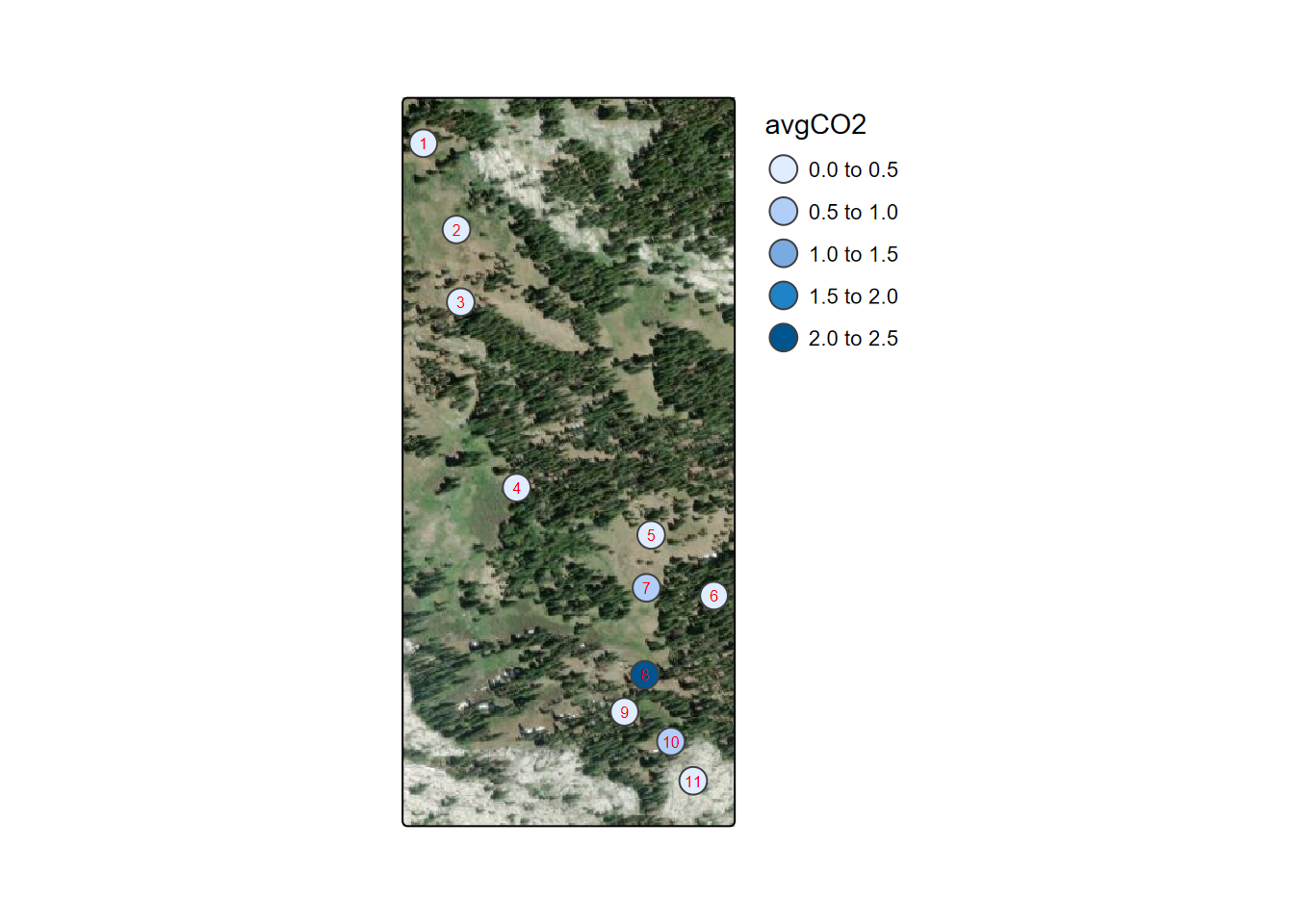
FIGURE 10.2: Marble Mountains average soil carbon dioxide per site
10.2.3 Generating pseudorandom numbers
Functions commonly used in R books for quickly creating a lot of numbers to display are those that generate pseudorandom numbers. These are also useful in statistical methods that need a lot of these, such as in Monte Carlo simulation. The two most commonly used are:
runif()generates a vector ofnpseudorandom numbers ranging by default frommin=0tomax=1(Figure 10.3).rnorm()generates a vector ofnnormally distributed pseudorandom numbers with a defaultmean=0andsd=0(Figures 10.4 and 10.5)
Figure 10.6 shows both in action as x and y.
x <- as_tibble(runif(n=1000, min=10, max=20))
names(x) <- 'x'
ggplot(x, aes(x=x)) + geom_histogram()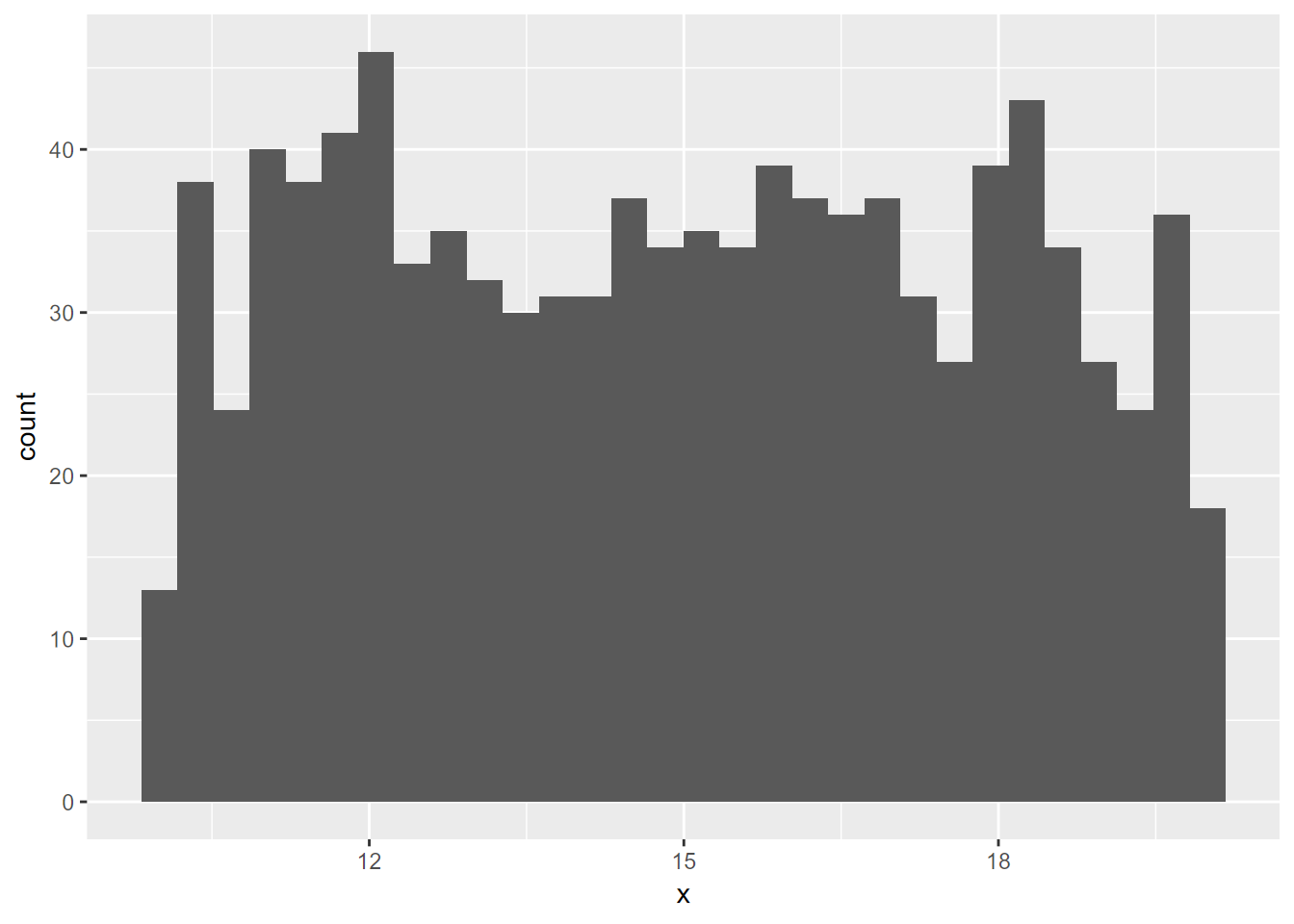
FIGURE 10.3: random uniform histogram
y <- as_tibble(rnorm(n=1000, mean=100, sd=10))
names(y) <- 'y'
ggplot(y, aes(x=y)) + geom_histogram()
FIGURE 10.4: random normal histogram
ggplot(y, aes(x=y)) + geom_density()
FIGURE 10.5: random normal density plot
xy <- bind_cols(x,y)ggplot(xy, aes(x=x,y=y)) + geom_point()
FIGURE 10.6: random normal plotted against random uniform
10.3 Correlation r and Coefficient of Determination r2
In the visualization chapter, we looked at creating scatter plots and also arrays of scatter plots where we could compare variables to visually see if they might be positively or negatively correlated. A statistic that is commonly used for this is the Pearson product-moment correlation coefficient or r statistic.
We’ll look at the formula for r below, but it’s easier to just use the
cor function. You just need the two variables as vector inputs in R to
return the r statistic. Squaring r to r2 is the coefficient of
determination and can be interpreted as the amount of the variation in
the dependent variable y that that is “explained” by variation in the
independent variable x. This coefficient will always be positive, with a
maximum of 1 or 100%.
If we create two random variables, uniform or normal, there shouldn’t be any correlation. We’ll do this 5 times each set:
for (i in 1:5) {print(paste(i, cor(rnorm(100), rnorm(100))))}## [1] "1 -0.204412739865431"
## [1] "2 -0.0999238439873436"
## [1] "3 -0.0324843786632077"
## [1] "4 -0.113866909161341"
## [1] "5 0.0414995669202227"for (i in 1:5) {print(paste(i, cor(runif(100), runif(100))))}## [1] "1 -0.04175948848328"
## [1] "2 -0.0657181150681941"
## [1] "3 0.0603411636573014"
## [1] "4 0.0624172840320831"
## [1] "5 -0.0664393031639701"for (i in 1:5) {print(paste(i, cor(rnorm(100), runif(100))))}## [1] "1 0.0966133821681494"
## [1] "2 -0.0670265120078233"
## [1] "3 -0.218585447586597"
## [1] "4 -0.0555677246203138"
## [1] "5 0.179855137626917"But variables such as temperature and elevation in the Sierra will be strongly negatively correlated, as seen in the scatter plot and the r value close to -1, and have a high r2 (Figure 10.7).
library(igisci); library(tidyverse)
sierra <- sierraFeb %>% filter(!is.na(TEMPERATURE))
elev <- sierra$ELEVATION; temp <- sierra$TEMPERATURE
plot(elev, temp)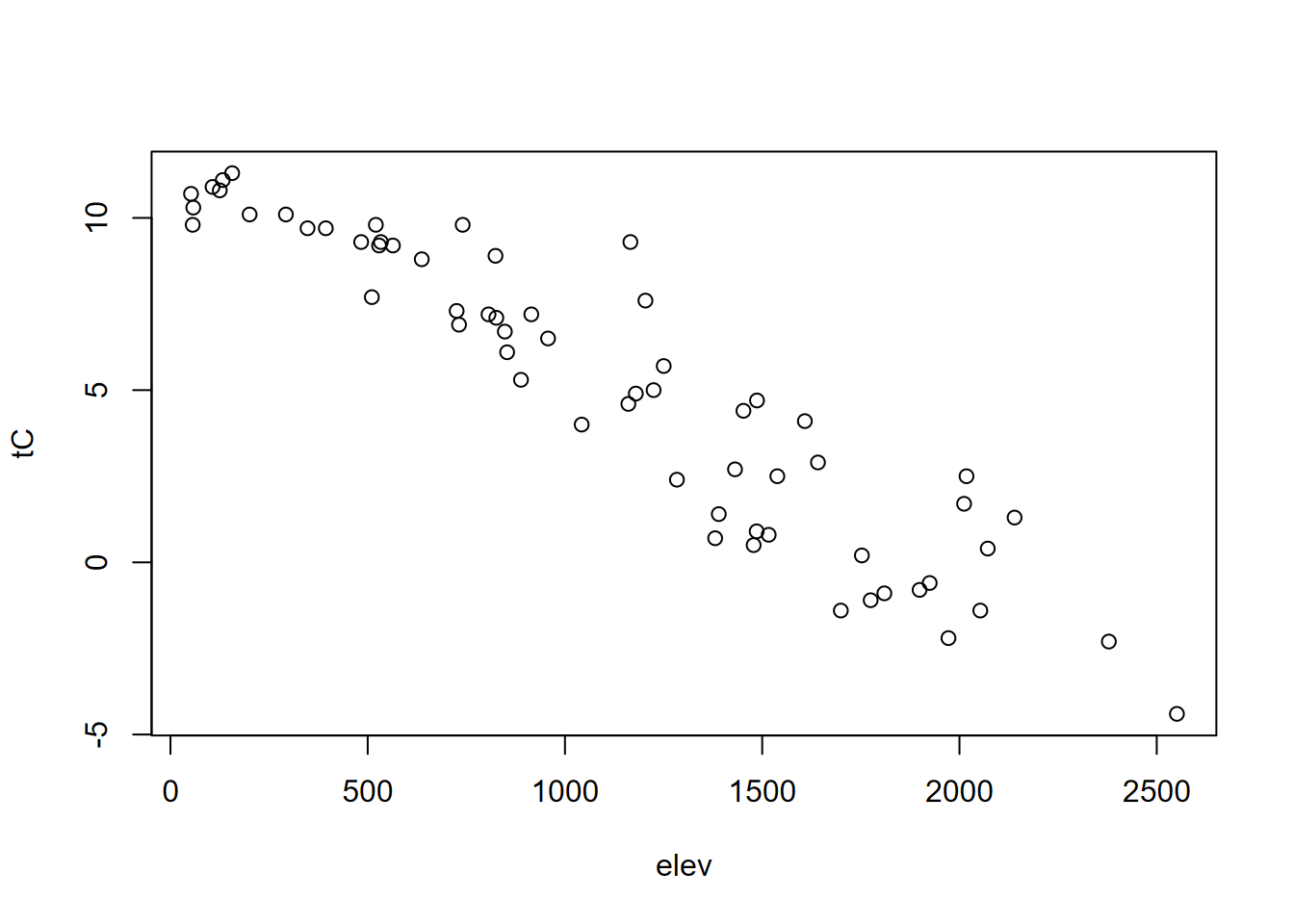
FIGURE 10.7: Scatter plot illustrating negative correlation
cor(elev, temp)## [1] -0.9357801cor(elev, temp)^2## [1] 0.8756845While you don’t need to use this, since the cor function is easier to
type, it’s interesting to know that the formula for Pearson’s
correlation coefficient is something that you can actually code in R,
taking advantage of its vectorization methods:
\[ r = \frac{\sum{(x_i-\overline{x})(y_i-\overline{y})}}{\sqrt{\sum{(x_i-\overline{x})^2\sum(y_i-\overline{y})^2}}} \]
r <- sum((elev-mean(elev))*(temp-mean(temp)))/
sqrt(sum((elev-mean(elev))^2*sum((temp-mean(temp))^2)))
r## [1] -0.9357801r^2## [1] 0.8756845Another version of the formula runs faster, so might be what R uses, but you’ll never notice the time difference:
\[ r = \frac{n(\sum{xy})-(\sum{x})(\sum{y})}{\sqrt{(n\sum{x^2}-(\sum{x})^2)(n\sum{y^2}-(\sum{y})^2)}} \]
n <- length(elev)
r <- (n*sum(elev*temp)-sum(elev)*sum(temp))/
sqrt((n*sum(elev^2)-sum(elev)^2)*(n*sum(temp^2)-sum(temp)^2))
r## [1] -0.9357801r^2## [1] 0.8756845… and as you can see, all three methods give the same results.
10.3.1 Displaying correlation in a pairs plot
We can use another type of pairs plot from the psych package to look at the correlation coefficient in the upper right part of the pairs plot, since correlation can be determined between x and y or y and x; the result is the same. In contrast to what we’ll see in regression models, there doesn’t have to be one explanatory (or independent) variable and one response (or dependent) variable; either one will do. The r value shows both the direction (positive or negative) and the magnitude of the correlation, with values closer to 1 or -1 being more correlated (Figure 10.8).
library(psych)
sierraFeb %>%
dplyr::select(ELEVATION:TEMPERATURE) %>%
pairs.panels(method = "pearson", # correlation method
hist.col = "#00AFBB",
density = TRUE, # show density plots
ellipses = F, smooth = F) # unneeded 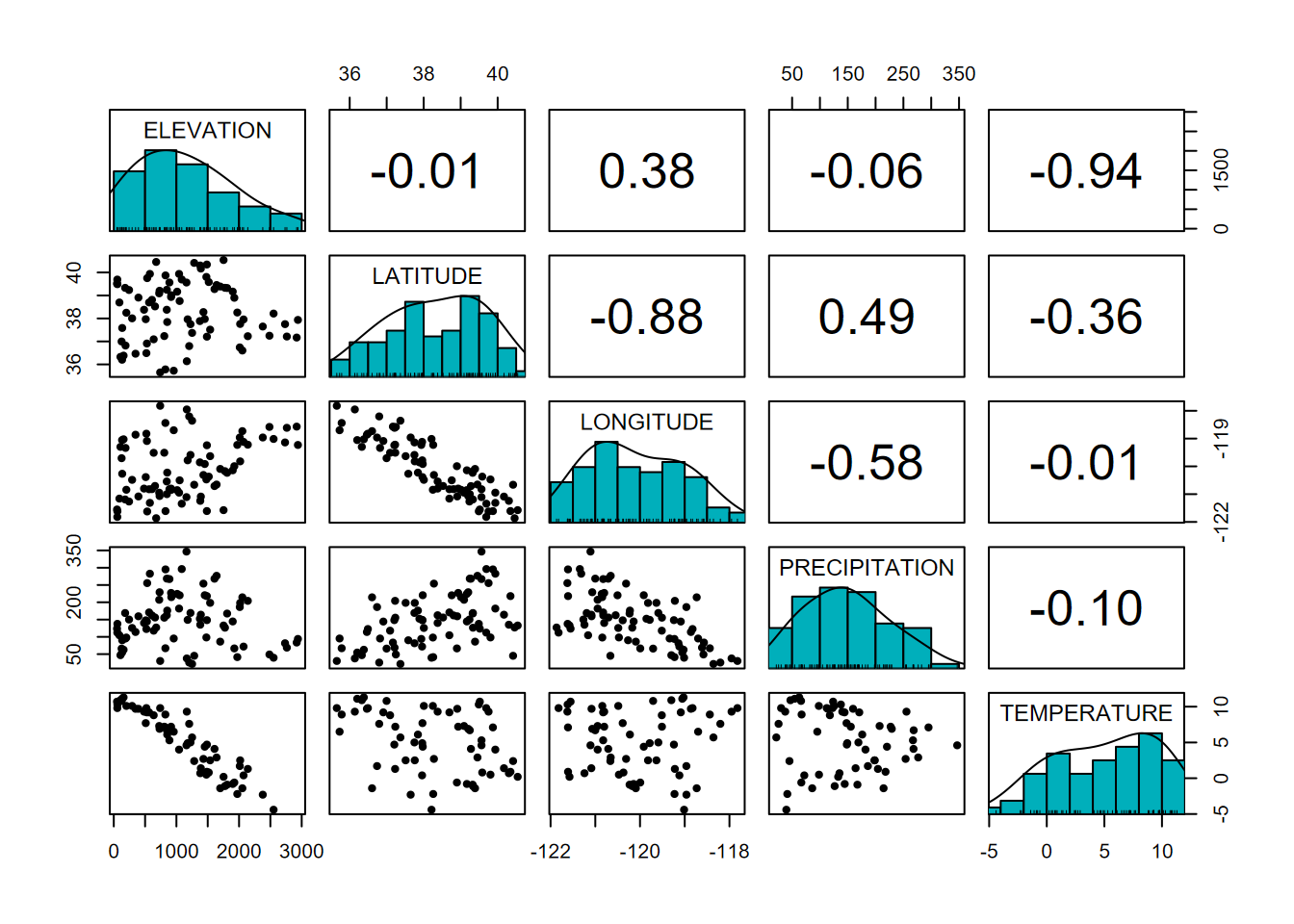
FIGURE 10.8: Pairs plot with r values
We can clearly see in the graphs the negative relationships between elevation and temperature and between latitude and longitude (what is that telling us?) and these correspond to strongly negative correlation coefficients.
One problem with Pearson: While there’s nothing wrong with the correlation coefficient, Pearson’s name, along with some other pioneers of statistics like Fisher, is tainted by an association with the racist field of eugenics. But the mathematics is not to blame, and the correlation coefficient is still as useful as ever. Maybe we can just say that Pearson discovered the correlation coefficient…
10.4 Statistical tests
Tests that compare our data to other data or look at relationships among variables are important statistical methods, and you should refer to statistical references to best understand how to apply the appropriate methods for your research.
10.4.1 Comparing samples and groupings with a t test and a non-parametric Kruskal-Wallis Rank Sum test
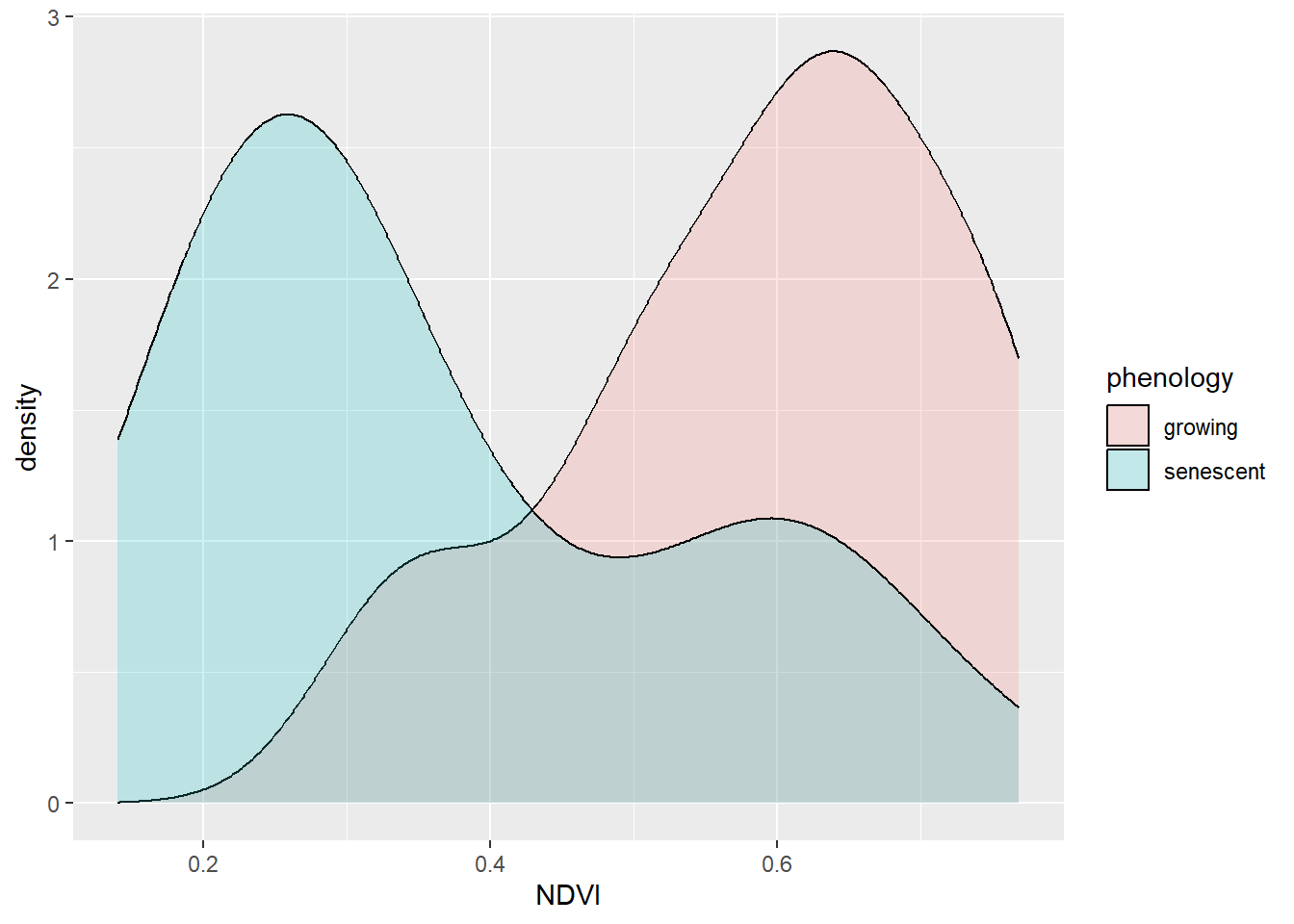
A common need in environmental research is to compare samples of a phenomenon (e.g. Figure 10.9) or compare samples with an assumed standard population. The simplest application of this is the t-test, which can only involve comparing two samples or one sample with a population. After this, we’ll look at analysis of variance, extending this to allow for more than two groups.
XSptsPheno %>%
ggplot(aes(NDVI, fill=phenology)) +
geom_density(alpha=0.2)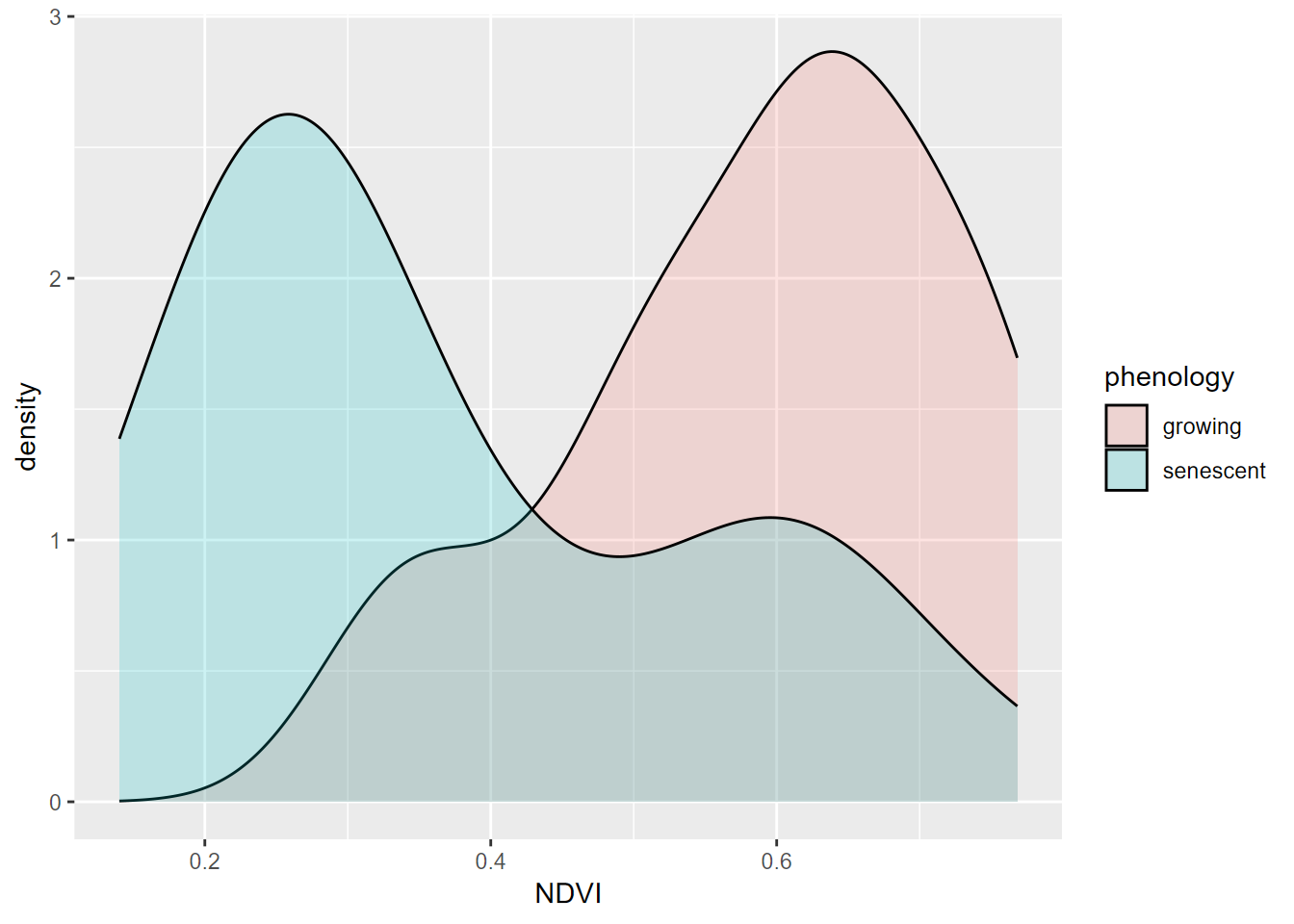
FIGURE 10.9: NDVI by phenology
t.test(NDVI~phenology, data=XSptsPheno) ##
## Welch Two Sample t-test
##
## data: NDVI by phenology
## t = 5.4952, df = 52.03, p-value = 1.19e-06
## alternative hypothesis: true difference in means between group growing and group senescent is not equal to 0
## 95 percent confidence interval:
## 0.1421785 0.3057412
## sample estimates:
## mean in group growing mean in group senescent
## 0.5901186 0.3661588One condition for using a t test is that our data are normally distributed. While these data sets appear reasonably normal, though with a bit of bimodality especially for the senescent group, the Shapiro-Wilk test (which uses a null hypothesis of normal) has a p value < 0.05 for the senescent group, so the data can’t be assumed to be normal.
shapiro.test(XSptsPheno$NDVI[XSptsPheno$phenology=="growing"])##
## Shapiro-Wilk normality test
##
## data: XSptsPheno$NDVI[XSptsPheno$phenology == "growing"]
## W = 0.93608, p-value = 0.07918shapiro.test(XSptsPheno$NDVI[XSptsPheno$phenology=="senescent"])##
## Shapiro-Wilk normality test
##
## data: XSptsPheno$NDVI[XSptsPheno$phenology == "senescent"]
## W = 0.88728, p-value = 0.004925Therefore we should use a non-parametric alternative such as the Kruskal-Wallis Rank Sum test:
kruskal.test(NDVI~phenology, data=XSptsPheno)##
## Kruskal-Wallis rank sum test
##
## data: NDVI by phenology
## Kruskal-Wallis chi-squared = 19.164, df = 1, p-value = 1.199e-05A bit of a review on significance tests and p values
First, each type of test will be testing a particular summary statistic, like the t test is comparing means and the analysis of variance will be comparing variances. In confirmatory statistical tests, you’re always seeing if you can reject the null hypothesis that there’s no difference, so in the t test or the rank sum test above that compares two samples, it’s that there’s no difference between two samples.
There will of course nearly always be some difference, so you might think that you’d always reject the null hypothesis that there’s no difference. That’s where random error and probability comes in. You can accept a certain amount of error – say 5% – to be able to say that the difference in values could have occurred by chance. That 5% or 0.05 is often called the “significance level” and is the probability of the two values being the same that you’re willing to accept. (The remainder 0.95 is often called the confidence level, the extent to which you’re confident that rejecting the null hypothesis and accepting the working hypothesis is correct.)
When R reports the p (or Pr) probability value, you compare that to that significance level to see if it’s lower, and then use that to possibly reject the null hypothesis and accept the working hypothesis. R will simply report the p value and commonly show asterisks along with it to indicate if it’s lower than various common significance levels, like 0.1, 0.05, 0.01, and 0.001.
10.4.1.1 Runoff and Sediment Yield under Eucalyptus vs Oaks – is there a difference?
Starting with the Data Abstraction chapter, one of the data sets we’ve been looking at is from a study of runoff and sediment yield under paired Eucalyptus and coast live oak sites, and we might want to analyze these data statistically to consider some basic research questions. These are discussed at greater length in Thompson, Davis, and Oliphant (2016), but the key questions are:
- Is the runoff under Eucalyptus canopy significantly different from that under oaks?
- Is the sediment yield under Eucalyptus canopy significantly different from that under oaks?
We’ll start with the first, since this was the focus on the first part of the study where multiple variables that influence runoff were measured, such as soil hydrophobicity resulting from the chemical effects of Eucalyptus, and any rainfall contrasts at each site and between sites. For runoff, we’ll then start by test for normality of each of the two samples (euc and oak) which shows clearly that both samples are non-normal.
shapiro.test(tidy_eucoak$runoff_L[tidy_eucoak$tree == "euc"])##
## Shapiro-Wilk normality test
##
## data: tidy_eucoak$runoff_L[tidy_eucoak$tree == "euc"]
## W = 0.74241, p-value = 4.724e-11shapiro.test(tidy_eucoak$runoff_L[tidy_eucoak$tree == "oak"])##
## Shapiro-Wilk normality test
##
## data: tidy_eucoak$runoff_L[tidy_eucoak$tree == "oak"]
## W = 0.71744, p-value = 1.698e-11So we might apply the non-parametric Kruskal-Wallis test …
kruskal.test(runoff_L~tree, data=tidy_eucoak)##
## Kruskal-Wallis rank sum test
##
## data: runoff_L by tree
## Kruskal-Wallis chi-squared = 2.2991, df = 1, p-value = 0.1294… and no significant difference can be seen. If we look at the data graphically, this makes sense, since the distributions are not dissimilar (Figure 10.10).
tidy_eucoak %>%
ggplot(aes(log(runoff_L),fill=tree)) +
geom_density(alpha=0.2)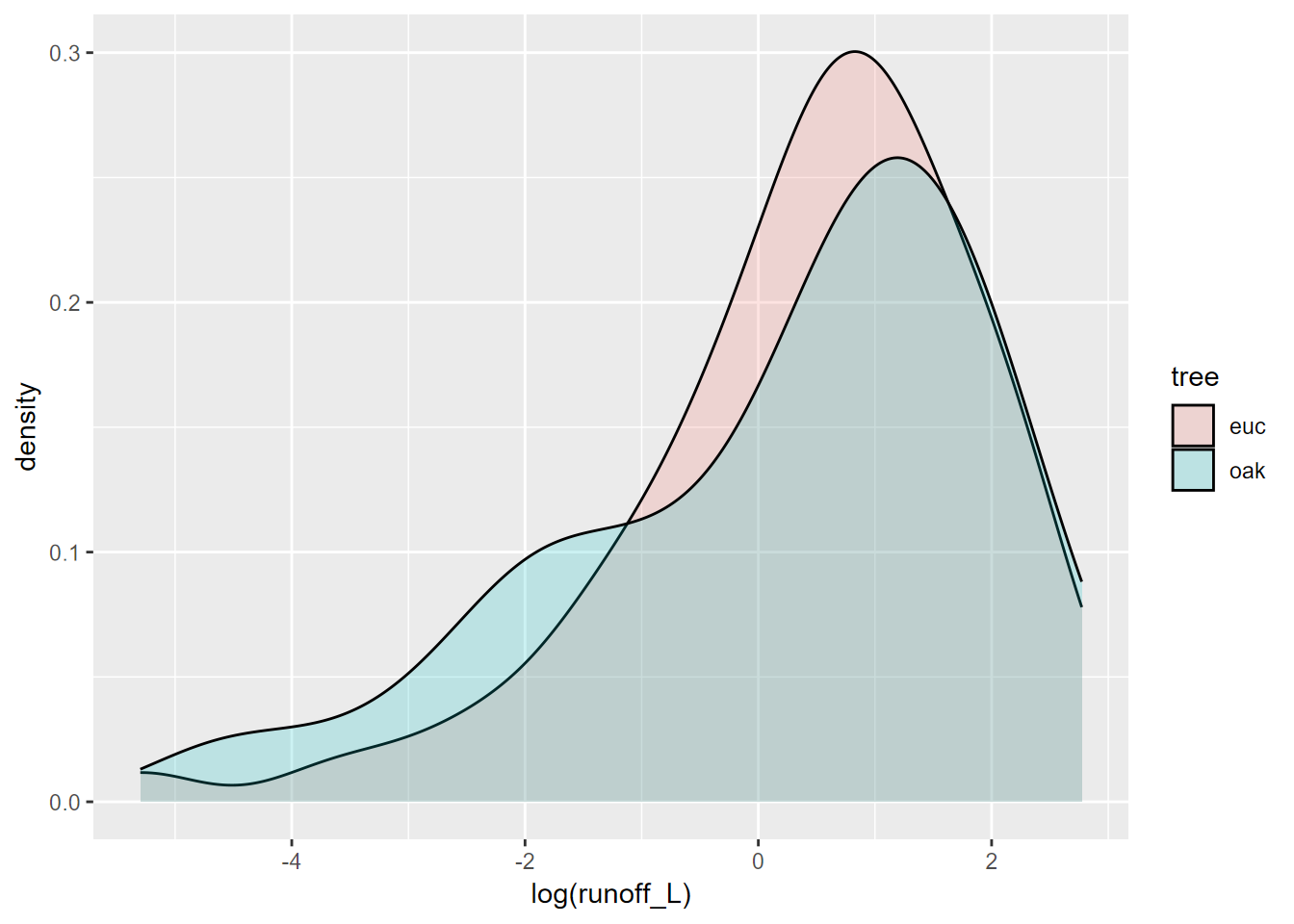
FIGURE 10.10: Runoff under Eucalyptus and Oak in Bay Area sites
However, some of this may result from major variations among sites, which is apparent in a site-grouped boxplot (Figure 10.11).
ggplot(data = tidy_eucoak) +
geom_boxplot(aes(x=site, y=runoff_L, color=tree))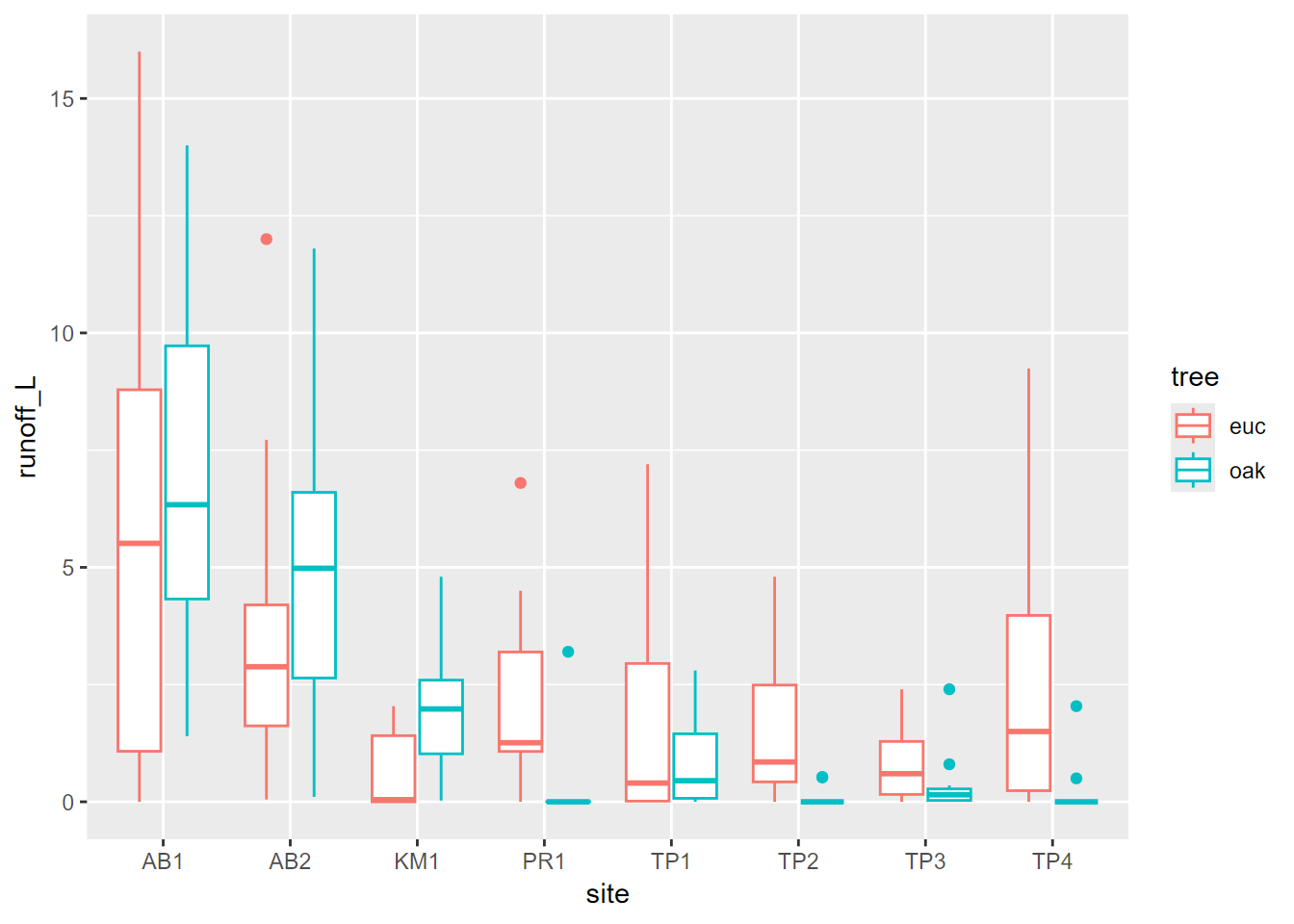
FIGURE 10.11: Runoff at various sites contrasting euc and oak
We might restrict our analysis to Tilden Park sites in the East Bay, where there’s more of a difference (Figure 10.12), but the sample size is very small.
tilden <- tidy_eucoak %>% filter(str_detect(tidy_eucoak$site,"TP"))
tilden %>%
ggplot(aes(log(runoff_L),fill=tree)) +
geom_density(alpha=0.2)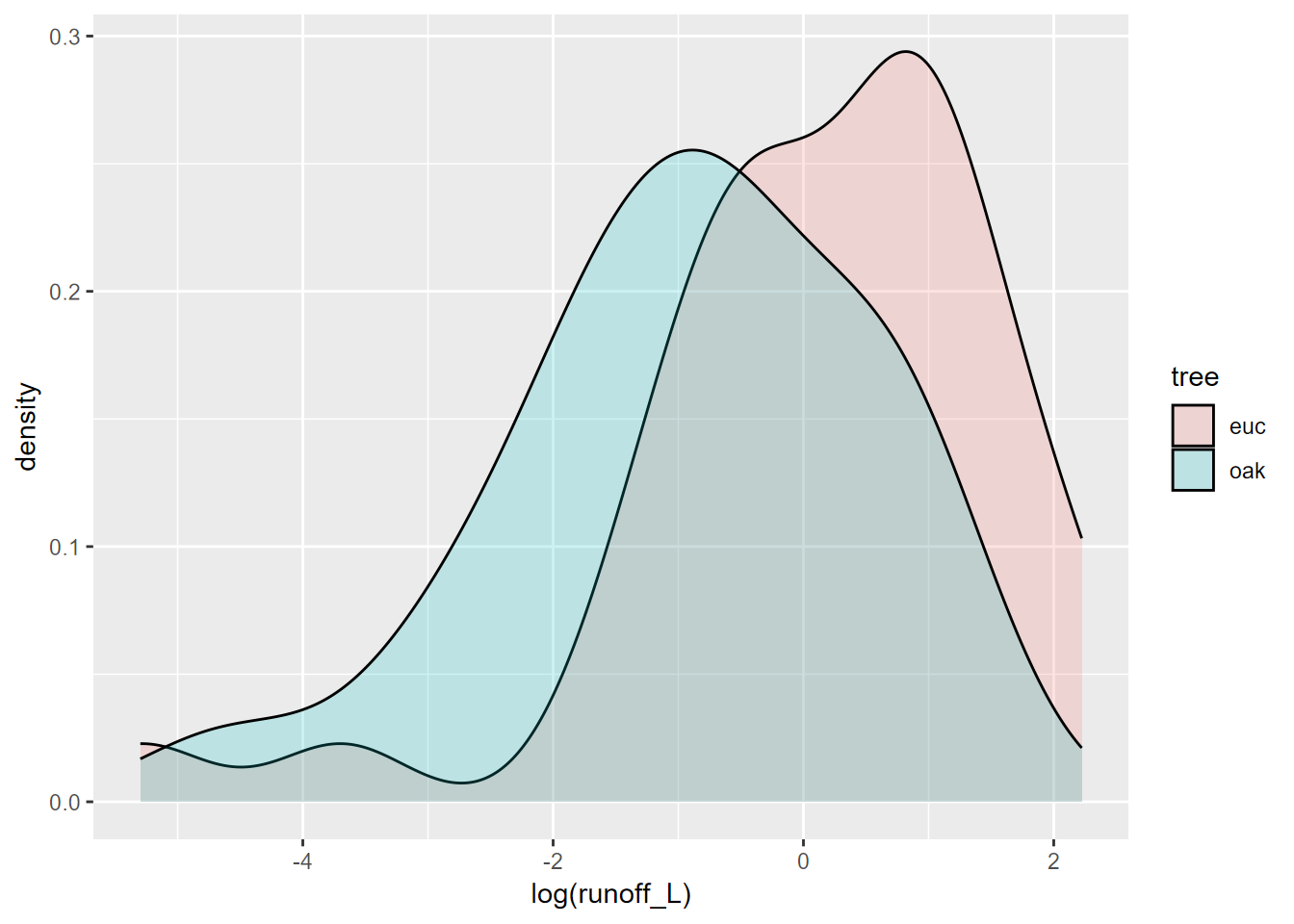
FIGURE 10.12: East Bay sites
shapiro.test(tilden$runoff_L[tilden$tree == "euc"])##
## Shapiro-Wilk normality test
##
## data: tilden$runoff_L[tilden$tree == "euc"]
## W = 0.73933, p-value = 1.764e-07shapiro.test(tilden$runoff_L[tilden$tree == "oak"])##
## Shapiro-Wilk normality test
##
## data: tilden$runoff_L[tilden$tree == "oak"]
## W = 0.59535, p-value = 8.529e-10So once again, as is common with small sample sets, we need a non-parametric test.
kruskal.test(runoff_L~tree, data=tilden)##
## Kruskal-Wallis rank sum test
##
## data: runoff_L by tree
## Kruskal-Wallis chi-squared = 14.527, df = 1, p-value = 0.0001382Sediment Yield
In the year runoff was studied, there were no runoff events sufficient to mobilize sediments. The next year, January had a big event, so we collected sediments and processed them in the lab.
From the basic sediment yield question listed above we can consider two variants:
- Is there a difference between eucs and oaks in terms of fine sediment yield?
- Is there a difference between eucs and oaks in terms of total sediment yield? (includes litter)
So here, we will need to extract fine and total sediment yield from the data and derive group statistics by site (Figure 10.13). As usual, we’ll use a faceted density plot to visualize the distributions (Figure 10.14). Then we’ll run the test.
eucoaksed <- read_csv(ex("eucoak/eucoaksediment.csv"))
summary(eucoaksed)## id site trtype slope
## Length:14 Length:14 Length:14 Min. : 9.00
## Class :character Class :character Class :character 1st Qu.:12.00
## Mode :character Mode :character Mode :character Median :21.00
## Mean :20.04
## 3rd Qu.:25.00
## Max. :32.00
##
## bulkDensity litter Jan08rain mean_runoff_ratio
## Min. :0.960 Min. : 25.00 Min. :228.1 Min. :0.00450
## 1st Qu.:1.060 1st Qu.: 51.25 1st Qu.:290.8 1st Qu.:0.02285
## Median :1.125 Median : 77.00 Median :301.1 Median :0.04835
## Mean :1.156 Mean : 76.64 Mean :298.5 Mean :0.06679
## 3rd Qu.:1.245 3rd Qu.: 95.75 3rd Qu.:317.0 3rd Qu.:0.12172
## Max. :1.490 Max. :135.00 Max. :328.5 Max. :0.16480
##
## med_runoff_ratio std_runoff_ratio fines_g litter_g
## Min. :0.00000 Min. :0.01070 Min. : 7.50 Min. :14.00
## 1st Qu.:0.01105 1st Qu.:0.01642 1st Qu.:13.30 1st Qu.:18.80
## Median :0.04950 Median :0.02740 Median :18.10 Median :40.40
## Mean :0.06179 Mean :0.04355 Mean :27.77 Mean :41.32
## 3rd Qu.:0.09492 3rd Qu.:0.05735 3rd Qu.:45.00 3rd Qu.:57.50
## Max. :0.16430 Max. :0.11480 Max. :66.70 Max. :97.80
## NA's :1 NA's :1
## total_g fineTotalRatio fineRainRatio
## Min. : 23.50 Min. :0.1300 Min. :0.025
## 1st Qu.: 35.00 1st Qu.:0.2700 1st Qu.:0.044
## Median : 60.50 Median :0.3900 Median :0.064
## Mean : 69.12 Mean :0.3715 Mean :0.097
## 3rd Qu.: 95.50 3rd Qu.:0.4900 3rd Qu.:0.141
## Max. :125.90 Max. :0.5500 Max. :0.293
## NA's :1 NA's :1 NA's :1eucoaksed %>%
group_by(trtype) %>%
summarize(meanfines = mean(fines_g, na.rm=T), sdfines = sd(fines_g, na.rm=T),
meantotal = mean(total_g, na.rm=T), sdtotal = sd(total_g, na.rm=T))## # A tibble: 2 × 5
## trtype meanfines sdfines meantotal sdtotal
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 euc 14.2 3.50 48.6 35.0
## 2 oak 39.4 20.4 86.7 26.2eucoakLong <- eucoaksed %>%
pivot_longer(col=c(fines_g,litter_g),
names_to = "sed_type",
values_to = "sed_g")
eucoakLong %>%
ggplot(aes(trtype, sed_g, col=sed_type)) +
geom_boxplot()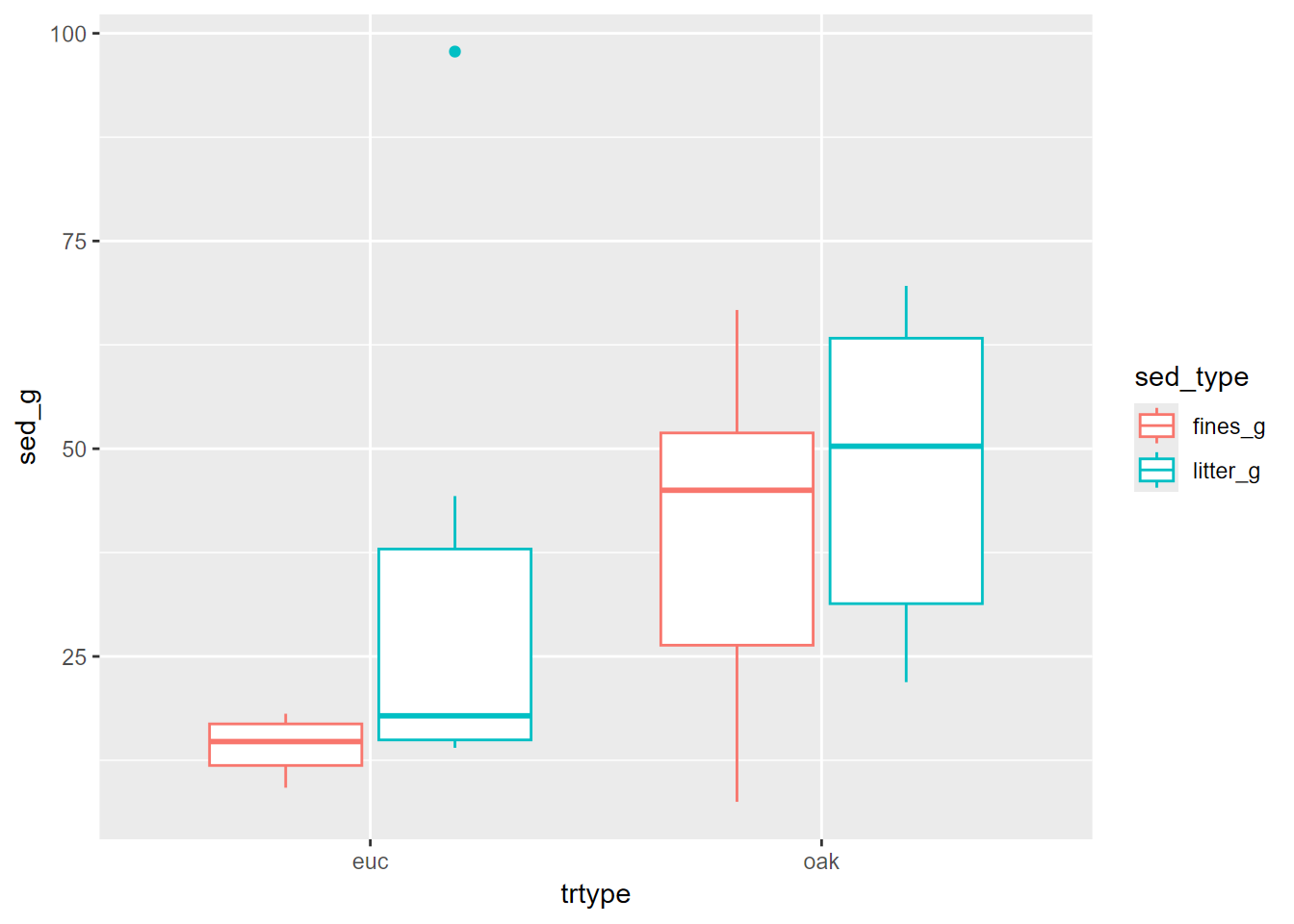
FIGURE 10.13: Eucalyptus and Oak sediment runoff box plots
eucoakLong %>%
ggplot(aes(sed_g, col=sed_type)) +
geom_density() +
facet_grid(trtype ~ .)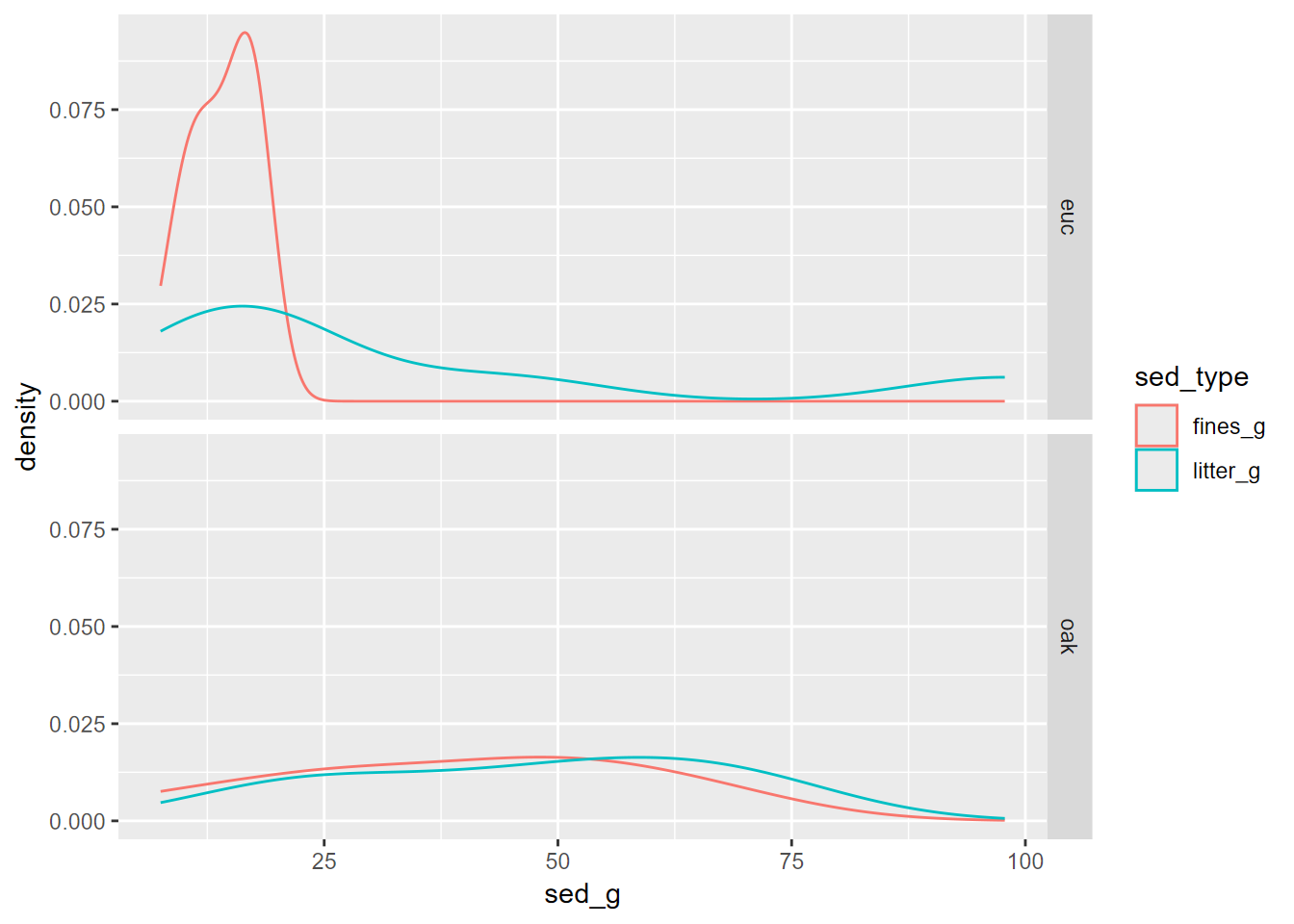
FIGURE 10.14: facet density plot of Eucalpytus and Oak sediment runoff
Tests of euc vs oak based on fine sediments:
shapiro.test(eucoaksed$fines_g[eucoaksed$trtype == "euc"])
shapiro.test(eucoaksed$fines_g[eucoaksed$trtype == "oak"])
t.test(fines_g~trtype, data=eucoaksed) ##
## Shapiro-Wilk normality test
##
## data: eucoaksed$fines_g[eucoaksed$trtype == "euc"]
## W = 0.9374, p-value = 0.6383##
## Shapiro-Wilk normality test
##
## data: eucoaksed$fines_g[eucoaksed$trtype == "oak"]
## W = 0.96659, p-value = 0.8729##
## Welch Two Sample t-test
##
## data: fines_g by trtype
## t = -3.2102, df = 6.4104, p-value = 0.01675
## alternative hypothesis: true difference in means between group euc and group oak is not equal to 0
## 95 percent confidence interval:
## -44.059797 -6.278299
## sample estimates:
## mean in group euc mean in group oak
## 14.21667 39.38571Tests of euc vs oak based on total sediments:
shapiro.test(eucoaksed$total_g[eucoaksed$trtype == "euc"])
shapiro.test(eucoaksed$total_g[eucoaksed$trtype == "oak"])
kruskal.test(total_g~trtype, data=eucoaksed) ##
## Shapiro-Wilk normality test
##
## data: eucoaksed$total_g[eucoaksed$trtype == "euc"]
## W = 0.76405, p-value = 0.02725##
## Shapiro-Wilk normality test
##
## data: eucoaksed$total_g[eucoaksed$trtype == "oak"]
## W = 0.94988, p-value = 0.7286##
## Kruskal-Wallis rank sum test
##
## data: total_g by trtype
## Kruskal-Wallis chi-squared = 3.449, df = 1, p-value = 0.06329So we used a t test for the fines_g, and the test suggests that there’s a significant difference in sediment yield for fines, but the Kruskal-Wallis test on total sediment (including litter) did not show a significant difference. Both results support the conclusion that oaks in this study produced more soil erosion, largely because the Eucalyptus stands generate so much litter cover, and that litter also made the total sediment yield not significantly different. See Thompson, Davis, and Oliphant (2016) for more information on this study and its conclusions.
10.4.2 Analysis of Variance
The purpose of Analysis of Variance (ANOVA) is to compare groups based upon continuous variables. It can be thought of as an extension of a t test where you have more than two groups, or as a linear model where one variable is a factor. In a confirmatory statistical test, you’ll want to see if you can reject the null hypothesis that there’s no difference between the within-sample variances and the between-sample variances.
- The response variable is a continuous variable
- The explanatory variable is the grouping – categorical (a factor in R)
From a study of a karst system in Tennessee (Jerry D. Davis and Brook 1993), we might ask the question
Are water samples from streams draining sandstone, limestone, and shale (Figure 10.15) different based on solutes measured as total hardness?

FIGURE 10.15: Water sampling in varying lithologies in a karst area
We can look at this spatially (Figure 10.16) as well as by variables graphically (Figure 10.17).
wChemData <- read_excel(ex("SinkingCove/SinkingCoveWaterChem.xlsx")) %>%
mutate(siteLoc = str_sub(Site,start=1L, end=1L))
wChemTrunk <- wChemData %>% filter(siteLoc == "T") %>%
mutate(siteType = "trunk")
wChemDrip <- wChemData %>% filter(siteLoc %in% c("D","S")) %>%
mutate(siteType = "dripwater")
wChemTrib <- wChemData %>% filter(siteLoc %in% c("B", "F", "K", "W", "P")) %>%
mutate(siteType = "tributary")
wChemData <- bind_rows(wChemTrunk, wChemDrip, wChemTrib)
sites <- read_csv(ex("SinkingCove/SinkingCoveSites.csv"))
wChem <- wChemData %>%
left_join(sites, by = c("Site" = "site")) %>%
st_as_sf(coords = c("longitude", "latitude"), crs = 4326)
library(terra)
tmap_mode("plot")
DEM <- rast(ex("SinkingCove/DEM_SinkingCoveUTM.tif"))
slope <- terrain(DEM, v='slope')
aspect <- terrain(DEM, v='aspect')
hillsh <- shade(slope/180*pi, aspect/180*pi, angle=40, direction=330)
bounds <- st_bbox(wChem)
xrange <- bounds$xmax - bounds$xmin
yrange <- bounds$ymax - bounds$ymin
xMIN <- as.numeric(bounds$xmin - xrange/10)
xMAX <- as.numeric(bounds$xmax + xrange/10)
yMIN <- as.numeric(bounds$ymin - yrange/10)
yMAX <- as.numeric(bounds$ymax + yrange/10)
#st_bbox(c(xmin = 16.1, xmax = 16.6, ymax = 48.6, ymin = 47.9), crs = st_crs(4326))
newbounds <- st_bbox(c(xmin=xMIN, xmax=xMAX, ymin=yMIN, ymax=yMAX), crs= st_crs(4326))
tm_shape(hillsh,bbox=newbounds) +
tm_raster(palette="-Greys",legend.show=F,n=20, alpha=0.5) + tm_shape(wChem) +
tm_symbols(size="TH", col="Lithology", scale=2, shape="siteType") +
tm_legend() +
tm_layout(legend.position = c("left", "bottom")) +
tm_graticules(lines=F)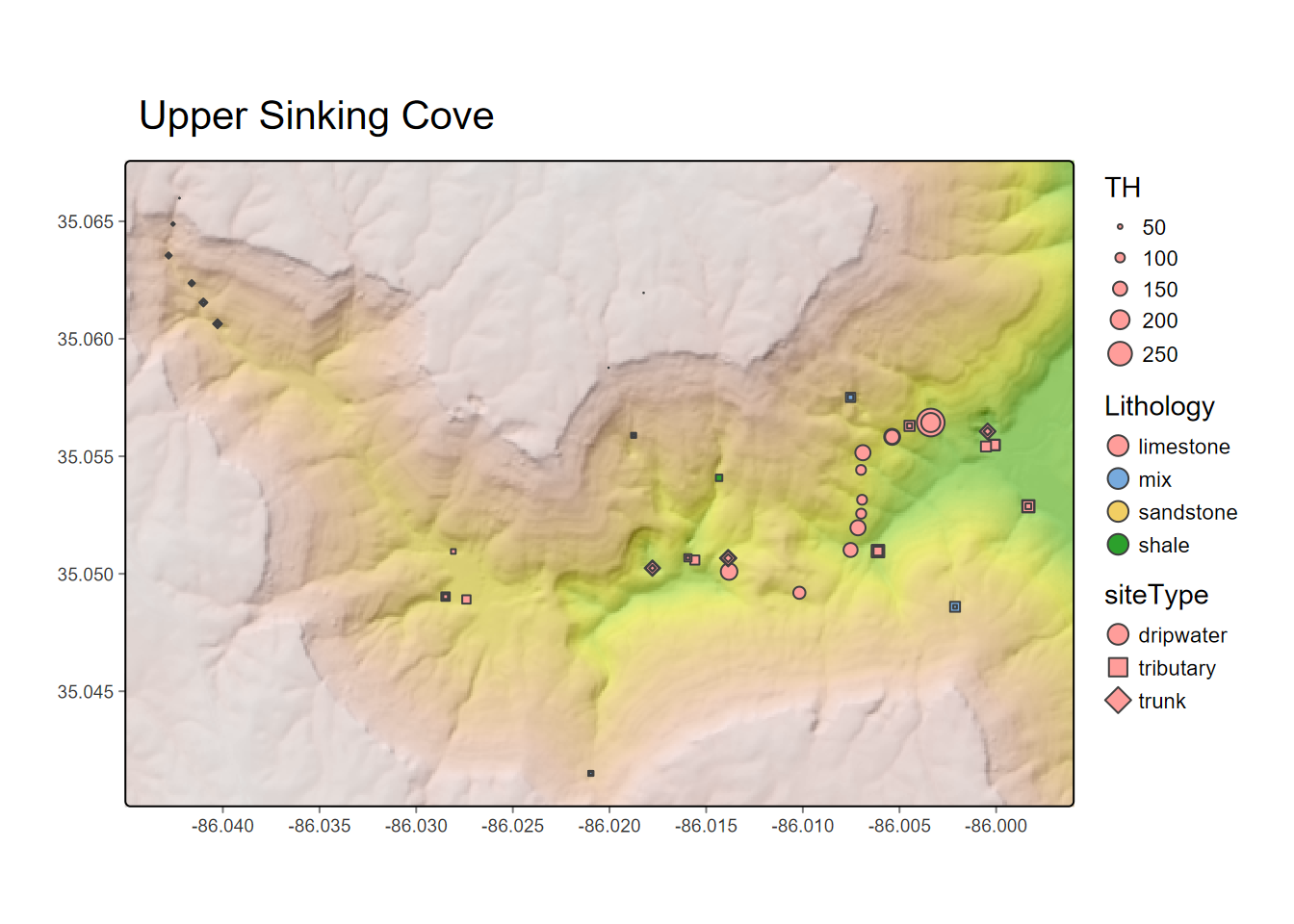
FIGURE 10.16: Total hardness from dissolved carbonates at water sampling sites in Upper Sinking Cove, TN
summary(aov(TH~siteType, data = wChemData))## Df Sum Sq Mean Sq F value Pr(>F)
## siteType 2 79172 39586 20.59 1.07e-07 ***
## Residuals 67 128815 1923
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(aov(TH~Lithology, data = wChemData))## Df Sum Sq Mean Sq F value Pr(>F)
## Lithology 3 98107 32702 19.64 3.28e-09 ***
## Residuals 66 109881 1665
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1wChemData %>%
ggplot(aes(x=TH, fill=siteType)) +
geom_histogram() +
facet_grid(Lithology ~ .)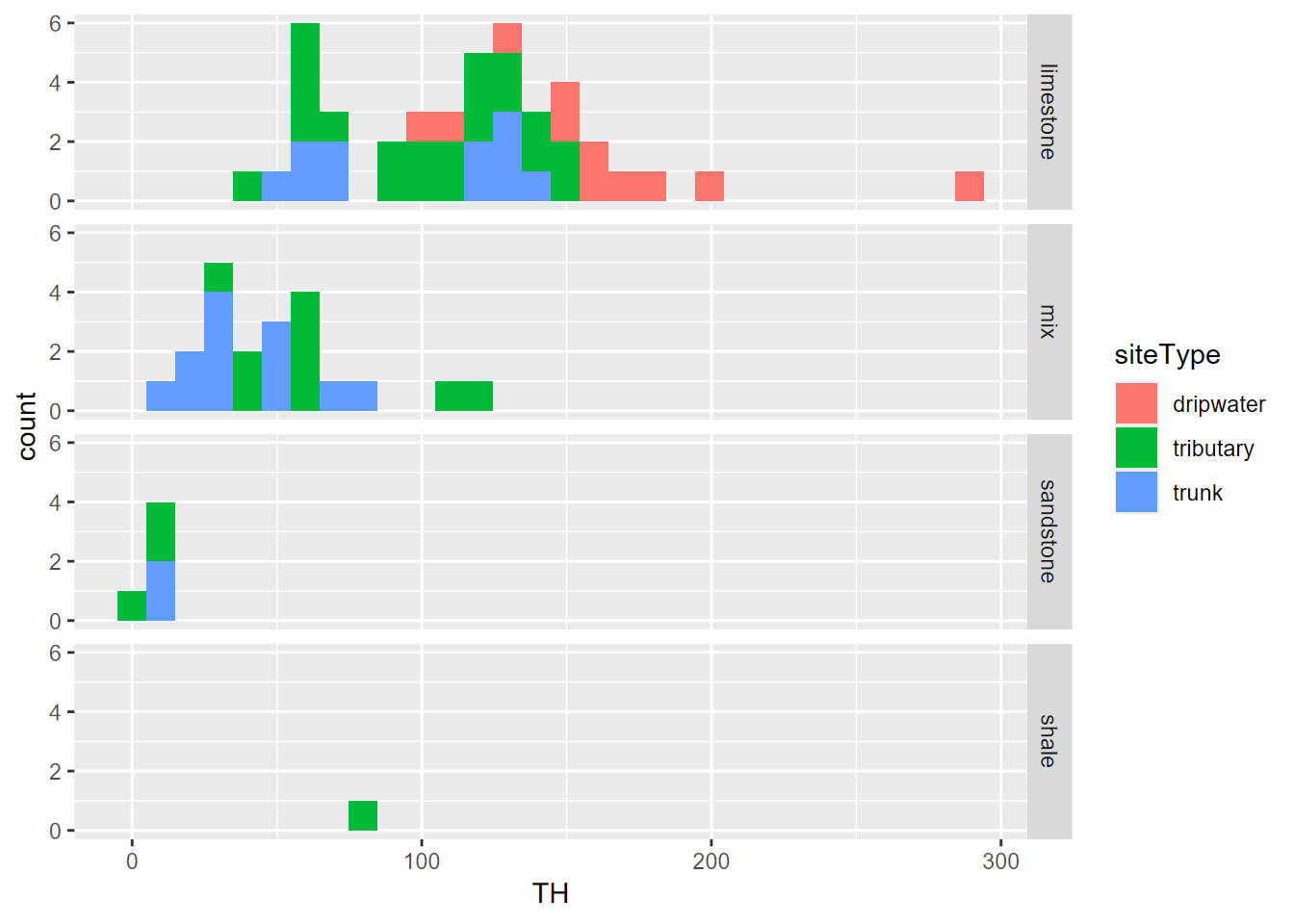
FIGURE 10.17: Sinking Cove dissolved carbonates as total hardness by lithology
Some observations and caveats from the above:
There’s pretty clearly a difference between surface waters (trunk and tributary) and cave dripwaters (from stalactites) in terms of solutes. Analysis of variance simply confirms the obvious.
There’s also pretty clearly a difference among lithologies on the basis of solutes, not surprising since limestone is much more soluble than sandstones. Similarly, analysis of variance confirms the obvious.
The data may not be sufficiently normally distributed, and limestone hardness values are bimodal (largely due to the inaccessibility of waters in the trunk cave passages travelling 2 km through the Bangor limestone 2), though analysis of variance may be less sensitive to this than a t test.
While shale creates springs, shale strata are very thin, with most of them in the “mix” category, or form the boundary between the two major limestone formations. Tributary streams appear to cross the shale in caves that were inaccessible for sampling. We visually confirmed this in one cave, but this exploration required some challenging rappel work to access, so we were not able to sample.
The geologic structure here is essentially flat, with sandstones on the plateau surface and the most massive limestones – the Bangor and Monteagle limestones – all below 400 m elevation (Figure 10.18).
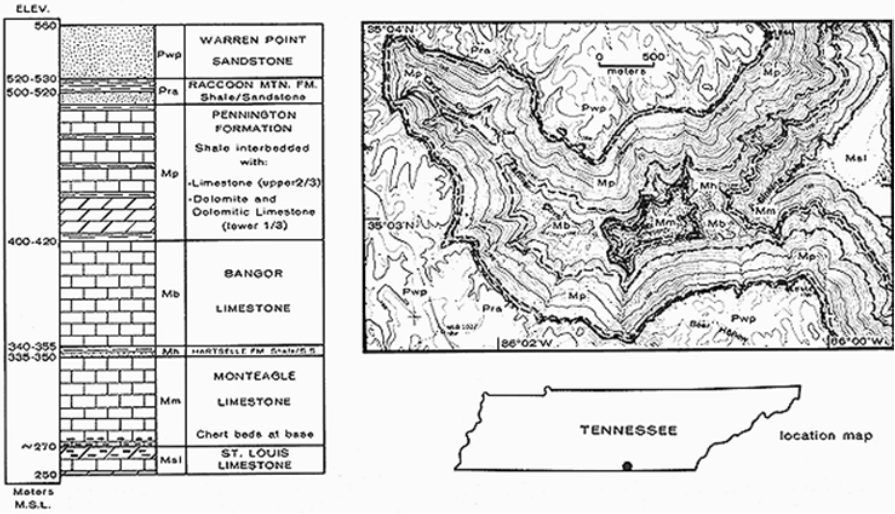
FIGURE 10.18: Upper Sinking Cove stratigraphy
- While the rapid increase in solutes happens when Cave Cove Creek starts draining through the much more soluble limestone until reaches saturation, the distance traveled by the water (reflected by a drop in elevation) can be seen (Figure 10.19).
wChemData %>%
ggplot(aes(x=Elevation, y=TH, col=Lithology)) +
geom_point() +
geom_smooth(method= "lm")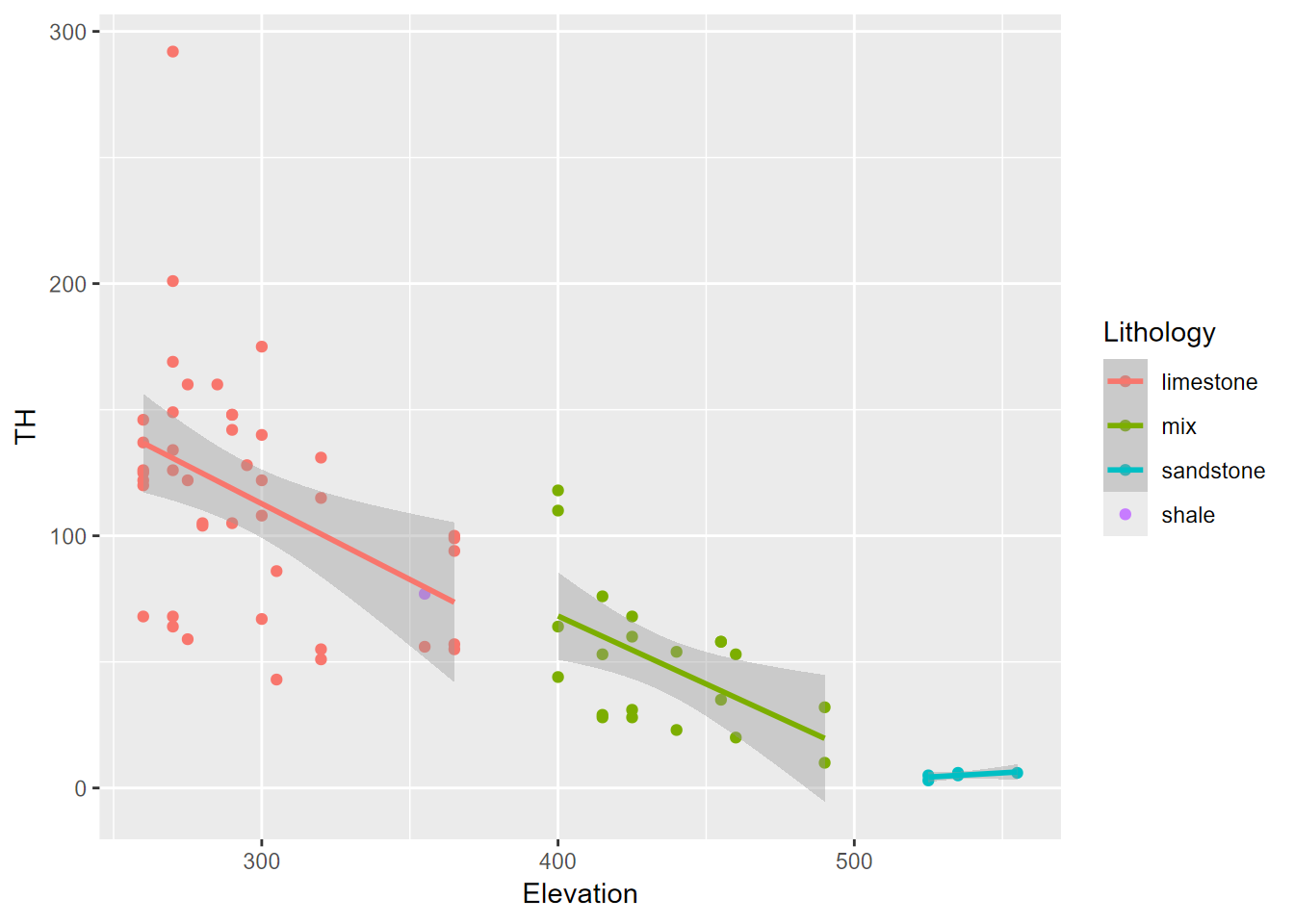
FIGURE 10.19: Sinking Cove dissolved carbonates as TH and elevation by lithology
10.4.3 Testing a correlation
We earlier looked at the correlation coefficient r. One test we can do is whether that correlation is significant:
cor.test(sierraFeb$TEMPERATURE, sierraFeb$ELEVATION)##
## Pearson's product-moment correlation
##
## data: sierraFeb$TEMPERATURE and sierraFeb$ELEVATION
## t = -20.558, df = 60, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.9609478 -0.8952592
## sample estimates:
## cor
## -0.9357801So we can reject the null hypothesis that the correlation is not equal to zero: the probability of the getting a correlation of -0.936 is less than \(2.2\times 10^{-16}\) and thus the “true correlation is not equal to 0”. So we can accept an alternative working hypothesis that they’re negatively correlated, and that – no surprise – it gets colder as we go to higher elevations, at least in February in the Sierra, where our data come from.
In the next chapter, we’ll use these data to develop a linear model and get a similar result comparing the slope of the model predicting temerature from elevation…
Exercises
Exercise 10.1 Build a soilvegJuly data frame.
- Create a new RStudio project named ‘Meadows’
- Create a soilveg tibble from “meadows/SoilVegSamples.csv” in the extdata.
- Have a look at this data frame and note that there is NA for SoilMoisture and NDVI for 8 of the records. These represent observations made in August, while the rest are all in July. While we have drone imagery and thus NDVI for these sites, but as they are during the senescent period we don’t want to compare these with the July samples.
- Filter the data frame to only include records that are not NA (!is.na) for SoilMoisture, and assign that to a new data frame ‘soilvegJuly’.
## # A tibble: 21 × 7
## Meadow id DominantVegetation veg BulkDensity SoilMoisture NDVI
## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 Loney L1 JUNNEV JUN 1.84 0.505 0.804
## 2 Loney L2 CARNEB CAR 0.916 0.711 0.849
## 3 Loney L3 upland UPL 3.08 0.296 0.838
## 4 Loney L4 JUNBAL JUN 3.90 0.239 0.756
## 5 Loney L5 JUNBAL JUN 1.63 0.508 0.865
## 6 Loney L6 grass GRA 2.59 0.366 0.84
## 7 Knuthson Q1 CARPEL CAR 0.31 0.433 0.833
## 8 Knuthson Q2 grass GRA 0.867 0.183 0.692
## 9 Knuthson Q3 JUNNEV JUN 0.942 0.114 0.665
## 10 Knuthson Q4 JUNNEV JUN 0.805 0.327 0.729
## # … with 11 more rowsExercise 10.2 Visualizations:
Create a scatter plot of Soil Moisture vs NDVI, colored by veg (the 3-character abbreviation of major vegetation types –
CARfor Carex/sedge,JUNfor Juncus/rush,GRAfor mesic grasses and forbs, andUPLfor more elevated (maybe by a meter) areas of sagebrush), forsoilvegJuly. What we can see is that this is a small sample. This study involved a lot of drone imagery, probably 100s of GB of imagery, which was the main focus of the study – to detect channels – but a low density of soil and vegetation ground samples.Create a histogram of soil moisture colored by veg, also for the July data. We see the same story, with not very many samples, though suggestive of a multimodal distribution overall.
Create a density plot of the same, using alpha=0.5 to see everything with transparency.
Exercise 10.3 Tests, July data
Using either aov() or anova(lm()), run an analysis of variance test of soil moisture ~ veg. Remember to specify the data, which should be just the July data., then do the same test for NDVI ~ veg.
Exercise 10.4 Meadow differences
- Now compare the meadows based on soil moisture in July, using a boxplot
- Then run an ANOVA test on this meadow grouping
Exercise 10.5 For the meadow data, create a pairs plot to find which variables are correlated along with their r values, and test the significance of that correlation and provide percentage of variation of one variable is explained by that of the other.
Exercise 10.6 Bulk density test, all data
We’ll now look at bulk density for all samples (soilveg), including both July and August. Soil moisture and NDVI won’t be a part of this analysis, only bulk density and vegetation. Look at the distribution of all bulk density values, using both a histogram with 20 bins and a density plot, then run an ANOVA test of bulk density predicted by (~) veg. What does the Pr(>F) value indicate?
Exercise 10.7 Carex or not?
Derive a bulkDensityCAR data frame by mutating a new variable CAR derived as a boolean result of veg == "CAR". This will group the vegetation points as either Carex or not, then use that in another ANOVA test to predict bulk density. What does the Pr(>F) value indicate?
References
We tried very hard to get into that cave that must extend from upper Cave Cove then under Farmer Cove to a spring in Wolf Cove – we have die traces to prove it↩︎