11 Modeling in R
The purpose of a statistical model is to help understand what variables might best predict a phenomenon of interest, which ones have more or less influence, define a predictive equation with coefficients for each of the variables, and then apply that equation to predict values using the same input variables for other areas. This process requires samples with observations of the explanatory (or independent) and response (or dependent) variables in question.
We’ll start with a simple linear model using our Sierra February climate data to model temperature (response variable) as predicted by elevation (explanatory variable):
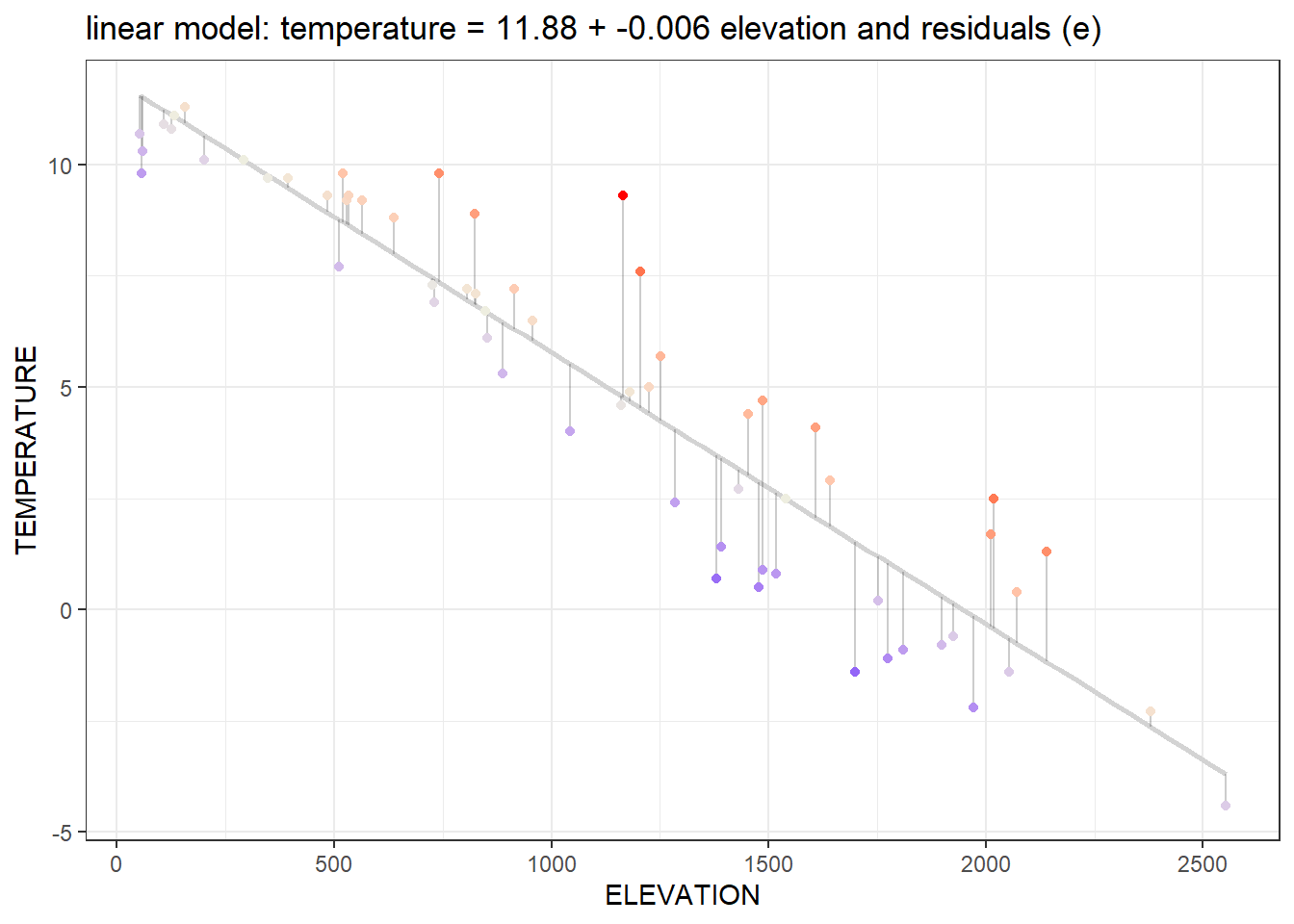
Figure 11.1: Linear model
11.1 Some common statistical models
There are many types of statistical models. Variables may be nominal (categorical) or interval/ratio data. You may be interested in predicting a continuous interval/ratio variable from other continuous variables, or predicting the probability of an occurrence (e.g. of a species), or maybe the count of something (also maybe a species). You may be needing to classify your phenomena based on continuous variables. Here are some examples:
lm(y ~ x)linear regression model with one explanatory variablelm(y ~ x1 + x2 + x3)multiple regression, a linear model with multiple explanatory variablesglm(y ~ x, family = poisson)generalized linear model, poisson distribution; see ?family to see those supported, including binomial, gaussian, poisson, etc.glm(y ~ x + y, family = binomial)glm for logistic regressionaov(y ~ x)analysis of variance (same as lm except in the summary)gam(y ~ x)generalized additive modelstree(y ~ x)orrpart(y ~ x)regression/classification trees
11.2 Linear model (lm)
If we look at the Sierra February climate example, the regression line in the graph above shows the response variable temperature predicted by the explanatory variable elevation. Here’s the code that produced the model and graph:
library(igisci); library(tidyverse)
sierra <- sierraFeb %>%
filter(!is.na(TEMPERATURE))
model1 = lm(TEMPERATURE ~ ELEVATION, data = sierra)
cc = model1$coefficients
sierra$resid = resid(model1)
sierra$predict = predict(model1)
eqn = paste("temperature =",
(round(cc[1], digits=2)), "+",
(round(cc[2], digits=3)), "elevation + e")
ggplot(sierra, aes(x=ELEVATION, y=TEMPERATURE)) +
geom_smooth(method="lm", se=FALSE, color="lightgrey") +
geom_segment(aes(xend=ELEVATION, yend=predict), alpha=.2) +
geom_point(aes(color=resid)) +
scale_color_gradient2(low="blue", mid="ivory2", high="red") +
guides(color="none") +
theme_bw() +
ggtitle(paste("Residuals (e) from model: ",eqn))The summary() function can be used to look at the results statistically:
summary(model1)##
## Call:
## lm(formula = TEMPERATURE ~ ELEVATION, data = sierra)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.9126 -1.0466 -0.0027 0.7940 4.5327
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.8813804 0.3825302 31.06 <2e-16 ***
## ELEVATION -0.0061018 0.0002968 -20.56 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.533 on 60 degrees of freedom
## Multiple R-squared: 0.8757, Adjusted R-squared: 0.8736
## F-statistic: 422.6 on 1 and 60 DF, p-value: < 2.2e-16Probably the most important statistic is the p value for the explanatory variable ELEVATION, which in this case is very small: \(<2.2\times10^{-16}\).
The graph shows not only the linear prediction line, but also the scatter plot of input points displayed with connecting offsets indicating the magnitude of the residual (error term) of the data point away from the prediction.
Making Predictions
We can use the linear equation and the coefficients derived for the intercept and the explanatory variable (and rounded a bit) to predict temperatures given the explanatory variable elevation, so:
\[ Temperature_{prediction} = 11.88 - 0.006{elevation} \]
So with these coefficients, we can apply the equation to a vector of elevations to predict temperature from those elevations:
a <- model1$coefficients[1]
b <- model1$coefficients[2]
elevations <- c(500, 1000, 1500, 2000)
elevations## [1] 500 1000 1500 2000tempEstimate <- a + b * elevations
tempEstimate## [1] 8.8304692 5.7795580 2.7286468 -0.3222645Next, we’ll plot predictions and residuals on a map.
11.3 Spatial Influences on Statistical Analysis
Spatial statistical analysis brings in the spatial dimension to a statistical analysis, ranging from visual analysis of patterns to specialized spatial statistical methods. There are many applications for these methods in environmental research, since spatial patterns are generally highly relevant. We might ask:
- What patterns can we see?
- What is the effect of scale?
- Relationships among variables – do they vary spatially?
In addition to helping to identify variables not considered in the model, the effect of local conditions and tendency of nearby observations to be related is rich for further exploration. Readers are encouraged to learn more about spatial statistics, and some methods are explored in Hijmans (n.d.).
But we’ll use a fairly straightforward method that can help enlighten us about the effect of other variables and the influence of proximity – mapping residuals. Mapping residuals is often enlightening since they can illustrate the influence of other variables. There’s even a recent blog on this: https://californiawaterblog.com/2021/10/17/sometimes-studying-the-variation-is-the-interesting-thing/?fbclid=IwAR1tfnj2SM_du6-jEd9h-AApRPO7w88TiPUbvTFz5dkagpQ1RMV04ZZYAr8
11.3.1 Mapping Residuals
If we start with a map of February temperatures in the Sierra and try to model these as predicted by elevation, we might see the following result. (First we’ll build the model again, though this is probably still in memory.)
library(tidyverse)
library(igisci)
library(sf)
sierra <- st_as_sf(filter(sierraFeb, !is.na(TEMPERATURE)), coords=c("LONGITUDE", "LATITUDE"), crs=4326)
modelElev <- lm(TEMPERATURE ~ ELEVATION, data = sierra)
summary(modelElev)##
## Call:
## lm(formula = TEMPERATURE ~ ELEVATION, data = sierra)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.9126 -1.0466 -0.0027 0.7940 4.5327
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.8813804 0.3825302 31.06 <2e-16 ***
## ELEVATION -0.0061018 0.0002968 -20.56 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.533 on 60 degrees of freedom
## Multiple R-squared: 0.8757, Adjusted R-squared: 0.8736
## F-statistic: 422.6 on 1 and 60 DF, p-value: < 2.2e-16We can see from the model summary that ELEVATION is significant as a predictor for TEMPERATURE, with a very low P value, and the R-squared value tells us that 87% of the variation in temperature might be “explained” by elevation. We’ll store the residual (resid) and prediction (predict), and set up our mapping environment to create maps of the original data, prediction, and residuals.
cc <- modelElev$coefficients
sierra$resid <- resid(modelElev)
sierra$predict <- predict(modelElev)
eqn = paste("temperature =",
(round(cc[1], digits=2)), "+",
(round(cc[2], digits=3)), "elevation")
ct <- st_read(system.file("extdata","sierra/CA_places.shp",package="igisci"))
ct$AREANAME_pad <- paste0(str_replace_all(ct$AREANAME, '[A-Za-z]',' '), ct$AREANAME)
bounds <- st_bbox(sierra)The original data
library(tmap); library(terra); library(igisci)
hillsh <- rast(ex("CA/ca_hillsh_WGS84.tif"))
tm_shape(hillsh, bbox=bounds) + tm_raster(palette="-Greys", style="cont", legend.show=F) +
tm_shape(st_make_valid(CA_counties)) + tm_borders() +
tm_shape(ct) + tm_dots() + tm_text("AREANAME", size=0.5, just=c("left","top")) +
tm_shape(sierra) + tm_symbols(col="TEMPERATURE", palette="-RdBu", size=0.5) +
tm_layout(legend.position=c("right","top")) +
tm_graticules(lines=F) +
tm_layout(main.title="February Normals",
main.title.position = c("right"), main.title.size = 0.8)
Figure 11.2: Original February temperature data
The prediction map
library(tmap)
tm_shape(hillsh, bbox=bounds) + tm_raster(palette="-Greys", style="cont", legend.show=F) +
tm_shape(st_make_valid(CA_counties)) + tm_borders() +
tm_shape(ct) + tm_dots() + tm_text("AREANAME", size=0.5, just=c("left","top")) +
tm_shape(sierra) + tm_symbols(col="predict", palette="-RdBu", size=0.5) +
tm_layout(legend.position=c("right","top")) +
tm_graticules(lines=F) +
tm_layout(main.title=eqn,
main.title.position = c("right"), main.title.size = 0.8)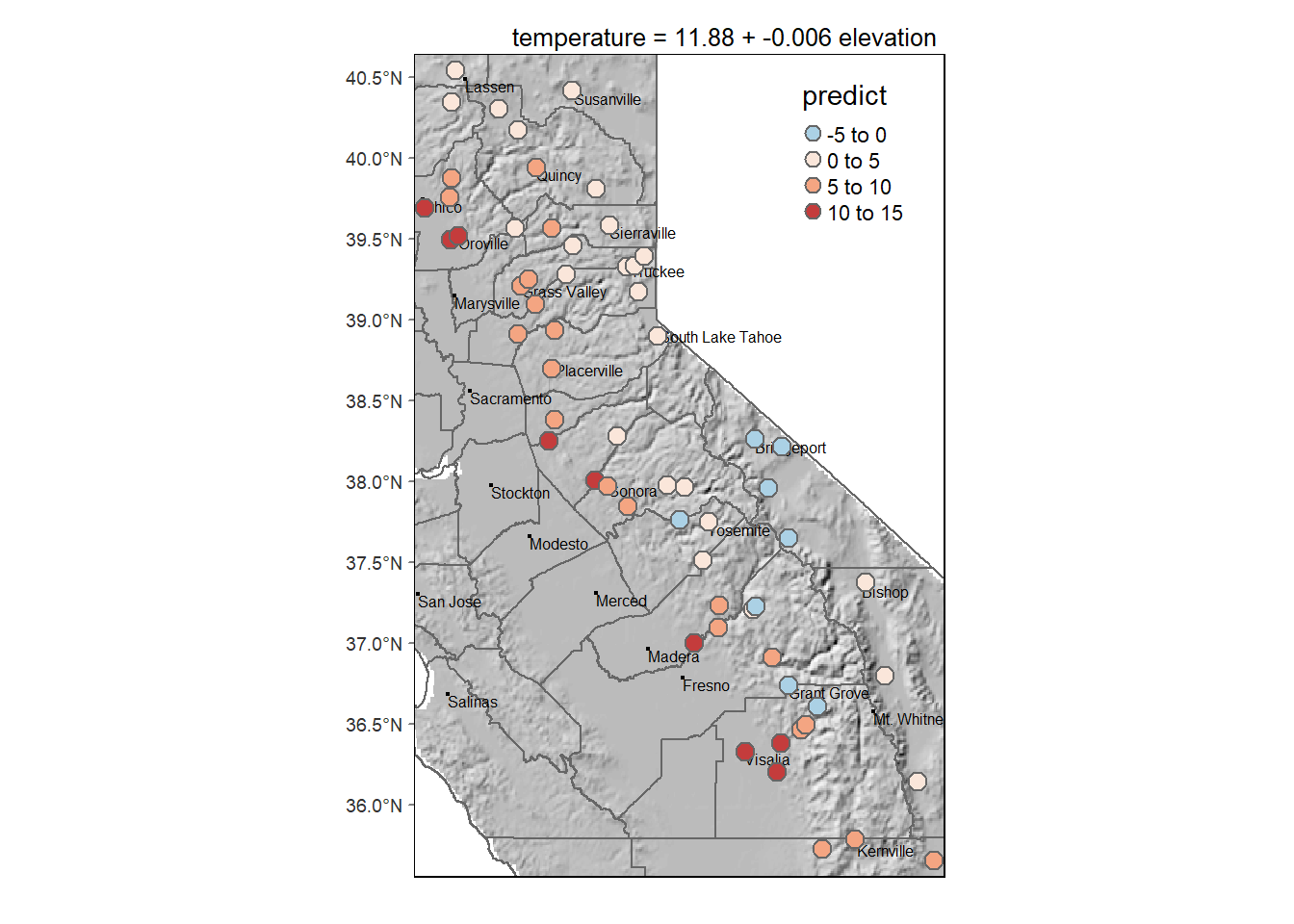
Figure 11.3: Temperature predicted by elevation model
We can also use the model to predict temperatures from a raster of elevations, which should match the elevations at the weather stations, allowing us to predict temperature for the rest of the study area. We should have more confidence in the area (the Sierra Nevada and nearby areas) actually sampled by the stations, so we’ll crop with the extent covering that area (though this will include more coastal areas that are likely to differ in February temperatures from patterns observed in the area sampled).
We’ll use GCS elevation raster data.
library(igisci)
library(tmap); library(terra)
elev <- rast(ex("CA/ca_elev_WGS84.tif"))
elevSierra <- crop(elev, ext(-122, -118, 35, 41)) # GCS
b0 <- coef(modelElev)[1]
b1 <- coef(modelElev)[2]
tempSierra <- b0 + b1 * elevSierra
names(tempSierra) = "Predicted Temperature"
#tempCA <- b0 + b1 * elev
tm_shape(tempSierra) + tm_raster(palette="-RdBu") + tm_graticules(lines=F) +
tm_legend(position = c("right", "top")) +
tm_shape(st_make_valid(CA_counties)) + tm_borders() +
tm_shape(ct) + tm_dots() + tm_text("AREANAME", size=0.5, just=c("left","top")) +
tm_layout(main.title=eqn,
main.title.position = c("right"), main.title.size = 0.7)
Figure 11.4: Temperature predicted by elevation raster
The residuals
library(tmap)
tm_shape(hillsh, bbox=bounds) + tm_raster(palette="-Greys", style="cont", legend.show=F) +
tm_shape(st_make_valid(CA_counties)) + tm_borders() +
tm_shape(ct) + tm_dots() + tm_text("AREANAME", size=0.5, just=c("left","top")) +
tm_shape(sierra) + tm_symbols(col="resid", palette="-RdBu", size=0.5) +
tm_layout(legend.position=c("right","top"),
main.title = paste("e from",eqn,"+ e"),
main.title.size = 0.7,
main.title.position = "right") +
tm_graticules(lines=F)
Figure 11.5: Residuals
Statistically, if the residuals from regression are spatially autocorrelated, we should look for patterns in the residuals to find other explanatory variables. However we can visually see, based upon the pattern of the residuals, that there’s at least one important explanatory variable not included in the model: latitude. We’ll leave that for you to look at in the exercises.
11.3.2 Analysis of Covariance
Analysis of Covariance, or ANCOVA, has the same purpose as Analysis of Variance that we looked at under tests earlier, but also takes into account the influence of other variables called covariates. In this way, analysis of covariance combines a linear model with an analysis of variance.
“Are water samples from streams draining sandstone, limestone, and shale different based on carbonate solutes, while taking into account elevation?”
Response variable is modeled from the factor (ANOVA) plus the covariate (regression)
ANOVA:
TH ~ rocktypewhereTHis total hardness, a measure of carbonate solutesRegression:
TH ~ elevationANCOVA:
TH ~ rocktype + elevation- Yet shouldn’t involve interaction between
rocktype(factor) andelevation(covariate):
- Yet shouldn’t involve interaction between
Example: stream types distinguished by discharge and slope
Three common river types are meandering, braided and anastomosed. For each, their slope varies by bankfull discharge in a relationship that looks something like:
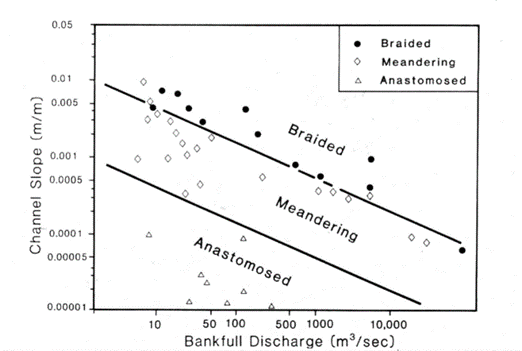
Figure 11.6: Slope by Q, river types

Figure 11.7: Braided river

Figure 11.8: Meandering river

Figure 11.9: Anastomosed river
Requirements:
- No relationship between discharge (covariate) and channel type (factor).
- Another interpretation: the slope of the relationship between the covariate and response variable is about the same for each group; only the intercept differs. Assumes parallel slopes.
log10(S) ~ strtype * log10(Q) … interaction between covariate and factor
log10(S) ~ strtype + log10(Q) … no interaction, parallel slopes
If models are not significantly different, remove interaction term due to parsimony, and satisfies this ANCOVA requirement.
library(tidyverse)
csvPath <- system.file("extdata","streams.csv", package="igisci")
streams <- read_csv(csvPath)
streams$strtype <- factor(streams$type, labels=c("Anastomosing","Braided","Meandering"))
summary(streams)## type Q S strtype
## Length:41 Min. : 6 Min. :0.000011 Anastomosing: 8
## Class :character 1st Qu.: 15 1st Qu.:0.000100 Braided :12
## Mode :character Median : 40 Median :0.000700 Meandering :21
## Mean : 4159 Mean :0.001737
## 3rd Qu.: 550 3rd Qu.:0.002800
## Max. :100000 Max. :0.009500ggplot(streams, aes(Q, S, color=strtype)) +
geom_point()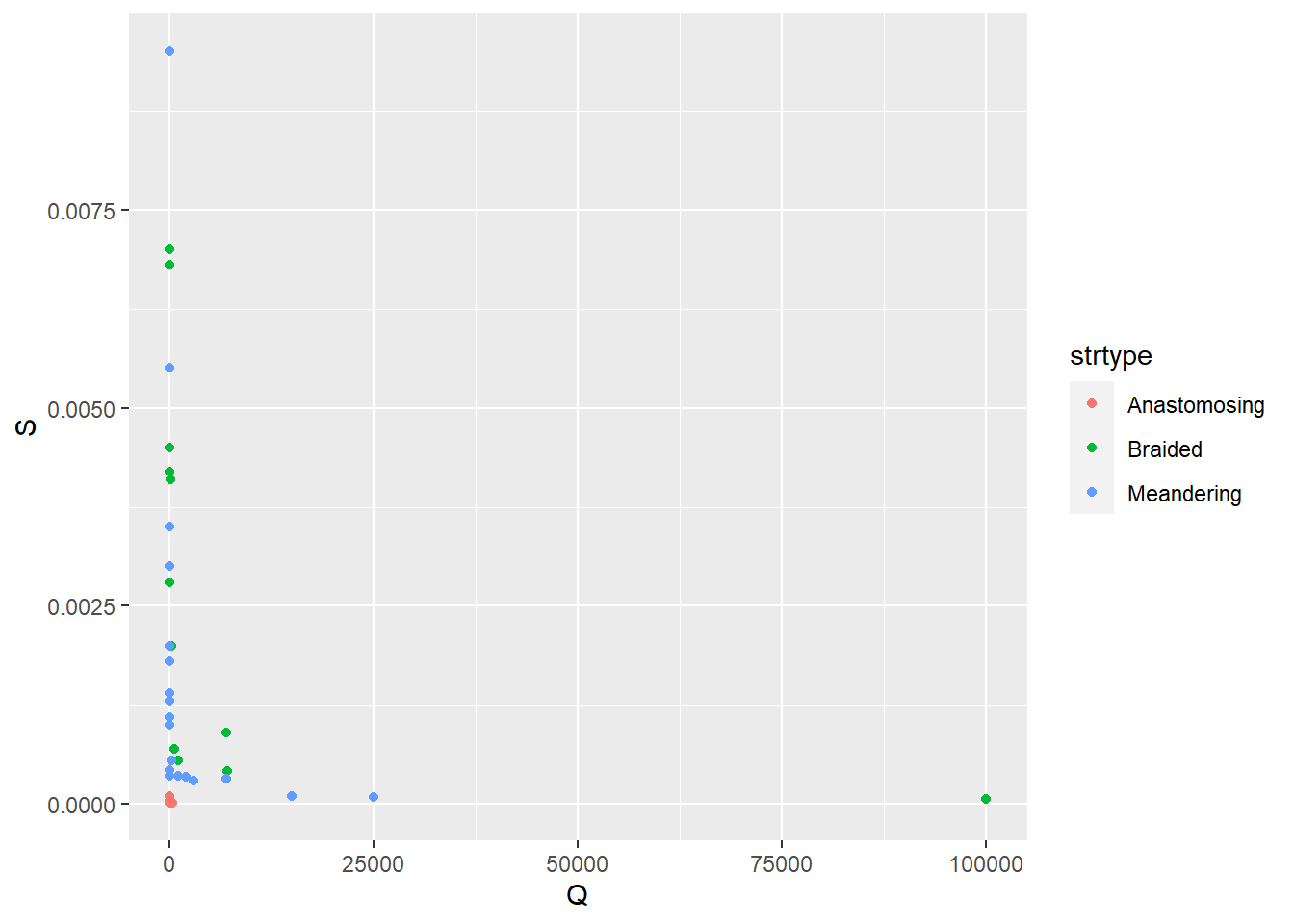
Figure 11.10: Q vs S: needs log scaling
library(scales) # needed for the trans_format function belowggplot(streams, aes(Q, S, color=strtype)) +
geom_point() + geom_smooth(method="lm", se = FALSE) +
scale_x_continuous(trans=log10_trans(),
labels = trans_format("log10", math_format(10^.x))) +
scale_y_continuous(trans=log10_trans(),
labels = trans_format("log10", math_format(10^.x)))
Figure 11.11: log scaled Q vs S with stream type
ancova = lm(log10(S)~strtype*log10(Q), data=streams)
summary(ancova)##
## Call:
## lm(formula = log10(S) ~ strtype * log10(Q), data = streams)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.63636 -0.13903 -0.00032 0.12652 0.60750
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.91819 0.31094 -12.601 1.45e-14 ***
## strtypeBraided 2.20085 0.35383 6.220 3.96e-07 ***
## strtypeMeandering 1.63479 0.33153 4.931 1.98e-05 ***
## log10(Q) -0.43537 0.18073 -2.409 0.0214 *
## strtypeBraided:log10(Q) -0.01488 0.19102 -0.078 0.9384
## strtypeMeandering:log10(Q) 0.05183 0.18748 0.276 0.7838
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2656 on 35 degrees of freedom
## Multiple R-squared: 0.9154, Adjusted R-squared: 0.9033
## F-statistic: 75.73 on 5 and 35 DF, p-value: < 2.2e-16anova(ancova)## Analysis of Variance Table
##
## Response: log10(S)
## Df Sum Sq Mean Sq F value Pr(>F)
## strtype 2 18.3914 9.1957 130.3650 < 2.2e-16 ***
## log10(Q) 1 8.2658 8.2658 117.1821 1.023e-12 ***
## strtype:log10(Q) 2 0.0511 0.0255 0.3619 0.6989
## Residuals 35 2.4688 0.0705
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Now an additive model, which does not have that interaction
ancova2 = lm(log10(S)~strtype+log10(Q), data=streams)
anova(ancova2)## Analysis of Variance Table
##
## Response: log10(S)
## Df Sum Sq Mean Sq F value Pr(>F)
## strtype 2 18.3914 9.1957 135.02 < 2.2e-16 ***
## log10(Q) 1 8.2658 8.2658 121.37 3.07e-13 ***
## Residuals 37 2.5199 0.0681
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(ancova,ancova2) # not significantly different, so simplification is justified## Analysis of Variance Table
##
## Model 1: log10(S) ~ strtype * log10(Q)
## Model 2: log10(S) ~ strtype + log10(Q)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 35 2.4688
## 2 37 2.5199 -2 -0.051051 0.3619 0.6989# Now we remove the strtype term
ancova3 = update(ancova2, ~ . - strtype)
anova(ancova2,ancova3) # Goes too far: removing strtype significantly different## Analysis of Variance Table
##
## Model 1: log10(S) ~ strtype + log10(Q)
## Model 2: log10(S) ~ log10(Q)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 37 2.5199
## 2 39 25.5099 -2 -22.99 168.78 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Alternatively, we can use R’s step method for a more automated approach.
ancova = lm(log10(S)~strtype*log10(Q), data=streams)
step(ancova)## Start: AIC=-103.2
## log10(S) ~ strtype * log10(Q)
##
## Df Sum of Sq RSS AIC
## - strtype:log10(Q) 2 0.051051 2.5199 -106.36
## <none> 2.4688 -103.20
##
## Step: AIC=-106.36
## log10(S) ~ strtype + log10(Q)
##
## Df Sum of Sq RSS AIC
## <none> 2.5199 -106.364
## - log10(Q) 1 8.2658 10.7857 -48.750
## - strtype 2 22.9901 25.5099 -15.455##
## Call:
## lm(formula = log10(S) ~ strtype + log10(Q), data = streams)
##
## Coefficients:
## (Intercept) strtypeBraided strtypeMeandering log10(Q)
## -3.9583 2.1453 1.7294 -0.4109ANOVA & ANCOVA are applications of a linear model. They use the lm model and the response variable is continuous and assumed normally distributed. The linear model for the stream types employing slope (S) and the covariate discharge (log10Q) was produced using:
mymodel <- lm(log10(S) ~ strtype + log10(Q))
Then as with standard ANOVA, we displayed the results using:
anova(mymodel)
11.4 Generalized Linear Model (GLM)
The glm in R allows you to work with various types of data using various distributions, described as families such as:
gaussian: normal distribution – what is used with lmbinomial: logit – used with probabilities.- used for logistic regression
poisson: for counts. Commonly used for species counts.
See help(glm) for other examples
11.4.1 Binomial family: Logistic GLM with streams
When the glm family is binomial, we might do what’s sometimes called logistic regression where we look at the probability of a categorical value (might be a species occurrence, for instance) given various independent variables.
A simple example of predicting a dog panting or not (a binomial, since the dog either panted or didn’t) related to temperature can be found at: https://bscheng.com/2016/10/23/logistic-regression-in-r/
Let’s try this with the streams data we just used for analysis of covariance, to predict the probability of a particular stream type from slope and discharge:
library(igisci)
library(tidyverse)
streams <- read_csv(ex("streams.csv"))
streams$strtype <- factor(streams$type, labels=c("Anastomosing","Braided","Meandering"))For logistic regression, we need probability data, so locations where we know the probability of something being true. If you think about it, that’s pretty difficult to know for an observation, but we might know whether something is true or not, like we observed the phenomenon or not, and so we just assign a probability of 1 if something is observed, and 0 if it’s not. Since in the case of the stream types, we really have three different probabilities: whether it’s true that the stream is anastomosing, whether it’s braided and whether it’s meandering, so we’ll create three dummy variables for that with values of 1 or 0: if it’s braided, the value for braided is 1, otherwise it’s 0; the same applies to all three dummy variables:
streams <- streams %>%
mutate(braided = ifelse(type == "B", 1, 0),
meandering = ifelse(type == "M", 1, 0),
anastomosed = ifelse(type == "A", 1, 0))
streams## # A tibble: 41 × 7
## type Q S strtype braided meandering anastomosed
## <chr> <dbl> <dbl> <fct> <dbl> <dbl> <dbl>
## 1 B 9.9 0.0045 Braided 1 0 0
## 2 B 11 0.007 Braided 1 0 0
## 3 B 16 0.0068 Braided 1 0 0
## 4 B 25 0.0042 Braided 1 0 0
## 5 B 40 0.0028 Braided 1 0 0
## 6 B 150 0.0041 Braided 1 0 0
## 7 B 190 0.002 Braided 1 0 0
## 8 B 550 0.0007 Braided 1 0 0
## 9 B 1100 0.00055 Braided 1 0 0
## 10 B 7100 0.00042 Braided 1 0 0
## # … with 31 more rowsThen we can run the logistic regression on each one:
summary(glm(braided ~ log(Q) + log(S), family=binomial, data=streams))##
## Call:
## glm(formula = braided ~ log(Q) + log(S), family = binomial, data = streams)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.00386 -0.49007 -0.00961 0.15789 1.58088
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 17.5853 6.7443 2.607 0.00912 **
## log(Q) 2.0940 0.8135 2.574 0.01005 *
## log(S) 4.3115 1.6173 2.666 0.00768 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 49.572 on 40 degrees of freedom
## Residual deviance: 23.484 on 38 degrees of freedom
## AIC: 29.484
##
## Number of Fisher Scoring iterations: 8summary(glm(meandering ~ log(Q) + log(S), family=binomial, data=streams))##
## Call:
## glm(formula = meandering ~ log(Q) + log(S), family = binomial,
## data = streams)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.5469 -1.2515 0.8197 1.1073 1.3072
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.43255 1.38078 1.762 0.0781 .
## log(Q) 0.04984 0.13415 0.372 0.7103
## log(S) 0.34750 0.19471 1.785 0.0743 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 56.814 on 40 degrees of freedom
## Residual deviance: 53.074 on 38 degrees of freedom
## AIC: 59.074
##
## Number of Fisher Scoring iterations: 4summary(glm(anastomosed ~ log(Q) + log(S), family=binomial, data=streams))##
## Call:
## glm(formula = anastomosed ~ log(Q) + log(S), family = binomial,
## data = streams)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.815e-05 -2.110e-08 -2.110e-08 -2.110e-08 2.244e-05
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -176.09 786410.69 0 1
## log(Q) -11.81 77224.35 0 1
## log(S) -24.18 70417.40 0 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 4.0472e+01 on 40 degrees of freedom
## Residual deviance: 1.3027e-09 on 38 degrees of freedom
## AIC: 6
##
## Number of Fisher Scoring iterations: 25So what we can see from this admittedly small sample is that:
- Predicting braided character from Q and S works pretty well, distinguishing these characteristics from the characteristics of all other streams (
braided==0) - Predicting anastomosed or meandering however isn’t significant.
We really need a larger sample size, and North American geomorphology has recently discovered the “anabranching” stream type (of which anastomosed is a type) that has long been recognized in Australia, and its characteristics range across meandering at least, so muddying the waters…
11.4.2 Logistic landslide model
With its active tectonics, steep slopes and relatively common intense rain events during the winter season, coastal California has a propensity for landslides. Pacifica has been the focus of many landslide studies by the USGS and others, with events ranging from coastal erosion influenced by wave action to landslides and debris flows on steep hillslopes driven by positive pore pressure (Ellen and Wieczorek (1988)).

Figure 11.12: Landslide in San Pedro Creek watershed

Figure 11.13: Sediment source analysis
Also see the relevant section in the San Pedro Creek Virtual Fieldtrip story map: J. Davis (n.d.).
Landslides detected in San Pedro Creek Watershed in Pacifica, CA, are in the SanPedro folder of extdata. Landslides were detected on aerial photography from 1941, 1955, 1975, 1983, and 1997, and confirmed in the field during a study in the early 2000’s (Sims (2004), J. Davis and Blesius (2015)). We’ll create a logistic regression to compare landslide probability to various environmental factors. We’ll use elevation, slope and other derivatives, distance to streams, distance to trails, and the results of a physical model predicting slope stability as a stability index (SI), using slope and soil transmissivity data.
library(igisci); library(sf); library(tidyverse); library(terra)
slides <- st_read(ex("SanPedro/slideCentroids.shp")) %>%
mutate(IsSlide = 1)
slides$Visible <- factor(slides$Visible)
trails <- st_read(ex("SanPedro/trails.shp"))
streams <- st_read(ex("SanPedro/streams.shp"))
wshed <- st_read(ex("SanPedro/SPCWatershed.shp"))ggplot(data=slides) + geom_sf(aes(col=Visible)) +
scale_color_brewer(palette="Spectral") +
geom_sf(data=streams, col="blue") +
geom_sf(data=wshed, fill=NA)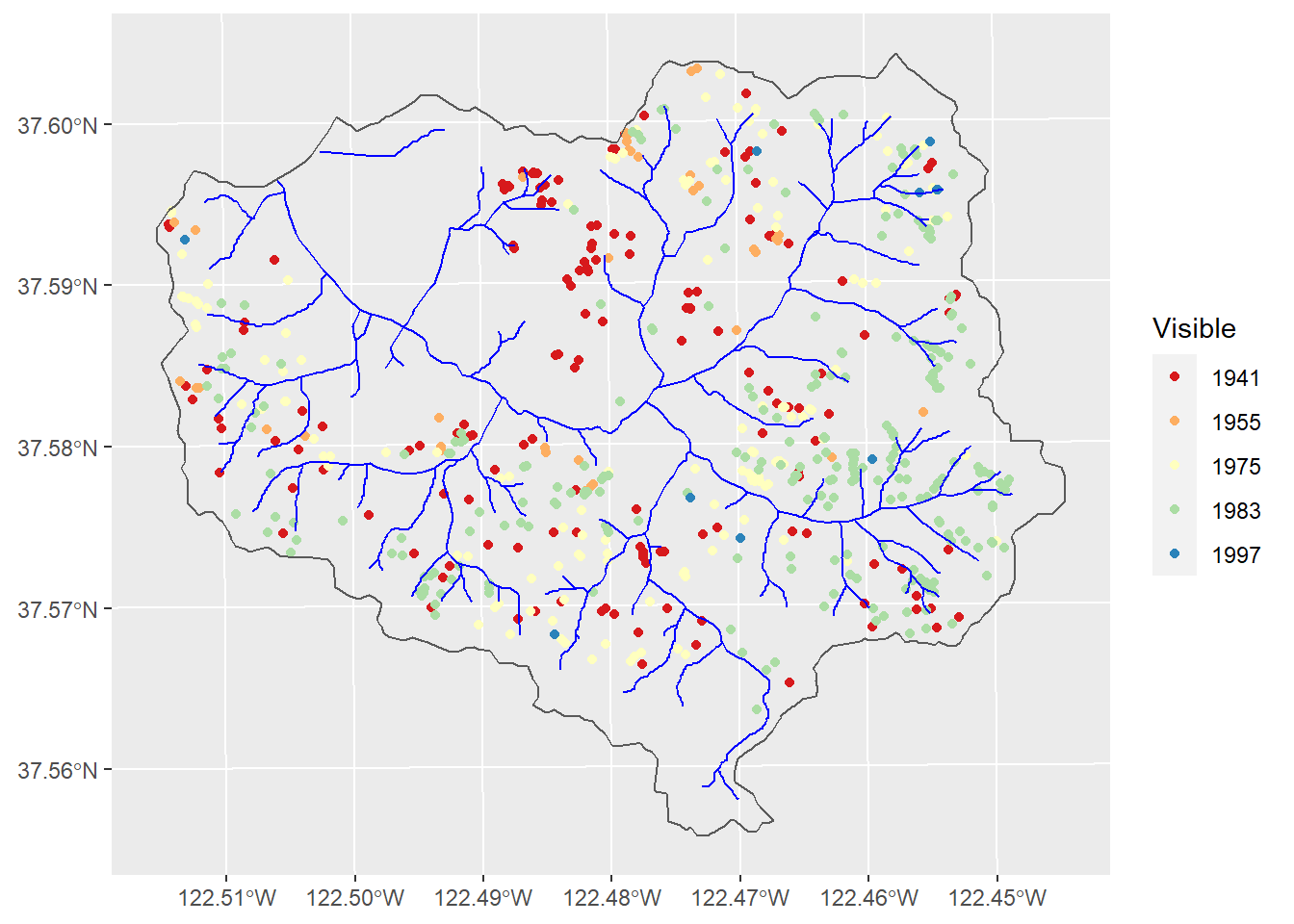
Figure 11.14: Landslides in San Pedro Creek watershed
At this point, we have data for occurrences of landslides, and so for each point we assign the dummy variable IsSlide = 1. We don’t have any absence data, but we can create some using random points and assign them IsSlide = 0. It would probably be a good idea to avoid areas very close to the occurrences, but we’ll just put random points everywhere and just remove the ones that don’t have SI data.
For the random locations, we’ll set a seed so for the book the results will stay the same; and if we’re good with that since it doesn’t really matter what seed we use, we might as well use the answer to everything: 42.
library(terra)
elev <- rast(ex("SanPedro/dem.tif"))
SI <- rast(ex("SanPedro/SI.tif"))
npts <- length(slides$Visible) * 2 # up it a little to get enough after clip
set.seed(42)
x <- runif(npts, min=xmin(elev), max=xmax(elev))
y <- runif(npts, min=ymin(elev), max=ymax(elev))
rsampsRaw <- st_as_sf(data.frame(x,y), coords = c("x","y"), crs=crs(elev))
ggplot(data=rsampsRaw) + geom_sf(size=0.5) +
geom_sf(data=streams, col="blue") +
geom_sf(data=wshed, fill=NA)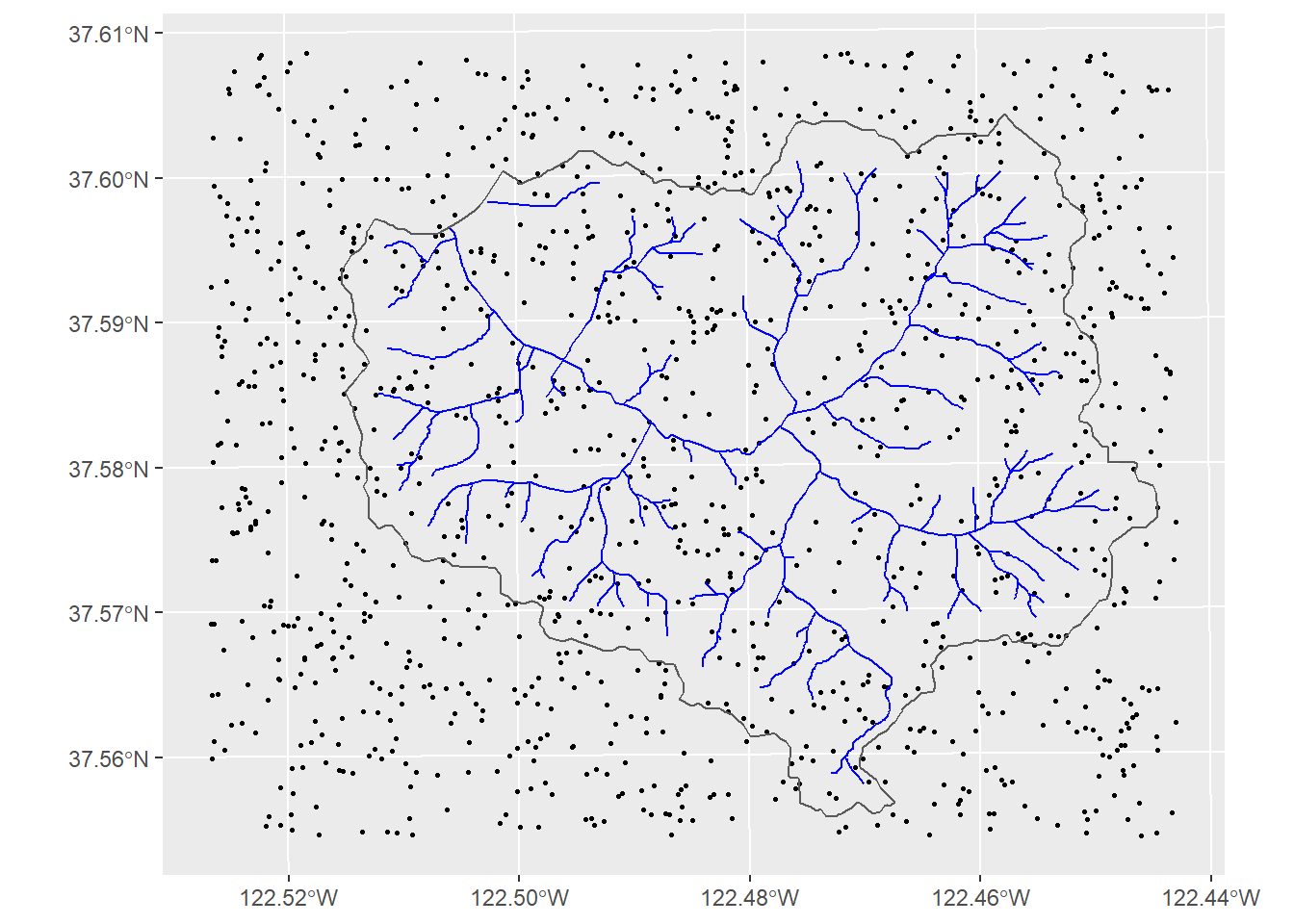
Figure 11.15: Raw random points
Now we have twice as many random points as we have landslides, within the rectangular extend of the watershed, as defined by the elevation raster. We doubled these because we need to exclude some points, yet still have enough to be roughly as many random points as slides. We’ll exclude:
- all points outside the watershed
- points within 100 m of the landslide occurrences, the distance based on knowledge of the grain of landscape features (like spurs and swales) that might influence landslide occurrence
slideBuff <- st_buffer(slides, 100)
wshedNoSlide <- st_difference(wshed, st_union(slideBuff))The 100 m buffer excludes all areas around all landslides in the data set. We’re going to run the model on specific years, but the best selection of landslide absences will be to exclude areas around all landslides we know of.
ggplot(data=slides) + geom_sf(aes(col=Visible)) +
scale_color_brewer(palette="Spectral") +
geom_sf(data=streams, col="blue") +
geom_sf(data=wshedNoSlide, fill=NA)
Figure 11.16: Landslides and buffers to exclude from random points
rsamps <- st_intersection(rsampsRaw,wshedNoSlide) %>%
mutate(IsSlide = 0)
allPts <- bind_rows(slides, rsamps)ggplot(data=allPts) + geom_sf(aes(col=IsSlide)) +
geom_sf(data=streams, col="blue") +
geom_sf(data=wshed, fill=NA)
Figure 11.17: Landslides and random points (excluded from slide buffers)
Now we’ll derive some environmental variables as rasters and extract their values to the slide/noslide point data set. We’ll use the shade function to create an exposure raster with the sun at the average noon angle from the south. Note the use of dplyr::rename to create meaningful variable names for rasters that had names like "lyr1" (who knows why?) which I determined by running it without the rename and seeing what it produced.
slidesV <- vect(allPts)
strms <- rasterize(vect(streams),elev)
tr <- rasterize(vect(trails),elev)
stD <- terra::distance(strms); names(stD) = "stD"
trD <- terra::distance(tr); names(trD) = "trD"
slope <- terrain(elev, v="slope")
curv <- terrain(slope, v="slope")
aspect <- terrain(elev, v="aspect")
exposure <- shade(slope/180*pi,aspect/180*pi,angle=53,direction=180)
elev_ex <- terra::extract(elev, slidesV) %>% rename(elev=dem) %>% dplyr::select(-ID)
SI_ex <- terra::extract(SI, slidesV) %>% dplyr::select(-ID)
slope_ex <- terra::extract(slope, slidesV) %>% dplyr::select(-ID)
curv_ex <- terra::extract(curv, slidesV) %>% rename(curv = slope) %>% dplyr::select(-ID)
exposure_ex <- terra::extract(exposure, slidesV) %>% rename(exposure=lyr1) %>% dplyr::select(-ID)
stD_ex <- terra::extract(stD, slidesV) %>% dplyr::select(-ID)
trD_ex <- terra::extract(trD, slidesV) %>% dplyr::select(-ID)
slidePts <- cbind(allPts,elev_ex,SI_ex,slope_ex,curv_ex,exposure_ex,stD_ex,trD_ex)
slidesData <- as.data.frame(slidePts) %>%
filter(!is.nan(SI)) %>% st_as_sf(crs=st_crs(slides))We’ll filter for just the slides in the 1983 imagery, and for the model also include all of the random points (detected with NA values for Visible):
slides83 <- slidesData %>% filter(Visible == 1983)
slides83plusr <- slidesData %>% filter(Visible == 1983 | is.na(Visible))The logistic regression in the glm model uses the binomial family:
summary(glm(IsSlide ~ SI + curv + elev + slope + exposure + stD + trD,
family=binomial, data=slides83plusr))##
## Call:
## glm(formula = IsSlide ~ SI + curv + elev + slope + exposure +
## stD + trD, family = binomial, data = slides83plusr)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.3819 -0.5882 -0.0002 0.7378 3.9146
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.1426071 1.0618610 0.134 0.89317
## SI -1.8190286 0.3639202 -4.998 5.78e-07 ***
## curv 0.0059237 0.0113657 0.521 0.60223
## elev -0.0025050 0.0014398 -1.740 0.08190 .
## slope 0.0623201 0.0211010 2.953 0.00314 **
## exposure 2.6971912 0.6603844 4.084 4.42e-05 ***
## stD -0.0052639 0.0019765 -2.663 0.00774 **
## trD -0.0020730 0.0006532 -3.174 0.00150 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 668.29 on 483 degrees of freedom
## Residual deviance: 402.90 on 476 degrees of freedom
## AIC: 418.9
##
## Number of Fisher Scoring iterations: 8So while we might want to make sure that we’ve picked the right variables, some conclusions from this might be that stability index (SI) is not surprisingly a strong predictor of landslides, but also that other than elevation and curvature, the other variables are also significant.
11.4.2.1 Map the logistic result
Should be able to, just need to use the formula for the model, which in our case will have 6 explanatory variables SI (\(X_1\)), elev (\(X_2\)), slope (\(X_3\)), exposure (\(X_4\)), stD (\(X_5\)) and trD (\(X_6\)): \[p = \frac{e^{b_0+b_1X_1+b_2X_2+b_3X_3+b_4X_4+b_5X_5}}{1+e^{b_0+b_1X_1+b_2X_2+b_3X_3+b_4X_4+b_5X_5}}\]
Then we retrieve the coefficients with coef() and use map algebra to create the prediction map, including dots for the landslides actually observed in 1983:
library(tmap)
SI_stD_model <- glm(IsSlide ~ SI + slope + exposure + stD + trD, family=binomial, data=slides83plusr)
b0 <- coef(SI_stD_model)[1]
b1 <- coef(SI_stD_model)[2]
b2 <- coef(SI_stD_model)[3]
b3 <- coef(SI_stD_model)[4]
b4 <- coef(SI_stD_model)[5]
b5 <- coef(SI_stD_model)[6]
predictionMap <- (exp(b0+b1*SI+b2*slope+b3*exposure+b4*stD+b5*trD))/
(1 + exp(b0+b1*SI+b2*slope+b3*exposure+b4*stD+b5*trD))
names(predictionMap) <- "slide_probability_1983"
tm_shape(predictionMap) + tm_raster() +
tm_shape(streams) + tm_lines(col="blue") +
tm_shape(wshed) + tm_borders(col="black") +
tm_shape(slides83) + tm_dots(col="green") +
tm_layout(title="Predicted by SI, slope, exposure, streamD, trailD") +
tm_graticules(lines=F)
Figure 11.18: Logistic model prediction of 1983 landslide probability
11.4.3 Poisson regression
Poission regression (family=poisson in glm) is for analyzing counts. You might use this to determine which variables are significant predictors, or you might want to see where or when counts are particularly high, or higher than expected. Or it might be applied to compare groupings. For example, if instead of looking at differences among rock types in Sinking Cove based on chemical properties in water samples or measurements (where we applied ANOVA), we looked at differences in fish counts, that might be an application of poisson regression, as long as other data assumptions hold.
- An explanation of the poisson distribution using meteor showers at: https://towardsdatascience.com/the-poisson-distribution-and-poisson-process-explained-4e2cb17d459
- An explanation of the poisson distribution applied to schooling data: https://stats.oarc.ucla.edu/r/dae/poisson-regression/
11.4.3.1 Seabird Poisson Model
This model is further developed in a case study where we’ll map a prediction, but we’ll look at the basics for applying a poisson family model in glm: seabird observations. The data is potentially suitable since it’s counts with known time intervals of observation effort and initial review of the data suggests that the mean counts is reasonably similar to the variance. The data were collected through the ACCESS program (Applied California Current Ecosystem Studies (n.d.)) and a thorough analysis provided by Studwell et al. (2017).
library(igisci); library(sf); library(tidyverse); library(tmap)
library(maptiles)
transects <- st_read(ex("SFmarine/transects.shp"))One of the seabirds studies, the black-footed albatross, has the lowest counts so a relatively rare bird, and studies of its distribution may be informative. We’ll look at counts collected during transect cruises in July 2006.
tmap_mode("plot")
oceanBase <- get_tiles(transects, provider="Esri.OceanBasemap")
transJul2006 <- transects %>% filter(month==7 & year==2006 & avg_tem>0 & avg_sal>0 & avg_fluo>0)
tm_shape(oceanBase) + tm_rgb() +
tm_shape(transJul2006) + tm_symbols(col="bfal", size="bfal")
Figure 11.19: Black-footed albatross counts, July 2006
Prior studies have suggested that temperature, salinity, fluorescence, depth and various distances might be good explanatory variables to use to look at spatial patterns, so we’ll use these in the model.
summary(glm(bfal~avg_tem+avg_sal+avg_fluo+avg_dep+dist_land+dist_isla+dist_200m+dist_cord, data=transJul2006,family=poisson))##
## Call:
## glm(formula = bfal ~ avg_tem + avg_sal + avg_fluo + avg_dep +
## dist_land + dist_isla + dist_200m + dist_cord, family = poisson,
## data = transJul2006)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.2935 -0.4646 -0.2445 -0.0945 4.7760
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.754e+02 7.032e+01 -2.495 0.01260 *
## avg_tem 7.341e-01 3.479e-01 2.110 0.03482 *
## avg_sal 5.202e+00 2.097e+00 2.480 0.01312 *
## avg_fluo -6.978e-01 1.217e+00 -0.574 0.56626
## avg_dep -3.561e-03 8.229e-04 -4.328 1.51e-05 ***
## dist_land -2.197e-04 6.194e-05 -3.547 0.00039 ***
## dist_isla 1.372e-05 1.778e-05 0.771 0.44043
## dist_200m -4.696e-04 1.037e-04 -4.528 5.95e-06 ***
## dist_cord -5.213e-06 1.830e-05 -0.285 0.77570
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 152.14 on 206 degrees of freedom
## Residual deviance: 105.73 on 198 degrees of freedom
## AIC: 160.37
##
## Number of Fisher Scoring iterations: 7We can see in the model coefficients table several predictive variables that appear to be significant, which we’ll explore further in the case study.
- avg_tem
- avg_sal
- avg_dep
- dist_land
- dist_200m
Note R will allow you to run glm on any family, but it’s up to you to make sure it’s appropriate. For example, if you provide a response variable that is not count data or doesn’t fit the requirements for a poisson model, R will create a result but it’s bogus.
11.5 Models Employing Machine Learning
Models using machine learning algorithms are commonly used in data science, fitting with its general exploratory and data-mining approach. There are many machine learning algorithms, and many resources for learning more about them, but they all share a basically black-box approach where a collection of variables are explored for patterns in input variables that help to explain a response variable. The latter is similar to more conventional statistical modeling describe above, with the difference being the machine learning approach – think of robots going through your data looking for connections.
We’ll explore machine learning methods in a later chapter when we attempt to use them to classify satellite imagery, an important environmental application. As this application is in the spatial domain, we might want to look further into spatial statistical methods.
Exercises
Exercise 11.1 Start by creating a new RStudio project “modeling” including a “data” folder we’ll use for the last question when you bring in your own data.
Exercise 11.2 Add LATITUDE as a second independent variable after ELEVATION in the model predicting February temperatures. Note that you’ll need to change a setting in the st_as_sf to not remove LATITUDE and LONGITUDE, and then you’ll need to change the lm regression formula to include both ELEVATION + LATITUDE. First derive and display the model summary results, and then answer the questions – is the explanation better based on the \(r^2\)?
Exercise 11.3 Now map the predictions and residuals.
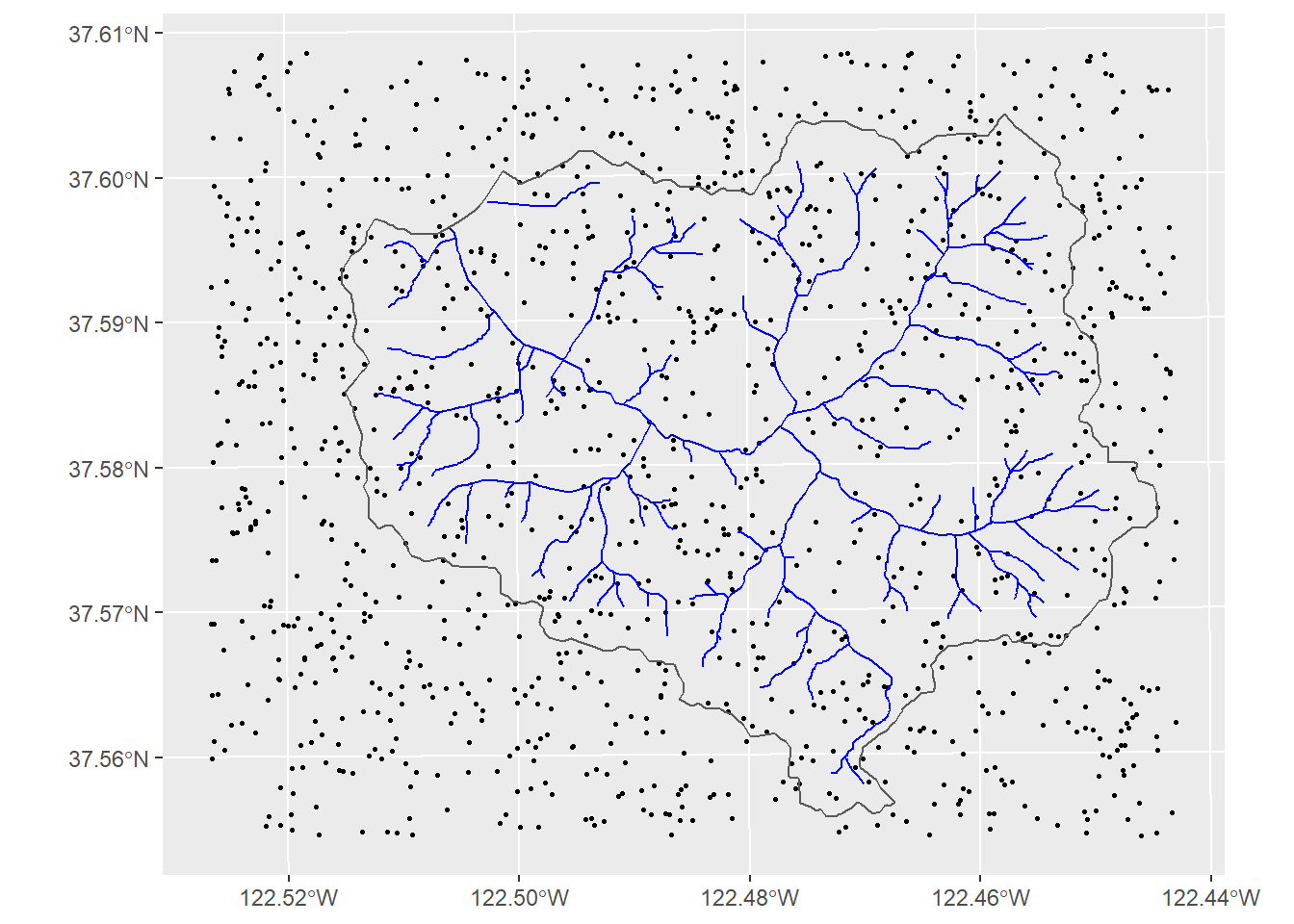
Figure 11.20: Goal
Exercise 11.4 Can you see any potential for additional variables? What evidence might there be for localized effects?
Exercise 11.5 Let’s build a prediction raster from the above model. Start by reading in the ca_elev_WGS84.tif raster as was done earlier, with the same crop, and again assigning it to elevSierra, and get the three coefficients b0, b1, and b2.
- Now use the following code to create a raster of the same dimensions as
elevSierra, but with latitude assigned as z values to the cells:
lats <- yFromCell(elevSierra, 1:ncell(elevSierra))
latitude <- setValues(elevSierra,lats)
plot(latitude)
Figure 11.21: Latitude raster
- Then build a raster prediction of temperature from the model and the two explanatory rasters.
Figure 11.22: Goal
Exercise 11.6 Modify the code for the San Pedro Creek Watershed logistical model to look at 1975 landslides. Are the conclusions different?
Exercise 11.7 Using your own data, that should have location information as well as other attributes, create a statistical model of your choice, and provide your assessment of the results, a prediction map, and where appropriate mapped residuals.
Exercise 11.8 Optionally, using your own data, no location data needed, create a glm binomial model. If you don’t have anything obvious, consider doing something like the study of a pet dog panting based on temperature. https://bscheng.com/2016/10/23/logistic-regression-in-r/