# Instalar el paquete (si no está instalado)
install.packages("pedtools")
# Cargar la librería
library(pedtools)Utilidad de R en ciencias forenses
En R existen muchas librerías de utilidad para las ciencias forenses, algunas de ellas son:
strvalidator: Esta librería se utiliza para validar marcadores STR y comparar perfiles genéticos.pedtools: Es un conjunto de paquetes enfocados en el análisis de pedigríes, útil para análisis de relaciones familiares, como paternidad o parentesco. Los paquetes más importantes dentro de esta suite son:pedigree: Para análisis de relaciones familiares.bdsim: Para simulación de identidades por descendencia (IBD).
forrel: Este paquete está diseñado específicamente para genética forense. Permite realizar análisis de pruebas de parentesco utilizando el método de razón de verosimilitud (LR). DNAtools: Proporciona herramientas para análisis probabilísticos de perfiles genéticos forenses, con enfoque en el cálculo de LR.relMix: Orientado a casos de mezcla de ADN (cuando hay ADN de múltiples individuos en una muestra), común en genética forense.haplo.stats: Útil para el análisis de haplotipos, que son series de alelos en cromosomas relacionados entre sí, y pueden ser usados en estudios de linajes.
En este documento nos vamos a enfocar en la librería pedtools para realizar un análisis de parentesco y de relaciones familiares.
Librería pedtools
“El objetivo de pedtools es proporcionar un conjunto de herramientas liviano pero completo para crear, manipular y visualizar pedigríes con o sin datos de marcadores. Las estructuras de pedigrí comunes se generan rápidamente con funciones personalizadas, mientras que una variedad de utilidades permiten modificaciones como agregar o eliminar individuos, extraer subconjuntos, romper bucles y fusionar pedigríes. La función de trazado importa maquinaria del paquete kinship2”.
https://github.com/magnusdv/pedtools
Con las siguientes lineas de código vamos a generar un pedigrí básico
# Crear un pedigrí básico
ped <- nuclearPed(father = "Padre", mother = "Madre", children = "Hijo 1")
# nuclearPed genera un pedigrí nuclear con una familia básica de padre, madre e hijoCon el siguiente código podemos graficar:
plot(ped)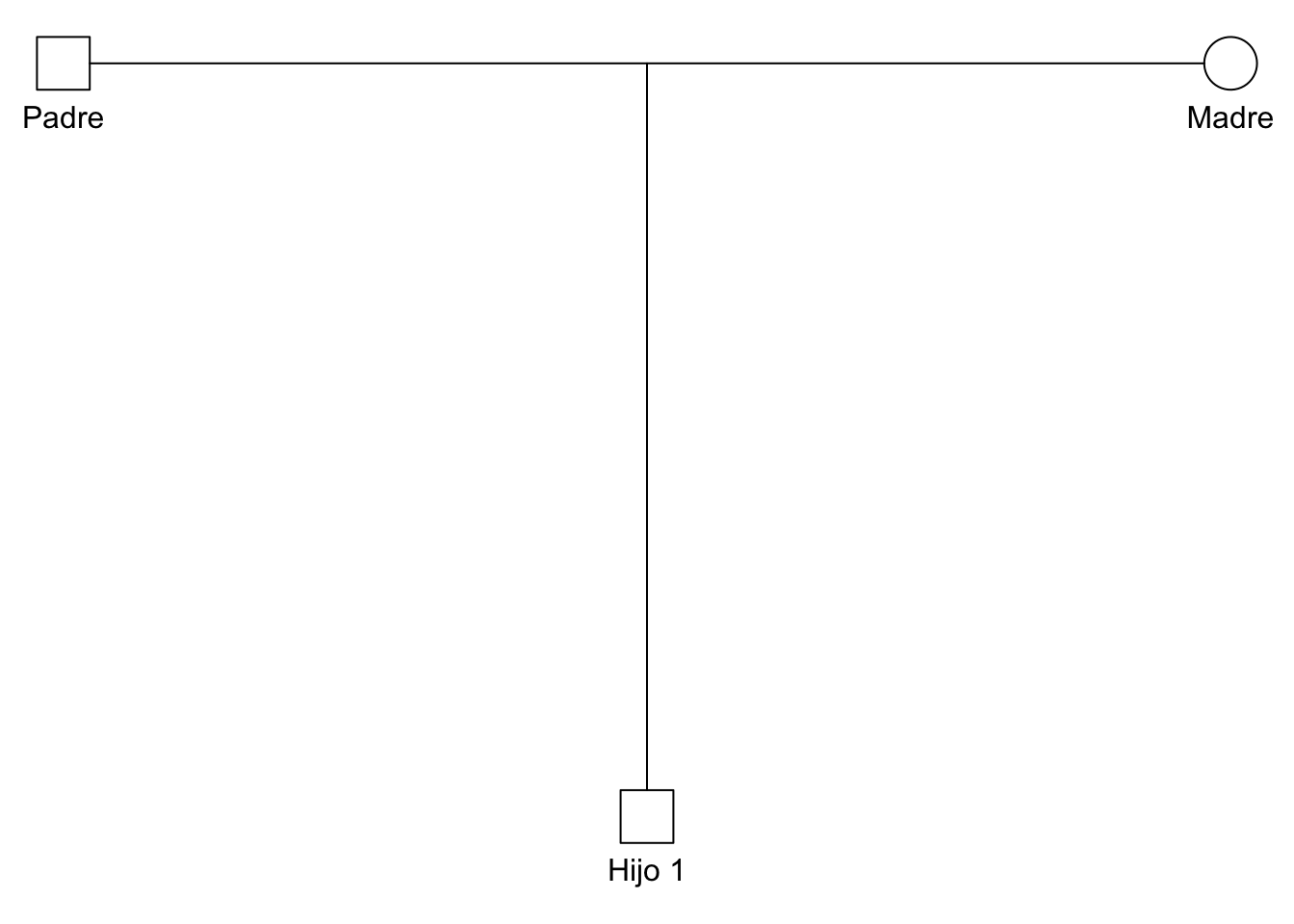
Podemos modificar nuestro pedigrí para agregar más hijos:
# Crear un pedigrí modificado
ped <- nuclearPed(father = "Padre", mother = "Madre",
children = c("Hijo 1", "Hijo 2"),
sex = c(1,2))
# Crear un pedigrí básico con un padre, una madre y dos hijos.
# 'nuclearPed' crea una familia nuclear con los padres y los hijos.
# Especificamos los nombres del padre y la madre, así como los nombres de los hijos.
# El argumento 'sex' indica el sexo de los hijos: 1 para masculino y 2 para femenino (según la convención en genética).
plot(ped)
Se pueden añadir más hijos y especificar el sexo de cada uno:
# Crear un pedigrí con más generaciones
ped <- nuclearPed(father = "Abuelo", mother = "Abuela",
children = c("Padre", "Tío"),nch = 4)Ahora podemos añadir más hijos al pedigrí:
ped <- addChildren(x = ped, father = "Padre",
mother = "Madre", nch = 4, sex=c(1,2,1,1), ids = c("Hijo 1", "Hijo 2", "Hijo 3", "Hijo 5"))Creating new mother: Madre# Mostrar el pedigrí
plot(ped)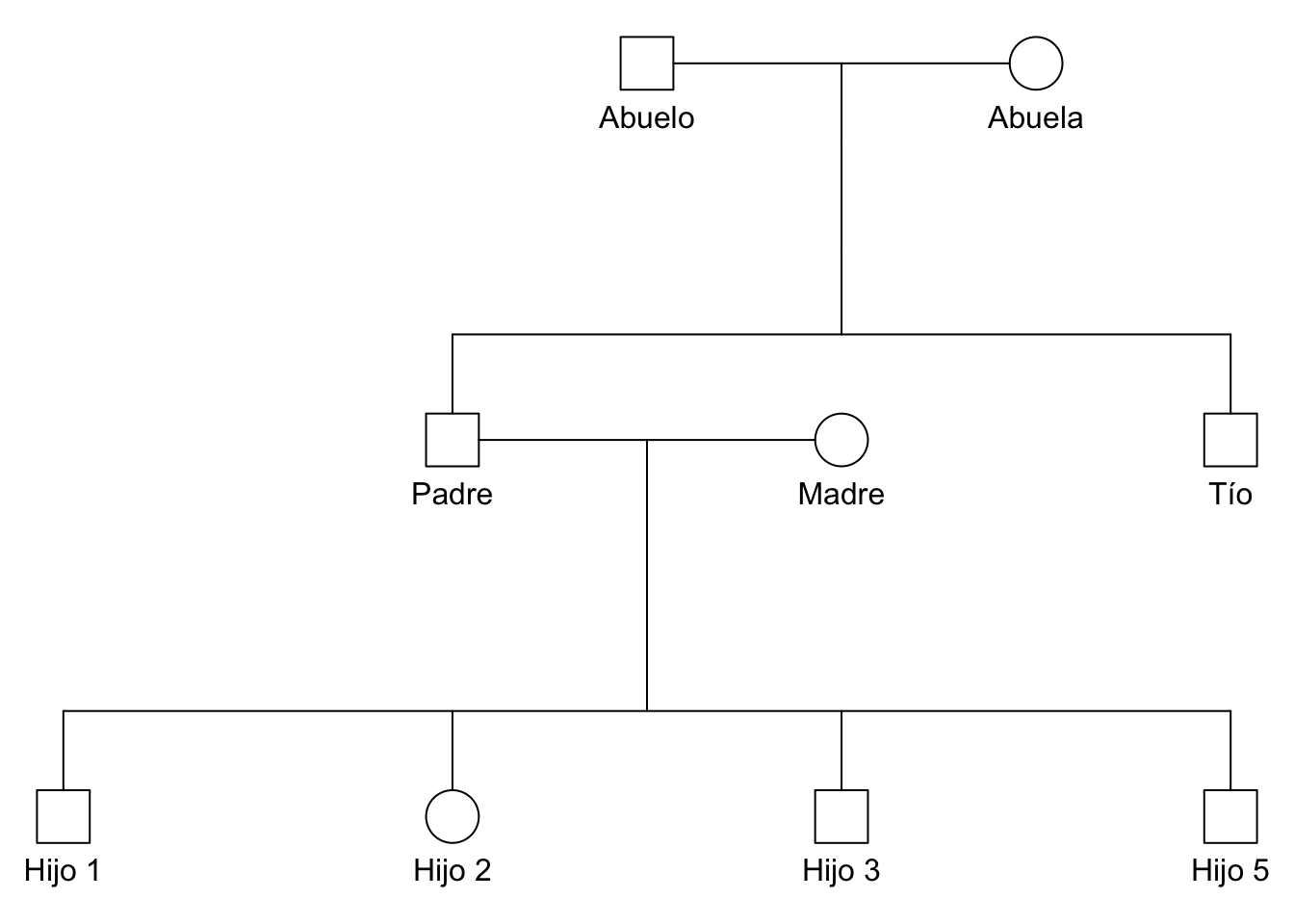
El siguiente ejemplo ilustra una creación paso a paso de un pedigrí con un objeto marcador:
library(pedtools)
# Start with two half brothers
x = halfSibPed(type = "paternal")
# Make 5 female
x = swapSex(x, 5)
# Add a sister to 5 (parents are 2 and 3)
x = addDaughter(x, parents = 2:3)
# Add inbred child
x = addSon(x, parents = 4:5)
# Create marker
x = addMarker(x, "7" = "a/b")
# Plot pedigree with genotypes
plot(x, marker = 1, hatched = 7)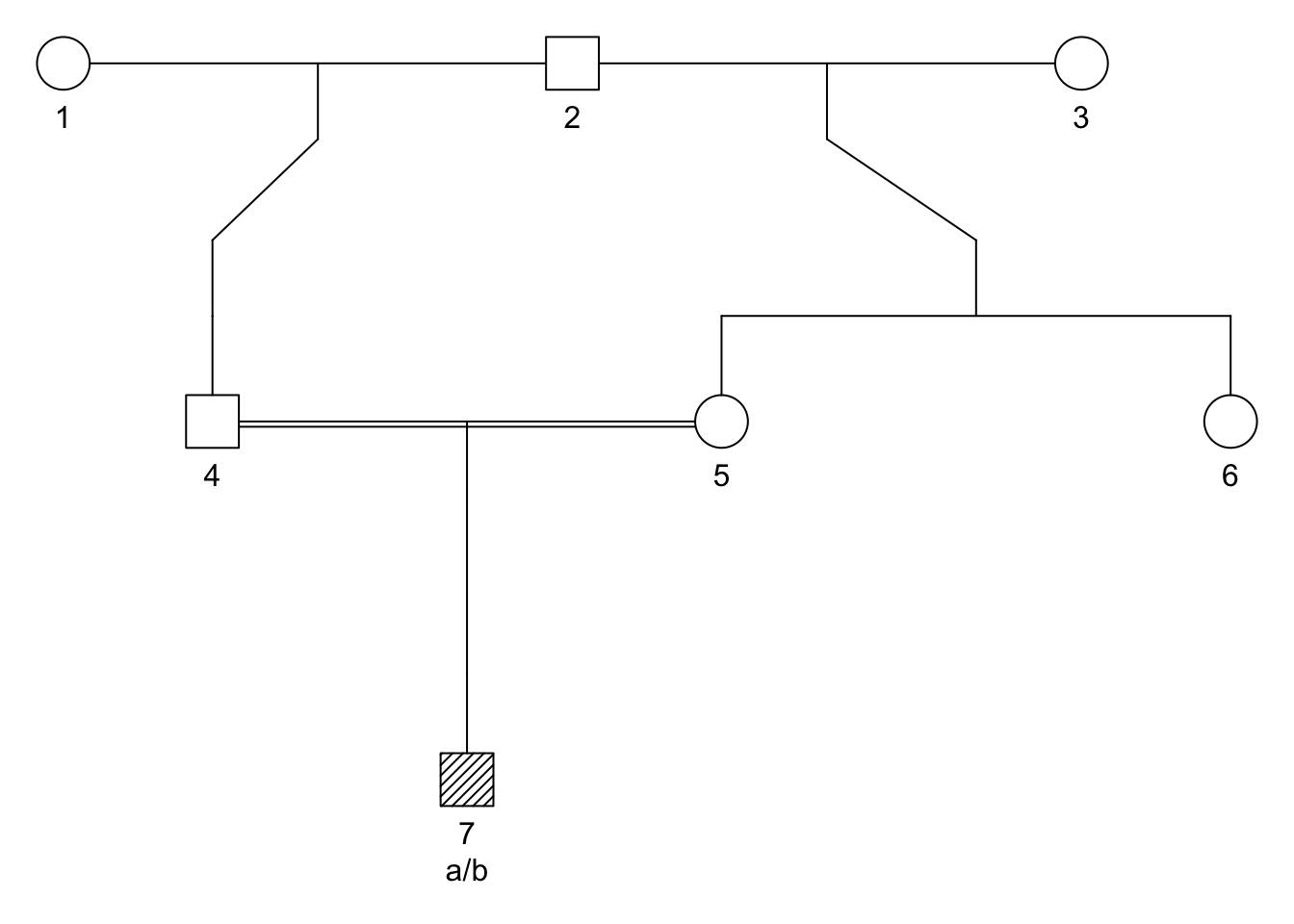
Utilizando pipes el código anterior se puede simplificar:
x = halfSibPed(type = "paternal") |>
swapSex(5) |>
addDaughter(parents = 2:3) |>
addSon(parents = 4:5) |>
addMarker("7" = "a/b")Prueba de parentesco para paternidad usando forrel
La librería forrel es una herramienta útil para realizar análisis de pruebas de parentesco utilizando el método de razón de verosimilitud (LR). En este ejemplo, vamos a utilizar forrel para realizar una prueba de paternidad.
El siguiente ejemplo fue tomado de: https://github.com/magnusdv/forrel
Primero demostramos la simulación de datos de marcadores para un par de hermanos. Luego, fingiendo que la relación es desconocida para nosotros, estimamos la relación entre los hermanos utilizando los datos simulados. Si todo va bien, la estimación debería estar cerca del valor esperado para los hermanos.
# Llamar a librería
library(forrel)Warning: package 'forrel' was built under R version 4.4.1Comenzamos creando y trazando un pedigrí con dos hermanos, llamados bro1y bro2
x = nuclearPed(children = c("bro1", "bro2"))
plot(x)
Ahora simulemos los genotipos de 100 SNP independientes para los cuatro miembros de la familia. Cada SNP tiene los alelos 1 y 2, con frecuencias iguales por defecto. Este es un ejemplo de simulación incondicional , ya que no damos ningún genotipo para condicionar.
x = markerSim(x, N = 100, alleles = 1:2, seed = 1234, verbose = FALSE)
#> Unconditional simulation of 100 autosomal markers.
#> Individuals: 1, 2, bro1, bro2
#> Allele frequencies:
#> 1 2
#> 0.5 0.5
#> Mutation model: No
#>
#> Simulation finished.
#> Calls to `likelihood()`: 0.
#> Total time used: 0.02 seconds.Explicación línea por línea:markerSim(x, N = 100, alleles = 1:2, seed = 1234):
x: El pedigrí ya existente que contiene a los cuatro individuos. -N = 100: Se especifica que se quieren simular 100 marcadores.alleles = 1:2: Define los alelos posibles para cada SNP, en este caso los alelos “1” y “2”, con frecuencias alélicas iguales (0.5 para cada alelo, por defecto).seed = 1234: Establece una semilla aleatoria para garantizar que los resultados sean reproducirles. Es decir, cada vez que se ejecute el código con esta semilla, se obtendrán los mismos resultados.
Podemos llamar a nuestros datos simulados:
print(x)FALSE id fid mid sex <1> <2> <3> <4> <5>
FALSE 1 * * 1 1/2 1/2 1/1 2/2 2/2
FALSE 2 * * 2 1/1 1/2 1/1 1/1 2/2
FALSE bro1 1 2 1 1/1 1/2 1/1 1/2 2/2
FALSE bro2 1 2 1 1/1 1/2 1/1 1/2 2/2FALSE Only 5 (out of 100) markers are shown.Supongamos que uno de los hermanos es homocigoto 1/1 y que queremos simular genotipos para el otro hermano. Esto se logra con el siguiente código, donde después de adjuntar primero un marcador al pedigrí, especificando el genotipo conocido, lo condicionamos haciendo referencia a él en markerSim().
y = nuclearPed(children = c("bro1", "bro2")) |>
addMarker(bro1 = "1/1", alleles = 1:2, name = "snp1") |>
markerSim(N = 100, ids = "bro2", partialmarker = "snp1",
seed = 321, verbose = FALSE)
y id fid mid sex <1> <2> <3> <4> <5>
1 * * 1 -/- -/- -/- -/- -/-
2 * * 2 -/- -/- -/- -/- -/-
bro1 1 2 1 1/1 1/1 1/1 1/1 1/1
bro2 1 2 1 2/2 1/2 1/1 1/1 1/1Only 5 (out of 100) markers are shown.Estimación de coeficientes de IBD
La ibdEstimate()función estima los coeficientes de identidad por descendencia (IBD) entre pares de individuos a partir de los datos de marcadores disponibles. Probemos con los genotipos simulados que acabamos de generar:
k = ibdEstimate(y, ids = c("bro1", "bro2"))Estimating 'kappa' coefficientsInitial search value: (0.333, 0.333, 0.333) Pairs of individuals: 1 bro1 vs. bro2: estimate = (0.28, 0.54, 0.18), iterations = 10
Total time: 0.00257 secs#> Estimating 'kappa' coefficients
#> Initial search value: (0.333, 0.333, 0.333)
#> Pairs of individuals: 1
#> bro1 vs. bro2: estimate = (0.28, 0.54, 0.18), iterations = 10
#> Total time: 0.00339 secs
k id1 id2 N k0 k1 k2
1 bro1 bro2 100 0.28001 0.53998 0.18001#> id1 id2 N k0 k1 k2
#> 1 bro1 bro2 100 0.28001 0.53998 0.18001Visualmente podemos verlo:
showInTriangle(k, labels = TRUE)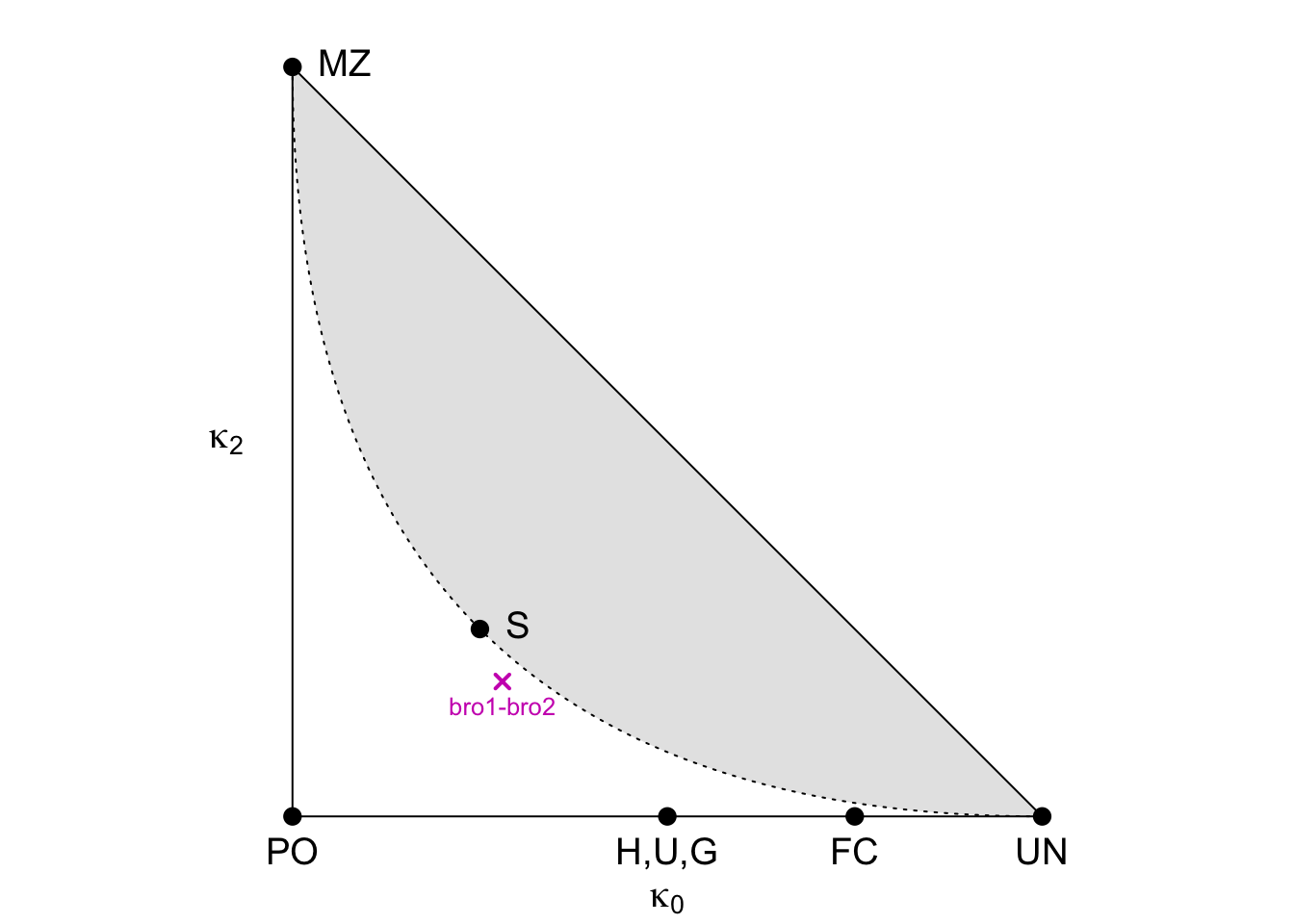
Esta gráfica representa un triángulo de relaciones de parentesco o triángulo de identidad genética, que se utiliza en estudios de genética para visualizar las relaciones de parentesco entre dos individuos en términos de los coeficientes de identidad por descendencia (IBD). En este triángulo se representan las proporciones de tres coeficientes: \(k_0\), \(k_1\) y \(k_2\), que describen la probabilidad de que dos individuos compartan 0, 1 o 2 alelos idénticos por descendencia, respectivamente.
La gráfica muestra cómo los hermanos simulados (“bro1” y “bro2”) se ubican en el triángulo de parentesco en función de los coeficientes \(k_0\), \(k_1\) y \(k_2\). La posición de “bro1-bro2” sugiere que estos dos individuos tienen una relación genética típica de hermanos completos, ya que comparten algunos alelos pero no todos, y caen en una región cercana al punto “S”, que corresponde a esa relación. Esta gráfica es una herramienta útil en genética forense y estudios de parentesco para visualizar cómo las relaciones genéticas entre individuos se comparan con relaciones conocidas (como gemelos, padres e hijos, hermanos, etc.).