Pruebas de hipótesis para la comparación de una media

Pérez-Guerrero Edsaúl Emilio

Instituto de Investigación en Ciencias Biomédicas

2024-04-10

Contenido

¿Cuándo se deben utilizar?
Prueba Z
Ejemplos prueba Z
Prueba t para la comparación de media
Ejemplo prueba t

Ejemplo hipotético 1

A los trabajadores de un hospital les interesa saber si el tiempo promedio que se tarda en atender a los pacientes en el departamento de urgencias ha cambiado con respecto al tiempo estándar de 30 minutos. Se conoce que la desviación estándar de estos tiempos, basada en datos históricos, es de 8 minutos.

\(H_0\): El tiempo promedio de atención es igual a 30 minutos. (\(\mu = 30\))
\(H_1\): El tiempo promedio de atención es diferente de 30 minutos. (\(\mu \neq 30\))

Supongamos que se toma una muestra de 100 pacientes recientes y se encuentra que el tiempo promedio de atención es de 32 minutos.

Ejemplo hipotético 1

Se quiere comparar los valores de la media con una media hipotética
Se conoce la desviación estándar
Se puede intuir que la desviación estándar histórica es la desviación estándar histórica

La prueba Z es la ideal para este ejemplo

Ejemplo hipotético 2

En ese mismo hospital se ha implementado un nuevo sistema de gestión para mejorar el tiempo de atención en el departamento de urgencias. Sin embargo, no se conoce la desviación estándar histórica de los tiempos de atención con este nuevo sistema.

Supongamos que se selecciona una muestra aleatoria de 25 pacientes atendidos bajo el nuevo sistema y se encuentra que el tiempo promedio de atención es de 28 minutos, con una desviación estándar de la muestra de 5 minutos.

\(H_0\): El tiempo promedio de atención es igual a 30 minutos. (\(\mu = 30\))
\(H_1\): El tiempo promedio de atención es diferente de 30 minutos. (\(\mu \neq 30\))

Ejemplo hipotético 2

Dado que no conocemos la desviación estándar de la población se podría utilizar la prueba T para comparar el tiempo promedio de atención bajo el nuevo sistema con el estándar.

La prueba de hipótesis para este caso es la prueba t student para una muestra

\(Z-test\)

Comparación de media con Distribución normal y varianza poblacional conocida

Z-test ¿Qué es?

Cuando se tiene una población con distribución normal (o aproximada a la normal) y se conoce la varianza es posible emplear el estadístico \(Z\) para la prueba de hipótesis.
Se parte del supuesto que \(H_0: \mu= \mu_0\)
El estadístico de prueba es:

\[z= \frac{ \bar{x}- \mu_0}{\sigma/ \sqrt{n}}\] Donde: \(\bar{x}\) es la media de mis datos, \(\mu_0\) es la media hipotética con la que me quiero comparar, \(\sigma\) es la desviación estándar poblacional y \(n\) provienen de mis datos de estudio.

Se utiliza relativamente poco ya que requiere de conocer la varianza de la población.

Ejemplo práctico 1. Z-test

Un grupo de investigadores desean conocer la edad media de cierta población. Saben por estudios anteriores, que la edad de los individuos en la población se distribuye normalmente con \(\sigma^2=27\). Para iniciar su estudio se preguntan ¿Si la media de edad de la población es diferente de 30?. Los investigadores quieren realizar su estudio con un 95% de confianza

Ejemplo práctico 1. Z-test

Los investigadores tomaron una muestra 50 sujetos con las siguiente edades:

edades <- c(32, 44, 35, 40, 42, 31, 38, 27, 23, 30, 39, 
          20, 30, 43, 26, 23, 22, 20, 36, 35, 25, 27, 
          27, 43, 22, 30, 26, 27, 32, 41, 42, 30, 43, 
          22, 42, 24, 22, 30, 27, 45, 26, 29, 45, 32, 
          31, 38, 25, 37, 31, 44)

Se sabe por experiencia que los datos provienen de una población aproximadamente normal.

Del problema obtenemos:

\(\sigma^2=27\)
\(\mu_0 \neq 30\)

Pasos para una prueba de hipótesis. Para la clase

Preguntas ¿Qué quiero probar?¿Las medias son iguales? ¿las proporciones son distintas?¿Qué quiero hacer con mi prueba estadística?
Hipótesis: Formular las hipótesis estadísticas
Estadística descriptiva y Datos:

Entender los datos
Medidas descriptivas
Gráficas
Tomar en cuenta los datos con los que se cuenta:
- Medias
- variación
- Distribución

Pasos para una prueba de hipótesis. Para la clase

Estadística de prueba: Tomando en cuenta mi hipótesis, la distribución de mis datos y los datos obtenidos del problema ¿Qué tipo de prueba voy a utilizar?

Utilizar diagrama

5.Evaluación de los supuestos

¿Qué necesito cumplir para poder utilizar la prueba?
¿Mis datos cumplen con los supuestos?
Si no se cumplen debo seleccionar otra prueba

Pasos para una prueba de hipótesis. Para la clase

Regla de decisión:¿Que voy a considerar como mi valor crítico?¿Cual es mi zona de rechazo o aceptación?
Estadístico de prueba: Determinar el valor de mi estadístico de prueba
Decisión: ¿Acepto o rechazo?
Conclusión
Valor de \(p\)

Resolución. Ejemplo práctico 1. Z-test

Preguntas. Paso 1

¿Qué quiero probar?¿Las medias son iguales? ¿las proporciones son distintas?¿Qué quiero hacer con mi prueba estadística?

¿La media de edad de la población es diferente de 30?

Del problema obtenemos:

\(\sigma^2=27\)
\(\mu_0 \neq 30\)
Distribución normal

Resolución. Ejemplo práctico 1. Z-test

Hipótesis

Hipótesis nula

\(H_0\): La media de la edad de la población es igual a 30
\(H_0\): \(\mu = 30\)

Hipótesis alterna

\(H_1\): La media de la edad de la población es diferente de 30
\(H_1\): \(\mu \neq 30\)

Resolución. Ejemplo práctico 1. Z-test

Estadística descriptiva

Entender los datos
Medidas descriptivas
Gráficas

summary(edades) # Resumen de los datos
hist(edades, main = "Histograma para las edades") # Histograma
abline(v=mean(edades))

density(edades)|>
  plot(main = "Gráfico de densidades para las edades", 
       xlab="Edades")
abline(v=mean(edades))

boxplot(edades, ylab="Edades", col = "cyan4")

Resolución. Ejemplo práctico 1. Z-test

Estadística descriptiva

Resumen de los datos

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  20.00   26.00   30.50   32.02   38.75   45.00

Resolución. Ejemplo práctico 1. Z-test

Estadística descriptiva

Histograma

Resolución. Ejemplo práctico 1. Z-test

Estadística descriptiva

Gráfico de densidad

Resolución. Ejemplo práctico 1. Z-test

Estadística descriptiva

Boxplot

Resolución. Ejemplo práctico 1. Z-test

Estadística de prueba:

Del problema obtenemos:

\(\sigma^2=27\)
\(\mu_0 \neq 30\)
Distribución normal

Tomando en cuenta mi hipótesis, la distribución de mis datos y los datos del problema ¿Qué tipo de prueba voy a utilizar?

Z-test

Resolución. Ejemplo práctico 1. Z-test

Evaluación de los supuestos

¿Qué necesito cumplir para poder utilizar la prueba?
- Distribución normal
- Conocer la varianza población
¿Mis datos cumplen con los supuestos?
- Del problema se puede obtener:
  - Distribución normal (del problema)
  - Varianza poblacional (del problema)
Si no se cumplen debo seleccionar otra prueba

Resolución. Ejemplo práctico 1. Z-test

Regla de decisión:

¿Que voy a considerar como mi valor crítico?
¿Cual es mi zona de rechazo o aceptación?
En este punto debemos de definir ¿Qué valores consideraremos para aceptar o rechazar nuestra \(H_0\)?
Del problema podemos deducir que:
- Hipótesis bilateral (solo nos interesa que sea diferente de 30)
- \(\alpha=0.05\). Los investigadores quieren realizar su estudio con un 95% de confianza
  - el \(\alpha=0.05\) es el valor que se utiliza habitualmente

¿Qué es \(\alpha\)?

El nivel de significancia, también denotado como \(\alpha\), es la probabilidad de rechazar la hipótesis nula cuando es verdadera.
Cuando se toma la decisión de rechazar o no la Hipótesis Nula podemos acertar o cometer errores. La probabilidad de cometer errores de tipo I es \(\alpha\).
Es la probabilidad de rechazar la hipótesis nula cuando es verdadera.
“Es un umbral de probabilidad establecido a priori como regla de decisión, de modo que cuando \(p\) sea inferior a \(\alpha\), se rechazará la hipótesis nula. Un riesgo \(\alpha\) del 5% supone aceptar que en 5 de cada 100 muestras que pudieran tomarse cuando \(H_0\) sea cierta se concluirá erróneamente que hubo diferencias significativas.”¹

¿Qué es \(\alpha\)?

Es la probabilidad de ocurrencia de los valores del estadístico en la región de rechazo cuando la Hipótesis Nula es verdadera.
El valor de \(\alpha\), también denominado nivel de significación, es definido por el investigador antes de recoger los datos, y la costumbre es hacer \(\alpha\)=0.05 o \(\alpha\)=0.01
Cuando la hipótesis es bilateral el valor \(\alpha\) se divide en ambas regiones
Cuando el valor de \(p\) es menor que \(\alpha\) se rechaza la \(H_0\)

Resolución. Ejemplo práctico 1. Z-test

Regla de decisión:

¿Qué rechazamos y qué aceptamos?
Dado que elegimos \(\alpha=0.05\) y dado que nuestra hipótesis es bilateral buscamos en tablas el valor \(Z\) adecuado.
En r lo podemos estimar con la función qnorm

qnorm(0.025)# para la cola superior (alfa/2)

[1] -1.959964

qnorm(0.025, lower.tail = F)# para la cola inferior (alfa/2)

[1] 1.959964

El valor con el que nos vamos a comparar es 1.96 y -1.96

Ejemplo práctico 1. Z-test

Paso 6. Regla de decisión

Ejemplo práctico 1. Z-test

Paso 6. Regla de decisión

rnorm(1000000, mean=0, sd=1)|>
  density()|>
  plot(main = "Regla de decisión ejemplo práctico 1",
     xlab = "Valores de Z", ylab = "")
abline(v=1.96, col="red", lw=4)
abline(v=-1.96, col="red", lw=4)

Ejemplo práctico 1. Z-test

Paso 6. Regla de decisión. Utilizando ggplot

Ejemplo práctico 1. Z-test

Paso 6. Regla de decisión. Utilizando ggplot

library(ggplot2)
ggplot(mapping = aes(x=rnorm(1000000, mean=0, sd=1)))+
  geom_density()+
  ylab("Densidad")+
  xlab("Valores de Z")+
  ggtitle("Gráfico de decisión",
          subtitle = "Zona de aceptación entre las lineas")+
  geom_vline(xintercept = c(1.96, -1.96), 
                color = "red", size=1.5)

Resolución. Ejemplo práctico 1. Z-test

Regla de decisión:

y <- (rnorm(10000000, mean=0, sd=1))
den <- density(y)
plot(den,  main="Regla de decisión ejemplo práctico 1", xlab="Valores de Z")
value <- 1.96
polygon(c(den$x[den$x >= value ], value),
        c(den$y[den$x >= value ], 0),
        col = "slateblue1",
        border = 1)
value <- -1.96
polygon(c(den$x[den$x <= value ], value),
        c(den$y[den$x <= value ], 0),
        col = "slateblue1",
        border = 1)

Ejemplo 1 Para Z-test

Regla de decisión:

Ejemplo 1 Para Z-test

Paso 7. Calcular estadístico con los datos de prueba

Para este punto nos basamos en la formula:

\[z= \frac{ \bar{x}- \mu_0}{\sigma/ \sqrt{n}}\] - Sustituyendo con los datos del Ejemplo 1

\[z= \frac{ mean(edades)-30}{\sqrt{27/50}}\]

Ejemplo 1 Para Z-test

Paso 7. Calcular estadístico con los datos de prueba

\[z= \frac{ mean(edades)-30}{\sqrt{27/50}}\]

Da como resultado: 2.7488718
El código en R es:

(mean(edades)-30)/sqrt(27/50)

[1] 2.748872

Ejemplo práctico 1. Z-test

Paso 8. Decisión

Con base en la regla de decisión, se puede rechazar la hipótesis nula porque 2.7489 está en la región de rechazo. Se puede decir que el valor calculado de la prueba estadística tiene un nivel de significación de .05 a dos colas

El valor que estimamos es mayor al valor de referencia de tablas

Ejemplo práctico 1. Z-test

Paso 8. Decisión

plot(density(rnorm(1000000, mean=0, sd=1)), main="Gráfico para la zona de rechazo")
legend(x="topleft", legend = "Zona aceptación entre lineas rojas y 
       la linea verde estadístico obtenido")
abline(v=1.96, col="red", lw=4)
abline(v=-1.96, col="red", lw=4)
abline(v=2.7489, col="green", lw=4)

Ejemplo práctico 1. Z-test

Paso 8. Decisión

Ejemplo práctico 1. Z-test

Paso 8. Decisión

Ejemplo práctico 1. Z-test

Paso 8. Decisión

y <- (rnorm(10000000, mean=0, sd=1))
den <- density(y)
plot(den,  main="Regla de decisión ejemplo práctico 1", xlab="Valores de Z")
value <- 1.96
polygon(c(den$x[den$x >= value ], value),
        c(den$y[den$x >= value ], 0),
        col = "slateblue1",
        border = 1)
value <- -1.96
polygon(c(den$x[den$x <= value ], value),
        c(den$y[den$x <= value ], 0),
        col = "slateblue1",
        border = 1)
legend(x="topleft", legend = "Zona aceptación zona blanca y 
       la linea verde estadístico obtenido")
abline(v=2.7489, col="green", lw=4)

Ejemplo práctico 1. Z-test

Paso 8. Decisión. ggplot

y <- (rnorm(10000000, mean=0, sd=1))
ggplot(mapping = aes(x=y))+
  geom_density()+
  ylab("Densidad")+
  xlab("Valores de Z")+
  ggtitle("Gráfico de decisión",
          subtitle = "Zona de aceptación entre las lineas")+
  geom_vline(xintercept = c(1.96, -1.96), 
                color = "red", size=1.5)+
  geom_vline(xintercept = 2.7489, 
                color = "green", size=1.5)

Ejemplo práctico 1. Z-test

Paso 8. Decisión. ggplot

Ejemplo práctico 1. Z-test

Paso 9. Conclusión

Con un 95% de confianza podemos decir que la media es distinta de 30

Ejemplo práctico 1. Z-test

Paso 10. Valor de p

Podemos estimar la probabilidad de encontrar en nuestra población el valor de \(Z\) estimado.
Este valor lo podemos obtener de tablas
En r lo podemos calcular con la función pnorm

pnorm(2.7489, lower.tail = F)# para el valor de la cola superior.

[1] 0.002989781

pnorm(-2.7489, lower.tail = T)# para la cola inferior

[1] 0.002989781

Tome en cuenta que: lower.tail debe ser verdadero cuando \(P[X≤ x]\)

Ejemplo práctico 1. Z-test

Paso 10. Valor de p

Dado que nuestra hipótesis es bilateral debemos de sumar las dos probabilidades
Nos da como resultado: 0.0059796
Podemos decir que en nuestra población la probabilidad de encontrar una media igual a 30 es de 0.0059796
Podemos decir los resultados observados se deben al azar en 0.5979563%

Ejemplo práctico 1. Z-test

Paso 10. Valor de p

Si el valor \(p\) es menor o igual que \(\alpha\), es posible rechazar la hipótesis nula; si el valor p es mayor que \(\alpha\) no es posible rechazar la hipótesis nula.
“El valor \(p\) no es la probabilidad de que \(H_0\) sea cierta. La probabilidad de que \(H_0\) sea cierta no se puede calcular con un valor p. Es más, hay que asumir que \(H_0\) es cierta para poder calcular el valor \(p\). El valor \(p\) es una probabilidad condicionada y su condición es \(H_0\).”¹

Valores de \(p\) ¹

P < 0.05	P ≥ 0.10
Se rechaza la hipótesis nula	No se puede rechazar la hipótesis nula
No parece que el azar lo explique todo	No se puede descartar que el azar lo explique todo
El “efecto” es mayor que el “error”	El “efecto” es similar al “error”
Hay diferencias estadísticamente significativas	No hay diferencias estadísticamente significativas
Existen evidencias a favor de la hipótesis alternativa	No existen evidencias a favor de la hipótesis alternativa
Los datos encontrados son poco compatibles con H0	Los datos encontrados son compatibles con H0

Nota: Los límites 0,05 y 0,10 son arbitrarios, pero comúnmente aceptados.

Ejemplo práctico 2. Z-test

Otro grupo de investigadores decidió replicar el estudio con el siguiente conjunto de datos:

edades2<-c(25, 29, 26, 34, 34, 35, 34, 29, 27, 
           31, 35, 35, 34, 33, 29, 33, 30, 30, 
           26, 33, 27, 26, 30, 25, 28, 32, 27, 
           30, 27, 35, 32, 33, 25, 29, 30, 32, 
           34, 33, 32, 27, 33, 32, 25, 33, 34, 
           27, 29, 34, 32, 32)

Ejemplo práctico 2. Z-test

Pasos del 1 al 6

Todos los pasos del 1 al 5 son iguales al problema anterior

Ejemplo práctico 2. Z-test

Paso 6. Calcular estadístico con los datos de prueba

Para este punto nos basamos en la formula:

\(z= \frac{ \bar{x}- \mu_0}{\sigma/ \sqrt{n}}\)

Sustituyendo con los datos del Ejemplo 2

\(z= \frac{ mean(edades2)-30}{\sqrt{27/50}}\)

Da como resultado: 0.7348469

Ejemplo práctico 2. Z-test

Paso 8. Decisión

Ejemplo práctico 2. Z-test

Paso 8. Decisión

Con base en la regla de decisión, NO existen argumentos para rechazar la \(H_0\) 0.73 está en la región de aceptación.

El valor que estimamos es mayor al valor de referencia de tablas

Ejemplo práctico 2. Z-test

Paso 9. Conclusión

No existen argumentos para decir que la media es distinta de 30 con un 95% de confianza

Ejemplo práctico 2. Z-test

Paso 10. Valor de p

Podemos estimar la probabilidad de encontrar en nuestra población el valor de \(z\) estimado.
Este valor lo podemos obtener de tablas
En r lo podemos calcular con la función pnorm

pnorm(0.74, lower.tail = F)# para el valor de la cola superior.

[1] 0.22965

pnorm(-0.74)# para la cola inferior

[1] 0.22965

Hipótesis unilateral

Si la hipótesis es unilateral no se divide el valor de \(\alpha\)
Nuestro criterio de rechazo quedaría en uno de los lados de la curva

Ejemplo práctico 3. Hipótesis unilateral

Los investigadores ahora desean saber si la media de la edad es mayor a 30.
El criterio de rechazo quedaría:

Ejemplo práctico 3. Hipótesis unilateral

Ahora el estadístico con el que nos vamos a comparar es: \(z=1.64\) que corresponde a la cola superior con un \(\alpha=0.05\)
En R lo podemos calcular de la siguiente manera:

qnorm(0.05, lower.tail = F)

[1] 1.644854

Ejemplo práctico 3. Hipótesis unilateral

Paso 8. Decisión

Ejemplo práctico 3. Hipótesis unilateral

Con base en la regla de decisión, podemos rechazar la \(H_0\)
Existe evidencia con un 95% de confianza de que la media es mayor que 30
El valor de \(p\) quedaría repartido en un solo lado

pnorm(2.7489, lower.tail = F)

[1] 0.002989781

Ejemplo práctico 3. Hipótesis unilateral

¿Y si buscáramos que nuestra media fuera menor de 30?
- \(H_A: \mu<30\)

Ejemplo práctico 3. Hipótesis unilateral \(H_A: \mu<30\)

¿Cómo hacerlo en `R`?

install.packages("BSDA")

Se utiliza la función:

z.test(x, y = NULL, alternative = "two.sided", mu = 0, 
       sigma.x = NULL, sigma.y = NULL, conf.level = 0.95)

¿Cómo hacerlo en `R`?

Argumentos z.test

x
- numeric vector; NAs and Infs are allowed but will be removed.
y
- numeric vector; NAs and Infs are allowed but will be removed.
alternative
- character string, one of “greater”, “less” or “two.sided”, or the initial letter of each, indicating the specification of the alternative hypothesis.
mu
- a single number representing the value of the mean or difference in means specified by the null hypothesis
sigma.x
- a single number representing the population standard deviation for x
conf.level
- confidence level for the returned confidence interval, restricted to lie between zero and one

¿Cómo hacerlo en `R`?

Ejemplo práctico 3. Prueba Z en R.

z.test(x=edades, alternative = "two.sided", mu=30, sigma.x = sqrt(27))


    One-sample z-Test

data:  edades
z = 2.7489, p-value = 0.00598
alternative hypothesis: true mean is not equal to 30
95 percent confidence interval:
 30.57973 33.46027
sample estimates:
mean of x 
    32.02

¿Cómo hacerlo en `R`?

Ejemplo práctico 3. Prueba Z en R.

Si buscamos \(H_A: \mu>30\)

z.test(edades, alternative = "greater", mu=30, sigma.x = sqrt(27))


    One-sample z-Test

data:  edades
z = 2.7489, p-value = 0.00299
alternative hypothesis: true mean is greater than 30
95 percent confidence interval:
 30.81128       NA
sample estimates:
mean of x 
    32.02

¿Cómo hacerlo en `R`?

Ejemplo práctico 4. Prueba Z en R.

z.test(edades2, alternative = "two.sided", mu=30, sigma.x = sqrt(27))


    One-sample z-Test

data:  edades2
z = 0.73485, p-value = 0.4624
alternative hypothesis: true mean is not equal to 30
95 percent confidence interval:
 29.09973 31.98027
sample estimates:
mean of x 
    30.54

Prueba \(t\) para una media

Recordando

Prueba de hipótesis para media de una sola población
- Usando Z-test (Distribución normal con varianza conocida). Revisada la clase anterior
- Usando t-test (Distribución normal con varianza desconocida)

Algunos autores sugieren que la prueba Z sea utilizada para muestras de \(n>30\) basados en el teorema del límite central

Recordando

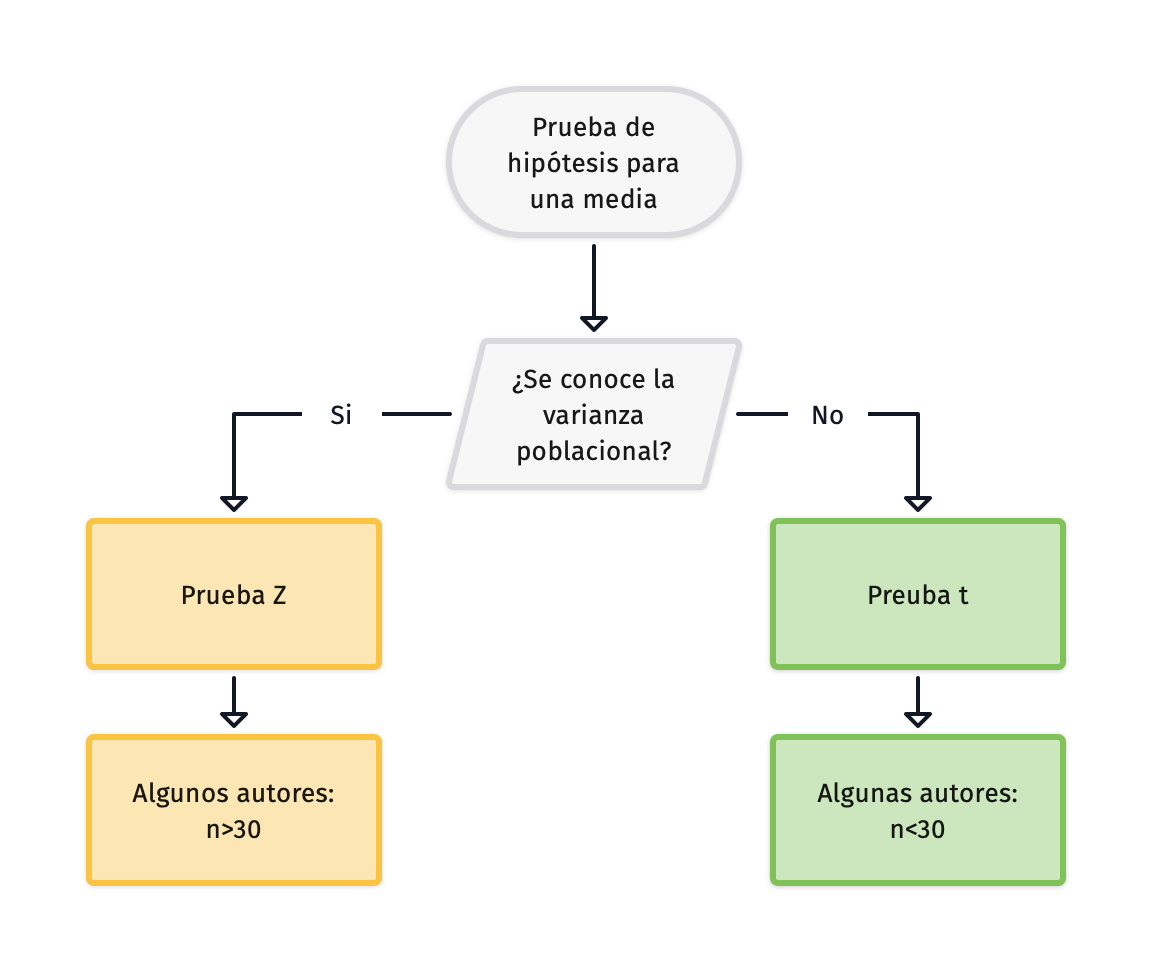
Selección de prueba

Teorema del límite central

El Teorema del Límite Central afirma que, si se toma una cantidad suficientemente grande de muestras aleatorias de una población, con una media y varianza definidas, entonces la distribución de las medias de esas muestras tenderá a seguir una distribución normal (o gaussiana), no importa la forma de la distribución de la población original.

Recordando

Cuando se conoce la varianza poblacional y los datos siguen una distribución normal podemos emplear el estadísticos \(Z\) para:
- Saber si la media es menor o mayor a una media hipotética
- Saber si la media de la población es igual a un determinado valor
La gran desventaja de emplear el estadístico \(Z\) es que difícilmente se conoce la varianza o la desviación estándar poblacional
Cuando no se conoce la varianza poblacional debemos de emplear la prueba t de student

Prueba t de student

Cuando el muestreo se realiza a partir de una población que sigue una distribución normal con una varianza desconocida la estadística de prueba para \(H_0: \mu= \mu_0\) es:

\[t= \frac{ \bar{x}- \mu_0}{s/ \sqrt{n}}\]

Prueba t de student

\[t= \frac{ \bar{x}- \mu_0}{s/ \sqrt{n}}\]

\(t\):el valor estimado de t con \(n-1\) grados de libertad
\(\bar{x}\): es la media de los datos que estamos trabajando o que deseamos probar
\(\mu_0\): es la media hipotética con la que nos vamos a comparar
\(s\): es la desviación estándar muestral
\(n\): la cantidad de datos de la muestra

Distribución \(t-student\)

Tiene media de 0.
Es simétrica con respecto a la media.
La media, la mediana y la moda coinciden.
Varianza mayor que 1. Aunque tiene a 1 cuando la \(n\) aumenta.
La variable \(t\) va de \(-\infty\) a \(\infty\).
Es una familia de distribuciones. Hay una distribución para cada valor de \(n\).
Es menos espigada y mas alargada que la distribución normal.
Se aproxima a la distribución normal a medida que \(n-1\) se aproxima al \(\infty\).
Si tenemos una muestra de tamaño n, entonces tendremos una distribución t con \((n-1)\) grados de libertad.

Distribución t-student

Distribución t-student con distintos grados de libertad

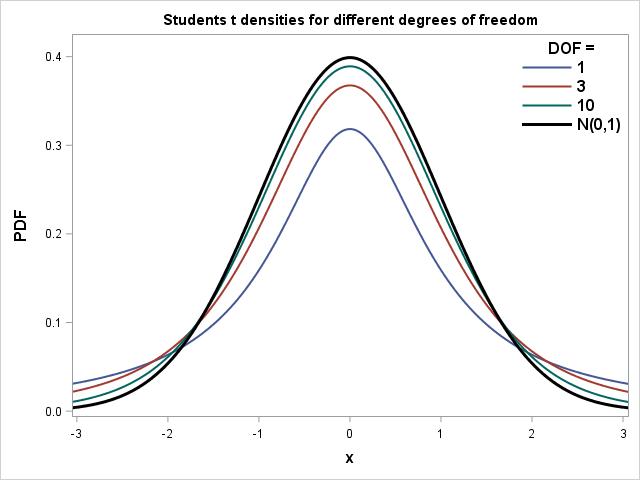
Grados de libertad

En matemáticas: Se definen como la dimensión del dominio de un vector aleatorio
En estadística: Se definen frecuentemente como el número de observaciones (piezas de información) en los datos que pueden variar libremente al estimar parámetros estadísticos

Grados de libertad

Distribucuón t-student

Los valores de tablas (de referencia) se pueden obtener
- https://www.stat.tamu.edu/~lzhou/stat302/T-Table.pdf
En R se utiliza la función qt() dada por:
- qt(p, df, ncp, lower.tail = TRUE, log.p = FALSE)
Por ejemplo el valor de \(t\) para una probabilidad de 0.05 para la cola inferior para una \(n\) de 50 es:

qt(p=0.05, df=49) # Los grados de libertad n-1

[1] -1.676551

Distribución \(t-student\)

En R se utiliza la función qt() dada por:
- qt(p, df, ncp, lower.tail = TRUE, log.p = FALSE)
Por ejemplo el valor de \(t\) para una probabilidad de 0.05 para la cola superior para un n de 50 es:

qt(p=0.05, df=49, lower.tail = F)# grados de libertad es n-1

[1] 1.676551

qt(p=0.95, df=49)# grados de libertad es n-1

[1] 1.676551

Distribución \(t-student\)

Si lo que se quiere es conocer la probabilidad de encontrar un valor determinado de \(t\) en R se utiliza la función

pt(q, df, ncp, lower.tail = TRUE, log.p = FALSE)

Por ejemplo para encontrar la probabilidad de encontrar un valor \(t\) de \(1.67\) en la cola superior se utiliza:

pt(q=1.67, df=49, lower.tail = F)

[1] 0.05064816

La parte de la derecha de la curva se utiliza por ejemplo cuando se busca una media mayor a…

Distribución \(t\) student

Para encontrar la probabilidad de encontrar un valor de \(-1.67\) en la cola inferior se utiliza:

pt(q=-1.67, df=49)

[1] 0.05064816

La parte de la derecha de la curva se utiliza por ejemplo cuando se busca una media menor a…

Prueba de hipótesis t-test Pasos

Ejemplo práctico 5. `t.test`

Los investigadores Castillo y Lillioja describieron una técnica, desarrollada por ellos, para la canulación linfática periférica en seres humanos. Los autores afirman que su técnica simplifica el procedimiento y permite la recolección de volúmenes convenientes de linfa para estudios metabólicos y cinéticos. Los individuos estudiados fueron 14 adultos varones sanos representativos de un rango amplio de pesos corporales. Los datos provienen de una población normal. Una de las variables de medición fue el índice de masa corporal IMC. Los resultados se muestran en objeto llamado “IMC”. ¹

Ejemplo práctico 5. `t.test`

IMC<-c(23,25,21,37,39,21,23,24,32,57,23,26,31,45)

Se pretende saber si es posible concluir que la media del IMC para la población de la que se extrajo la muestra no es 35. Resuelva el ejercicio utilizando los pasos para la prueba de hipótesis.

Pregunta

¿Qué es lo que ser pretende responder?
Si la media del IMC en un grupo de individuos es distinto de 35
La media del IMC para un grupo de individuos no es 35
La media la población para el IMC de cual se extrajeron los datos no es 35

Hipótesis

\(H_0: \mu=35\).
\(H_A: \mu \neq 35\). Es una hipótesis bilateral

Datos

¿Qué datos tenemos disponibles?
- \(s=\) No la conocemos pero se puede estimar
- \(n=14\)
- \(\mu=\) No la conocemos pero se puede estimar
- \(x_0=35\)
- \(\alpha=0.05\) aunque no describe explicitamente, podemos utilizar un valor 0.05 por ser el valor más utilizado.
- Población normal (establecida por el problema)

Conozcamos nuestros datos. Estadística descriptiva

summary(IMC)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  21.00   23.00   25.50   30.50   35.75   57.00

Conozcamos nuestros datos. Estadística descriptiva

hist(IMC)
abline(v=mean(IMC), col="red")

Conozcamos nuestros datos. Estadística descriptiva

boxplot(IMC, col="cyan4")

Selección de mi prueba estadística

No conocemos la varianza poblacional
Nuestra intención es comparar una media hipotética con la media de nuestros datos
Utilizando el diagrama de decisión de la clase y los datos del problema la prueba estadística es:

t student para una muestra

t student

\[t= \frac{ \bar{x}- \mu_0}{s/ \sqrt{n}}\] Necesitamos conocer por lo tanto: - \(s\) - \(n\) - \(\mu_0\)

Determinar datos faltantes para resolverlo con R

sd(IMC)

[1] 10.63919

length(IMC)

[1] 14

mean(IMC)

[1] 30.5

Validar los supuestos

En este caso podemos suponer que:
- Los datos vienen de una población con distribución normal. Significa que podemos utilizar estadísticos que se basan en una distribución normal
- No se conoce el valor de la varianza poblacional. No se puede emplear el estadístico \(z\)
- Empleamos la distribución y el estadístico \(t\)

Reglas decisión y valores críticos

En este punto se identifican los valores críticos que definirán nuestro zona de aceptación.

Datos que tenemos
- Tipo de hipótesis: Bilateral
- Nivel de confianza: 95%
- \(\alpha=\)0.05. Es necesario dividir el valor de alfa entre dos. Ya que estamos trabajando con una hipótesis bilateral

Reglas decisión y valores críticos

Lo que se necesita calcular
- Estadístico t con el que nos vamos a comparar: Necesitamos el valor del lado izquierdo y del lado derecho ya que nuestra \(H_A: \mu \neq 35\). En R utilizamos la función qt

Estamos buscando cuales el valor de la distribución t para una probabilidad de 0.025 a cada lado de la curva

qt(0.025, df=13)#valor del lado izquierdo

[1] -2.160369

qt(0.025, df=13, lower.tail = F)#Valor del lado derecho

[1] 2.160369

Reglas decisión y valores críticos

Lo que se necesita calcular
- Estadístico t con el que nos vamos a comparar: Necesitamos el valor del lado izquierdo y del lado derecho ya que nuestra \(H_A: \mu \neq 35\). En R utilizamos la función qt

Estamos buscando cuales el valor de la distribución t para una probabilidad de 0.025 a cada lado de la curva

o de la siguiente manera

qt(c(0.025,0.975), df=13)

[1] -2.160369  2.160369

Regla de decisión y Gráficas

Se creo una gráfica con 1000 datos, 999 grados de libertad. Está gráfica es solamente ilustrativa y permite identificar visualemte cuál es nuestra zona de rechazo y cual la de aceptación.

El código fue:

plot(densisty(hist(rt(1000, df=999), main = "Gráfica para regla de decisión", 
     xlab = "Valor de t", ylab="")))
abline(v=(qt(0.025, df=13)), col="red", lw=4)
abline(v=qt(0.975, df=13), col="red", lw=4)

Regla de decisión y Gráficas

y <- (rt(1000000, df=999999))
den <- density(y)
plot(den,  main="Regla de decisión prueba t", xlab="Valores de t")
value <- qt(0.975, df=13)
polygon(c(den$x[den$x >= value ], value),
        c(den$y[den$x >= value ], 0),
        col = "slateblue1",
        border = 1)
value <-  qt(0.025, df=13)
polygon(c(den$x[den$x <= value ], value),
        c(den$y[den$x <= value ], 0),
        col = "slateblue1",
        border = 1)
legend(x="topleft", legend = "Zona aceptación en blanco")

Regla de decisión y Gráficas

Calcular el valor t de nuestros datos

Es neceserio calcular el valor de t de nuestros datos para después compararlo con los valores críticos

Para este punto nos basamos en la formula:

\(t= \frac{ \bar{x}- \mu_0}{s/ \sqrt{n}}\)

Sustituyendo con los datos del ejercicio

\(t= \frac{ 30.5-35}{10.64 /\sqrt{14}}\)

Calcular el valor t de nuestros datos

En R lo podemos hacer utilizando el siguiente código:

(mean(IMC)-35)/(sd(IMC)/sqrt(length(IMC)))

[1] -1.582589

Redondeando a dos cifras da -1.58

Decisión

Con base en la regla de decisión (valores críticos), no existe evidencia para rechazar la hipótesis nula porque \(-1.58\) no es mayor que 2.1603687 ni menor que -2.1603687

Decisión

y <- (rt(1000000, df=999999))
den <- density(y)
plot(den,  main="Regla de decisión prueba t", xlab="Valores de t")
value <- qt(0.975, df=13)
polygon(c(den$x[den$x >= value ], value),
        c(den$y[den$x >= value ], 0),
        col = "slateblue1",
        border = 1)
value <-  qt(0.025, df=13)
polygon(c(den$x[den$x <= value ], value),
        c(den$y[den$x <= value ], 0),
        col = "slateblue1",
        border = 1)
legend(x="topleft", legend = "Zona aceptación en blanco")
abline(v=(-1.58), col="green", lw=4)

Decisión

Conclusión

Con un 95% de confianza podemos decir que la media para IMC de la población no es distinta de 35

Valor de p

En r lo podemos calcular con la función pt

pt(-1.58, df=13, lower.tail = T)#Para el de la izquierda

[1] 0.06906086

pt(-(-1.58), df=13, 
   lower.tail = F) #Para el de la derecha. Se tiene que poner en negativo

[1] 0.06906086

Dado que nuestra hipótesis es unilateral debemos de sumar probabilidades. Da como resultado= 0.1381217.

Valor de p

Podemos concluir que existe una alta probabilidad que los resultados sean debidos al azar. Da como resultado= 0.1381217.
El valor de p es mayor que \(\alpha\) no existen argumentos para rechazar la \(H_0\)

¿Cómo hacerlo utilizando una función de `R`?

Función `t.test`

En R podemos utilizar la función t.test para determinar si una media de una población es igual a otra media hipotética
Para conocer la función puede acceder al menú de ayuda utilizando el siguiente código

help("t.test")

Argumentos de la función `t.test`

t.test(x, ...)

## Default S3 method:
t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"),
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)

Argumentos de la función `t.test`

x
- a (non-empty) numeric vector of data values.
y
- an optional (non-empty) numeric vector of data values.
alternative
- a character string specifying the alternative hypothesis, must be one of “two.sided” (default), “greater” or “less”. You can specify just the initial letter.

Argumentos de la función `t.test`

mu
- a number indicating the true value of the mean (or difference in means if you are performing a two sample test).
paired
- a logical indicating whether you want a paired t-test.
var.equal
- a logical variable indicating whether to treat the two variances as being equal. If TRUE then the pooled variance is used to estimate the variance otherwise the Welch (or Satterthwaite) approximation to the degrees of freedom is used.
conf.level
- confidence level of the interval

Ejemplo práctico 6. Utilizando `t.test`

t.test(x=IMC, mu=35, alternative = "two.sided")


    One Sample t-test

data:  IMC
t = -1.5826, df = 13, p-value = 0.1375
alternative hypothesis: true mean is not equal to 35
95 percent confidence interval:
 24.35712 36.64288
sample estimates:
mean of x 
     30.5

Ejemplo práctico 6. Utilizando `t.test`

t.test(x=IMC, mu=35, alternative = "greater")#para una media mayor a 35


    One Sample t-test

data:  IMC
t = -1.5826, df = 13, p-value = 0.9312
alternative hypothesis: true mean is greater than 35
95 percent confidence interval:
 25.46445      Inf
sample estimates:
mean of x 
     30.5

Ejemplo práctico 6. Utilizando `t.test`

t.test(x=IMC, mu=35, alternative = "less")#para una media menor a 35


    One Sample t-test

data:  IMC
t = -1.5826, df = 13, p-value = 0.06877
alternative hypothesis: true mean is less than 35
95 percent confidence interval:
     -Inf 35.53555
sample estimates:
mean of x 
     30.5

Ejemplo práctico 6. Utilizando `t.test`

t.test(x=IMC, mu=35, 
       alternative = "less", 
       conf.level = 0.99)#para una media menor a 35 y alfa de 0.01


    One Sample t-test

data:  IMC
t = -1.5826, df = 13, p-value = 0.06877
alternative hypothesis: true mean is less than 35
99 percent confidence interval:
   -Inf 38.036
sample estimates:
mean of x 
     30.5

Ejemplo práctico 7. Utilizando `t.test`

Ahora los investigadores se pregunta si la media del IMC es menor que 32, resuelva esta pregunta utilizando la función t.test