low age lwt race smoke ptl ht ui ftv bwt
85 0 19 182 2 0 0 0 1 0 2523
86 0 33 155 3 0 0 0 0 3 2551
87 0 20 105 1 1 0 0 0 1 2557
88 0 21 108 1 1 0 0 1 2 2594
89 0 18 107 1 1 0 0 1 0 2600
91 0 21 124 3 0 0 0 0 0 2622Prueba de hipótesis para la comparación de dos proporciones
Bioestadística básica
Posgrados CUCS
Contenido
- Distribución \(\chi^2\)
- Tablas de contingencia
- Prueba de \(\chi^2\)
- Prueba exacta de Fisher
Introducción
Un grupo de investigadores desea conocer si saltarse el desayuno se asocia con la obesidad. Para ello, plantean un estudio en el que se incluyó dos grupos de individuos: uno integrado por individuos que si se saltaban el desayuno y otro grupo en el que los individuos desayunaban todos los días. Se identificó cuantas personas con sobrepeso había en cada uno de los grupos y se realizó la prueba estadística pertinente.
La prueba indicada para resolver esta pregunta es la prueba \(\chi^2\)
Distribución \(\chi^2\)
Propiedades de la distribución \(\chi^2\)
- Es una distribución que contiene solo valores positivos
- No sigue un forma de campana
- Esta formada por cada uno de los valores de \(Z\) de datos aleatorios elevada al cuadrado
- Se describe por una función exponencial
- Tiene \(n\) grados de libertad
Definición de la distribución \(\chi^2\)
Dada una variable aleatoria \(y\) que sigue una distribución normal, con media \(\mu\) y varianza \(\sigma^2\) cada valor puede transformarse en la variable normal estándar \(z\) por medio de la siguiente formula:
\[z= \frac{y_i-\mu}{\sigma}\]
Definición de la distribución \(\chi^2\)
Cada valor de \(z\) puede elevarse al cuadrado para obtener \(z^2\). Cuando se estudia la distribución muestra de \(z^2\), se observa que sigue una distribución \(\chi^2\) con 1 grado de libertad. Es decir:
\[\chi^2_{(1)}= \lgroup\frac{y_i-\mu}{\sigma}\rgroup=z^2\]
Definición de la distribución \(\chi^2\)
Si todos los datos aleatorios de una muestra se eleva al cuadrado se obtiene:
\[\chi^2_{(n)}= z^2_1+z^2_2+ \cdot \ \cdot \ \cdot+ z^2_n\] Es la suma de los valores \(z^2\) resultantes tendrá una distribución \(\chi^2\), con \(n\) grados de libertad
Después de realizar una integral, la formula matemática de las distribución \(\chi^2\) es la siguiente:
\[f(u)=\frac{1}{\lgroup\frac{k}{2}-1\rgroup!}\ \frac{1}{2^{k/2}}u^{(k/2)-1}e^{-(u/2)}, u>0\]
Definición de la distribución \(\chi^2\)
\[f(u)=\frac{1}{\lgroup\frac{k}{2}-1\rgroup!}\ \frac{1}{2^{k/2}}u^{(k/2)-1}e^{-(u/2)}, u>0\]
Donde:
- \(e\) es el número irracional 2.71828
- \(k\) es el numero de grados de libertad.
- \(u\) es \(\chi\)
La media y la variancia de la distribución \(\chi^2\) son, respectivamente, \(k\) y \(2k\).
Gráfica de la distribución \(\chi^2\)
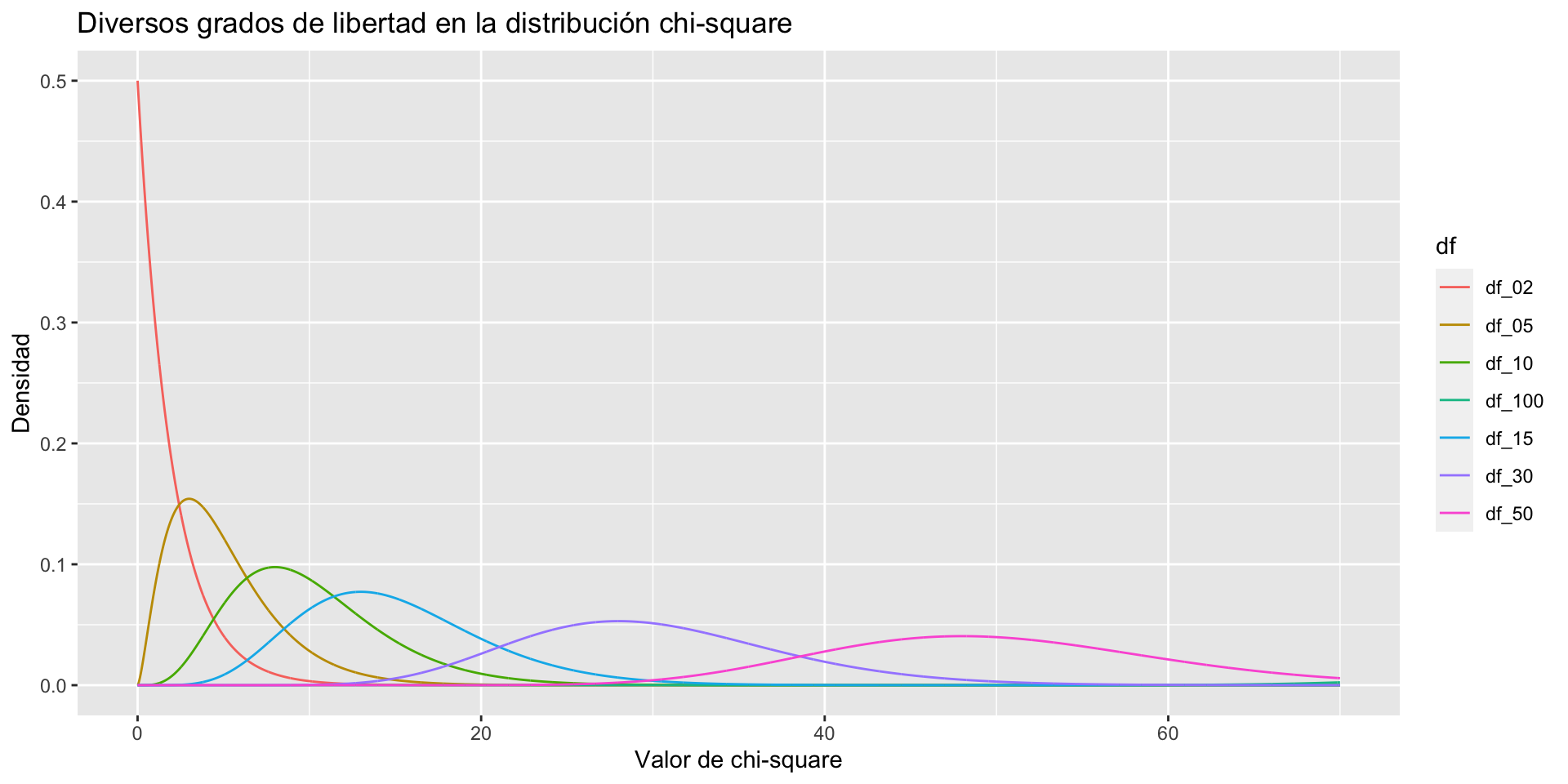
Funciones para la distribución \(\chi^2\) en R
dchisqes la función densidad, permite graficar una distribuciónpchisqdado un valor de \(\chi^2\) con \(n\) grados de libertad devuelve la probabilidad de encontrar ese valorqchisqdada una probabilidad devuelve de encontrar ese valor en la distribución \(\chi^2\) con \(n\) grados de libertadrchisqgenera datos a aleatorios de una distribución \(\chi^2\)
Tablas de contingencia
Las tablas de contingencia permiten resumir datos de variables categóricas, es el primer paso para la realización de una prueba \(\chi^2\)
Tablas de contingencia
- Es una de las formas más comunes de resumir datos categóricos
- Se realizan para estudiar si existe asociación entre una variable categórica (fila) y otra variable categórica (columna). De forma general, se acepta que en las filas se muestra la exposición y en las columnas el evento.
- Una tabla de contingencia es una tabla que cuenta las observaciones por múltiples variables categóricas. Las filas y columnas de las tablas corresponden a estas variables categóricas.
- Se consideran \(X\) y \(Y\) dos variables categóricas con \(I\) y \(J\) categorías
Ejemplo
- Sea \(X\) una variable categórica que indica si toma aspirina o placebo (I=2)
- Sea \(Y\) una variable categórica que indica si sufrió ataque cardíaco (J=3)
| Mortal | No mortal | No ataque | Totales | |
|---|---|---|---|---|
| Placebo | 18 | 171 | 10845 | 11304 |
| Aspirina | 5 | 99 | 10933 | 11037 |
La función table en R
Importar base para ejemplo
La función table en R
Si queremos conocer cuantos pacientes fuman y de forma separada cuantos recién nacidos presentaron bajo peso al nacer podemos emplear el siguiente código:
La función table en R
Si queremos conocer cuantos pacientes fuman y de forma separada cuantos recién nacidos presentaron bajo peso al nacer podemos emplear el siguiente código:
smoke
0 1
115 74 low
0 1
130 59 Las anteriores son solo tablas de frecuencias, no una tabla de contingencia.
La función table en R
Se pueden crear tablas de contingencia con la función table ingresando dos variables.
La función table en R
low
smoke 0 1
0 86 29
1 44 30 smoke
low 0 1
0 86 44
1 29 30La función table en R
¿Y si quisieramos proporciones?
race
smoke 1 2 3
0 0.44 0.16 0.55
1 0.52 0.10 0.12 smoke
race 0 1
1 0.44 0.52
2 0.16 0.10
3 0.55 0.12El resultado anterior también se puede hacer utilizando la función prop.table
La función prop.table
Con esta función podemos obtener tablas de contingencia con proporciones
race
smoke 1 2 3
0 0.23280423 0.08465608 0.29100529
1 0.27513228 0.05291005 0.06349206 smoke
race 0 1
1 0.23280423 0.27513228
2 0.08465608 0.05291005
3 0.29100529 0.06349206La función prop.table
Se puede calcular las proporciones por columnas o por filas, cambiando un argumento. Se utiliza 1 para filas y 2 para columnas.
race
smoke 1 2 3
0 0.3826087 0.1391304 0.4782609
1 0.7027027 0.1351351 0.1621622 smoke
race 0 1
1 0.3826087 0.7027027
2 0.1391304 0.1351351
3 0.4782609 0.1621622Algunos ejemplos de tablas de contingencia
Ejemplo de tabla de contingencia

Ejemplo de tabla de contingencia
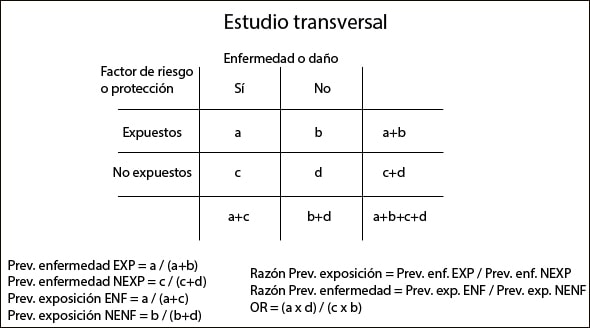
Prueba de \(\chi^2\)
Prueba de \(\chi^2\)
La prueba de ji cuadrado (\(\chi^2\)) de Pearson es una prueba estadística de contraste de hipótesis que se aplica para analizar datos recogidos en forma de número de observaciones en cada categoría (conteos):
- Número de éxitos que ha tenido una intervención.
- Porcentaje de pacientes que presentan una característica.
- Proporción de resultados favorables obtenidos de grupo de pacientes con tratamientos distintos.
La prueba de chi-cuadrada se basa en la independencia de dos criterios de clasificación
Datos observados vs Datos esperados
La prueba de \(\chi^2\) utiliza la diferencia de valores observados vs los datos esperado
Las frecuencias observadas son el número de objetos o individuos en la muestra que caen dentro de las diversas categorías de la variable de interés
Las frecuencias esperadas son el número de objetos o de individuos en la muestra que se esperaría observar si alguna hipótesis nula respecto a la variable es verdadera
Entre más grande sea la diferencia entre los valores esperados y los observados menos probabilidad hay que los resultados sean debidos al azar
El estadístico de prueba
Para obtener el estadístico de prueba se emplea la siguiente formula:
\[\chi^2= \displaystyle\sum_{i=1}^{r} \displaystyle\sum_{j=1}^{c}\bigg[\frac{(O_{ij}-E_{ij})^2}{E{ij}}\bigg]\]
donde: donde \(O_{ij}\) es la frecuencia observada y \(E_{ij}\) es la frecuencia esperada para la celda ij
Pasos para la prueba de \(\chi^2\)
Tomar muestras aleatorias de las poblaciones de interés. Las variables deben ser independientes
Clasificar cada sujeto según las categorías de cada variable en estudio. Tablas de contingencia
Anotar los conteos o frecuencias en un cuadro de contingencia.
Calcular las frecuencias esperadas para cada celda.
Comparar las frecuencias esperadas y observadas mediante.
Comparar el valor calculado de \(\chi^2\) con el valor tabulado de \(\chi^2\)
Determinar el valor de \(p\)
Determinación de las frecuencias esperadas
Cuando dos eventos son independientes, la probabilidad de su ocurrencia conjunta es igual al producto de sus probabilidades individuales. La probabilidad de que un sujeto tomado al azar en esta población esté caracterizado por algún nivel de ambos criterios se estima mediante:
\[E_{ij}=\bigg(\frac{n_i}{n}\bigg)\bigg(\frac{n_j}{n}\bigg)n\]
o bien:
\[E_{ij}=\frac{(n_i)(n_j)}{n}\]
Determinación de las frecuencias esperadas
\[E_{ij}=\frac{(n_i)(n_j)}{n}\]
| Tratamiento | Favorable | Desfavorable | Total |
|---|---|---|---|
| Placebo | 16 (a) | 48 (b) | 64 \((n_j)\) |
| Test | 40 (c) | 20 (d) | 60 \((n_j)\) |
| Total | 56 \((n_i)\) | 68 \((n_i)\) | 124 \((n)\) |
Determinación de las frecuencias esperadas
\[E_{ij}=\frac{(n_i)(n_j)}{n}\]
| Tratamiento | Favorable | Desfavorable | Total |
|---|---|---|---|
| Placebo | 16 (a) | 48 (b) | 64 \((n_j)\) |
| Test | 40 (c) | 20 (d) | 60 \((n_j)\) |
| Total | 56 \((n_i)\) | 68 \((n_i)\) | 124 \((n)\) |
\[a=\frac{(56)(64)}{124}=56\]
Determinación de las frecuencias esperadas
\[E_{ij}=\frac{(n_i)(n_j)}{n}\]
| Tratamiento | Favorable | Desfavorable | Total |
|---|---|---|---|
| Placebo | 16 (a) | 48 (b) | 64 \((n_j)\) |
| Test | 40 (c) | 20 (d) | 60 \((n_j)\) |
| Total | 56 \((n_i)\) | 68 \((n_i)\) | 124 \((n)\) |
\[a=\frac{(56)(64)}{124}=56\]
Determinación de las frecuencias esperadas
\[E_{ij}=\frac{(n_i)(n_j)}{n}\]
| Tratamiento | Favorable | Desfavorable | Total |
|---|---|---|---|
| Placebo | 16 (a) | 48 (b) | 64 \((n_j)\) |
| Test | 40 (c) | 20 (d) | 60 \((n_j)\) |
| Total | 56 \((n_i)\) | 68 \((n_i)\) | 124 \((n)\) |
Determinar los otros valores
Determinación de las frecuencias esperadas
\[b=\frac{(68)(64)}{124}=35.1\] \[c=\frac{(56)(60)}{124}=27.1\]
\[d=\frac{(68)(60)}{124}=32.9\]
Grados de libertad
Para calcular los grados de libertad se utiliza la fórmula: \(gl = (r – 1)(c – 1)\), donde \(gl\) son los grados de libertad, \(r\) es el número de renglones o filas y \(c\) es el número de columnas.
Para una tabla de dos por dos los grados de libertad son 1
Ejemplo 1
Ejemplo 1.
Dado el siguiente conjunto de datos, determine si la proporción con dos o más hipoglucemiantes orales es independiente entre los grupos. Utilice \(\alpha=0.10\)
| Tratamiento | Dos hipoglucemiantes | Un hipoglucemiante | Total |
|---|---|---|---|
| Grupo 1 | 16 (a) | 134 (b) | 150 \((n_j)\) |
| Grupo 2 | 6 (c) | 119 (d) | 125 \((n_j)\) |
| Total | 22 \((n_i)\) | 253 \((n_i)\) | 275 (n) |
Hipótesis
\(H_0:\) el uso de dos o más hipoglucemiantes orales por parte de un enfermo de diabetes es independiente del grupo al que pertenece (no hay relación entre las variables)
\(H_A\):el uso de dos o más hipoglucemiantes orales por parte de un enfermo de diabetes no es independiente del grupo al que pertenece (hay relación entre la variables)
\(H_A\):el uso de dos o más hipoglucemiantes orales por parte de un enfermo de diabetes es dependiente del grupo al que pertenece (hay relación entre la variables)
Supuestos y datos
Descripción de la población que interesa y planteamiento de los supuestos necesarios.
La población es nominal. Para este caso, las respuestas son del tipo “sí” o “no”.
No existen frecuencias esperadas pequeñas (en todo caso, este supuesto puede confirmarse durante el procedimiento mediante el cual se calcula el estadístico de prueba).
Los sujetos que conforman las muestras han sido seleccionados de manera independiente.
El estadístico indicado es \(\chi^2\)
Determinar los valores esperados
Dado el siguiente conjunto de datos, determine si la proporción con dos o más hipoglucemiantes orales es independiente entre los grupos. Utilice \(\alpha=0.10\)
| Tratamiento | Dos hipoglucemiantes | Un hipoglucemiante | Total |
|---|---|---|---|
| Grupo 1 | 16 (a) | 134 (b) | 150 \((n_j)\) |
| Grupo 2 | 6 (c) | 119 (d) | 125 \((n_j)\) |
| Total | 22 \((n_i)\) | 253 \((n_i)\) | 275 (n) |
Determinar los valores esperados
\[a=\frac{(22)(150)}{275}=12\] \[b=\frac{(253)(150)}{275}=138\] \[c=\frac{(22)(125)}{275}=10\] \[d=\frac{(253)(125)}{275}=115\]
Calculo del valor de \(\chi^2\) de mis datos
\[\chi^2= \displaystyle\sum_{i=1}^{r} \displaystyle\sum_{j=1}^{c}\bigg[\frac{(O_{ij}-E_{ij})^2}{E{ij}}\bigg]\]
\[\chi^2=\frac{(16-12)^2}{12}+\frac{(134-138)^2}{138}+\frac{(6-10)^2}{10}+\frac{(119-115)^2}{115}=3.2\]
Criterios de decisión
El valor crítico de la prueba, que define las regiones de rechazo y aceptación, se localiza de la siguiente manera:
La prueba de \(\chi^2\) siempre es una prueba a una cola (derecha).
Para la prueba de \(\chi^2\),la región de rechazo se encuentra a la derecha de la distribución y está formada por aquella parte de la distribución \(\chi^2\) que incluye todos los valores de \(\chi^2\) tales que, cuando \(H_0\) es verdadera, la probabilidad de ocurrencia aleatoria de una p de ese tamaño o menor es igual o mayor de \(alpha\)
Criterios de decisión
- lo que intentamos probar es la dependencia de los datos
la región de rechazo se encuentra a la derecha de la distribución
Valor de \(\chi^2\) de tablas
Para calcular los grados de libertad se utiliza la fórmula: \(gl = (r – 1)(c – 1)\), donde \(gl\) son los grados de libertad, \(r\) es el número de renglones o filas y \(c\) es el número de columnas.
Para una tabla de dos por dos los grados de libertad son 1
Gráfica hipotética para el valor crítico
Gráfica hipotética para el valor crítico
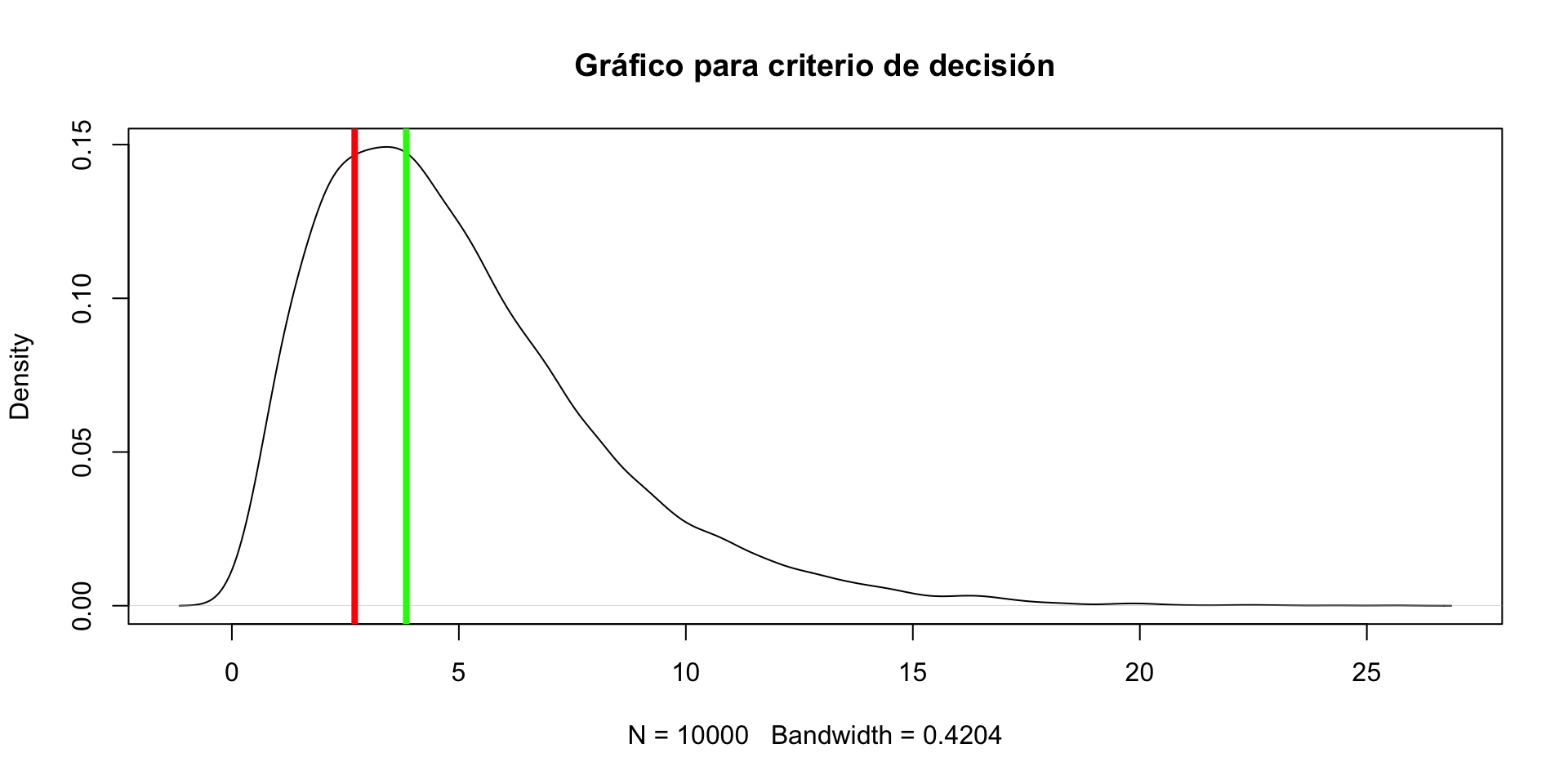
Gráfica hipotética para el valor crítico
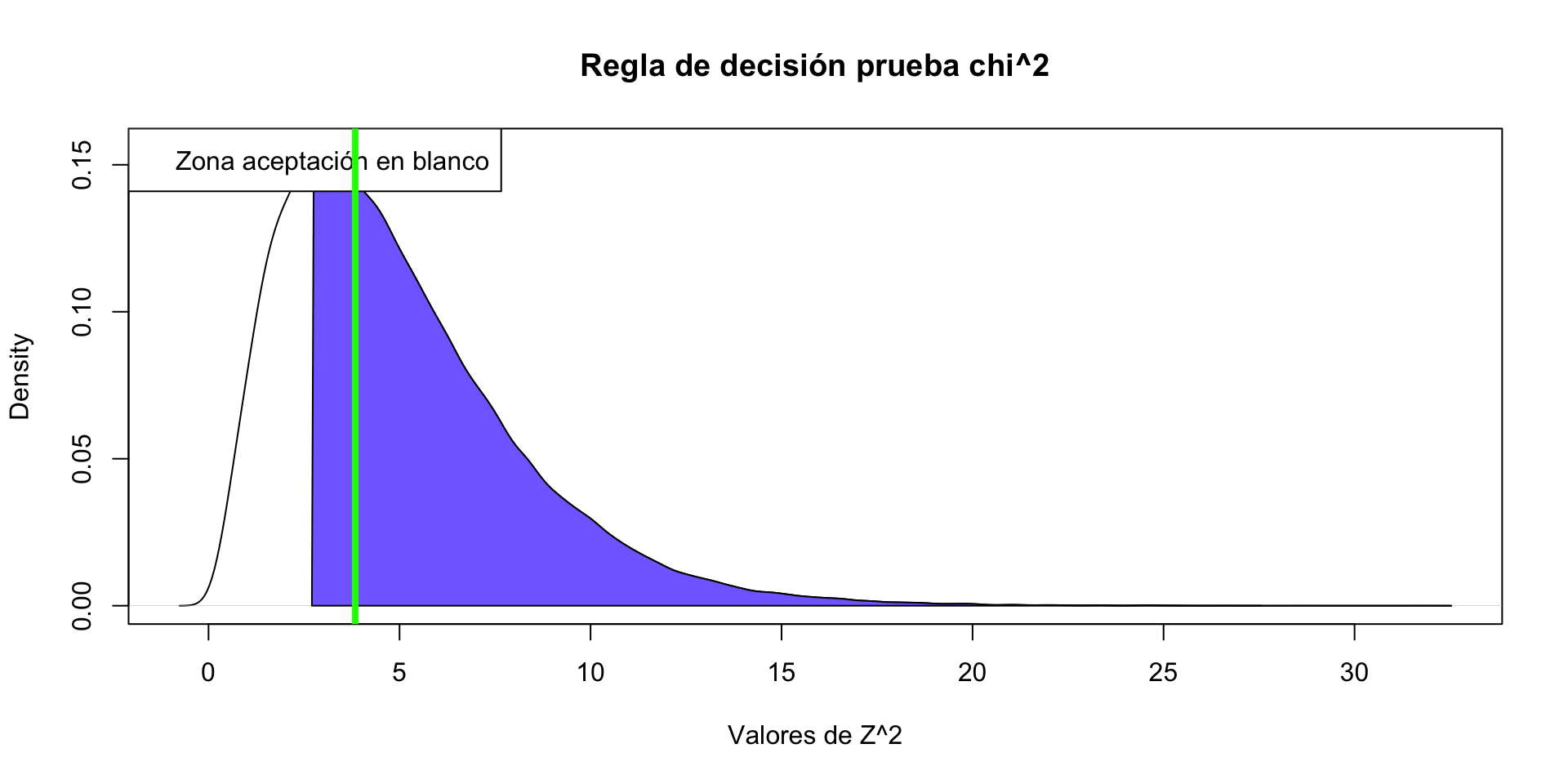
Gráfica hipotética para el valor crítico
Decisión y conclusión.
Se rechaza la \(H_0\) porque 3.12 es mayor a 2.7, es decir, está más a la derecha de la curva. la región de rechazo se encuentra a la derecha de la distribución
Estos valores nos indican que los datos son dependientes, es decir, que el valor observado en las frecuencias del uso de dos hipoglucemiantes, si depende del grupo.
Decisión y conclusión.
- La proporción de individuos con dos o más hipoglucemiantes es distinta entre los grupos. En el grupo 1 la proporción fue de 0.107 mientras que la del grupo 2 fue 0.048
Calculo de \(p\)
En R se utiliza la función pchisq
Ejemplo práctico
Ejemplo práctico
El propósito de un estudio realizado por Vermund et al. era investigar la hipótesis de que las mujeres infectadas con VIH que también están infectadas con el papiloma virus humano (PVR), tienen mas probabilidad de tener anormalidades citológicas cervicales que las mujeres con uno de los dos virus mencionados.
Ejemplo práctico
Los datos son los siguientes:
| PVH | Seropositivo sintomático | Seropositivo asintomático | Seronegativo | Total |
|---|---|---|---|---|
| Positivo | 23 | 4 | 10 | 37 |
| Negativo | 10 | 14 | 35 | 59 |
| Total | 33 | 18 | 45 | 96 |
Se pretende conocer si es posibles concluir que existe relación entre el estadio del PVH y la etapa de la infección
Hipótesis
- \(H_0\):
- Las variable son independientes.
- No hay relación entre el estadio del PVH y la etapa de la infección por VIH.
- Las proporciones de mujeres en las distintas etapas del VIH son iguales independientemente de la co-infección por PVH
Hipótesis
- \(H_A\):
- las variables son dependientes
- Hay relación entre el estadio del PVH y la etapa de la infección por VIH.
- Las proporciones de mujeres en las distintas etapas del VIH son diferentes independientemente de la co-infección por PVH
Frecuencias observadas y esperadas
Para la primer casilla en el lado superior izquierdo el cálculo es: 33*37/96
| PVH | Seropositivo sintomático | Seropositivo asintomático | Seronegativo | Total |
|---|---|---|---|---|
| Positivo | 23 (12.72) | 4 (6.94) | 10 (17.34) | 37 |
| Negativo | 10 (20.28) | 14 (11.06) | 35 (27.66) | 59 |
| Total | 33 | 18 | 45 | 96 |
Valor de \(\chi^2\) de mis datos
\[\chi^2= \displaystyle\sum_{i=1}^{r} \displaystyle\sum_{j=1}^{c}\bigg[\frac{(O_{ij}-E_{ij})^2}{E{ij}}\bigg]\]
Sustituyendo:
\[\chi^2=\frac{(23-12.72)^2}{12.72}+\frac{(4-6.94)^2}{6.94}+\cdot \cdot \cdot+\frac{(35-27.66)^2}{27.66}=20.60\]
Valor de \(\chi^2\) de tablas
Para calcular los grados de libertad se utiliza la fórmula: \(gl = (r – 1)(c – 1)\), donde \(gl\) son los grados de libertad, \(r\) es el número de renglones o filas y \(c\) es el número de columnas.
\(gl = (2 – 1)(3 – 1)=2\)
Valor de \(p\)
Ejercicio 2 de práctica
Ejercicio 2 de práctica
Un grupo de investigadores desea conocer, si el fumar en el primer trimestre del embarazo se asocia al bajo peso de los recién nacidos. Estos datos fueron capturados en la base de datos “birthwt”. Utilice \(\alpha\) de 0.05, construya un gráfico de barras y reporte los valores esperados por casilla
Ejercicio 2 de práctica
Se puede crear una tabla con los datos para facilitar la resolución del ejercicio.
Ejercicio 2 de práctica
Se puede crear un gráfico de barras para que nos oriente de las frecuencias de los recién nacidos con peso bajo entre las mujeres que fumaron en el primer trimestre del embarazo y las que no
Ejercicio 2 de práctica
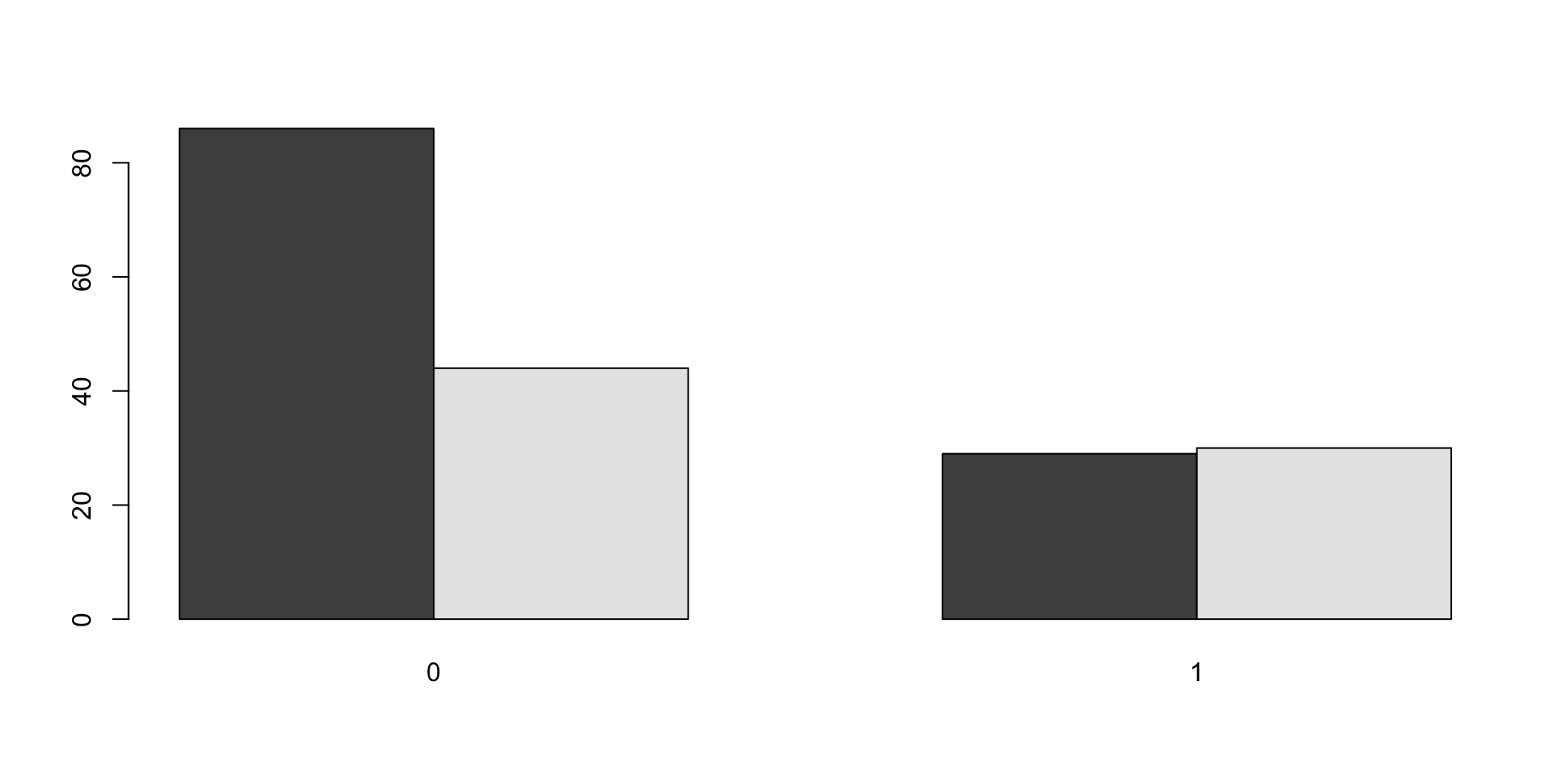
Ejercicio 2 de práctica
Para realizar la prueba de \(\chi^2\) utilice el siguiente código
Pearson's Chi-squared test with Yates' continuity correction
data: tab1
X-squared = 4.2359, df = 1, p-value = 0.03958Corrección de Yates
Con frecuencia utilizamos aproximaciones con distribuciones de probabilidad continuas para resolver contrastes de hipótesis con variables que siguen una distribución discreta. En estos casos, debemos aplicar una corrección de continuidad, siendo la más conocida la corrección de continuidad de Yates.
La distribución \(\chi^2\) puede perder su continuidad cuando se tienen valores pequeños en las casillas de la tabla de contingencia
¿Cómo concluiría?
¿Cómo concluirían?
Extraer parámetros
Es posible extraer parámetros de la función chis.test si se guarda en un objeto
Utilizando ggstatplot
En ggstastplot también se puede realizar la prueba de \(\chi^2\) aunque no permite la realización de la prueba exacta de Fisher (que veremos más adelante).
Responda la sigueinte pregunta:
¿Fumar durante el embarazo se asocia al bajo peso al nacer?
Utilizando ggstatplot
Utilizando ggstatplot
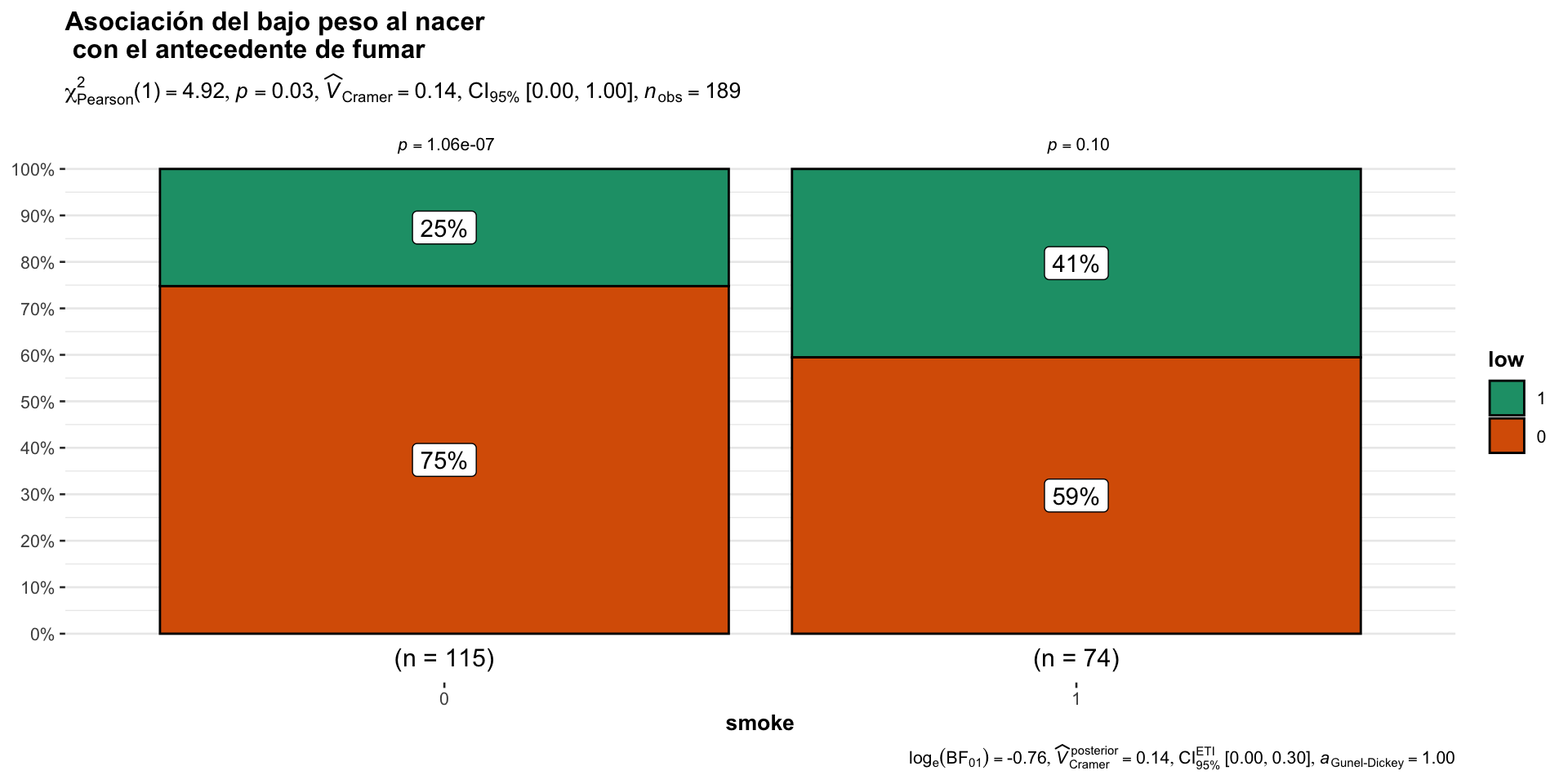
Prueba exacta de fisher
Frecuencias esperadas pequeñas
- Cuando las frecuencias esperadas para cada celda son grandes, el estadístico X 2 calculado se aproxima a la distribución chi-cuadrada. Sin embargo, cuando las frecuencias esperadas son pequeñas, esta aproximación no es tan cercana y su utilización puede conducir a errores de interpretación.
Frecuencias esperadas pequeñas
- Se considera que, cuando las frecuencias esperadas son iguales o mayores de 5, son lo suficientemente grandes para utilizar la distribución de chi-cuadrada, aunque generalmente se acepta como adecuada su utilización en cuadros de contingencia con más de cuatro celdascuando en menos de 20% de las celdas se encuentran frecuencias esperadas menores de 5
Corrección de Mantel-Haenszel
- Cuando las muestras son pequeñas y las frecuencias esperadas menores de 5, se puede utilizar las correcciones propuestas por Mantel-Haenszel y por Yates. Estas correcciones modifican el valor de n en la fórmula de tal manera que, a medida que la muestra es más pequeña, la prueba es más estricta. La chi-cuadrada con corrección de Mantel-Haenszel se calcula mediante:
\[\chi^2_{MH}=\frac{(n-1)(ad-bc)^2}{(a+c)(b+d)(a+b)(c+d)}\]
Prueba exacta de Físher
- Es un procedimiento estadístico de prueba de hipótesis que se basa en los totales observados en columnas y renglones.
- Al igual que para la prueba chi-cuadrada, con este procedimiento se evalúa la independencia entre las categorías correspondientes a los renglones y las columnas, y se puede probar la hipótesis nula.
- A diferencia de otras pruebas estadísticas (p. ej., z o chi-cuadrada), el resultado de la prueba exacta de Fisher es el valor de p.
\[\frac{(a+c)!(a+b)!(b+d)!(c+d)!}{n!a!b!c!d!}\]
Prueba exacta de Físher
Suponga que en el ejercicio practico 2 se presentaron valores esperados menores a 5. Resuelva el mismo problema utilizando la prueba exacta de Físher
Fisher's Exact Test for Count Data
data: tab1
p-value = 0.03618
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.028780 3.964904
sample estimates:
odds ratio
2.014137 Ejercicio práctico 3
¿Es posible concluir que el peso de bajo al nacer depende de la raza de las mujeres embarazadas? Construya una gráfico de barras y reporte los valores esperados. Utilice las variables low y race
Ejercicio práctico 4
¿Es posible concluir que el estatus de los pacientes con melanoma se asocia a la presencia de úlceras y a al sexo de los pacientes?
utilice la base de datos Melanoma de la librería MASS, además compruebe sus resultados utilizando ggstatplot.