Población y muestreo

Bioestadística básica/Posgrados CUCS

Pérez-Guerrero Edsaúl Emilio

Instituto de Investigación en Ciencias Biomédicas

2024-08-25

Contenido

  1. Población
  2. Muestras
  3. Muestreo utilizando R

Proceso del análisis de datos

Etapas en del análisis de datos

Población

Población

  • En estadística una población puede entenderse como el grupo objetivo del cual se eligen los sujetos de la muestra y para quienes se generalizarían los resultados

  • El grupo objetivo debe tener características previamente definidas

  • Cuando se investiga todos los sujetos de la población objetivo se denomina enumeración completa o censo.

Población

Algunos ejemplos de población son:

  • En un estudio descriptivo de infección respiratoria aguda (IRA) en un país, la población objetivo podría ser todos los casos de IRA existentes en ese país.
  • Para un programa de control del cáncer cervicouterino, la población objetivo podría ser todas las mujeres casadas mayores de 40 años.
  • Para estudiar los factores de riesgo del agrandamiento de la próstata, la población de interés podría ser todos los hombres de 50 años o más en un área.

Población

Algunas limitaciones en la definición de población:

  • Algunos autores sostienen que debe de incluir a los a los pasados y a los futuros casos1
  • Hay algunas poblaciones que no se pueden delimitar
  • En algunos casos es imposible incluir todos los casos

¿Qué carcterísticas tiene una población?

¿Por qué no es posible investigar una población entera?

Muestreo

Ventajas de la muestra

  • Puede ser el único método factible para la recopilación de datos relevantes en algunos casos. Ventaja

  • Menor costo y menor demanda de recursos (personal, laboratorio, etc.) Ventaja

  • Se puede recopilar información confiable si lo métodos son adecuados. Ventaja

Desventajas de la muestra

  • Una muestra de una población con toda probabilidad será diferente de la segunda muestra. Desventaja
  • No todas las muestras son representativas. Desventaja
  • Cuando se requiere información para segmentos pequeños que contienen pocos individuos, el muestreo puede no proporcionar información lo suficientemente precisa sobre ellos. Desventaja
  • A veces, se necesita un recuento completo, como para un diagnóstico y perfil de resultados de los casos ingresados en un hospital cada año. Desventaja

Conceptos

Unidad de investigación y unidad de muestreo

  • La unidad de investigación es el tema sobre el que se obtiene información

  • La unidad de muestreo es la que se utiliza para realizar el muestreo.

En una encuesta comunitaria sobre desnutrición, la unidad de muestreo podría ser una familia, pero la unidad de investigación podría ser un niño menor de 5 años. Una unidad de muestreo puede tener múltiples unidades o ninguna unidad de investigación sobre la cual investigar.

Unidad de investigación y unidad de muestreo

Se realiza una investigación sobre la prevalencia de DM en hospitales de segundo nivel del área metropolitana de Guadalajara.

  • ¿Quién es la unidad de investigación?
  • ¿Quien es la unidad de muestreo?
  • ¿Es posible definir una población?
  • ¿Que problemas podríamos encontrar en la realización del muestreo para esta población?

Marco de muestreo

Se refiere a la lista de todas las unidades de muestreo en la población objetivo se denomina marco de muestreo.

  • Las unidades se eligen de este marco.
  • Las unidades deben ser mutuamente excluyentes y el marco debe ser una lista exhaustiva
  • La preparación del marco requiere una definición precisa de la unidad, así como de la población. Criterios de inclusión y de exclusión
  • A veces hace referencia a lista de unidades de investigación

Marco de muestreo

Se pretende realizar un estudio para medir la prevalencia de hipertensión y diabetes en el barrio del Santuario de la ciudad de Guadalajara.

  • ¿Quienes formarían el marco de muestreo?

  • ¿Incluimos diabéticos e hipertensos? ¿Solo pacientes con una de las dos enfermedades?

  • ¿Cómo podría definir mi unidad de muestreo y mi unidad de investigación?

Tamaño de muestra

  • Se refiere el número de sujetos o unidades de muestreo

  • Se utiliza la letra \(n\) para referirnos a ella

  • Debe ser lo suficientemente grande para responder nuestra pregunta de investigación y para permitirnos encontrar diferencias y/o asociaciones

  • Es el tamaño mínimo que se necesita para ver diferencias

Tamaño de muestra

  • Depende de:
    • La variación de la población
    • Del tamaño del efecto (diferencias)
    • Del poder estadístico (la capacidad de la prueba para ver diferencias)
    • Del nivel de confianza de la prueba

Muestreo aleatorio y no aleatorio

  • Una muestra se denomina aleatoria cuando la inclusión o exclusión de un sujeto elegible en particular depende del azar y no se puede predecir de antemano.

  • Para hacer un muestreo aleatorio necesitamos:

    • Un gran número de unidades de muestreo.
    • O conocer todos los individuos que reúnen con mi criterios de inclusión y exclusión

Muestreo aleatorio y no aleatorio

La selección aleatoria es solo una estrategia para obtener una muestra representativa. Cuanto mayor sea la muestra en relación con el tamaño de la población, mayor será la probabilidad de que sea representativa, aleatoria o no. Pero el muestreo aleatorio asigna probabilidades que ayudan a hacer inferencias estadísticamente sólidas. 1

Un problema muy grande con la muestra

  • La fluctuación de la muestra depende:
    • Método del muestreo
    • Tamaño de muestra
    • Variación

Métodos de muestreo

Métodos de muestreo

  1. Muestreo aleatorio simple
  2. Muestreo aleatorio estratificado
  3. Muestreo aleatorio multietapa
  4. Muestreo aleatorio por conglomerados (clusters)
  5. Muestreo aleatorio sistemático
  6. Muestreo consecutivo
  7. Muestreo secuencial

Muestreo aletorio simple

  • Muestreo en el que todos los individuos tienen las mismas oportunidades de ser seleccionados
  • Estrictamente, todas las muestras, independientemente de su tamaño, tienen las mismas posibilidades de ser seleccionadas
  • Requiere de la disponibilidad del marco muestral. Debemos de conocer todo nuestro marco muestral

Muestreo aletorio simple

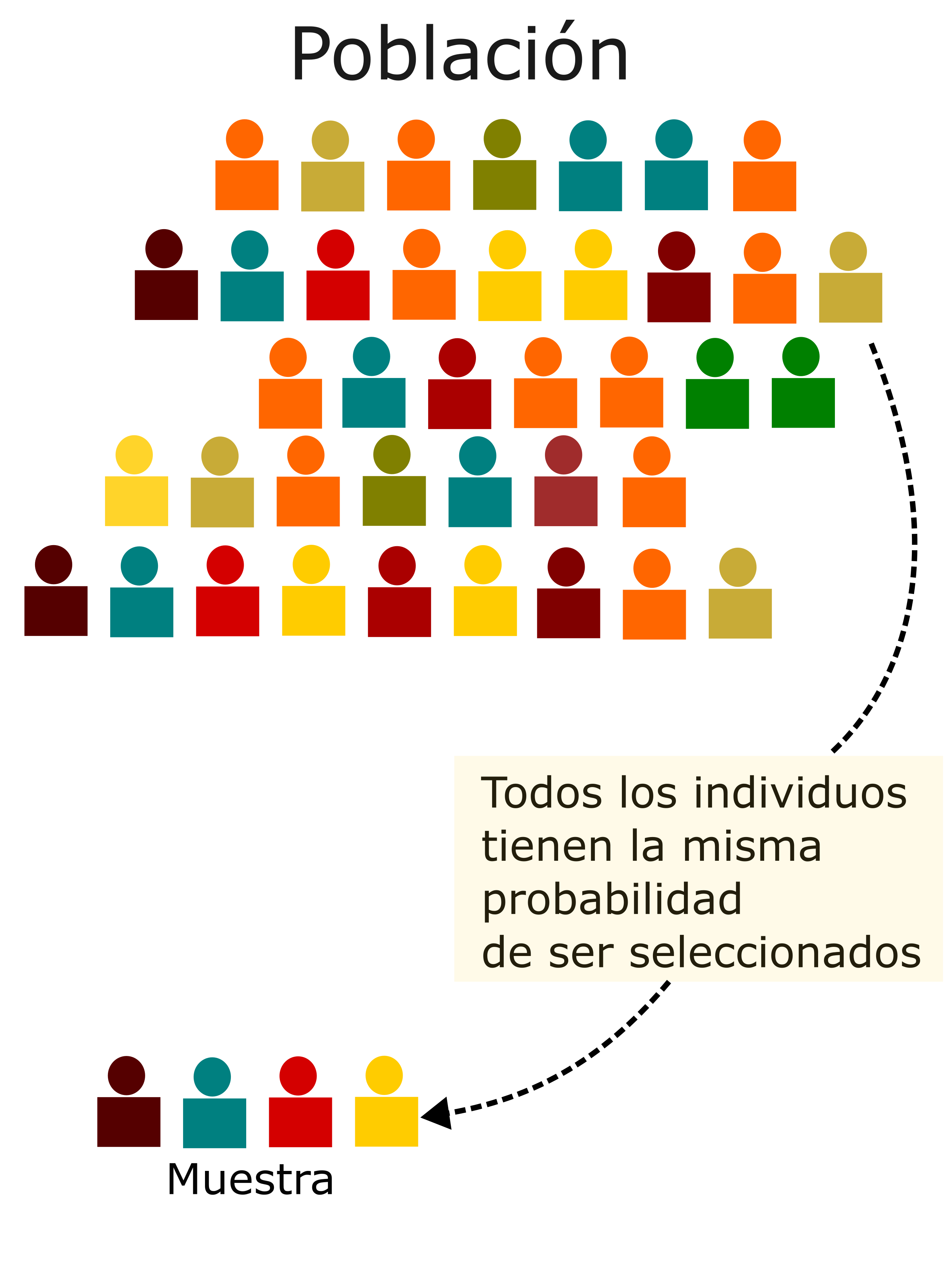
Figure 1: Muestreo aletorio simple

Muestreo aletorio simple

¿Que pasaría si requiere una muestra de subgrupos poco representativos?

Muestreo aletorio estratificado

En el muestreo por estratos, la población se divide en subgrupos o estratos homogéneos basados en una característica específica, como la edad, el género, la ubicación geográfica, el nivel socioeconómico o la condición de salud. Luego, se selecciona una muestra aleatoria de cada estrato.

Muestreo aletorio estratificado

Se realiza un estudio para evaluar los niveles de una hormona en mujeres. Se espera que la muestra sea representativa de todos los hospitales de segundo nivel de Guadalajara. ¿Cómo nos aseguramos de que todos los hospitales tengan una representación adecuada?

  • Primero se realiza la identificación de los estratos (los hospitales)
  • Después se realiza un muestreo aleatorio para cada estrato
  • Se determina el tamaño de la muestra para cada estrato
  • Una muestra obtenida por muestreo aleatorio estratificado implica que la muestra de cada estrato está en la misma proporción que en la población

Muestreo por estratos

Supongamos que deseas llevar a cabo un estudio para evaluar la prevalencia de la diabetes en una población de adultos mayores en una ciudad determinada. Sabe que esta población se compone de cuatro estratos en función de la ubicación geográfica: centro de la ciudad, suburbios, áreas rurales y áreas costeras. Cada estrato tiene una población de adultos mayores con características socioeconómicas y de acceso a la atención médica ligeramente diferentes

Muestreo aleatorio estratificado

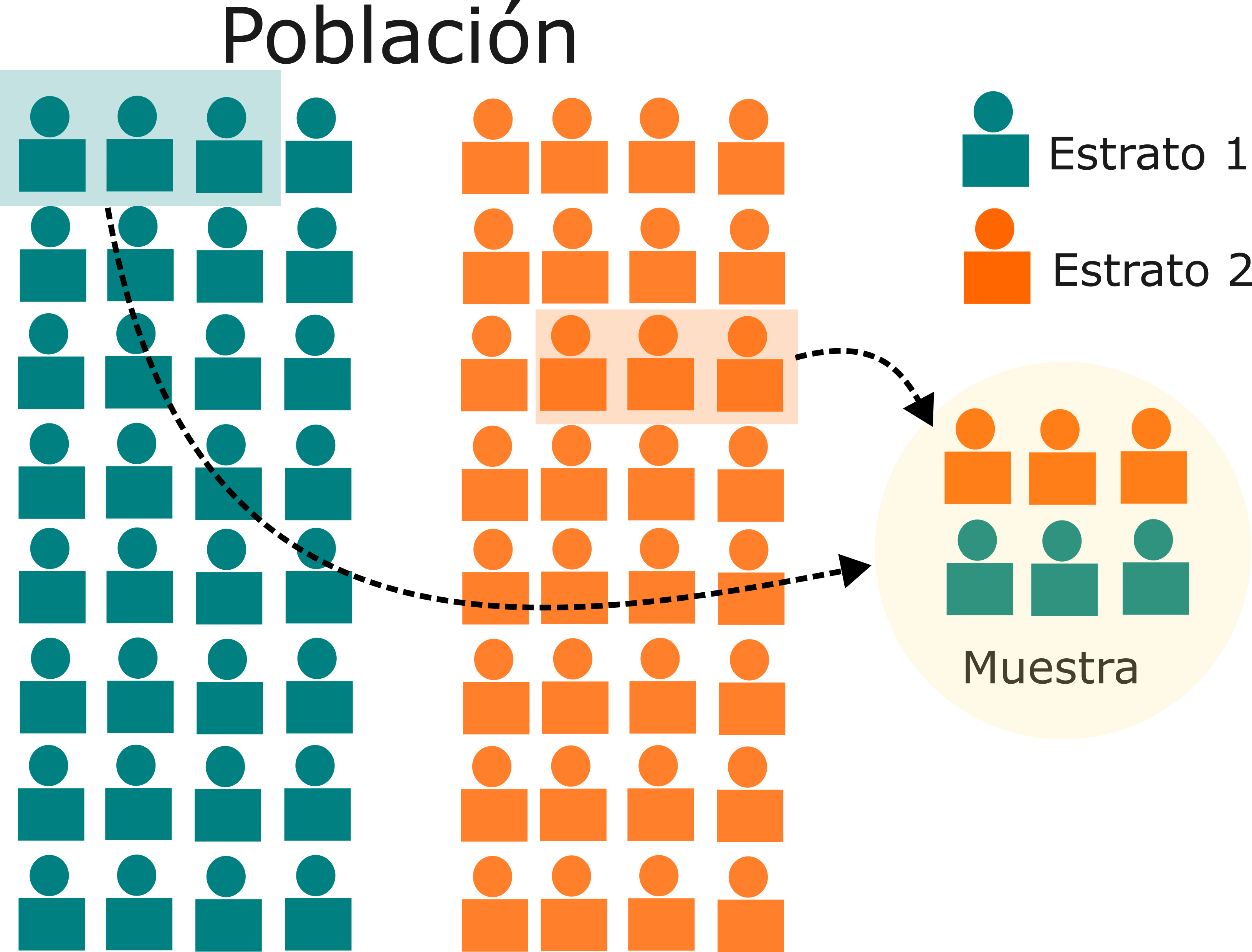
Figure 2: Muestreo por estratos

Ventajas y desventajas del muestreo por estratos

Ventajas

  • Permite obtener estimaciones precisas para cada estrato, lo que es útil cuando se sabe que diferentes estratos tienen diferentes tasas o características de interés.
  • Puede proporcionar una representación equitativa de cada estrato, lo que es útil para garantizar la inclusión de grupos minoritarios en la muestra.
  • Facilita un análisis detallado de cada estrato por separado.

Ventajas y desventajas del muestreo por estratos

Desventajas

  • Puede ser más costoso y requerir más tiempo que otras técnicas de muestreo.
  • Requiere información precisa sobre la población en términos de estratos.

Muestreo aletorio por clústers (conglomerados)

  • A diferencia del análisis por estratos, el análisis por clústers permite que ciertas unidades de muestreo, sobre todo cuando son pequeñas o reúnen ciertas características, no sean incluidas.

Muestreo aletorio por clústers (conglomerados)

  • La diferencia más importante entre el muestreo por clústers y por estratos es que el primero se aprovecha de divisiones ya hechas en la población mientras que el segundo no. Además el muestreo por clúster permite la no inclusión de ciertas unidades de muestreo.

Muestreo aletorio por clústers (conglomerados)

Imagine que realiza un estudio para evaluar la prevalencia de enfermedades transmitidas por vectores, como el dengue y el zika, en una región rural de un país. En lugar de realizar un muestreo por estratos, donde dividiría la población en grupos basados en alguna característica específica, opta por el muestreo por clústers debido a la falta de una lista completa y actualizada de todos los hogares en la región. Por lo tanto realiza un muestreo por localidades, omitiendo a aquellas localidades pequeñas.

Muestreo aleatorio por clúster (conglomerados)

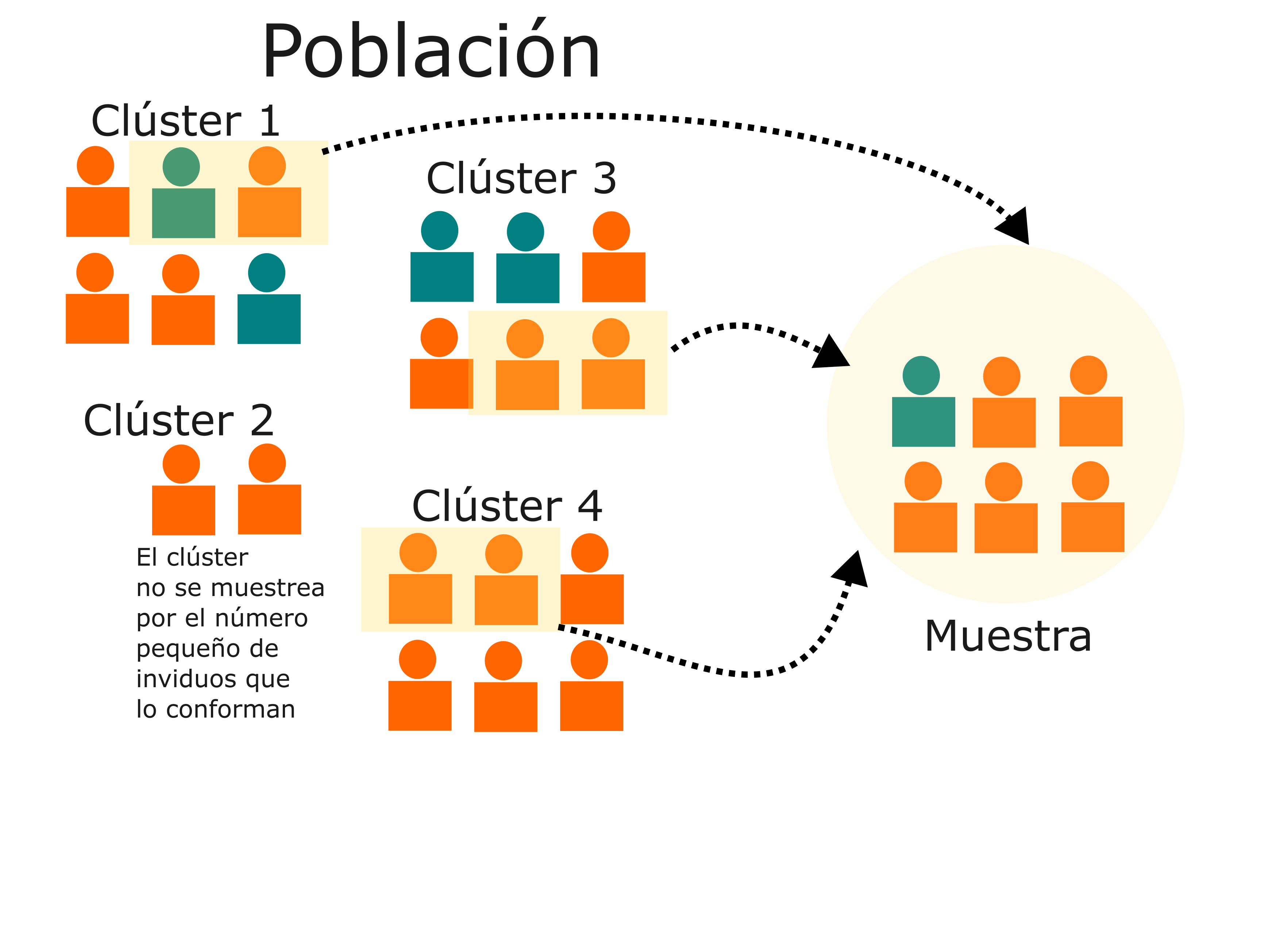
Figure 3: Muestro por conglomerados

Muestreo aleatorio por clusters

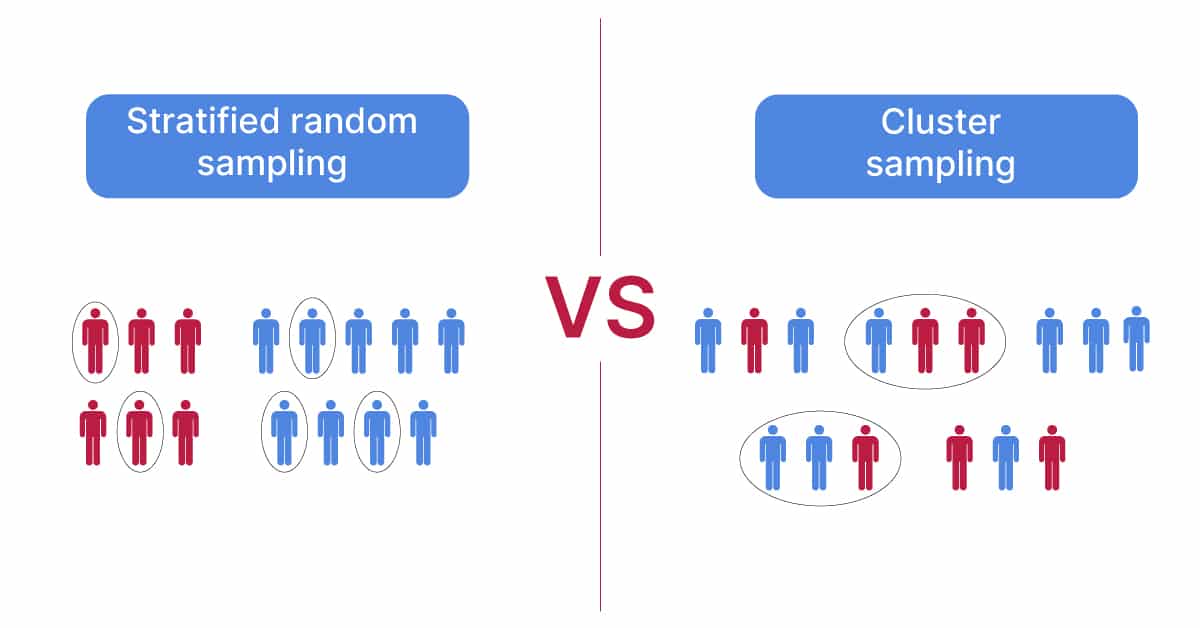
Diferencias entre el muestreo por clústers y estratos

¿Cómo plantearía el muestreo por clúster para un estudio para estimar la prevalencia de DM2 en los hospitales de segundo nivel del área metropolitana de Guadalajara?

¿Cómo plantearía el muestreo por estratos para un estudio para estimar la prevalencia de DM2 en los hospitales de segundo nivel del área metropolitana de Guadalajara?

Muestreo aleatorio multietapa

  • Útil para poblaciones de gran tamaño
  • Consiste en extraer las muestras por etapas
  • Se realiza el muestreo de la unidad mayor a unidad menor

Muestreo aletorio multietapa

En un estudio para encontrar la prevalencia del tabaquismo en mujeres de 20 años se puede, por ejemplo, seleccionar primero 4 municipios, luego 12 ciudades censales dentro de cada municipio seleccionado y luego 50 familias dentro de cada bloque seleccionado, todo por método aleatorio.

Todas las mujeres mayores de 20 años en las familias seleccionadas podrían ser la unidad de investigación, aunque las unidades de muestreo son condados, bloques y familias.

Muestreo aleatorio multietapa

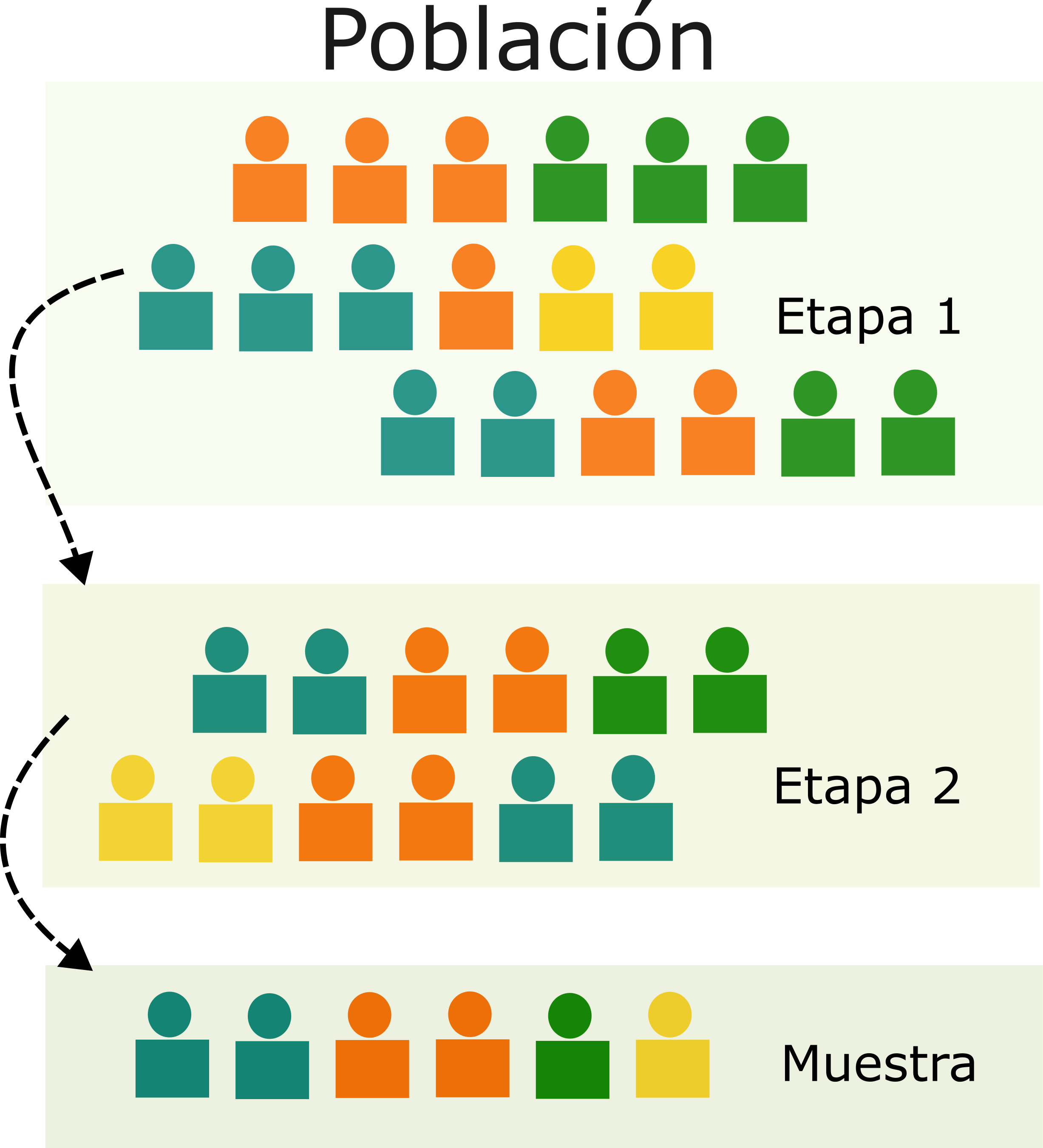
Figure 4

Muestro aleatorio sistemático

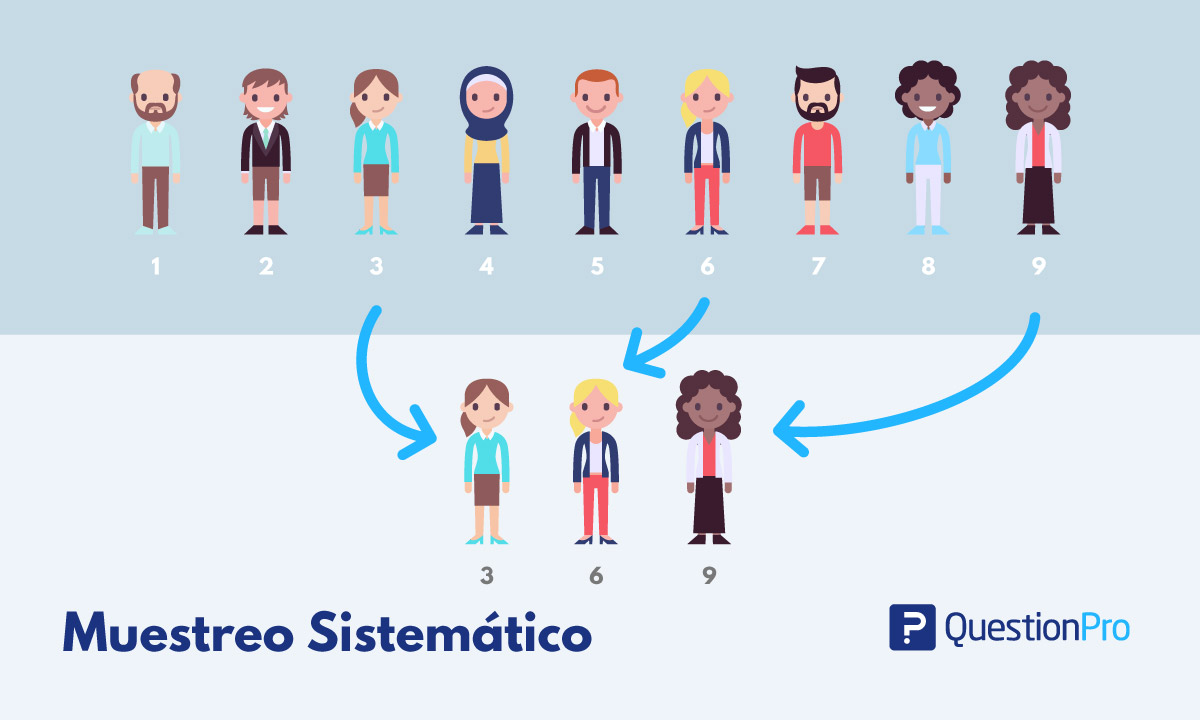
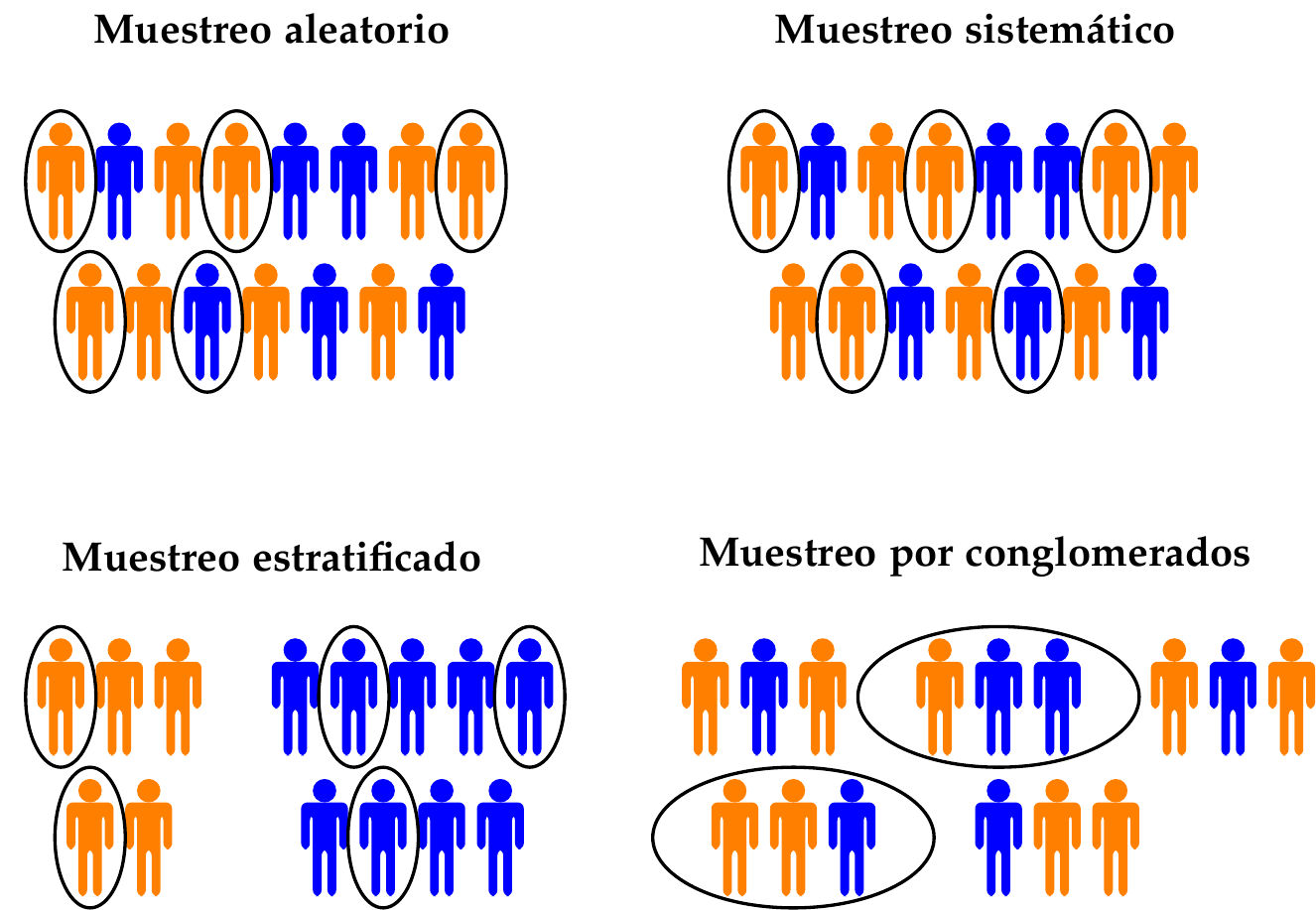
Muestreos aleatorios

Casos consecutivos

  • Pacientes incluidos de una consulta
  • Se selecciona a los pacientes que asistan a determinado sitio siempre y cuando cumplan con los criterios de inclusión.
  • Se debe evitar el sesgo de los días.
  • Es un muestreo no probabilístico

Muestreo secuencial

En el muestreo secuencial, los sujetos elegibles de la población objetivo se seleccionan uno a uno de manera aleatoria y se evalúan. El muestreo posterior se detiene tan pronto como se dispone de un resultado fiable en un sentido u otro. Este método de muestreo no es tan popular en medicina.

Es un método no probabilístico

Muestreo en R

Muestreo aletorio simple en R

  • sample(). Devuelve un número determinado de datos de un objeto
  • La función sample() requiere de al menos los siguientes argumentos:
    • un objeto del que vamos a extraer los datos
    • la cantidad de datos que vamos extraer
    • un argumento lógico para indicar si se quiere remplazo

Función sample()

Suponga que tiene una lista de 2000 pacientes con DM2, de los cuales debe seleccionar aletoriamente 100 para ser incluidos en un estudio que trata de estima la prevalencia de retinopatía diabética

set.seed(4) # Sembrando la misma semilla

sample(1:2000, size=100, replace = FALSE)
  [1] 1528  587  819 1795   71  684  371  757  698  307  312  414 1086  614 1154
 [16]  152 1409 1620  767 1771 1827  411 1389 1584 1200  869 1917  898 1952  303
 [31] 1324  197 1935  893  150 1477 1856  880  433   54 1535  203 1616 1934 1429
 [46] 1716 1089  304 1985  892 1782 1339 1824  397  980 1340 1150 1944 1612  573
 [61]  645  489  434  234  436  974 1977  200  418  250  128  811  158  534  251
 [76]  779  538  278 1421  625  703 1764 1794  948 1315 1201 1495  446  119  533
 [91] 1464 1940 1416 1012  458  321  904  225 1953 1076

Función sample()

Cree un objeto con 10 de los nombres de los los alumnos de la clase. Extraiga una muestra aleatoria con reemplazo de 50.

03:00

Función sample() aplicada a bases de datos

De la base de datos pima.tr2 de la librería mass, seleccione al azar 20 datos

03:00

Ejercicio resolución

library(MASS)# Cargar paquete
data("Pima.tr2") # cargar data set
sample(Pima.tr2$age, size=20)
 [1] 23 69 30 26 58 25 37 45 45 31 24 22 41 34 26 32 31 33 29 24

Con el código anterior utilizó la variable age para hacer la aleatorización, pero no es lo más adecuada

Otra forma de resolución (la correcta)

Pima.tr2$ID <- 1:300 # Creamos una variable de indexación

Si utilizamos el símbolo $ y llamamos a una variable que no existe, en realidad la estamos creando. Con el código anterior creamos una variable llamada ID con números del 1 al 300

head(Pima.tr2) # Muestra los primero 6 datos de un data frame
  npreg glu bp skin  bmi   ped age type ID
1     5  86 68   28 30.2 0.364  24   No  1
2     7 195 70   33 25.1 0.163  55  Yes  2
3     5  77 82   41 35.8 0.156  35   No  3
4     0 165 76   43 47.9 0.259  26   No  4
5     0 107 60   25 26.4 0.133  23   No  5
6     5  97 76   27 35.6 0.378  52  Yes  6

Otra forma de resolución

Ahora podemos hacer la aletorización

sample(Pima.tr2$ID, size=20)
 [1] 261  41 196 152  36  73 147 191  87 282   9 299 179 227 121 185 165  76  98
[20] 126

Muestreo sistemático

set.seed(4) # Todos los mismos datos
n <- sample(Pima.tr2$ID, size=20)
n+5
 [1]  80 264  76 177 250 191  67 107 135 157  89 260 240  53 181 202 155  59 208
[20]  85

¿Qué es lo que hace el código anterior?

countdown::countdown(minutes = 2)
02:00

Muestreo por conglomerados en R

# Crear una población ficticia con 1000 individuos divididos en 10 conglomerados
set.seed(123)  # Sembrando un semilla
poblacion <- data.frame(
  Conglomerado = rep(1:10, each = 100),
  Individuo = 1:1000
)

# Realizar el muestreo aleatorio de 3 conglomerados
conglomerados_muestreados <- sample(1:10, 3)

# Extraer los datos de los conglomerados seleccionados
muestra <- poblacion[poblacion$Conglomerado %in% conglomerados_muestreados, ]

Muestreo por conglomerados en R

head(muestra,6)
    Conglomerado Individuo
101            2       101
102            2       102
103            2       103
104            2       104
105            2       105
106            2       106

El uso de %in%

El operador %in% en R se utiliza para verificar si un elemento se encuentra dentro de un conjunto (vector, lista, etc.). Retorna un vector lógico que indica si cada elemento del primer conjunto se encuentra presente en el segundo conjunto.

Por ejemplo, si tienes un vector a y un vector b, puedes usar %in% para verificar si los elementos de a están presentes en b. El resultado será un vector de valores booleanos, TRUE si el elemento de a está en b y FALSE si no lo está

El uso de %in%

a <- c(1, 2, 3)
b <- c(2, 3, 4, 5)

resultado <- a %in% b

Muestreo con otros paquetes

# Instalar el paquete dplyr
install.packages("dplyr")

# Otra alternativa de instalación
install.packages("devtools")
devtools::install_github("tidyverse/dplyr")
  • dplyr: Es un paquete de manipulación de datos que proporciona un conjunto consistente de verbos que lo ayudan a resolver los desafíos de manipulación de datos más comunes

Muestro con otros paquetes

library(dplyr) # Librería necesaria
#Objeto con muestra:
muestra <- Pima.tr2 |>
  sample_n(size=20, replace=F)

Muestreo con otros paquetes

head(muestra)
  npreg glu bp skin  bmi   ped age type  ID
1     4 148 60   27 30.9 0.150  29  Yes 118
2     0  73 NA   NA 21.1 0.342  25   No 299
3     4 114 65   NA 21.9 0.432  37   No 229
4     4 128 70   NA 34.3 0.303  24   No 244
5    12  92 62    7 27.6 0.926  44  Yes  14
6     0 198 66   32 41.3 0.502  28  Yes 153

Muestreo con propoción de casos

muestra2 <- Pima.tr2 |>
  sample_frac(0.10)# Extraer el 10% de lo casos

Muestreo con propoción de casos

head(muestra2)
  npreg glu bp skin  bmi   ped age type  ID
1     2 122 70   27 36.8 0.340  27   No 143
2     3 148 66   25 32.5 0.256  22   No  32
3     1 143 74   22 26.2 0.256  21   No 109
4     0 119 NA   NA 32.4 0.141  24  Yes 263
5     4  83 86   19 29.3 0.317  34   No  23
6     3 191 68   15 30.9 0.299  34   No 135

Muestreo estratificado

muestra_estra <- Pima.tr2 |>
  group_by(type) |> #Estratificamos o agrupamos
  sample_frac(0.04) # obentemos el 4% para cada grupo

Muestreo estratificado

# A tibble: 12 × 9
# Groups:   type [2]
   npreg   glu    bp  skin   bmi   ped   age type     ID
   <int> <int> <int> <int> <dbl> <dbl> <int> <fct> <int>
 1     7   137    90    41  32   0.391    39 No      178
 2     2   121    70    32  39.1 0.886    23 No       74
 3     5   123    74    40  34.1 0.269    28 No       47
 4     0   107    60    25  26.4 0.133    23 No        5
 5     2    99    70    16  20.4 0.235    27 No       21
 6     3    99    80    11  19.3 0.284    30 No      103
 7     5   155    84    44  38.7 0.619    34 No      192
 8     7   136    90    NA  29.9 0.21     50 No      233
 9     7   168    88    42  38.2 0.787    40 Yes     156
10     5   158    84    41  39.4 0.395    29 Yes      71
11     4   158    78    NA  32.9 0.803    31 Yes     255
12    12   140    82    43  39.2 0.528    58 Yes      96

Muestreo por estratificado

Suppose we wish to randomize 100 subjects, stratifying by sex into two intervention groups (A and B). The following code statements contain the resolution for this stratification1:

# 1. Creation of an object with stratified randomization 
  # the sex stratum contains two levels:
    # 1 = female and 2 = male 
  # the group stratum contains two levels:
    # 1 = A and 2 = B 
random <- psych::block.random(n=100, 
                              ncond=c(sex=2, groups = 2)) 
# 2. View the results 
random

Bioestadística básica/Posgrados CUCS