qf(0.05, 2, 27, lower.tail = F)[1] 3.354131ANOVA de una vía
Bioestadística
CUCS/UDG
CUCS/UDG
ANOVA de una vía
La prueba de ANOVA (Análisis de Varianza) es una técnica estadística utilizada para comparar las medias de dos o más grupos y determinar si existen diferencias significativas entre ellos. Para aplicar correctamente una prueba de ANOVA, se deben cumplir varios supuestos:
Independencia de las Observaciones: Cada grupo o muestra debe ser independiente de los demás. Esto significa que la selección de un individuo en un grupo no debe influir en la selección de individuos en otro grupo.
Normalidad: Los datos en cada grupo deben distribuirse normalmente. Esto es más relevante en muestras pequeñas, ya que las pruebas ANOVA son “robustas” a este supuesto en muestras grandes.
Homogeneidad de Varianzas: Las varianzas de los grupos deben ser aproximadamente iguales. Este supuesto, conocido como homocedasticidad, es importante porque la ANOVA compara las varianzas entre los grupos. Si las varianzas son muy diferentes, las conclusiones de la ANOVA podrían no ser válidas.
Nivel de Medición: Las variables dependientes deben ser medidas al menos a nivel de intervalo o de razón. Esto significa que los datos deben ser numéricos y permitir comparaciones significativas de tamaño.
En este documento se explica como obtener el valor de F de tablas, como resolver una ANOVA de forma manual utilizando R, como resolver un ANOVA utilizando la función aov y como resolver un ANOVA utilizando la función oneway.test()
Cálculo del valor F de tablas
En R se utliza la familia de funciones pf, qf
- pf: se utiliza para obtener la probabilidad dado un valor de F
- pf(q, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)
- qf: dada una probabilidad y grados de libertad devuelve el valor de F
- qf(p, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)
Por ejemplo:
- Con un alfa de 0.05 (generalmente se emplea una hipótesis unilateral ya que el valor de F siempre es positivo)
- Con 2 grados de libertad para los tratamientos
- Con 27 grados de libertad para el error
Calculo manual del ANOVA utilizando R
Creación de objetos
Envase_A<-c(23,28,21,27,35,41,37,30,32,36)
Envase_B<-c(35,36,29,40,43,49,51,28,50,52)
Envase_C<-c(50,43,36,34,45,52,52,43,49,34)Suma de cuadrados total
SCT<-sum(Envase_A^2, Envase_B^2, Envase_C^2)-
((sum(Envase_A, Envase_B, Envase_C)^2)/30)
SCT[1] 2488.3Suma de cuadrados del tratamiento
SCtrata<-sum(Envase_A)^2/length(Envase_A)+
sum(Envase_B)^2/length(Envase_B)+
sum(Envase_C)^2/length(Envase_C)-
((sum(Envase_A, Envase_B, Envase_C)^2)/30)
SCtrata[1] 920.6Suma de cuadrados del error (dentro de muestras)
SCerror<-SCT-SCtrata
SCerror[1] 1567.7Cuadrados medios de los tratamientos (entre mtas)
CMtrat<-SCtrata/(3-1)#Son tres tratamientos
CMtrat[1] 460.3Cuadrados medios de los tratamientos (dentro de muestras)
CMerror<-SCerror/(30-3)#Se tienen 30 datos y tres tratamientos
CMerror[1] 58.06296Valor de F
Fcal<-CMtrat/CMerror
Fcal[1] 7.927601Cálculo desde una base de datos utilizando R
En la elaboración de un nuevo producto se quiere comparar el efecto en el tipo de envase sobre la vida de anaquel de un suero fetal bovino. Para ello se tomaron 3 tipos de envase, con los cuales se realizaron 10 réplicas en cada uno y se midieron los días de duración. Los resultados fueron los siguientes:
- Envase A: 23, 28, 21, 27, 35, 41, 37, 30, 32, 36
- Envase B: 35, 36, 29, 40, 43, 49, 51, 28, 50, 52
- Envase C: 50, 43, 36, 34, 45, 52, 52, 43, 49, 34
¿Existe evidencia significativa para demostrar que el tipo de envase influye en la vida de anaquel en el producto? Utilice \(\alpha\)=0.05.
Importar base de datos
Importe y descargue la base de datos BaseANOVA.xls
Una vez descargada guardela en su carpeta de bases e importela
df <- readxl::read_excel("Bases/BasesANOVA.xlsx", sheet = "Ejercicio 1")Estadística descriptiva
Realice gráfica y estadística descriptiva
tapply(df$Dias, INDEX = df$Envase, summary)$`Envase A`
Min. 1st Qu. Median Mean 3rd Qu. Max.
21.00 27.25 31.00 31.00 35.75 41.00
$`Envase B`
Min. 1st Qu. Median Mean 3rd Qu. Max.
28.00 35.25 41.50 41.30 49.75 52.00
$`Envase C`
Min. 1st Qu. Median Mean 3rd Qu. Max.
34.00 37.75 44.00 43.80 49.75 52.00 library(ggplot2)
library(dplyr)
Attaching package: 'dplyr'The following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, uniondf %>%
ggplot(mapping = aes(x=Envase, y=Dias, fill = Envase)) +
geom_boxplot()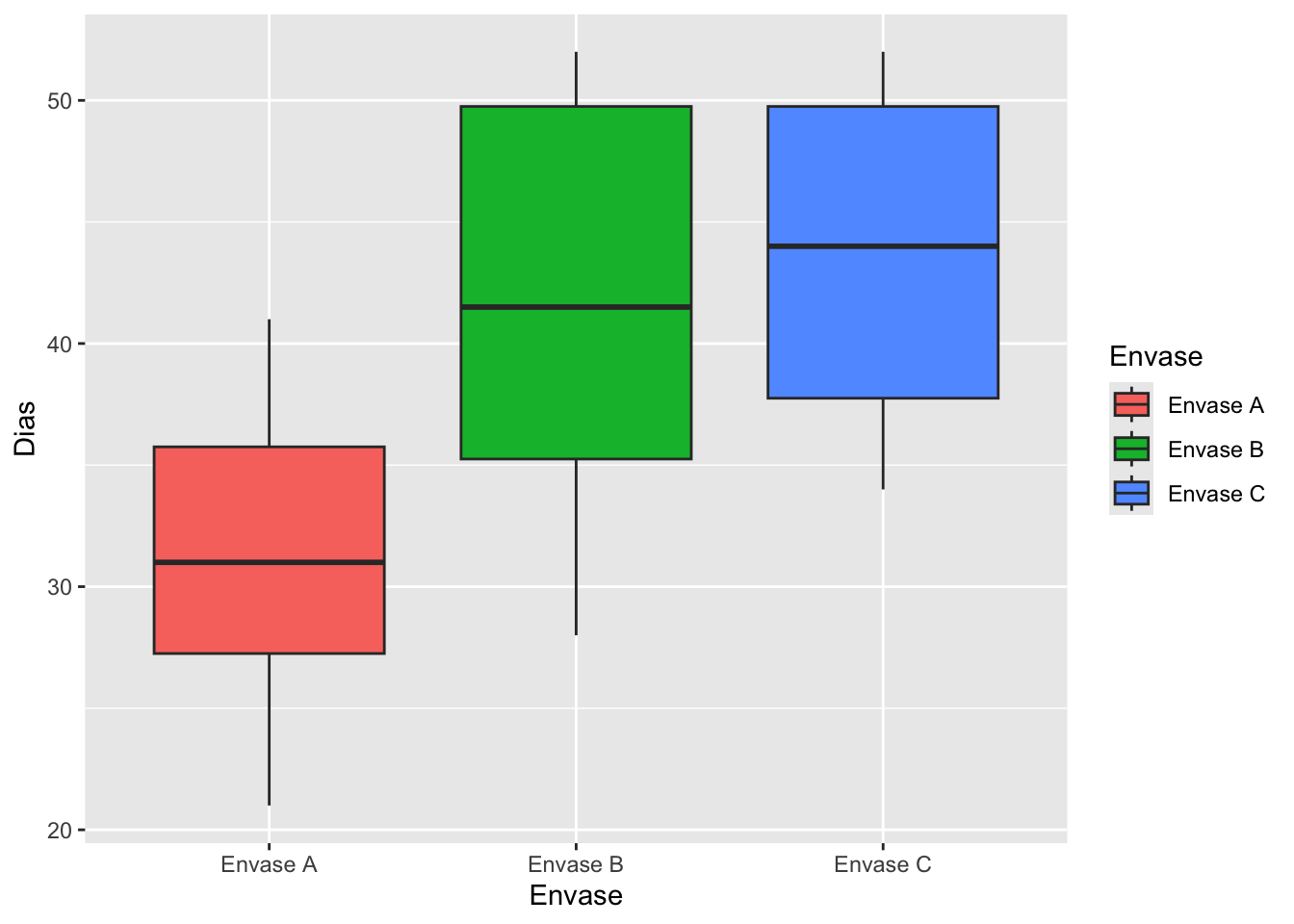
gplots::plotmeans(df$Dias~df$Envase)
paleta <- c("#C1C1C1", "#2C4251", "#D16666", "#B6C649")
boxplot(df$Dias~df$Envase, col=paleta, main="Días de vida de anquel de un suero bovino",
ylab = "Días", xlab = "Tipo de envase")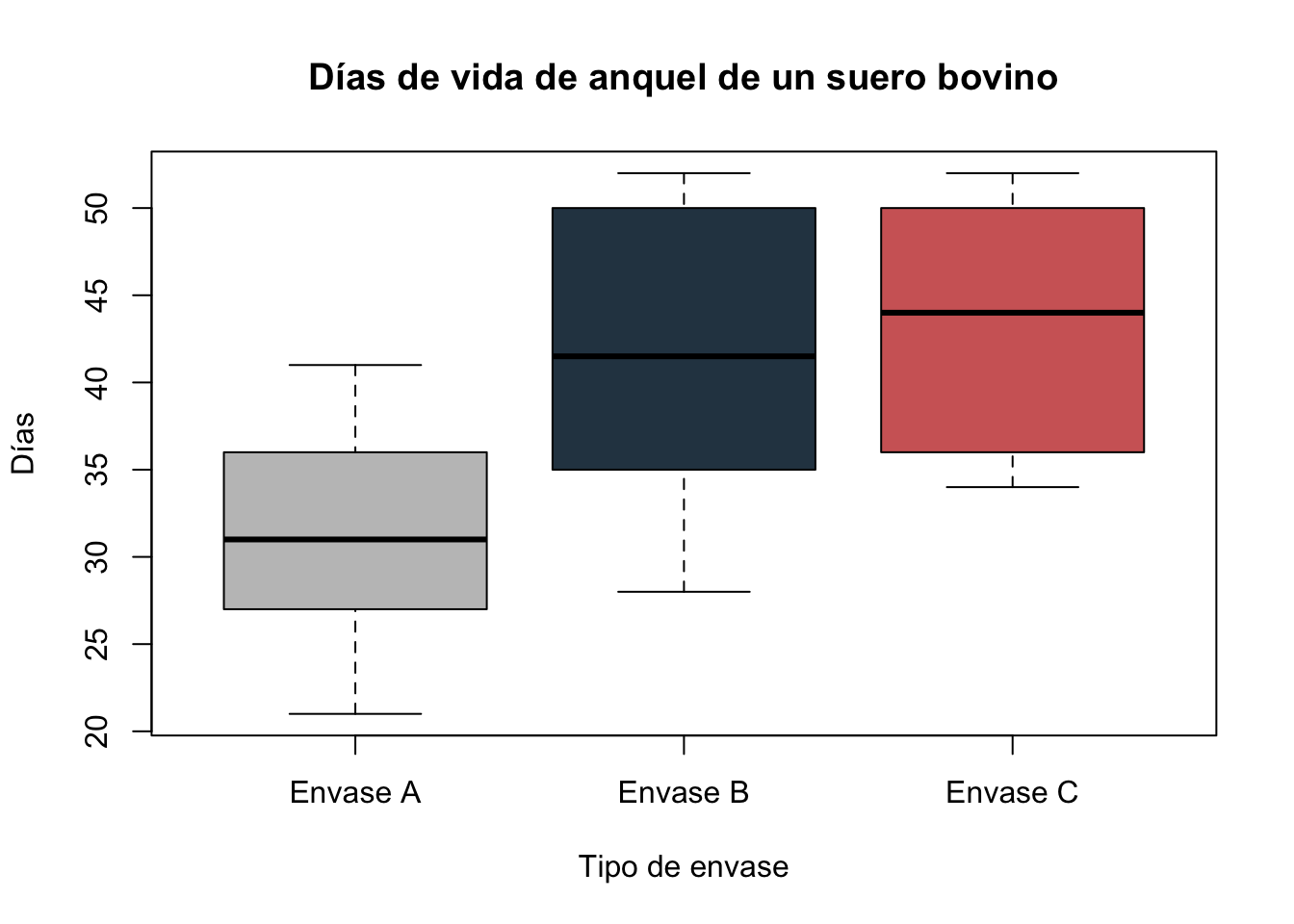
Función aov
aov(df$Dias~df$Envase)|>
summary() Df Sum Sq Mean Sq F value Pr(>F)
df$Envase 2 920.6 460.3 7.928 0.00196 **
Residuals 27 1567.7 58.1
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La función aov asume virianzas iguales, si es neceario evaluar la homogenidad podemos utilizar la función de bartlett.test() o car::leveneTest()
bartlett.test(df$Dias~df$Envase)
Bartlett test of homogeneity of variances
data: df$Dias by df$Envase
Bartlett's K-squared = 1.1525, df = 2, p-value = 0.562car::leveneTest(df$Dias~df$Envase)Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 2 1.247 0.3034
27 Si se presentan varianzas diferentes utilice la función: oneway.test()
oneway.test(df$Dias~df$Envase)
One-way analysis of means (not assuming equal variances)
data: df$Dias and df$Envase
F = 9.5867, num df = 2.000, denom df = 17.674, p-value = 0.001515Ejercicio 2
Se desea conocer si existen diferencia en el peso de 4 cepas distintas de ratas (DOC, WKY, DOC-Ca WKY-Ca). Tome un nivel de confianza de 0.05
| No Caso | DOC | wky | doc-ca | wky-ca |
|---|---|---|---|---|
| 1 | 336 | 328 | 304 | 342 |
| 2 | 346 | 315 | 292 | 284 |
| 3 | 269 | 343 | 299 | 334 |
| 4 | 346 | 368 | 293 | 348 |
| 5 | 323 | 353 | 277 | 315 |
| 6 | 309 | 374 | 303 | 313 |
| 7 | 322 | 356 | 303 | 301 |
| 8 | 316 | 339 | 320 | 354 |
| 9 | 300 | 343 | 324 | 346 |
| 10 | 309 | 343 | 340 | 319 |
| 11 | 276 | 334 | 299 | 289 |
| 12 | 306 | 333 | 279 | 322 |
| 13 | 310 | 313 | 305 | 308 |
| 14 | 302 | 333 | 290 | 325 |
| 15 | 269 | 372 | 300 | |
| 16 | 311 | 312 |
Los datos se encuentran en la hoja Ejercicio 2 de las base BaseANOVA
Realice: - Gráficas - Estadística descriptiva - Homogenidad de vairanzas - Test de ANOVA
Base de datos Cushings
Para ejemplificar como resolver la prueba de ANOVA utilizando la función aov en R vamos a utilizar la base de datos cushings de la librería MASS
Descripción de la base cushings
El conjunto de datos de Cushings [2], que está disponible en el paquete MASS. El síndrome de Cushing es un trastorno hormonal asociado con un alto nivel de cortisol secretado por la glándula suprarrenal. El conjunto de datos de Cushings incluye 27 observaciones (n = 27). Para cada individuo de la muestra, se registran las tasas de excreción urinaria de dos metabolitos de esteroides. Estos son la tasa de excreción urinaria (mg/24 h) de tetrahidrocortisona y la tasa de excreción urinaria (mg/24 h) de pregnanetriol. La variable Tipo en el conjunto de datos muestra el tipo de síndrome subyacente, que puede ser una de cuatro categorías: adenoma (a), hiperplasia bilateral (b), carcinoma (c) y desconocido (u)
Resolución ANOVA con la base cushings
Adjuntar las base de datos y observar los primeros 6 datos
library(MASS)
Attaching package: 'MASS'The following object is masked from 'package:dplyr':
selectdata(Cushings)
attach(Cushings) # Evita el uso de $
head(Cushings) # Primeros 6 datos Tetrahydrocortisone Pregnanetriol Type
a1 3.1 11.70 a
a2 3.0 1.30 a
a3 1.9 0.10 a
a4 3.8 0.04 a
a5 4.1 1.10 a
a6 1.9 0.40 aLos nombres de esta base, son un tanto complicados. Podemos obtener los nombres de un objeto con la función names
names(Cushings)[1] "Tetrahydrocortisone" "Pregnanetriol" "Type" ¿Existe diferencia entre los niveles de tetrahidrocortisona entre los tipos de Cushings?
Vamos a graficar
gplots::plotmeans(Tetrahydrocortisone~Type)Warning in arrows(x, li, x, pmax(y - gap, li), col = barcol, lwd = lwd, :
zero-length arrow is of indeterminate angle and so skippedWarning in arrows(x, ui, x, pmin(y + gap, ui), col = barcol, lwd = lwd, :
zero-length arrow is of indeterminate angle and so skipped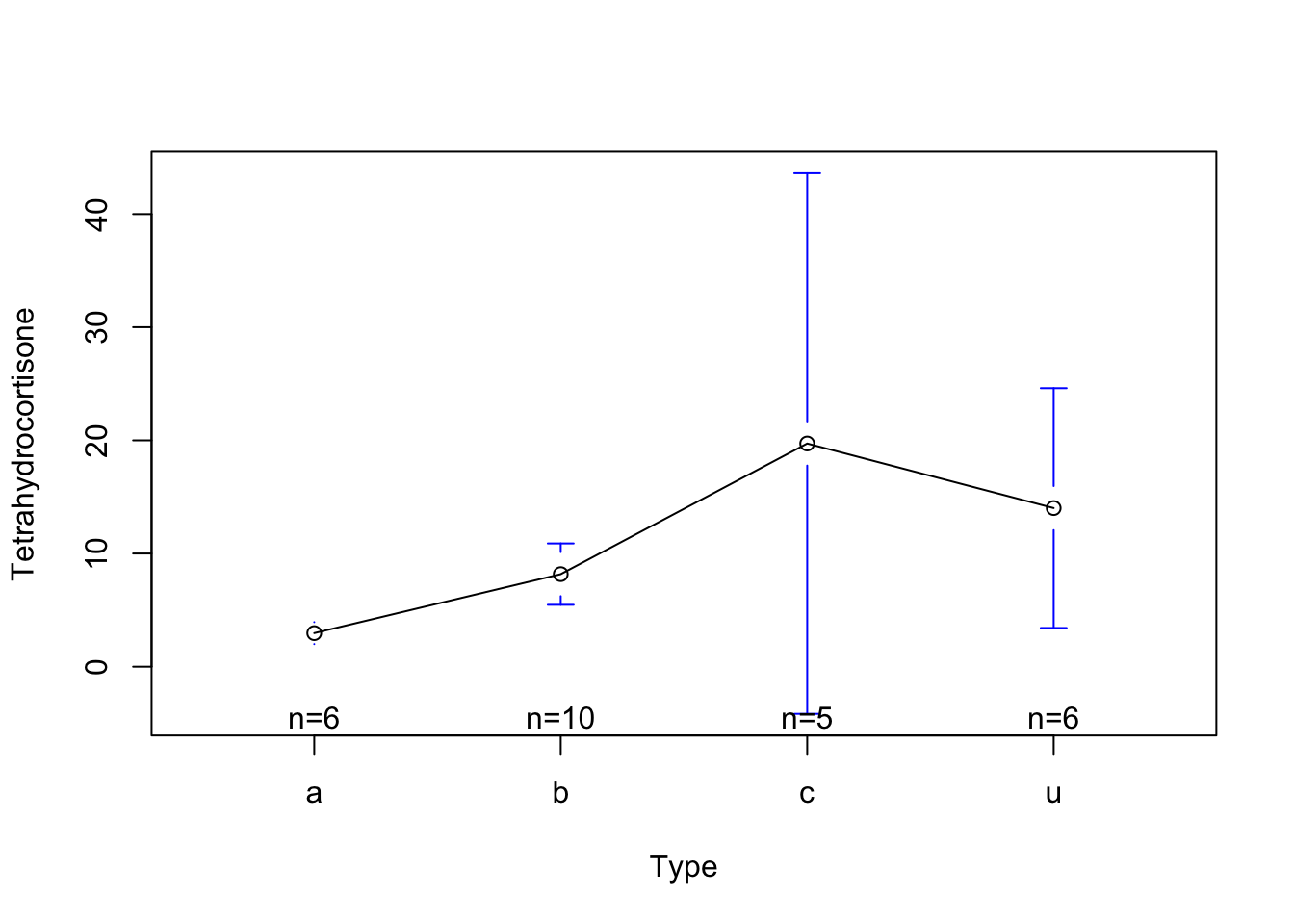
Para realizar el ANOVA se utiliza la función aov, Es recomendable guardar el ANOVA en un objeto para acceder fácilmente a los resultados
ANOVA1<-aov(Tetrahydrocortisone~Type)
summary(ANOVA1)## Con esto vemos el resultado del ANOVA Df Sum Sq Mean Sq F value Pr(>F)
Type 3 893.5 297.84 3.226 0.0412 *
Residuals 23 2123.6 92.33
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Otra forma utilizando los pipes es:
aov(Tetrahydrocortisone~Type)|>
summary() Df Sum Sq Mean Sq F value Pr(>F)
Type 3 893.5 297.84 3.226 0.0412 *
Residuals 23 2123.6 92.33
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Podemos comprobar gráficamente nuestro ANOVA utilizando la librería ggstatsplot.
library(ggstatsplot)ggbetweenstats( # Para comparar grupos independientes
data = Cushings, #Objeto con la base de datos
x = Type, # Nombre de la variable de agrupación
y = Tetrahydrocortisone, # Nombre de las variable numerica
title = "Comparación de las concentraciones de hormonas entre pacientes con Cushing", # titulo
type = "p")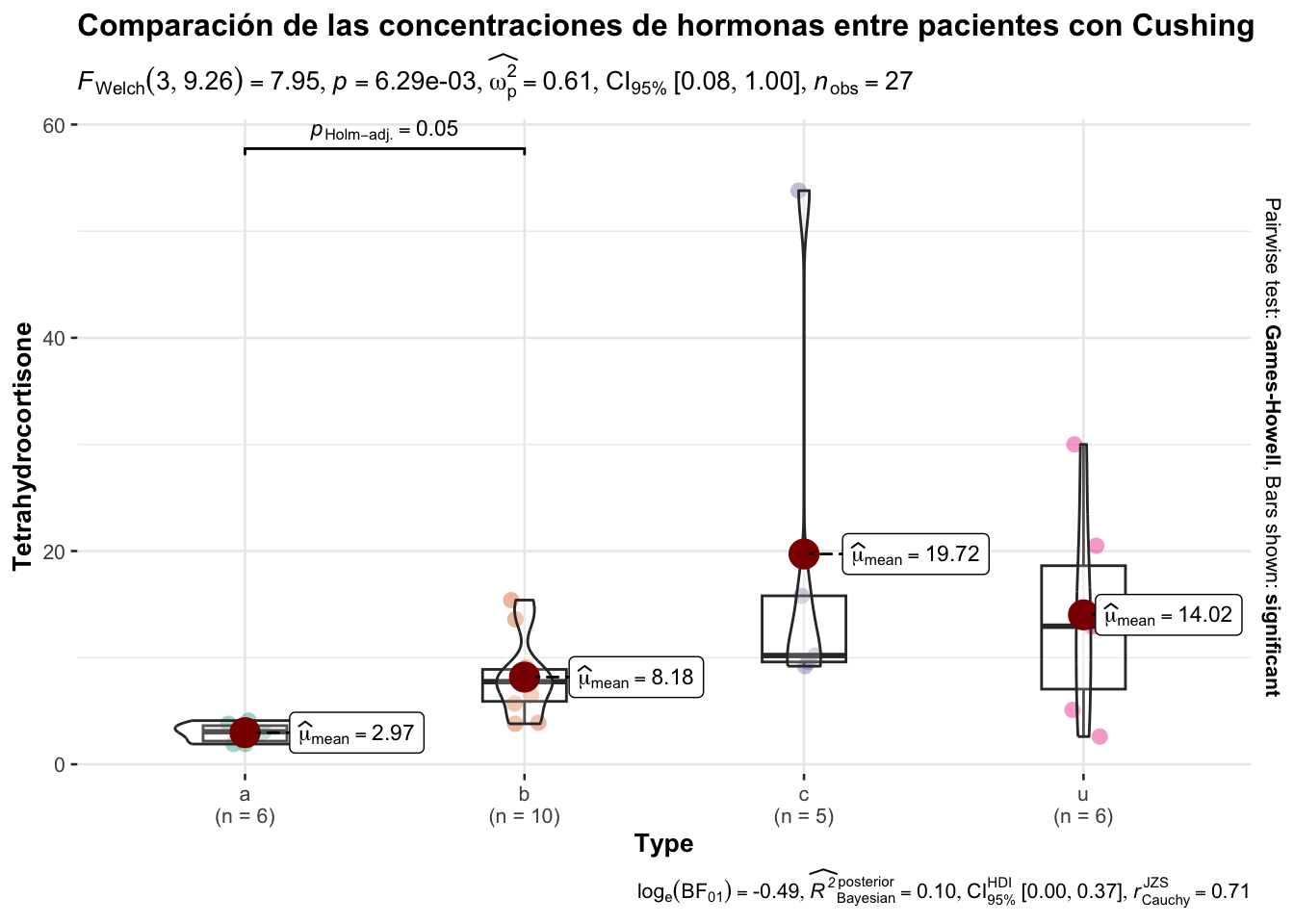
Los resultados anteriores nos indican que si hay diferencia entre los niveles de tetrahidrocortisona entre los tipos de Cushings.
Note como el valor de F no coincide. Esto debido a hasta el momento no hemos evaluado la homogenidead de las varianzas (lo haremos más adelatnes).
Podemos una prueba posthoc utilizando la función TukeyHSD alimentada por el objeto de nuestro ANOVA.
TukeyHSD(ANOVA1)# Para hacer la prueba de tukey, se alimenta con el objeto del ANOVA Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = Tetrahydrocortisone ~ Type)
$Type
diff lwr upr p adj
b-a 5.213333 -8.5181810 18.94485 0.7219961
c-a 16.753333 0.6517055 32.85496 0.0393613
u-a 11.050000 -4.3022998 26.40230 0.2200574
c-b 11.540000 -3.0244704 26.10447 0.1551716
u-b 5.836667 -7.8948477 19.56818 0.6473881
u-c -5.703333 -21.8049612 10.39829 0.7619359Podemos realizar una gráfica de nuestra prueba posthoc con el siguiente código:
plot(TukeyHSD(ANOVA1))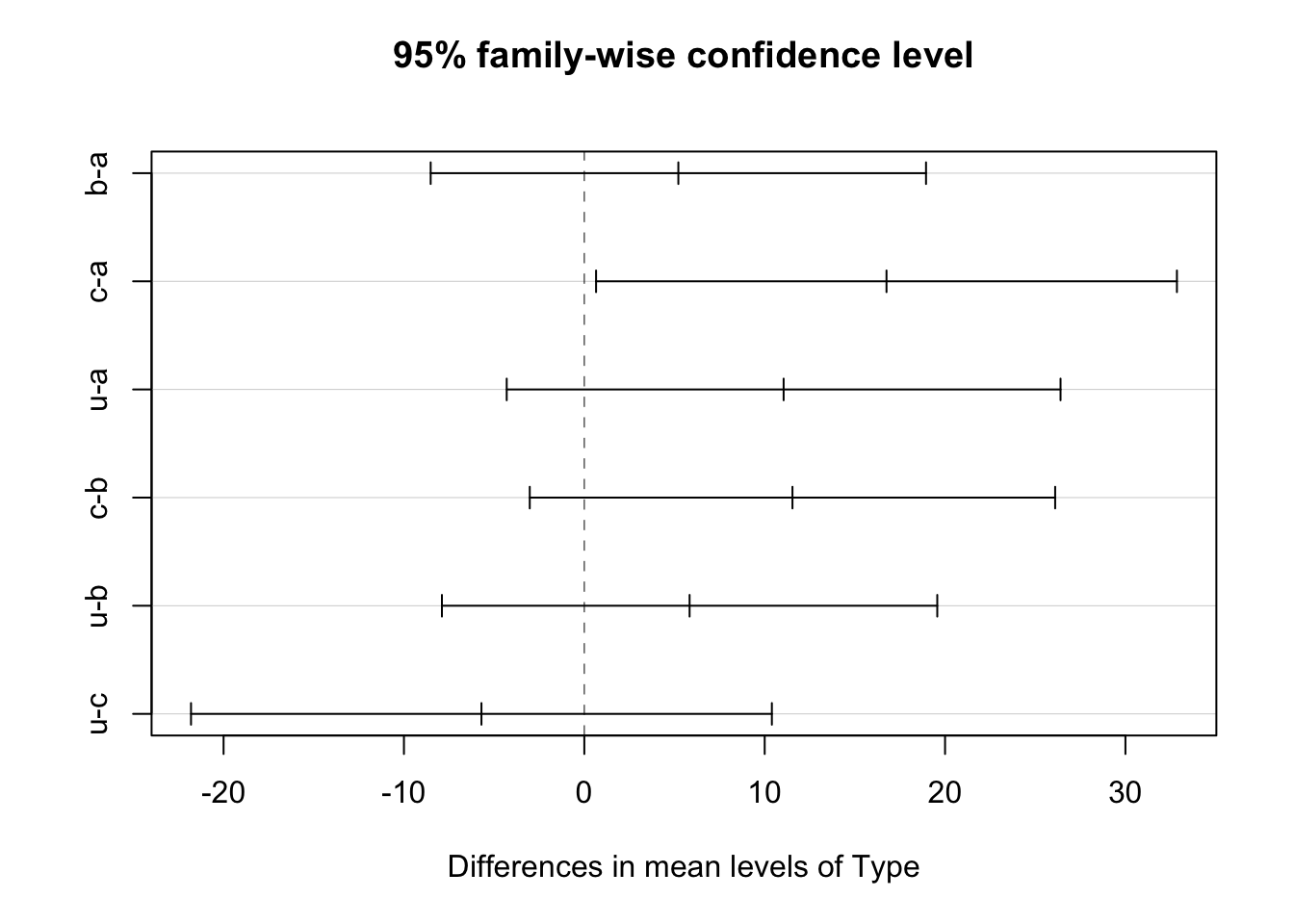
Otra forma utilizando los pipes es:
aov(Tetrahydrocortisone~Type)|>
TukeyHSD()|>
plot()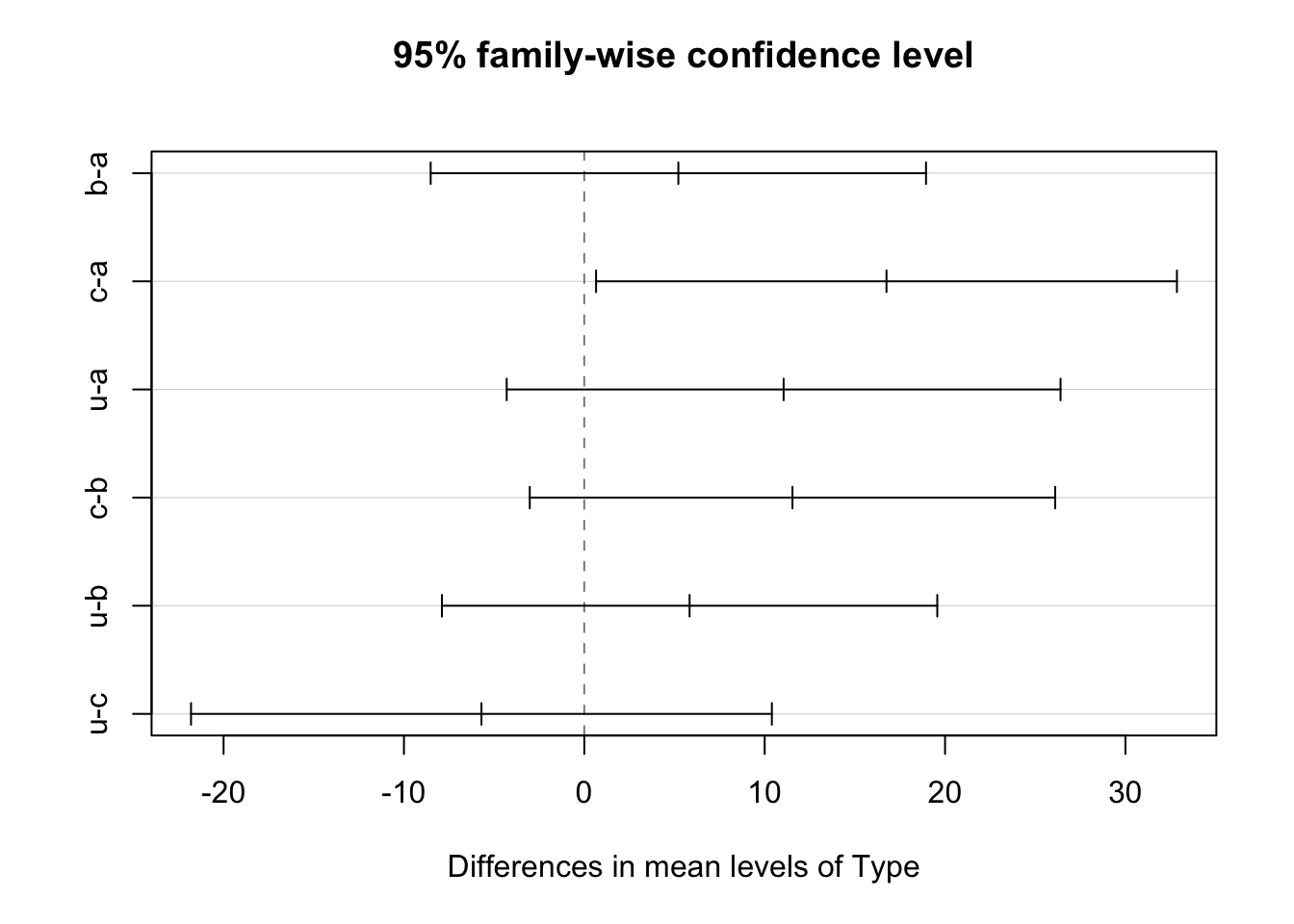
Uno de los supuestos que se deben de evaluar en el ANOVA es la homogenidad de varianzas. Para hacerlo puede utilizar algunas de las funciones que ya se revisaron en la clase como: car::LeveneTest() o bartlett.test(). Vamos a retomar el ejemplo de la base Chusings
car::leveneTest(Tetrahydrocortisone~Type)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 3 1.4638 0.2505
23 Aunque se cumple el supuesto de homogenidad de varianzas evaluado con Levene, la gráfica de medias indica que tenemos una variación muy grande entre los grupos, especificamente en el grupo C, por lo tanto realizar el ANOVA sin corregir el valor de F no es lo más indicado. Vamos a utilizar la función oneway.test(), la cual proporciona una corrección para el valor F en situaciones donde el supuesto de homogeneidad de varianzas no se cumple. Esta corrección hace que la prueba sea más robusta en situaciones donde las varianzas de los grupos no son iguales, lo cual es un supuesto clave del ANOVA clásico.
La corrección más común aplicada por oneway.test() es la corrección de Welch, que ajusta los grados de libertad de la estadística F, haciendo que la prueba sea más adecuada para datos con varianzas desiguales. Esta corrección es similar a la que se usa en la prueba t de Welch para dos muestras, que también ajusta los grados de libertad cuando se comparan las medias de dos grupos con varianzas desiguales.
El código en R sería:
oneway.test(Tetrahydrocortisone~Type)
One-way analysis of means (not assuming equal variances)
data: Tetrahydrocortisone and Type
F = 7.9544, num df = 3.0000, denom df = 9.2558, p-value = 0.006293Ahora si nuestro valor de F coincide con el estima en ggstastplot.
Ejercicios
Instrucciones generales
Conteste a cada uno de los siguientes cuestionamientos, realice para ello, una prueba de ANOVA de una vía, gráficas y una prueba post-hoc (tukey)
Ejercicio 1
Un investigador desea conocer la efectividad de varios suplementos alimenticios (feed) sobre la tasa de crecimiento (weight) de los pollos. Cargue la base de datos chickwts que se encuentra en R. Use ANOVA para examinar la efectividad de los suplementos alimenticios. La linea de comando para cargar la base chickwts es data("chickwts"). Ejercicio tomado de: Biostatistics with R. Shahbaba (2012). Springer
Ejercicio 2
Usando la libreria MASS llame a la base de datos “genotype”. Esta base de datos contiende los resultados de una investigación realizad por Bailey y cols. en 1953 enla que investigaron la herencia del y su asociación con el crecimiento de varios grupo de ratas. En este estudio, las camadas de ratas se separaron de sus madres naturales, y fueron criadas por madres adoptivas. Las madres y las camadas pueden tener cuatro genotipos diferentes: A, B, I y J. Supongamos que queremos investigar si el aumento de peso (Wt) de la camada (en gramos) a los 28 días está relacionado con el genotipo de la madre adoptiva Madre (A, B, I y J). Utilice la prueba de ANOVA de una vía y realice gráficos de caja y bigotes. Ejercicio tomado de: Biostatistics with R. Shahbaba (2012). Springer
Ejercicio 3
Cargue el conjunto de datos de anorexia del paquete MASS. Este conjunto de datos se recopiló para investigar la efectividad de diferentes tratamientos (Treat) en el aumento de peso para pacientes jóvenes con anorexia. Cree una nueva variable llamada Diferencia restando el peso del paciente antes del período de estudio (Prewt) de su peso después del período de estudio (Postwt): Diferencia = Postwt - Prewt. Use una gráfica de medios para visualizar cómo cambia esta variable según el tipo de tratamiento. Use ANOVA para investigar si el tipo de tratamiento hace una diferencia en la cantidad de aumento de peso. Ejercicio tomado de: Biostatistics with R. Shahbaba (2012). Springer
Ejercicio 4
Una investigación realizada por Singh et al. y publicada en la revista Clinical Immunology and Immunopathology se refiere a las anormalidades inmunológicas en tresg grupos de niós. Como parte de su investigación, tomaron mediciones de la concentración sérica de un antígeno en tres muestras de niños de diez años o menos de edad. Las mediciones en unidades por milímetro de suero son las siguientes:
- Grupo 1 (n = 23): 755,385,380,215,400,343,415,360,345, 450,410,435,460,360,225,900,365,440,820,400, 170,300,325
- Grupo 2 (n = 33); 165,390,290,435,235,345,320,330,205, 375,345,305,220,270,355,360,335,305,325,245,285,370,345,345, 230,370,285,315,195,270,305,375,220
- Grpo 3 (n= 15): 380,510, 315,565,715,380,390,245,155,335,295,200,105,105,245
¿Existe diferencia entre las concentraciones del antígeno y los grupos estudiados?. Realice una prueba pos-hoc para conocer entre que grupos está diferencia (si es que la hay). Ejercicio tomado de: Bioestadística. Base para el análisis de las ciencias de la salud. WAYNE W. DANIEL (2011). LIMUSA WILEY