Estadística y Elementos de Quimiometría
Probabilidad y Estadística - 2021

Curvas de calibrado

---

1 Introducción.

El método de calibración es un procedimiento analítico muy utilizado en análisis cuantitativo en química analítica que implica la construcción de una “curva de calibración” para determinar la concentración de una sustancia (analito) en una muestra problema. Una curva de calibración es la representación gráfica de una señal que se mide en función de la concentración de un analito. Conociendo esta relación funcional, será posible conocer la concentración en una muestra dada mediante la medida de esa señal.

1.1 Ejemplo 1: calidad de agua para consumo humano.

La reglamentación técnico-sanitaria para el abastecimiento y control de la calidad de las aguas potables de consumo público califica al zinc de componente no deseable y fija en un máximo tolerable de hasta 5000 microgramos por litro su concentración en el agua. La determinación de dicha concentración constituye un criterio orientado, entre otros, a la comprobación de la calidad del agua analizada.

¿Cómo podemos determinar el contenido de Zn en agua potable para evaluar la calidad de la misma?

Este es un ejemplo típico de uso de la curva de calibración. ¿Cómo?

A grandes rasgos, para construir la recta de calibrado, primero medimos la absorbancia de una serie de disoluciones que contienen concentraciones concocidas de Zn(II). Supongamos por ejemplo que, por medio de espectrofotometría de absorción atómica, medimos disoluciones con las siguientes concentraciones: \(0.000,\; 0.025,\; 0.050,\; 0.100,\; 0.150,\; 0.200\;\;\) y \(0.250\;\) mg/L (ppm), obtenidas por dilución con agua destilada a partir de una disolución de Zn(II) de \(5.0\;\) mg/L.

A partir de los pares de puntos (concentración, señal) obtenidos, ajustamos un modelo lineal (como ya hemos estudiado en la unidad “Regresión Lineal”). Finalmente utilizamos la recta estimada para predecir la concentración de Zn en la muestra de interés, en este caso, en muestras de agua potable.

Esto que, en apariencia es lo mismo que ya hicimos cuando estudiamos regresión lineal, presenta una diferencia no menor: lo que queremos predecir aquí es un valor de la variable predictora. Por esto se habla también de predicción inversa y, de alguna manera, es uno de los motivos que justifican que tratemos el tema separadamente.

En particular, en esta unidad abordaremos el tema de la calibración analítica mediante el modelo lineal, y veremos algunas estrategias para asegurar que el modelo lineal es correcto y adecuado a nuestras necesidades.

¿Por qué se necesita de la calibración en Química Analítica? Porque se necesita una escala con la cual después medir la concentración de un compuesto de interés en una muestra.

¿Hay técnicas que no requieren calibración? Sí, son pocas pero existe. Una de ellas es la gravimetría, una técnica que consiste en pesar directamente en una balanza el compuesto que nos interesa. Pero para eso el compuesto tiene que estar puro. Aislar un compuesto puro es complicado y por eso la aplicación de la gravimetría está limitada.

En general, la mayoría de los químicos analíticos tienen que calibrar. ¿Y qué es la calibración? La calibración es un modelo matemático que genera una escala con la cual medir la concentración del compuesto de interés (el analito). Y para eso necesitamos un serie de medidas instrumentales (con un equipo que puede ser óptico, eléctrico o de otra naturaleza) sobre un conjunto de muestras –de calibración– donde interviene el compuesto de interés en estado puro y en concentraciones conocidas y con las medidas realizadas a esas muestras de calibración se genera un modelo. El modelo después se aplica a una muestra de ensayo –incógnita–, y en esa muestra incógnita se logra el objetivo de determinar la concentración del compuesto de interés.

Por lo tanto, a grandes rasgos, podemos considerar que la calibración tiene dos etapas:

1 La de calibración propiamente dicha.

2 La de la predicción o de la estimación de la concetración del analito en la muestra de interés.

Es importante destacar que, el análisis mediante recta de calibración, puede hacerse cuando solo el analito presenta señal analítica o respuesta (absorbancia, fluorescencia, potencial eléctrico, corriente, etc.), o cuando la señal del blanco es constante.

Existen tres tipos de calibraciones en química analítica:

• Clásica o univariada

• Multivariada

• Multi-modo o multi-vía

Un único dato (escalar) medido para una muestra analítica dada se clasifica como univariado, mientras que múltiples datos instrumentales registrados para una única muestra se consideran multivariados. Cuando los datos multivariados para una muestra pueden organizarse en una tabla o matriz de datos con dos dimensiones diferentes, o cuando los datos para un conjunto de varias muestras se pueden organizar en un objeto matemático de al menos tres dimensiones (arreglo tri-dimensional), se dice que pertenecen a la clase multi-vía.

En este curso aprenderemos la calibración clásica. La Figura 1.1 ilustra este tipo de calibración.

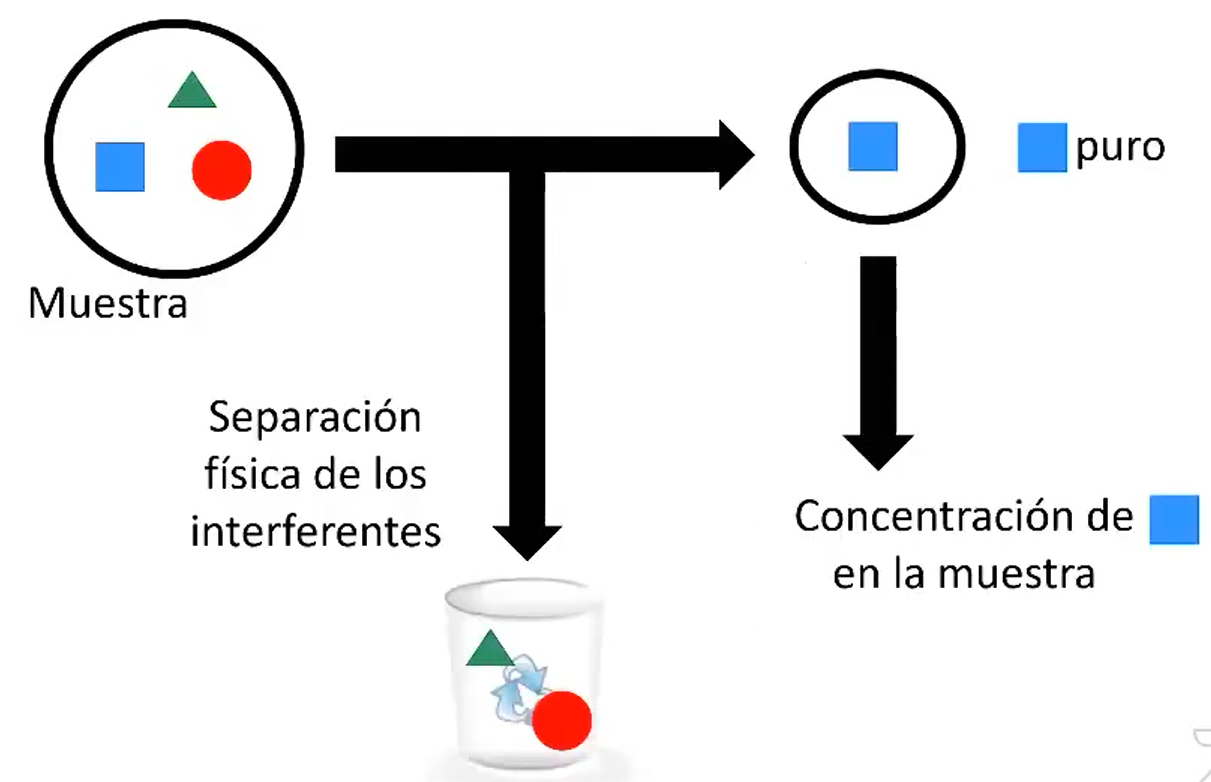
Figura 1.1: Representación gráfica del tipo de calibración univariada. Extraída de la conferencia Olivieri (2021).

En este tipo de problemas, tenemos una muestra (que para simplificar, en este ejemplo, la muestra tiene solo tres componentes (el azul, el rojo y el verde) y supongamos que nos interesa determinar el compuesto azul. En este tipo de calibración es imprescendible separar físicamente al verde y al rojo (sustancias que en química analítica se las denomina interferentes) y aislar ese compuesto puro de alguna manera para poder determinar su concentración en la muestra. El requerimiento de separación física de los interferentes es la principal dificultad que tiene esta calibración.

2 Gráficas de calibrado en análisis instrumental.

El procedimiento habitual es el siguiente. El analista toma una serie de materiales (normalmente al menos tres o cuatro, y posiblemente algunos más) de los que se conoce la concentración de analito (disoluciones patrón o estándar). Estos patrones de calibración se miden en el instrumento analítico bajo las mismas condiciones que las utilizadas posteriormente para los materiales de ensayo (es decir, los «desconocidos»). Una vez establecida la gráfica de calibrado, puede obtenerse la concentración de analito por interpolación en cualquier material de ensayo.

Así vemos que las etapas o pasos que deben seguirse en un análisis mediante recta de calibración son:

1 Etapa de calibración:

• Determinación del extremo superior del rango lineal.

• Preparación de los patrones.

• Medición de la respuesta de los patrones.

• Estimación de los parámetros de la regresión.

• Cálculo de las cifras de mérito del método.

2 Etapa de predicción.

• Estimación de la concetración del analito en la muestra de interés.

Este procedimiento general plantea varias cuestiones estadísticas importantes:

1. El gráfico de calibración ¿muestra una relación lineal? De no ser así, ¿qué forma tiene dicha curva?


2. Teniendo en cuenta que cada uno de los puntos de la línea de calibrado está sujeto a errores, ¿cuál es la mejor línea recta (o curva) que pasa por esos puntos?


3. Suponiendo que el calibrado es realmente lineal, ¿cuáles son los errores y límites de confianza de la pendiente y ordenada en el origen de la recta?


4. Cuando el gráfico de calibrado se usa para el análisis de un material de ensayo, ¿cuáles son los errores y límites de confianza de la concentración determinada?


5. ¿Cuál es el límite de detección del método? Esto es, ¿cuál es la menor concentración de analito que puede detectarse con un predeterminado nivel de confianza?

Antes de abordar estas cuestiones detalladamente, veamos algunas consideraciones importantes en el trazado de las líneas de calibrado.

2.1 Algunos aspectos importantes en el trazado de las líneas de calibrado.

1. En primer lugar, resulta habitualmente esencial que los patrones de calibrado cubran el intervalo completo de concentraciones requerido en subsiguientes análisis. Con la importante excepción del método de las adiciones estándar, que es tratado aparte en una sección posterior, la concentración de los materiales de ensayo se determina normalmente por interpolación y no por extrapolación.


2. Siempre el punto cero o valor de un blanco se debe incluir en la curva de calibrado. El blanco no contiene ningún analito adicionado deliberadamente, pero contiene los mismos disolventes, reactivos, etc., que los otros materiales de ensayo, y está sujeto exactamente a la misma secuencia del procedimiento analítico. La señal del instrumento dada por el blanco a veces no será cero. Esta señal está sometida a errores, como los demás puntos del gráfico calibrado, y no tiene sentido, en principio, restar el valor del blanco de los otros valores estándar antes de dibujar la curva de calibrado. Esto es debido a que, como vimos cuando estudiamos Propagación de incertidumbres, cuando se restan dos cantidades, la incertidumbre en el resultado final no puede obtenerse por simple resta. La resta del valor del blanco de cualquier otra señal del instrumento antes de dibujar el gráfico proporciona una información incorrecta de las incertidumbres del proceso de calibración.


3. Finalmente, se debe subrayar que la curva de calibrado se establece siempre con la respuesta del instrumento en el eje vertical (\(Y\)) y la concentración del patrón sobre el eje horizontal (\(X\)). Esto es debido a que muchos de los procedimientos que se describen en las secciones siguientes suponen que todos los errores residen en los valores de \(Y\) y que las concentraciones de los patrones (valores de \(X\)) se encuentran libres de error.

2.2 Determinación del rango lineal.

Esta etapa es fundamental, ya que la regresión lineal está basada en la suposición de que los datos de respuesta analítica están linealmente relacionados con la concentración del analito. Si se sospecha que existen desvíos de la linealidad, se recomienda realizar un análisis exploratorio previo cuyo objeto es extender el rango de aplicabilidad de la técnica analítica a la máxima concentración posible. En dicho análisis, se incluyen patrones de concentración conocida del analito desde cero hasta valores que se desvíen visiblemente de la linealidad. Una prueba estadística apropiada permitirá luego decidir hasta qué concentración se cumple la relación lineal respuesta-concentración. Sin embargo, dado que los parámetros a emplear en esta prueba se obtienen del análisis matemático-estadístico de la regresión, diferiremos el cálculo detallado para más adelante.

2.3 Preparación de patrones.

Una vez estimado el extremo superior del rango lineal de la técnica, deben prepararse patrones de concentración conocida dentro de dicho rango, e incluyendo el valor cero de concentración del analito (blanco). Usualmente, se preparan varios patrones (como mínimo cinco) con concentraciones igualmente espaciadas entre cero y el extremo superior del rango lineal, y cada patrón se analiza por triplicado.

Debe ponerse especial cuidado en la preparación de los patrones del analito para la calibración, de manera que las concentraciones de calibrado se conozcan con la máxima precisión posible. Este requisito se relaciona con el hecho de que la recta de regresión se ajusta mediante ecuaciones que suponen que los valores del eje x (concentraciones) tienen una incertidumbre considerablemente menor que los del eje y (respuestas).

Solo a modo de ejemplo, si se realizan mediciones de absorbancia como respuesta, podemos suponer que el nivel de incertidumbre en la respuesta puede ser de alrededor de 0.005 unidades de absorbancia. Si los valores de las respuestas son, en promedio, de 1 unidad de absorbancia, esto implica un nivel relativo de incertidumbre de aproximadamente \(0.5\%\;\) en la respuesta. Por lo tanto, se deben preparar patrones de calibrado cuyas concentraciones se conozcan con un error menor al \(0.5\%\;\). Preparar soluciones de calibrado, por ejemplo, con incertidumbres del orden del \(0.1\%\;\) en promedio, requiere pesar más de 100 mg de reactivo, preparar soluciones en matraces calibrados de al menos 100 mL, tomar alícuotas con pipetas aforadas calibradas, etc.

2.4 Medición de la respuesta de los patrones.

Una vez preparados los patrones de concentración conocida, se miden sus respuestas analíticas, incluyendo réplicas de cada medición. Usualmente cada patrón se mide por triplicado.

Notación: A lo largo del apunte, utilizaremos la siguiente notación para indicar la cantidad de patrones y cantidad de mediciones en total. Por ejemplo, si se emplean 6 patrones, cada uno por triplicado, entonces el número de niveles diferentes de concentración \((k)\;\) es 6, y el número total de puntos de la recta de calibrado \((N)\;\) es 18.

3 Modelo lineal.

El uso de una recta de calibración para determinar la concentración de un analito en una muestra es una aplicación importante de la regresión lineal. Como lo mencionamos en la sección precedente, la variable \(Y\) representa las medidas de respuesta (señal del instrumento) y la variable \(X\) la concentración de las soluciones estándar. Los errores cometidos en la preparación de las soluciones estándar suelen ser insignificantes en comparación con los errores de medición. Por lo tanto, la suposición de que la variable \(X\) se conoce exactamente y, en consecuencia, no tiene error, está justificada en la calibración. La variable \(X\) es entonces la variable independiente (predictora) e \(Y\) la variable dependiente (respuesta).

La función de calibración se puede obtener ajustando un modelo matemático adecuado a través de los datos experimentales.

En términos generales, suponemos el siguiente modelo para la respuesta experimental observada \[\begin{align} Y &= f(X)+\varepsilon \end{align}\] donde \(f(X)\) es la curva de calibración que tenemos que estimar. Para hacer esto, necesitamos \(N\) observaciones, \(y_i\) de \(k\) estándares diferentes. Por supuesto que, si no hay observaciones replicadas, \(N=k\) , en otro caso \(N>k\) . Para cada valor observado \(y_i\) la correspondiente concentración del estándar la denotamos \(x_i\), sin distinguir si son iguales (réplicas) o no. Por lo tanto \[\begin{align} y_i &= f(x_i)+\varepsilon_i, \;\;\; i=1, \ldots, N. \end{align}\] En muchos problemas de calibración se consideran las siguientes hipótesis cuya compatibilidad con los resultados experimentales debemos comprobar cuidadosamente:

a. La verdadera función de calibración \(f\) es lineal en el rango de concentraciones estudiado. Por lo tanto \[\begin{align} y_i&=\beta_0 +\beta_1 x_i + \varepsilon_i, \;\;\; i=1, \ldots, N. \tag{3.1} \end{align}\]

b. Los valores de la variable predictora \((x_i, \;\;i = 1, \ldots , N)\) son valores controlados y su incertidumbre experimental puede despreciarse en comparación con la incertidumbre en la determinación de la respuesta.

c. Los errores en la respuesta observada son independientes, tienen media cero, \(E(\varepsilon_i)=0\;\) y la misma varianza, \(Var(\varepsilon_i)=\sigma^2\) , para \(i=1, \ldots, N\;\).

La evaluación y análisis de los estimadores de los parámetros en una calibración (\(\hat \beta_0, \hat \beta_1\) y \(S_{y|x}^2\)) es un problema de inferencia estadística porque todos los estimadores son variables aleatorias que dependen de la distribución del error \(\varepsilon\) . El único supuesto necesario sobre la distribución de los errores en el método de mínimos cuadrados es que tienen una varianza constante \(\sigma^2\) independiente de la concentración \(x_i\). Sin embargo, si queremos inferir estadísticamente algo sobre los parámetros correspondientes, es necesario disponer de información adicional sobre su distribución.

Por este motivo, adicionalmente consideramos los siguientes supuestos

d. los datos están distribuidos normalmente y, en consecuencia, para cada \(x\), la respuesta experimental es una variable aleatoria normal (\(Y|X=x\sim \mathcal{N}(\beta_0+\beta_1 x , \sigma^2)\;\))).

La Figura 3.1 ilustra el significado de las hipótesis asumidas: para cada concentración \(x_i\) y debido al carácter aleatorio de \(\varepsilon\), se puede obtener cualquier valor de la señal, pero los valores cercanos a \(\beta_0+\beta_1 x_i\) son más probables, por ser este el valor medio esperado cuando se usa una función de densidad de probabilidad de una distribución normal, independiente de una concentración a otra y con varianza común \(\sigma^2\).

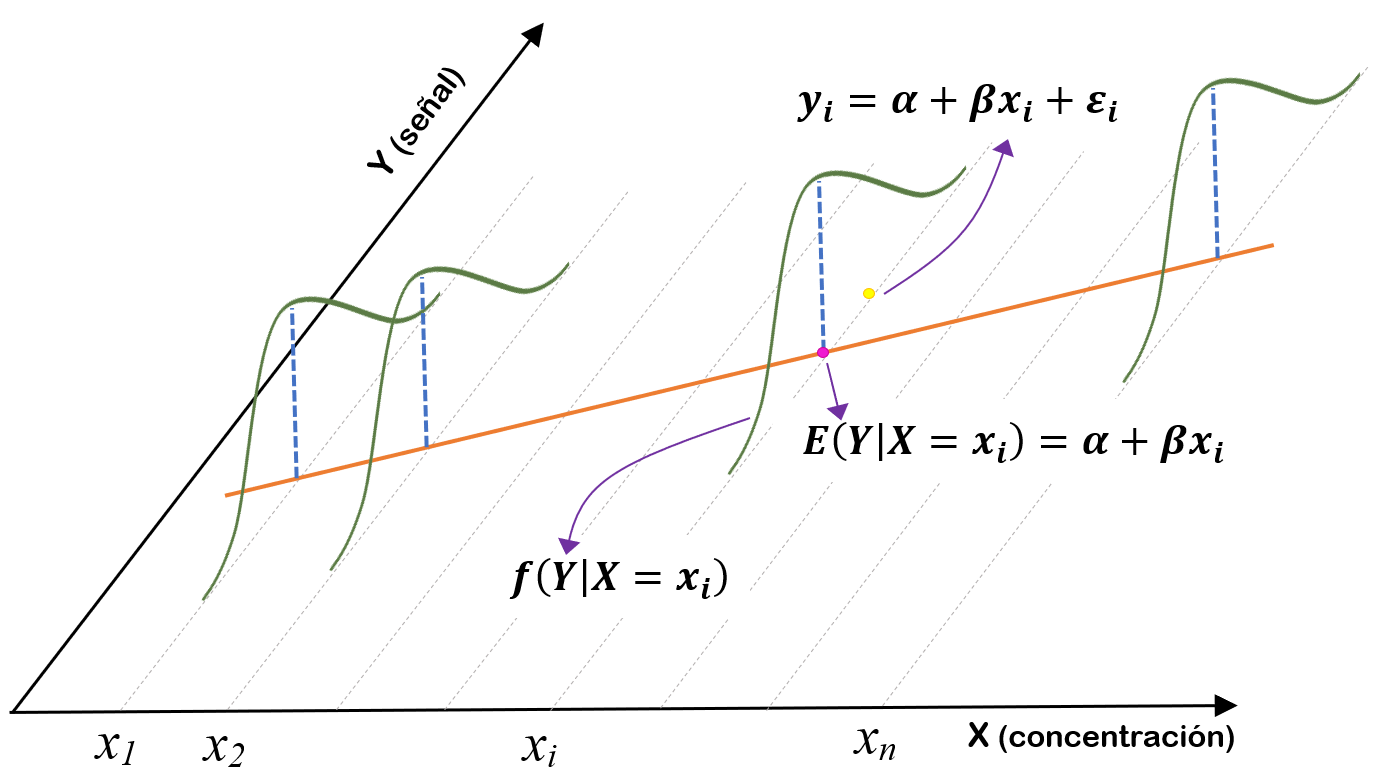
Figura 3.1: Modelo de calibración de Eq. (2.1), asumiendo que la señal registrada proviene de una distribución normal.

Proponer un modelo de calibración específico, como el de la Ecuación (3.1), para algunos datos experimentales es consecuencia del conocimiento teórico del problema, pero su validez debe verificarse sobre la base de un examen crítico de los resultados experimentales. El modelo \(f(x)\) es una hipótesis de trabajo y debe modificarse si los datos experimentales están en contra.

Cuando decimos que un modelo es lineal o no lineal, nos referimos a la linealidad o no linealidad en los coeficientes. El valor de la mayor potencia de una variable predictora en el modelo se denomina orden del modelo. Por ejemplo, \[\begin{align} y_i&=\beta_0 +\beta_1 x_i + \beta_2 x_i^2 + \varepsilon_i, \;\;\; i=1, \ldots, N. \tag{3.2} \end{align}\] es un modelo de regresión lineal (en las \(\beta\) ’s) de segundo orden (en \(x\)). El modelo de calibración de la Ecuación (3.2) es cuadrático; no es una calibración lineal pero sino una regresión lineal.

3.1 Estimación por mínimos cuadrados

El método de mínimos cuadrados ordinarios (OLS por sus siglas en inglés -Ordinary Least Squares-) no requiere ninguna hipótesis sobre la distribución de los errores, \(\varepsilon\) en la Ecuación (3.1). Para obtener las estimaciones \(\hat \beta_0\) y \(\hat \beta_1\) de \(\beta_0\) y \(\beta_1\), respectivamente, se determina la recta que mejor describe los datos experimentales. El argumento es el siguiente: para cada par de valores \(a\) y \(b\), se obtiene una recta diferente, \(\hat{y}= a+bx\) , cuyos residuos son \(e_i = y_i - \hat{y}_i\) ; \(i = 1, \ldots ,N\). Los estimadores OLS de \(\beta_0\) y \(\beta_1\) son los valores que minimizan la suma de cuadrados de estos residuos (\(SSE\)), \[\begin{align} SSE(a,b) &= \sum\limits_{i=1}^N e_i^2 = \sum\limits_{i=1}^N (y_i - \hat{y}_i)^2 = \sum\limits_{i=1}^N (y_i - a-bx_i)^2 \tag{3.3} \end{align}\]

La recta que se obtiene al minimizar \(SSE\) en función de a y b es la que minimiza la suma de las distancias “en vertical” entre los datos experimentales y los estimados con la línea ajustada (ver Figura 3.2).

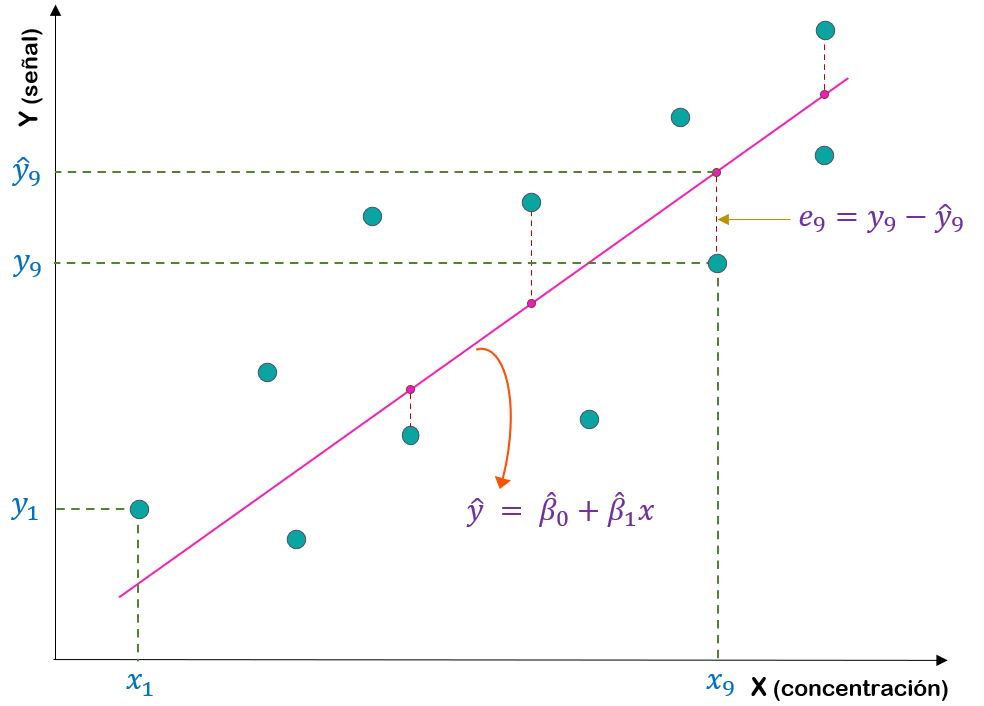
Figura 3.2: Ilustración del método de mínimos cuadrados: la recta de calibración ajustada es la que minimiza la suma de cuadrados de todas las distancias verticales \(e_i\).

Es evidente que si un conjunto de \(N\) residuos es grande, entonces el ajuste del modelo no es bueno. Residuos pequeños son indicadores de un ajuste adecuado. Notemos que, de la definición del residuo \(e_i\) se deduce que \[\begin{align} y_i&=\hat{\beta}_0 +\hat{\beta}_1 x_i + e_i, \;\;\; i=1, \ldots, N. \tag{3.4} \end{align}\] La Ecuación (3.4) debería aclarar la diferencia entre los residuos \(e_i\) y los errores aleatorios \(\varepsilon_i\) del modelo (3.1).

La Figura 3.3 muestra la recta ajustada a partir de un conjunto de datos, a saber \(\hat{y} = \hat{\beta}_0 +\hat{\beta}_1x\) , y la recta que refleja el modelo, \(\mu_{Y| x}= \beta_0+\beta_1x\) . Desde luego, \(\beta_0\) y \(\beta_1\) son parámetros desconocidos. La recta ajustada es un estimación de la recta correspondiente al modelo estadístico.

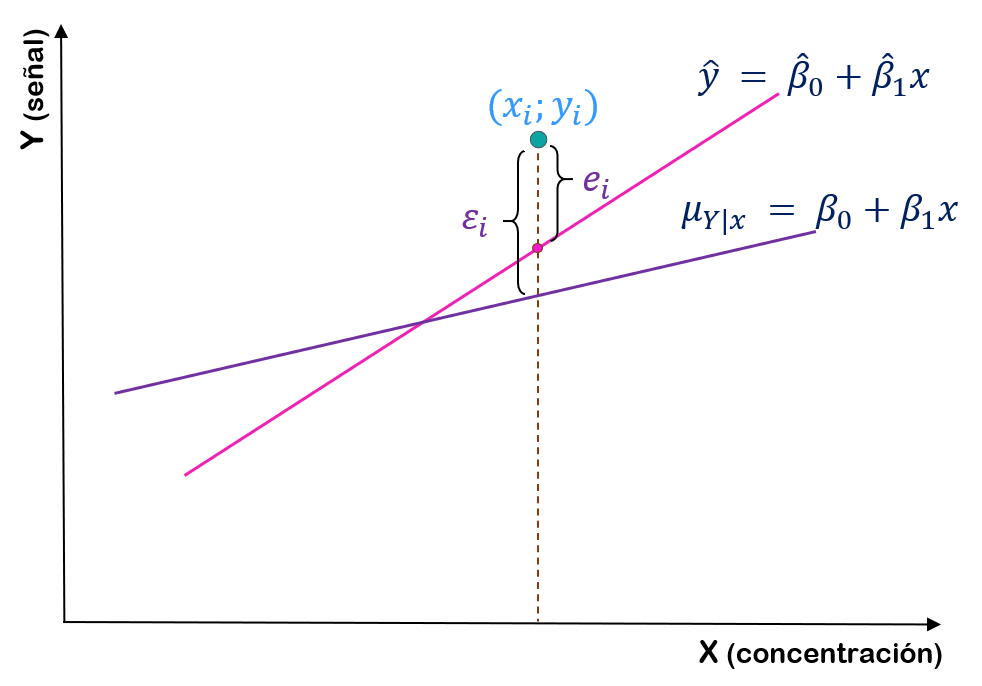
Figura 3.3: Comparación de \(\varepsilon_i\) con el residuo \(e_i\).

Se puede probar analíticamente que la función \(SSE(a, b)\) en la Ecuación (3.3) tiene un mínimo único (excepto cuando \(x_1 = x_2 = \ldots = x_N\) , una situación claramente sin sentido en calibración) que puede determinarse explícitamente. Esta solución proporciona los estimadores OLS que, como ya hemos visto, vienen dados por las ecuaciones

\[\begin{align} \hat{\beta}_1 & = \frac{\sum\limits_{i=1}^{N}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^N(x_i-\bar{x})^2}=\frac{Cov(x,y)}{S_x^2}=\frac{S_{xy}}{S_x^2} \tag{3.5}\\ \hat{\beta}_0 & = \bar{y}-\hat{\beta_1}\bar{x} \tag{3.6} \end{align}\]

donde \(\bar{y}=\frac{1}{N}\sum\limits_{i=1}^N y_i\) , el promedio de las \(y_i\) , \(\bar{x}=\frac{1}{N}\sum\limits_{i=1}^N x_i\) , el promedio de las \(x_i\) y \(S_x^2\) denota la varianza muestral de las \(x\)’s

La línea determinada por estas ecuaciones se conoce como recta de regresión de \(Y\) sobre \(X\), es decir, la recta que indica cómo varía \(Y\) cuando \(X\) se ajusta a los valores elegidos. Es muy importante hacer constar que la recta de regresión de \(X\) sobre \(Y\) no es la misma recta (excepto en el caso muy improbable en que todos los puntos caigan sobre una línea recta, exactamente cuando \(r = 1\) o \(r= -1\)). La recta de regresión de \(X\) sobre \(Y\) supone que todos los errores ocurren en la dirección de \(X\). Si se mantiene rigurosamente el convenio que la señal analítica se representa siempre sobre el eje \(Y\) y la concentración sobre el eje \(X\), la recta de regresión de \(Y\) sobre \(X\) es la que se debe usar siempre en los experimentos de calibración.

El método OLS no proporciona una estimación para \(\sigma^2\). Sin embargo, esta puede obtenerse a partir de la suma de cuadrado de los residuos y basándose en las estimaciones OLS de \(\beta_0\) y \(\beta_1\). Llamamos a \(\hat{\sigma}^2\) varianza de la regresión, es habitualmente denotada por \(S^2_{Y|x}\) y está definida por \[\begin{align} \tag{3.7} S^2_{y|x} &= \frac{1}{N-2}\sum\limits_{i=1}^N (y_i-\hat{\beta}_0 - \hat{\beta}_1 x_i)^2 = \frac{1}{N-2}\sum\limits_{i=1}^N (y_i-\hat{y}_i)^2 = \frac{1}{N-2}\sum\limits_{i=1}^N e_i^2 \end{align}\] El parámetro \(\sigma^2\) refleja la variación aleatoria o variación del error experimental alrededor de la recta de regresión.

---

3.1.1 Ejemplo 2

Enunciado

Como primer ejemplo práctico, vamos a considerar una serie de medidas realizadas durante un experimento de emisión luminiscente. La intensidad de la emisión fluorescente de las sustancias químicas que presentan esta propiedad, es directamente proporcional a la concentración de dicha sustancia.

Se han examinado una serie de soluciones patrón de fluoresceína en un espectrómetro de fluorescencia, y han conducido a las siguientes intensidades de fluorescencia (en unidades arbitrarias):

Construir la recta de regresión, en el caso que sea adecuado, indicando cuál se considera como variable predictora y cuál será la variable respuesta.

---

Solución:

Definamos en primer lugar las variables con las que vamos a trabajar.

• Y : “Intensidad de fluorescencia” \(\leadsto\) Variable respuesta.
• X : “Concentración de fluoresceína (pg/mL)” \(\rightsquigarrow\) Variable predictora.

Para decidir si tiene sentido construir la recta de regresión, comencemos con un análisis exploratorio. Para ello vamos a graficar los puntos y calculemos el coeficiente de correlación lineal muestral \(r\).

concentracion <- c(0,2,4,6,8,10,12)
intensidad <- c(2.1,5.0,9.0,12.6,17.3,21.0,24.7)
(r <- cor(concentracion,intensidad))

## [1] 0.9988796

mydata <- data.frame(cbind(intensidad,concentracion))
ggplot(mydata, aes(x=concentracion, y=intensidad)) + 
  geom_point(size=3,color="purple3") +
  labs(x="Concentración (pg/mL)", y="Intensidad de fluorescencia") +
  theme_ipsum(
    base_size = 11.5,
    axis_title_size = 12,
    axis_title_just = "rt")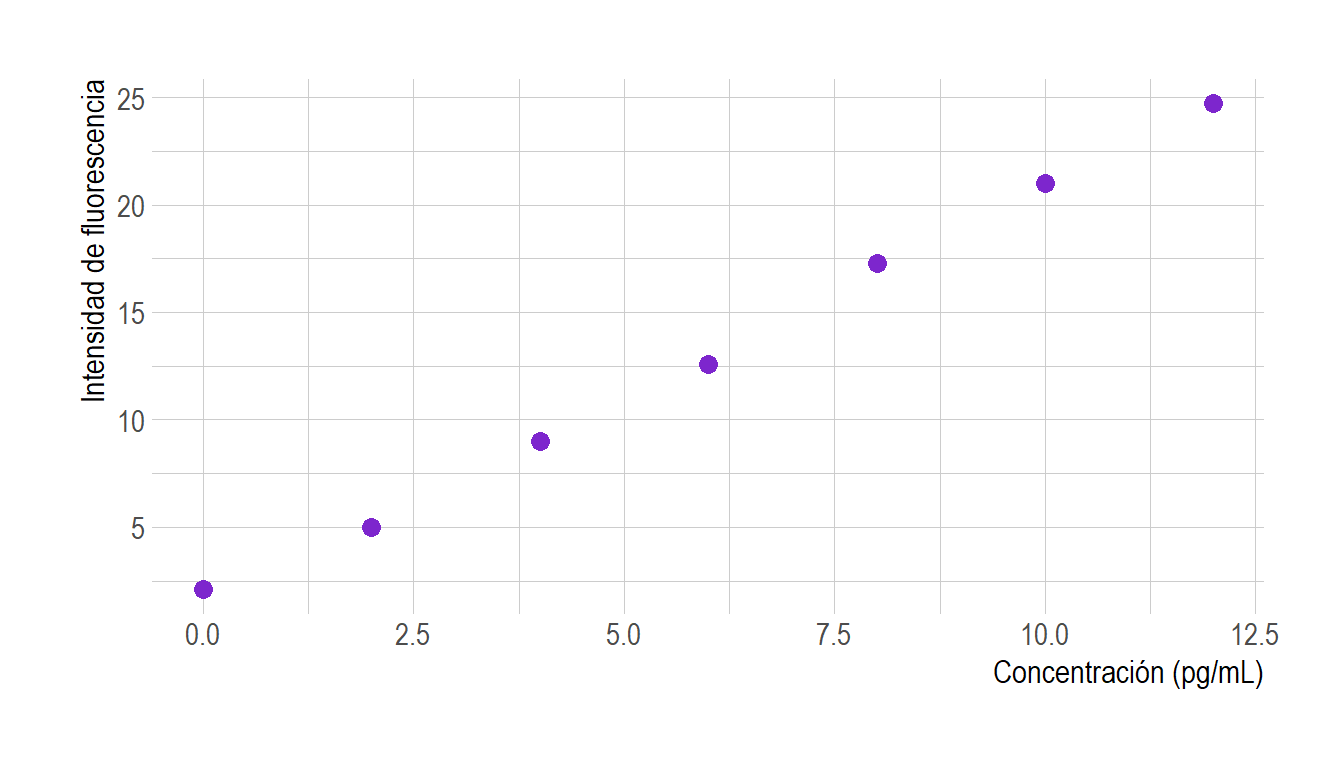

Figura 3.4: Gráfica de dispersión para los datos de fluoresceína.

Según podemos observar en el gráfico y a partir del valor estimado para el coeficiente de correlación lineal muestral, muy próximo a la unidad y positivo, parece existir una relación lineal fuerte y creciente entre las variables, es decir, que el aumento de la concentración produce un aumento en la Intensidad de fluorescencia. Por lo tanto, tiene sentido construir la recta de regresión.

library(ggthemes)
ajuste <- lm(intensidad~concentracion)
summary(ajuste)

## 
## Call:
## lm(formula = intensidad ~ concentracion)
## 
## Residuals:
##        1        2        3        4        5        6        7 
##  0.58214 -0.37857 -0.23929 -0.50000  0.33929  0.17857  0.01786 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     1.5179     0.2949   5.146  0.00363 ** 
## concentracion   1.9304     0.0409  47.197 8.07e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4328 on 5 degrees of freedom
## Multiple R-squared:  0.9978, Adjusted R-squared:  0.9973 
## F-statistic:  2228 on 1 and 5 DF,  p-value: 8.066e-08

ggplot(mydata, aes(x=concentracion, y=intensidad)) +
  geom_abline(intercept=coefficients(ajuste)[1],slope=coefficients(ajuste)[2], color="#e67e1b", size=1)+
  geom_point(size=3,color="purple3") +
  labs(x="Concentración (pg/mL)", y="Intensidad de fluorescencia") +
  scale_x_continuous(limits = c(-.2,12.2),breaks=concentracion,expand = c(0,0))+
  scale_y_continuous(limits = c(-0.5,25.5),expand = c(0,0))+
  annotate(geom="text", x=3.2, y=1.52, label="Ordenada al origen = 1.52",
              color="#21512a")+
  geom_segment(aes(x = 0.14, y = 1.52, xend = 1, yend = 1.52),
                  arrow = arrow(length = unit(2, "mm"),ends="first", type = "closed"))+
  geom_segment(aes(x = 4, y = (coefficients(ajuste)[1]+coefficients(ajuste)[2]*4), xend = 6, yend = (coefficients(ajuste)[1]+coefficients(ajuste)[2]*4)), linetype='dashed')+
  geom_segment(aes(x = 6, y = (coefficients(ajuste)[1]+coefficients(ajuste)[2]*4), xend = 6, yend = (coefficients(ajuste)[1]+coefficients(ajuste)[2]*6)), linetype='dashed')+
  annotate(geom="text", x=7.5, y=10, label="Pendiente = 1.93",
              color="#21512a")+
  geom_segment(aes(x = -0.2, y = 0, xend = 12.2, yend=0),col="#595e5e")+
  geom_segment(aes(x = 0, y = -0.5, xend = 0, yend=25.5), col="#595e5e")+
  theme_ipsum(
    base_size = 11.5,
    axis_title_size = 12,
    axis_title_just = "rt")+
  theme(legend.position = "none")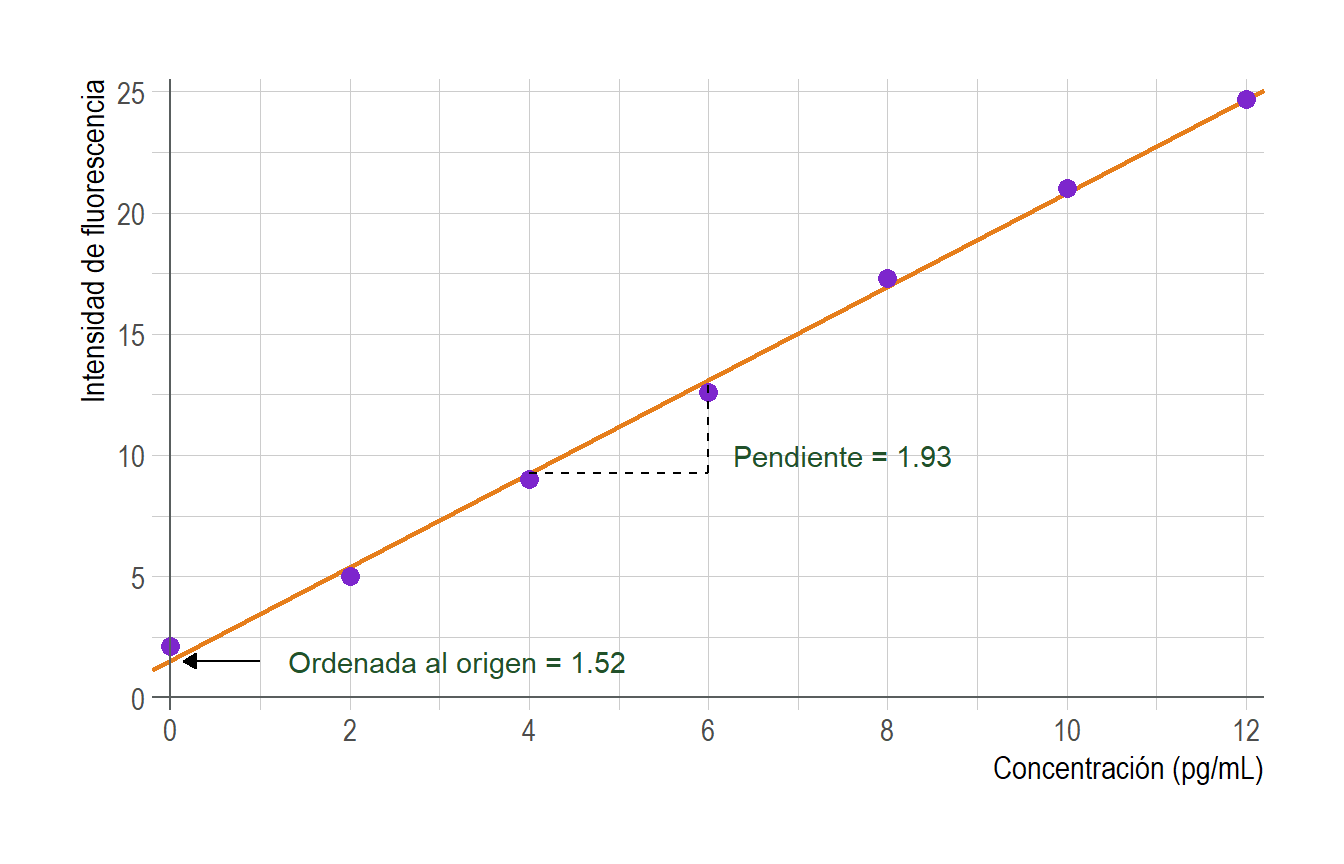

Figura 3.5: Gráfica de calibrado para los datos de fluoresceína.

Por lo tanto la recta estimada es \(\hat{y}=1.52 + 1.93 x\;\).

O bien podemos escribir \(Inte\hat{ns}idad = 1.52 + 1.93 \cdot concentracion\;\).

La recta estimada, junto con los valores estimados de la pendiente y la ordenada origen se muestran en la Figura 3.5. Es importante recalcar que la estimación de la recta solo será útil cuando un estudio previo (cálculo de \(r\) y análisis exploratorio de los datos) indique que una línea recta es coherente con el experimento que se trata. Y como ya lo hemos mencionado anteriormente, debemos analizar la validez del modelo propuesto. Dicho análisis lo haremos a partir del estudio de los residuos del modelo.

Validación de las hipótesis del modelo: Análisis de los residuos.

par(mfrow=c(1,2))
plot(ajuste,c(1,2))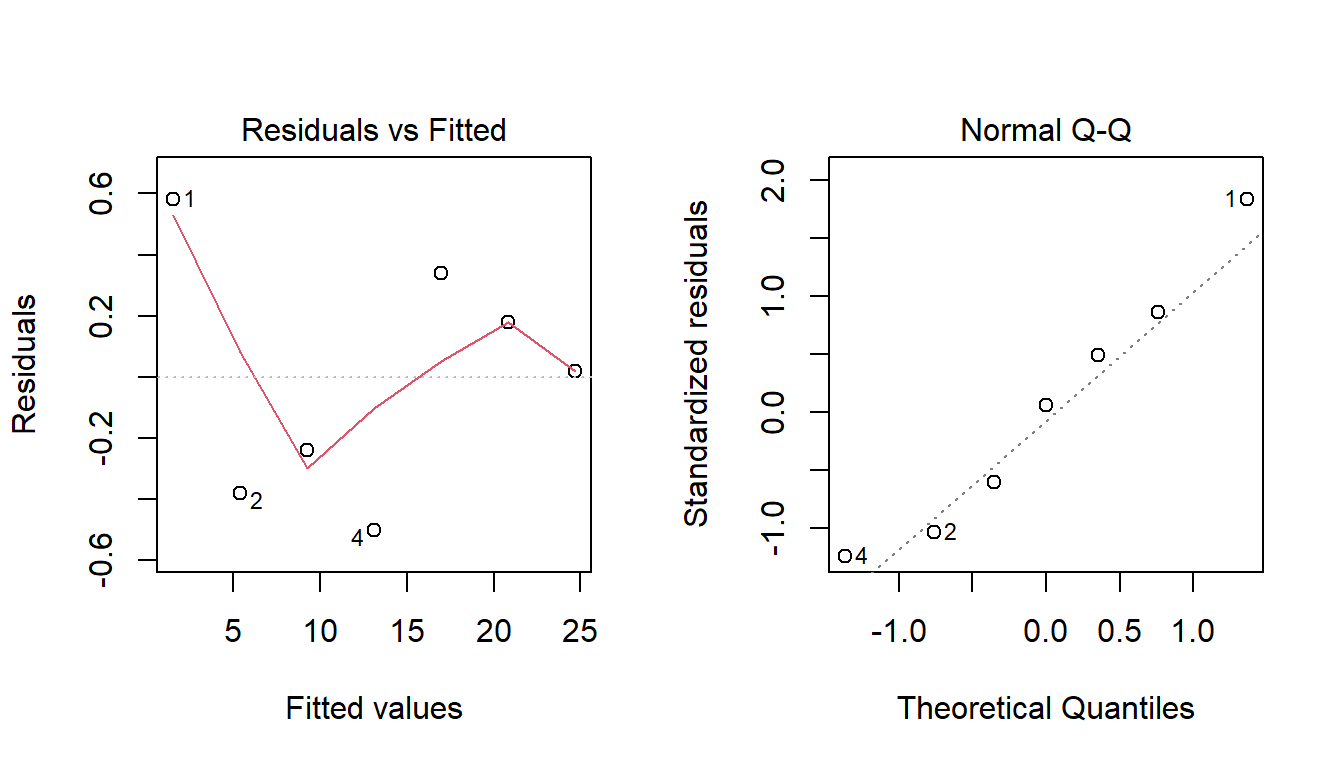

Figura 3.6: Análisis de residuos para Ejemplo 2.

ncvTest(ajuste)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 1.390008, Df = 1, p = 0.2384

shapiro.test(ajuste$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  ajuste$residuals
## W = 0.965, p-value = 0.8603

Analizamos también la existencia de datos atípicos (outliers).

outlierTest(ajuste)

## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
##   rstudent unadjusted p-value Bonferroni p
## 1 2.884165           0.044825      0.31377

influenceIndexPlot(ajuste)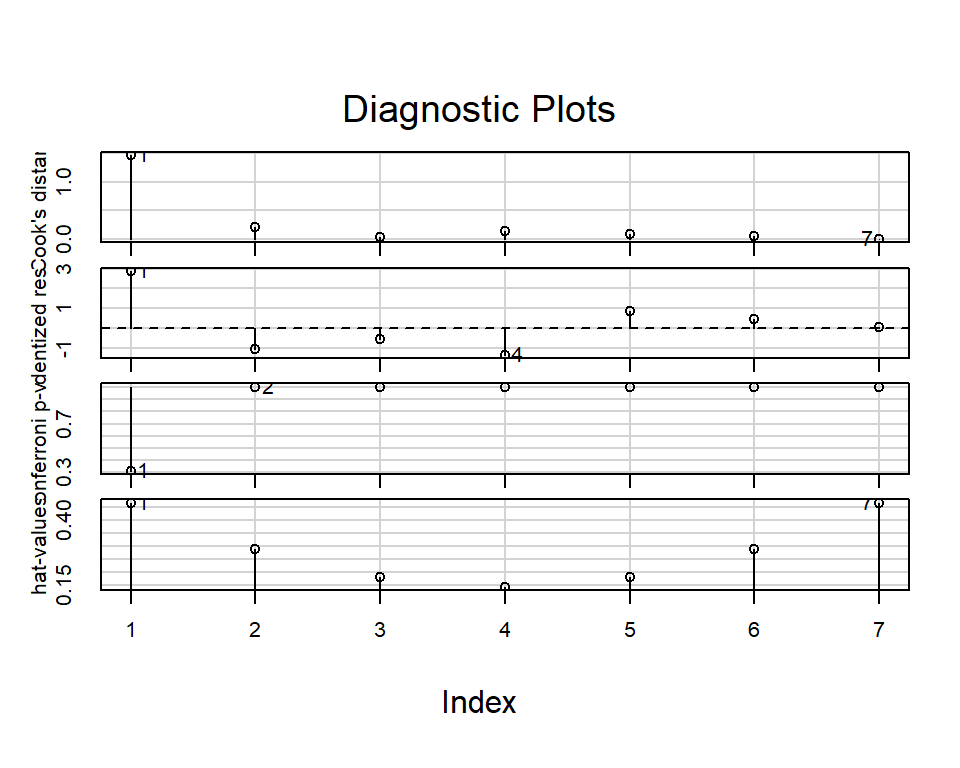

A partir de estos gráficos y de los resultados de los test, no parece haber problemas con los supuestos del modelo (normalidad y varianza constantes de los errores.)

---

3.2 Errores en la pendiente y ordenada en el origen de la recta de regresión

Para estimar las incertidumbres (expresadas como desviaciones estándar) de la pendiente y la ordenada en el origen, análicemos la de incertidumbre de las ecuaciones (3.5) y (3.6).

En primer lugar notemos que los estimadores \(\hat \beta_0\) y \(\hat \beta_1\) son combinaciones lineales de las \(y_i\)’s. En consecuencia, sus incertidumbres están relacionadas con la incertidumbre al medir los valores de \(Y\). En efecto: \[\begin{align} \hat{\beta}_1 &= \sum\limits_{i=1}^{N}\frac{x_i-\bar{x}}{\sum_{i=1}^n(x_i-\bar{x})^2}y_i =\sum\limits_{i=1}^{N}c_i y_i \end{align}\] donde \(c_i = \frac{x_i-\bar{x}}{\sum_{i=1}^N(x_i-\bar{x})^2}\;\) y por lo tanto \[\begin{align} Var(\hat{\beta}_1) &= Var(\sum\limits_{i=1}^{N}c_i y_i)\\ &=\sum\limits_{i=1}^{N}\Big[\frac{x_i-\bar{x}}{\sum_{i=1}^N(x_i-\bar{x})^2}\Big]^2Var(y_i)\\ &=\sum\limits_{i=1}^{N}\frac{(x_i-\bar{x})^2}{\Big[\sum_{i=1}^N(x_i-\bar{x})^2\Big]^2}\sigma^2\\ &=\frac{\sigma^2}{\sum\limits_{i=1}^N(x_i-\bar{x})^2} \tag{3.8} \end{align}\]

Por otro lado, \[\begin{align} Var(\hat{\beta}_0) &= Var(\bar{y}-\hat{\beta_1}\bar{x})\\ &= Var(\bar{y})+Var(\hat{\beta_1}\bar{x})-2Cov(\bar{y},\hat{\beta_1}\bar{x})\\ &=\frac{\sigma^2}{N}+(\bar{x})^2Var(\hat{\beta_1})-2\bar{x}Cov(\bar{y},\hat{\beta_1}) \end{align}\] Pero tenemos que \[\begin{equation} \begin{split} Cov(\bar{y},\hat{\beta_1})&= Cov\Big(\frac{1}{N}\sum_iy_i,\sum_ic_iy_i\Big)\\ &=\frac{1}{N}\sum_ic_iCov(y_i,y_i)\\ &=\frac{\sigma^2}{N}\sum_ic_i\\ &=0 \end{split} \tag{3.9} \end{equation}\]

Por lo tanto, \[\begin{align} \tag{3.10} Var(\hat{\beta}_0) = \sigma^2\Big[\frac{1}{N}+\frac{(\bar x)^2}{\sum\limits_{i=1}^N(x_i-\bar{x})^2}\Big] \end{align}\]

Adicionalmente, tenemos que \[\begin{align} \tag{3.11} Cov(\hat{\beta}_0,\hat{\beta}_1)=-\sigma^2\frac{\bar{x}}{\sum\limits_{i=1}^N(x_i-\bar{x})^2} \end{align}\]

De las ecuacionces (3.8), (3.10) y (3.11), y utilizando el estimador \(S_{y|x}\) de \(\sigma\) obtenido en la sección anterior, tenemos que, estimadores para las errores estándar de la pendiente (\(\beta_1\)) y ordenada al origen (\(\beta_0\)) y la covarianza entre ellos, vienen dadas por:

\[\begin{align} S_{\hat \beta_1} & = \frac{S_{y|x}}{\sqrt{\sum\limits_{i}(x_i-\bar{x})^2}}\\ S_{\hat \beta_0} & = S_{y|x}\sqrt{\frac{\sum\limits_{i}x_i^2}{N\sum\limits_{i}(x_i-\bar{x})^2}}\\ C\hat{o}v(\hat{\beta}_0,\hat{\beta}_1)&=-S_{y|x}^2\frac{\bar{x}}{\sum\limits_{i=1}^N(x_i-\bar{x})^2} \end{align}\]

Los valores de \(S_{\hat \beta_1}\) y \(S_{\hat \beta_0}\) se pueden utilizar de la manera usual para obtener intervalos de confianza para la pendiente y la ordenada al origen. Así pues los límites de confianza de la pendiente vienen dados por \(\hat{\beta_1} \pm t_{\alpha/2,n-2}S_{\hat \beta_1}\) donde el valor de \(t_{\alpha/2,n-2}\) es el cuantil \(1-\alpha/2\) de la distribución \(t\) con \(n-2\) grados de libertad. Similarmente los límites de confianza para la ordenada al origen vienen dados por \(\hat{\beta_0} \pm t_{\alpha/2,n-2}S_{\hat \beta_0}\).

---

3.2.1 Ejemplo 2 (continuación):

Enunciado:

Para los datos de concentración de fluoresceína, queremos determinar los intervalos de confianza para la pendiente y la ordenada al origen.

---

Solución:

De la tabla resumen del ajuste lineal, obtenemos

res <- summary(ajuste)
beta0 <- res$coefficients[1,1]
sdbeta0 <- res$coefficients[1,2]
beta1 <- res$coefficients[2,1]
sdbeta1 <- res$coefficients[2,2]
alpha = 0.05
n <- length(res$residuals)
qt <- qt(1-alpha/2,n-2)
ICbeta0 <- beta0 + c(-1,1)*qt*sdbeta0
ICbeta1 <- beta1 + c(-1,1)*qt*sdbeta1

# Estos intervalos también pueden obtenerse directamente usando la función confint()  
confint(ajuste,level=0.95)

##                 2.5 %   97.5 %
## (Intercept)   0.75970 2.276014
## concentracion 1.82522 2.035495

\(S_{y|x} =0.4328\) , \(S_{\hat \beta_1} = 0.0409\) y \(S_{\hat \beta_0} = 0.2949\) . Así, un intervalo de confianza del 95% para \(\beta_1\) es \((1.83\;,\;2.04)\;\), mientras que para \(\beta_0\) resulta \((0.76\;,\; 2.28)\;\).

Observación: Notar como hemos utilizado todas las cifras decimales disponibles al hacer los cálculo y solo hemos redondeado al final, al reportar el IC obtenido.

---

3.3 Región de confianza conjunta para \(\beta_0\) y \(\beta_1\).

En el ejemplo anterior, los intervalos de confianza para \(\beta_0\;\) y \(\beta_1\;\) los calculamos por separado. Estos especifican rangos para los parámetros individuales independientemente del valor del otro parámetro. Sin embargo, la Ecuación (3.11) muestra que la pendiente y la ordenada al origen estimadas, \(\hat \beta_1\;\) y \(\hat \beta_0\;\), están relacionadas: si, por ejemplo, en la Figura 3.5, otro conjunto de puntos de medición tomados de la misma población da lugar a un valor mayor para \(\hat \beta_1\;\), es probable que esto conduzca a un valor más chico para \(\hat \beta_0\;\). Los estimadores de pendiente y ordenada al origen no son variables aleatorias estadísticamente independientes y el valor de uno de los parámetros influye automáticamente en el del otro. Por lo tanto, a partir de los intervalos individuales de \(100(1 - \alpha)\%\;\), no podemos decir con el mismo grado de confianza que las hipótesis nulas \(\beta_0 = 0\;\) y \(\beta_1 = 1\;\) son simultáneamente aceptables. Esto es comparable con el problema de comparaciones múltiples discutido en ANOVA.

Si queremos testear la hipótesis conjunta de que \(\beta_0 = 0\;\) y \(\beta_1 = 1\;\), necesitamos usar una prueba de hipótesis compuesta o un intervalo de confianza conjunto (esto es, una región de confianza) para la pendiente y la ordenada al origen. Estas tienen en cuenta la correlación entre las estimaciones \(\hat \beta_1\;\) y \(\hat \beta_0\;\).

La región de confianza conjunta toma la forma de una elipse con el centro \((\hat \beta_0\;,\hat \beta_1)\;\) (los estimadores \(OLS\;\) de \(\beta_0\;\) y \(\beta_1\;\) respectivamente, y se define como el conjunto de de todos los puntos \((\beta_0, \beta_1)\;\) que verifican la siguiente desigualdad: \[\begin{equation} \tag{3.12} \frac{N(\beta_0-\hat{\beta}_0)^2+2\sum\limits_{i=1}^N x_i(\beta_0-\hat{\beta}_0)(\beta_1-\hat{\beta}_1) +\sum\limits_{i=1}^N x_i^2(\beta_1-\hat{\beta}_1)}{2 S_{y|x}^2}\leq F_{\alpha; 2, N-2} \end{equation}\]

donde \(F_{\alpha; 2, N-2}\;\) es el cuantil \(1-\alpha\;\) de la distribución \(F\;\) con \(2\;\) y \(N-2\;\) grados de libertad.

Esta región es útil para establecer la precisión de un método de análisis en un rango de concentraciones y para comparar diferentes métodos analíticos y/o calibraciones.

Para analizar la precisión de un método analítico, el procedimiento es el siguiente. Una vez obtenido el modelo de calibración, se utiliza para estimar las concentraciones \(\hat x_i\;\) correspondientes a los estándares de calibración \(x_i\;\). Si el método es preciso, entonces la regresión de los valores \(\hat x_i\;\) versus \(x_i\;\) debe ser una recta con pendiente 1 y ordenada al origen 0. La recta de regresión \(\hat x = \hat b_0 + \hat b_1 x\;\) y su correspondiente \(S_{\hat{x} x}\;\) son suficientes para obtener la región de confianza de nivel \(1 – \alpha\;\) para \((b_0, b_1)\) (notar el cambio de notación en la pendiente y ordenada al origen, la cual obedece al hecho de que estamos considerando la regresión de los valores predichos \(\hat x_i\;\) en \(x_i\;\) y no la regresión correspondiente a la calibración). Si el punto \((0, 1)\;\) pertenece a esa región, se puede concluir que el método no tiene sesgo.

Por su parte, la representación conjunta de las regiones para varios métodos de calibración equipados con las mismas señales analíticas permite una comparación entre ellos; cuanto más pequeña sea la superficie de la región de confianza, más preciso será el método de calibración.

Comentarios adicionales:

• De forma análoga al intervalo de confianza, la región de confianza se puede utilizar para efectuar contrastes de hipótesis, sin más que examinar si el punto establecido en dicha hipótesis se encuentra dentro o fuera de la región de confianza. Si dicho punto está dentro, no se rechaza la hipótesis nula y si está fuera se rechaza.

• Por otra parte, al igual que ocurre en los intervalos de confianza para un solo parámetro, las dimensiones de la elipse dependen directamente de las varianzas estimadas de los estimadores de los parámetros: a mayor varianza, mayor será la elipse y viceversa (y esto, por lo tanto, da una idea de la precisión del método que se está probando). La inclinación de la elipse depende de la covarianza entre los dos estimadores: la elipse asciende de izquierda a derecha si tal covarianza es positiva, descendiendo en caso contrario. En el caso particular de calibración, al analizar la Ecuación (3.11), podemos notar que, debido que que los valores \(x_i\;\) no pueden ser negativos (pues son valores de concentraciones), siempre tendremos \(\bar x> 0\;\) y, en consecuencia, la covarianza entre \(\hat \beta_0\;\) y \(\hat \beta_1\;\) es siempre negativa.

• Podemos comparar la región de confianza bidimensional con los intervalos de confianza individuales, para lo cual tenemos que trazar dos líneas paralelas a cada eje que pasen por los límites de los intervalos individuales. Con ello queda claro que la región de confianza conjunta no es necesariamente la intersección de los intervalos de confianza individuales y, por tanto, los contrastes individuales y conjuntos son independientes. Es decir, se puede aceptar la hipótesis nula de los parámetros a nivel individual y no a nivel conjunto, y viceversa.

---

3.3.1 Ejemplo 2 (continuación): Región de confianza

Enunciado:

Para los datos de concentración de fluoresceína, queremos determinar la región de confianza para la pendiente y la ordenada al origen.

---

Solución:

Para graficar la elipse que corresponde a la región de confianza que estamos buscando, podemos usar la función confidenceEllipse() (que está incluída en el paquete car y por lo tanto para acceder a la misma debemos primero llamar la librería correspondiente)

confidenceEllipse(ajuste, which.coef = c("concentracion","(Intercept)"), main = "Región de confianza del 95%")

Pero la vida no es así de simple…

puntos <- confidenceEllipse(ajuste, which.coef = c("(Intercept)","concentracion"),draw = FALSE,segments=1000)
df <- data.frame(puntos)
colnames(df) <- c('ordenada','pendiente')
beta0hat <- as.numeric(ajuste$coefficients[1])
beta1hat <- as.numeric(ajuste$coefficients[2])
ggplot(df, aes(x=pendiente, y=ordenada))+ 
  #geom_line(color="#e67e1b")+
  geom_point(size=0.5,col='darkorange')+
  annotate("point", x = beta1hat, y = beta0hat, colour = "darkred", size=2)+
  annotate("text", x=beta1hat, y=(beta0hat+0.1), parse = TRUE, label='paste(\'( \', hat(beta)[1], \',\',hat(beta)[0],\')\')',size=4,col='#536d4a')+
  labs(title='Region de confianza del 95%',y="Ordenada al Origen", x="Pendiente") +
  geom_vline(xintercept=c(ICbeta1[1],ICbeta1[2]), linetype='longdash', color='coral4', size=0.5)+
  geom_hline(yintercept=c(ICbeta0[1],ICbeta0[2]), linetype='longdash', color='coral4', size=0.7)+
  theme_ipsum(
    base_size = 11.5,
    axis_title_size = 12,
    axis_title_just = "rt")+
  theme(plot.title = element_text(face='bold', colour='black', size=13,hjust=0.5))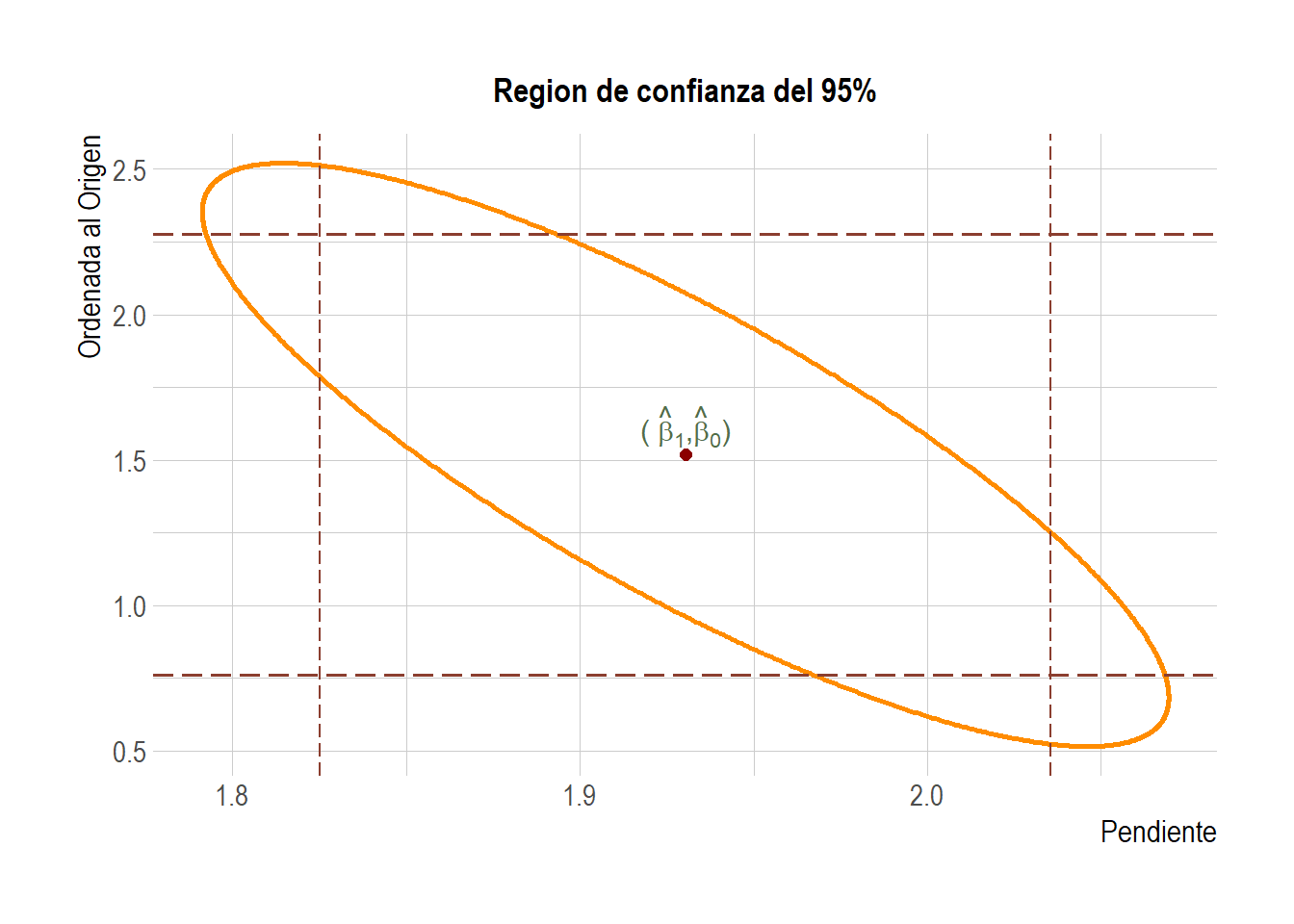

Figura 3.7: Región de confianza conjunta para \(\beta_1\) y \(\beta_0\). También se muestran los IC individuales para cada parámetro.

# execute the function on the model object and provide the restrictions 
# to be tested as a character vector
linearHypothesis(ajuste, c("(Intercept) = 0", "concentracion = 1"))

## Linear hypothesis test
## 
## Hypothesis:
## (Intercept) = 0
## concentracion = 1
## 
## Model 1: restricted model
## Model 2: intensidad ~ concentracion
## 
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1      7 450.75                                  
## 2      5   0.94  2    449.81 1200.4 1.969e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

---

4 Cálculo de una concentración y su error aleatorio

La aplicación más importante de una recta de calibración es la determinación de la concentración de un analito en una muestra problema.

Una vez que han sido determinadas la pendiente y la ordenada en el origen de la recta de calibración, es fácil calcular la concentración (valor de \(X\)) correspondiente a cualquier señal medida en el instrumento (valor de \(Y\)). Es decir, el problema ahora es, para un valor especificado de \(Y\), digamos \(y_{inc}\), obtener un valor estimado, \(\hat x_{inc}\;\), de la concentración en la muestra incógnita, así como también un intervalo de confianza para dicho valor.

Para ello, comencemos notando que, como para el par de puntos \((x_{inc},y_{inc})\) se verifica \(y_{inc} = \beta_0 +\beta_1 x_{inc}+\varepsilon_i\) (recta de calibración poblacional), podemos obtener la concentración estimada del analito en la muestra usando la recta estimada, es decir: \[\begin{equation} \tag{4.1} \hat{x}_{inc} = \frac{y_{inc}-\hat{\beta}_0}{\hat{\beta}_1} \end{equation}\]

Como vemos, el cálculo de una estimación para \(x_{inc}\) a partir de un valor dado \(y_{inc}\) involucra las estimaciones tanto de la pendiente (\(\hat \beta_1\)) como de la ordenada en el origen (\(\hat \beta_0\)) y, como se vio en la sección anterior, ambos valores están sujetos a error. Además, la señal del instrumento derivada del material de ensayo también está sujeta a errores aleatorios. Como resultado, la determinación de la incertidumbre global en la concentración correspondiente es extremadamente compleja. Una alternativa (amplimante utilizada) es aproximarla propagando las incertidumbres. Para ello tenemos:

• Cantidad de interés: \(x_{inc}\) que es función de \(\beta_0\), \(\beta_1\) e \(y_{inc}\) a través de la función \(f(x,y,z)=\frac{x-y}{z}\).

• Estimador \(\displaystyle \hat{x}_{inc} = \frac{{y}_{inc}-\hat{\beta}_0}{\hat{\beta}_1}\)

El problema que tenemos aquí es que los estimadores involucrados no son independientes (como lo hemos pedido al obtener la expresión para la incertidumbre del nuevo estimador). Pero notemos que podemos escribir \[\begin{align} \hat{x}_{inc} &= \frac{ y_{inc}-\hat{\beta}_0}{\hat{\beta}_1} \\ &= \frac{ y_{inc}-\bar{y}+\hat{\beta}_1\bar{x}}{\hat{\beta}_1} \\ & = \frac{y_{inc}-\bar{y}}{\hat{\beta}_1}+\bar{x} \tag{4.2} \end{align}\] De esta última expresión, notemos que \[\begin{align} Cov( y_{inc}-\bar{y},\hat{\beta}_1)&=Cov( y_{inc},\hat{\beta}_1)-Cov(\bar{y},\hat{\beta}_1) \end{align}\] Como lo probamos en (3.9), el segundo término es 0, mientras que \(Cov(y_{inc},\hat{\beta}_1)\) es cero pues, recordemos que \(\hat{\beta}_1=\sum\limits_{i=1}^N c_iy_i\;\) y por lo tanto, por el supuesto de independendia de las observaciones, \(y_{inc}\) resulta indepediente de \(\hat{\beta}_1\). Por el mismo motivo \(y_{inc}\) es también independiente de \(\bar{y}\).

Si aplicamos entonces la regla que obtuvimos para propagar incertidumbres a la relación dada en la Ecuación (4.2), obtenemos la siguiente fórmula para en estimador del error estándar de \(\hat x_0\) \[\begin{align} \tag{4.3} S_{\hat x_{inc}} &= \frac{S_{y|x}}{\hat \beta_1}\sqrt{1+\frac{1}{N}+\frac{(y_{inc}-\bar{y})^2}{\hat \beta_1^2\sum\limits_{i=1}^N(x_i-\bar{x})^2}} \end{align}\] En algunos casos el analista puede realizar varias lecturas de la muestra problema para obtener el valor de \(y_{inc}\). Si disponemos de \(m\) lecturas, entonces la ecuación para \(S_{\hat x_{inc}}\) se convierte en: \[\begin{align} \tag{4.4} S_{\hat x_{inc}} &= \frac{S_{y|x}}{\hat \beta_1}\sqrt{\frac{1}{m}+\frac{1}{N}+\frac{(\bar{y}_{inc}-\bar{y})^2}{\hat \beta_1^2\sum\limits_{i=1}^N(x_i-\bar{x})^2}} \end{align}\] Notar que la Ecuación (4.4) se reduce a la (4.3) cuando \(m=1\) como es de esperar.

Por otro lado notemos que, si utilizamos la relación dada en la Ecuación (4.1), podemos reexpresar la Ecuación (4.4) de la siguiente manera: \[\begin{align} \tag{4.5} S_{\hat x_{inc}} &= \frac{S_{y|x}}{\hat\beta_1}\sqrt{\frac{1}{m}+\frac{1}{N}+ \frac{(\hat{x}_{inc}-\bar{x})^2}{\sum\limits_{i=1}^N(x_i-\bar{x})^2}} \end{align}\] Es importante descatar, como podemos observar de la Ecuación (4.5), que la incertidumbre en la predicción depende de cada muestra y no de la calibración en forma global, ya que para cada muestra incógnita hay un valor predicho de la concentración (\(\hat x_{inc}\)) y por lo tanto un valor asociado del desvío estándar \(S_{\hat x_{inc}}\).

Una vez que hemos calculado -estimado- el error estándar de \(\hat x_{inc}\), podemos construir un intervalo de confianza del \(100(1-\alpha) \%\) para la verdadera concentración \(x_{inc}\), a saber: \[\begin{equation} \tag{4.6} \hat x_{inc} \pm t_{\alpha/2,n-2}S_{\hat x_{inc}} \end{equation}\]

---

4.1 Ejemplo 2 (continuación): Cálculo de una concentración.

Enunciado

A partir de la recta de calibración que obtuvimos en la sección anterior, queremos ahora calcular la concentración (sus límites de confianza) para soluciones con intensidades de fluorescencia de 2.9, 13.5 y 23.0 unidades.

Solución

Vamos a estimar los valores de concentración utilizando la Ecuación (4.1):

y0 <- c(2.9,13.5,23.0)
x0hat <- (y0-beta0)/beta1
# Límites de confianza
n <- length(res$residuals)
Sres <- res$sigma
ybarra <- mean(intensidad)
Sxx <- sum((concentracion-mean(concentracion))^2)
Sx0 <- Sres/beta1*sqrt(1+1/n+(y0-ybarra)^2/(beta1^2*Sxx))
alpha <- 0.05
qt <- qt(1-alpha/2,n-2)
x0hat[1] + c(-1,1)*qt*Sx0[1]

## [1] 0.03590545 1.39610195

x0hat[2] + c(-1,1)*qt*Sx0[2]

## [1] 5.590908 6.823523

x0hat[3] + c(-1,1)*qt*Sx0[3]

## [1] 10.45202 11.80514

• Por lo tanto, los valores estimados para las concentraciones son 0.72, 6.21 y 11.13 pg/ml con errores estándar de 0.26, 0.24 y 0.26 pg/ml respectivamente.

• Los intervalos de confianza a partir de dichas estimaciones son 0.72 \(\pm\) 0.68, 6.21 \(\pm\) 0.62 y 11.13 \(\pm\) 0.68.

---

Este ejemplo pone en relieve un punto importante. Muestra que los límites de confianza son más pequeños (es decir, mejores) para la intesidad \(y_{inc} = 13.5\;\) que para los otros dos valores. En efecto, si analizamos la Ecuación (4.3), podemos ver que cuando \(y_{inc}\) se aproxima a \(\bar y\), el numerador del tercer término se aproxima a cero, y \(S_{\hat x_{inc}}\) entonces se aproxima a un valor mínimo. Esto nos dice que, un experimento de calibración de este tipo, proporcionará los resultados más precisos cuando la señal medida en el instrumento corresponda a un punto próximo al centro de gravedad \((\bar x, \bar y)\) de la recta de regresión.

La Figura 4.1 muestra las bandas de confianza para las concentraciones estimadas con este modelo de calibración. Además resalta los intervalos de confianza obtenidos para las tres concentraciones estimadas en el ejemplo. Notar que, a diferencia de lo que sucede en la regresión lineal convencional, estos intervalos de confianza son para valores de abscisas y no de ordenadas.

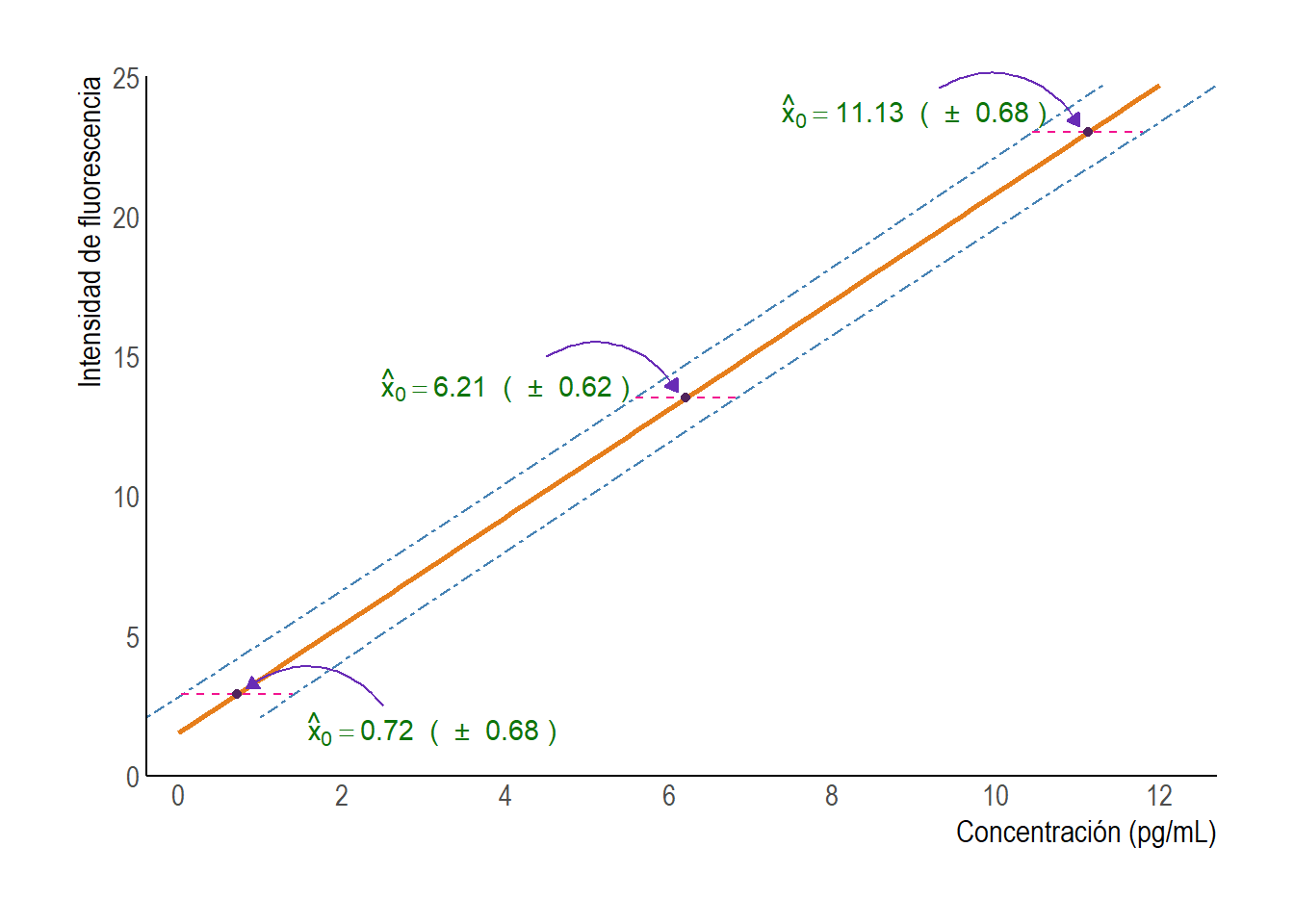
Figura 4.1: Bandas de confianza para concentraciones de fluoresceína calculadas a partir de la recta de calibración.

5 Cálculo de las cifras de mérito.

1. Las cifras de mérito de un método analítico se utilizan regularmente con el propósito de calificar un determinado método y compararlo con otros que ya están publicados y con protocolos oficiales que determina la Unión Internacional de Química Pura y Aplicada.

2. Condensan las propiedades de conjuntos de datos en unos pocos indicadores numéricos.

Incluyen, entre otras, las siguientes:

• Sensibilidad de calibración

• Sensibilidad analítica

• Límite de detección

• Límite de cuantificación

• Rango dinámico

• Rango lineal

5.1 Sensibilidad de la calibración.

Es el cambio en la señal de respuesta por unidad de cambio en la concentración del analito.
\[\begin{align} SEN & = \hat{\beta}_1 \end{align}\] La sensibilidad de la calibración es entonces la pendiente de la curva de calibración, y sus unidades son señal \(\times\;\)concentración\(^{-1}\).

5.2 Sensibilidad Analítica.

La sensibilidad de calibración no es adecuada para comparar dos métodos analíticos cuando estos están basados en respuestas de diferente naturaleza (por ejemplo, absorbancia y fluorescencia, o absorbancia y medidas electroquímicas, etc.). Para ello es preferible utilizar la llamada sensibilidad analítica \(\gamma\;\), definida por el cociente entre la sensibilidad y el ruido instrumental: \[\begin{align} \gamma & = \frac{SEN}{S_y} \end{align}\] donde \(S_y\;\) es una medida conveniente del nivel de ruido en la respuesta. Para estimar el nivel de ruido pueden usarse dos procedimientos, que en teoría deberían coincidir. En el primero, se estima el ruido instrumental a través de los desvíos de las réplicas de las mediciones de calibrado respecto de sus promedios: \[\begin{align} \tag{5.1} S_y & = \sqrt{\frac{\sum_{i=1}^k\sum_{j=1}^r(y_{ij}-\bar{y}_i)^2}{N-k}} \end{align}\] donde \(k\;\) es el número de niveles de concentración estudiados en la recta, \(r\;\) es el número de réplicas por cada nivel, \(y_{ij}\;\) es el valor de la respuesta correspondiente a cada nivel y réplica e \(\bar y\;\) es el promedio de las respuestas de las réplicas para cada nivel de concentración. En la Ecuación (5.1), el número de grados de libertad es \(N — k\;\), ya que de los \(N\;\) datos disponibles, \(k\;\) grados de libertad se reservan para el cálculo de las \(k\;\) medias \(\bar y_i\;\).

En el segundo método de estimación del nivel de ruido, se lo estima como el desvío estándar de los residuos de la regresión lineal \(S_{y|x}\;\) cuya fórmula de cálculo obtuvimos anteriormente (Ecuación (3.7)).

Si los datos estudiados cumplen la relación lineal entre respuesta y concentración, los dos métodos anteriormente descritos deben proveer resultados similares en cuanto a la estimación del ruido instrumental.

5.3 Límites de detección

El límite de detección (LOD) se define como la cantidad o concentración mínima de sustancia que puede ser detectada de manera confiable por un método analítico determinado. Intuitivamente, el LOD sería la concentración mínima obtenida a partir de la medida de una muestra (que contiene el analito) que seríamos capaces de discriminar de la concentración obtenida a partir de la medida de un blanco, es decir, de una muestra sin analito presente. Dicho de otro modo, es la mínima concentracion de analito que es significativamente mayor que cero.

5.3.1 Falsos positivos y falsos negativos

El LOD se calcula mediante una prueba de hipótesis estadística. Vamos a imaginar un determinado método analítico y vamos a situarnos mentalmente en el eje de las concentraciones. Vamos a suponer también que el método analítico tiene una precisión conocida a lo largo de los diferentes niveles de concentración y que los resultados obtenidos con dicho método siguen una distribución normal. Si analizáramos blancos de muestra con el método, bien seguro obtendríamos una distribución de valores de concentración como la que muestra la Figura 5.1

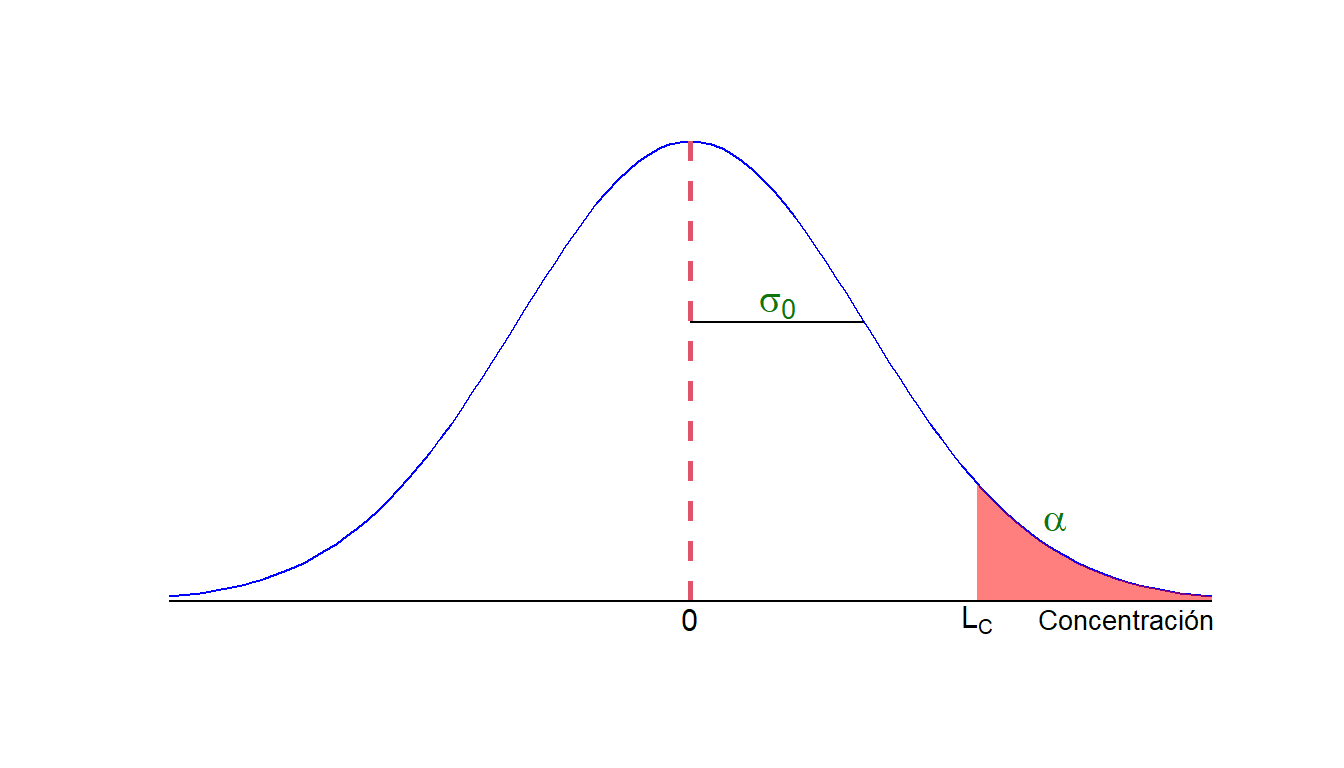
Figura 5.1: Distribución de valores alrededor de cero y nivel crítico.

Los valores de concentración (en ausencia de un error sistemático) se distribuirían alrededor de cero con una desviación estándar \(\sigma_0\;\). Quiere decir que como resultado de la medida de un blanco, y debido a los errores experimentales del método (reflejados en \(\sigma_0\;\)) podríamos obtener una concentración que no fuese cero. Como responsables de los resultados generados en el laboratorio, lo que nos gustaría es poder acotar la distribución en algún punto. Dicho punto es el valor crítico, \(L_C\;\), que nos permitirá, una vez medida la muestra, tomar la decisión de si el analito se halla presente o no. Si la concentración obtenida es superior a \(L_C\;\) entonces resulta poco probable que corresponda al blanco y podemos decir que el analito está presente en la muestra. Existe, sin embargo, un riesgo al acotar la distribución en \(L_C\;\) (probabilidad de que el análisis de un blanco diese como resultado una concentración superior a \(L_C\;\), con lo que falsamente concluiríamos que el analito está presente) Dicha probabilidad, \(\alpha\;\), como ya hemos estudiado, es error de tipo I o probabilidad de falso positivo.

Es decisión del laboratorio la elección del valor de \(\alpha\;\), en función al riesgo, que se está dispuesto a asumir, de equivocarnos. Podríamos establecer, por ejemplo, el valor crítico a concentración cero. El riesgo en ese caso de cometer un falso positivo sería del 50% (cualquier valor de concentración por encima de cero sería considerado como debido a la presencia de analito). Si \(\alpha\;\) se toma igual a \(0.05\;\), entonces una concentración superior a \(L_C\;\) tendrá solo un \(5\%\;\) de probabilidades de constituir un falso positivo.

Ahora bien, ¿podemos adoptar el valor de \(L_C\;\) de la Figura 5.1 como el límite de detección de nuestro método analítico? Supongamos que es así y que dicho valor corresponde a una concentración de 2 ppb. Es decir, el laboratorio está asumiendo que es capaz de detectar analitos en muestra a un nivel de concentración igual o superior a 2 ppb. Imaginemos que un cliente del laboratorio le suministra un lote de muestras con un contenido de 2 ppb de analito. El laboratorio analiza dichas muestras y obtiene una distribución de valores semejante a la mostrada en la Figura 5.2 (en rojo):

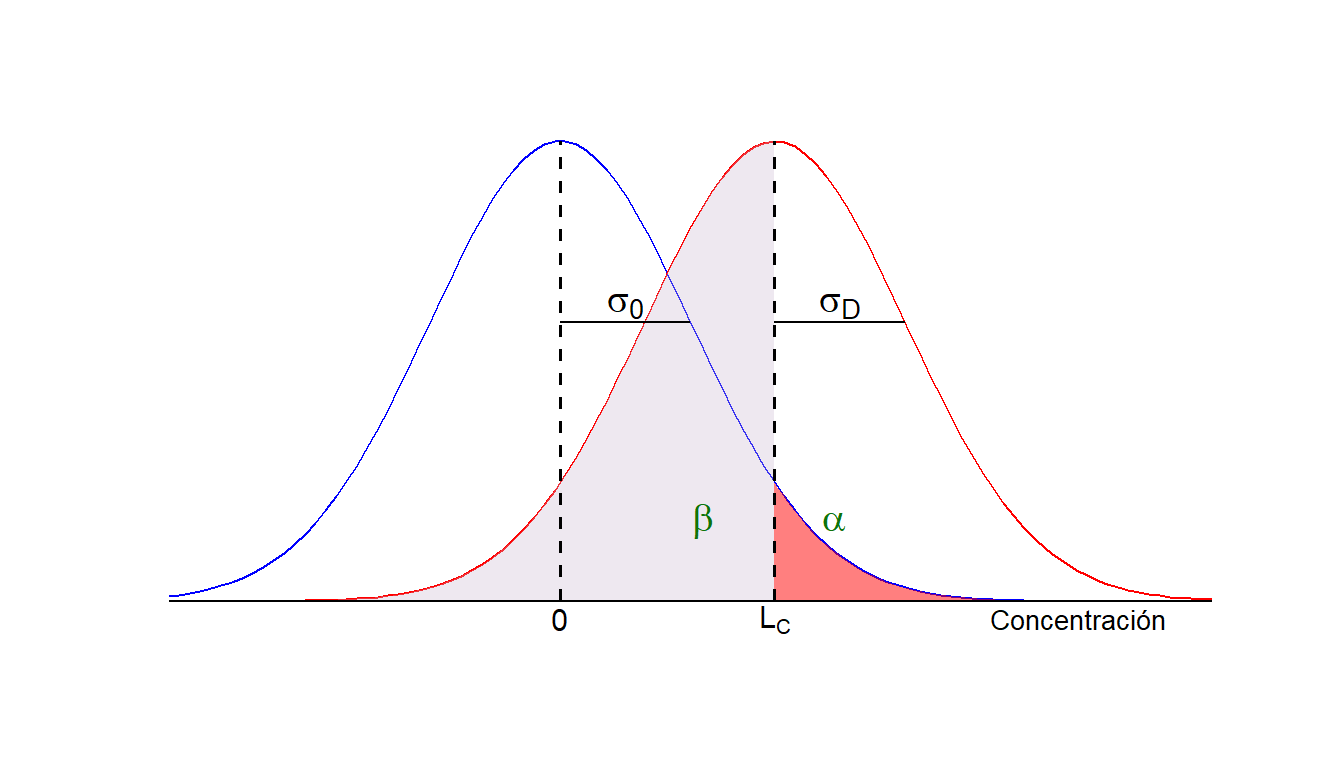
Figura 5.2: Nivel crítico y límite de detección para una probabilidad \(\alpha\). El riesgo de cometer un falso negativo es del 50%.

Las concentraciones se distribuirían aproximadamente alrededor de 2 ppb, mitad hacia arriba y mitad hacia abajo. ¿Cuál sería la consecuencia? Pues que aproximadamente en la mitad de los casos el laboratorio diría que no hay analito en la muestra, o que no puede detectarlo, puesto que las concentraciones caen por debajo del valor crítico, \(L_C\:\). ¿Cómo es posible? El laboratorio había asegurado que es capaz de detectar a un nivel de 2 ppb y ahora, a este nivel de concentración, se equivoca la mitad de las veces. Existe pues un riesgo de concluir erróneamente que el analito no está presente cuando en realidad si lo está. Como sabemos, dicha probabilidad, \(\beta\;\), es el error de tipo II o probabilidad de falso negativo.

Es nuevamente decisión del laboratorio la elección del valor de \(\beta\;\). ¿Podemos permitirnos un 50% de errores? En caso negativo, la única alternativa para reducir el riesgo de falsos negativos es aumentar el LOD, como en el ejemplo de la Figura 5.3.

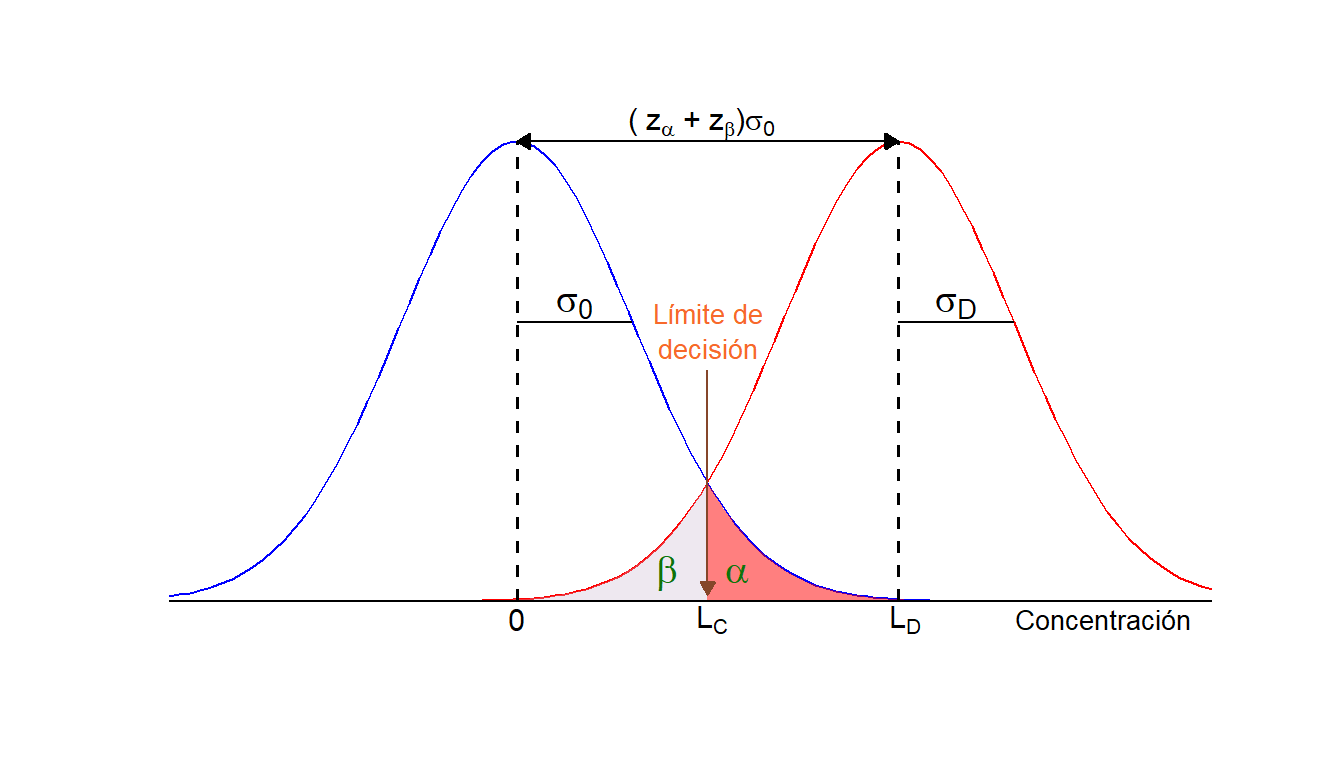
Figura 5.3: Nivel crítico y límite de detección para \(\alpha=\beta\).

Al aumentar el LOD el laboratorio se protege contra los falsos negativos. Imaginemos que ahora el LOD = 4 ppb. Claramente, si un cliente envía muestras conteniendo 4 ppb de analito, el laboratorio ahora corre un riesgo mucho menor de asegurar que el analito no está presente cuando en realidad sí lo está y a una concentración de 4 ppb.

5.3.2 Expresiones para el cálculo del valor crítico y del límite de detección

La decisión de si un determinado analito está presente o no en una muestra se basa en la comparación de la concentración predicha del analito con el nivel crítico, \(L_C\;\) , que se define como: \[\begin{align} \tag{5.2} L_C & = z_{\alpha}\sigma_0 \end{align}\] donde \(z_{\alpha}\;\) es el cuantil \(1-\alpha\) de la distribución normal estándar y \(\sigma_0\;\) es la desviación estándar de la concentración neta cuando el analito no está presente en la muestra (i.e, de la distribución del blanco). \(L_C\;\) se define para marcar un valor mínimo a partir del cual una concentración predicha se considera causada por el analito. De esta forma, existe un riesgo a de cometer un error de tipo I (o falso positivo). Sin embargo, si queremos mantener un riesgo (llamado \(\beta\;\)) pequeño de cometer un falso negativo, el LOD del método, \(L_D\;\), debe ser mayor. Así pues, tomando en consideración ambas probabilidades de error: \[\begin{align} \tag{5.3} L_D &=z_{\alpha}\sigma_0+z_{\beta}\sigma_D \end{align}\] donde \(z_{\beta}\;\) es el cuantil \(1-\beta\) de la distribución normal estándar y \(\sigma_D\;\) es la desviación estándar de la concentración neta cuando el analito está presente en la muestra al nivel del LDD. En las ecuaciones (5.2) y (5.3) se ha asumido que las concentraciones siguen una distribución normal con varianza conocida.

Como podemos notar, el valor del LOD depende de \(\alpha\;\) y de \(\beta\;\), y de los desvíos estándar \(\sigma_0\;\) y \(\sigma_D\;\) de las dos distribuciones gaussianas de la Figura 5.3. En general ambas probabilidades se toman iguales a \(0.05\;\), mientras que los desvíos estándar se suponen iguales (hipótesis de varianza constante). De esta modo, la ecuación (5.3) se transforma en: \[\begin{align} \tag{5.4} L_D &=2z_{\alpha}\sigma_0 \approx 3.3\sigma_0 \end{align}\]

Si no se conoce la varianza, debe estimarse a partir de análisis replicados. De la misma forma, los valores de \(z\;\), basados en distribuciones normales deben ser reemplazados por los correspondientes valores \(t\;\) de una distribución \(t\) con \(\nu=N-2\;\) grados de libertad. Así, (tomando \(\alpha = \beta\;\)) las expresiones para \(L_C\;\) y \(L_D\;\) (asumiendo varianza constante) son: \[\begin{align} \tag{5.5} L_C & =t_{\alpha,\nu}s_0 \end{align}\] \[\begin{align} \tag{5.6} L_D &= 2t_{\alpha,\nu}s_0 \end{align}\]

Como se puede observar, las ecuaciones para el cálculo de \(L_C\) y \(L_D\) son bastante simples. La dificultad mayor proviene de la estimación de \(s_0\). En la definición moderna, el LOD se calcula en función del desvío estándar de la concentración predicha para una muestra blanco, lo que significa que para obtener la estimación \(s_0\;\), utilizamos la fórmula de la Ecuación (4.5).

Si su ponemos que se analiza una muestra por triplicado (lo más usual es \(m = 3\;\)) en la que el analito no está presente (\(x_0=0\;\)), la Ecuación (4.5) se reduce a: \[\begin{align} \tag{5.7} S_{0} &= \frac{S_{y|x}}{\hat \beta_1} \sqrt{\frac{1}{3}+\frac{1}{N}+\frac{\bar{x}^2}{\sum\limits_{i=1}^N(x_i-\bar{x})^2}} \end{align}\]

5.4 Límite de cuantificación

Es la mínima concentración cuantificable en forma confiable. Este parámetro (LOQ) se toma como la concentración correspondiente a 10 veces el desvío estándar (en unidades de concentración) del blanco, con lo cual: \[\begin{align} LOQ & = 10s_0 \end{align}\] De este modo, coeficiente de variación (CV) para una concentración media igual al LOQ es del \(10\%\;\), nivel que se toma convencionalmente como el máximo RSD aceptable para cuantificar el analito en una muestra.

Las relaciones entre los tres niveles y su significado en el análisis se muestran en la Figura 5.4.

Figura 5.4: Representación gráfica de las decisiones tomadas en función de la concentración. (Currie 1968)

5.5 Rango dinámico

Se considera que va desde la menor concentración detectable (el LOD) hasta la pérdida de relación entre respuesta y concentración. El rango dinámico es también el rango de aplicabilidad de la técnica. En la zona de pérdida de la linealidad, podría aplicarse, en principio, un método de regresión polinómica para la calibración (o algún otro de naturaleza no lineal), de modo que nada impide que dicha zona sea utilizada con propósitos predictivos.

5.6 Rango lineal

Se considera que el rango lineal comprende desde la menor concentración que puede medirse (el LOQ) hasta la pérdida de la linealidad (ver Figura 5.5). Una manera conveniente de medir el cumplimiento de la linealidad es a través de la relación que existe entre la varianza de la regresión, medida por \(S_{y|x}^2\;\) (ver Ecuación (3.7)), y la del ruido instrumental, medida por \(S_y^2\;\) (ver Ecuación (5.1)). Si la primera es significativamente mayor que la segunda, se supone que hay causas de desvío del modelo lineal que son estadísticamente superiores al ruido en la respuesta. Para emplear esta prueba es esencial que se cumpla el supuesto bajo el cual se realiza el ajuste lineal, esto es, que los errores en concentración de calibrado sean menores que en respuesta. De lo contrario, se acumularían en \(S_{y|x}^2\;\) incertidumbres derivadas de la imprecisión en las concentraciones de los patrones, que nada tienen que ver con el ruido instrumental o la falta de linealidad. La prueba estadística para determinar si los datos se ajustan al modelo lineal utiliza el estadístico \(F\;\), cuyo valor observado, \(F_{obs}\;\), viene dado por: \[\begin{align} F_{obs} =\frac{S_{y|x}^2}{S_{y}^2}. \end{align}\] Este valor se compara con el cuantil \(1-\alpha\;\) de la distribución \(F_{N-2,N-k}\;\) (\(F\;\) con \(N-2\;\) y \(N-k\;\) grados de libertad).

Si \(F_{obs}<f_{\alpha;\;N-2,N-k}\;\) se rechaza la hipótesis de que los datos se comportan de manera lineal.

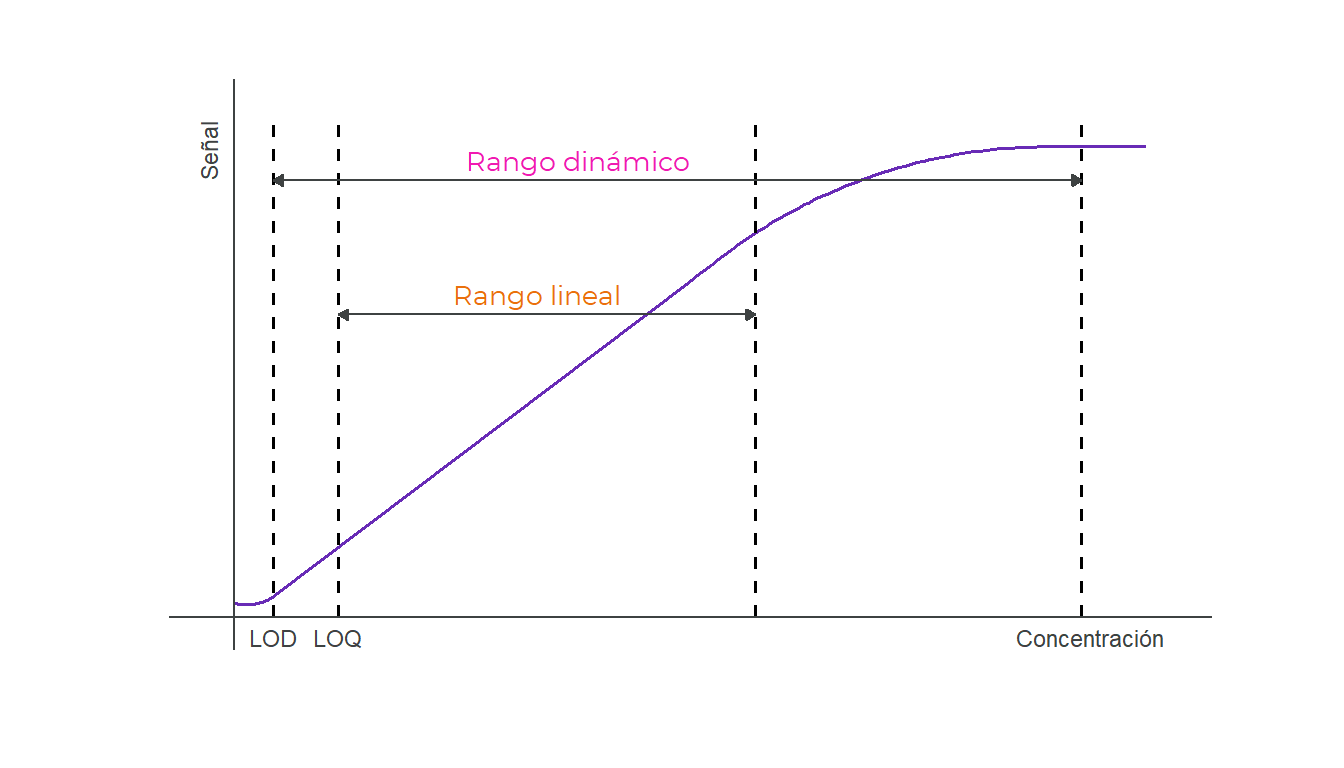
Figura 5.5: Rangos dinámico y lineal de un método analítico.

---

6 Ejemplo 1: resolución.

Enunciado

La reglamentación técnico-sanitaria para el abastecimiento y control de la calidad de las aguas potables de consumo público califica al zinc de componente no deseable y fija en un máximo tolerable de hasta 5000 microgramos por litro su concentración en el agua. La determinación de dicha concentración constituye un criterio orientado, entre otros, a la comprobación de la calidad del agua analizada.

Se determinó el contenido de Zn en diferentes muestras de aguas por espectrofotometría de absorción atómica. Para el calibrado se mide la absorbancia de una serie de disoluciones que contienen las siguientes concentraciones de Zn(II): 0.000, 0.010, 0.025, 0.050, 0.100, 0.150, 0.200 y 0.250 mg/L (ppm), obtenidas por dilución con agua destilada a partir de una disolución de Zn(II) de 5.0 mg/L.

La determinación de Zn(II) en las diferentes muestras de agua se realizó tomando 1 mL y diluyendo con agua desionizada hasta 100 mL y midiendo la absorbancia suministrada, excepto en el caso del agua de mar en que 0.1 mL de esta se diluyeron en un matraz de 100 mL.

Calcular la concentración de Zn(II) en las muestras a partir de los datos obtenidos en el calibrado (resumidos en la siente tabla).

Solución

ESQUEMA DEL EXPERIMENTO

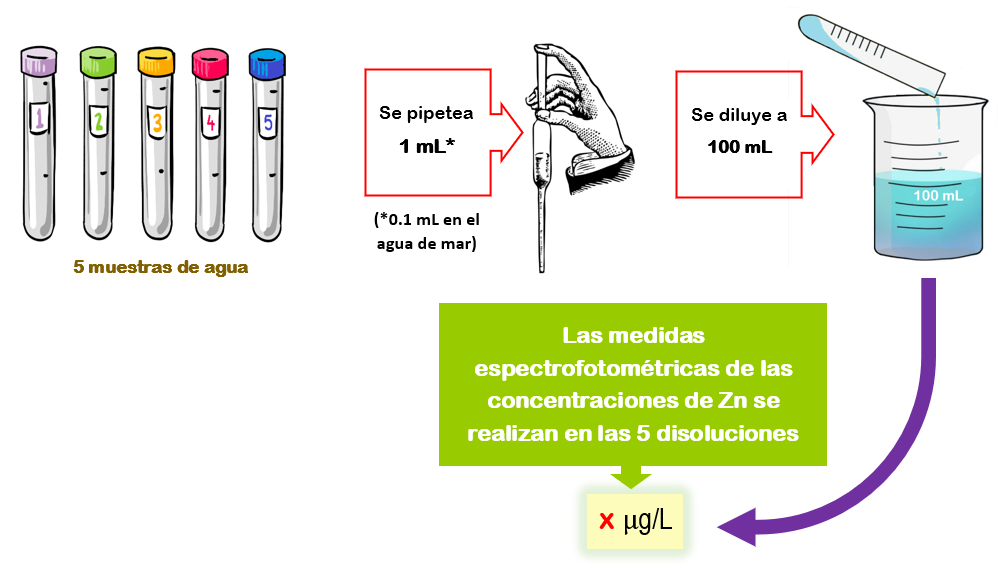
Recta de Calibrado.

Como lo haces siempre comencemos con un análisis exploratorio de los datos. Para esto, representemos graficamente los datos de calibración proporcionados en la Tabla 6.1.

Zn <- c(0.000, 0.010, 0.025, 0.050, 0.100, 0.150, 0.200, 0.250)
A1 <- c(0.000, 0.004, 0.003, 0.008, 0.020, 0.025, 0.036, 0.043)
A2 <- c(0.001, 0.001, 0.006, 0.011, 0.017, 0.029, 0.034, 0.041)
A3 <- c(0.002, 0.001, 0.005, 0.009, 0.019, 0.027, 0.035, 0.045)
mydata <- data.frame(A1,A2,A3,Zn)
mydata = tidyr::gather(mydata,"id", "value", 1:3) 
ggplot(mydata,aes(x=Zn, y=value)) +
  geom_point(size=3,color="blue3") +
  labs(x="Zn -patrón- (ppm)", y="Absorbancia") +
  theme_ipsum(
    base_size = 11.5,
    axis_title_size = 12,
    axis_title_just = "rt")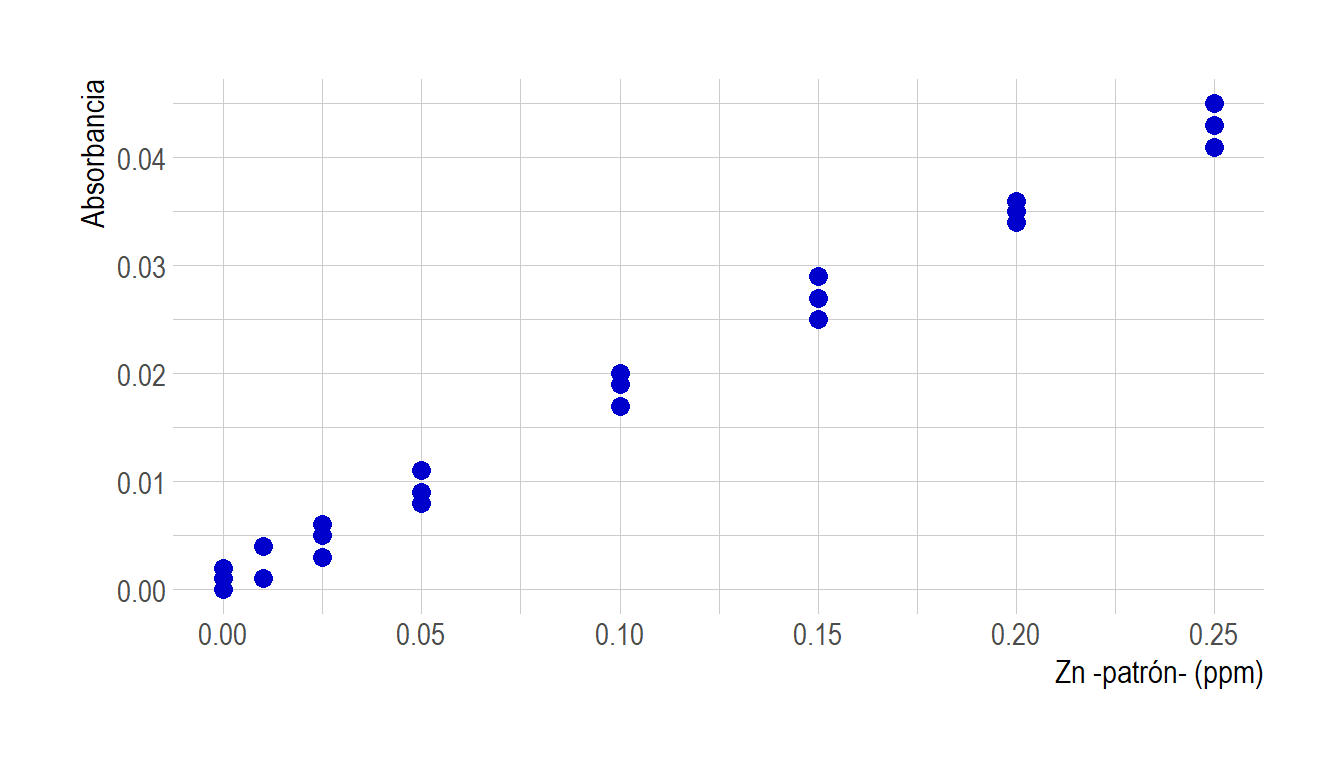

Figura 6.1: Gráfica de dispersión para los datos de análisis de aguas.

Según podemos observar en el gráfico, los puntos parecen estar linealmente relacionados en todo el rango medido (igualmente debemos chequearlo!). En efecto, se obtiene un valor de \(F_{obs}=0.818\) con un \(p-\)valor asociado de 0.675 (más adelante se muestran los cálculos en detalle)

Ajustemos entonces la recta de mínimos cuadrados ordinarios.

ajuste <- lm(value~Zn,data=mydata)
summary(ajuste)

## 
## Call:
## lm(formula = value ~ Zn, data = mydata)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -2.560e-03 -1.094e-03 -4.203e-05  1.122e-03  2.544e-03 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.0008001  0.0004386   1.824   0.0818 .  
## Zn          0.1710395  0.0033371  51.254   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.00143 on 22 degrees of freedom
## Multiple R-squared:  0.9917, Adjusted R-squared:  0.9913 
## F-statistic:  2627 on 1 and 22 DF,  p-value: < 2.2e-16

ggplot(mydata, aes(x=Zn, y=value))+ 
  geom_abline(intercept=coefficients(ajuste)[1],slope=coefficients(ajuste)[2], color="#e67e1b")+
  geom_point(size=3,color="blue3") +
  labs(x="Zn -patrón- (ppm)", y="Absorbancia") +
  theme_ipsum(
    base_size = 11.5,
    axis_title_size = 12,
    axis_title_just = "rt")

Figura 6.2: Gráfica de calibrado para los datos de análisis de aguas.

Tenemos entonces que, los estimadores de la pendiente y ordenada al origen son: \[\begin{align} \hat{\beta_1} &= 0.171\; (\pm 0.003)\\ \hat{\beta_0} &= 0.0008\;(\pm 0.0004) \end{align}\] y por lo tanto, la recta estimada es \(\hat{y} = 0.0008 + 0.171 x\;\;\) o, equivalentemente, \(\hat{\text{A}} = 0.0008 + 0.171\; \text{Zn}\;\).

Validación de los supuestos.

Linealidad.

medias <- with(mydata,tapply(value,Zn,mean))
var <- with(mydata,tapply(value,Zn,var))
ns <- with(mydata,tapply(value,Zn,length))
N <- sum(ns)
k <- length(ns)

sy <- sum((ns-1)*var)/(N-k)  # esta es la pooled
syx <- sigma(ajuste)
# Estadístico F ~ F_{N-2,N-k}
Fobs <- syx^2/sy
alpha <- 0.05
Fcrit <- qf(1-alpha,N-2,N-k)
Fobs>Fcrit  #FALSE

## [1] FALSE

pf(Fobs,N-2,N-k,lower.tail = FALSE)

## [1] 0.6749769

Como \(F_{obs}<f_{N-2,N-k}\), no rechazo la hipótesis nula de linealidad. (La conclusión es la misma, por supuesto, se consideramos que el \(p-\)valor es mayor que \(\alpha\))

Residuos.

par(mfrow=c(1,2))
plot(ajuste,c(1,2))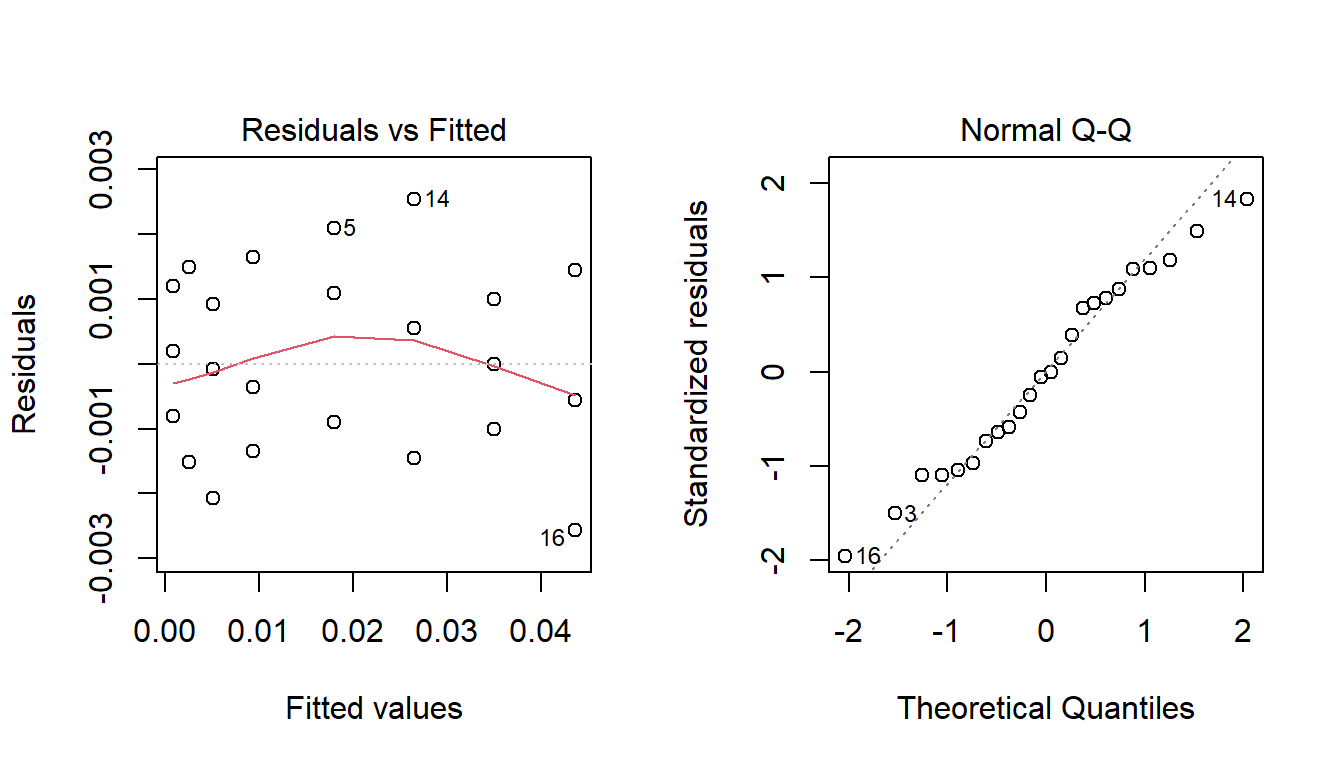

Figura 6.3: Análisis de residuos para Ejemplo 1.

ncvTest(ajuste)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.3042428, Df = 1, p = 0.58123

shapiro.test(ajuste$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  ajuste$residuals
## W = 0.97073, p-value = 0.6851

Analizamos también la existencia de datos atípicos (outliers).

outlierTest(ajuste)

## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
##     rstudent unadjusted p-value Bonferroni p
## 16 -2.110379           0.046993           NA

influenceIndexPlot(ajuste)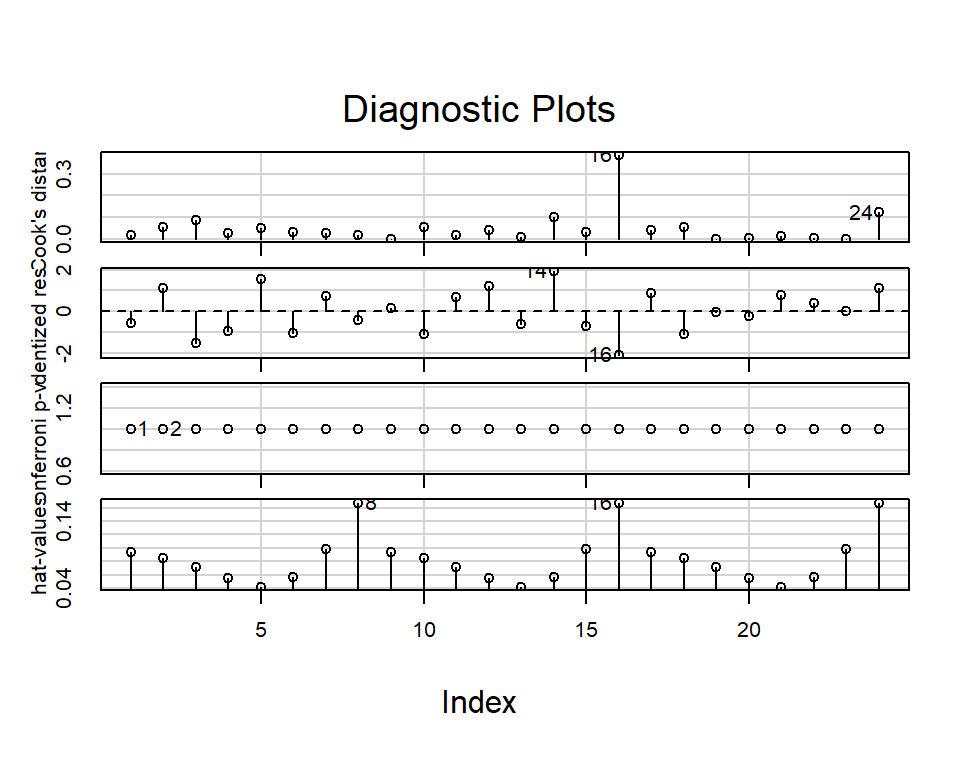

A partir de estos gráficos y de los resultados de los test, no parece haber problemas con los supuestos del modelo (normalidad y varianza constantes de los errores.)

Estimación de las concentraciones en muestras problema.

Tenemos entonces el modelo estimado a partir del cual vamos a estimar la concentración de zinc en cada una de las muestras de interés.

Muestra	Respuesta promedio (\(y_{inc}\))	Concentración predicha \((\hat{x}_{inc})\)	Error estándar \((S_{\hat{x}_{inc}})\)	\(CV(\%)=\frac{100\; S_{\hat{x}_{inc}}}{\hat{x}_{inc}}\)
Agua de grifo	0.015	0.083	0.005	6.176
Agua de río	0.030	0.173	0.005	3.082
Agua de pozo	0.008	0.040	0.005	13.059
Agua residual	0.040	0.227	0.006	2.511
Agua de mar	0.003	0.011	0.005	49.433

Puede notarse que las concentraciones predichas se acotaron a tres decimales, teniendo en cuenta sus desvíos estándar (que son todos aproximadamente 0.005 unidades). Notemos también que el coeficiente de variación (CV) es mucho mayor para la muestra de agua de mar, para la cual la concentración predicha es más chica. Esto está relacionado con la mínima concentración detectable por la técnica, que se considerará a continuación.

Para calcular las concentraciones de Zn en las muestras originales, hay que tener en cuenta que el volumen de muestra tomado (1mL en todas las aguas excepto en la de mar, de la que se tomaron 0.1 mL) se aumentó a 100 mL. Hubo pues, una dilución.

Con los valores obtenidos a partir de la recta de calibrado, hemos calculado la concentración de Zn en las disoluciones diludas finales, no en las originales. Para conocer entonces las concentraciones en las muestras originales, deberemos aplicar la fórmula \[\begin{align} V_{inicial}\times c_{inicial} = V_{final}\times c_{final} \end{align}\] En cada caso tenemos los valores de \(c_{final}\;\) y queremos \(c_{inicial}\;\).

Por otra parte, estas concentraciones (finales) predichas están en ppm o mg/L (porque en esas unidades vienen dadas las concentraciones en los patrones). Luego, si queremos comparar el valor predicho para el contenido de zinc en agua potable con el valor reglamentado por la OMS, deberíamos unificar las unidades. Recordemos que el máximo permitido para el contenido de zinc en aguas para consumo humano es de 5000 \(\mu\)g/L, lo que es equivalente a 5 mg/L.

Equivalencias
1 mL \(\times\;c_{inicial}=\) 100 mL \(\times\) 0.083
1 mL \(\times\;c_{inicial}=\) 100 mL \(\times\) 0.173
1 mL \(\times\;c_{inicial}=\) 100 mL \(\times\) 0.040
1 mL \(\times\;c_{inicial}=\) 100 mL \(\times\) 0.227
1 mL \(\times\;c_{inicial}=\) 100 mL \(\times\) 0.011

Como podemos ver, la concentración en la muestra de agua de grifo resulta 8.30 mg/L \(\pm\) 0.05 mg/L, que mayor al límite legal señalado por la OMS (5 mg/L). Por supuesto que esta conclusión es solamente exploratoria, para poder responder estadísticamente a la cuestión (por ejemplo para ver si se autoriza o no el consumo humano del agua) deberíamos hacer un test de hipótesis.

Tarea para el hogar: Averiguar y comentar sobre los niveles de zinc encontrados en las muestras restantes si son niveles aceptables o no (por ejemplo: máximo permitido en aguas residuales)

Cálculo de las cifras de mérito.

1 Sensibilidad:

En el presente ejemplo la sensibilidad está dada por \(SEN=0.171\;\) mg\(^{-1}\)L (la absorbancia no tiene unidades)

2 Sensibilidad analítica:

Para el cálculo de la sensibilidad analítica, necesitamos una estimación del ruido instrumental. Como vimos, hay dos métodos a partir de los cuales podemos estimar dicho valor:

• a través de los desvíos de las réplicas de las mediciones de calibrado respecto de sus promedios:

# Las concentraciones y las señales medidas
Zn <- c(0.000, 0.010, 0.025, 0.050, 0.100, 0.150, 0.200, 0.250)
A1 <- c(0.000, 0.004, 0.003, 0.008, 0.020, 0.025, 0.036, 0.043)
A2 <- c(0.001, 0.001, 0.006, 0.011, 0.017, 0.029, 0.034, 0.041)
A3 <- c(0.002, 0.001, 0.005, 0.009, 0.019, 0.027, 0.035, 0.045)
y <- c(A1,A2,A3)
# Calculamos las medias por nivel de concentración
medias <- colMeans(rbind(A1,A2,A3))
N <- length(y)
k <- length(Zn)
# calculamos el desvío
Sy <- sqrt(sum((y-rep(medias,3))^2/(N-k)))

Por lo tanto, el nivel de ruido instrumental obtenido por este método, es \(S_y=0.0016\).

• a través del desvío estándar de los residuos de la regresión lineal.

Si nos fijamos en la salida de R (summary(ajuste)) tenemos que \(S_{y|x}=0.0014\).

Tenemos pues, que ambos métodos conducen a estimaciones de ruido similares. Utilizando 0.0014 como niel de ruido, podemos calcular la sensibilidad analítica como \(\gamma =\frac{0.171}{0.0014}=119.6197\;\) mg\(^{-1}\)L. El informe correcto deberá tener 3 CS porque la pendiente tiene 3 CS (mientras que \(S_{y|x}\) tiene 4 CS). Luego, \(\gamma=120\;\) mg\(^{-1}\)L

3 Límite de detección:

Para determinar el LOD necesitamos calcular \(S_0\), el desvío estándar en la concentración predicha para una muestra blanco (Ecuación (5.7))

x <- rep(Zn,3)
Syx <- sigma(ajuste)
beta1hat <- coefficients(ajuste)[2]
N <- length(x)
xbarra_cuad <- mean(x)^2
Sxx <- sum((x-mean(x))^2)
S0 <- Syx/beta1hat*sqrt(1/3+1/N+xbarra_cuad/Sxx)
alpha <- 0.05
LOD <- 2*qt(1-alpha,N-2)*S0

Resulta entonces que \(LOD=2 t_{0.95,22} S_0 = 0.019\;\;\) ppm.

Este resultado se interpreta diciendo que la técnica es capaz de detectar al analito cuando está en concentraciones superiores a \(0.019\;\) ppm.

4 Límite de cuantificación:

El límite de cuantificación se calcula como \(0.05\) ppm, y se interpreta como la menor concentración que se puede cuantificar, esto es, en el intervalo de concentración entre \(0.02\) y \(0.05\) la técnica puede detectar pero no cuantificar el analito.

Con esto se prueba que la concentración predicha para el agua de mar (así como también para el agua de pozo) está por debajo del \(LOQ\), lo cual explica el alto valor \(CV\) para esas predicciones.

5 Rango dinámico:

La máxima concentración probada fue \(0.250\). Hasta esa concentración, existe un cambio en la respuesta al cambiar la concentración, por lo que, a falcta de mayor información, supondremos que el rango dinámico está entre \(0.02\) y \(0.25\) .

6 Rango lineal:

Finalmente, para calcular el rango lineal, necesitamos el valor de \(F_{obs}=\frac{S_{y|x}^2}{S^2_y}\) que, como ya vimos, es igual a \(0.818\) con un \(p-\)valor asociado de \(0.675\) indicando que, en el rango de concentraciones medido, se mantiene la linealidad. De este modo, tenemos que el rango lineal está entre \(0.05\) y \(0.25\).

---

7 Metodo de las adiciones de estándar.

La matriz es todo lo que hay en el problema, que no sea el analito. Se define el efecto de matriz como el cambio que experimenta una señal analítica por todo lo que hay en la muestra excepto el analito.

La preparación de estándares que reproduzcan la composición de la muestra es muy complicada cuando se trata del análisis de muestras complejas (suelos, minerales, sangre completa, orina, etc.) ya que en este tipo de muestras, usualmente, los componentes de la matriz afectan las medidas de la señal analítica ya sea por exceso o por defecto.

Con el objetivo de minimizar los efectos de la matriz, se utiliza el método de adición de estándar en el que la muestra se utiliza como una especie de “blanco” al que se añade más analito. Para ello, se añaden cantidades conocidas y crecientes del analito a determinar a alícuotas de la muestra desconocida y todas se diluyen al mismo volumen final. Posteriormente, se procede a determinar la señal de todas estas soluciones (las muestras enriquecidas y la desconocida) y se representa gráficamente la señal analítica en función de la concentración del estándar añadido.

Este método no elimina las interferencias, solo las compensa ya que se obtienen todas las señales analíticas bajo las mismas condiciones.

La Figura 7.1 muestra un fuerte efecto de matriz en el análisis de perclorato (ClO\(_4^-\;\) ) por espectrometría de masas. Se tiene que controlar el perclorato en agua potable porque por encima de \(18\;\) µg/L puede reducir la producción de hormonas tiroideas. Disoluciones patrón de ClO\(_4^-\;\) en agua pura (calidad reactivo) origina la curva de calibrado superior que aparece en la Figura 7.1. La respuesta a disoluciones patrón con la misma concentración de ClO\(_4^-\;\) en agua subterránea es 15 veces menor, como se ve en la curva inferior. La disminución de la señal del ClO\(_4^-\;\) es el efecto de matriz atribuido a otros aniones presentes en el agua subterránea.

Figura 7.1: Curvas de calibrado del perclorato en agua pura y en agua subterránea. (Harris 2016).

Dado que diferentes aguas subterráneas tienen diferentes concentraciones de muchos aniones, no es posible construir una curva de calibrado para este análisis que pueda aplicarse a más de una determinada agua subterránea. Y de ahí que se requiera el método de la adición de estándar. Si se añade un pequeño volumen de una disolución concentrada de patrón al problema desconocido, no se modifica mucho la concentración de la matriz. El supuesto que se hace en el método de adición de estándar es que la influencia de la matriz es la misma en el analito añadido que en el analito original de la muestra problema.

En la Figura 7.2 se ilustra una manera de llevar a cabo el método de adición de estándar. Se pipetea en cada matraz volumétrico volúmenes iguales de la muestra problema. A continuación se añaden volúmenes crecientes de estándar a cada matraz. Finalmente, se diluye cada matraz hasta el enrase. Cada matraz contiene, pues, la misma concentración de muestra problema y diferentes concentraciones de estándar.

Figura 7.2: Análisis aplicando el método de adiciones de estándar. Inicialmente en cada matraz añade el mismo volumen de muestra (por ej. 5 mL). Se adiciona 0, 5, 10, 15 y 20 mL de estándar. Se enrasa a Volumen Final (por ej. 50 mL). (Harris 2016).

7.1 Procedimiento

El procedimiento experimental para un análisis de adiciones de estándar es el siguiente. Se añaden volúmenes iguales, \(V_x\), de una solución de analito de concentración desconocida, \(c_x\), a una serie de matraces volumétricos de volumen \(V_t\). Se utiliza una solución estándar de analito de concentración \(c_s\) para enriquecer los matraces utilizando un volumen diferente, \(V_s\), en cada caso. Normalmente, se utilizan incrementos regulares de \(V_s\). A continuación, se añaden los reactivos adecuados y finalmente, cada matraz aforado se llena hasta el enrase con el disolvente apropiado. De esta manera, la concentración del analito en cada uno de los matraces aforados es \[\begin{align} c_{analito} &= \frac{c_s V_s}{V_t} + \frac{c_x V_x}{V_t} \end{align}\]

Usando el método de adiciones de estándar, dentro del rango de calibración lineal, se supone que la señal de respuesta, \(R\), del instrumento de análisis es directamente proporcional a la concentración de analito; es decir \[\begin{align} \tag{7.1} R &= k\Big(\frac{c_s V_s}{V_t} + \frac{c_x V_x}{V_t}\Big) = k\Big[\frac{V_x}{V_t}\Big(\frac{c_s V_s}{V_x}\Big) + \frac{c_x V_x}{V_t}\Big] \end{align}\]

Definiendo \(c'\) como el aumento en la concentración de analito en el volumen de muestra original (\(V_x\)) debido a los estándares añadidos, tenemos que \[\begin{align} c' &= \frac{c_s V_s}{V_x} \end{align}\]

Por consiguiente, la Ecuación (7.1) puede escribirse en forma lineal \[\begin{align} \tag{7.2} R &= m c' + b \end{align}\] con pendiente \[\begin{align} \tag{7.3} m & = k\frac{V_x}{V_t} \end{align}\] y ordenada al origen \[\begin{align} \tag{7.4} b &= k\frac{c_xV_x}{V_t} \end{align}\]

La abscisa al origen, o intercepto con eje \(x\;\), \(c'_0\;\), ocurre cuando \(R=0\;\) y \(b=-mc'_0\;\), de donde podemos escribir \(c'_0=-\frac{b}{m}\;\).

Sustituyendo la pendiente y la ordenada al origen con las Ecuaciones (7.3) y (7.4) respectivamente, tenemos que la concentración en la muestra incógnita, \(c_x\;\), es \[\begin{align} \tag{7.5} c_x &= -c'_0 = \frac{b}{m} \end{align}\]

Por lo tanto, usando esta relación, la concentración de analito en la muestra problema se puede obtener a partir de la regresión de \(R\;\) en \(c'\;\) (i.e. la señal de instrumento en función de las cantidades de estándar añadidas) por extrapolación el punto de corte con el eje \(c'\;\). Veamos ahora cuál es la precisión de \(c_x\;\), expresada por el error estándar \(S_{c_x}\;\).

7.2 Error de la estimación

En el siguiente desarrollo, las coordenadas \((c',R)\;\) se reemplazarán por las más convencionales \((x,y)\;\) y consideremos que tenemos \(N\;\) puntos \((x_i,y_i)\,\) en el gráfico de calibración de adición de estándar.

Como vimos en la sección precedente, \(c_x =f(b,m) = \frac{b}{m}\;\). Dado que \(m\;\) y \(b\;\) están sujetos a error (Sección 3.2), el valor calculado también lo estará. Entonces, para estimar el error de esta estimación, podemos propagar errores pero deberemos consider que \(m\;\) y \(b\;\) no son independientes (recordar que en la deducción que hicimos de propagación de errores en expresiones multiplicativas, un supuesto imporante que consideramos fue que los estimadores eran estadísticamente independientes) (En realidad nos alcanza con que sean no correlacionados).

1. En este caso podemos considerar que \(c_x\;\) es función de la ordenada al origen y de la pendiente a través de la función \(f(x,y) = \frac{x}{y}\;\). Luego:

• \(\frac{\partial f}{\partial x} = \frac{1}{y}\;\).

• \(\frac{\partial f}{\partial y} = -\frac{x}{y^2}\;\).

Luego el desarrollo en Taylor de primer orden de la \(f\;\) resulta \[\begin{align} c_x \approx \frac{b}{m} +\frac{1}{m}(b-\alpha) -\frac{b}{m^2}(m - \beta) \end{align}\]

2. Calculado la varianza en ambos miembros tenemos \[\begin{align} Var(c_x) &\approx \frac{1}{m^2}Var(b) +\frac{b^2}{m^4}Var(m) +2Cov(\frac{1}{m}b,-\frac{b}{m^2}m)\\ &= \frac{1}{m^2}\frac{S_{y|x}^2\sum\limits_{i}x_i^2}{N\sum\limits_{i}(x_i-\bar{x})^2} +\frac{b^2}{m^4}\frac{S_{y|x}^2}{\sum\limits_{i}(x_i-\bar{x})^2} +2\frac{b}{m^3}\frac{S_{y|x}^2\bar{x}}{\sum\limits_{i}(x_i-\bar{x})^2}\\ &= \frac{S_{y|x}^2}{m^2}\left[\frac{\sum\limits_{i}x_i^2}{N\sum\limits_{i}(x_i-\bar{x})^2} +\frac{b^2}{m^2}\frac{1}{\sum\limits_{i}(x_i-\bar{x})^2} +2\frac{b}{m}\frac{\bar{x}}{\sum\limits_{i}(x_i-\bar{x})^2}\right]\\ &= \frac{S_{y|x}^2}{m^2}\left[\frac{m^2\sum\limits_{i}x_i^2+Nb^2+2Nmb\bar{x}}{Nm^2\sum\limits_{i}(x_i-\bar{x})^2}\right]\\ &= \frac{S_{y|x}^2}{m^2}\left[\frac{m^2\sum\limits_{i}(x_i-\bar{x})^2+Nm^2\bar{x}^2+Nb^2+2Nmb\bar{x}}{Nm^2\sum\limits_{i}(x_i-\bar{x})^2}\right]\\ &= \frac{S_{y|x}^2}{m^2}\left[\frac{1}{N}+\frac{(m\bar{x}+b)^2}{m^2\sum\limits_{i}(x_i-\bar{x})^2}\right]\\ &= \frac{S_{y|x}^2}{m^2}\left[\frac{1}{N}+\frac{\bar{y}^2}{m^2\sum\limits_{i}(x_i-\bar{x})^2}\right] \end{align}\]

De esta manera, la fórmula para el error estándar de la concentración en la muestra problema resulta: \[\begin{align} \tag{7.6} S_{c_x} = \frac{S_{y|x}}{m}\sqrt{\frac{1}{N}+\frac{\bar{y}^2}{m^2\sum\limits_{i}(x_i-\bar{x})^2}} \end{align}\]

Notar que esta expresión no es igual a la que obtuvimos antes cuando calculamos la predicción de una concentración a partir del modelo de calibración (Ecuación (4.4)). Esto se debe a que, en este caso, la cantidad no se predice a partir de una valor medido de \(y\;\), sino que que extrapolamos la curva de calibración al corte con el eje \(x\;\) y por lo tanto el valor de \(y\;\) para la incógnita es \(0\;\) y el término \(1/m\;\) está ausente.

7.3 Ejemplo 3 : Adición de estándar.

Enunciado

Se pipetearon alícuotas de \(10.00\;\) mL de una muestra de agua natural en matraces aforados de \(50.00\;\) mL. A cada uno se le añadieron exactamente \(0.00,\; 5.00,\; 10.00,\; 15.00 \;\;\) y \(20.00\;\) mL de una solución estándar que contenía \(11.1\;\) ppm de Fe\(^{3+}\;\), seguido de un exceso de ión tiocianato para dar el complejo rojo Fe(SCN)\(^{2+}\;\). Después de la dilución a volumen, se midieron las absorbancias a una longitud de onda analítica apropiada. Las lecturas de absorbancia, \(R\;\), para las cinco soluciones fueron \(0.240,\; 0.437,\; 0.621,\; 0.809\;\;\) y \(1.009\;\), respectivamente.

(a) ¿Cuál es la concentración de Fe\(^{3+}\;\) en la muestra de agua?

(b) Calcule la desviación estándar en la concentración de Fe\(^{3+}\;\).

---

Solución

En este ejemplo, \(c_s=11.1\;\) ppm, \(V_x = 10.00\;\) mL y \(V_t =50.00\;\) mL.

Grafiquemos en primer lugar los datos. (Figura 7.3)

Figura 7.3: Gráfico de calibración lineal para el método de adiciones estándar.

Aquí debemos tener cuidado en que necetitamos la regresión de la absorbancia \(R\;\) en \(c'\;\) que es el aumento de concentración de analito en el volumen de muestra original (\(V_x\)) debido a los estándares añadidos, que como vimos antes, \(c'= \frac{c_s V_s}{V_x}\;\).

Al aplicar la regresión lineal al conjunto de datos \((R, c')\;\) se obtiene \(m = 0.0344\;(\pm 0.0003)\;\) , \(b = 0.241\;(\pm 0.004)\;\) y, el cociente entre estas dos cantidades, proporciona la concentración de Fe\(^{3+}\;\) en la muestra de agua de \(c_x\;\) (o \(c_{Fe}\;\)) \(= 7.008691\;\) ppm. Para expresar correctamente el resultado de esta estimación, necesitamos calcular el error asociado a la misma (expresado por el desvío estándar) utilizando la Ecuación (7.6).

Vs <- seq(0,20,by=5)
absorbancia <- c(0.240, 0.437, 0.621, 0.809, 1.009)
cs <- 11.1
Vx <- 10.00
aumento <- cs*Vs/Vx
ajuste <- lm(absorbancia~aumento)
m <- coefficients(ajuste)[2]
b <- coefficients(ajuste)[1]
cx <- b/m
Sxx <- sum((aumento-mean(aumento))^2)
N <- length(Vs)
Se <- sigma(ajuste)
desvio_cx <- Se/m*sqrt(1/N+mean(absorbancia)^2/(m^2*Sxx)) 

Por lo tanto, la concentración de Fe\(^{3+}\;\) en la muestra es \(7.01\;\pm\;0.16\;\) ppm.

---

8 Exactitud y comparación de dos métodos analíticos.

En esta sección vamos a ver una aplicación de la regresión lineal al análisis de la exactitud de un método analítico y para la comparación de dos métodos analíticos diferentes.

Para el estudio de la exactitud de un método analítico, es usual preparar una serie de patrones con concentraciones conocidas del analito, diferentes a las utilizadas en la etapa de calibración. Luego se determina la concentración del analito en cada uno de ellos por interpolación en la recta de calibrado, y se analiza la exactitud de la determinación a través de la recuperación de las concentraciones nominales del analito.

Por otro lado, cuando se desean comparar dos métodos analíticos, se determina, por ambos métodos, el contenido de un analito en una serie de muestras en las que su concentración es variable (dentro del rango lineal de cada uno de ellos).

En ambos casos se trata de comparar pares de valores que idealmente serían iguales, y estudiar el posible desvío de esta situación ideal, en un contexto estadístico y con un cierto nivel de confianza.

8.1 Exactitud de un método analítico.

Si se dispone de una serie de patrones de concentración conocida para la validación de un método analítico, se procede del modo siguiente. En primer lugar se miden sus respuestas, incluyendo réplicas de cada medición (usualmente cada patrón se mide por triplicado). Se estima la concentración a partir de cada respuesta analítica, se promedian los valores para cada nivel y se calcula el desvío estándar asociado. Luego se realiza una regresión lineal de los promedios en función de las concentraciones nominales de cada nivel.

Una aclaración sobre notación: En lo que resta de la sección, vamos a llamar:

• \(X\) a la concentración nominal de cada nivel,
• \(Y\) a la concentración promedio predicha para las réplicas de cada nivel,
• \(r\) es el número de réplicas en cada patrón,
• \(q\) el número de niveles de validación estudiados (i.e. la cantidad de patrones utilizados en el estudio de validación),
• \(s_{y_i}\) el desvío estándar en la señal para cada nivel de concentración (\(x_i\)), por lo tanto tenemos \(q\) desvíos estándar, y los mismos están dados por: \[\begin{align} s_{y_i} &= \sqrt{\frac{\sum\limits_{j=1}^r(y_{ij}-\bar{y}_i)^2}{r-1}} \end{align}\] donde \(y_{ij}\) es la concentración predicha para el patrón \(i\) en la réplica \(j\) e \(\bar{y}_i\) es el promedio de las \(r\) réplicas para el nivel \(i\).

Una observación importante que debemos hacer es que para realizar un estudio por regresión lineal simple un supuesto importante es es que la varianza de la variable \(Y|X\) es constante (homocedasticidad).

En la calibración de datos analíticos se supone que la distribución del ruido instrumental es constante a lo largo del rango de calibración, o en otras palabras, que la respuesta analítica es homocedástica. Esto no es necesariamente cierto, sin embargo, cuando la variable \(Y\) es la concentración predicha para patrones de validación, y no la respuesta analítica.

Como lo hemos estudiado (Sección 4), el desvío estándar en la concentración predicha mediante una recta de calibrado no es constante para diferentes muestras, sino que varía con la concentración del analito. Es decir que, en principio, la variable \(Y\) que estamos considerando ahora no es homocedástica. En estos casos, se recomienda realizar una regresión lineal mediante cuadrados mínimos ponderados (WLS, por weighted least squares) y no una regresión ordinaria (OLS). Por supuesto que primero debemos verificar si la varianza puede considerarse o no constante para luego decidir que regresión debemos ajustar a los datos.

En las unidades de Intervalo de confianza y Test de hipótesis bajo normalidad, ya hemos estudiado cómo decidir si dos varianzas pueden considerarse iguales o no. La idea aquí es utilizar ese mismo test, pero considerando la máxima y la mínima varianza muestral (¿por qué?). De este modo, el estadístico \(F\) a utilizar será \[\begin{align} F=\frac{\max(s_{y_i}^2)}{\min(s_{y_i}^2)} \end{align}\] que, bajo la hipótesis nula de igualdad de varianzas poblacionales, tiene distribución aproximadamente \(F_{r-1,r-1}\) (a diferecia del estadístico que utilizamos para comparar dos varianzas, aquí tenemos el cociente entre dos de los que se denominan “estadísticos de orden”, y por este motivo la distribución no es exactamente una \(F\)). El valor del estadístico calculado con la muestra se compara con el cuantil \(1-\alpha\) de la distribución correspondiente. Si \(F_{obs}>f_{1-\alpha;r-1,r-1}\) entonces rechazamos la hipotesis nula y en tal caso lo recomendable es utilizar WLS para estimar el modelo de regresión.

Un estudio detallado de como se obtienen las estimaciones de los parámetros \(\beta_0\) y \(\beta_1\) utilizando WLS se escapa del alcance de este curso, pero nos parece importante (e interesante!) mencionarlo para futuras referencias.

8.1.1 Región de confianza cuando las varianzas son constantes.

Consideremos primero el caso en que el test de igualdad de varianza no conduce a rechazar la hipótesis nula y, por o tanto, pudimos obtener los estimadores de \(\beta_0\) y \(\beta_1\) vía OLS. ¿Cómo podemos hacer para determinar si las concentraciones estimadas de los patrones de validación se diferencian estadísticamente (o no), de las nominales?

Pensemos… En el caso ideal, el valor de concentración estimado debería estar muy cerca del verdadero valor (valor nominal) del estándar de validación. Si esto fuera cierto, ¿cómo les parece que sería el gráfico de puntos concentración estimada versus concentración nominal?

Tiene sentido pensar que, en tal caso, los puntos en dicho gráfico deberían estar prácticamente sobre la recta identidad, ¿verdad? Bueno, eso es justamente lo que tenemos que chequear. Es decir, debemos considerar el intervalo de confianza conjunto para la pendiente y la ordenada al origen. Ya vimos (Sección 3.3) que dicho intervalo conjunto es una región en el plano de las dos variables (pendiente y ordenada al origen) que tiene forma elíptica. Por este motivo, la prueba estadística correcta consiste en investigar si el punto (1,0) está contenido en la región elíptica de confianza conjunta de la pendiente y la ordenada al origen.

8.1.2 Regresión ponderada

Si los datos no cumplen con la prueba de varianza constante, el análisis de los datos de validación debe hacerse mediante regresión lineal ponderada. Como ya lo hemos dicho, no vamos a hacer un estudio en profundidad de este caso, pero veamos como cambian las estimaciones cuando usamos regresión con pesos.

En este caso, las estimaciones de la pendiente y la ordena al origen se calculan minimizando la siguiente suma ponderada de cuadrados \[\begin{equation} \tag{8.1} SSE_w = \sum\limits_{i=1}^{q}w_i(y_i-\hat{y}_i)^2 \end{equation}\] donde \(w_i\) son los pesos o ponderaciones aplicado a cada punto de la regresión, \(q\) es la cantidad total de puntos (los niveles de validación), \(y_i\) es el valor de la variable \(Y\) en cada punto (i.e promedio \(\bar{y}_i\) de las \(r\) réplicas del nivel \(i\)) e \(\hat{y}_i\) es el valor ajustado por la recta.

En la regresión de mínimos cuadrados ponderados, el problema de la heterocedasticidad se mitiga introduciendo factores de ponderación inversamente proporcionales a la varianza: \[\begin{equation*} w_i = \frac{1}{s_{y_i}^2} \end{equation*}\]

El efecto concreto del pesado de los datos en forma inversamente proporcional a su variancia es dar mayor contribución, en la regresión, a los datos más precisos, y comparativamente menor peso a los menos precisos. Esto significa que queremos que la recta calculada pase más cerca de estos puntos más precisos que de los puntos menos precisos. La pendiente y la ordenada al origen vienen dadas por: \[\begin{align} \hat{\beta}_1 & = \frac{\sum\limits_{i=1}^{q}w_i(x_i-\bar{x}_{w})(y_i-\bar{y}_w)}{\sum_{i=1}^qw_i(x_i-\bar{x}_w)^2} \\ \hat{\beta}_0 & = \bar{y}_w-\hat{\beta_1}\bar{x}_w \end{align}\] donde \(x_i\) es la concnetración (nominal) de cada uno de los \(q\) patrones de validación, y \(\displaystyle \bar{x}_w=\frac{\sum w_ix_i}{\sum w_i}\) y \(\displaystyle \bar{y}_w=\frac{\sum w_iy_i}{\sum w_i}\).

En el método WLS \(s_{y|x}\) (desvío estándar de los residuos de la regresión) está dado por: \[\begin{align} s_{y|x} = \sqrt{\frac{\sum_{i=1}^q w_i(y_i-\hat{y}_i)^2}{q-2}} \end{align}\] donde \(y_i\) es la respuesta experimental e \(\hat{y}_i\) es la respuesta estimada en cada punto.

8.1.3 Región de confianza en el caso de varianza no constante.

Cuando se aplica el método WLS para determinar \(\hat \beta_0\) y \(\hat{\beta}_1\), la prueba de exactitud del método analítico es idéntica a la estudiada en el caso OLS, excepto que la ecuación que describe la elipse de confianza conjunta es: \[\begin{equation*} \frac{(\beta_1-\hat{\beta}_1)\sum\limits_{i=1}^q w_i +2(\beta_0-\hat{\beta}_0)(\beta_1-\hat{\beta}_1)\sum\limits_{i=1}^q w_ix_i +(\beta_0-\hat{\beta}_0)^2\sum\limits_{i=1}^q w_ix_i^2}{2 S_{y|x}^2}\leq F_{\alpha; 2, N-2} \end{equation*}\]

8.1.4 Ejemplo 3 Estudio de exactitud:

Enunciado:

La Tabla 8.1 muestra datos para analizar la exactitud de un método analítico. Determine si el método es exacto mediante regresión lineal y estudio de la región eliptica de confianza conjunta para \(\beta_0\) y \(\beta_1\).

---

Solución:

Lo que primero debemos fijarnos es si debemos justar el modelo mediando OLS o WLS.

Test de varianza constante.

La prueba, como vimos, se basa en el estadístico \(F=\frac{\max(s_{y_i}^2)}{\min(s_{y_i}^2)}\). Según los datos proporcionados en la Tabla 8.1 \(\max(s_{y_i}^2)=0.06^2\;\) y \(\min(s_{y_i}^2)=0.02^2\). Luego, el valor del estádistico observado en la muestra es\(F_{obs}=\frac{0.0036}{0.0004}=9\). Este valor observado debemos compararlo con el cuantil \(1-\alpha\) de la distribución \(F_{4,4}\). Vamos a utilizar \(\alpha=0.05\) y por lo tanto \(f_{0.05;4,4}=6.39\). Como \(F_{obs}>f_{0.05;4,4}\), rechazamos la hipotesis nula de varianzas constantes. Luego debemos emplear el método WLS para el análisis de exactitud por regresión lineal.

En R podemos hacerlo agregando el argumento weights a la función lm().

nominal <- c(0.05, 5.16, 9.91, 14.90, 19.80, 24.90, 30.00)
predicha <- c(0.06, 5.02, 10.00, 15.20, 19.90, 25.00, 30.00)
desvio <- c(0.06, 0.05, 0.04, 0.02, 0.03, 0.04, 0.06)
q <- length(nominal)
w <- (q/desvio^2)/(sum(1/desvio^2)) # pesos tal que suman q
ajuste.w <- lm(predicha~nominal,weights = w)
summary(ajuste.w)

## 
## Call:
## lm(formula = predicha ~ nominal, weights = w)
## 
## Weighted Residuals:
##        1        2        3        4        5        6        7 
## -0.06444 -0.18997 -0.04794  0.24746 -0.07999 -0.07068 -0.11206 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.121337   0.153476   0.791    0.465    
## nominal     1.002416   0.008977 111.665 1.09e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1598 on 5 degrees of freedom
## Multiple R-squared:  0.9996, Adjusted R-squared:  0.9995 
## F-statistic: 1.247e+04 on 1 and 5 DF,  p-value: 1.092e-09

confidenceEllipse(ajuste.w,fill = T,lwd = 0,which.coef = c("(Intercept)", "nominal"),main = "Región de confianza del 95%",xlab=expression(paste("Ordenanda al origen ", beta[0])), ylab=expression(paste("Pendiente  ", beta[1])),col='#f0c289')
text(coefficients(ajuste.w)[1],y=(coefficients(ajuste.w)[2]+0.005),labels=expression(paste('( ', hat(beta)[0], ',',hat(beta)[1],')')),col='#536d4a')
points(0,1,pch=19,col='darkred')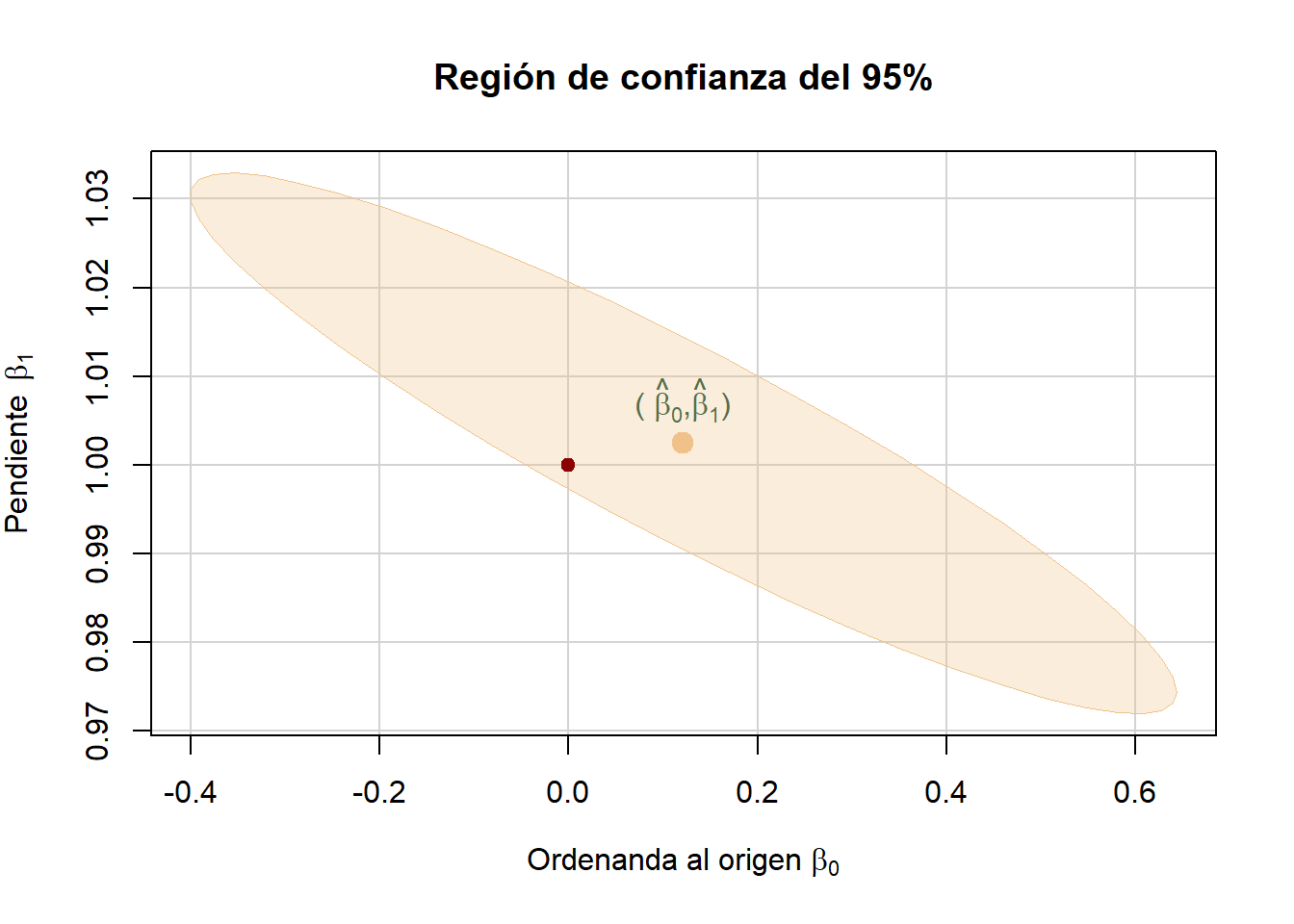

myFont1 <- "Montserrat"
puntos <- confidenceEllipse(ajuste.w,fill = T,lwd = 0,which.coef = c("(Intercept)", "nominal"),segments=1000,draw=FALSE)
df <- data.frame(puntos)
colnames(df) <- c('ordenada','pendiente')
beta0hat <- as.numeric(ajuste.w$coefficients[1])
beta1hat <- as.numeric(ajuste.w$coefficients[2])
ggplot(df, aes(x=pendiente, y=ordenada))+ 
  geom_point(size=0.5,col='darkorange')+
  annotate("point", x = beta1hat, y = beta0hat, colour = "orange", size=2)+
  annotate("point", x = 1, y = 0, colour = "darkred", size=2)+
  annotate("text", x=beta1hat, y=(beta0hat+0.07), parse = TRUE, label='paste(\'( \', hat(beta)[1], \',\',hat(beta)[0],\')\')',size=4,col='#536d4a')+
  labs(title='Región de confianza del 95%',y="Ordenada al Origen", x="Pendiente") +
  theme_ipsum(
    base_size = 11.5,
    axis_title_size = 12,
    axis_title_just = "rt")+
  theme(plot.title = element_text(family=myFont1, face='bold', colour='black', size=12,hjust=0.5))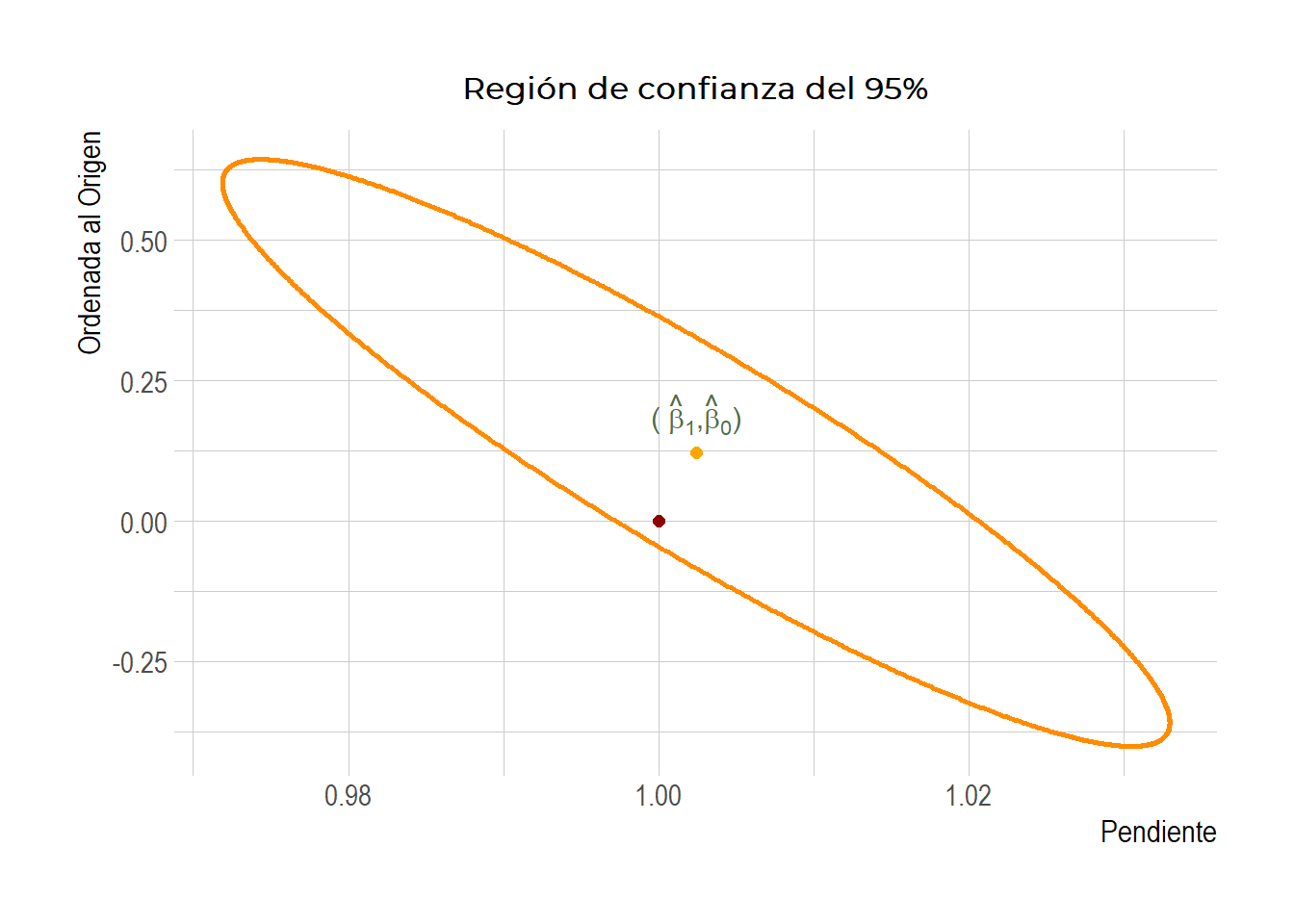

Figura 8.1: Región de confianza conjunta para \(\beta_1\) y \(\beta_0\) con la pendiente en el eje horizontal.

Como podemos observar, punto ideal \((1,0)\) está contenido en la elipse, por lo que no tenemos evidencia en contra de la exactitud del método analizado.

8.2 Comparación de métodos analíticos

La comparación de dos métodos se lleva a cabo disponiendo de una serie de muestras para las que se ha determinado el contenido de un analito por dos métodos alternativos.

Usualmente se mide cada muestra por triplicado por ambos métodos, y se aplica un modelo de regresión lineal para verificar si los resultados provistos por ambos métodos son comparables.

Cada muestra estudiada proporciona entonces una concentración predicha por cada uno de los dos métodos, acompañadas por sus respectivas incertidumbres. Supongamos que los resultados determinados por el método 1 se consideran la variable \(X\) y los provistos por el método 2 la variable \(Y\) (en la comparación de un método dado frente a otro considerado como referencia, este último se toma como método 1). Ambas variables, por lo tanto, tienen asociada una incertidumbre. La regresión lineal de \(Y\) sobre \(X\) en este caso difiere tanto del método OLS como del WLS, ya que en estos dos últimos la suposición básica es que no hay error en la variable \(X\), aunque en realidad debería decirse que en OLS y WLS la incertidumbre asociada a la variable \(X\) (concentración nominal de patrones) es significativamente menor que la asociada a la variable \(Y\) (respuesta analítica de los patrones, o concentración predicha por un método dado). Este supuesto no se cumple en la comparación de métodos analíticos, y es necesario recurrir a un método de regresión que tenga en cuenta los errores en ambos ejes. Un método popular para estos casos es el de cuadrados mínimos bivariados o BLS (por bivariate least squares).

En la técnica BLS la pendiente y la ordenada al origen de la recta ajustada se obtienen minimizando una función idéntica a la mostrada en la Ecuación (8.1), excepto que los pesos son una función de las variancias en ambas variables: \[\begin{equation} \tag{8.2} w_i = \big[s_{y_i}^2+ \hat{\beta}_1^2s_{x_i}^2\big]^{-1} \end{equation}\]

En otras palabras, los pesos de la regresión “doblemente ponderada” BLS se eligen como inversamente proporcionales a una combinación de las varianzas en \(X\) y en \(Y\). No existen fórmulas explícitas para estimar la pendiente y la ordenada al origen cuando los pesos tienen la forma dada por la Ecuación (8.2), y debemos recurrir a un algoritmo matemático iterativo. Esto es así porque en la Ecuación (8.2) interviene la pendiente estimada \(\hat{\beta_1}\), que a su vez depende de los pesos. En R podemos hacerlo utilizando la función BLS.ht() contenida en el paquete BivRegBLS

Observación: hay ocasiones en que no es imprescindible aplicar el método BLS: cuando la variancia en la variable \(X\) es significativamente menor que en la variable \(Y\), la comparación puede realizarse con éxito empleando el método WLS, asumiendo que no hay error en la \(X\). De hecho, podemos notar que la Ecuación (8.2) se reduce al caso WLS con peso \(w_i = s^{-2}_{y_i}\) cuando \(s_{x_i}\) es chico, digamos cercano a 0. Por este motivo se aconseja asignar, para la regresión lineal, la variable \(X\) a los valores hallados por el método más preciso, y la variable \(Y\) al método menos preciso.

Si puede hacerse esta última aproximación, la comparación de métodos consiste en el cálculo de la pendiente y ordenada al origen mediante WLS, y consideración de la región elíptica de confianza conjunta, tal como se describió para el estudio de exactitud. Si el punto ideal (1,0) está contenido dentro de la elipse, los métodos son comparables estadísticamente en cuanto a la predicción de la concentración del analito en las muestras de validación.

8.2.1 Ejemplo 4 Estudio de exactitud: Comparación de dos métodos.

Enunciado:

La Tabla 8.2 muestra datos para la comparación de dos métodos analíticos (promedios de tres réplicas en cada caso) incluyendo los desvíos de cada uno. Determine si los métodos conducen al mismo resultado mediante regresión lineal y estudio de la región eliptica de confianza conjunta.

---

Solución:

Se trata aquí de comparar dos métodos analíticos. Como hemos visto, lo más adecuado es utilizar BLS.

Metodo1 <- c(0.05, 5.16, 9.91, 14.90, 19.80, 24.90, 30.00)
desvio1 <- c(0.03, 0.02, 0.02, 0.01, 0.02, 0.01, 0.03)
Metodo2 <- c(0.06, 5.02, 10.00, 15.20, 19.90, 25.00, 30.00)
desvio2 <- c(0.06, 0.05, 0.04, 0.02, 0.03, 0.04, 0.06)
df.x <- rep(2,length(desvio1))
df.y <- rep(2,length(desvio2))
datos <- data.frame(M1=Metodo1, V1=desvio1^2, M2=Metodo2, V2=desvio2^2,df.x=df.x, df.y=df.y)

library(BivRegBLS)
res <- BLS.ht(data = datos, xcol = 1, ycol = 3,var.x.col = 2, var.y.col = 4,df.var.x.col = 5,df.var.y.col = 6)
res$Estimate.BLS.ht

##              H0          Estimate           Std Error        Lower 95%CI
## Intercept     0 0.116122396981041   0.152789387727558 -0.276635227789413
## Slope         1  1.00266884411628 0.00890266212557988  0.979783822567453
## Joint     (0,1)                                                         
##                 Upper 95%CI    pvalue
## Intercept 0.508880021751494 0.4815238
## Slope       1.0255538656651 0.7764070
## Joint                       0.1509522

Tenemos entonces que las estimaciones de la pendiente y la ordenada al origen mediante BLS son: \[\begin{align} \hat{\beta}_1 &=1.00 \; \pm \; 0.01\\ \hat{\beta}_0 &= 0.12 \; \pm \; 0.15 \end{align}\]

Notar que son casi idénticos a los hallados mediante la técnica WLS. Esto se debe a que los valores de la variable \(X\) (las concentraciones estimadas mediante el método analítico 1) tienen desvios estándar menores que los de la \(Y\) (las concentraciones estimadas mediante el método analítico 2). Como consecuencia, es prácticamente lo mismo realizar el análisis mediante WLS o mediante BLS.

Finalmente para concluir acerca de si los métodos son equivalentes o no, determinamos la región de confianza para \(\beta_0\) y \(\beta_1\).

df <- data.frame(res$Ellipse.BLS.ht)
colnames(df) <- c('pendiente','ordenada')
beta0hat <- as.numeric(res$Estimate.BLS.ht$Estimate[1])
beta1hat <- as.numeric(res$Estimate.BLS.ht$Estimate[2])
ggplot(df, aes(y=ordenada, x=pendiente))+ 
  #geom_line(color="#e67e1b")+
  geom_point(size=0.5,col='darkorange')+
  annotate("point", y = beta0hat, x = beta1hat, colour = "darkred", size=2)+
  annotate("text", y=beta0hat, x=(beta1hat+0.004), parse = TRUE, label='paste(\'( \', hat(beta)[1], \',\',hat(beta)[0],\')\')',size=4,col='#536d4a')+
  annotate("point", x = 1, y = 0, colour = "magenta", size=3,shape=17)+
  annotate("text", x = 1, y = 0.07, label='(1,0)', colour = "darkblue", size=4)+
  labs(y="Ordenada al Origen", x="Pendiente") +
  theme_ipsum(
    base_size = 11.5,
    axis_title_size = 12,
    axis_title_just = "rt")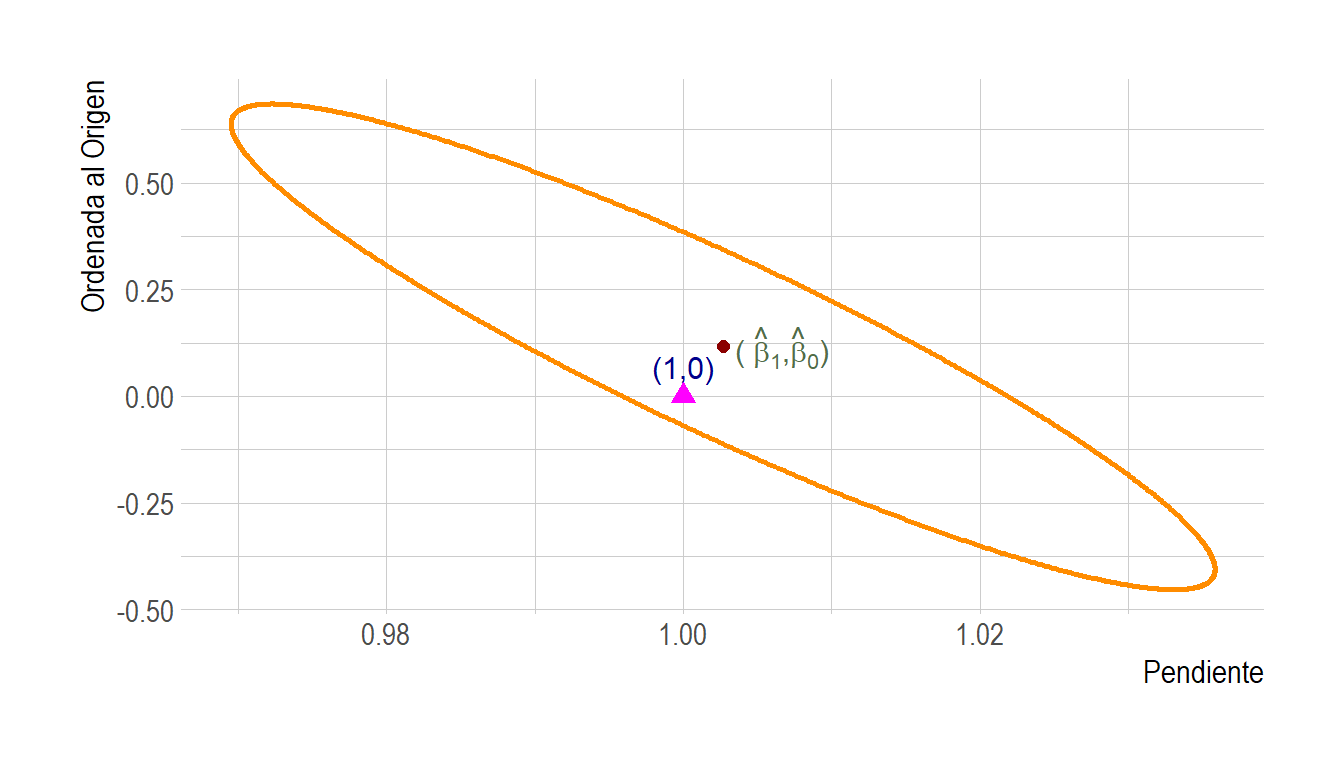

Figura 8.2: Región de confianza para la comparación de métodos.

Como el punto ideal \((1,0)\) pertenece a la región de confianza, no rechazamos la hipótesis nula de equivalencia entre los dos métodos analíticos, es decir, no encontramos envidencia en los datos experimentales de que los métodos conduzcan a resultados diferentes.

---

Referencias

Currie, L. A. (1968). LIMITS FOR QUALITATIVE DETECTION AND QUANTITATIVE DETERMINATION. APPLICATION TO RADIOCHEMISTRY. Anal. Chem., 40: 586-93 (Mar. 1968). doi:10.1021/ac60259a007.

Goicoechea, H. and Olivieri, A. C. (2007). La calibración en química analítica. Ed. UNL.

Harris, D. C. (2016). Análisis químico cuantitativo. 3rd ed. Editorial Reverté.

Olivieri, A. (2021). Quimiometría: Un matrimonio de conveniencia entre química y matemática. https://www.youtube.com/watch?v=ySXaRG7xyjw.