2.3 Principal component analysis
Principal Component Analysis (PCA) is a useful technique for exploratory data analysis, which allows a better visualization of the variability present in a dataset with many variables. This “better visualization” is achieved by transforming a set of covariates into a smaller set of principal components.
A principal component can be thought of as the direction where there is the most variance or, geometrically speaking, where the data is most spread out. In practical terms, to derive the first principal component that describe our mixture, we try to find the straight line that best spreads the data out when it is projected along it, thus explaining the most substantial variance in the data. The following Figure shows the first principal component in a simple setting with only 3 covariates of interest (so that we could graphically represent it):
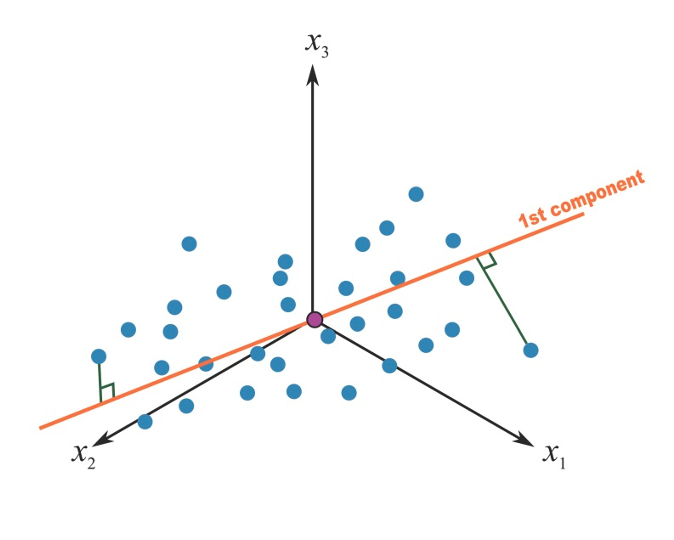
Figure 2.5: First principal component in a 3-covariates setting
Mathematically speaking, this first component \(t_1\) is calculated as a linear combination of the \(p\) original predictors \(T=XW_p\), where \(W_p\) are weights that would maximize the overall explained variability. For those math-oriented readers, it turns out that such weights are the eigenvectors of the correlation matrix of the original exposures.
Once a first component has been retrieved, we proceed by calculating a second component that would maximize the residual variance. Of interest in our context, the procedure adds a constraints of orthogonality to this second component, that is, it will be uncorrelated to the first one, as presented in Figure 2.6.
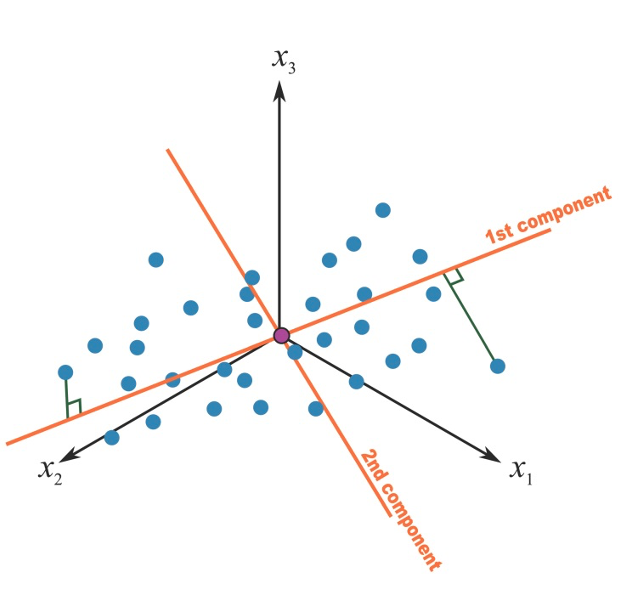
Figure 2.6: Second principal component in a 3-covariates setting
Mathematically, this is obtained by another linear combination where the weights are the eigenvectors corresponding to the second largest eigenvalue. In this way we can proceed to derive a full set of \(p\) components from our original \(p\) covariates, until all variance has been explained. In summary, PCA is a set of linear transformation that fits the matrix of exposures into a new coordinate system so that the most variance is explained by the first coordinate, and each subsequent coordinate is orthogonal to the last and has a lesser variance. Practically, we are transforming a set of \(p\) correlated variables into a set of \(p\) uncorrelated principal components. PCA is sensitive to unscaled covariates, so it is usually recommended to standardize your matrix of exposures before running a PCA analysis.
2.3.1 Fitting a PCA in R
There are several options to conduct PCA in R. Here we will use prcomp but alternative options are available (princomp and principal). PCA is also available in the aforementioned rexposome package. To prepare nice figures for presentations or usage in manuscripts one could also consider the factoextra package, which creates a ggplot2-based elegant visualization (link).
The prcomp( ) function produces a basic principal component analysis. The command requires the raw data we want to reduce (the exposure matrix) and will extract principal components. Here we are also centering and scaling all exposures.
fit <- prcomp(X, center=TRUE, scale=TRUE)2.3.2 Choosing the number of components
One of the most interesting features of PCA is that, while it is possible to calculate \(p\) components from a set of \(p\) covariates, we usually need a smaller number to successfully describe most of the variance of the original matrix of exposures. In practical terms, not only we are reshaping the original set of exposures into uncorrelated principal components, but we are also able to reduce the dimension of the original matrix into a smaller number of variables that describe the mixture. How many components do we actually need? Before getting to describe the several tools that can guide us on this decision, it is important to stress that this step will be purely subjective. Sometimes these tools will lead to the same evident conclusion, but other times it might not be straightforward to identify a clear number of components that describe the original data. In general, the three common tools used to select a number of components include:
- Select components that explain at least 70 to 80% of the original variance
- Select components corresponding to eigenvalues larger than 1
- Look at the point of inflation in the scree plot
Let’s take a look at these approaches in our illustrative example. These are the results of the PCA that we ran with the previous R command:
summary(fit)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 2.4627 1.7521 1.12071 0.89784
## Proportion of Variance 0.4332 0.2193 0.08971 0.05758
## Cumulative Proportion 0.4332 0.6525 0.74219 0.79977
## PC5 PC6 PC7 PC8
## Standard deviation 0.83905 0.72337 0.63861 0.60268
## Proportion of Variance 0.05029 0.03738 0.02913 0.02594
## Cumulative Proportion 0.85006 0.88744 0.91657 0.94251
## PC9 PC10 PC11 PC12
## Standard deviation 0.4892 0.46054 0.43573 0.29751
## Proportion of Variance 0.0171 0.01515 0.01356 0.00632
## Cumulative Proportion 0.9596 0.97476 0.98832 0.99464
## PC13 PC14
## Standard deviation 0.25542 0.09904
## Proportion of Variance 0.00466 0.00070
## Cumulative Proportion 0.99930 1.00000(Square roots of) eigenvalues are reported in the first line, while the second and third lines present, respectively, the proportion of variance explained by each given component (note that, as expected, this decreases as we proceed with the estimation), and the cumulative variance explained.
The scree plot is the plot of the descending eigenvalues. Ideally we would like to identify a point of inflation (also known as “elbow” of the curve), signifying that after a certain number of components, the proportion of variance that is additionally explained becomes minimal.
plot(fit,type="lines")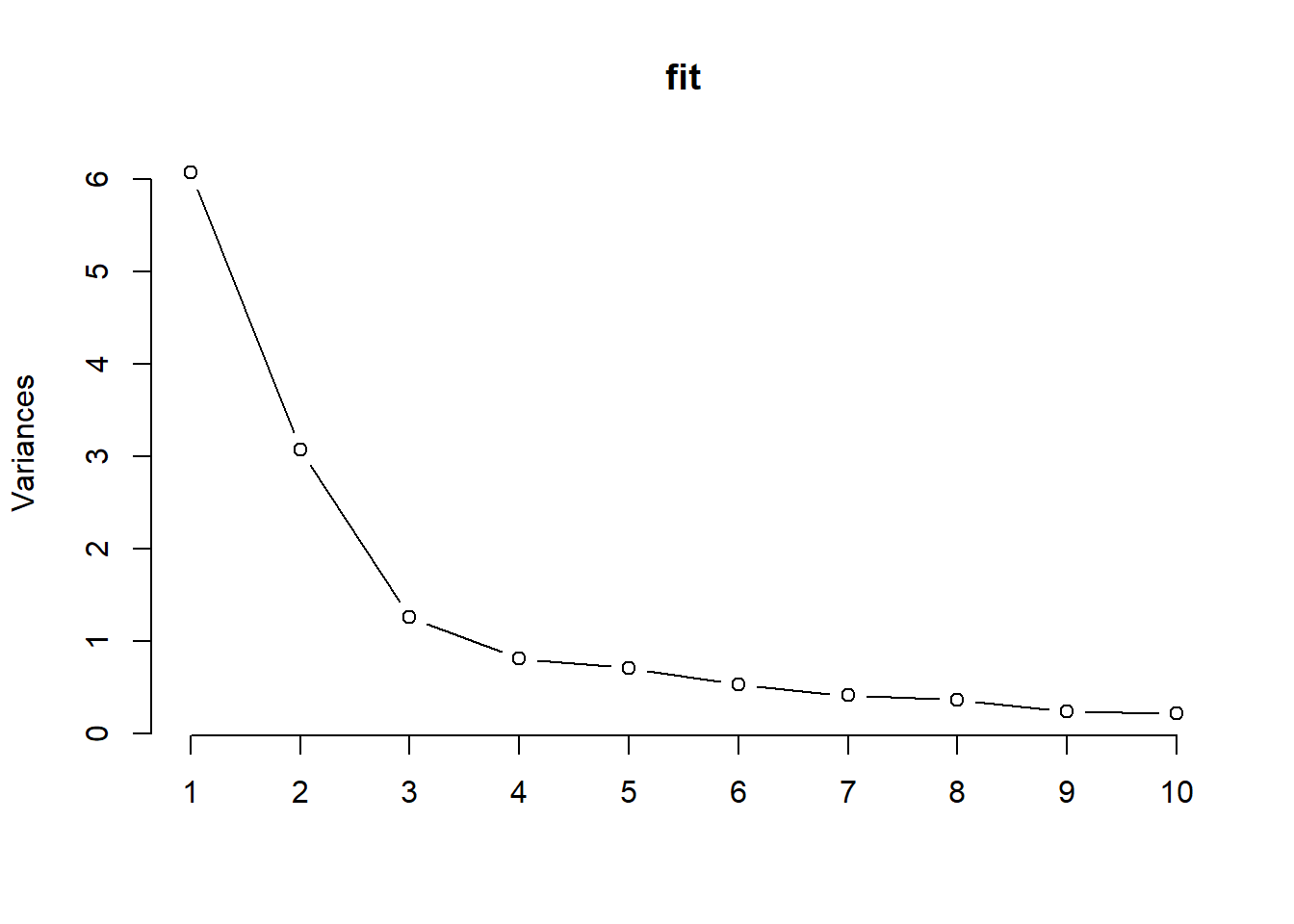
Figure 2.7: Scree plot
All these techniques seem to indicate that 3 components might successfully describe the original set of 14 exposures.
2.3.3 Getting sense of components interpretation
A PCA is made by three steps. Fitting the model is the easiest part as it only requires a line of coding (assuming that the pre-processing has been carefully conducted). The second step, selecting the number of components, requires some levels of subjectivity but is also relatively simple in most settings. The third step is usually the more complicated ones, as we are now tasked with providing some interpretation to the set of principal components that we have selected. To get a sense of what principal components represent, we usually look at loading factors, the correlation coefficients between the derived components and the original covariates. In practical terms they inform us on how much of the original variance of each covariate is explained by each component. Loading factors for the illustrative example are presented in Table 2.2. It is not simple to identify any clear pattern. Loading factors are generally low, and several covariates seem to equally load to more components. However, there is a trick that can be tried out to improve the interpretation of the components, consisting in rotating the axes. The most common approach to do that is called “varimax”.
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | PC10 | PC11 | PC12 | PC13 | PC14 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 0.00 | 0.30 | 0.36 | 0.43 | 0.77 | 0.02 | -0.06 | 0.04 | 0.01 | -0.01 | 0.01 | -0.01 | 0.00 | -0.01 |
| x2 | 0.03 | 0.28 | 0.47 | 0.45 | -0.58 | -0.35 | -0.03 | 0.20 | 0.03 | -0.04 | 0.00 | -0.01 | 0.02 | 0.00 |
| x3 | 0.36 | -0.14 | 0.27 | -0.13 | -0.03 | 0.16 | -0.21 | -0.09 | -0.13 | -0.02 | -0.06 | -0.10 | 0.45 | -0.67 |
| x4 | 0.36 | -0.13 | 0.28 | -0.12 | -0.02 | 0.16 | -0.20 | -0.10 | -0.13 | -0.02 | -0.05 | -0.08 | 0.33 | 0.74 |
| x5 | 0.35 | -0.13 | 0.28 | -0.10 | -0.04 | 0.14 | -0.22 | -0.10 | -0.11 | -0.02 | -0.08 | 0.15 | -0.80 | -0.07 |
| x6 | 0.31 | 0.01 | -0.03 | -0.06 | 0.12 | -0.62 | 0.44 | -0.50 | -0.22 | -0.02 | -0.06 | -0.01 | 0.00 | -0.01 |
| x7 | 0.24 | 0.33 | -0.24 | -0.14 | 0.03 | -0.28 | -0.53 | -0.19 | 0.60 | 0.05 | 0.02 | 0.12 | 0.04 | 0.01 |
| x8 | 0.36 | -0.05 | -0.01 | -0.01 | 0.03 | 0.02 | 0.25 | 0.32 | 0.13 | 0.78 | 0.27 | -0.01 | -0.02 | 0.00 |
| x9 | 0.20 | 0.35 | -0.31 | -0.18 | 0.08 | -0.22 | -0.24 | 0.51 | -0.57 | -0.08 | -0.07 | -0.03 | -0.02 | 0.01 |
| x10 | 0.27 | -0.02 | -0.41 | 0.53 | -0.09 | 0.23 | 0.04 | -0.08 | 0.01 | 0.11 | -0.63 | -0.04 | 0.01 | 0.00 |
| x11 | 0.32 | -0.05 | -0.31 | 0.39 | -0.06 | 0.18 | -0.01 | -0.10 | -0.07 | -0.34 | 0.70 | -0.02 | -0.01 | -0.01 |
| x12 | 0.03 | 0.52 | 0.04 | -0.12 | -0.12 | 0.36 | 0.24 | -0.19 | -0.12 | 0.04 | 0.02 | 0.67 | 0.12 | -0.01 |
| x13 | 0.01 | 0.53 | 0.02 | -0.17 | -0.12 | 0.29 | 0.14 | -0.23 | 0.01 | 0.05 | 0.03 | -0.71 | -0.14 | -0.01 |
| x14 | 0.34 | 0.02 | 0.06 | -0.20 | 0.07 | 0.05 | 0.44 | 0.43 | 0.43 | -0.50 | -0.15 | -0.01 | 0.00 | 0.00 |
Let’s take a look at the rotated loading factors for the first three components (the ones that we have selected) in our example:
rawLoadings_3<- fit$rotation[,1:3]
rotatedLoadings_3 <- varimax(rawLoadings_3)$loadings
rotatedLoadings_3##
## Loadings:
## PC1 PC2 PC3
## x1 0.162 0.428
## x2 0.163 0.123 0.506
## x3 0.452 -0.102
## x4 0.455
## x5 0.450
## x6 0.275 0.105 -0.115
## x7 0.435 -0.152
## x8 0.332 -0.131
## x9 0.473 -0.198
## x10 0.178 -0.446
## x11 0.182 0.134 -0.382
## x12 0.466 0.227
## x13 0.473 0.218
## x14 0.332
##
## PC1 PC2 PC3
## SS loadings 1.000 1.000 1.000
## Proportion Var 0.071 0.071 0.071
## Cumulative Var 0.071 0.143 0.214Interpretation remains a bit tricky and very subjective, but it definitely improves. With three rotated components we observe covariates groupings that recall what we observed in the network analysis: we have \(X_1, X_2\) with higher loading on PC3, \(X_7, X_9, X_{12}, X_{13}\) loading on PC2, and all other exposures loading on PC1.
2.3.4 Using principal components in subsequent analyses
We have here discussed PCA as an unsupervised technique for describing the mixture. Principal components, however, can be used in further analysis, for example including the selected components into a regression model instead of the original exposures. This approach is very appealing in the context of environmental mixtures as it would result into incorporating most of the information of our exposure matrix into a regression models by using uncorrelated covariates, thus overcoming one of the major limitations of using multiple regression in this context (see Section 3). Nevertheless, the validity of this approach is strictly dependent on whether a good interpretation of the components has been determined; in our example we would not conclude that the PCA clearly summarizes exposures into well defined groups, and we would get negligible advantages by including such components into a regression model. The next subsection will present some published papers that applied this technique in environmental epidemiology. Furthermore, if subgroups of exposures are clearly identified from a PCA, this information can be incorporated into subsequent modeling technique that will be discussed later.
2.3.5 PCA in practice
Despite several techniques developed ad-hoc for the analysis of environmental mixtures have emerged, PCA remains a very common choice among environmental epidemiologists. Most of the times, the method is used to reduce the dimension of a mixture of correlated exposures into a subset of uncorrelated components that are later included in regression analysis.
As a first example, let’s consider a paper by Lee et al. (2017) evaluating the association between pregnancy exposure to 28 contaminants (metals, pesticides, PCBs, phthalates, PFAS, BPA) and socio-economic status in the MIREC study. To summarize the mixture, the Authors conduct a PCA that suggests selecting 11 principal components. The following figure presents the loading factors, as included in the paper:
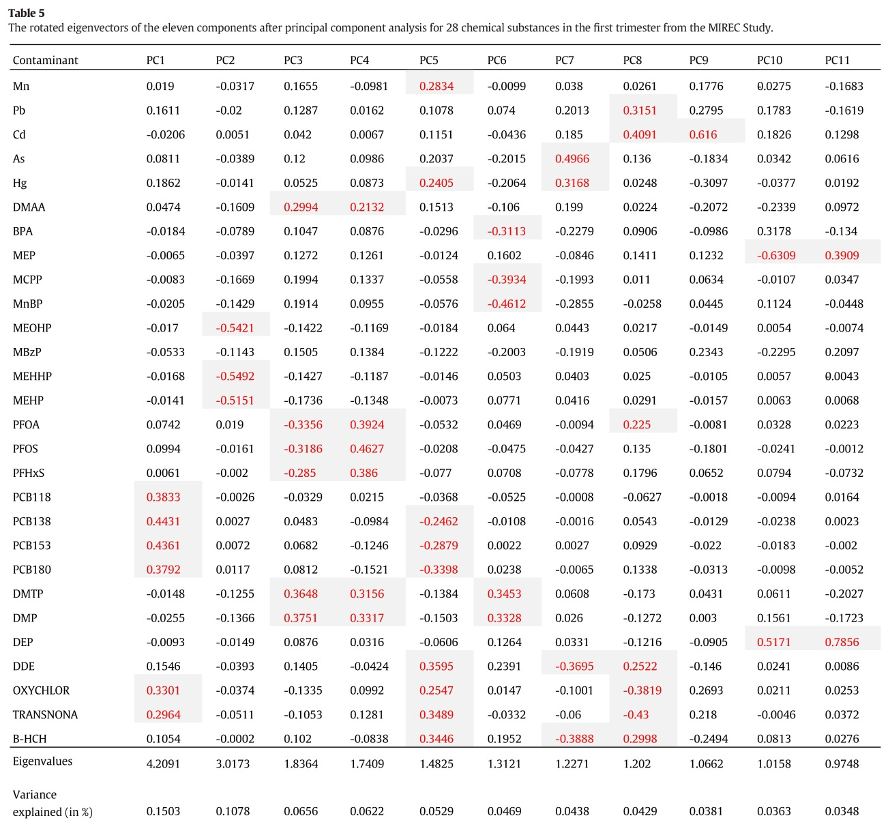
Figure 2.8: Loading factors from Lee et al., 2017
The interpretation of such components is not straightforward (the paper does not mention whether a rotation was considered). The first component has higher loadings on PCBs, while the second component has high loadings on DEHP metabolites. All other components have high loadings on specific subsets of exposures, but fail to uniquely identify clusters of exposures within the mixture. For example, to describe exposure to organochlorine pesticides, we find similar loading factors in PC1, PC5, and PC9. Similarly, organophosphate pesticides equivalently load on PC3, PC4, and PC6. As described in the previous paragraphs, this has relevant implications when attempting to evaluate PCA components in a regression model. The following figure presents results from such regression in the paper:
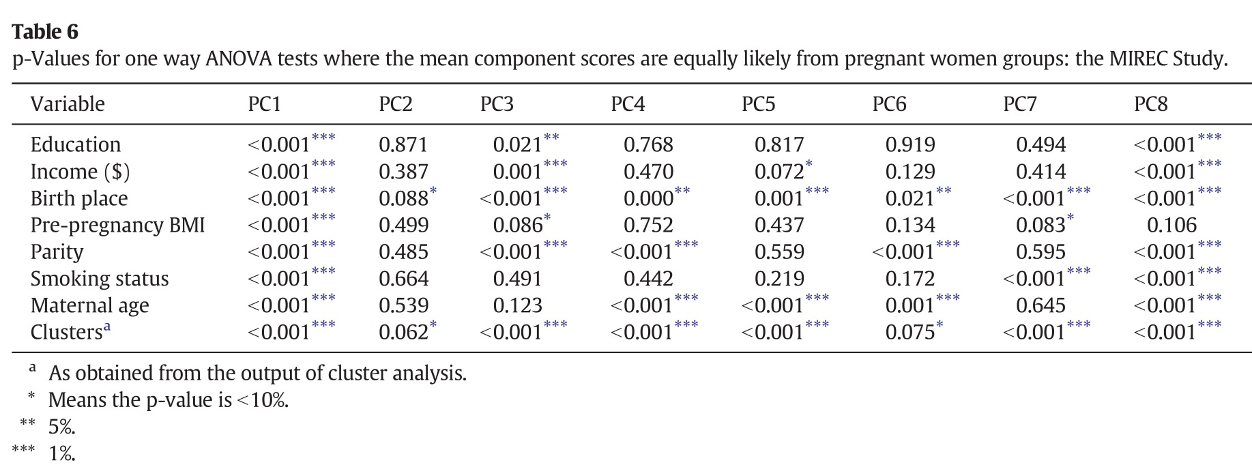
Figure 2.9: Regression results from Lee et al., 2017
From this table we might be able to conclude that PCBs are associated with the outcome of interest (as they load on PC1), but it is not easy to draw any conclusion about other sets of exposures, whose variability is captured by multiple components. To conclude, the real information that a PCA model is giving us in this example is that the mixture is very complex and we do not observe clearly defined subgroups of exposures based on the correlation structure. In such setting, a PCA analysis might not be the best option to evaluate exposure-outcome associations, and other methods should be considered.
A second interesting example can be found in Sanchez et al. (2018), evaluating metals and socio-demographic characteristics in the HEALS study in Bangladesh. Out of a mixture of 15 metals, a rotated PCA identified 6 principal components explaining 81% of the total variability. Differently from the previous examples, such components better identify subgroups of exposures (Figure 2.10).
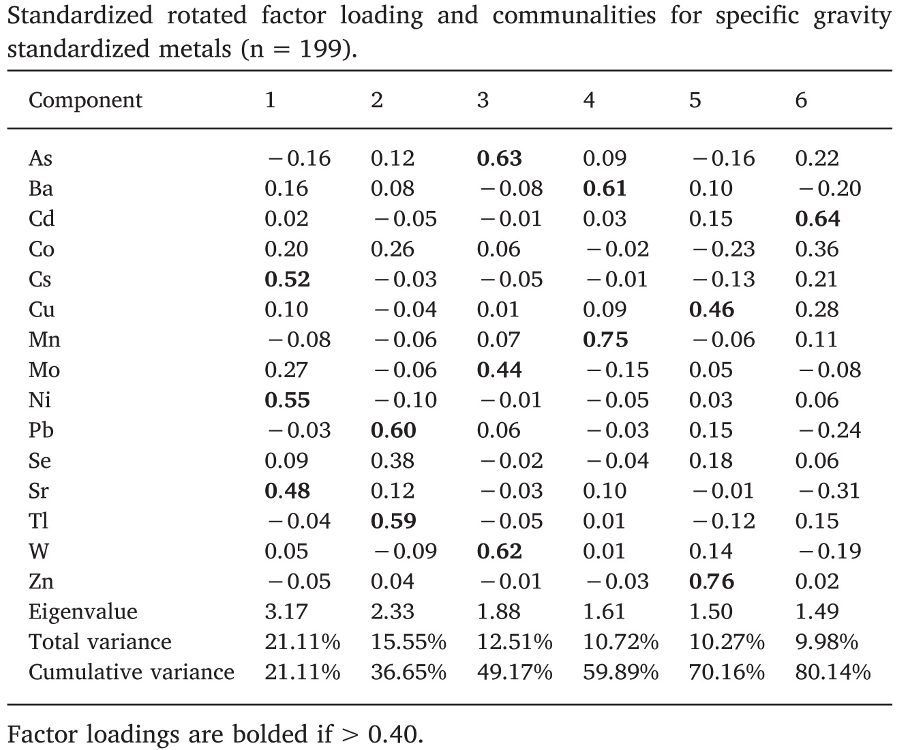
Figure 2.10: Loading factors from Sanchez et al., 2018
If we look at these loading factors by row, we see that each metal has a high loading factor with one component, and low loading to all others. For example arsenic (row 1) is described by PC3, cadmium (row 3) by PC6, and so on down to zinc, described by PC5. In this situation, a regression model that includes the principal components will have a better interpretation; for example, associations between PC3 and the outcome can be used to retrieve information on the joint associations between arsenic, molybdenum, and tungsten, on the outcome.
Nevertheless, it is important to note some critical limitations of this approach, that remain valid also when a perfect interpretation can be provided. Let’s think of this third principal component that is well describing the variability of arsenic, molybdenum, and tungsten. A regression coefficient linking PC3 with the outcome would only tell us how the subgroup of these 3 exposures is associated with the outcome, but would not inform us on which of the three is driving the association, whether all three exposures have effects in the same direction, nor whether there is any interaction between the three components. Moreover, let’s not forget that components are calculated as linear combinations of the exposures and without taking the relationship with the outcome into account.
For these reasons, we can conclude that PCA is very powerful tool to be considered in the preliminary unsupervised assessment of the mixture as it can inform subsequent analyses. On the other hand, using derived components into regression modeling must be done with caution, and is usually outperformed by most supervised approaches that we will describe later.
Finally, it is important to mention that several extensions of the classical PCA have been developed, including a supervised version of the approach. These techniques, however, were developed in other fields and have not gained too much popularity in the context of environmental exposures, where alternative supervised approaches, presented in the following sections, are generally used.