Chi²-Vierfeldertest

_Statistik

Prof. Dr. Armin Eichinger

TH Deggendorf

28.02.2024

Überblick

• Einführung
• \(\chi²\)-Vierfeldertest
• 🚬 Beispiel: Geschlecht und Rauchverhalten

Einführung

Verschiedene \(\chi²\)-Tests

Verfahren für Häufigkeitsdaten (meist auf nominalem Skalenniveau)

Homogenitätstest

• Erhebung mehrerer Stichproben bezüglich eines Merkmals
• Fragestellung: Sind die Daten verschiedener Stichproben identisch verteilt?
• Beispiel: Sonntagsfrage (prozentualer Anteil von politischen Parteien) für unterschiedliche Stichproben
• “Der Homogenitätstest kann auch als Unabhängigkeitstest interpretiert werden, wenn man die Stichproben als Ausprägungen eines zweiten Merkmals ansieht.” (Wikipedia)

Anpassungstest (auch: Verteilungstest)

• Erhebung einer Stichprobe bezüglich eines Merkmals
• Fragestellung: Sind die Daten einer Stichprobe auf eine bestimmte Art verteilt?
• Beispiel: Sind die Daten normalverteilt?

▶ Unabhängigkeitstest

• Erhebung einer Stichprobe bezüglich zweier Merkmale
• Daten in Kontingenztabelle (auch Kreuztabelle); je ein Merkmal entlang den Zeilen bzw. Spalten
• Fragestellung: Gibt es einen Zusammenhang zwischen den beiden Merkmalen?
• Beispiel: Hängen Geschlecht und Rauchverhalten zusammen?
• Spezialfall: Beide Merkmale sind dichotom (\(\rightarrow \chi²\)-Vierfeldertest)

\(\chi²\)-Vierfeldertest

Signifikanztest

• Forschungshypothese H₁: Die beiden Variablen sind abhängig (= nicht unabhängig).

• Teststatistik:

  • \(\chi^{2}=\sum _{{j=1}}^{2}\sum _{{i=1}}^{2}{\frac {(n_{{ij}}-E_{{ij}})^{2}}{E_{{ij}}}}\)
    
  • Allgemein (auch für mehr als 2 Kategorien):
    \(\chi^{2}=\sum _{{j=1}}^{k}\sum _{{i=1}}^{m}{\frac {(n_{{ij}}-E_{{ij}})^{2}}{E_{{ij}}}}\)
    

  mit
  n\(_{ij}\): Tatsächliche Anzahl Fälle in Kategorie ij
  E\(_{ij}\): Erwartete Fälle in Kategorie ij
  \(k, m\): Anzahl Zeilen bzw. Spalten
  n: Gesamte Anzahl

• Berechnung der Erwartungen E\(_{ij}\)

  • \(E_{ij} = \frac{n_{i•} n_{•j}}{n}\),
    

  mit
  n\(_{•j}\): Summe Anzahl über alle Zeilen
  n\(_{i•}\): Summe Anzahl über alle Spalten

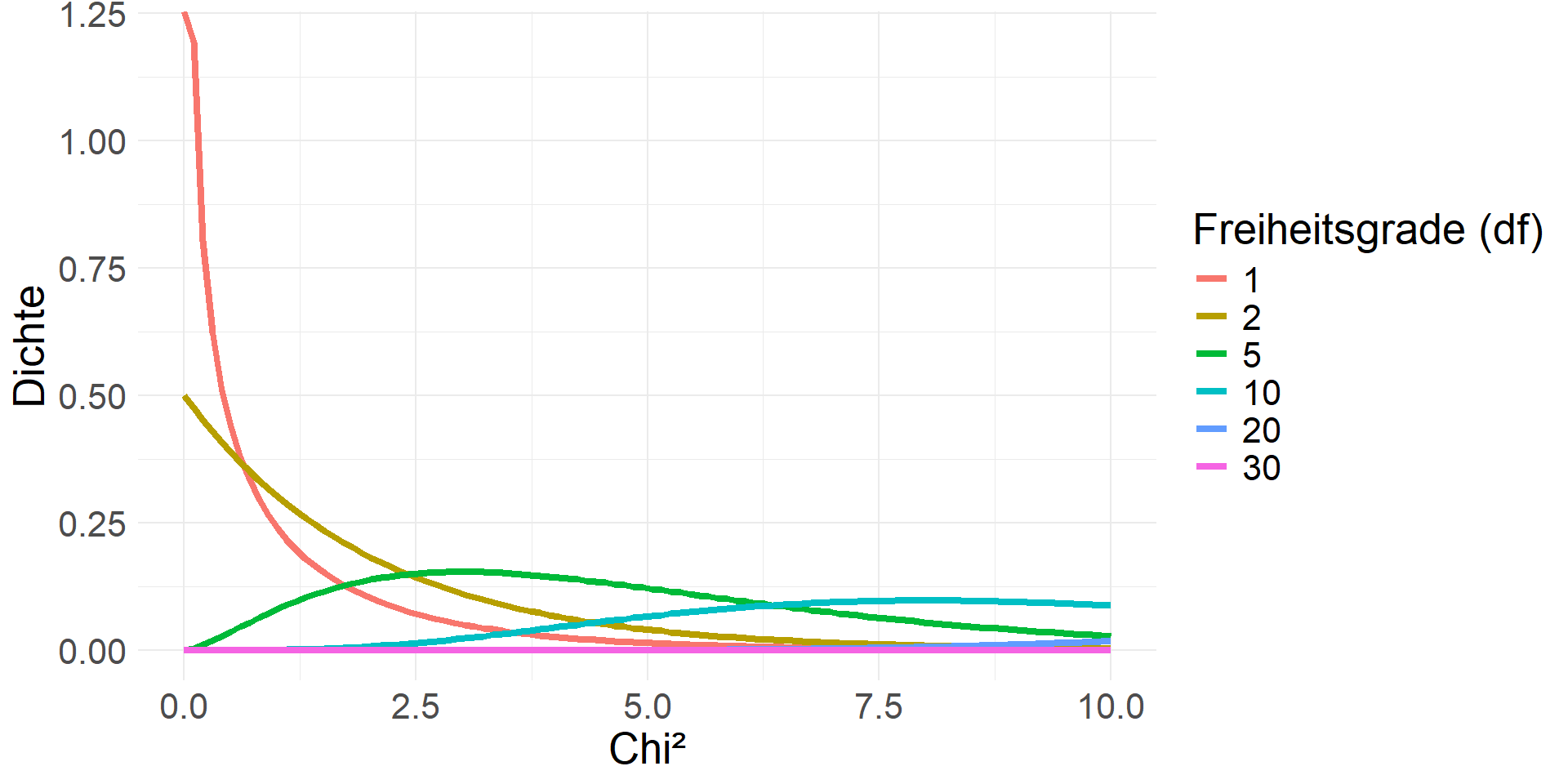
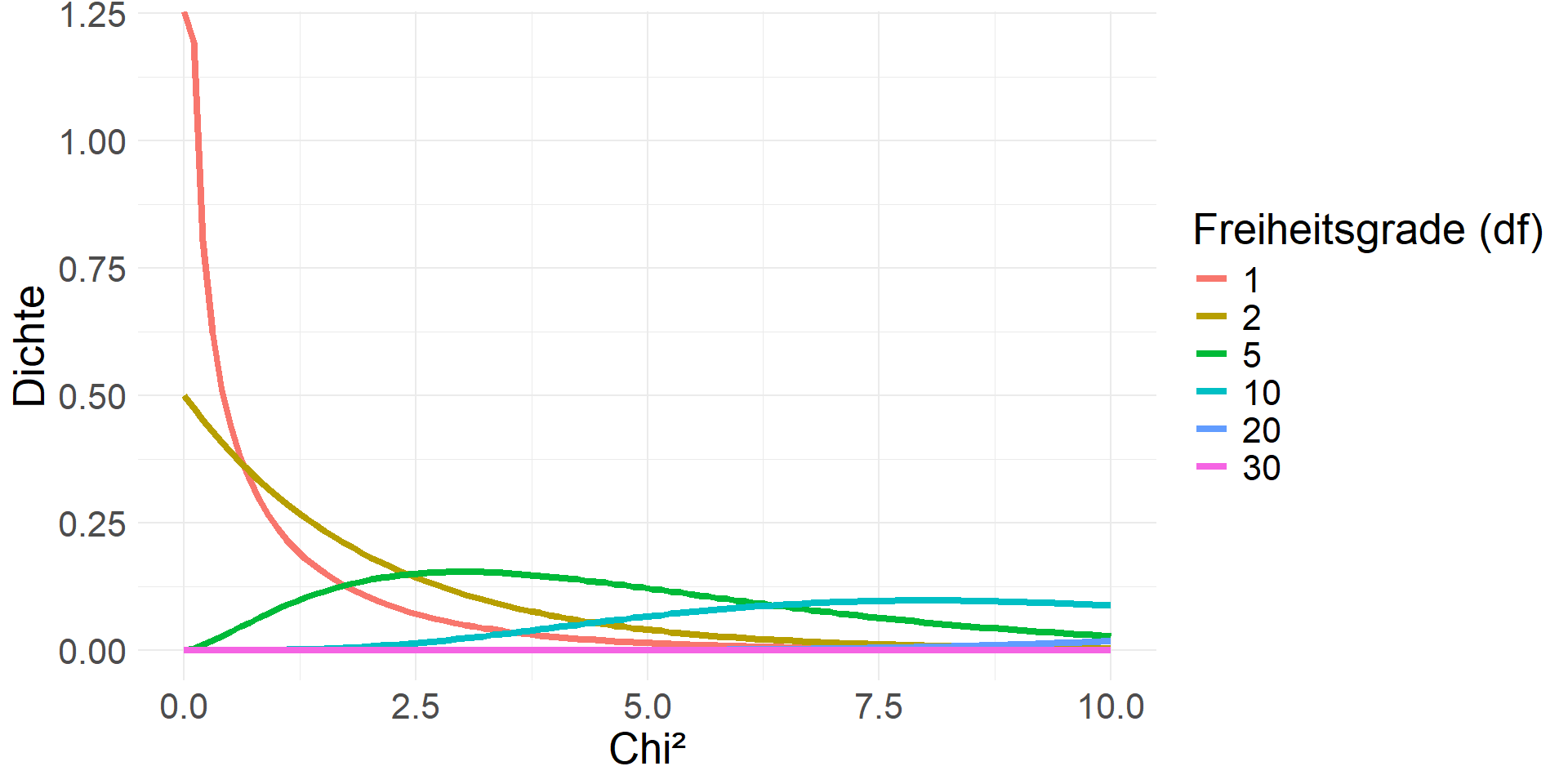
\(\chi²\)-Verteilung

Beispiel Kreuztabelle

	NR	R
w	90	10	100
m	80	20	100
	170	30	200

Signifikanztest

• Freiheitsgrade: \(\textit{df} = (m - 1)(k - 1)\)
  

• Vierfeldertest: \(\textit{df} = (2-1)(2-1) = 1\)

• Entscheidung:

  • Vierfeldertest: nicht unabhängig (und damit abhängig), wenn \(\chi^{2}_{emp} > \chi^{2}_{krit}(1) =\) 3.841
  • \((i \times j)\)-Felder: nicht unabhängig (und damit abhängig), wenn \(\chi^{2}_{emp} > \chi^{2}_{krit}(\textit{df})\)

• Effektstärke: Cramer’s V
  \(V = \sqrt{\frac{\chi²}{n(k - 1)}}\),
  mit k = min(Kategorienzahl)

\(\chi²\)-Verteilung

df	Kritische_Werte
1	3.841459
2	5.991465
3	7.814728
4	9.487729
5	11.070498
6	12.591587
7	14.067140
8	15.507313
9	16.918978
10	18.307038
11	19.675138
12	21.026070
13	22.362033
14	23.684791
15	24.995790
16	26.296228
17	27.587112
18	28.869299
19	30.143527
20	31.410433
21	32.670573
22	33.924439
23	35.172462
24	36.415028
25	37.652484
26	38.885139
27	40.113272
28	41.337138
29	42.556968
30	43.772972

Annahmen

• Skalenniveau:
  • allgemein: Variablen nominal oder ordinal
  • Vierfeldertest: dichotom
• Unabhängigkeit der einzelnen Messungen
• Jede Zelle hat fünf oder mehr Beobachtungen
• Alternative: Exakter Test nach Fisher

🚬 Beispiel: Geschlecht und Rauchverhalten

🚬 Beispiel

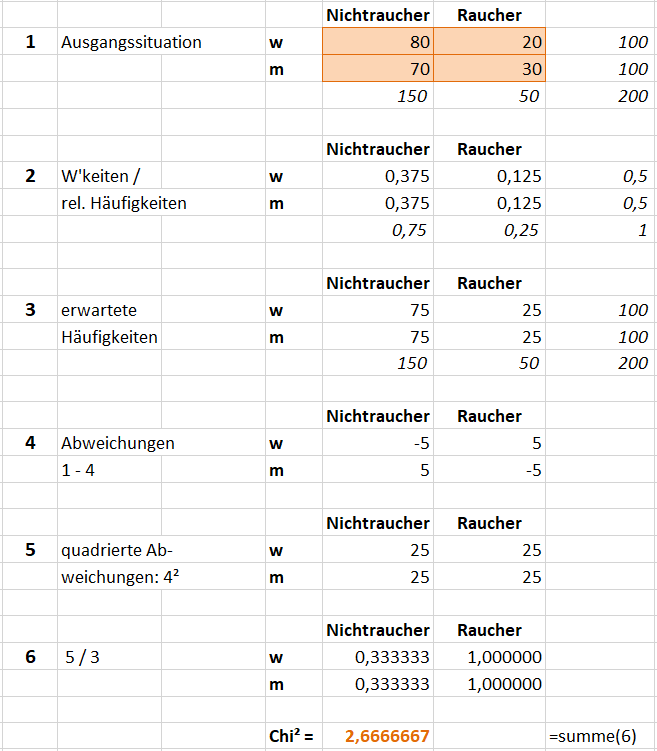
Ausgangszahlen mit Randsummen (Beobachtung)

🚬 Beispiel

Relative Häufigkeiten

🚬 Beispiel

Erwartete Häufigkeiten

🚬 Beispiel

Abweichung Beobachtung - Erwartung

🚬 Beispiel

Quadrierte Abweichung

🚬 Beispiel

Quadrierte Abweichung geteilt durch die Erwartung

🚬 Beispiel

Vorgehen im Überblick

    Pearson's Chi-squared test

data:  vierfelder
X-squared = 2.6667, df = 1, p-value = 0.1025

Cramer V 
  0.1155