Varianzanalyse – ANOVA, zweifaktoriell

_Statistik

Prof. Dr. Armin Eichinger

TH Deggendorf

12.03.2024

Überblick

• Einführung
• Beispiel
• Signifikanztest
• Voraussetzungen & Post-Hoc-Vergleiche
• Interaktion

Einführung

Begriffe & Klassifikation

• Bisher: Einfaktorielle Versuchspläne (oder Designs); mit bzw. ohne Messwiederholung

• Mehrfaktorielle Designs untersuchen den Einfluss und das Zusammenwirken mehrerer UVs (Faktoren) auf eine AV

• Konvention der Namensgebung für Faktoren: A, B, C, …

• Beispiel Zweifaktorielles Design:

  • Untersuchung des Einflusses von Faktor A (= Haupteffekt A), Faktor B (= Haupteffekt B)und des Zusammenwirkens A x B (= Interaktionseffekt AxB)
  • Annahme: Faktor A hat 2 Ausprägungen, Faktor B hat 3 Ausprägungen
    \(\rightarrow\) (2 x 3)-Design
  • Mögliche Kombinationen:
    • Beide Faktoren ohne MW
    • Beide Faktoren mit MW
    • Ein Faktor mit ein Faktor ohne MW (sog. Mixed Design)

Beispiel

Beispiel: Beer Goggles 🍺👓

• Fragestellungen:

  1. Ändert sich die Attraktivität der Gesprächspartner:innen mit zunehmendem Alkoholkonsum? (Haupteffekt A)
  2. Unterscheidet sich die Attraktivität der Gesprächspartner:innen zwischen den Geschlechtern? (Haupteffekt B)
  3. Ändert sich die Attraktivität der Gesprächspartner:innen mit zunehmendem Alkoholkonsum für die beiden Geschlechter unterschiedlich? (Interaktionseffekt)

• Abhängige Variable (AV): Attraktivität der Gesprächspartner anhand einer Skala von 1 bis 100; Annahme der objektiven Operationalisierung (z. B. durch die gemittelte Bewertung einer ausgewählten Jury o. ä.)

• Unabhängige Variablen (UVs)

  • Faktor A: Geschlecht; zwei Stufen
    • Stufe 1: Female (weiblich)
    • Stufe 2: Male (männlich)
  • Faktor B: Alkoholkonsum; drei Stufen
    • Stufe 1: 0 Pint
    • Stufe 2: 2 Pint
    • Stufe 3: 4 Pint

🍺👓 Beispiel

🍺👓 Beispiel

Interaktionsdiagramm – Sicht 1

🍺👓 Beispiel

Interaktionsdiagramm – Sicht 2

🍺👓 Beispiel

                   Df Sum Sq Mean Sq F value   Pr(>F)    
Geschlecht          1    169   168.7   2.032    0.161    
Alkohol             2   3332  1666.1  20.065 7.65e-07 ***
Geschlecht:Alkohol  2   1978   989.1  11.911 7.99e-05 ***
Residuals          42   3488    83.0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

                      eta.sq eta.sq.part
Geschlecht         0.0188197  0.04615385
Alkohol            0.3716310  0.48862074
Geschlecht:Alkohol 0.2206087  0.36192110

Signifikanztest

Hypothesen

Haupteffekte A, B:

1. H\(_{0_A}\): \(\mu_{A_1} = \mu_{A_2} = \dots = \mu_{A_k}\)
   H\(_{1_A}\): \(\mu_{A_i} \neq \mu_{A_j}\) (für mindestens ein i, j; i \(\neq\) j)

2. H\(_{0_B}\): \(\mu_{B_1} = \mu_{B_2} = \dots = \mu_{B_l}\)
   H\(_{1_B}\): \(\mu_{B_i} \neq \mu_{B_j}\) (für mindestens ein i, j; i \(\neq\) j)

Interaktonseffekt A \(\times\) B:

3. H\(_{0_{A\times B}}\): \(\mu_{ij} = \mu_{A_i} + \mu_{B_j} - \mu\)
   H\(_{1_{A\times B}}\): \(\mu_{ij} \neq \mu_{A_i} + \mu_{B_j} - \mu\)

Quadratsummen: Zerlegung

Quadratsummen: Formeln

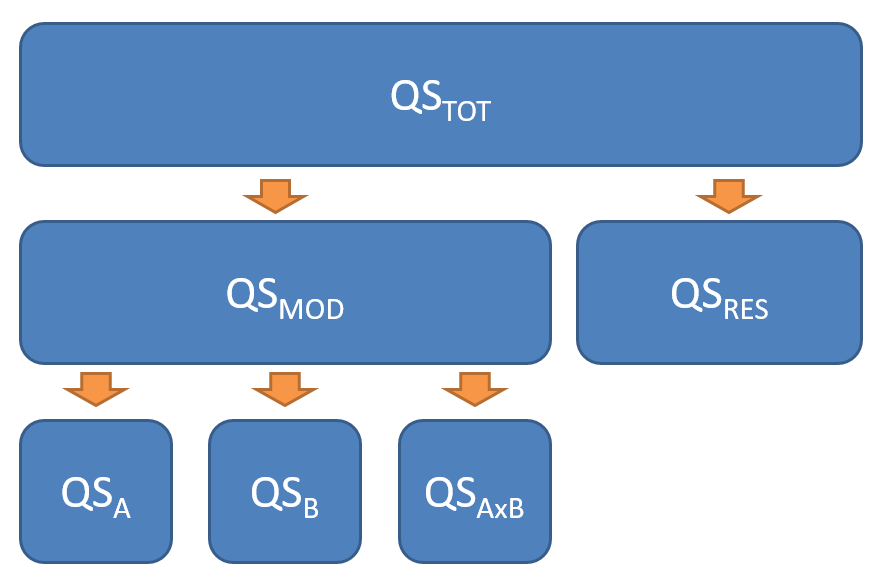
Totale Quadratsumme:

• \(QS_{tot} = \sum_{i}^{n}(x_i - \bar{x})^2\) (analog zur einfaktoriellen ANOVA)

Modellquadratsumme (drei Effekte)

• \(QS_{A} = \sum_{a}^{A} n_a(\bar{x}_a - \bar{x})^2\) (Haupteffekt A)

• \(QS_{B} = \sum_{b}^{B} n_b(\bar{x}_b - \bar{x})^2\) (Haupteffekt B)

• \(QS_{A\times B} = \sum_{a}^{A}\sum_{b}^{B} n_{ab}(\bar{x}_{ab} - (\bar{x}_{a} + \bar{x}_b - \bar{x})) ^2\) (Interaktionseffekt)

Residuale Quadratsumme

• \(QS_{res} = \sum_{a}^{A}\sum_{b}^{B} \sum_{i}^{n_{ab}} (x_i - \bar{x}_{ab})^2\)
  oder
  
• \(QS_{res} = QS_{tot} - QS_{A} - QS_{B} - QS_{A\times B}\)

\(i\): Laufindex für die einzelnen Zellen der Matrix (= Messwerte der AV)
\(a\) bzw. \(b\): Laufindex für die Stufen des Faktors A bzw. B
\(A\) bzw. \(B\): Anzahl Stufen des Faktors A bzw. B
\(n\): Anzahl Merkmalsträger

Teststatistik

Vorgehen: Analog zur ANOVA ohne MW

Freiheitsgrade:

• Freiheitsgrade Faktor A: \(\textit{df}_{A}\) = Anzahl Faktorstufen - 1
• Freiheitsgrade Faktor B: \(\textit{df}_{B}\) = Anzahl Faktorstufen - 1
• Freiheitsgrade Interaktionseffekt \(\textit{df}_{A \times B}\) = \(\textit{df}_{A} \times \textit{df}_{B}\)
• Freiheitsgrade der Residuen: \(\textit{df}_{res}\) = \(n - \textit{df}_{A} - \textit{df}_{B} - \textit{df}_{A \times B} - 1\)

Mittlere Quadratsummen:

• \(MQS_{A} = QS_{A}/\textit{df}_{A}\)
• \(MQS_{B} = QS_{B}/\textit{df}_{B}\)
• \(MQS_{A \times B} = QS_{A \times B}/\textit{df}_{A \times B}\)
• \(MQS_{res} = QS_{res}/\textit{df}_{res}\)

Teststatistiken:

• \(F_{A} = MQS_{A}/MQS_{res}\)
• \(F_{B} = MQS_{B}/MQS_{res}\)
• \(F_{A \times B} = MQS_{A \times B}/MQS_{res}\)

F-Verteilung

Kritische Werte der F-Verteilung

Werte der F-Verteilung

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	40	50	100	Inf
1	161.45	199.50	215.71	224.58	230.16	233.99	236.77	238.88	240.54	241.88	242.98	243.91	244.69	245.36	245.95	246.46	246.92	247.32	247.69	248.01	248.31	248.58	248.83	249.05	249.26	249.45	249.63	249.80	249.95	250.10	251.14	251.77	253.04	254.31
2	18.51	19.00	19.16	19.25	19.30	19.33	19.35	19.37	19.38	19.40	19.40	19.41	19.42	19.42	19.43	19.43	19.44	19.44	19.44	19.45	19.45	19.45	19.45	19.45	19.46	19.46	19.46	19.46	19.46	19.46	19.47	19.48	19.49	19.50
3	10.13	9.55	9.28	9.12	9.01	8.94	8.89	8.85	8.81	8.79	8.76	8.74	8.73	8.71	8.70	8.69	8.68	8.67	8.67	8.66	8.65	8.65	8.64	8.64	8.63	8.63	8.63	8.62	8.62	8.62	8.59	8.58	8.55	8.53
4	7.71	6.94	6.59	6.39	6.26	6.16	6.09	6.04	6.00	5.96	5.94	5.91	5.89	5.87	5.86	5.84	5.83	5.82	5.81	5.80	5.79	5.79	5.78	5.77	5.77	5.76	5.76	5.75	5.75	5.75	5.72	5.70	5.66	5.63
5	6.61	5.79	5.41	5.19	5.05	4.95	4.88	4.82	4.77	4.74	4.70	4.68	4.66	4.64	4.62	4.60	4.59	4.58	4.57	4.56	4.55	4.54	4.53	4.53	4.52	4.52	4.51	4.50	4.50	4.50	4.46	4.44	4.41	4.36
6	5.99	5.14	4.76	4.53	4.39	4.28	4.21	4.15	4.10	4.06	4.03	4.00	3.98	3.96	3.94	3.92	3.91	3.90	3.88	3.87	3.86	3.86	3.85	3.84	3.83	3.83	3.82	3.82	3.81	3.81	3.77	3.75	3.71	3.67
7	5.59	4.74	4.35	4.12	3.97	3.87	3.79	3.73	3.68	3.64	3.60	3.57	3.55	3.53	3.51	3.49	3.48	3.47	3.46	3.44	3.43	3.43	3.42	3.41	3.40	3.40	3.39	3.39	3.38	3.38	3.34	3.32	3.27	3.23
8	5.32	4.46	4.07	3.84	3.69	3.58	3.50	3.44	3.39	3.35	3.31	3.28	3.26	3.24	3.22	3.20	3.19	3.17	3.16	3.15	3.14	3.13	3.12	3.12	3.11	3.10	3.10	3.09	3.08	3.08	3.04	3.02	2.97	2.93
9	5.12	4.26	3.86	3.63	3.48	3.37	3.29	3.23	3.18	3.14	3.10	3.07	3.05	3.03	3.01	2.99	2.97	2.96	2.95	2.94	2.93	2.92	2.91	2.90	2.89	2.89	2.88	2.87	2.87	2.86	2.83	2.80	2.76	2.71
10	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	3.02	2.98	2.94	2.91	2.89	2.86	2.85	2.83	2.81	2.80	2.79	2.77	2.76	2.75	2.75	2.74	2.73	2.72	2.72	2.71	2.70	2.70	2.66	2.64	2.59	2.54
11	4.84	3.98	3.59	3.36	3.20	3.09	3.01	2.95	2.90	2.85	2.82	2.79	2.76	2.74	2.72	2.70	2.69	2.67	2.66	2.65	2.64	2.63	2.62	2.61	2.60	2.59	2.59	2.58	2.58	2.57	2.53	2.51	2.46	2.40
12	4.75	3.89	3.49	3.26	3.11	3.00	2.91	2.85	2.80	2.75	2.72	2.69	2.66	2.64	2.62	2.60	2.58	2.57	2.56	2.54	2.53	2.52	2.51	2.51	2.50	2.49	2.48	2.48	2.47	2.47	2.43	2.40	2.35	2.30
13	4.67	3.81	3.41	3.18	3.03	2.92	2.83	2.77	2.71	2.67	2.63	2.60	2.58	2.55	2.53	2.51	2.50	2.48	2.47	2.46	2.45	2.44	2.43	2.42	2.41	2.41	2.40	2.39	2.39	2.38	2.34	2.31	2.26	2.21
14	4.60	3.74	3.34	3.11	2.96	2.85	2.76	2.70	2.65	2.60	2.57	2.53	2.51	2.48	2.46	2.44	2.43	2.41	2.40	2.39	2.38	2.37	2.36	2.35	2.34	2.33	2.33	2.32	2.31	2.31	2.27	2.24	2.19	2.13
15	4.54	3.68	3.29	3.06	2.90	2.79	2.71	2.64	2.59	2.54	2.51	2.48	2.45	2.42	2.40	2.38	2.37	2.35	2.34	2.33	2.32	2.31	2.30	2.29	2.28	2.27	2.27	2.26	2.25	2.25	2.20	2.18	2.12	2.07
16	4.49	3.63	3.24	3.01	2.85	2.74	2.66	2.59	2.54	2.49	2.46	2.42	2.40	2.37	2.35	2.33	2.32	2.30	2.29	2.28	2.26	2.25	2.24	2.24	2.23	2.22	2.21	2.21	2.20	2.19	2.15	2.12	2.07	2.01
17	4.45	3.59	3.20	2.96	2.81	2.70	2.61	2.55	2.49	2.45	2.41	2.38	2.35	2.33	2.31	2.29	2.27	2.26	2.24	2.23	2.22	2.21	2.20	2.19	2.18	2.17	2.17	2.16	2.15	2.15	2.10	2.08	2.02	1.96
18	4.41	3.55	3.16	2.93	2.77	2.66	2.58	2.51	2.46	2.41	2.37	2.34	2.31	2.29	2.27	2.25	2.23	2.22	2.20	2.19	2.18	2.17	2.16	2.15	2.14	2.13	2.13	2.12	2.11	2.11	2.06	2.04	1.98	1.92
19	4.38	3.52	3.13	2.90	2.74	2.63	2.54	2.48	2.42	2.38	2.34	2.31	2.28	2.26	2.23	2.21	2.20	2.18	2.17	2.16	2.14	2.13	2.12	2.11	2.11	2.10	2.09	2.08	2.08	2.07	2.03	2.00	1.94	1.88
20	4.35	3.49	3.10	2.87	2.71	2.60	2.51	2.45	2.39	2.35	2.31	2.28	2.25	2.22	2.20	2.18	2.17	2.15	2.14	2.12	2.11	2.10	2.09	2.08	2.07	2.07	2.06	2.05	2.05	2.04	1.99	1.97	1.91	1.84
21	4.32	3.47	3.07	2.84	2.68	2.57	2.49	2.42	2.37	2.32	2.28	2.25	2.22	2.20	2.18	2.16	2.14	2.12	2.11	2.10	2.08	2.07	2.06	2.05	2.05	2.04	2.03	2.02	2.02	2.01	1.96	1.94	1.88	1.81
22	4.30	3.44	3.05	2.82	2.66	2.55	2.46	2.40	2.34	2.30	2.26	2.23	2.20	2.17	2.15	2.13	2.11	2.10	2.08	2.07	2.06	2.05	2.04	2.03	2.02	2.01	2.00	2.00	1.99	1.98	1.94	1.91	1.85	1.78
23	4.28	3.42	3.03	2.80	2.64	2.53	2.44	2.37	2.32	2.27	2.24	2.20	2.18	2.15	2.13	2.11	2.09	2.08	2.06	2.05	2.04	2.02	2.01	2.01	2.00	1.99	1.98	1.97	1.97	1.96	1.91	1.88	1.82	1.76
24	4.26	3.40	3.01	2.78	2.62	2.51	2.42	2.36	2.30	2.25	2.22	2.18	2.15	2.13	2.11	2.09	2.07	2.05	2.04	2.03	2.01	2.00	1.99	1.98	1.97	1.97	1.96	1.95	1.95	1.94	1.89	1.86	1.80	1.73
25	4.24	3.39	2.99	2.76	2.60	2.49	2.40	2.34	2.28	2.24	2.20	2.16	2.14	2.11	2.09	2.07	2.05	2.04	2.02	2.01	2.00	1.98	1.97	1.96	1.96	1.95	1.94	1.93	1.93	1.92	1.87	1.84	1.78	1.71
26	4.23	3.37	2.98	2.74	2.59	2.47	2.39	2.32	2.27	2.22	2.18	2.15	2.12	2.09	2.07	2.05	2.03	2.02	2.00	1.99	1.98	1.97	1.96	1.95	1.94	1.93	1.92	1.91	1.91	1.90	1.85	1.82	1.76	1.69
27	4.21	3.35	2.96	2.73	2.57	2.46	2.37	2.31	2.25	2.20	2.17	2.13	2.10	2.08	2.06	2.04	2.02	2.00	1.99	1.97	1.96	1.95	1.94	1.93	1.92	1.91	1.90	1.90	1.89	1.88	1.84	1.81	1.74	1.67
28	4.20	3.34	2.95	2.71	2.56	2.45	2.36	2.29	2.24	2.19	2.15	2.12	2.09	2.06	2.04	2.02	2.00	1.99	1.97	1.96	1.95	1.93	1.92	1.91	1.91	1.90	1.89	1.88	1.88	1.87	1.82	1.79	1.73	1.65
29	4.18	3.33	2.93	2.70	2.55	2.43	2.35	2.28	2.22	2.18	2.14	2.10	2.08	2.05	2.03	2.01	1.99	1.97	1.96	1.94	1.93	1.92	1.91	1.90	1.89	1.88	1.88	1.87	1.86	1.85	1.81	1.77	1.71	1.64
30	4.17	3.32	2.92	2.69	2.53	2.42	2.33	2.27	2.21	2.16	2.13	2.09	2.06	2.04	2.01	1.99	1.98	1.96	1.95	1.93	1.92	1.91	1.90	1.89	1.88	1.87	1.86	1.85	1.85	1.84	1.79	1.76	1.70	1.62
40	4.08	3.23	2.84	2.61	2.45	2.34	2.25	2.18	2.12	2.08	2.04	2.00	1.97	1.95	1.92	1.90	1.89	1.87	1.85	1.84	1.83	1.81	1.80	1.79	1.78	1.77	1.77	1.76	1.75	1.74	1.69	1.66	1.59	1.51
50	4.03	3.18	2.79	2.56	2.40	2.29	2.20	2.13	2.07	2.03	1.99	1.95	1.92	1.89	1.87	1.85	1.83	1.81	1.80	1.78	1.77	1.76	1.75	1.74	1.73	1.72	1.71	1.70	1.69	1.69	1.63	1.60	1.52	1.44
100	3.94	3.09	2.70	2.46	2.31	2.19	2.10	2.03	1.97	1.93	1.89	1.85	1.82	1.79	1.77	1.75	1.73	1.71	1.69	1.68	1.66	1.65	1.64	1.63	1.62	1.61	1.60	1.59	1.58	1.57	1.52	1.48	1.39	1.28
Inf	3.84	3.00	2.60	2.37	2.21	2.10	2.01	1.94	1.88	1.83	1.79	1.75	1.72	1.69	1.67	1.64	1.62	1.60	1.59	1.57	1.56	1.54	1.53	1.52	1.51	1.50	1.49	1.48	1.47	1.46	1.39	1.35	1.24	1.00

ANOVA-Tabelle

Quelle	QS	df	MQS	F	p
Faktor A	QS\(_{A}\)	df\(_{A}\)	MQS\(_{A}\)	F\(_A\)	p\(_A\)
Faktor B	QS\(_{B}\)	df\(_{B}\)	MQS\(_{B}\)	F\(_B\)	p\(_B\)
A x B	QS\(_{A \times B}\)	df\(_{A \times B}\)	MQS\(_{A \times B}\)	F\(_{A \times B}\)	p\(_{A \times B}\)
Residuen	QS\(_{res}\)	df\(_{res}\)	MQS\(_{res}\)
Gesamt	QS\(_{tot}\)	df\(_{tot}\)

Erläuterungen:

• QS\(_{tot}\) = QS\(_{mod}\) + QS\(_{res}\) = QS\(_{A}\) + QS\(_{B}\) + QS\(_{A \times B}\) + QS\(_{res}\)
• df\(_{tot}\) = df\(_{mod}\) + df\(_{res}\) = df\(_{A}\) + df\(_{B}\) + df\(_{A \times B}\) + df\(_{res}\)
• MQS\(_{A}\) = QS\(_{A}\)/df\(_{A}\); analog B bzw. A \(\times\) B
• MQS\(_{res}\) = QS\(_{res}\)/df\(_{res}\)
• F\(_{A}\) = MQS\(_{A}\)/MQS\(_{res}\); analog B bzw. A \(\times\) B
• p: p(F | H\(_0\))

🍺👓 Beispiel

                   Df Sum Sq Mean Sq F value   Pr(>F)    
Geschlecht          1    169   168.7   2.032    0.161    
Alkohol             2   3332  1666.1  20.065 7.65e-07 ***
Geschlecht:Alkohol  2   1978   989.1  11.911 7.99e-05 ***
Residuals          42   3488    83.0                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

                      eta.sq eta.sq.part
Geschlecht         0.0188197  0.04615385
Alkohol            0.3716310  0.48862074
Geschlecht:Alkohol 0.2206087  0.36192110

Voraussetzungen & Post-Hoc-Vergleiche

Voraussetzungen

• Unabhängigkeit der Gruppen (insbes. keine Messwiederholung)
• Intervallskalierung der AV
• Normalverteilung der AV in den Gruppen
  • bei ähnlich großen Gruppen kein Problem
  • allgemein: robust gegenüber Verletzung
  • Prüfung: häufig grafisch; alternativ: Kolmogorow-Smirnow-Test
• Varianzhomogenität
  • bei ähnlich großen Gruppen kein Problem
  • robust gegenüber Verletzung
  • Prüfung: Levene-Test; bei Verletzung: z. B. Korrektur nach White

NV-Test grafisch: QQ-Plot

Levene-Test

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  5  1.4252 0.2351
      42               

ANOVA ohne/mit Korrektur bei Inhomogenität

ANOVA Table (type II tests)

              Effect DFn DFd      F        p p<.05   pes
1         Geschlecht   1  42  2.032 1.61e-01       0.046
2            Alkohol   2  42 20.065 7.65e-07     * 0.489
3 Geschlecht:Alkohol   2  42 11.911 7.99e-05     * 0.362

ANOVA Table (type II tests)

              Effect DFn DFd      F        p p<.05
1         Geschlecht   1  42  1.406 0.242000      
2            Alkohol   2  42  9.173 0.000495     *
3 Geschlecht:Alkohol   2  42 10.679 0.000178     *

Post-hoc-Vergleiche

• Bei signifikanten Haupteffekten: Wo sind die Unterschiede?
• Post-Hoc-Vergleiche nur für mehr als zwei Faktorstufen sinnvoll
• Verschiedene Verfahren; z. B. Bonferroni, Tukey

🍺👓 Beispiel (Tukey, Bonferroni)

Faktor “Alkohol”

 contrast          estimate   SE df t.ratio p.value
 2 Pints - 4 Pints   18.125 3.22 42   5.626  <.0001
 2 Pints - None       0.938 3.22 42   0.291  0.9544
 4 Pints - None     -17.188 3.22 42  -5.335  <.0001

Results are averaged over the levels of: Geschlecht 
P value adjustment: tukey method for comparing a family of 3 estimates 

 contrast          estimate   SE df t.ratio p.value
 2 Pints - 4 Pints   18.125 3.22 42   5.626  <.0001
 2 Pints - None       0.938 3.22 42   0.291  1.0000
 4 Pints - None     -17.188 3.22 42  -5.335  <.0001

Results are averaged over the levels of: Geschlecht 
P value adjustment: bonferroni method for 3 tests 

Faktor “Geschlecht”

Achtung: Post-Hoc-Vergleiche nicht sinnvoll, da nur zwei Faktorstufen!

 contrast      estimate   SE df t.ratio p.value
 Female - Male     3.75 2.63 42   1.426  0.1614

Results are averaged over the levels of: Alkohol 

 contrast      estimate   SE df t.ratio p.value
 Female - Male     3.75 2.63 42   1.426  0.1614

Results are averaged over the levels of: Alkohol 

Interaktion

Arten von Interaktion

Ordinale Interaktion

• Gleiche Trends für alle Linien in beiden Diagrammen
• Beide Haupteffekte sind global interpretierbar

Hybride Interaktion o. semidisordinale Interaktion

• Gleiche Trends in einem Diagramm, entgegengesetzte Trends im anderen
• Nur ein Haupteffekt ist global interpretierbar

Disordinale Interaktion

• Entgegengesetzte Trends in beiden Diagrammen
• Kein Haupteffekt ist global interpretierbar

Darstellung von Interaktion – Beispiel

Welche Arten der Interaktion
finden wir wo?