Varianzanalyse – ANOVA, einfaktoriell

_Statistik

Prof. Dr. Armin Eichinger

TH Deggendorf

16.05.2024

Überblick

• Einführung
• Signifikanztest
• Multiples Testen
• Voraussetzungen & Effektstärke
• Post-hoc-Vergleiche

Einführung

Das meint GPT:

Begriffe & Klassifikation

• Varianzanalyse ≙ Analysis of Variance ≙ ANOVA
• Unabhängige Variable (UV; auch: Faktor o. Treatment): Nominalskala (bzw. kategorial)
• Abhängige Variable (AV): mind. Intervallskala
• Fragestellung (alle Formulierungen sind äquivalent!):
  1. Unterscheiden sich die Ausprägungen der UV (also des Faktors) hinsichtlich der Ausprägung der AV?
  2. Hat der Faktor (die UV) einen Einfluss auf die AV?
  3. Gibt es einen Zusammenhang zwischen UV und AV?
• Versuchspläne mit und ohne Messwiederholung (engl. repeated measures design)
• Mehrfaktorielle ANOVA: Mehr als eine UV; z. B. zweifaktorielle ANOVA
• Beispiel dreifaktorielle ANOVA:
  • Faktor A hat vier, Faktor B hat drei und Faktor C hat zwei Ausprägungen
  • Versuchsdesign: (4 x 3 x 2)-Design

Beispiel 🐕

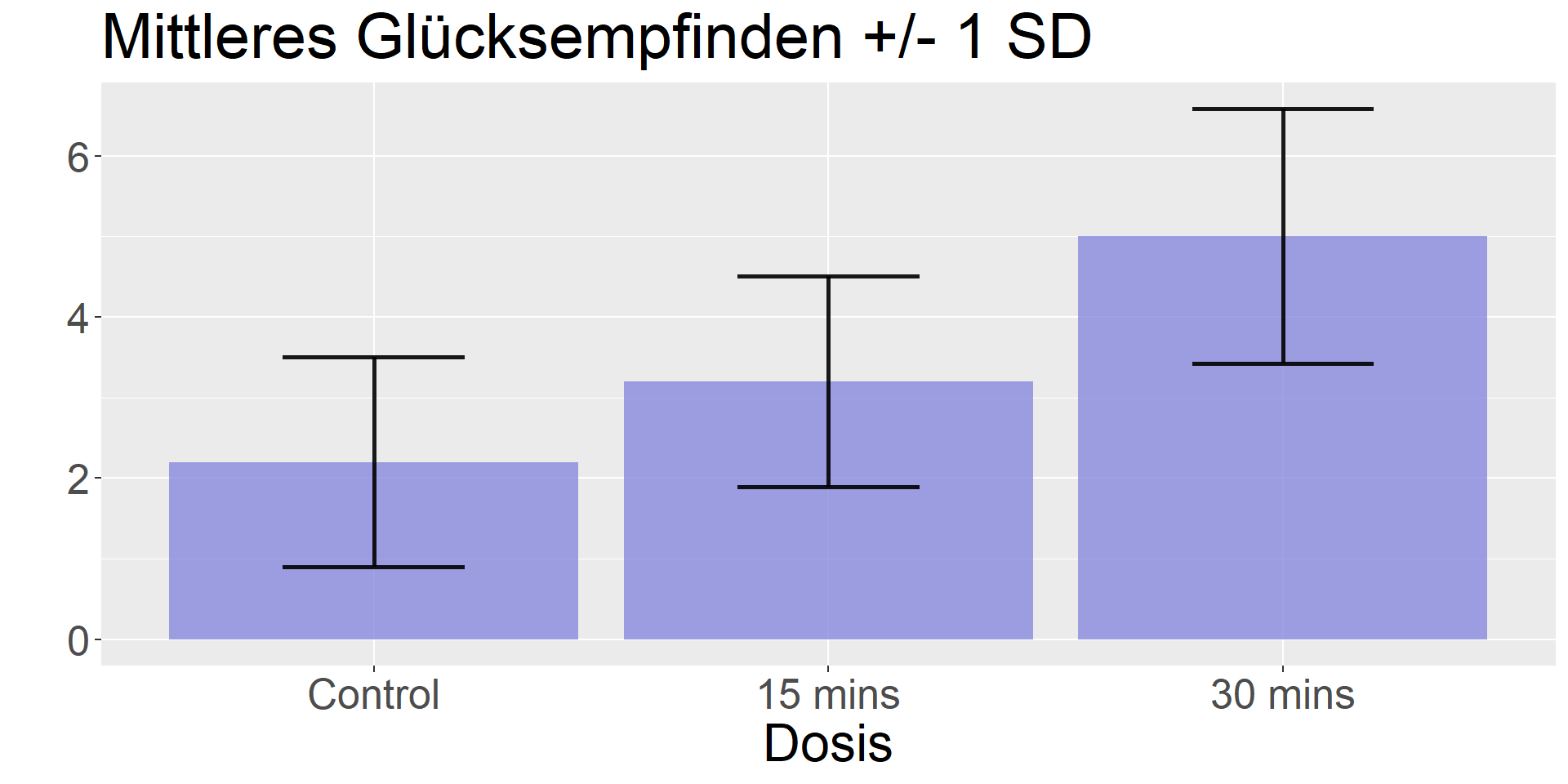
• Fragestellung: Steigert der Umgang mit Welpen unser Glückserleben?
• UV: Zwei Experimentalbedingungen (15 min + 30 min) und eine Kontrollbedingung (= insgesamt drei Faktorstufen)
• AV: Glücksindex (von 1 bis 10)

       id    dose happiness
1  25hto3 Control         3
2  121118 Control         2
3  t54p42 Control         1
4  s6u853 Control         1
5  tcs14p Control         4
6  oum4t7 15 mins         5
7  kfl7lq 15 mins         2
8  2gi51b 15 mins         4
9  d3j771 15 mins         2
10 eu23ns 15 mins         3
11 b343ey 30 mins         7
12 5nvg7h 30 mins         4
13 5ta11l 30 mins         5
14 82e7va 30 mins         3
15 667x5j 30 mins         6

Beispiel 🐕

Output der ANOVA:

Analysis of Variance Table

Response: happiness
          Df Sum Sq Mean Sq F value  Pr(>F)  
dose       2 20.133 10.0667  5.1186 0.02469 *
Residuals 12 23.600  1.9667                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Erläuterungen:

• “Df” (df): Freiheitsgrade des Modells (“dose”) sowie der Residuen; df\(_{mod}\) = Anzahl Faktorstufen - 1; df\(_{res}\) = n - Anzahl Faktorstufen
• “Sum Sq” (QS): Quadratsummen des Modells sowie der Residuen (QS\(_{mod}\), QS\(_{res}\))
• “Mean Sq” (MQS): Mittlere Quadratsummen (= QS/df) des Modells sowie der Residuen (MQS\(_{mod}\), MQS\(_{res}\))
• “F value” (F): F-Wert (= MQS\(_{mod}\)/MQS\(_{res}\)); unsere Teststatistik
• “Pr(>F)” (p): p-Wert; Wahrscheinlichkeit des Werts der Teststatistik unter Annahme von H\(_0\)

Signifikanztest

Hypothesen

Ausgangspunkt: Kein Effekt; d.h. die Mittelwerte
in den k Bedingungen unterscheiden sich nicht

H\(_0\): \(\mu_1 = \mu_2 = \dots = \mu_k\)

H\(_1\): \(\mu_i \neq \mu_j\) (für mindestens ein i, j; i \(\neq\) j)

Achtung - NICHT
H\(_1\): \(\mu_1 \neq \mu_2 \neq \dots \neq \mu_k\)

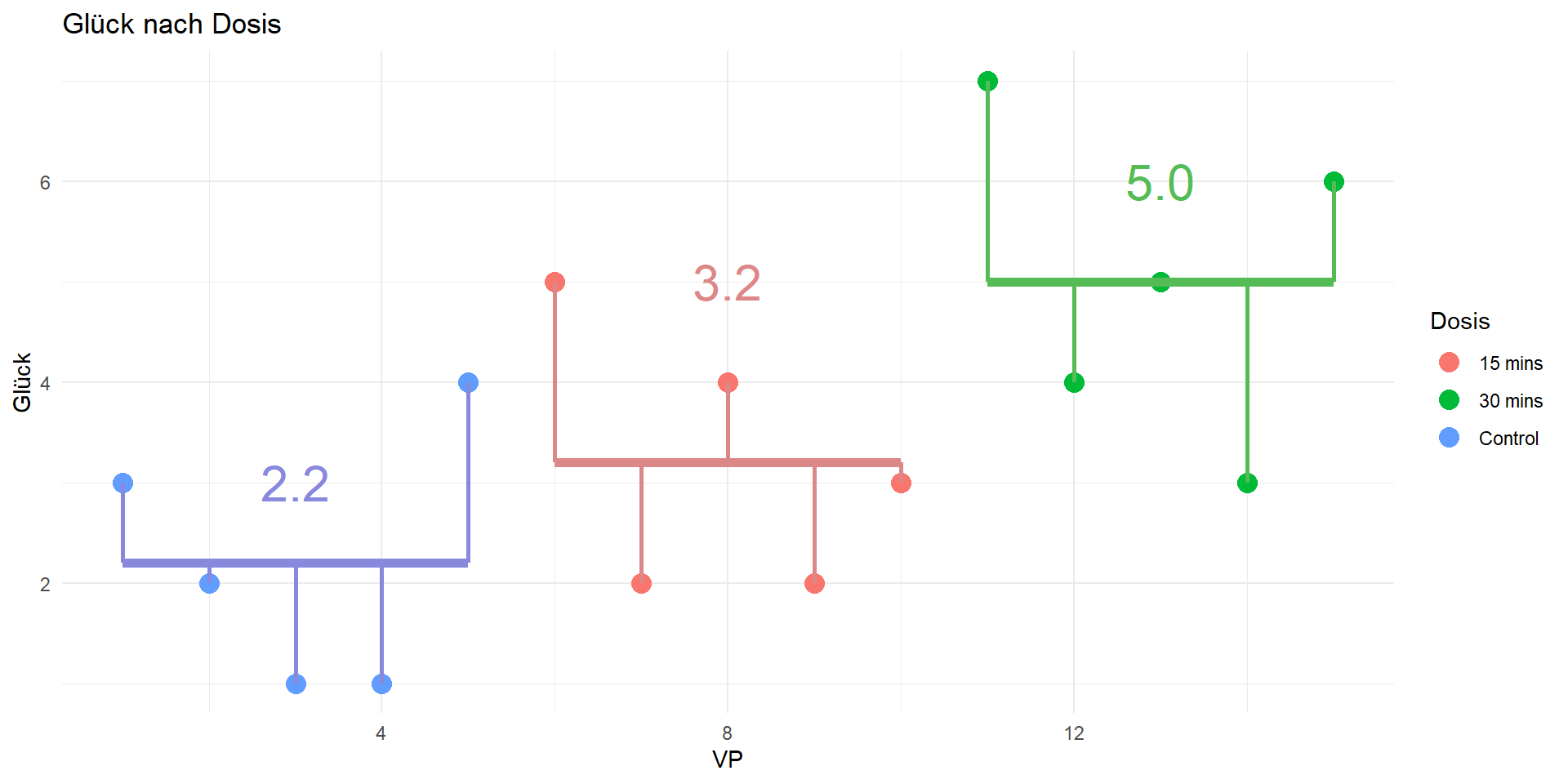
Quadratsummen

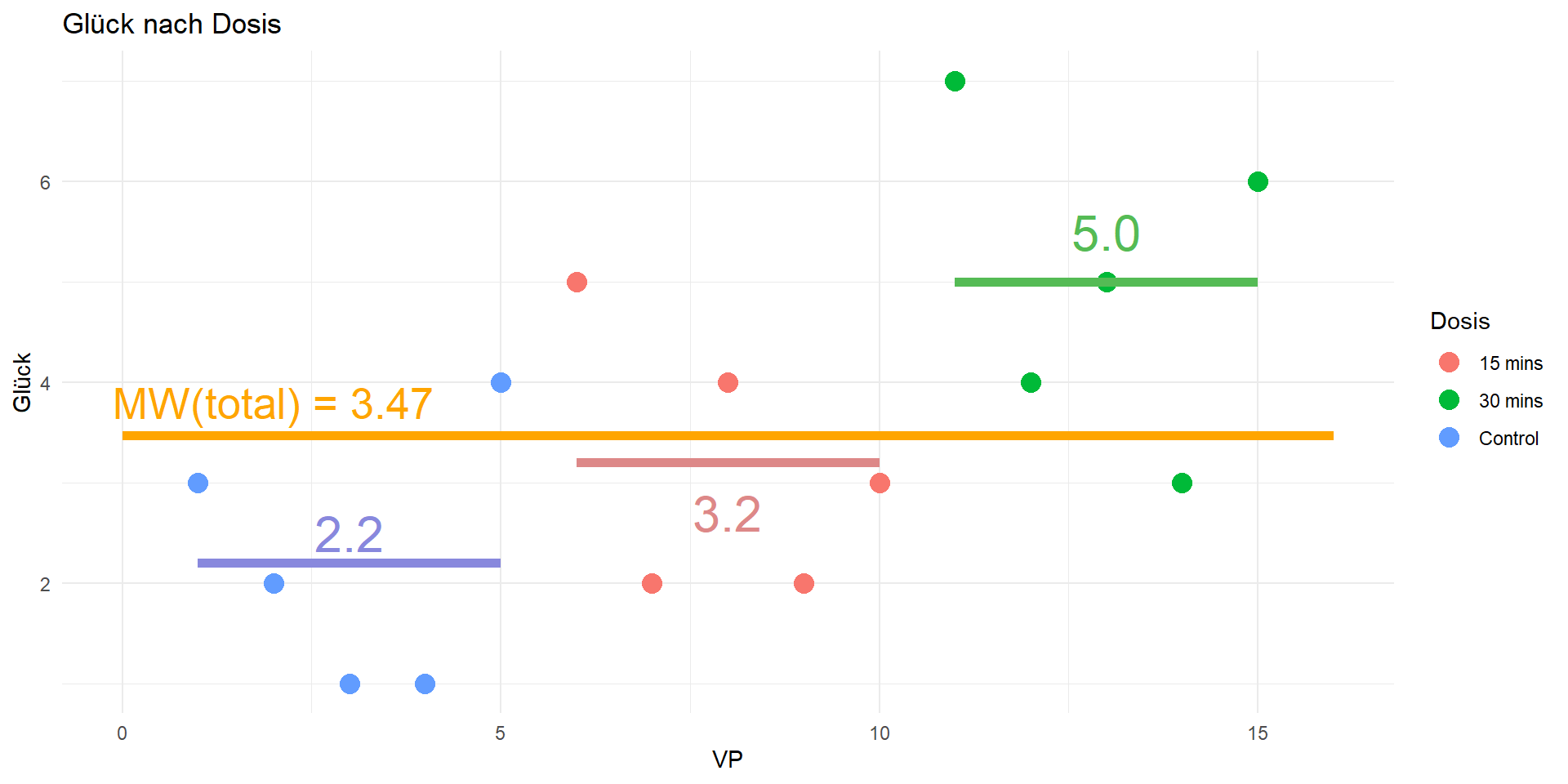
Totale Quadratsumme

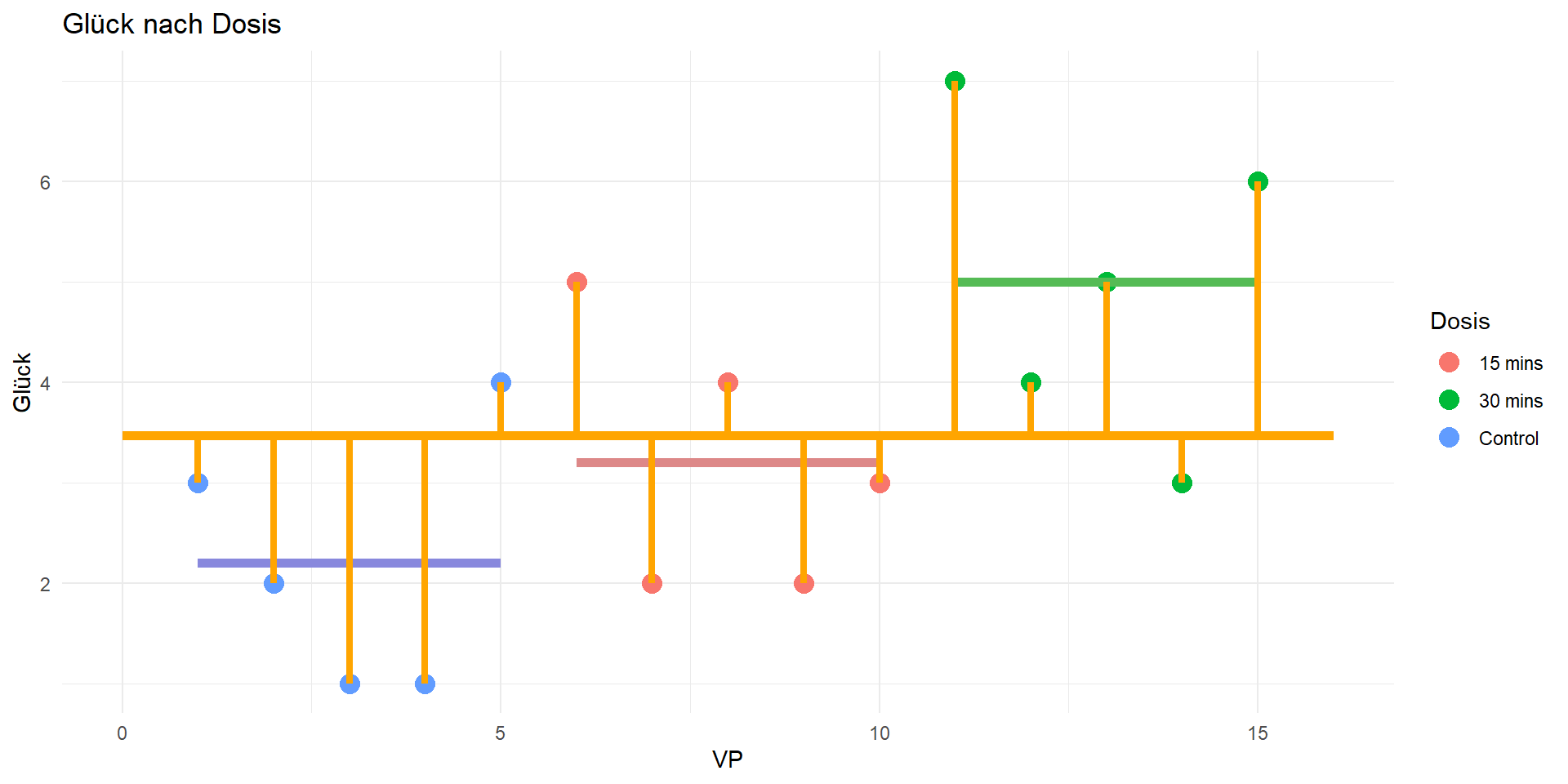
Modellquadratsumme

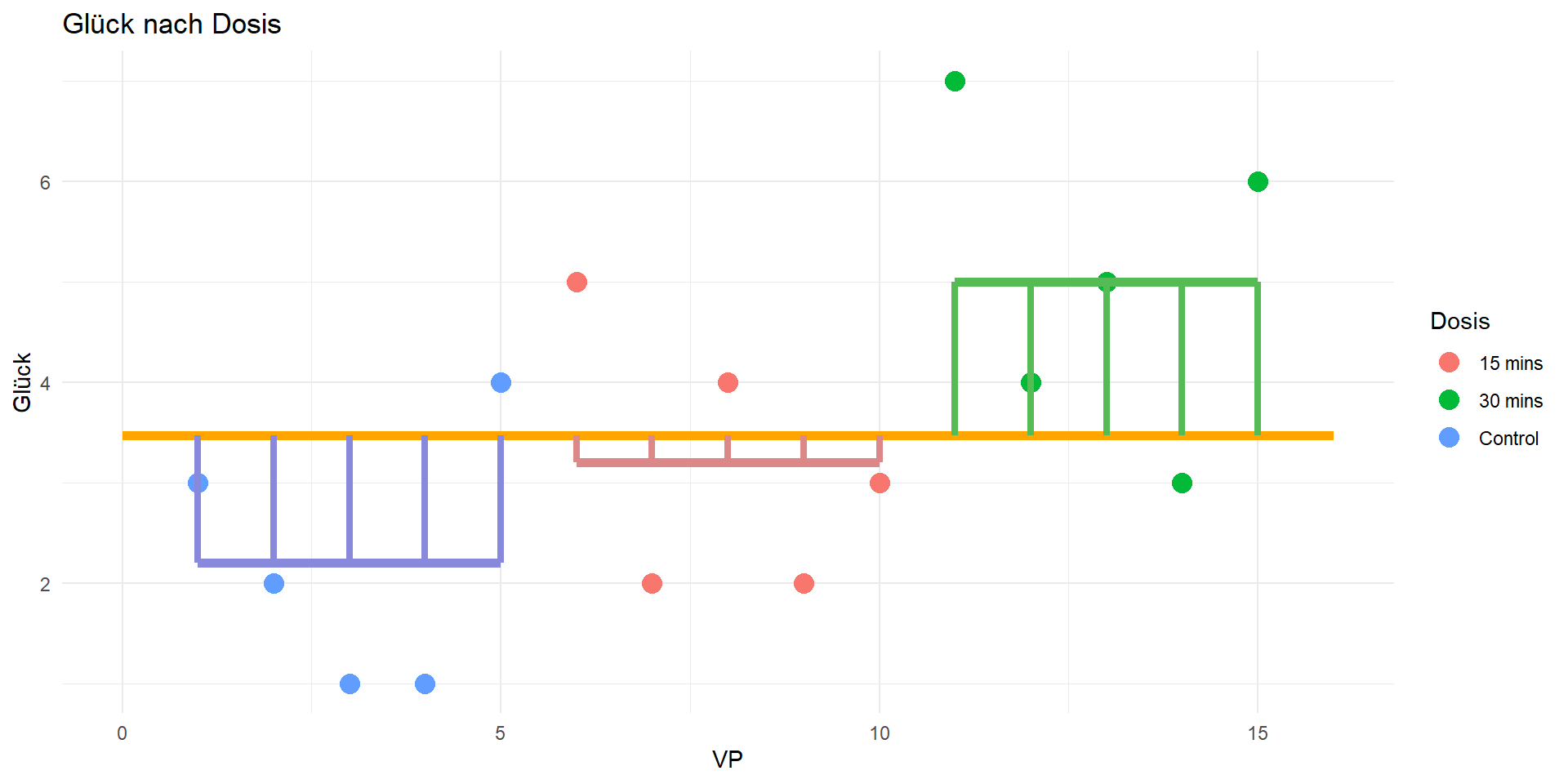
Residualquadratsumme

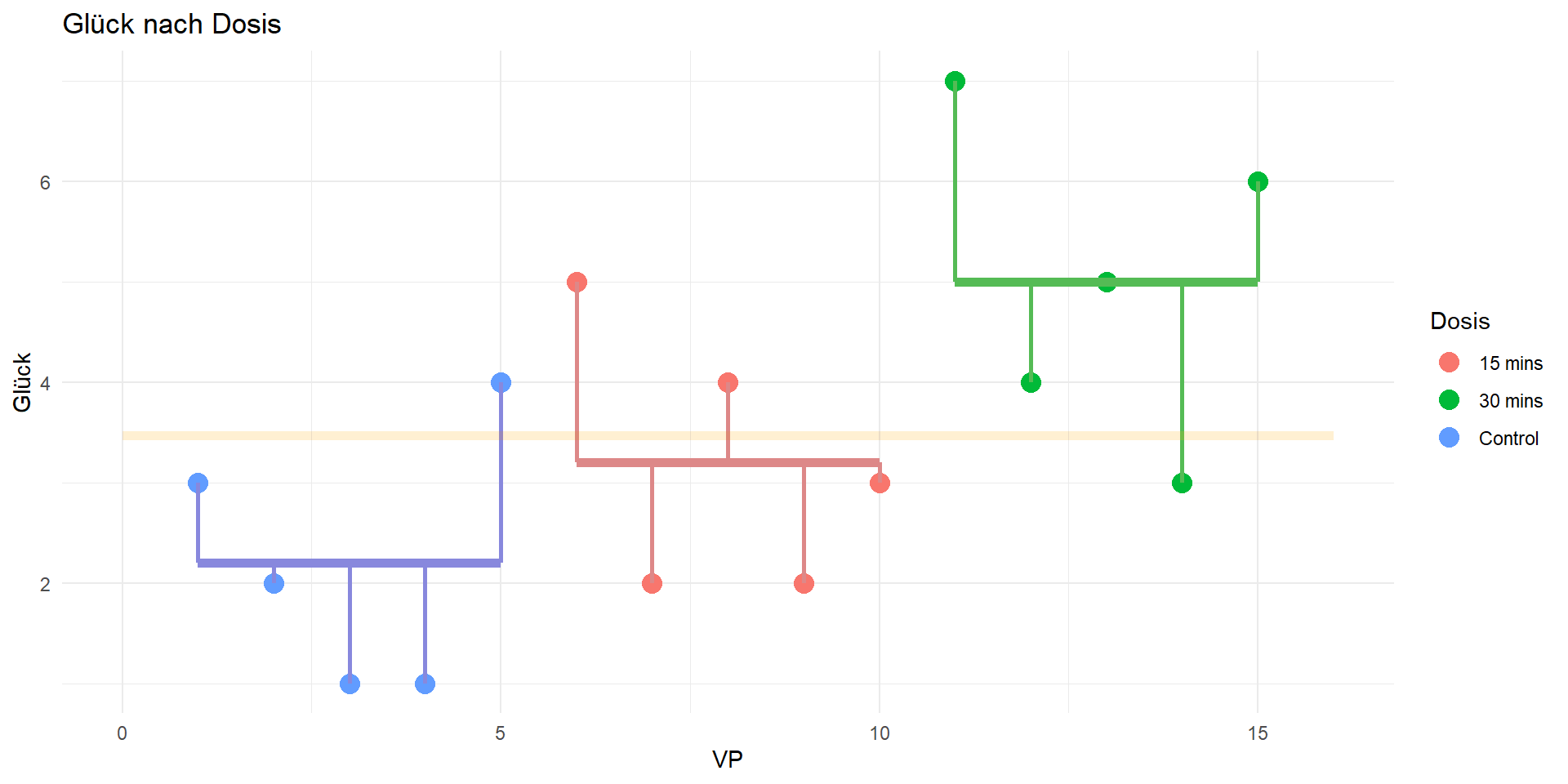
Quadratsummen: Zusammenhang

\(QS_{tot} = QS_{mod} + QS_{res}\)

Formeln:

• \(QS_{tot} = \sum_{i}^{n}(x_i - \bar{x})^2\)
• \(QS_{mod} = \sum_{l}^{k} n_l(\bar{x}_l - \bar{x})^2\)
• \(QS_{res} = \sum_{l}^{k}\sum_{i}^{n_l}(x_{li} - \bar{x}_l)^2\)
  
  \(k\): Anzahl der Bedingungen
  \(n_l\): Anzahl Merkmalsträger in Bedingung \(l\)
  \(\bar{x}_l\): Mittelwert in Bedingung \(l\)

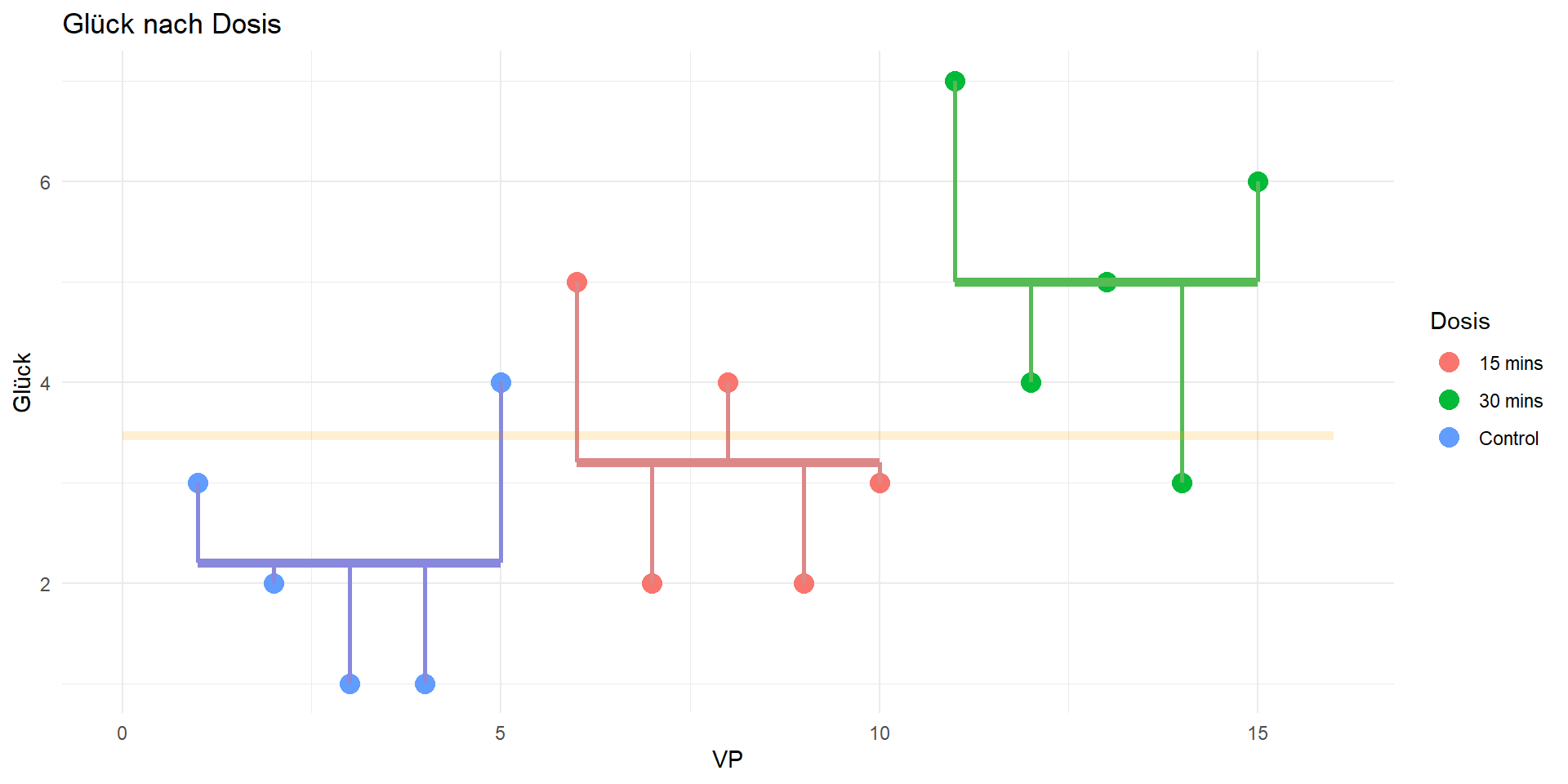
Teststatistik

Vorgehen: Analog zur Regressionsanalyse

Mittlere Quadratsummen & Freiheitsgrade:

• Freiheitsgrade des Modells: \(\textit{df}_{mod}\) = Anzahl Faktorstufen - 1
• Mittlere Modell-Quadratsumme: \(MQS_{mod} = QS_{mod}/\textit{df}_{mod}\)
• Freiheitsgrade der Residuen: \(\textit{df}_{res}\) = n - Anzahl Faktorstufen
• Mittlere Residualquadratsumme: \(MQS_{res} = QS_{res}/\textit{df}_{res}\)

Teststatistik:

• \(F = MQS_{mod}/MQS_{res}\)
• F-Verteilung: Abb. rechts

F-Verteilung

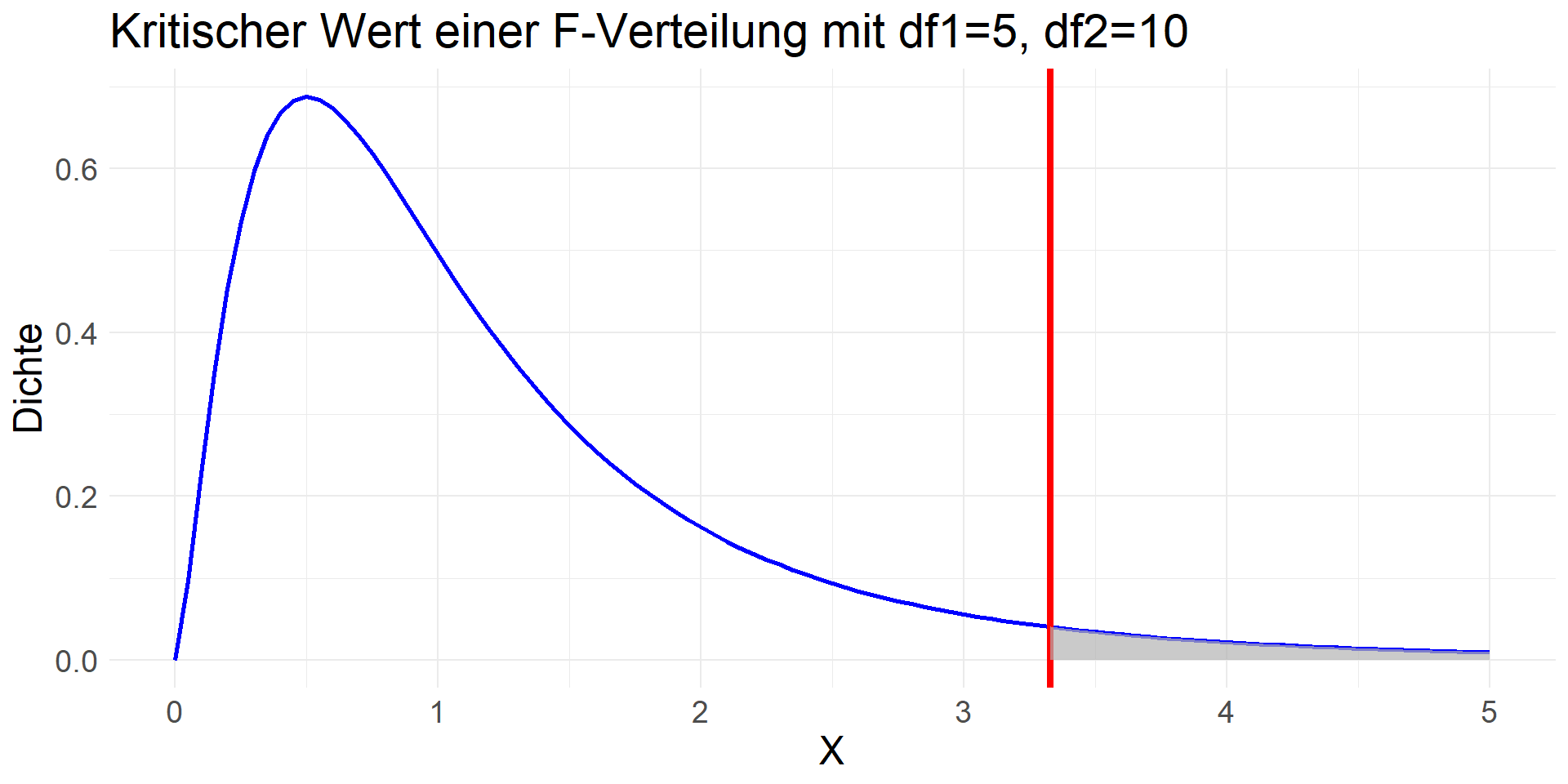
Kritische Werte der F-Verteilung

Werte der F-Verteilung

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	40	50	100	Inf
1	161.45	199.50	215.71	224.58	230.16	233.99	236.77	238.88	240.54	241.88	242.98	243.91	244.69	245.36	245.95	246.46	246.92	247.32	247.69	248.01	248.31	248.58	248.83	249.05	249.26	249.45	249.63	249.80	249.95	250.10	251.14	251.77	253.04	254.31
2	18.51	19.00	19.16	19.25	19.30	19.33	19.35	19.37	19.38	19.40	19.40	19.41	19.42	19.42	19.43	19.43	19.44	19.44	19.44	19.45	19.45	19.45	19.45	19.45	19.46	19.46	19.46	19.46	19.46	19.46	19.47	19.48	19.49	19.50
3	10.13	9.55	9.28	9.12	9.01	8.94	8.89	8.85	8.81	8.79	8.76	8.74	8.73	8.71	8.70	8.69	8.68	8.67	8.67	8.66	8.65	8.65	8.64	8.64	8.63	8.63	8.63	8.62	8.62	8.62	8.59	8.58	8.55	8.53
4	7.71	6.94	6.59	6.39	6.26	6.16	6.09	6.04	6.00	5.96	5.94	5.91	5.89	5.87	5.86	5.84	5.83	5.82	5.81	5.80	5.79	5.79	5.78	5.77	5.77	5.76	5.76	5.75	5.75	5.75	5.72	5.70	5.66	5.63
5	6.61	5.79	5.41	5.19	5.05	4.95	4.88	4.82	4.77	4.74	4.70	4.68	4.66	4.64	4.62	4.60	4.59	4.58	4.57	4.56	4.55	4.54	4.53	4.53	4.52	4.52	4.51	4.50	4.50	4.50	4.46	4.44	4.41	4.36
6	5.99	5.14	4.76	4.53	4.39	4.28	4.21	4.15	4.10	4.06	4.03	4.00	3.98	3.96	3.94	3.92	3.91	3.90	3.88	3.87	3.86	3.86	3.85	3.84	3.83	3.83	3.82	3.82	3.81	3.81	3.77	3.75	3.71	3.67
7	5.59	4.74	4.35	4.12	3.97	3.87	3.79	3.73	3.68	3.64	3.60	3.57	3.55	3.53	3.51	3.49	3.48	3.47	3.46	3.44	3.43	3.43	3.42	3.41	3.40	3.40	3.39	3.39	3.38	3.38	3.34	3.32	3.27	3.23
8	5.32	4.46	4.07	3.84	3.69	3.58	3.50	3.44	3.39	3.35	3.31	3.28	3.26	3.24	3.22	3.20	3.19	3.17	3.16	3.15	3.14	3.13	3.12	3.12	3.11	3.10	3.10	3.09	3.08	3.08	3.04	3.02	2.97	2.93
9	5.12	4.26	3.86	3.63	3.48	3.37	3.29	3.23	3.18	3.14	3.10	3.07	3.05	3.03	3.01	2.99	2.97	2.96	2.95	2.94	2.93	2.92	2.91	2.90	2.89	2.89	2.88	2.87	2.87	2.86	2.83	2.80	2.76	2.71
10	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	3.02	2.98	2.94	2.91	2.89	2.86	2.85	2.83	2.81	2.80	2.79	2.77	2.76	2.75	2.75	2.74	2.73	2.72	2.72	2.71	2.70	2.70	2.66	2.64	2.59	2.54
11	4.84	3.98	3.59	3.36	3.20	3.09	3.01	2.95	2.90	2.85	2.82	2.79	2.76	2.74	2.72	2.70	2.69	2.67	2.66	2.65	2.64	2.63	2.62	2.61	2.60	2.59	2.59	2.58	2.58	2.57	2.53	2.51	2.46	2.40
12	4.75	3.89	3.49	3.26	3.11	3.00	2.91	2.85	2.80	2.75	2.72	2.69	2.66	2.64	2.62	2.60	2.58	2.57	2.56	2.54	2.53	2.52	2.51	2.51	2.50	2.49	2.48	2.48	2.47	2.47	2.43	2.40	2.35	2.30
13	4.67	3.81	3.41	3.18	3.03	2.92	2.83	2.77	2.71	2.67	2.63	2.60	2.58	2.55	2.53	2.51	2.50	2.48	2.47	2.46	2.45	2.44	2.43	2.42	2.41	2.41	2.40	2.39	2.39	2.38	2.34	2.31	2.26	2.21
14	4.60	3.74	3.34	3.11	2.96	2.85	2.76	2.70	2.65	2.60	2.57	2.53	2.51	2.48	2.46	2.44	2.43	2.41	2.40	2.39	2.38	2.37	2.36	2.35	2.34	2.33	2.33	2.32	2.31	2.31	2.27	2.24	2.19	2.13
15	4.54	3.68	3.29	3.06	2.90	2.79	2.71	2.64	2.59	2.54	2.51	2.48	2.45	2.42	2.40	2.38	2.37	2.35	2.34	2.33	2.32	2.31	2.30	2.29	2.28	2.27	2.27	2.26	2.25	2.25	2.20	2.18	2.12	2.07
16	4.49	3.63	3.24	3.01	2.85	2.74	2.66	2.59	2.54	2.49	2.46	2.42	2.40	2.37	2.35	2.33	2.32	2.30	2.29	2.28	2.26	2.25	2.24	2.24	2.23	2.22	2.21	2.21	2.20	2.19	2.15	2.12	2.07	2.01
17	4.45	3.59	3.20	2.96	2.81	2.70	2.61	2.55	2.49	2.45	2.41	2.38	2.35	2.33	2.31	2.29	2.27	2.26	2.24	2.23	2.22	2.21	2.20	2.19	2.18	2.17	2.17	2.16	2.15	2.15	2.10	2.08	2.02	1.96
18	4.41	3.55	3.16	2.93	2.77	2.66	2.58	2.51	2.46	2.41	2.37	2.34	2.31	2.29	2.27	2.25	2.23	2.22	2.20	2.19	2.18	2.17	2.16	2.15	2.14	2.13	2.13	2.12	2.11	2.11	2.06	2.04	1.98	1.92
19	4.38	3.52	3.13	2.90	2.74	2.63	2.54	2.48	2.42	2.38	2.34	2.31	2.28	2.26	2.23	2.21	2.20	2.18	2.17	2.16	2.14	2.13	2.12	2.11	2.11	2.10	2.09	2.08	2.08	2.07	2.03	2.00	1.94	1.88
20	4.35	3.49	3.10	2.87	2.71	2.60	2.51	2.45	2.39	2.35	2.31	2.28	2.25	2.22	2.20	2.18	2.17	2.15	2.14	2.12	2.11	2.10	2.09	2.08	2.07	2.07	2.06	2.05	2.05	2.04	1.99	1.97	1.91	1.84
21	4.32	3.47	3.07	2.84	2.68	2.57	2.49	2.42	2.37	2.32	2.28	2.25	2.22	2.20	2.18	2.16	2.14	2.12	2.11	2.10	2.08	2.07	2.06	2.05	2.05	2.04	2.03	2.02	2.02	2.01	1.96	1.94	1.88	1.81
22	4.30	3.44	3.05	2.82	2.66	2.55	2.46	2.40	2.34	2.30	2.26	2.23	2.20	2.17	2.15	2.13	2.11	2.10	2.08	2.07	2.06	2.05	2.04	2.03	2.02	2.01	2.00	2.00	1.99	1.98	1.94	1.91	1.85	1.78
23	4.28	3.42	3.03	2.80	2.64	2.53	2.44	2.37	2.32	2.27	2.24	2.20	2.18	2.15	2.13	2.11	2.09	2.08	2.06	2.05	2.04	2.02	2.01	2.01	2.00	1.99	1.98	1.97	1.97	1.96	1.91	1.88	1.82	1.76
24	4.26	3.40	3.01	2.78	2.62	2.51	2.42	2.36	2.30	2.25	2.22	2.18	2.15	2.13	2.11	2.09	2.07	2.05	2.04	2.03	2.01	2.00	1.99	1.98	1.97	1.97	1.96	1.95	1.95	1.94	1.89	1.86	1.80	1.73
25	4.24	3.39	2.99	2.76	2.60	2.49	2.40	2.34	2.28	2.24	2.20	2.16	2.14	2.11	2.09	2.07	2.05	2.04	2.02	2.01	2.00	1.98	1.97	1.96	1.96	1.95	1.94	1.93	1.93	1.92	1.87	1.84	1.78	1.71
26	4.23	3.37	2.98	2.74	2.59	2.47	2.39	2.32	2.27	2.22	2.18	2.15	2.12	2.09	2.07	2.05	2.03	2.02	2.00	1.99	1.98	1.97	1.96	1.95	1.94	1.93	1.92	1.91	1.91	1.90	1.85	1.82	1.76	1.69
27	4.21	3.35	2.96	2.73	2.57	2.46	2.37	2.31	2.25	2.20	2.17	2.13	2.10	2.08	2.06	2.04	2.02	2.00	1.99	1.97	1.96	1.95	1.94	1.93	1.92	1.91	1.90	1.90	1.89	1.88	1.84	1.81	1.74	1.67
28	4.20	3.34	2.95	2.71	2.56	2.45	2.36	2.29	2.24	2.19	2.15	2.12	2.09	2.06	2.04	2.02	2.00	1.99	1.97	1.96	1.95	1.93	1.92	1.91	1.91	1.90	1.89	1.88	1.88	1.87	1.82	1.79	1.73	1.65
29	4.18	3.33	2.93	2.70	2.55	2.43	2.35	2.28	2.22	2.18	2.14	2.10	2.08	2.05	2.03	2.01	1.99	1.97	1.96	1.94	1.93	1.92	1.91	1.90	1.89	1.88	1.88	1.87	1.86	1.85	1.81	1.77	1.71	1.64
30	4.17	3.32	2.92	2.69	2.53	2.42	2.33	2.27	2.21	2.16	2.13	2.09	2.06	2.04	2.01	1.99	1.98	1.96	1.95	1.93	1.92	1.91	1.90	1.89	1.88	1.87	1.86	1.85	1.85	1.84	1.79	1.76	1.70	1.62
40	4.08	3.23	2.84	2.61	2.45	2.34	2.25	2.18	2.12	2.08	2.04	2.00	1.97	1.95	1.92	1.90	1.89	1.87	1.85	1.84	1.83	1.81	1.80	1.79	1.78	1.77	1.77	1.76	1.75	1.74	1.69	1.66	1.59	1.51
50	4.03	3.18	2.79	2.56	2.40	2.29	2.20	2.13	2.07	2.03	1.99	1.95	1.92	1.89	1.87	1.85	1.83	1.81	1.80	1.78	1.77	1.76	1.75	1.74	1.73	1.72	1.71	1.70	1.69	1.69	1.63	1.60	1.52	1.44
100	3.94	3.09	2.70	2.46	2.31	2.19	2.10	2.03	1.97	1.93	1.89	1.85	1.82	1.79	1.77	1.75	1.73	1.71	1.69	1.68	1.66	1.65	1.64	1.63	1.62	1.61	1.60	1.59	1.58	1.57	1.52	1.48	1.39	1.28
Inf	3.84	3.00	2.60	2.37	2.21	2.10	2.01	1.94	1.88	1.83	1.79	1.75	1.72	1.69	1.67	1.64	1.62	1.60	1.59	1.57	1.56	1.54	1.53	1.52	1.51	1.50	1.49	1.48	1.47	1.46	1.39	1.35	1.24	1.00

ANOVA-Tabelle

(analog zur Regressionsanalyse)

Quelle	QS	df	MQS	F	p
Modell	QS\(_{mod}\)	df\(_{mod}\)	MQS\(_{mod}\)	F	p
Residuen	QS\(_{res}\)	df\(_{res}\)	MQS\(_{res}\)
Gesamt	QS\(_{tot}\)	df\(_{tot}\)

Erläuterungen:

• QS\(_{tot}\) = QS\(_{mod}\) + QS\(_{res}\)
• df\(_{tot}\) = df\(_{mod}\) + df\(_{res}\)
• MQS\(_{mod}\) = QS\(_{mod}\)/df\(_{mod}\)
• MQS\(_{res}\) = Q\(S_{res}\)/df\(_{res}\)
• F = MQS\(_{mod}\)/MQS\(_{res}\)
• p: p(F | H\(_0\))

Beispiel 🐕

Analysis of Variance Table

Response: happiness
          Df Sum Sq Mean Sq F value  Pr(>F)  
dose       2 20.133 10.0667  5.1186 0.02469 *
Residuals 12 23.600  1.9667                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Multiples Testen

Warum nicht mehrere t-Tests?

• Idee: Statt einer ANOVA mehrere t-Tests rechnen

• Beispiel mit 4 Gruppen: 6 t-Tests

  1. Gruppe 1 vs. 2
  2. Gruppe 1 vs. 3
  3. Gruppe 1 vs. 4
  4. Gruppe 2 vs. 3
  5. Gruppe 2 vs. 4
  6. Gruppe 3 vs. 4

• Allgemein: Für \(k\) Gruppen \(\frac{k(k - 1)}{2}\) einzelne t-Tests

• Beispiel 20 Versuchsbedingungen: \(\frac{20(20 - 1)}{2}\) = 190 Einzelvergleiche

• Problem: Jeder einzelne Test weist eigenen α-Fehler auf

• α-Fehler = Fehler 1. Art: Annahme der H\(_1\), obwohl H\(_0\) gilt

α-Fehler-Inflation

• P(α-Fehler für einen Test) = α = 0.05
  \(\Rightarrow\) P(keinen α-Fehler für einen Test) = 1 - 0.05 = 0.95

• P(keinen α-Fehler für sechs Tests) = 0.95\(^6\)
  \(\Rightarrow\) P(mindestens ein α-Fehler für sechs Tests) = 1 - 0.95\(^6\) = 0.265 = 26.5 %

• Offensichtlich: 26.5 \(\gg\) 5 % ❌
  \(\rightarrow\) α-Fehler-Inflation

• Beispiel 20 Versuchsbedingungen:
  P(mindestens ein α-Fehler für 190 Tests) = 1 - 0.95\(^{190}\) = 0.99994 = 99.994 %

• Alternative ANOVA: α-Fehler = 5 % ✅

Voraussetzungen & Effektstärke

Voraussetzungen

(Vergleichbar t-Test, da Erweiterung)

• Unabhängigkeit der Gruppen (insbes. keine Messwiederholung)
• Intervallskalierung der AV
• Normalverteilung der AV in den Gruppen
  • bei ähnlich großen Gruppen kein Problem
  • allgemein: robust gegenüber Verletzung
  • Prüfung: häufig grafisch; alternativ: Kolmogorow-Smirnow-Test
• Varianzhomogenität
  • bei ähnlich großen Gruppen kein Problem
  • robust gegenüber Verletzung
  • Prüfung: Levene-Test; bei Verletzung: z. B. Welch-Test

Effektstärke

• Maße der Effektstärke: \(\eta^2\) (verbreiteter) und \(\omega^2\)

• \(\eta^2\): unbereinigtes Effektstärkemaß (überschätzt Effekt tendenziell)

• \(\eta^2 = \frac{QS_{mod}}{QS_{tot}} = R^2\)

• \(\omega^2\): bereinigtes Effektstärkemaß

• \(\omega^2 = \frac{QS_{mod} - df_{mod}MQS_{res}}{QS_{tot}+MQS_{res}}\)

• Es gilt (für MQS\(_{res}\) > 0): \(\eta^2 > \omega^2\)

• Einordnung (gilt auch für \(\omega^2\))

  • kleiner Effekt: \(\eta^2\) = .01
  • mittlerer Effekt: \(\eta^2\) = .06
  • großer Effekt: \(\eta^2\) = .14

🐕 Beispiel

        eta.sq eta.sq.part
dose 0.4603659   0.4603659

Post-hoc-Vergleiche

Post-hoc: Grundlegendes

• F-Test (Omnibus-Test):

  • Antwort auf die Frage: Existiert ein Unterschied zwischen den Gruppen?
  • Keine Antwort auf die Frage: Zwischen welchen Gruppen existiert ein Unterschied?

• Post-hoc-Tests untersuchen die Unterschiede zwischen einzelnen Gruppen

• Aber: Multiples Testen führt zu α-Fehler-Inflation

• Post-hoc-Vergleiche sind multiple Tests, die nicht zu α-Fehler-Inflation führen

• Vorgehen: Korrektur/Anpassen des α-Fehlers

• Verschiedene Verfahren: Bonferroni, Tukey, Dunnett, Scheffe, …

Verfahren: Bonferroni

• Beispiel: Vier Gruppen (Versuchsbedingungen)

• Ausgangspunkt: F-Test ist signifikant

• Frage: Zwischen welchen Gruppen besteht ein Unterschied?

• Vorgehen:

  • Anpassen des Signifikanzniveaus α
  • Neues Signifikanzniveau α\('\) = α / (Anzahl Einzelvergleiche)
  • Bei vier Gruppen: sechs Einzelvergleiche
    \(\Rightarrow\) α\('\) = α/6 ≈ 0.05/6 = 0.00833 = 0.833 %

Carlo Emilio Bonferroni (Quelle: Wikipedia)

Post-hoc: Beispiel 🐕

• Signifikanter Omnibus-Test (p < 0.05)

• Welche(r) Unterschied(e) ist/sind signifikant?

• Bonferroni-Korrektur:

  • 3 Bedingungen, also 3 Einzelvergleiche (mittels t-Tests)
  • Korrektur von \(\alpha_{neu}\) = \(\alpha\)/3 = 0.05/3 \(\approx\) 0.0167 = 1.67%

• 3 t-Tests

  • Kontrollgruppe vs. 15 Minuten: p = 0.2598 (> 0.0167)
  • Kontrollgruppe vs. 30 Minuten: p = 0.0157 (< 0.0167; also signifikanter Unterschied)
  • 15 Minuten vs. 30 Minuten: p = 0.0851 (> 0.0167)

• Ergebnis in einem Satz: Post-hoc-Vergleiche nach Bonferroni ergaben signifikante Unterschiede zwischen den Bedingungen Control und 30 Minuten.

Omnibus-Test

Analysis of Variance Table

Response: happiness
          Df Sum Sq Mean Sq F value  Pr(>F)  
dose       2 20.133 10.0667  5.1186 0.02469 *
Residuals 12 23.600  1.9667                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Einzelvergleiche – Bonferroni

    Pairwise comparisons using t tests with non-pooled SD 

data:  data_puppies_orig$happiness and data_puppies_orig$dose 

        15 mins 30 mins
30 mins 0.259   -      
Control 0.780   0.049  

P value adjustment method: bonferroni 

Einzelvergleiche – mehrfache t-Tests

    Pairwise comparisons using t tests with non-pooled SD 

data:  data_puppies_orig$happiness and data_puppies_orig$dose 

        15 mins 30 mins
30 mins 0.259   -      
Control 0.780   0.049  

P value adjustment method: bonferroni 

    Two Sample t-test

data:  happiness by dose
t = 1.2127, df = 8, p-value = 0.2598
alternative hypothesis: true difference in means between group 15 mins and group Control is not equal to 0
95 percent confidence interval:
 -0.9015797  2.9015797
sample estimates:
mean in group 15 mins mean in group Control 
                  3.2                   2.2 

    Two Sample t-test

data:  happiness by dose
t = 3.0551, df = 8, p-value = 0.0157
alternative hypothesis: true difference in means between group 30 mins and group Control is not equal to 0
95 percent confidence interval:
 0.6865123 4.9134877
sample estimates:
mean in group 30 mins mean in group Control 
                  5.0                   2.2 

    Two Sample t-test

data:  happiness by dose
t = -1.964, df = 8, p-value = 0.08514
alternative hypothesis: true difference in means between group 15 mins and group 30 mins is not equal to 0
95 percent confidence interval:
 -3.9134877  0.3134877
sample estimates:
mean in group 15 mins mean in group 30 mins 
                  3.2                   5.0 

ANOVA als Regressionsmodell?!

• Skalenniveaus bei der multiplen Regressionsanalyse?

• Skalenniveaus bei der ANOVA?

• Modell?