Vergleich von t-Test und Korrelationsanalyse

Statistik: Übung

Author

Affiliation

Prof. Dr. Armin Eichinger

TH Deggendorf

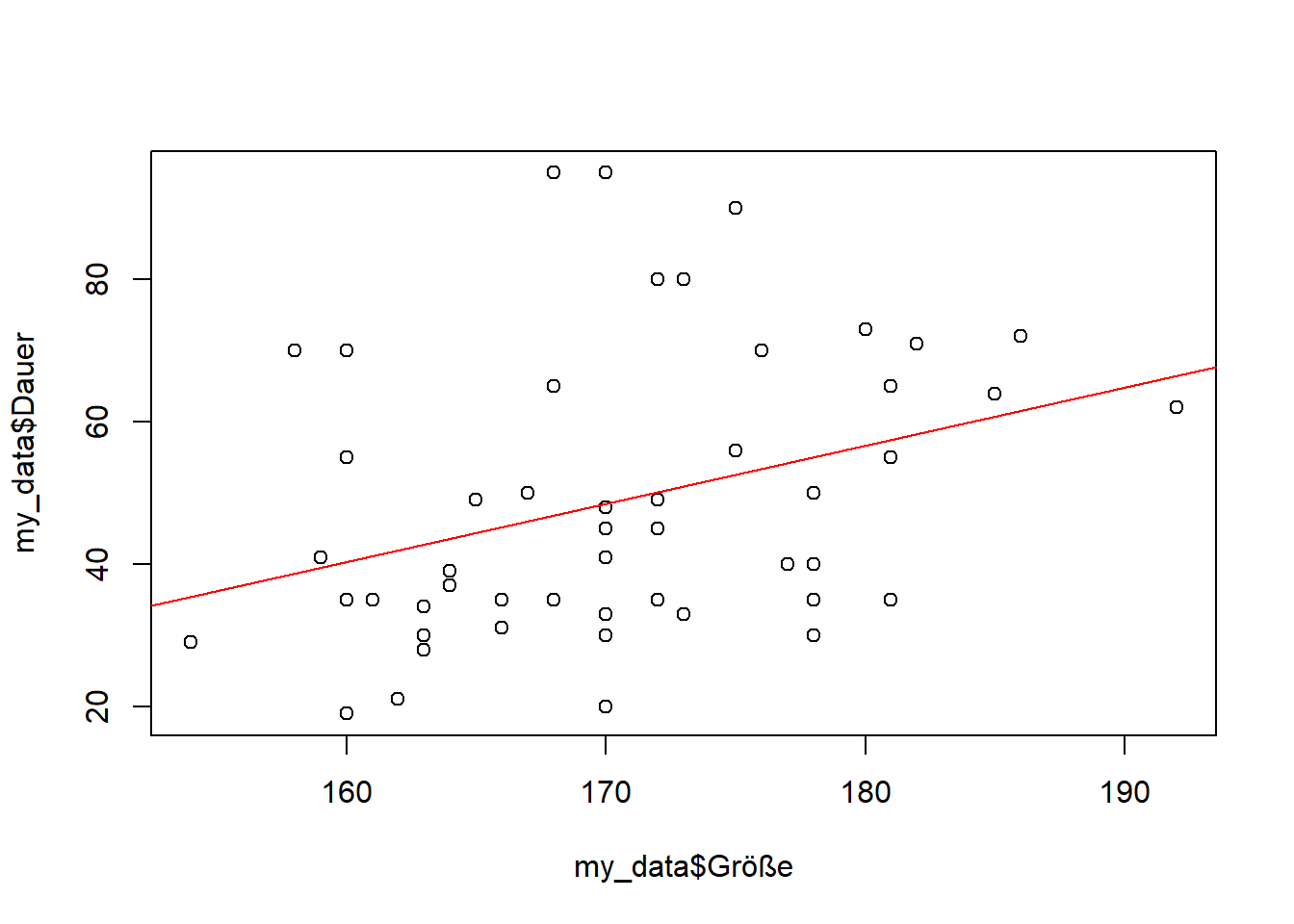
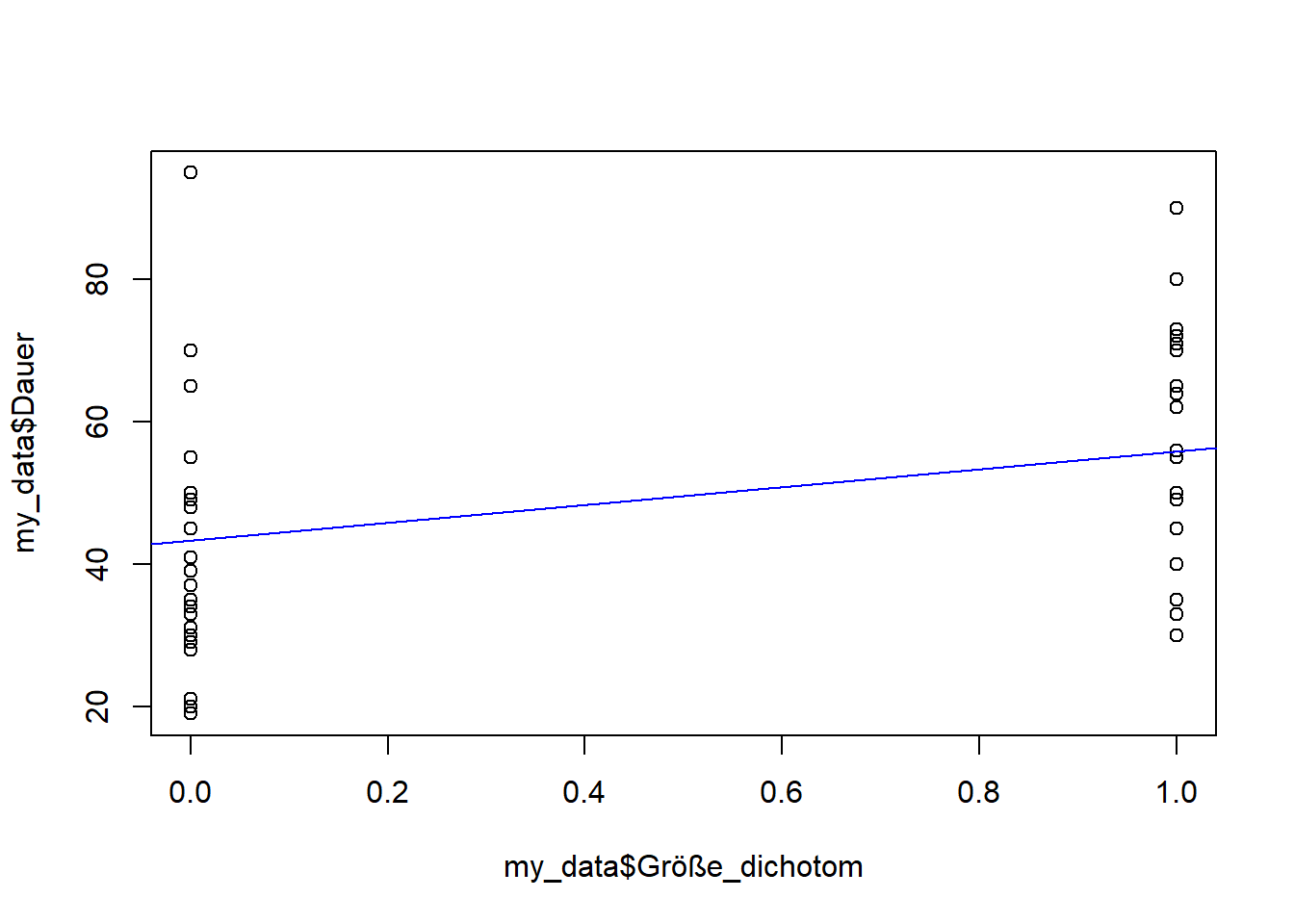
Ausgangspunkt sind die in einer Vorlesung erhobenen Daten: Wie lange konnten die Studierenden die Luft anhalten (in Sekunden) und wie groß sind sie (in cm). Die Daten finden Sie hier.

Untersucht wird die Fragestellung, ob große Menschen die Luft länger anhalten können als kleine Menschen; bzw. ob Größe und Zeitdauer positiv zusammenhängen.

Versuchen Sie, die Analyse anhand der Kommentare im Code nachzuvollziehen.

# Brauchen wir für das mutate
library(tidyverse)

# Daten einlesen
my_data <- read.csv2("data/luft_anhalten_data.csv")

# Nicht prüfungsrelevant!
# Erzeugen einer neuen Spalte, die für Größe den Median-Split umsetzt:
# Werte < Median(Größe) --> 0
# Werte > Median(Größe) --> 1
my_data <- my_data |>
  mutate(Größe_dichotom = if_else(my_data$Größe > median(my_data$Größe), 1, 0))

# Schauen wir uns das Ergebnis an
my_data

   Größe Dauer Größe_dichotom
1    163    34              0
2    178    40              1
3    178    50              1
4    192    62              1
5    163    30              0
6    158    70              0
7    170    30              0
8    161    35              0
9    172    45              1
10   181    55              1
11   159    41              0
12   172    49              1
13   160    35              0
14   166    35              0
15   163    28              0
16   173    33              1
17   165    49              0
18   181    35              1
19   160    55              0
20   160    70              0
21   181    65              1
22   170    33              0
23   175    90              1
24   177    40              1
25   164    39              0
26   170    48              0
27   170    20              0
28   185    64              1
29   176    70              1
30   166    31              0
31   182    71              1
32   170    41              0
33   162    21              0
34   154    29              0
35   170    95              0
36   170    45              0
37   168    35              0
38   178    30              1
39   180    73              1
40   168    65              0
41   167    50              0
42   164    37              0
43   172    35              1
44   160    19              0
45   186    72              1
46   172    80              1
47   173    80              1
48   175    56              1
49   178    35              1
50   168    95              0

# t-Test: H1: Große Menschen können die Luft länger anhalten
# zur Erinnerung: alternative = "two.sided", "less" oder "greater"
t.test(my_data$Dauer~my_data$Größe_dichotom, alternative="less", var.equal = TRUE) 

    Two Sample t-test

data:  my_data$Dauer by my_data$Größe_dichotom
t = -2.3144, df = 48, p-value = 0.01248
alternative hypothesis: true difference in means between group 0 and group 1 is less than 0
95 percent confidence interval:
      -Inf -3.445987
sample estimates:
mean in group 0 mean in group 1 
       43.39286        55.90909 

# Korrelationskoeffizient r
cor(my_data$Größe,my_data$Dauer)

[1] 0.3418082

# Signifikanztest für r
# Wir erwarten einen positiven Zusammenhang, daher "greater"
cor.test(my_data$Größe,my_data$Dauer, alternative="greater")

    Pearson's product-moment correlation

data:  my_data$Größe and my_data$Dauer
t = 2.5199, df = 48, p-value = 0.00756
alternative hypothesis: true correlation is greater than 0
95 percent confidence interval:
 0.1156916 1.0000000
sample estimates:
      cor 
0.3418082 

# Lineares Modell für das Diagramm - noch kein Stoff
my_model <- lm(my_data$Dauer~my_data$Größe)
#plot(my_model)
#summary(my_model)

# Scatterplot plus lineares Modell
plot(my_data$Größe, my_data$Dauer)
abline(my_model, col = "red")

#################
# Ab hier wird es ungewöhnlich!
#################

# Korrelationskoeffizient r für die dichotome Größe!
# Vergleichen Sie mit dem anderen r
cor(my_data$Größe_dichotom,my_data$Dauer)

[1] 0.3168484

# Lineares Modell für das Diagramm - noch kein Stoff
my_model_dichotom <- lm(my_data$Dauer~my_data$Größe_dichotom)

# "Scatterplot" plus lineares Modell
plot(my_data$Größe_dichotom, my_data$Dauer)
abline(my_model_dichotom, col = "blue")

# Signifikanztest für das dichotome r
# Vergleichen Sie t- und p-Werte mit denen des t-Tests oben
cor.test(my_data$Größe_dichotom,my_data$Dauer, alternative="greater")

    Pearson's product-moment correlation

data:  my_data$Größe_dichotom and my_data$Dauer
t = 2.3144, df = 48, p-value = 0.01248
alternative hypothesis: true correlation is greater than 0
95 percent confidence interval:
 0.08798521 1.00000000
sample estimates:
      cor 
0.3168484 

Anhang

SNV

Achtung: Die Tabelle hat zwei Hälften – oben negative unten positive z-Werte

	-.00	-.01	-.02	-.03	-.04	-.05	-.06	-.07	-.08	-.09
0	0.5000	0.4960	0.4920	0.4880	0.4840	0.4801	0.4761	0.4721	0.4681	0.4641
-0.1	0.4602	0.4562	0.4522	0.4483	0.4443	0.4404	0.4364	0.4325	0.4286	0.4247
-0.2	0.4207	0.4168	0.4129	0.4090	0.4052	0.4013	0.3974	0.3936	0.3897	0.3859
-0.3	0.3821	0.3783	0.3745	0.3707	0.3669	0.3632	0.3594	0.3557	0.3520	0.3483
-0.4	0.3446	0.3409	0.3372	0.3336	0.3300	0.3264	0.3228	0.3192	0.3156	0.3121
-0.5	0.3085	0.3050	0.3015	0.2981	0.2946	0.2912	0.2877	0.2843	0.2810	0.2776
-0.6	0.2743	0.2709	0.2676	0.2643	0.2611	0.2578	0.2546	0.2514	0.2483	0.2451
-0.7	0.2420	0.2389	0.2358	0.2327	0.2296	0.2266	0.2236	0.2206	0.2177	0.2148
-0.8	0.2119	0.2090	0.2061	0.2033	0.2005	0.1977	0.1949	0.1922	0.1894	0.1867
-0.9	0.1841	0.1814	0.1788	0.1762	0.1736	0.1711	0.1685	0.1660	0.1635	0.1611
-1	0.1587	0.1562	0.1539	0.1515	0.1492	0.1469	0.1446	0.1423	0.1401	0.1379
-1.1	0.1357	0.1335	0.1314	0.1292	0.1271	0.1251	0.1230	0.1210	0.1190	0.1170
-1.2	0.1151	0.1131	0.1112	0.1093	0.1075	0.1056	0.1038	0.1020	0.1003	0.0985
-1.3	0.0968	0.0951	0.0934	0.0918	0.0901	0.0885	0.0869	0.0853	0.0838	0.0823
-1.4	0.0808	0.0793	0.0778	0.0764	0.0749	0.0735	0.0721	0.0708	0.0694	0.0681
-1.5	0.0668	0.0655	0.0643	0.0630	0.0618	0.0606	0.0594	0.0582	0.0571	0.0559
-1.6	0.0548	0.0537	0.0526	0.0516	0.0505	0.0495	0.0485	0.0475	0.0465	0.0455
-1.7	0.0446	0.0436	0.0427	0.0418	0.0409	0.0401	0.0392	0.0384	0.0375	0.0367
-1.8	0.0359	0.0351	0.0344	0.0336	0.0329	0.0322	0.0314	0.0307	0.0301	0.0294
-1.9	0.0287	0.0281	0.0274	0.0268	0.0262	0.0256	0.0250	0.0244	0.0239	0.0233
-2	0.0228	0.0222	0.0217	0.0212	0.0207	0.0202	0.0197	0.0192	0.0188	0.0183
-2.1	0.0179	0.0174	0.0170	0.0166	0.0162	0.0158	0.0154	0.0150	0.0146	0.0143
-2.2	0.0139	0.0136	0.0132	0.0129	0.0125	0.0122	0.0119	0.0116	0.0113	0.0110
-2.3	0.0107	0.0104	0.0102	0.0099	0.0096	0.0094	0.0091	0.0089	0.0087	0.0084
-2.4	0.0082	0.0080	0.0078	0.0075	0.0073	0.0071	0.0069	0.0068	0.0066	0.0064
-2.5	0.0062	0.0060	0.0059	0.0057	0.0055	0.0054	0.0052	0.0051	0.0049	0.0048
-2.6	0.0047	0.0045	0.0044	0.0043	0.0041	0.0040	0.0039	0.0038	0.0037	0.0036
-2.7	0.0035	0.0034	0.0033	0.0032	0.0031	0.0030	0.0029	0.0028	0.0027	0.0026
-2.8	0.0026	0.0025	0.0024	0.0023	0.0023	0.0022	0.0021	0.0021	0.0020	0.0019
-2.9	0.0019	0.0018	0.0018	0.0017	0.0016	0.0016	0.0015	0.0015	0.0014	0.0014
-3	0.0013	0.0013	0.0013	0.0012	0.0012	0.0011	0.0011	0.0011	0.0010	0.0010

	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
0	0.5000	0.5040	0.5080	0.5120	0.5160	0.5199	0.5239	0.5279	0.5319	0.5359
0.1	0.5398	0.5438	0.5478	0.5517	0.5557	0.5596	0.5636	0.5675	0.5714	0.5753
0.2	0.5793	0.5832	0.5871	0.5910	0.5948	0.5987	0.6026	0.6064	0.6103	0.6141
0.3	0.6179	0.6217	0.6255	0.6293	0.6331	0.6368	0.6406	0.6443	0.6480	0.6517
0.4	0.6554	0.6591	0.6628	0.6664	0.6700	0.6736	0.6772	0.6808	0.6844	0.6879
0.5	0.6915	0.6950	0.6985	0.7019	0.7054	0.7088	0.7123	0.7157	0.7190	0.7224
0.6	0.7257	0.7291	0.7324	0.7357	0.7389	0.7422	0.7454	0.7486	0.7517	0.7549
0.7	0.7580	0.7611	0.7642	0.7673	0.7704	0.7734	0.7764	0.7794	0.7823	0.7852
0.8	0.7881	0.7910	0.7939	0.7967	0.7995	0.8023	0.8051	0.8078	0.8106	0.8133
0.9	0.8159	0.8186	0.8212	0.8238	0.8264	0.8289	0.8315	0.8340	0.8365	0.8389
1	0.8413	0.8438	0.8461	0.8485	0.8508	0.8531	0.8554	0.8577	0.8599	0.8621
1.1	0.8643	0.8665	0.8686	0.8708	0.8729	0.8749	0.8770	0.8790	0.8810	0.8830
1.2	0.8849	0.8869	0.8888	0.8907	0.8925	0.8944	0.8962	0.8980	0.8997	0.9015
1.3	0.9032	0.9049	0.9066	0.9082	0.9099	0.9115	0.9131	0.9147	0.9162	0.9177
1.4	0.9192	0.9207	0.9222	0.9236	0.9251	0.9265	0.9279	0.9292	0.9306	0.9319
1.5	0.9332	0.9345	0.9357	0.9370	0.9382	0.9394	0.9406	0.9418	0.9429	0.9441
1.6	0.9452	0.9463	0.9474	0.9484	0.9495	0.9505	0.9515	0.9525	0.9535	0.9545
1.7	0.9554	0.9564	0.9573	0.9582	0.9591	0.9599	0.9608	0.9616	0.9625	0.9633
1.8	0.9641	0.9649	0.9656	0.9664	0.9671	0.9678	0.9686	0.9693	0.9699	0.9706
1.9	0.9713	0.9719	0.9726	0.9732	0.9738	0.9744	0.9750	0.9756	0.9761	0.9767
2	0.9772	0.9778	0.9783	0.9788	0.9793	0.9798	0.9803	0.9808	0.9812	0.9817
2.1	0.9821	0.9826	0.9830	0.9834	0.9838	0.9842	0.9846	0.9850	0.9854	0.9857
2.2	0.9861	0.9864	0.9868	0.9871	0.9875	0.9878	0.9881	0.9884	0.9887	0.9890
2.3	0.9893	0.9896	0.9898	0.9901	0.9904	0.9906	0.9909	0.9911	0.9913	0.9916
2.4	0.9918	0.9920	0.9922	0.9925	0.9927	0.9929	0.9931	0.9932	0.9934	0.9936
2.5	0.9938	0.9940	0.9941	0.9943	0.9945	0.9946	0.9948	0.9949	0.9951	0.9952
2.6	0.9953	0.9955	0.9956	0.9957	0.9959	0.9960	0.9961	0.9962	0.9963	0.9964
2.7	0.9965	0.9966	0.9967	0.9968	0.9969	0.9970	0.9971	0.9972	0.9973	0.9974
2.8	0.9974	0.9975	0.9976	0.9977	0.9977	0.9978	0.9979	0.9979	0.9980	0.9981
2.9	0.9981	0.9982	0.9982	0.9983	0.9984	0.9984	0.9985	0.9985	0.9986	0.9986
3	0.9987	0.9987	0.9987	0.9988	0.9988	0.9989	0.9989	0.9989	0.9990	0.9990

t-Verteilung

df	0.01	0.025	0.05	0.10	0.25	0.5	0.75	0.90	0.95	0.975	0.99
1	-31.8205	-12.7062	-6.3138	-3.0777	-1.0000	0	1.0000	3.0777	6.3138	12.7062	31.8205
2	-6.9646	-4.3027	-2.9200	-1.8856	-0.8165	0	0.8165	1.8856	2.9200	4.3027	6.9646
3	-4.5407	-3.1824	-2.3534	-1.6377	-0.7649	0	0.7649	1.6377	2.3534	3.1824	4.5407
4	-3.7469	-2.7764	-2.1318	-1.5332	-0.7407	0	0.7407	1.5332	2.1318	2.7764	3.7469
5	-3.3649	-2.5706	-2.0150	-1.4759	-0.7267	0	0.7267	1.4759	2.0150	2.5706	3.3649
6	-3.1427	-2.4469	-1.9432	-1.4398	-0.7176	0	0.7176	1.4398	1.9432	2.4469	3.1427
7	-2.9980	-2.3646	-1.8946	-1.4149	-0.7111	0	0.7111	1.4149	1.8946	2.3646	2.9980
8	-2.8965	-2.3060	-1.8595	-1.3968	-0.7064	0	0.7064	1.3968	1.8595	2.3060	2.8965
9	-2.8214	-2.2622	-1.8331	-1.3830	-0.7027	0	0.7027	1.3830	1.8331	2.2622	2.8214
10	-2.7638	-2.2281	-1.8125	-1.3722	-0.6998	0	0.6998	1.3722	1.8125	2.2281	2.7638
11	-2.7181	-2.2010	-1.7959	-1.3634	-0.6974	0	0.6974	1.3634	1.7959	2.2010	2.7181
12	-2.6810	-2.1788	-1.7823	-1.3562	-0.6955	0	0.6955	1.3562	1.7823	2.1788	2.6810
13	-2.6503	-2.1604	-1.7709	-1.3502	-0.6938	0	0.6938	1.3502	1.7709	2.1604	2.6503
14	-2.6245	-2.1448	-1.7613	-1.3450	-0.6924	0	0.6924	1.3450	1.7613	2.1448	2.6245
15	-2.6025	-2.1314	-1.7531	-1.3406	-0.6912	0	0.6912	1.3406	1.7531	2.1314	2.6025
16	-2.5835	-2.1199	-1.7459	-1.3368	-0.6901	0	0.6901	1.3368	1.7459	2.1199	2.5835
17	-2.5669	-2.1098	-1.7396	-1.3334	-0.6892	0	0.6892	1.3334	1.7396	2.1098	2.5669
18	-2.5524	-2.1009	-1.7341	-1.3304	-0.6884	0	0.6884	1.3304	1.7341	2.1009	2.5524
19	-2.5395	-2.0930	-1.7291	-1.3277	-0.6876	0	0.6876	1.3277	1.7291	2.0930	2.5395
20	-2.5280	-2.0860	-1.7247	-1.3253	-0.6870	0	0.6870	1.3253	1.7247	2.0860	2.5280
21	-2.5176	-2.0796	-1.7207	-1.3232	-0.6864	0	0.6864	1.3232	1.7207	2.0796	2.5176
22	-2.5083	-2.0739	-1.7171	-1.3212	-0.6858	0	0.6858	1.3212	1.7171	2.0739	2.5083
23	-2.4999	-2.0687	-1.7139	-1.3195	-0.6853	0	0.6853	1.3195	1.7139	2.0687	2.4999
24	-2.4922	-2.0639	-1.7109	-1.3178	-0.6848	0	0.6848	1.3178	1.7109	2.0639	2.4922
25	-2.4851	-2.0595	-1.7081	-1.3163	-0.6844	0	0.6844	1.3163	1.7081	2.0595	2.4851
26	-2.4786	-2.0555	-1.7056	-1.3150	-0.6840	0	0.6840	1.3150	1.7056	2.0555	2.4786
27	-2.4727	-2.0518	-1.7033	-1.3137	-0.6837	0	0.6837	1.3137	1.7033	2.0518	2.4727
28	-2.4671	-2.0484	-1.7011	-1.3125	-0.6834	0	0.6834	1.3125	1.7011	2.0484	2.4671
29	-2.4620	-2.0452	-1.6991	-1.3114	-0.6830	0	0.6830	1.3114	1.6991	2.0452	2.4620
30	-2.4573	-2.0423	-1.6973	-1.3104	-0.6828	0	0.6828	1.3104	1.6973	2.0423	2.4573
31	-2.4528	-2.0395	-1.6955	-1.3095	-0.6825	0	0.6825	1.3095	1.6955	2.0395	2.4528
32	-2.4487	-2.0369	-1.6939	-1.3086	-0.6822	0	0.6822	1.3086	1.6939	2.0369	2.4487
33	-2.4448	-2.0345	-1.6924	-1.3077	-0.6820	0	0.6820	1.3077	1.6924	2.0345	2.4448
34	-2.4411	-2.0322	-1.6909	-1.3070	-0.6818	0	0.6818	1.3070	1.6909	2.0322	2.4411
35	-2.4377	-2.0301	-1.6896	-1.3062	-0.6816	0	0.6816	1.3062	1.6896	2.0301	2.4377
36	-2.4345	-2.0281	-1.6883	-1.3055	-0.6814	0	0.6814	1.3055	1.6883	2.0281	2.4345
37	-2.4314	-2.0262	-1.6871	-1.3049	-0.6812	0	0.6812	1.3049	1.6871	2.0262	2.4314
38	-2.4286	-2.0244	-1.6860	-1.3042	-0.6810	0	0.6810	1.3042	1.6860	2.0244	2.4286
39	-2.4258	-2.0227	-1.6849	-1.3036	-0.6808	0	0.6808	1.3036	1.6849	2.0227	2.4258
40	-2.4233	-2.0211	-1.6839	-1.3031	-0.6807	0	0.6807	1.3031	1.6839	2.0211	2.4233
41	-2.4208	-2.0195	-1.6829	-1.3025	-0.6805	0	0.6805	1.3025	1.6829	2.0195	2.4208
42	-2.4185	-2.0181	-1.6820	-1.3020	-0.6804	0	0.6804	1.3020	1.6820	2.0181	2.4185
43	-2.4163	-2.0167	-1.6811	-1.3016	-0.6802	0	0.6802	1.3016	1.6811	2.0167	2.4163
44	-2.4141	-2.0154	-1.6802	-1.3011	-0.6801	0	0.6801	1.3011	1.6802	2.0154	2.4141
45	-2.4121	-2.0141	-1.6794	-1.3006	-0.6800	0	0.6800	1.3006	1.6794	2.0141	2.4121
46	-2.4102	-2.0129	-1.6787	-1.3002	-0.6799	0	0.6799	1.3002	1.6787	2.0129	2.4102
47	-2.4083	-2.0117	-1.6779	-1.2998	-0.6797	0	0.6797	1.2998	1.6779	2.0117	2.4083
48	-2.4066	-2.0106	-1.6772	-1.2994	-0.6796	0	0.6796	1.2994	1.6772	2.0106	2.4066
49	-2.4049	-2.0096	-1.6766	-1.2991	-0.6795	0	0.6795	1.2991	1.6766	2.0096	2.4049
50	-2.4033	-2.0086	-1.6759	-1.2987	-0.6794	0	0.6794	1.2987	1.6759	2.0086	2.4033
51	-2.4017	-2.0076	-1.6753	-1.2984	-0.6793	0	0.6793	1.2984	1.6753	2.0076	2.4017
52	-2.4002	-2.0066	-1.6747	-1.2980	-0.6792	0	0.6792	1.2980	1.6747	2.0066	2.4002
53	-2.3988	-2.0057	-1.6741	-1.2977	-0.6791	0	0.6791	1.2977	1.6741	2.0057	2.3988
54	-2.3974	-2.0049	-1.6736	-1.2974	-0.6791	0	0.6791	1.2974	1.6736	2.0049	2.3974
55	-2.3961	-2.0040	-1.6730	-1.2971	-0.6790	0	0.6790	1.2971	1.6730	2.0040	2.3961
56	-2.3948	-2.0032	-1.6725	-1.2969	-0.6789	0	0.6789	1.2969	1.6725	2.0032	2.3948
57	-2.3936	-2.0025	-1.6720	-1.2966	-0.6788	0	0.6788	1.2966	1.6720	2.0025	2.3936
58	-2.3924	-2.0017	-1.6716	-1.2963	-0.6787	0	0.6787	1.2963	1.6716	2.0017	2.3924
59	-2.3912	-2.0010	-1.6711	-1.2961	-0.6787	0	0.6787	1.2961	1.6711	2.0010	2.3912
60	-2.3901	-2.0003	-1.6706	-1.2958	-0.6786	0	0.6786	1.2958	1.6706	2.0003	2.3901
61	-2.3890	-1.9996	-1.6702	-1.2956	-0.6785	0	0.6785	1.2956	1.6702	1.9996	2.3890
62	-2.3880	-1.9990	-1.6698	-1.2954	-0.6785	0	0.6785	1.2954	1.6698	1.9990	2.3880
63	-2.3870	-1.9983	-1.6694	-1.2951	-0.6784	0	0.6784	1.2951	1.6694	1.9983	2.3870
64	-2.3860	-1.9977	-1.6690	-1.2949	-0.6783	0	0.6783	1.2949	1.6690	1.9977	2.3860
65	-2.3851	-1.9971	-1.6686	-1.2947	-0.6783	0	0.6783	1.2947	1.6686	1.9971	2.3851
66	-2.3842	-1.9966	-1.6683	-1.2945	-0.6782	0	0.6782	1.2945	1.6683	1.9966	2.3842
67	-2.3833	-1.9960	-1.6679	-1.2943	-0.6782	0	0.6782	1.2943	1.6679	1.9960	2.3833
68	-2.3824	-1.9955	-1.6676	-1.2941	-0.6781	0	0.6781	1.2941	1.6676	1.9955	2.3824
69	-2.3816	-1.9949	-1.6672	-1.2939	-0.6781	0	0.6781	1.2939	1.6672	1.9949	2.3816
70	-2.3808	-1.9944	-1.6669	-1.2938	-0.6780	0	0.6780	1.2938	1.6669	1.9944	2.3808
71	-2.3800	-1.9939	-1.6666	-1.2936	-0.6780	0	0.6780	1.2936	1.6666	1.9939	2.3800
72	-2.3793	-1.9935	-1.6663	-1.2934	-0.6779	0	0.6779	1.2934	1.6663	1.9935	2.3793
73	-2.3785	-1.9930	-1.6660	-1.2933	-0.6779	0	0.6779	1.2933	1.6660	1.9930	2.3785
74	-2.3778	-1.9925	-1.6657	-1.2931	-0.6778	0	0.6778	1.2931	1.6657	1.9925	2.3778
75	-2.3771	-1.9921	-1.6654	-1.2929	-0.6778	0	0.6778	1.2929	1.6654	1.9921	2.3771
76	-2.3764	-1.9917	-1.6652	-1.2928	-0.6777	0	0.6777	1.2928	1.6652	1.9917	2.3764
77	-2.3758	-1.9913	-1.6649	-1.2926	-0.6777	0	0.6777	1.2926	1.6649	1.9913	2.3758
78	-2.3751	-1.9908	-1.6646	-1.2925	-0.6776	0	0.6776	1.2925	1.6646	1.9908	2.3751
79	-2.3745	-1.9905	-1.6644	-1.2924	-0.6776	0	0.6776	1.2924	1.6644	1.9905	2.3745
80	-2.3739	-1.9901	-1.6641	-1.2922	-0.6776	0	0.6776	1.2922	1.6641	1.9901	2.3739
81	-2.3733	-1.9897	-1.6639	-1.2921	-0.6775	0	0.6775	1.2921	1.6639	1.9897	2.3733
82	-2.3727	-1.9893	-1.6636	-1.2920	-0.6775	0	0.6775	1.2920	1.6636	1.9893	2.3727
83	-2.3721	-1.9890	-1.6634	-1.2918	-0.6775	0	0.6775	1.2918	1.6634	1.9890	2.3721
84	-2.3716	-1.9886	-1.6632	-1.2917	-0.6774	0	0.6774	1.2917	1.6632	1.9886	2.3716
85	-2.3710	-1.9883	-1.6630	-1.2916	-0.6774	0	0.6774	1.2916	1.6630	1.9883	2.3710
86	-2.3705	-1.9879	-1.6628	-1.2915	-0.6774	0	0.6774	1.2915	1.6628	1.9879	2.3705
87	-2.3700	-1.9876	-1.6626	-1.2914	-0.6773	0	0.6773	1.2914	1.6626	1.9876	2.3700
88	-2.3695	-1.9873	-1.6624	-1.2912	-0.6773	0	0.6773	1.2912	1.6624	1.9873	2.3695
89	-2.3690	-1.9870	-1.6622	-1.2911	-0.6773	0	0.6773	1.2911	1.6622	1.9870	2.3690
90	-2.3685	-1.9867	-1.6620	-1.2910	-0.6772	0	0.6772	1.2910	1.6620	1.9867	2.3685
91	-2.3680	-1.9864	-1.6618	-1.2909	-0.6772	0	0.6772	1.2909	1.6618	1.9864	2.3680
92	-2.3676	-1.9861	-1.6616	-1.2908	-0.6772	0	0.6772	1.2908	1.6616	1.9861	2.3676
93	-2.3671	-1.9858	-1.6614	-1.2907	-0.6771	0	0.6771	1.2907	1.6614	1.9858	2.3671
94	-2.3667	-1.9855	-1.6612	-1.2906	-0.6771	0	0.6771	1.2906	1.6612	1.9855	2.3667
95	-2.3662	-1.9853	-1.6611	-1.2905	-0.6771	0	0.6771	1.2905	1.6611	1.9853	2.3662
96	-2.3658	-1.9850	-1.6609	-1.2904	-0.6771	0	0.6771	1.2904	1.6609	1.9850	2.3658
97	-2.3654	-1.9847	-1.6607	-1.2903	-0.6770	0	0.6770	1.2903	1.6607	1.9847	2.3654
98	-2.3650	-1.9845	-1.6606	-1.2902	-0.6770	0	0.6770	1.2902	1.6606	1.9845	2.3650
99	-2.3646	-1.9842	-1.6604	-1.2902	-0.6770	0	0.6770	1.2902	1.6604	1.9842	2.3646
100	-2.3642	-1.9840	-1.6602	-1.2901	-0.6770	0	0.6770	1.2901	1.6602	1.9840	2.3642