Korrelationsanalyse

_Statistik

Prof. Dr. Armin Eichinger

TH Deggendorf

10.12.2024

Gesucht: Ein Maß für Zusammenhänge

Wunschliste: Anforderungen

Wie sollte ein Maß für Zusammenhänge beschaffen sein? Was sind unsere Anforderungen?
Obligatorisch:
1. Kongruenz: Je größer der Zusammenhang, desto größer der Wert und umgekehrt
2. Unterscheidbarkeit von positiven und negativen Zusammenhängen
3. Unabhängigkeit von der Einheit, in der die Variablen gemessen werden (z. B. Zentimeter oder Meter)
Optional:
1. Ein Wert von 0 bedeutet “kein Zusammenhang”.
2. Begrenzte Bandbreite der Werte (→ Minimal- und Maximalwerte)

Kovarianz

Ähnlichkeit zur Varianz (namentlich und formal)
Zur Erinnerung die Formel für die Varianz: \(s² = \hat{\sigma}² = \frac{\sum\limits_{i=1}^{n}(x_i - \overline{x})²}{n-1}\)
Formel der Kovarianz: \(Cov(x,y) = \frac{\sum\limits_{i=1}^{n}(x_{i} - \overline{x})(y_{i} - \overline{y})}{n-1}\)
Ersetzen wir \(y\) durch \(x\) erhalten wir die Varianz.
Anforderungen:
- Anforderungen 1 + 2 (Kongruenz + Unterscheidbarkeit) sind erfüllt
- Anforderung 3: Kovarianz ändert sich mit den verwendeten Einheiten; nicht erfüllt!
- Beispiel: Kovarianz von Größe und Gewicht
  \(Cov\)(Größe in cm, Gewicht in kg) \(=\) 100 \(\cdot\) \(Cov\)(Größe in m, Gewicht in kg)
- Anforderung 4 (0 = kein Zusammenhang) ist erfüllt
- Anforderung 5 (Bandbreite) ist nicht erfüllt

Korrelationskoeffizient \(r\)

Lösung: Standardisierung der Kovarianz (d. h. teilen durch die beiden beteiligten Standardabweichungen)
Ergebnis: Korrelationskoeffizient \(r\)
Formel: \(r(x,y) = \frac{Cov(x,y)}{s_x \cdot s_y}\)
Anforderungen:
- Anforderung 1 erfüllt: \(|r_1| > |r_2| \Rightarrow\) größerer Zusammenhang
- Anforderung 2 erfüllt: \(r > 0\) für positive Zusammenhänge; \(r < 0\) für negative Zusammenhänge
- Anforderung 3 erfüllt: \(r\) ändert sich nicht mit den verwendeten Einheiten.
  Alle Einheiten fallen weg; \(r\) ist dimensionslos.
  
  Beispiel: Korrelation von Größe und Gewicht
  \(r\)(Größe in cm, Gewicht in kg) \(=\) \(r\)(Größe in m, Gewicht in kg)
- Anforderungen 4 erfüllt: \(r = 0\) bedeutet “kein Zusammenhang”.
- Anforderung 5 erfüllt: \(r\) ist auf das Intervall \([-1; 1]\) begrenzt.

Darstellung von Korrelationen

Scatterplot (Streudiagramm)

Korrelationsmatrix:

          Height    Weight
Height 1.0000000 0.5143289
Weight 0.5143289 1.0000000

Ausgangsdaten
Height	Weight
190	95
169	79
165	75
160	71
163	55
176	65
199	90
180	70
179	57
190	80
179	81
190	78
192	60
157	58
196	77
168	77
153	63
165	84
194	79
185	90
160	72
192	73
193	87
163	59
154	59
183	94
174	92

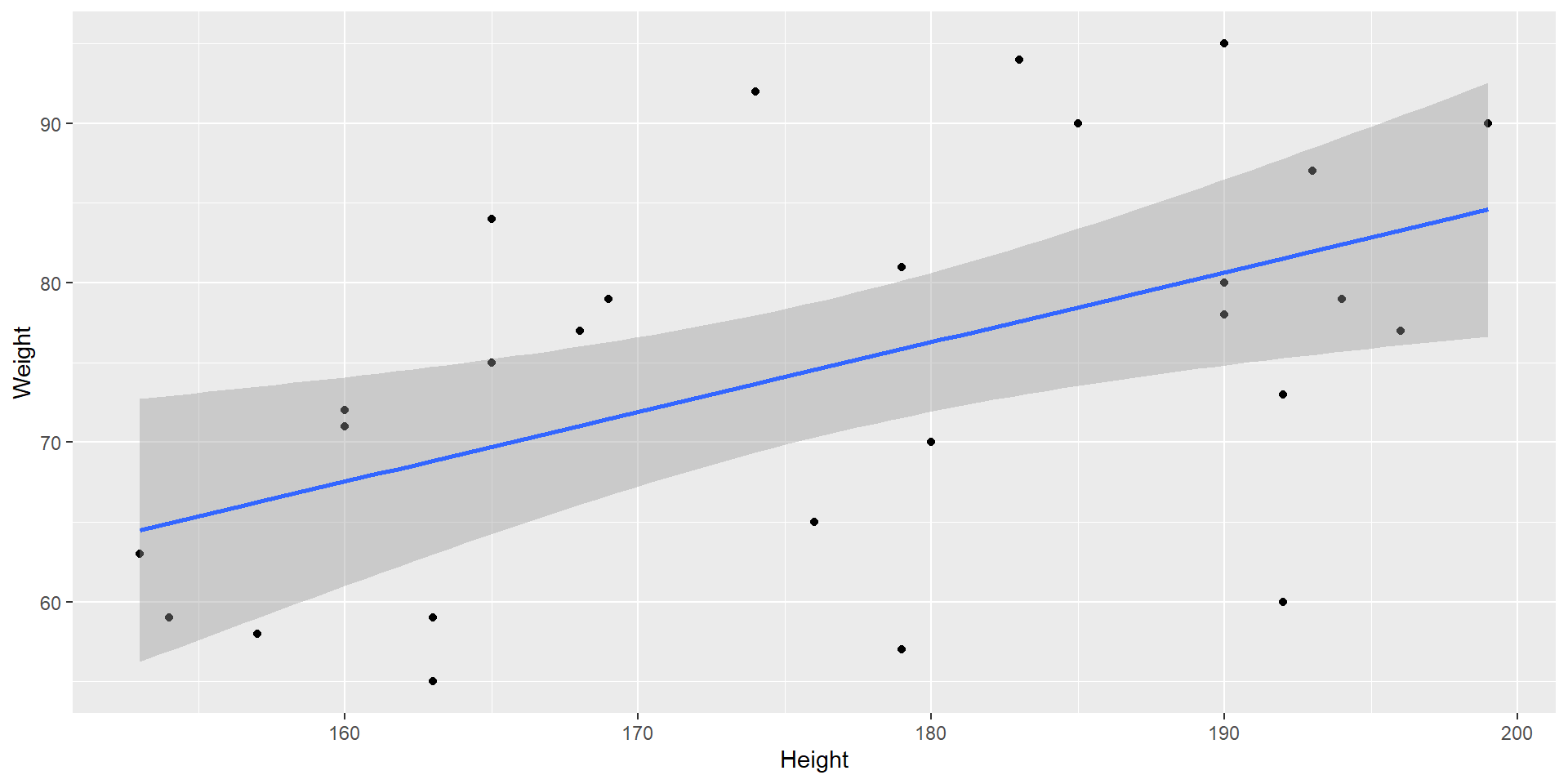
Scatterplot + Regressionsgerade

Korrelationsmatrix:

          Height    Weight
Height 1.0000000 0.5143289
Weight 0.5143289 1.0000000

Ausgangsdaten
Height	Weight
190	95
169	79
165	75
160	71
163	55
176	65
199	90
180	70
179	57
190	80
179	81
190	78
192	60
157	58
196	77
168	77
153	63
165	84
194	79
185	90
160	72
192	73
193	87
163	59
154	59
183	94
174	92

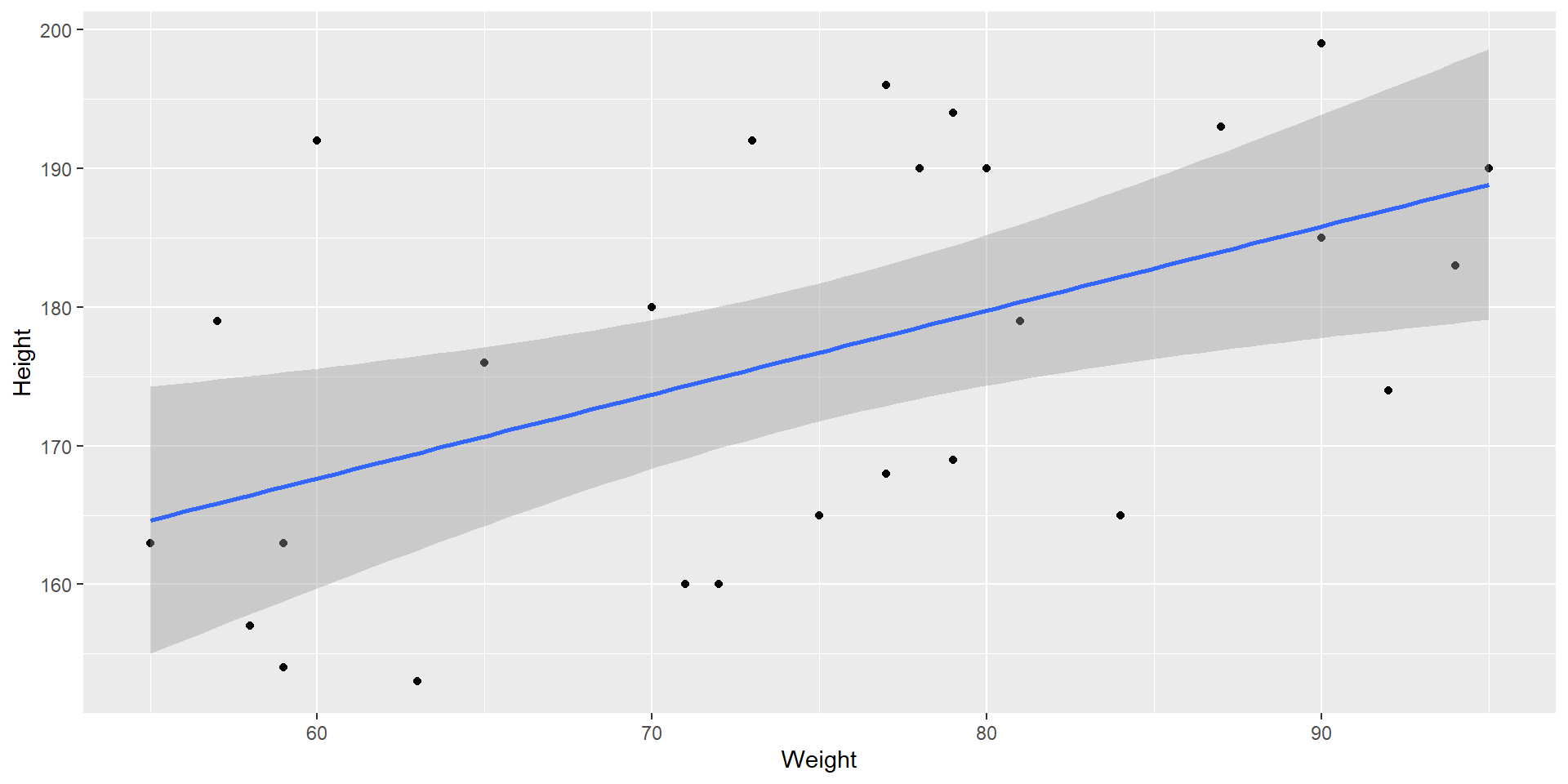
Scatterplot: X und Y vertauscht

Korrelationsmatrix:

          Height    Weight
Height 1.0000000 0.5143289
Weight 0.5143289 1.0000000

Ausgangsdaten
Height	Weight
190	95
169	79
165	75
160	71
163	55
176	65
199	90
180	70
179	57
190	80
179	81
190	78
192	60
157	58
196	77
168	77
153	63
165	84
194	79
185	90
160	72
192	73
193	87
163	59
154	59
183	94
174	92

Konfidenzintervall für \(r\)

KI: Allgemeines Schema

KI = Schätzwert \(\pm\) Teststatistik \(\cdot\) Standardfehler
Zur Erinnerung (1): 95%-KI für Stichprobenmittelwerte (bei Normalverteilung):
\[ \begin{eqnarray} 95\%\text{-}KI &=& \overline{x} \pm z_{0.975} \cdot \hat\sigma_{\overline{x}} \\\ &=& \overline{x} \pm 1.96 \cdot \hat\sigma_{\overline{x}} \\\ \end{eqnarray} \]
Zur Erinnerung (2): 95%-KI für Stichprobenmittelwerte (bei t-Verteilung):
\[ \begin{eqnarray} 95\%\text{-}KI &=& \overline{x} \pm t_{df, 0.975} \cdot \hat\sigma_{\overline{x}} \\\ \end{eqnarray} \]
Neu: Schätzwert ist ein Korrelationskoeffizient r

KI für Korrelationskoeffizient r

Eigentlich …: KI = \(r\) \(\pm\) Teststatistik \(\cdot\) Standardfehler
Problem: \(r\) als Schätzer einer Grundgesamtheit ist nicht symmetrisch verteilt (z. B. normal bzw. t-verteilt) wie Stichprobenmittelwerte
Damit können wir mit \(r\) nicht “rechnen” – z. B. Mittelwerte bilden o. ä.
Lösung: Fisher-z-Transformation
Standardfehler dieser transformierten Verteilung: \(\textit{SE}_z = \frac{1}{\sqrt{n - 3}}\)
KI(Fisher-z) = Fisher-z(r) \(\pm\) 1.96 \(\cdot \textit{SE}_z\)
Das Ergebnis ist von Fisher-z nach r rückzutransformieren (siehe wieder: Fisher-z-Transformation)

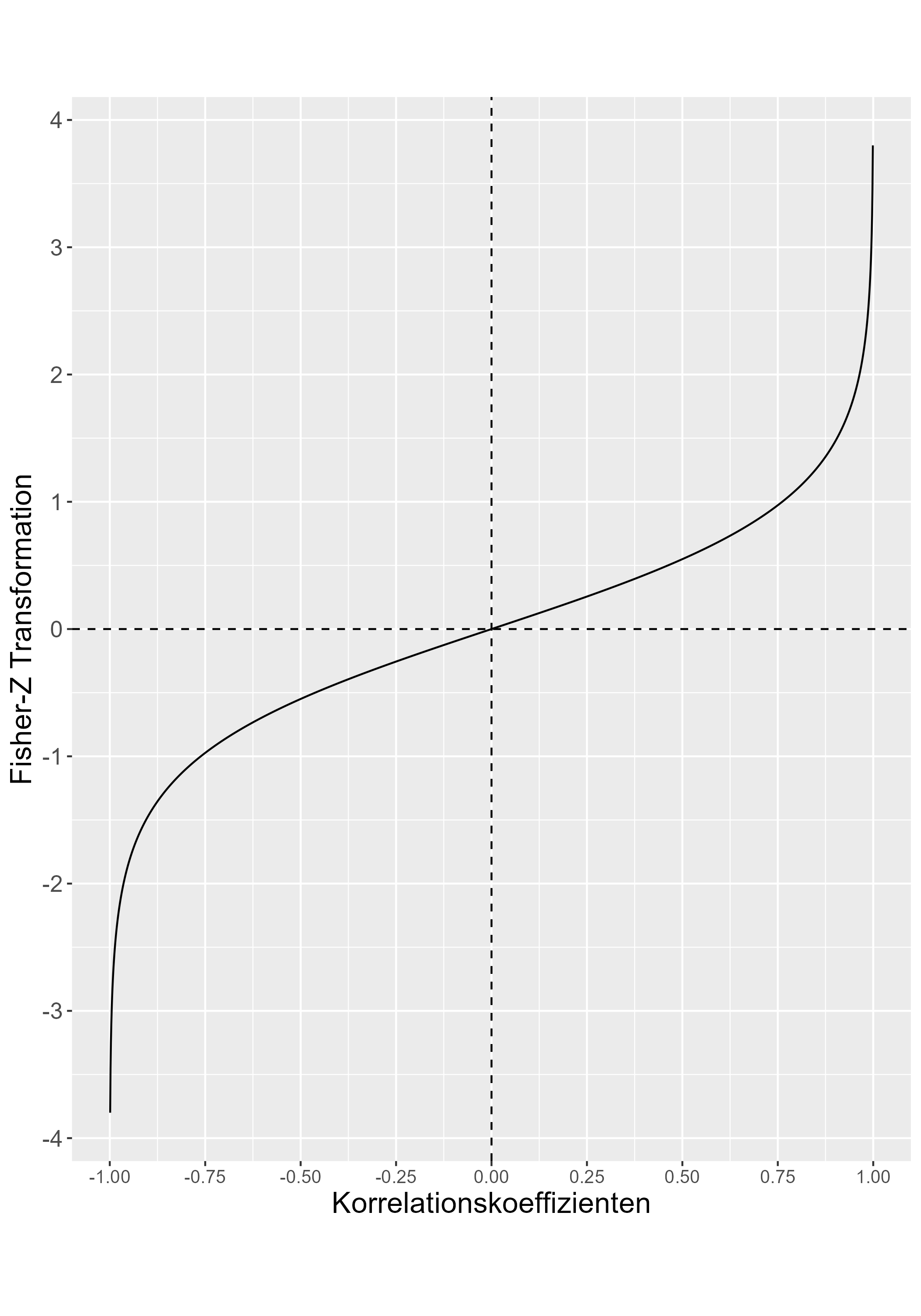
Fisher-z-Transformation

Transformation: r \(\rightarrow\) Fisher-z

\[ (Fisher\text{-})z = 0.5 \cdot ln{\frac{1 + r}{1 - r}} \]

Rücktransformation: Fisher-z \(\rightarrow\) r

\[ r = \frac{e^{2z}-1}{e^{2z}+1} \] Beispiel: Mittelwert von \(r_1\) = 0.1, \(r_2\) = 0.3, \(r_3\) = 0.8

Achtung: \(\bar{r} \neq\frac{.1+.3+.8}{3}\)
F.-z-Trafo.:
- 0.1 \(\rightarrow\) 0.1
- 0.3 \(\rightarrow\) 0.31
- 0.8 \(\rightarrow\) 1.099
\(\overline{z}\) = 0.503 \(\rightarrow \bar{r}\) = 0.464

Beispiel KI

95%-KI für die Korrelation zwischen Größe und Gewicht (n = 27)
r = 0.5143
\(\textit{SE}_z\) = \(\frac{1}{\sqrt{n - 3}}\) = 0.2041
Fisher-z(0.5143) = 0.5686
KI(Fisher-z)
- Untere Grenze = 0.5686 - 1.96 \(\cdot\) \(\frac{1}{\sqrt{24}}\) = 0.1685
- Obere Grenze = 0.5686 + 1.96 \(\cdot\) \(\frac{1}{\sqrt{24}}\) = 0.9686
KI(Fisher-z \(\rightarrow\) r)
- Untere Grenze = 0.1669
- Obere Grenze = 0.7481

Ausgangsdaten
Height	Weight
190	95
169	79
165	75
160	71
163	55
176	65
199	90
180	70
179	57
190	80
179	81
190	78
192	60
157	58
196	77
168	77
153	63
165	84
194	79
185	90
160	72
192	73
193	87
163	59
154	59
183	94
174	92

Beispiel KI: grafisch

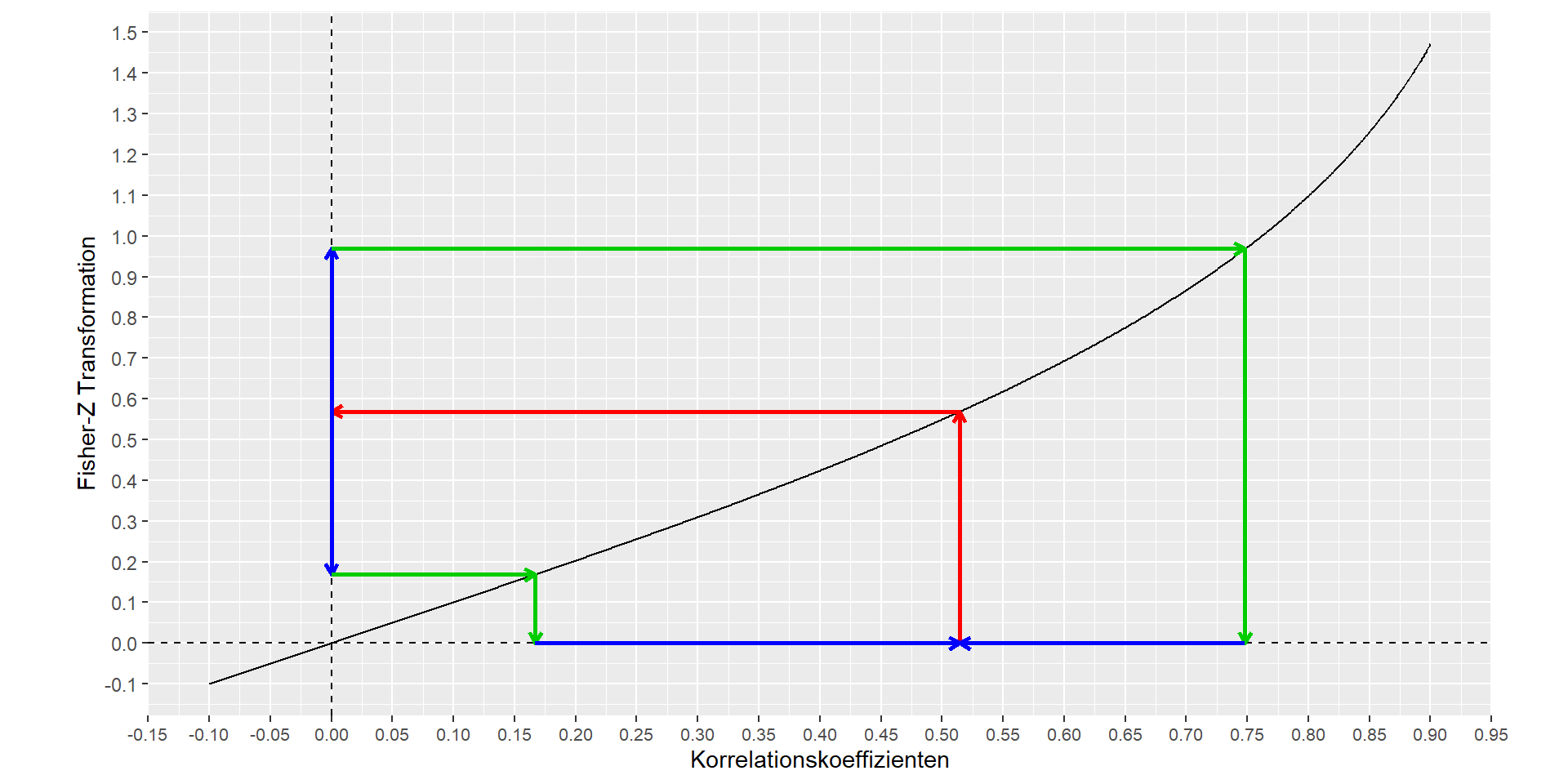
Signifikanztest für \(r\)

Übersicht

Fragestellung: Unterscheidet sich der Korrelationskoeffizient r einer Stichprobe von 0?
Mögliche Erweiterung der Fragestellung (bleibt hier unberücksichtigt): Unterscheidet sich der Korrelationskoeffizient r einer Stichprobe von einem Wert ungleich \(\rho \neq 0\) in der Population (\(\rho\) – “rho” – ist das griechische r)?
Voraussetzungen:
- Mindestens Intervallskalenniveau
- Linearität
- Normalverteilung
- Varianzhomogenität
Hypothesen:
- \(H_{0}\colon \rho =0; H_{1}\colon \rho \neq 0\) (zweiseitig)
- \(H_{0}\colon \rho \leq 0; H_{1}\colon \rho > 0\) bzw.
  \(H_{0}\colon \rho \geq 0; H_{1}\colon \rho < 0\) bzw. (einseitig)
Teststatistik/Prüfgröße: \(t = \frac{r \sqrt{n-2}}{\sqrt{1-r^2}}\)
\(t\) ist t-verteilt mit n - 2 Freiheitsgraden.
Nicht-parametrische Alternative für ordinale Daten: Rangkorrelation nach Spearman. Der Signifikanztest erfolgt analog.

Beispiel

Eine kleine Stichprobe von VPn (n = 5) sieht eine Anzahl von Werbungen und kauft im Anschluss eine bestimmte Anzahl an Produkten. Hängen beide Variablen signifikant positiv zusammen? Wie lautet das 95%-KI für r?

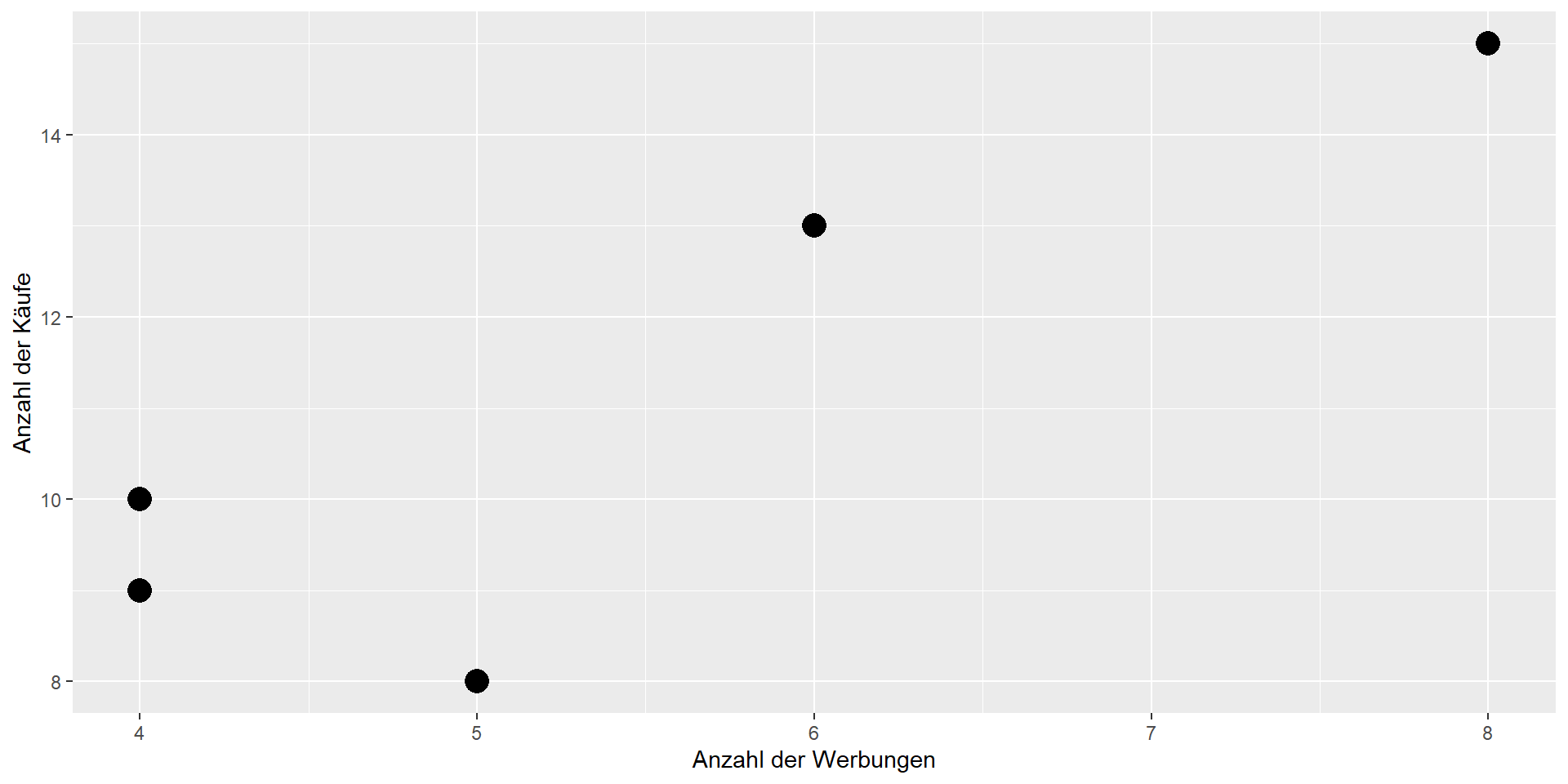
Ergebnisse der Rechenschritte:

Kovarianz: \(Cov(Werbungen,Käufe)=\) 4.25
Standardabweichung: \(\textit{SD}_{Werbungen}=\) 1.6733
Standardabweichung: \(\textit{SD}_{Käufe}=\) 2.9155
Korrelationskoeffizient: \(r=\) 0.8712
Empirischer t-Wert: \(t_{emp}(3)=\) 3.0737
Kritischer t-Wert: \(t_{krit, .95}(3) =\) 2.3534
Fisher-z-Wert: \(z =\) 1.338
95%-KI für r, untere Grenze: -0.0479
95%-KI für r, obere Grenze: 0.9914

Ausgangsdaten
Werbungen	Käufe
5	8
4	9
4	10
6	13
8	15

Korrelation für ordinale Daten

Rangkorrelation nach Spearman

Angenommen, die Daten sind nicht intervallskaliert – Problem …?!
Lösung: ordinale Information ausnutzen; (falls erforderlich Daten sortieren und) Rangplätze zuweisen
Rangkorrelation nach Spearman \(r_S\): Zusammenhangsmaß für zwei ordinalskalierte Merkmale
Monotoner statt linearer Zusammenhang
Aber: \(r_S\) ist linear in den Rängen!
Die Rangkorrelation nach Spearman ist identisch mit der Produkt-Moment-Korrelation nach Pearson der in Ränge transformierten Werte.
Rangkorrelation wird auch berechnet für den Zusammenhang zwischen einer ordinalskalierten und einer intervallskalierten Variablen.
Weiterer Einsatz von \(r_S\): nicht-linearer aber monotoner Zusammenhang zwischen metrischen Variablen
Zentrale Eigenschaften entsprechen denen des Produkt-Moment-Korrelationskoeffizienten:
- Grenzen: -1 ≤ \(r_S\) ≤ 1
- Interpretation des Determinationskoeffizienten

Beispiel

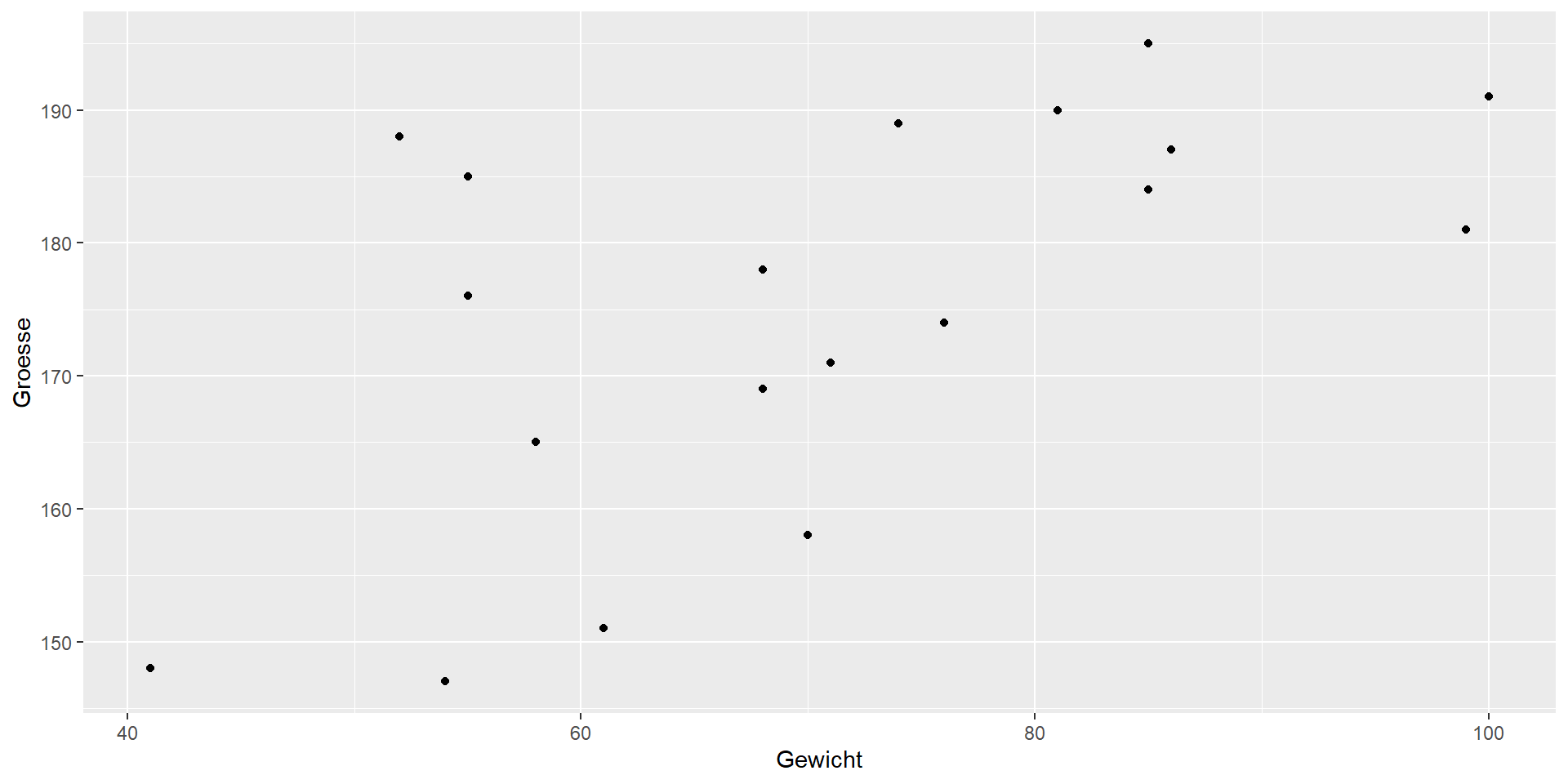
Korrelation der Rohwerte: 0.602

Korrelation der Ränge: 0.59

Ausgangsdaten
Groesse	Rang1	Gewicht	Rang2
147	19	54	17
187	6	86	3
158	16	70	10
195	1	85	4
190	3	81	6
165	15	58	14
174	12	76	7
185	7	55	15
169	14	68	11
184	8	85	4
189	4	74	8
181	9	99	2
191	2	100	1
178	10	68	11
148	18	41	19
151	17	61	13
188	5	52	18
176	11	55	15
171	13	71	9

Zum Nachdenken

Anscombe-Quartett

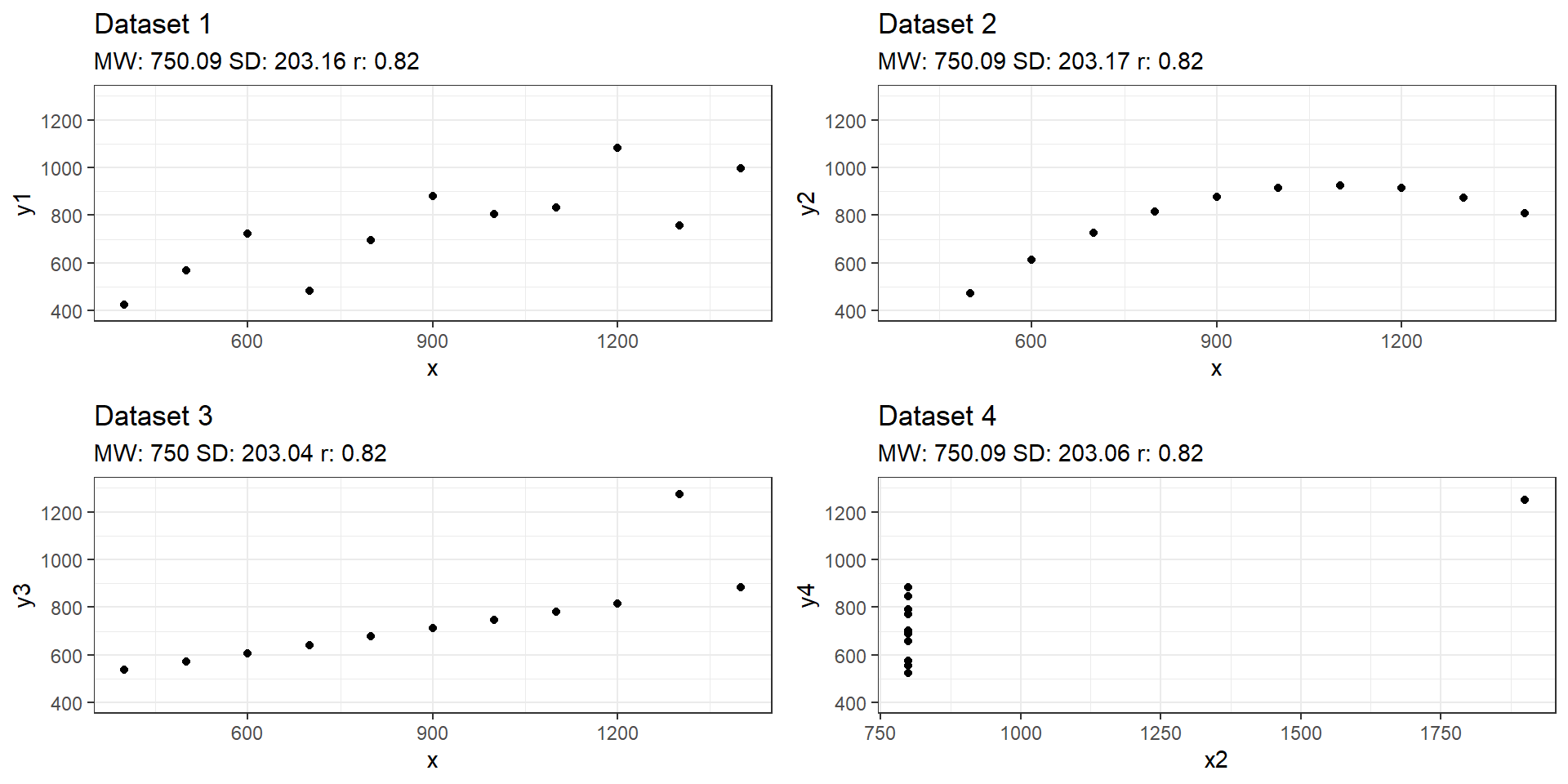
Anhang

SNV: Tabelle der z-Werte

Achtung: Die Tabelle hat zwei Hälften – oben negative unten positive z-Werte

	-.00	-.01	-.02	-.03	-.04	-.05	-.06	-.07	-.08	-.09
0	0.5000	0.4960	0.4920	0.4880	0.4840	0.4801	0.4761	0.4721	0.4681	0.4641
-0.1	0.4602	0.4562	0.4522	0.4483	0.4443	0.4404	0.4364	0.4325	0.4286	0.4247
-0.2	0.4207	0.4168	0.4129	0.4090	0.4052	0.4013	0.3974	0.3936	0.3897	0.3859
-0.3	0.3821	0.3783	0.3745	0.3707	0.3669	0.3632	0.3594	0.3557	0.3520	0.3483
-0.4	0.3446	0.3409	0.3372	0.3336	0.3300	0.3264	0.3228	0.3192	0.3156	0.3121
-0.5	0.3085	0.3050	0.3015	0.2981	0.2946	0.2912	0.2877	0.2843	0.2810	0.2776
-0.6	0.2743	0.2709	0.2676	0.2643	0.2611	0.2578	0.2546	0.2514	0.2483	0.2451
-0.7	0.2420	0.2389	0.2358	0.2327	0.2296	0.2266	0.2236	0.2206	0.2177	0.2148
-0.8	0.2119	0.2090	0.2061	0.2033	0.2005	0.1977	0.1949	0.1922	0.1894	0.1867
-0.9	0.1841	0.1814	0.1788	0.1762	0.1736	0.1711	0.1685	0.1660	0.1635	0.1611
-1	0.1587	0.1562	0.1539	0.1515	0.1492	0.1469	0.1446	0.1423	0.1401	0.1379
-1.1	0.1357	0.1335	0.1314	0.1292	0.1271	0.1251	0.1230	0.1210	0.1190	0.1170
-1.2	0.1151	0.1131	0.1112	0.1093	0.1075	0.1056	0.1038	0.1020	0.1003	0.0985
-1.3	0.0968	0.0951	0.0934	0.0918	0.0901	0.0885	0.0869	0.0853	0.0838	0.0823
-1.4	0.0808	0.0793	0.0778	0.0764	0.0749	0.0735	0.0721	0.0708	0.0694	0.0681
-1.5	0.0668	0.0655	0.0643	0.0630	0.0618	0.0606	0.0594	0.0582	0.0571	0.0559
-1.6	0.0548	0.0537	0.0526	0.0516	0.0505	0.0495	0.0485	0.0475	0.0465	0.0455
-1.7	0.0446	0.0436	0.0427	0.0418	0.0409	0.0401	0.0392	0.0384	0.0375	0.0367
-1.8	0.0359	0.0351	0.0344	0.0336	0.0329	0.0322	0.0314	0.0307	0.0301	0.0294
-1.9	0.0287	0.0281	0.0274	0.0268	0.0262	0.0256	0.0250	0.0244	0.0239	0.0233
-2	0.0228	0.0222	0.0217	0.0212	0.0207	0.0202	0.0197	0.0192	0.0188	0.0183
-2.1	0.0179	0.0174	0.0170	0.0166	0.0162	0.0158	0.0154	0.0150	0.0146	0.0143
-2.2	0.0139	0.0136	0.0132	0.0129	0.0125	0.0122	0.0119	0.0116	0.0113	0.0110
-2.3	0.0107	0.0104	0.0102	0.0099	0.0096	0.0094	0.0091	0.0089	0.0087	0.0084
-2.4	0.0082	0.0080	0.0078	0.0075	0.0073	0.0071	0.0069	0.0068	0.0066	0.0064
-2.5	0.0062	0.0060	0.0059	0.0057	0.0055	0.0054	0.0052	0.0051	0.0049	0.0048
-2.6	0.0047	0.0045	0.0044	0.0043	0.0041	0.0040	0.0039	0.0038	0.0037	0.0036
-2.7	0.0035	0.0034	0.0033	0.0032	0.0031	0.0030	0.0029	0.0028	0.0027	0.0026
-2.8	0.0026	0.0025	0.0024	0.0023	0.0023	0.0022	0.0021	0.0021	0.0020	0.0019
-2.9	0.0019	0.0018	0.0018	0.0017	0.0016	0.0016	0.0015	0.0015	0.0014	0.0014
-3	0.0013	0.0013	0.0013	0.0012	0.0012	0.0011	0.0011	0.0011	0.0010	0.0010

	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
0	0.5000	0.5040	0.5080	0.5120	0.5160	0.5199	0.5239	0.5279	0.5319	0.5359
0.1	0.5398	0.5438	0.5478	0.5517	0.5557	0.5596	0.5636	0.5675	0.5714	0.5753
0.2	0.5793	0.5832	0.5871	0.5910	0.5948	0.5987	0.6026	0.6064	0.6103	0.6141
0.3	0.6179	0.6217	0.6255	0.6293	0.6331	0.6368	0.6406	0.6443	0.6480	0.6517
0.4	0.6554	0.6591	0.6628	0.6664	0.6700	0.6736	0.6772	0.6808	0.6844	0.6879
0.5	0.6915	0.6950	0.6985	0.7019	0.7054	0.7088	0.7123	0.7157	0.7190	0.7224
0.6	0.7257	0.7291	0.7324	0.7357	0.7389	0.7422	0.7454	0.7486	0.7517	0.7549
0.7	0.7580	0.7611	0.7642	0.7673	0.7704	0.7734	0.7764	0.7794	0.7823	0.7852
0.8	0.7881	0.7910	0.7939	0.7967	0.7995	0.8023	0.8051	0.8078	0.8106	0.8133
0.9	0.8159	0.8186	0.8212	0.8238	0.8264	0.8289	0.8315	0.8340	0.8365	0.8389
1	0.8413	0.8438	0.8461	0.8485	0.8508	0.8531	0.8554	0.8577	0.8599	0.8621
1.1	0.8643	0.8665	0.8686	0.8708	0.8729	0.8749	0.8770	0.8790	0.8810	0.8830
1.2	0.8849	0.8869	0.8888	0.8907	0.8925	0.8944	0.8962	0.8980	0.8997	0.9015
1.3	0.9032	0.9049	0.9066	0.9082	0.9099	0.9115	0.9131	0.9147	0.9162	0.9177
1.4	0.9192	0.9207	0.9222	0.9236	0.9251	0.9265	0.9279	0.9292	0.9306	0.9319
1.5	0.9332	0.9345	0.9357	0.9370	0.9382	0.9394	0.9406	0.9418	0.9429	0.9441
1.6	0.9452	0.9463	0.9474	0.9484	0.9495	0.9505	0.9515	0.9525	0.9535	0.9545
1.7	0.9554	0.9564	0.9573	0.9582	0.9591	0.9599	0.9608	0.9616	0.9625	0.9633
1.8	0.9641	0.9649	0.9656	0.9664	0.9671	0.9678	0.9686	0.9693	0.9699	0.9706
1.9	0.9713	0.9719	0.9726	0.9732	0.9738	0.9744	0.9750	0.9756	0.9761	0.9767
2	0.9772	0.9778	0.9783	0.9788	0.9793	0.9798	0.9803	0.9808	0.9812	0.9817
2.1	0.9821	0.9826	0.9830	0.9834	0.9838	0.9842	0.9846	0.9850	0.9854	0.9857
2.2	0.9861	0.9864	0.9868	0.9871	0.9875	0.9878	0.9881	0.9884	0.9887	0.9890
2.3	0.9893	0.9896	0.9898	0.9901	0.9904	0.9906	0.9909	0.9911	0.9913	0.9916
2.4	0.9918	0.9920	0.9922	0.9925	0.9927	0.9929	0.9931	0.9932	0.9934	0.9936
2.5	0.9938	0.9940	0.9941	0.9943	0.9945	0.9946	0.9948	0.9949	0.9951	0.9952
2.6	0.9953	0.9955	0.9956	0.9957	0.9959	0.9960	0.9961	0.9962	0.9963	0.9964
2.7	0.9965	0.9966	0.9967	0.9968	0.9969	0.9970	0.9971	0.9972	0.9973	0.9974
2.8	0.9974	0.9975	0.9976	0.9977	0.9977	0.9978	0.9979	0.9979	0.9980	0.9981
2.9	0.9981	0.9982	0.9982	0.9983	0.9984	0.9984	0.9985	0.9985	0.9986	0.9986
3	0.9987	0.9987	0.9987	0.9988	0.9988	0.9989	0.9989	0.9989	0.9990	0.9990

t-Verteilung

df	0.01	0.025	0.05	0.10	0.25	0.75	0.90	0.95	0.975	0.99
1	-31.8205	-12.7062	-6.3138	-3.0777	-1.0000	1.0000	3.0777	6.3138	12.7062	31.8205
2	-6.9646	-4.3027	-2.9200	-1.8856	-0.8165	0.8165	1.8856	2.9200	4.3027	6.9646
3	-4.5407	-3.1824	-2.3534	-1.6377	-0.7649	0.7649	1.6377	2.3534	3.1824	4.5407
4	-3.7469	-2.7764	-2.1318	-1.5332	-0.7407	0.7407	1.5332	2.1318	2.7764	3.7469
5	-3.3649	-2.5706	-2.0150	-1.4759	-0.7267	0.7267	1.4759	2.0150	2.5706	3.3649
6	-3.1427	-2.4469	-1.9432	-1.4398	-0.7176	0.7176	1.4398	1.9432	2.4469	3.1427
7	-2.9980	-2.3646	-1.8946	-1.4149	-0.7111	0.7111	1.4149	1.8946	2.3646	2.9980
8	-2.8965	-2.3060	-1.8595	-1.3968	-0.7064	0.7064	1.3968	1.8595	2.3060	2.8965
9	-2.8214	-2.2622	-1.8331	-1.3830	-0.7027	0.7027	1.3830	1.8331	2.2622	2.8214
10	-2.7638	-2.2281	-1.8125	-1.3722	-0.6998	0.6998	1.3722	1.8125	2.2281	2.7638
11	-2.7181	-2.2010	-1.7959	-1.3634	-0.6974	0.6974	1.3634	1.7959	2.2010	2.7181
12	-2.6810	-2.1788	-1.7823	-1.3562	-0.6955	0.6955	1.3562	1.7823	2.1788	2.6810
13	-2.6503	-2.1604	-1.7709	-1.3502	-0.6938	0.6938	1.3502	1.7709	2.1604	2.6503
14	-2.6245	-2.1448	-1.7613	-1.3450	-0.6924	0.6924	1.3450	1.7613	2.1448	2.6245
15	-2.6025	-2.1314	-1.7531	-1.3406	-0.6912	0.6912	1.3406	1.7531	2.1314	2.6025
16	-2.5835	-2.1199	-1.7459	-1.3368	-0.6901	0.6901	1.3368	1.7459	2.1199	2.5835
17	-2.5669	-2.1098	-1.7396	-1.3334	-0.6892	0.6892	1.3334	1.7396	2.1098	2.5669
18	-2.5524	-2.1009	-1.7341	-1.3304	-0.6884	0.6884	1.3304	1.7341	2.1009	2.5524
19	-2.5395	-2.0930	-1.7291	-1.3277	-0.6876	0.6876	1.3277	1.7291	2.0930	2.5395
20	-2.5280	-2.0860	-1.7247	-1.3253	-0.6870	0.6870	1.3253	1.7247	2.0860	2.5280
21	-2.5176	-2.0796	-1.7207	-1.3232	-0.6864	0.6864	1.3232	1.7207	2.0796	2.5176
22	-2.5083	-2.0739	-1.7171	-1.3212	-0.6858	0.6858	1.3212	1.7171	2.0739	2.5083
23	-2.4999	-2.0687	-1.7139	-1.3195	-0.6853	0.6853	1.3195	1.7139	2.0687	2.4999
24	-2.4922	-2.0639	-1.7109	-1.3178	-0.6848	0.6848	1.3178	1.7109	2.0639	2.4922
25	-2.4851	-2.0595	-1.7081	-1.3163	-0.6844	0.6844	1.3163	1.7081	2.0595	2.4851
26	-2.4786	-2.0555	-1.7056	-1.3150	-0.6840	0.6840	1.3150	1.7056	2.0555	2.4786
27	-2.4727	-2.0518	-1.7033	-1.3137	-0.6837	0.6837	1.3137	1.7033	2.0518	2.4727
28	-2.4671	-2.0484	-1.7011	-1.3125	-0.6834	0.6834	1.3125	1.7011	2.0484	2.4671
29	-2.4620	-2.0452	-1.6991	-1.3114	-0.6830	0.6830	1.3114	1.6991	2.0452	2.4620
30	-2.4573	-2.0423	-1.6973	-1.3104	-0.6828	0.6828	1.3104	1.6973	2.0423	2.4573
31	-2.4528	-2.0395	-1.6955	-1.3095	-0.6825	0.6825	1.3095	1.6955	2.0395	2.4528
32	-2.4487	-2.0369	-1.6939	-1.3086	-0.6822	0.6822	1.3086	1.6939	2.0369	2.4487
33	-2.4448	-2.0345	-1.6924	-1.3077	-0.6820	0.6820	1.3077	1.6924	2.0345	2.4448
34	-2.4411	-2.0322	-1.6909	-1.3070	-0.6818	0.6818	1.3070	1.6909	2.0322	2.4411
35	-2.4377	-2.0301	-1.6896	-1.3062	-0.6816	0.6816	1.3062	1.6896	2.0301	2.4377
36	-2.4345	-2.0281	-1.6883	-1.3055	-0.6814	0.6814	1.3055	1.6883	2.0281	2.4345
37	-2.4314	-2.0262	-1.6871	-1.3049	-0.6812	0.6812	1.3049	1.6871	2.0262	2.4314
38	-2.4286	-2.0244	-1.6860	-1.3042	-0.6810	0.6810	1.3042	1.6860	2.0244	2.4286
39	-2.4258	-2.0227	-1.6849	-1.3036	-0.6808	0.6808	1.3036	1.6849	2.0227	2.4258
40	-2.4233	-2.0211	-1.6839	-1.3031	-0.6807	0.6807	1.3031	1.6839	2.0211	2.4233
41	-2.4208	-2.0195	-1.6829	-1.3025	-0.6805	0.6805	1.3025	1.6829	2.0195	2.4208
42	-2.4185	-2.0181	-1.6820	-1.3020	-0.6804	0.6804	1.3020	1.6820	2.0181	2.4185
43	-2.4163	-2.0167	-1.6811	-1.3016	-0.6802	0.6802	1.3016	1.6811	2.0167	2.4163
44	-2.4141	-2.0154	-1.6802	-1.3011	-0.6801	0.6801	1.3011	1.6802	2.0154	2.4141
45	-2.4121	-2.0141	-1.6794	-1.3006	-0.6800	0.6800	1.3006	1.6794	2.0141	2.4121
46	-2.4102	-2.0129	-1.6787	-1.3002	-0.6799	0.6799	1.3002	1.6787	2.0129	2.4102
47	-2.4083	-2.0117	-1.6779	-1.2998	-0.6797	0.6797	1.2998	1.6779	2.0117	2.4083
48	-2.4066	-2.0106	-1.6772	-1.2994	-0.6796	0.6796	1.2994	1.6772	2.0106	2.4066
49	-2.4049	-2.0096	-1.6766	-1.2991	-0.6795	0.6795	1.2991	1.6766	2.0096	2.4049
50	-2.4033	-2.0086	-1.6759	-1.2987	-0.6794	0.6794	1.2987	1.6759	2.0086	2.4033
51	-2.4017	-2.0076	-1.6753	-1.2984	-0.6793	0.6793	1.2984	1.6753	2.0076	2.4017
52	-2.4002	-2.0066	-1.6747	-1.2980	-0.6792	0.6792	1.2980	1.6747	2.0066	2.4002
53	-2.3988	-2.0057	-1.6741	-1.2977	-0.6791	0.6791	1.2977	1.6741	2.0057	2.3988
54	-2.3974	-2.0049	-1.6736	-1.2974	-0.6791	0.6791	1.2974	1.6736	2.0049	2.3974
55	-2.3961	-2.0040	-1.6730	-1.2971	-0.6790	0.6790	1.2971	1.6730	2.0040	2.3961
56	-2.3948	-2.0032	-1.6725	-1.2969	-0.6789	0.6789	1.2969	1.6725	2.0032	2.3948
57	-2.3936	-2.0025	-1.6720	-1.2966	-0.6788	0.6788	1.2966	1.6720	2.0025	2.3936
58	-2.3924	-2.0017	-1.6716	-1.2963	-0.6787	0.6787	1.2963	1.6716	2.0017	2.3924
59	-2.3912	-2.0010	-1.6711	-1.2961	-0.6787	0.6787	1.2961	1.6711	2.0010	2.3912
60	-2.3901	-2.0003	-1.6706	-1.2958	-0.6786	0.6786	1.2958	1.6706	2.0003	2.3901
61	-2.3890	-1.9996	-1.6702	-1.2956	-0.6785	0.6785	1.2956	1.6702	1.9996	2.3890
62	-2.3880	-1.9990	-1.6698	-1.2954	-0.6785	0.6785	1.2954	1.6698	1.9990	2.3880
63	-2.3870	-1.9983	-1.6694	-1.2951	-0.6784	0.6784	1.2951	1.6694	1.9983	2.3870
64	-2.3860	-1.9977	-1.6690	-1.2949	-0.6783	0.6783	1.2949	1.6690	1.9977	2.3860
65	-2.3851	-1.9971	-1.6686	-1.2947	-0.6783	0.6783	1.2947	1.6686	1.9971	2.3851
66	-2.3842	-1.9966	-1.6683	-1.2945	-0.6782	0.6782	1.2945	1.6683	1.9966	2.3842
67	-2.3833	-1.9960	-1.6679	-1.2943	-0.6782	0.6782	1.2943	1.6679	1.9960	2.3833
68	-2.3824	-1.9955	-1.6676	-1.2941	-0.6781	0.6781	1.2941	1.6676	1.9955	2.3824
69	-2.3816	-1.9949	-1.6672	-1.2939	-0.6781	0.6781	1.2939	1.6672	1.9949	2.3816
70	-2.3808	-1.9944	-1.6669	-1.2938	-0.6780	0.6780	1.2938	1.6669	1.9944	2.3808
71	-2.3800	-1.9939	-1.6666	-1.2936	-0.6780	0.6780	1.2936	1.6666	1.9939	2.3800
72	-2.3793	-1.9935	-1.6663	-1.2934	-0.6779	0.6779	1.2934	1.6663	1.9935	2.3793
73	-2.3785	-1.9930	-1.6660	-1.2933	-0.6779	0.6779	1.2933	1.6660	1.9930	2.3785
74	-2.3778	-1.9925	-1.6657	-1.2931	-0.6778	0.6778	1.2931	1.6657	1.9925	2.3778
75	-2.3771	-1.9921	-1.6654	-1.2929	-0.6778	0.6778	1.2929	1.6654	1.9921	2.3771
76	-2.3764	-1.9917	-1.6652	-1.2928	-0.6777	0.6777	1.2928	1.6652	1.9917	2.3764
77	-2.3758	-1.9913	-1.6649	-1.2926	-0.6777	0.6777	1.2926	1.6649	1.9913	2.3758
78	-2.3751	-1.9908	-1.6646	-1.2925	-0.6776	0.6776	1.2925	1.6646	1.9908	2.3751
79	-2.3745	-1.9905	-1.6644	-1.2924	-0.6776	0.6776	1.2924	1.6644	1.9905	2.3745
80	-2.3739	-1.9901	-1.6641	-1.2922	-0.6776	0.6776	1.2922	1.6641	1.9901	2.3739
81	-2.3733	-1.9897	-1.6639	-1.2921	-0.6775	0.6775	1.2921	1.6639	1.9897	2.3733
82	-2.3727	-1.9893	-1.6636	-1.2920	-0.6775	0.6775	1.2920	1.6636	1.9893	2.3727
83	-2.3721	-1.9890	-1.6634	-1.2918	-0.6775	0.6775	1.2918	1.6634	1.9890	2.3721
84	-2.3716	-1.9886	-1.6632	-1.2917	-0.6774	0.6774	1.2917	1.6632	1.9886	2.3716
85	-2.3710	-1.9883	-1.6630	-1.2916	-0.6774	0.6774	1.2916	1.6630	1.9883	2.3710
86	-2.3705	-1.9879	-1.6628	-1.2915	-0.6774	0.6774	1.2915	1.6628	1.9879	2.3705
87	-2.3700	-1.9876	-1.6626	-1.2914	-0.6773	0.6773	1.2914	1.6626	1.9876	2.3700
88	-2.3695	-1.9873	-1.6624	-1.2912	-0.6773	0.6773	1.2912	1.6624	1.9873	2.3695
89	-2.3690	-1.9870	-1.6622	-1.2911	-0.6773	0.6773	1.2911	1.6622	1.9870	2.3690
90	-2.3685	-1.9867	-1.6620	-1.2910	-0.6772	0.6772	1.2910	1.6620	1.9867	2.3685
91	-2.3680	-1.9864	-1.6618	-1.2909	-0.6772	0.6772	1.2909	1.6618	1.9864	2.3680
92	-2.3676	-1.9861	-1.6616	-1.2908	-0.6772	0.6772	1.2908	1.6616	1.9861	2.3676
93	-2.3671	-1.9858	-1.6614	-1.2907	-0.6771	0.6771	1.2907	1.6614	1.9858	2.3671
94	-2.3667	-1.9855	-1.6612	-1.2906	-0.6771	0.6771	1.2906	1.6612	1.9855	2.3667
95	-2.3662	-1.9853	-1.6611	-1.2905	-0.6771	0.6771	1.2905	1.6611	1.9853	2.3662
96	-2.3658	-1.9850	-1.6609	-1.2904	-0.6771	0.6771	1.2904	1.6609	1.9850	2.3658
97	-2.3654	-1.9847	-1.6607	-1.2903	-0.6770	0.6770	1.2903	1.6607	1.9847	2.3654
98	-2.3650	-1.9845	-1.6606	-1.2902	-0.6770	0.6770	1.2902	1.6606	1.9845	2.3650
99	-2.3646	-1.9842	-1.6604	-1.2902	-0.6770	0.6770	1.2902	1.6604	1.9842	2.3646
100	-2.3642	-1.9840	-1.6602	-1.2901	-0.6770	0.6770	1.2901	1.6602	1.9840	2.3642