| Zuckergehalt |
|---|
| 20.70 |
| 20.75 |
| 22.14 |
| 19.72 |
| 25.06 |
| 27.46 |
| 22.91 |
| 19.56 |
| 18.28 |
| 22.44 |
| 22.15 |
| 25.34 |
| 21.10 |
| 16.26 |
| 19.08 |
| 19.85 |
| 20.33 |
| 18.04 |
| 17.46 |
| 19.88 |
| 21.29 |
| 21.54 |
| 24.12 |
| 20.53 |
| 21.39 |
| 24.75 |
| 21.08 |
| 19.95 |
| 22.12 |
| 22.33 |
| 25.79 |
Test von Unterschiedshypothesen
_Statistik
TH Deggendorf
26.02.2024
Eine Stichprobe
(Einstichproben-)Gauß-Test
Fragestellung: Ist der Mittelwert einer Stichprobe ungleich (bzw. kleiner oder größer) einem gegebenen Populationsmittelwert \(\mu_0\)?
Voraussetzungen:
- Bekanntes \(\mu_0\) und bekannte Standardabweichung \(\sigma\)
UND - Normalverteilte Grundgesamtheit ODER n > 30
- Bekanntes \(\mu_0\) und bekannte Standardabweichung \(\sigma\)
Hypothesen:
- \(H_{0}\colon \mu_1 =\mu _{0}; {\displaystyle H_{1}\colon \mu_1 \neq \mu _{0}}\) (zweiseitig)
- \(H_{0}\colon \mu_1 \leq \mu _{0}; {\displaystyle H_{1}\colon \mu_1 > \mu _{0}}\) bzw.
\(H_{0}\colon \mu_1 \geq \mu _{0}; {\displaystyle H_{1}\colon \mu_1 < \mu _{0}}\) bzw. (einseitig)
Teststatistik/Prüfgröße: \(z={\frac {{\bar x}-\mu _{0}}{\sigma/\sqrt{n}}}\)
\(z\) ist standardnormalverteilt.
⚙️🔩 Beispiel
Eine Maschine produziert Schrauben. Die Länge der produzierten Schrauben ist normalverteilt um den Wert \(\mu\) = 100 mm. Die Standardabweichung \(\sigma\) beträgt 1 mm.
In regelmäßigen Abständen wird geprüft, ob die Maschine richtig eingestellt ist. Dazu wird eine Stichprobe der produzierten Schrauben (n = 150) gemessen. Für eine dieser Stichproben wird ein Mittelwert von \(\bar{x}\) = 98 mm festgestellt.
Ist diese Abweichung auf einem Signifikanzniveau von \(\alpha\) = 5 % statistisch bedeutsam? Testen Sie ungerichtet.
Lösung
H0: \(\mu\) \(=\) 100 mm
H1: \(\mu\) \(\neq\) 100 mmn > 30 \(\Rightarrow\) \(\bar{x}\) entstammt einer Normalverteilung mit der Standardabweichung \(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}\) bzw. \(\sigma_{\bar{x}} = \frac{1}{\sqrt{150}} = 0.082\).
Kritische z-Werte (da zweiseitig): \(z_{0.025}\) = -1.96; \(z_{0.975}\) = 1.96
Empirischer z-Wert: \(z_{emp} = \frac{\bar{x}-\mu_0}{\sigma_{\bar{x}}}= \frac{98-100}{0.082}\) = -24.39
Annahmebereich der ungerichteten \(H_0\): [\(\mu + z_{.025} \cdot \textit{SE}\); \(\mu + z_{.975} \cdot \textit{SE}\)] = [99.839; 100.161]
Die beiden Teilbereiche links und rechts dieses Bereiches addieren sich zu 5 % und bilden den Ablehnungsbereich der H0.
Unser Mittelwert der Stichprobe \(\bar{x}\) = 98 mm fällt in den Ablehnungsbereich der H0. Alternativ: \(z_{emp}\) ist betragsmäßig größer als \(z_{krit}\). Wir können die Nullhypothese daher ablehnen und stattdessen die Alternativhypothese H1 annehmen. Es gibt damit eine signifikante Abweichung vom Populationsmittelwert 100 mm. Unser Mittelwert ist signifikant kleiner als der Erwartungswert \(\mu\).
Einstichproben-t-Test
Fragestellung: Ist der Mittelwert einer Stichprobe ungleich (bzw. kleiner oder größer) einem gegebenen Populationsmittelwert \(\mu_0\)?
Voraussetzungen:
- Bekanntes \(\mu_0\) und Standardabweichung in der Population nicht bekannt
UND - Normalverteilte Grundgesamtheit ODER n > 30
- Bekanntes \(\mu_0\) und Standardabweichung in der Population nicht bekannt
Hypothesen:
- \(H_{0}\colon \mu_1 =\mu _{0}; {\displaystyle H_{1}\colon \mu_1 \neq \mu _{0}}\) (zweiseitig)
- \(H_{0}\colon \mu_1 \leq \mu _{0}; {\displaystyle H_{1}\colon \mu_1 > \mu _{0}}\) bzw.
\(H_{0}\colon \mu_1 \geq \mu _{0}; {\displaystyle H_{1}\colon \mu_1 < \mu _{0}}\) bzw. (einseitig)
Teststatistik/Prüfgröße: \(t={\frac {{\bar x}-\mu _{0}}{s/\sqrt{n}}}\)
\(t\) ist t-verteilt mit \(n-1\) Freiheitsgraden.
Unterschied zum Gauß-Test: Schätzen von \(\sigma\) über die Standardabweichung \(s\) der Stichprobe.
🍔 Beispiel
Eine Fastfood-Kette gibt an, dass ihr Vanilleeis 20 g Zucker pro 100 ml Eis enthält. Deutschlandweit wird an 31 verschiedenen Standorten je eine Probe entnommen, deren Zuckergehalt untersucht wird. Die Daten sind in der Tabelle rechts dargestellt.
Wir vermuten, dass die Kette tatsächlich mehr Zucker einsetzt als die angegebenen 20 g. Testen Sie diese Annahme gerichtet mit \(\alpha\) = 5 %.
Lösung
\(H_0\): \(\mu\) \(\leq\) 20 g
\(H_1\): \(\mu\) \(\gt\) 20 gn > 30 \(\Rightarrow\) \(\bar{x}\) entstammt einer Normalverteilung (NV-Annahme erfüllt)
Schätzen der Populationsvarianz über die Sichprobenvarianz: \(\hat{\sigma}\) bzw. \(\textit{SD}\)
Standardfehler: \(\hat{\sigma}_{\bar{x}} = \textit{SE} = \frac{\textit{SD}}{\sqrt{n}}\)
\(\bar{x}\) = 21.4; \(\textit{SD}\) = 2.542; \(\textit{SE}\) = 0.457;
Teststatistik: \(t_{emp}(\textit{df }) = t(30)=\frac{\bar{x}-\mu_{0}}{s/\sqrt{n}} = \frac{21.4 - 20}{0.457}\) = 3.063
\(t_{krit}(30)\) = \(t_{.95}(30)\) = 1.697
Ablehnungsbereich \(H_0\): \(\bar{x} >\) \(\mu + t_{krit} \cdot \textit{SE}\) = 20.776
Unser Mittelwert von \(\bar{x}\) = 21.4 fällt in den Ablehnungsbereich der H0. Wir nehmen daher die Alternativhypothese an. Es gibt einen signifikant höheren Zuckeranteil als 20 g.
Zwei Stichproben
t-Test für unabhängige (o. unverbundene) Stichproben
Fragestellung: Unterscheiden sich die Mittelwerte zweier unabhängiger Stichproben?
Mögliche Erweiterung der Fragestellung: Unterscheiden sich die Mittelwerte zweier unabhängiger Stichproben um einen bestimmten Wert? (Wird im folgenden nicht berücksichtigt)
Voraussetzungen:
- Unabhängigkeit der beiden Stichproben
- Beide Grundgesamtheiten normalverteilt ODER n > 30
- Varianzhomogenität
- \(\sigma\) unbekannt
Hypothesen:
- \(H_{0}\colon \mu_1 =\mu _{0}; {\displaystyle H_{1}\colon \mu_1 \neq \mu _{0}}\) (zweiseitig)
- \(H_{0}\colon \mu_1 \leq \mu _{0}; {\displaystyle H_{1}\colon \mu_1 > \mu _{0}}\) bzw.
\(H_{0}\colon \mu_1 \geq \mu _{0}; {\displaystyle H_{1}\colon \mu_1 < \mu _{0}}\) bzw. (einseitig)
Teststatistik/Prüfgröße: \(t={\frac {{\bar x_1}-{\bar x_2}}{s \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}}\),
wobei: \(s = \sqrt{{\frac {(n_1-1)s_{1}^{2}+(n_2-1)s_{2}^{2}}{n_1+n_2-2}}}\) (gepoolte Standardabweichung)Vereinfachung für gleichgroße Stichproben (\(n_1=n_2\)): \(s = \sqrt{ \frac{s_1^2 + s_2^2}{2}}\)
\(t\) ist t-verteilt mit n1 + n2 - 2 Freiheitsgraden.
Nicht-parametrische Alternative: Wilcoxon-Mann-Whitney-Test (andere Bezeichnungen: Mann-Whitney-U-Test, Wilcoxon-Rangsummentest)
💊 Beispiel
Ein neues Medikament soll adipösen Menschen das Abnehmen erleichtern. Zwei Stichproben von \(n_1\) = 48 und \(n_2\) = 45 Personen (alle adipös) erhalten in der Experimentalgruppe (\(n_1\)) das Medikament bzw. in der Kontrollbedingung (\(n_2\)) ein Placebo-Präparat. Neben einigen anderen medizinischen Indikatoren wird auch das Körpergewicht der Versuchsteilnehmer:innen erhoben.
Für die Experimentalgruppe ergibt sich nach der Behandlung ein Mittelwert von \(\bar{x}_1\) = 122.8 kg (SD = 22.7 kg); für die Kontrollgruppe betragen die entsprechenden Werte \(\bar{x}_2\) = 130.6 kg (SD = 20.3 kg).
Fragestellung: Hat die Experimentalgruppe nach Ablauf der Studie ein signifikant niedrigeres Körpergewicht?
Lösung
\(H_{0}\colon \mu_1 \geq \mu _{2}\)
\({\displaystyle H_{1}\colon \mu_1 < \mu _{2}}\)Gepoolte Standardabweichung: \(s = \sqrt{\frac{(48-1)\cdot22.7^2 + (45-1)\cdot20.3^2}{48 + 45 -2}}\) = 21.573
Teststatistik: \(t_{emp}\)(91) = \(\frac{122.8 - 130.6}{21.573 \cdot \sqrt{1/48 + 1/45}}\) = -1.742
\(t_{krit}\)(91) = \(t_{.05}\)(91) = - \(t_{.95}\)(91) = - 1.662
Achtung: Wir erwarten einen negativen Wert! Genauso gut könnte man die Berechnung mit vertauschten Mittelwerten durchführen. Dann würden wir einen positiven Wert für t erwarten.
Der empirische t-Wert \(t_{emp}\)(91) von -1.742 ist betragsmäßig größer als der kritische Wert von 1.662. Das Gewicht der Experimentalgruppe ist damit nach Ablauf der Studie signifikant kleiner als das der Kontrollgruppe. Das Medikament senkt das Körpergewicht signifikant.
t-Test für abhängige (o. verbundene) Stichproben
Fragestellung: Unterscheiden sich die Mittelwerte zweier abhängiger Stichproben?
Mögliche Erweiterung der Fragestellung: Unterscheiden sich die Mittelwerte zweier abhängiger Stichproben um einen bestimmten Wert? (Wird im folgenden nicht berücksichtigt)
Voraussetzungen:
- Abhängigkeit der beiden Stichproben (z. B. durch Identität bei Messwiederholung)
- Differenzen unabhängig und (normalverteilt ODER n > 30)
Hypothesen:
- \(H_{0}\colon \mu_1 =\mu _{0}; H_{1}\colon \mu_1 \neq \mu _{0}\) (zweiseitig)
- \(H_{0}\colon \mu_1 \leq \mu _{0}; H_{1}\colon \mu_1 > \mu _{0}\) bzw.
\(H_{0}\colon \mu_1 \geq \mu _{0}; H_{1}\colon \mu_1 < \mu _{0}\) bzw. (einseitig)
Teststatistik/Prüfgröße: \(t = \frac{\overline{x}_{d}}{s_{d}/\sqrt{n}}\),
wobei \(\overline{x}_{d} = {\frac {1}{n}}\sum _{i=1}^{n}x_{1i} - x_{2i} = {\frac {1}{n}}\sum _{i=1}^{n}d_{i}\)
und \(s_{d}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(d_{i}-{\overline{x}_{d}})^{2}}}\)\(t\) ist t-verteilt mit n - 1 Freiheitsgraden.
Nicht-parametrische Alternative: Wilcoxon-Vorzeichen-Rang-Test (andere Bezeichnungen: Wilcoxon-Test für gepaarte Stichproben)
🐁 Beispiel
Das Beispiel habe ich dem Skript Biology 304: Biological Data Analysis von Paul M. Magwene entnommen.
Wir messen die Expression des Gens YFG1 bei fünf Mäusen (die Genexpression wird in der Einheit “Transkripte pro Einheit Zeit” gemessen). Dann werden diese fünf Mäuse mit Medikament XY behandelt und nach einem geeigneten Zeitraum die Genexpression erneut gemessen.
Expression vor dem Treatment = 12, 11.75, 11.25, 10.5, 10;
Expression nach dem Treatment = 11, 10, 10.50, 8.75, 9.75;
die Reihenfolge der Versuchstiere ist in beiden Bedingungen dieselbe.Wir nehmen an, dass die Voraussetzung normalverteilter Differenzen erfüllt ist.
Gibt es einen Unterschied in der gemessenen Genexpression zwischen den beiden Zeitpunkten der Messung (vorher vs. nachher)? Alternativ: Gibt es einen Einfluss der Behandlung auf die Genexpression? Testen Sie ungerichtet.
Lösung
- \(H_{0}\colon \mu_1 = \mu _{2}\)
\({\displaystyle H_{1}\colon \mu_1 \neq \mu _{2}}\)
\(\bar{x}_{d}\) = \(\frac{(12-11) + (11.75-10) + (11.25-10.5) + (10.5-8.75) + (10-9.75)}{5}\) = 1.1
\(\textit{SD}_d\) = 0.652
Teststatistik: \(t_{emp}\)(4) = \(\frac{1.1}{0.652/\sqrt{5}}\) = 3.773
\(t_{krit}\)(4) = \(t_{.025}\)(4) bzw. \(t_{.975}\)(4) = -2.776 bzw. 2.776 (zweiseitiger Test!)
Der empirische t-Wert \(t_{emp}\)(4) von 3.773 ist größer als der kritische Wert von 2.776. H0 kann daher abgelehnt werden. Die Genexpression ist nach der Behandlung durch das Medikament signifikant kleiner.
Darstellung & Effektstärke
Darstellung: Balken- bzw. Säulendiagramm
- Übliche Darstellung mit Fehlerindikatoren
- Fehlerindikatoren stehen für:
- +/- 1 SD oder
- +/- 1 SE oder
- 95%-KI (wie im Bsp. rechts)
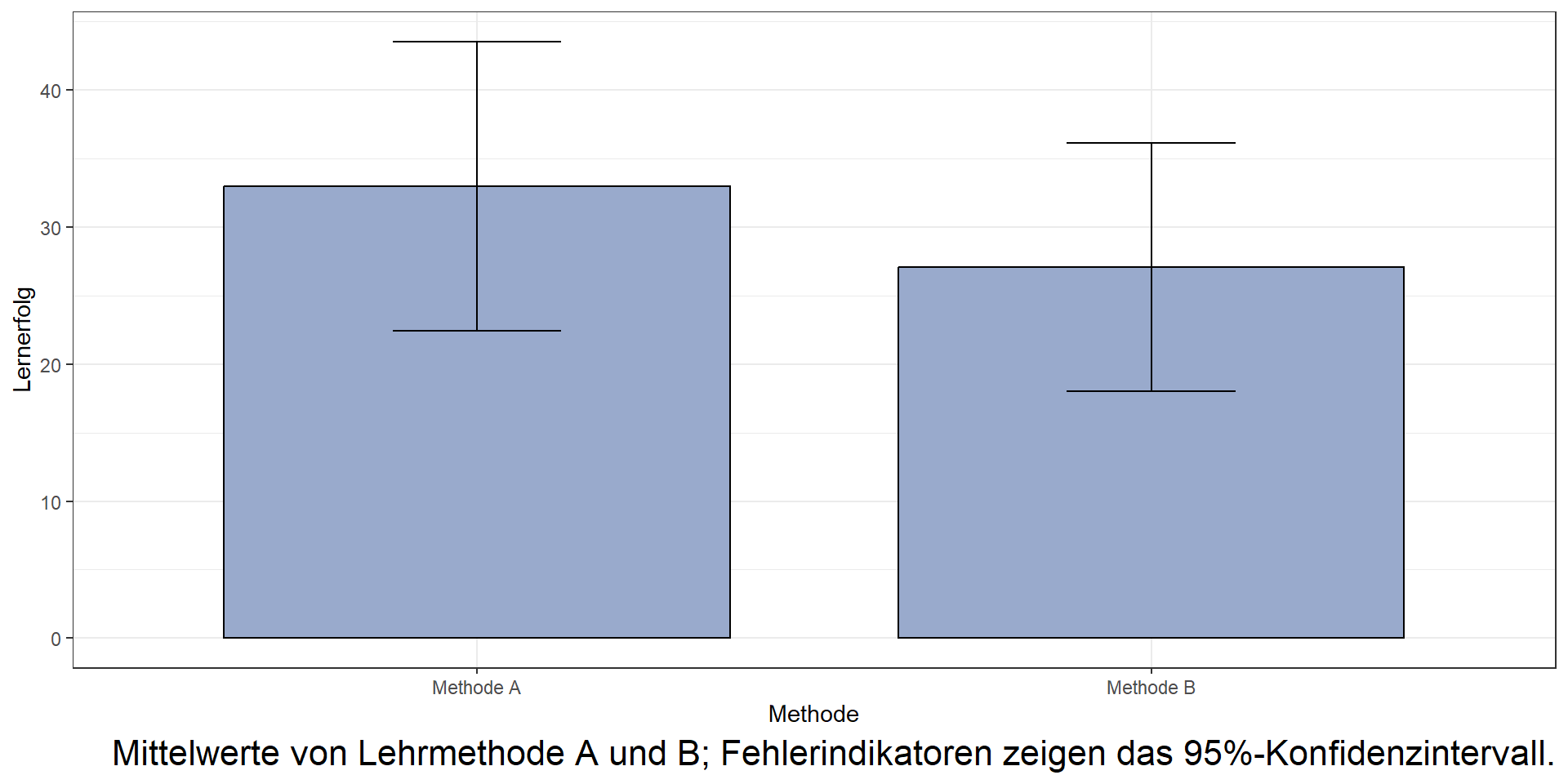
Ausgangsdaten
|
|
|---|---|
| Leistung | Methode |
| 15 | Methode A |
| 45 | Methode A |
| 16 | Methode A |
| 41 | Methode A |
| 7 | Methode A |
| 48 | Methode A |
| 46 | Methode A |
| 37 | Methode A |
| 40 | Methode A |
| 35 | Methode A |
| 5 | Methode B |
| 36 | Methode B |
| 18 | Methode B |
| 25 | Methode B |
| 10 | Methode B |
| 40 | Methode B |
| 43 | Methode B |
| 30 | Methode B |
| 35 | Methode B |
| 29 | Methode B |
Maß der Effektstärke
Korrelationskoeffizient r als Effektstärkemaß
Formel: \[r = \sqrt\frac{t^2}{t^2+\textit{df}}\]
Wertebereich: (hier) zwischen 0 und 1 (im Allgemeinen \([-1;+1]\)).
Interpretation:
- r ~ 0.1 → kleiner Effekt
- r ~ 0.3 → mittlerer Effekt
- r ~ 0.5 → großer Effekt
Anhang
SNV: Tabelle der z-Werte
Achtung: Die Tabelle hat zwei Hälften – oben negative unten positive z-Werte
| -.00 | -.01 | -.02 | -.03 | -.04 | -.05 | -.06 | -.07 | -.08 | -.09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5000 | 0.4960 | 0.4920 | 0.4880 | 0.4840 | 0.4801 | 0.4761 | 0.4721 | 0.4681 | 0.4641 |
| -0.1 | 0.4602 | 0.4562 | 0.4522 | 0.4483 | 0.4443 | 0.4404 | 0.4364 | 0.4325 | 0.4286 | 0.4247 |
| -0.2 | 0.4207 | 0.4168 | 0.4129 | 0.4090 | 0.4052 | 0.4013 | 0.3974 | 0.3936 | 0.3897 | 0.3859 |
| -0.3 | 0.3821 | 0.3783 | 0.3745 | 0.3707 | 0.3669 | 0.3632 | 0.3594 | 0.3557 | 0.3520 | 0.3483 |
| -0.4 | 0.3446 | 0.3409 | 0.3372 | 0.3336 | 0.3300 | 0.3264 | 0.3228 | 0.3192 | 0.3156 | 0.3121 |
| -0.5 | 0.3085 | 0.3050 | 0.3015 | 0.2981 | 0.2946 | 0.2912 | 0.2877 | 0.2843 | 0.2810 | 0.2776 |
| -0.6 | 0.2743 | 0.2709 | 0.2676 | 0.2643 | 0.2611 | 0.2578 | 0.2546 | 0.2514 | 0.2483 | 0.2451 |
| -0.7 | 0.2420 | 0.2389 | 0.2358 | 0.2327 | 0.2296 | 0.2266 | 0.2236 | 0.2206 | 0.2177 | 0.2148 |
| -0.8 | 0.2119 | 0.2090 | 0.2061 | 0.2033 | 0.2005 | 0.1977 | 0.1949 | 0.1922 | 0.1894 | 0.1867 |
| -0.9 | 0.1841 | 0.1814 | 0.1788 | 0.1762 | 0.1736 | 0.1711 | 0.1685 | 0.1660 | 0.1635 | 0.1611 |
| -1 | 0.1587 | 0.1562 | 0.1539 | 0.1515 | 0.1492 | 0.1469 | 0.1446 | 0.1423 | 0.1401 | 0.1379 |
| -1.1 | 0.1357 | 0.1335 | 0.1314 | 0.1292 | 0.1271 | 0.1251 | 0.1230 | 0.1210 | 0.1190 | 0.1170 |
| -1.2 | 0.1151 | 0.1131 | 0.1112 | 0.1093 | 0.1075 | 0.1056 | 0.1038 | 0.1020 | 0.1003 | 0.0985 |
| -1.3 | 0.0968 | 0.0951 | 0.0934 | 0.0918 | 0.0901 | 0.0885 | 0.0869 | 0.0853 | 0.0838 | 0.0823 |
| -1.4 | 0.0808 | 0.0793 | 0.0778 | 0.0764 | 0.0749 | 0.0735 | 0.0721 | 0.0708 | 0.0694 | 0.0681 |
| -1.5 | 0.0668 | 0.0655 | 0.0643 | 0.0630 | 0.0618 | 0.0606 | 0.0594 | 0.0582 | 0.0571 | 0.0559 |
| -1.6 | 0.0548 | 0.0537 | 0.0526 | 0.0516 | 0.0505 | 0.0495 | 0.0485 | 0.0475 | 0.0465 | 0.0455 |
| -1.7 | 0.0446 | 0.0436 | 0.0427 | 0.0418 | 0.0409 | 0.0401 | 0.0392 | 0.0384 | 0.0375 | 0.0367 |
| -1.8 | 0.0359 | 0.0351 | 0.0344 | 0.0336 | 0.0329 | 0.0322 | 0.0314 | 0.0307 | 0.0301 | 0.0294 |
| -1.9 | 0.0287 | 0.0281 | 0.0274 | 0.0268 | 0.0262 | 0.0256 | 0.0250 | 0.0244 | 0.0239 | 0.0233 |
| -2 | 0.0228 | 0.0222 | 0.0217 | 0.0212 | 0.0207 | 0.0202 | 0.0197 | 0.0192 | 0.0188 | 0.0183 |
| -2.1 | 0.0179 | 0.0174 | 0.0170 | 0.0166 | 0.0162 | 0.0158 | 0.0154 | 0.0150 | 0.0146 | 0.0143 |
| -2.2 | 0.0139 | 0.0136 | 0.0132 | 0.0129 | 0.0125 | 0.0122 | 0.0119 | 0.0116 | 0.0113 | 0.0110 |
| -2.3 | 0.0107 | 0.0104 | 0.0102 | 0.0099 | 0.0096 | 0.0094 | 0.0091 | 0.0089 | 0.0087 | 0.0084 |
| -2.4 | 0.0082 | 0.0080 | 0.0078 | 0.0075 | 0.0073 | 0.0071 | 0.0069 | 0.0068 | 0.0066 | 0.0064 |
| -2.5 | 0.0062 | 0.0060 | 0.0059 | 0.0057 | 0.0055 | 0.0054 | 0.0052 | 0.0051 | 0.0049 | 0.0048 |
| -2.6 | 0.0047 | 0.0045 | 0.0044 | 0.0043 | 0.0041 | 0.0040 | 0.0039 | 0.0038 | 0.0037 | 0.0036 |
| -2.7 | 0.0035 | 0.0034 | 0.0033 | 0.0032 | 0.0031 | 0.0030 | 0.0029 | 0.0028 | 0.0027 | 0.0026 |
| -2.8 | 0.0026 | 0.0025 | 0.0024 | 0.0023 | 0.0023 | 0.0022 | 0.0021 | 0.0021 | 0.0020 | 0.0019 |
| -2.9 | 0.0019 | 0.0018 | 0.0018 | 0.0017 | 0.0016 | 0.0016 | 0.0015 | 0.0015 | 0.0014 | 0.0014 |
| -3 | 0.0013 | 0.0013 | 0.0013 | 0.0012 | 0.0012 | 0.0011 | 0.0011 | 0.0011 | 0.0010 | 0.0010 |
| .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
t-Verteilung
| df | 0.01 | 0.025 | 0.05 | 0.10 | 0.25 | 0.5 | 0.75 | 0.90 | 0.95 | 0.975 | 0.99 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | -31.8205 | -12.7062 | -6.3138 | -3.0777 | -1.0000 | 0 | 1.0000 | 3.0777 | 6.3138 | 12.7062 | 31.8205 |
| 2 | -6.9646 | -4.3027 | -2.9200 | -1.8856 | -0.8165 | 0 | 0.8165 | 1.8856 | 2.9200 | 4.3027 | 6.9646 |
| 3 | -4.5407 | -3.1824 | -2.3534 | -1.6377 | -0.7649 | 0 | 0.7649 | 1.6377 | 2.3534 | 3.1824 | 4.5407 |
| 4 | -3.7469 | -2.7764 | -2.1318 | -1.5332 | -0.7407 | 0 | 0.7407 | 1.5332 | 2.1318 | 2.7764 | 3.7469 |
| 5 | -3.3649 | -2.5706 | -2.0150 | -1.4759 | -0.7267 | 0 | 0.7267 | 1.4759 | 2.0150 | 2.5706 | 3.3649 |
| 6 | -3.1427 | -2.4469 | -1.9432 | -1.4398 | -0.7176 | 0 | 0.7176 | 1.4398 | 1.9432 | 2.4469 | 3.1427 |
| 7 | -2.9980 | -2.3646 | -1.8946 | -1.4149 | -0.7111 | 0 | 0.7111 | 1.4149 | 1.8946 | 2.3646 | 2.9980 |
| 8 | -2.8965 | -2.3060 | -1.8595 | -1.3968 | -0.7064 | 0 | 0.7064 | 1.3968 | 1.8595 | 2.3060 | 2.8965 |
| 9 | -2.8214 | -2.2622 | -1.8331 | -1.3830 | -0.7027 | 0 | 0.7027 | 1.3830 | 1.8331 | 2.2622 | 2.8214 |
| 10 | -2.7638 | -2.2281 | -1.8125 | -1.3722 | -0.6998 | 0 | 0.6998 | 1.3722 | 1.8125 | 2.2281 | 2.7638 |
| 11 | -2.7181 | -2.2010 | -1.7959 | -1.3634 | -0.6974 | 0 | 0.6974 | 1.3634 | 1.7959 | 2.2010 | 2.7181 |
| 12 | -2.6810 | -2.1788 | -1.7823 | -1.3562 | -0.6955 | 0 | 0.6955 | 1.3562 | 1.7823 | 2.1788 | 2.6810 |
| 13 | -2.6503 | -2.1604 | -1.7709 | -1.3502 | -0.6938 | 0 | 0.6938 | 1.3502 | 1.7709 | 2.1604 | 2.6503 |
| 14 | -2.6245 | -2.1448 | -1.7613 | -1.3450 | -0.6924 | 0 | 0.6924 | 1.3450 | 1.7613 | 2.1448 | 2.6245 |
| 15 | -2.6025 | -2.1314 | -1.7531 | -1.3406 | -0.6912 | 0 | 0.6912 | 1.3406 | 1.7531 | 2.1314 | 2.6025 |
| 16 | -2.5835 | -2.1199 | -1.7459 | -1.3368 | -0.6901 | 0 | 0.6901 | 1.3368 | 1.7459 | 2.1199 | 2.5835 |
| 17 | -2.5669 | -2.1098 | -1.7396 | -1.3334 | -0.6892 | 0 | 0.6892 | 1.3334 | 1.7396 | 2.1098 | 2.5669 |
| 18 | -2.5524 | -2.1009 | -1.7341 | -1.3304 | -0.6884 | 0 | 0.6884 | 1.3304 | 1.7341 | 2.1009 | 2.5524 |
| 19 | -2.5395 | -2.0930 | -1.7291 | -1.3277 | -0.6876 | 0 | 0.6876 | 1.3277 | 1.7291 | 2.0930 | 2.5395 |
| 20 | -2.5280 | -2.0860 | -1.7247 | -1.3253 | -0.6870 | 0 | 0.6870 | 1.3253 | 1.7247 | 2.0860 | 2.5280 |
| 21 | -2.5176 | -2.0796 | -1.7207 | -1.3232 | -0.6864 | 0 | 0.6864 | 1.3232 | 1.7207 | 2.0796 | 2.5176 |
| 22 | -2.5083 | -2.0739 | -1.7171 | -1.3212 | -0.6858 | 0 | 0.6858 | 1.3212 | 1.7171 | 2.0739 | 2.5083 |
| 23 | -2.4999 | -2.0687 | -1.7139 | -1.3195 | -0.6853 | 0 | 0.6853 | 1.3195 | 1.7139 | 2.0687 | 2.4999 |
| 24 | -2.4922 | -2.0639 | -1.7109 | -1.3178 | -0.6848 | 0 | 0.6848 | 1.3178 | 1.7109 | 2.0639 | 2.4922 |
| 25 | -2.4851 | -2.0595 | -1.7081 | -1.3163 | -0.6844 | 0 | 0.6844 | 1.3163 | 1.7081 | 2.0595 | 2.4851 |
| 26 | -2.4786 | -2.0555 | -1.7056 | -1.3150 | -0.6840 | 0 | 0.6840 | 1.3150 | 1.7056 | 2.0555 | 2.4786 |
| 27 | -2.4727 | -2.0518 | -1.7033 | -1.3137 | -0.6837 | 0 | 0.6837 | 1.3137 | 1.7033 | 2.0518 | 2.4727 |
| 28 | -2.4671 | -2.0484 | -1.7011 | -1.3125 | -0.6834 | 0 | 0.6834 | 1.3125 | 1.7011 | 2.0484 | 2.4671 |
| 29 | -2.4620 | -2.0452 | -1.6991 | -1.3114 | -0.6830 | 0 | 0.6830 | 1.3114 | 1.6991 | 2.0452 | 2.4620 |
| 30 | -2.4573 | -2.0423 | -1.6973 | -1.3104 | -0.6828 | 0 | 0.6828 | 1.3104 | 1.6973 | 2.0423 | 2.4573 |
| 31 | -2.4528 | -2.0395 | -1.6955 | -1.3095 | -0.6825 | 0 | 0.6825 | 1.3095 | 1.6955 | 2.0395 | 2.4528 |
| 32 | -2.4487 | -2.0369 | -1.6939 | -1.3086 | -0.6822 | 0 | 0.6822 | 1.3086 | 1.6939 | 2.0369 | 2.4487 |
| 33 | -2.4448 | -2.0345 | -1.6924 | -1.3077 | -0.6820 | 0 | 0.6820 | 1.3077 | 1.6924 | 2.0345 | 2.4448 |
| 34 | -2.4411 | -2.0322 | -1.6909 | -1.3070 | -0.6818 | 0 | 0.6818 | 1.3070 | 1.6909 | 2.0322 | 2.4411 |
| 35 | -2.4377 | -2.0301 | -1.6896 | -1.3062 | -0.6816 | 0 | 0.6816 | 1.3062 | 1.6896 | 2.0301 | 2.4377 |
| 36 | -2.4345 | -2.0281 | -1.6883 | -1.3055 | -0.6814 | 0 | 0.6814 | 1.3055 | 1.6883 | 2.0281 | 2.4345 |
| 37 | -2.4314 | -2.0262 | -1.6871 | -1.3049 | -0.6812 | 0 | 0.6812 | 1.3049 | 1.6871 | 2.0262 | 2.4314 |
| 38 | -2.4286 | -2.0244 | -1.6860 | -1.3042 | -0.6810 | 0 | 0.6810 | 1.3042 | 1.6860 | 2.0244 | 2.4286 |
| 39 | -2.4258 | -2.0227 | -1.6849 | -1.3036 | -0.6808 | 0 | 0.6808 | 1.3036 | 1.6849 | 2.0227 | 2.4258 |
| 40 | -2.4233 | -2.0211 | -1.6839 | -1.3031 | -0.6807 | 0 | 0.6807 | 1.3031 | 1.6839 | 2.0211 | 2.4233 |
| 41 | -2.4208 | -2.0195 | -1.6829 | -1.3025 | -0.6805 | 0 | 0.6805 | 1.3025 | 1.6829 | 2.0195 | 2.4208 |
| 42 | -2.4185 | -2.0181 | -1.6820 | -1.3020 | -0.6804 | 0 | 0.6804 | 1.3020 | 1.6820 | 2.0181 | 2.4185 |
| 43 | -2.4163 | -2.0167 | -1.6811 | -1.3016 | -0.6802 | 0 | 0.6802 | 1.3016 | 1.6811 | 2.0167 | 2.4163 |
| 44 | -2.4141 | -2.0154 | -1.6802 | -1.3011 | -0.6801 | 0 | 0.6801 | 1.3011 | 1.6802 | 2.0154 | 2.4141 |
| 45 | -2.4121 | -2.0141 | -1.6794 | -1.3006 | -0.6800 | 0 | 0.6800 | 1.3006 | 1.6794 | 2.0141 | 2.4121 |
| 46 | -2.4102 | -2.0129 | -1.6787 | -1.3002 | -0.6799 | 0 | 0.6799 | 1.3002 | 1.6787 | 2.0129 | 2.4102 |
| 47 | -2.4083 | -2.0117 | -1.6779 | -1.2998 | -0.6797 | 0 | 0.6797 | 1.2998 | 1.6779 | 2.0117 | 2.4083 |
| 48 | -2.4066 | -2.0106 | -1.6772 | -1.2994 | -0.6796 | 0 | 0.6796 | 1.2994 | 1.6772 | 2.0106 | 2.4066 |
| 49 | -2.4049 | -2.0096 | -1.6766 | -1.2991 | -0.6795 | 0 | 0.6795 | 1.2991 | 1.6766 | 2.0096 | 2.4049 |
| 50 | -2.4033 | -2.0086 | -1.6759 | -1.2987 | -0.6794 | 0 | 0.6794 | 1.2987 | 1.6759 | 2.0086 | 2.4033 |
| 51 | -2.4017 | -2.0076 | -1.6753 | -1.2984 | -0.6793 | 0 | 0.6793 | 1.2984 | 1.6753 | 2.0076 | 2.4017 |
| 52 | -2.4002 | -2.0066 | -1.6747 | -1.2980 | -0.6792 | 0 | 0.6792 | 1.2980 | 1.6747 | 2.0066 | 2.4002 |
| 53 | -2.3988 | -2.0057 | -1.6741 | -1.2977 | -0.6791 | 0 | 0.6791 | 1.2977 | 1.6741 | 2.0057 | 2.3988 |
| 54 | -2.3974 | -2.0049 | -1.6736 | -1.2974 | -0.6791 | 0 | 0.6791 | 1.2974 | 1.6736 | 2.0049 | 2.3974 |
| 55 | -2.3961 | -2.0040 | -1.6730 | -1.2971 | -0.6790 | 0 | 0.6790 | 1.2971 | 1.6730 | 2.0040 | 2.3961 |
| 56 | -2.3948 | -2.0032 | -1.6725 | -1.2969 | -0.6789 | 0 | 0.6789 | 1.2969 | 1.6725 | 2.0032 | 2.3948 |
| 57 | -2.3936 | -2.0025 | -1.6720 | -1.2966 | -0.6788 | 0 | 0.6788 | 1.2966 | 1.6720 | 2.0025 | 2.3936 |
| 58 | -2.3924 | -2.0017 | -1.6716 | -1.2963 | -0.6787 | 0 | 0.6787 | 1.2963 | 1.6716 | 2.0017 | 2.3924 |
| 59 | -2.3912 | -2.0010 | -1.6711 | -1.2961 | -0.6787 | 0 | 0.6787 | 1.2961 | 1.6711 | 2.0010 | 2.3912 |
| 60 | -2.3901 | -2.0003 | -1.6706 | -1.2958 | -0.6786 | 0 | 0.6786 | 1.2958 | 1.6706 | 2.0003 | 2.3901 |
| 61 | -2.3890 | -1.9996 | -1.6702 | -1.2956 | -0.6785 | 0 | 0.6785 | 1.2956 | 1.6702 | 1.9996 | 2.3890 |
| 62 | -2.3880 | -1.9990 | -1.6698 | -1.2954 | -0.6785 | 0 | 0.6785 | 1.2954 | 1.6698 | 1.9990 | 2.3880 |
| 63 | -2.3870 | -1.9983 | -1.6694 | -1.2951 | -0.6784 | 0 | 0.6784 | 1.2951 | 1.6694 | 1.9983 | 2.3870 |
| 64 | -2.3860 | -1.9977 | -1.6690 | -1.2949 | -0.6783 | 0 | 0.6783 | 1.2949 | 1.6690 | 1.9977 | 2.3860 |
| 65 | -2.3851 | -1.9971 | -1.6686 | -1.2947 | -0.6783 | 0 | 0.6783 | 1.2947 | 1.6686 | 1.9971 | 2.3851 |
| 66 | -2.3842 | -1.9966 | -1.6683 | -1.2945 | -0.6782 | 0 | 0.6782 | 1.2945 | 1.6683 | 1.9966 | 2.3842 |
| 67 | -2.3833 | -1.9960 | -1.6679 | -1.2943 | -0.6782 | 0 | 0.6782 | 1.2943 | 1.6679 | 1.9960 | 2.3833 |
| 68 | -2.3824 | -1.9955 | -1.6676 | -1.2941 | -0.6781 | 0 | 0.6781 | 1.2941 | 1.6676 | 1.9955 | 2.3824 |
| 69 | -2.3816 | -1.9949 | -1.6672 | -1.2939 | -0.6781 | 0 | 0.6781 | 1.2939 | 1.6672 | 1.9949 | 2.3816 |
| 70 | -2.3808 | -1.9944 | -1.6669 | -1.2938 | -0.6780 | 0 | 0.6780 | 1.2938 | 1.6669 | 1.9944 | 2.3808 |
| 71 | -2.3800 | -1.9939 | -1.6666 | -1.2936 | -0.6780 | 0 | 0.6780 | 1.2936 | 1.6666 | 1.9939 | 2.3800 |
| 72 | -2.3793 | -1.9935 | -1.6663 | -1.2934 | -0.6779 | 0 | 0.6779 | 1.2934 | 1.6663 | 1.9935 | 2.3793 |
| 73 | -2.3785 | -1.9930 | -1.6660 | -1.2933 | -0.6779 | 0 | 0.6779 | 1.2933 | 1.6660 | 1.9930 | 2.3785 |
| 74 | -2.3778 | -1.9925 | -1.6657 | -1.2931 | -0.6778 | 0 | 0.6778 | 1.2931 | 1.6657 | 1.9925 | 2.3778 |
| 75 | -2.3771 | -1.9921 | -1.6654 | -1.2929 | -0.6778 | 0 | 0.6778 | 1.2929 | 1.6654 | 1.9921 | 2.3771 |
| 76 | -2.3764 | -1.9917 | -1.6652 | -1.2928 | -0.6777 | 0 | 0.6777 | 1.2928 | 1.6652 | 1.9917 | 2.3764 |
| 77 | -2.3758 | -1.9913 | -1.6649 | -1.2926 | -0.6777 | 0 | 0.6777 | 1.2926 | 1.6649 | 1.9913 | 2.3758 |
| 78 | -2.3751 | -1.9908 | -1.6646 | -1.2925 | -0.6776 | 0 | 0.6776 | 1.2925 | 1.6646 | 1.9908 | 2.3751 |
| 79 | -2.3745 | -1.9905 | -1.6644 | -1.2924 | -0.6776 | 0 | 0.6776 | 1.2924 | 1.6644 | 1.9905 | 2.3745 |
| 80 | -2.3739 | -1.9901 | -1.6641 | -1.2922 | -0.6776 | 0 | 0.6776 | 1.2922 | 1.6641 | 1.9901 | 2.3739 |
| 81 | -2.3733 | -1.9897 | -1.6639 | -1.2921 | -0.6775 | 0 | 0.6775 | 1.2921 | 1.6639 | 1.9897 | 2.3733 |
| 82 | -2.3727 | -1.9893 | -1.6636 | -1.2920 | -0.6775 | 0 | 0.6775 | 1.2920 | 1.6636 | 1.9893 | 2.3727 |
| 83 | -2.3721 | -1.9890 | -1.6634 | -1.2918 | -0.6775 | 0 | 0.6775 | 1.2918 | 1.6634 | 1.9890 | 2.3721 |
| 84 | -2.3716 | -1.9886 | -1.6632 | -1.2917 | -0.6774 | 0 | 0.6774 | 1.2917 | 1.6632 | 1.9886 | 2.3716 |
| 85 | -2.3710 | -1.9883 | -1.6630 | -1.2916 | -0.6774 | 0 | 0.6774 | 1.2916 | 1.6630 | 1.9883 | 2.3710 |
| 86 | -2.3705 | -1.9879 | -1.6628 | -1.2915 | -0.6774 | 0 | 0.6774 | 1.2915 | 1.6628 | 1.9879 | 2.3705 |
| 87 | -2.3700 | -1.9876 | -1.6626 | -1.2914 | -0.6773 | 0 | 0.6773 | 1.2914 | 1.6626 | 1.9876 | 2.3700 |
| 88 | -2.3695 | -1.9873 | -1.6624 | -1.2912 | -0.6773 | 0 | 0.6773 | 1.2912 | 1.6624 | 1.9873 | 2.3695 |
| 89 | -2.3690 | -1.9870 | -1.6622 | -1.2911 | -0.6773 | 0 | 0.6773 | 1.2911 | 1.6622 | 1.9870 | 2.3690 |
| 90 | -2.3685 | -1.9867 | -1.6620 | -1.2910 | -0.6772 | 0 | 0.6772 | 1.2910 | 1.6620 | 1.9867 | 2.3685 |
| 91 | -2.3680 | -1.9864 | -1.6618 | -1.2909 | -0.6772 | 0 | 0.6772 | 1.2909 | 1.6618 | 1.9864 | 2.3680 |
| 92 | -2.3676 | -1.9861 | -1.6616 | -1.2908 | -0.6772 | 0 | 0.6772 | 1.2908 | 1.6616 | 1.9861 | 2.3676 |
| 93 | -2.3671 | -1.9858 | -1.6614 | -1.2907 | -0.6771 | 0 | 0.6771 | 1.2907 | 1.6614 | 1.9858 | 2.3671 |
| 94 | -2.3667 | -1.9855 | -1.6612 | -1.2906 | -0.6771 | 0 | 0.6771 | 1.2906 | 1.6612 | 1.9855 | 2.3667 |
| 95 | -2.3662 | -1.9853 | -1.6611 | -1.2905 | -0.6771 | 0 | 0.6771 | 1.2905 | 1.6611 | 1.9853 | 2.3662 |
| 96 | -2.3658 | -1.9850 | -1.6609 | -1.2904 | -0.6771 | 0 | 0.6771 | 1.2904 | 1.6609 | 1.9850 | 2.3658 |
| 97 | -2.3654 | -1.9847 | -1.6607 | -1.2903 | -0.6770 | 0 | 0.6770 | 1.2903 | 1.6607 | 1.9847 | 2.3654 |
| 98 | -2.3650 | -1.9845 | -1.6606 | -1.2902 | -0.6770 | 0 | 0.6770 | 1.2902 | 1.6606 | 1.9845 | 2.3650 |
| 99 | -2.3646 | -1.9842 | -1.6604 | -1.2902 | -0.6770 | 0 | 0.6770 | 1.2902 | 1.6604 | 1.9842 | 2.3646 |
| 100 | -2.3642 | -1.9840 | -1.6602 | -1.2901 | -0.6770 | 0 | 0.6770 | 1.2901 | 1.6602 | 1.9840 | 2.3642 |
