Signifikanztest: Randi in R

Statistik: Übungen

1 Einführung

Wir wollen R verwenden, um das Beispiel des Wünschelrutengängers (WRG) zu bearbeiten. Den Text zu James Randi sollten Sie daher unbedingt gelesen haben.

Lassen Sie uns rekapitulieren:

• Es gibt 13 Versuchsdurchgänge; n = 13
• Die Wahrscheinlichkeit für einen zufälligen Treffer (also zufällig den korrekten Eimer auszuwählen), beträgt p = 0.1.
• James Randi legt die Latte hoch: Der WRG muss mindestens sieben mal richtig liegen; k = 7.

2 Aufgabe

Die Frage, die wir uns stellen, ist: Wie groß ist die Wahrscheinlichkeit dafür, dass der WRG zufällig sieben mal richtig liegt, wenn er es 13 mal versucht?

Dazu verwenden wir die Dichtefunktion der Binomialverteilung:

\[f(X=k|n) = {n\choose k}\cdot p^k \cdot q^{n-k}\]

Sie gibt an, wie groß die Wahrscheinlichkeit für k Treffer bei n versuchen und der Trefferwahrscheinlichkeit p ist (q ist einfach 1 - p).

Dafür gibt es in R die Funktion dbinom(k, n, p) mit drei Parametern. Diese Parameter kennen wir.

k <- 7
n <- 13
p <- 0.1
ergebnis <- dbinom(k, n, p)
ergebnis

[1] 9.119528e-05

format(ergebnis, scientific = FALSE)

[1] "0.00009119528"

Wenn wir uns mit der wissenschaftlichen Notation nicht so wohl fühlen, können wir die Funktion format() verwenden, die mit dem zweiten Parameter scientific = FALSE die klassische Notation erzwingt.

3 Aufgabe

Uns reicht es nicht, die Wahrscheinlichkeit für 7 Treffer zu kennen, da auch mehr Treffer (8, 9, …, 13) dazu führen, dass der WRG die Million gewinnt.

Wir müssen daher die Wahrscheinlichkeit für 7 oder mehr Treffer berechnen.

Auch dafür gibt es in R eine Funktion, die sich nur in einem Buchstaben von der vorherigen unterscheidet: pbinom(k, n, p). Die Parameter sind dieselben; k wird hier verwendet im Sinn von “\(\leq\) k Treffer”. Es werden alle Einzelwahrscheinlichkeiten (0 Treffer, 1 Treffer, … 7 Treffer) – also inklusive k summiert.

Wir suchen aber die Wahrscheinlichkeit von 7 oder mehr Treffern. Das Gegenereignis von 7 oder mehr ist 6 oder weniger – und genau das können wir mit der Funktion pnorm() ermitteln, wenn wir k = 6 setzen. Wir müssen nur daran denken, das Ergebnis von 1 abzuziehen.

k <- 6
n <- 13
p <- 0.1

ergebnis_kum <- pbinom(k, n, p)     # "kum" steht für kumuliert 
ergebnis_kum <- 1 - ergebnis_kum    # uns interessiert das Gegenereignis
format(ergebnis_kum, scientific = FALSE)

[1] "0.00009928549"

Die Wahrscheinlichkeit dafür, zufällig sieben oder mehr Treffer zu erzielen, beträgt 0.009929 %.

4 Aufgabe

Wie sieht eine Verteilung der zu erwartenden Ergebnisse aus, wenn die H₀ gilt; der WRG also nur rät?

Dazu können wir die Funktion rbinom() einsetzen. Wie schon für rnorm() steht das “r” hier für “random”. Die Funktion liefert also binomialverteilte Zufallszahlen. Diese stehen für die Anzahl Treffer bei einem binomialverteilten Zufallsexperiment.

Als Parameter erwartet rbinom() die Anzahl der Durchgänge; wählen Sie hier beispielsweise 1000. Die beiden weiteren Parameter entsprechen den Schwesterfuktionen von oben: n und p.

Die Funktion hist() kennen wir schon. Sie werden vielleicht feststellen, dass deren Parameter breaks (Anzahl der Kategorien) manchmal nicht so will, wie wir uns das vorstellen, wenn wir nur eine Zahl angeben. Wir können stattdessen auch die Kategoriegrenzen auf der X-Achse direkt mit Hilfe von c() angeben: breaks=c(0,1,2,3,4,5,6).

Erzeugen Sie das folgende Histogramm (wenn Sie set.seed(123) verwenden, sollte es identisch dem meinen sein):

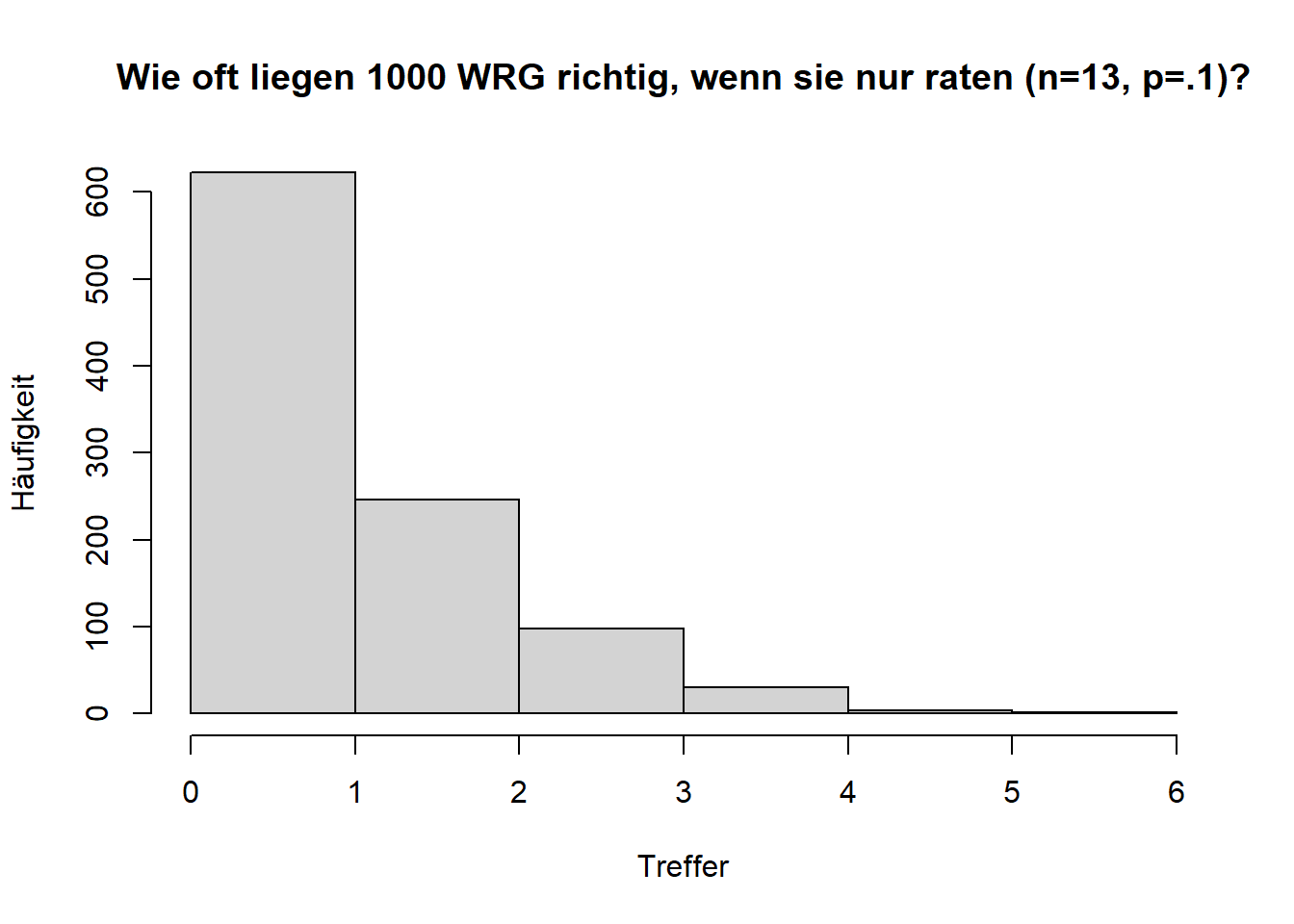
Die häufigste Anzahl an Treffern bei derartigen Experimenten (wenn wir die H₀ annehmen), sind damit 0 und 1. Sie machen zusammen über 80 Prozent der Fälle aus.

5 Aufgabe

Für das Beispiel zum neuen Trainingsverfahren gehen wir nun ganz ähnlich vor wie bei der Aufgabe eben.

Wir wollen diese Frage beantworten: Wie sieht eine Verteilung von Ergebnissen einzelner Merkmalsträger (hier: Menschen, die an dem Training teilnehmen) aus, wenn es nichts bringt; wenn also die H₀ gilt?

Erzeugen Sie als Antwort das folgende Histogramm:

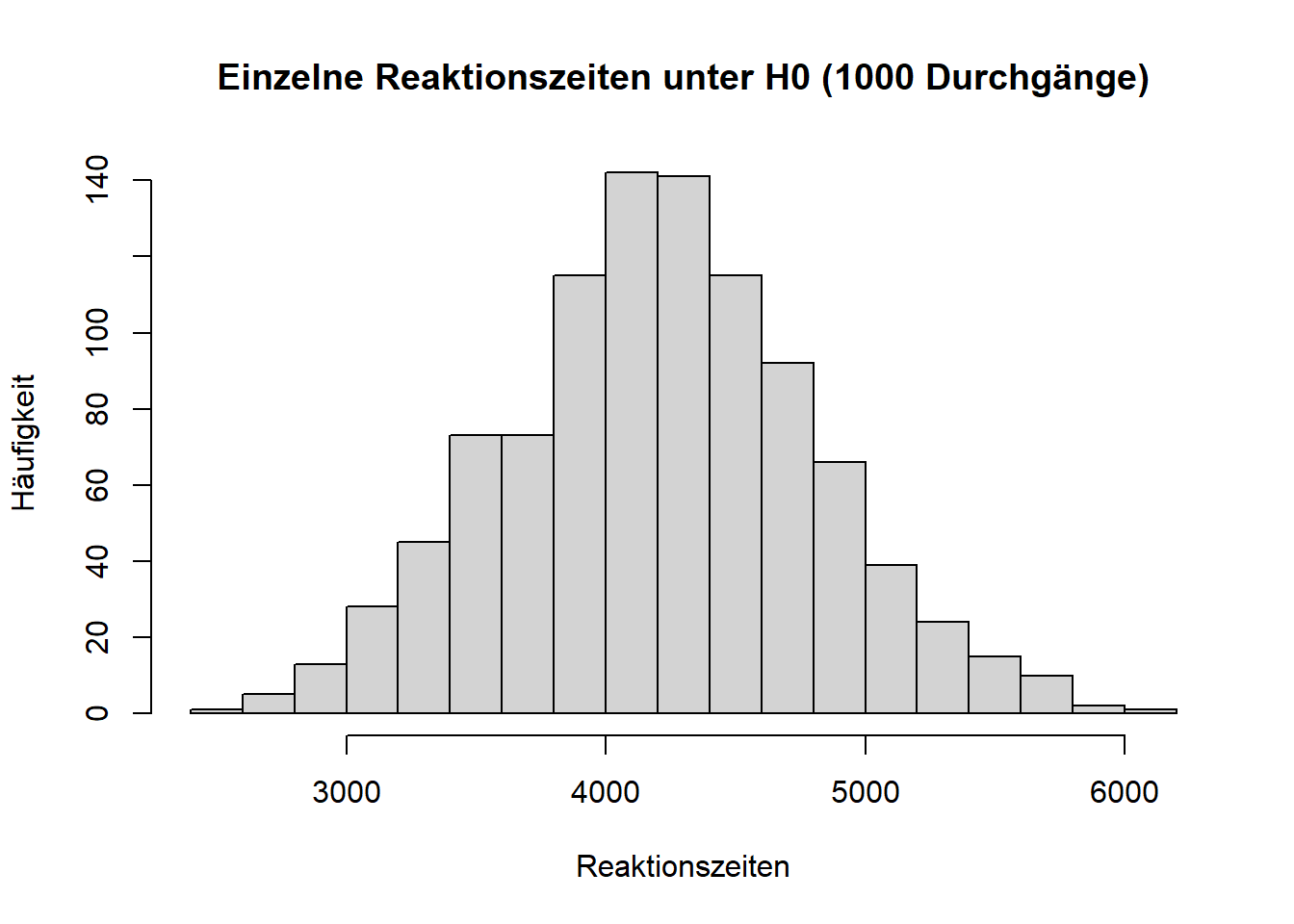
Unsere Trainingsstrichprobe hat einen MW von rund 3900 ms. Das wäre in unserem Histogramm gar nicht so ungewöhnlich. Aber Achtung: Wir vergleichen gerade Äpfel mit Birnen! Unser Histogramm stellt einzelne Reaktionszeiten dar, aber 3900 ist der Mittelwert einer Stichprobe.

Wir brauchen daher eine andere Verteilung, um unseren Mittelwert bewerten zu können: die Verteilung der Mittelwerte gleichartiger Stichproben; also Stichproben gleicher Größe, wenn die H₀ gilt.

Wir wissen, wie diese Verteilung aussieht. Sie ist auch normalverteilt, hat denselben Mittelwert, ist aber schmaler – hat also eine andere Standardabweichung, die hier Standardfehler heißt. Den Standardfehler erhalten wir, indem wir die SD durch \(\sqrt{n}\) teilen.

Erzeugen Sie mit Hilfe dieser Informationen das folgende Histogramm.

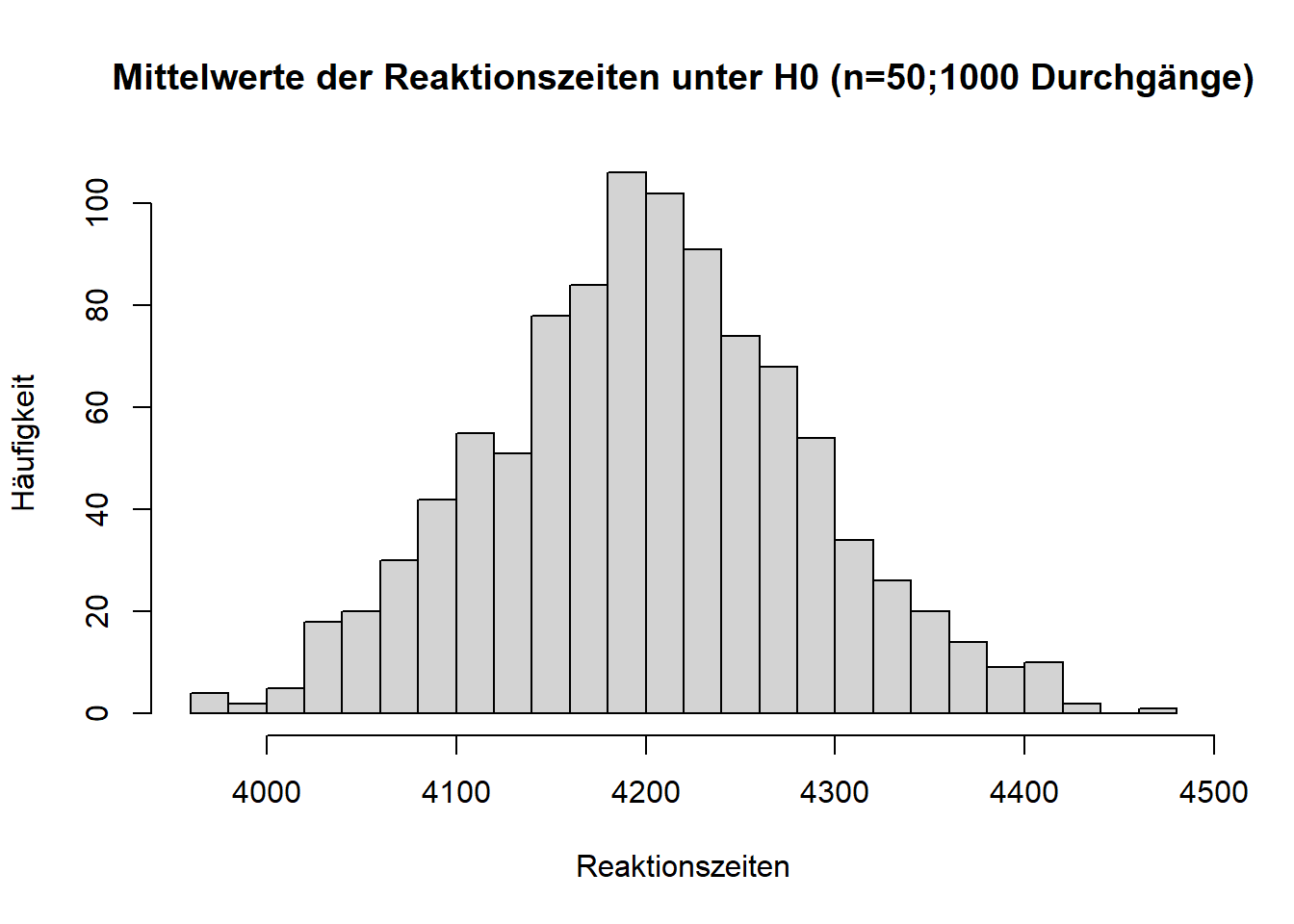
Vergleichen Sie die X-Achsen (Abszissen): Ein Mittelwert von 3900 ms ist hier scheinbar äußerst selten (=unwahrscheinlich).

Wie unwahrscheinlich genau? Das können wir leicht feststellen, indem wir berechnen, wie viele Standardfehler (= die Standardabweichung der Verteilung der Mittelwerte) unser Stichproben-MW vom großen MW (4200) entfernt ist; indem wir also den z-Wert berechnen und in der Tabelle nachsehen.

Wir können das auch der Funktion pnorm() überlassen (die kennen wir schon!), die als Parameter den MW unserer Stichprobe, den großen MW und den SE erwartet.

Antwort: Ein Stichprobenmittelwert von 3889.54 ms ist kleiner als etwa 99.99 Prozent der Mittelwerte, wenn die H₀ gilt.