Deskriptive Statistik (1)

_Statistik

Prof. Dr. Armin Eichinger

TH Deggendorf

12.02.2024

Eigenschaften

  • Wortbedeutung: deskriptiv = beschreibend

  • Empirische Daten (einer Stichprobe) werden geeignet nummerisch (tabellarisch) oder auch grafisch dargestellt

  • In Abgrenzung zu: induktive = schließende = inferentielle Statistik (von Eigenschaften einer Stichprobe auf eine Grundgesamtheit bzw. Population schließen)

  • Fließende Übergänge (z. B. Konfidenzintervalle)

  • Keine Hypothesentests

  • Beispiele

    • Berechnung von Kennzahlen (Mittelwerte, Streuungsmaße, …)
    • Darstellung von Verteilungen (Histogramm, Boxplot-Darstellung)
    • Rechnen mit Verteilungen (z-Transformation/Standardisierung)

Beispiel

Fiktive Daten zur Körpergröße

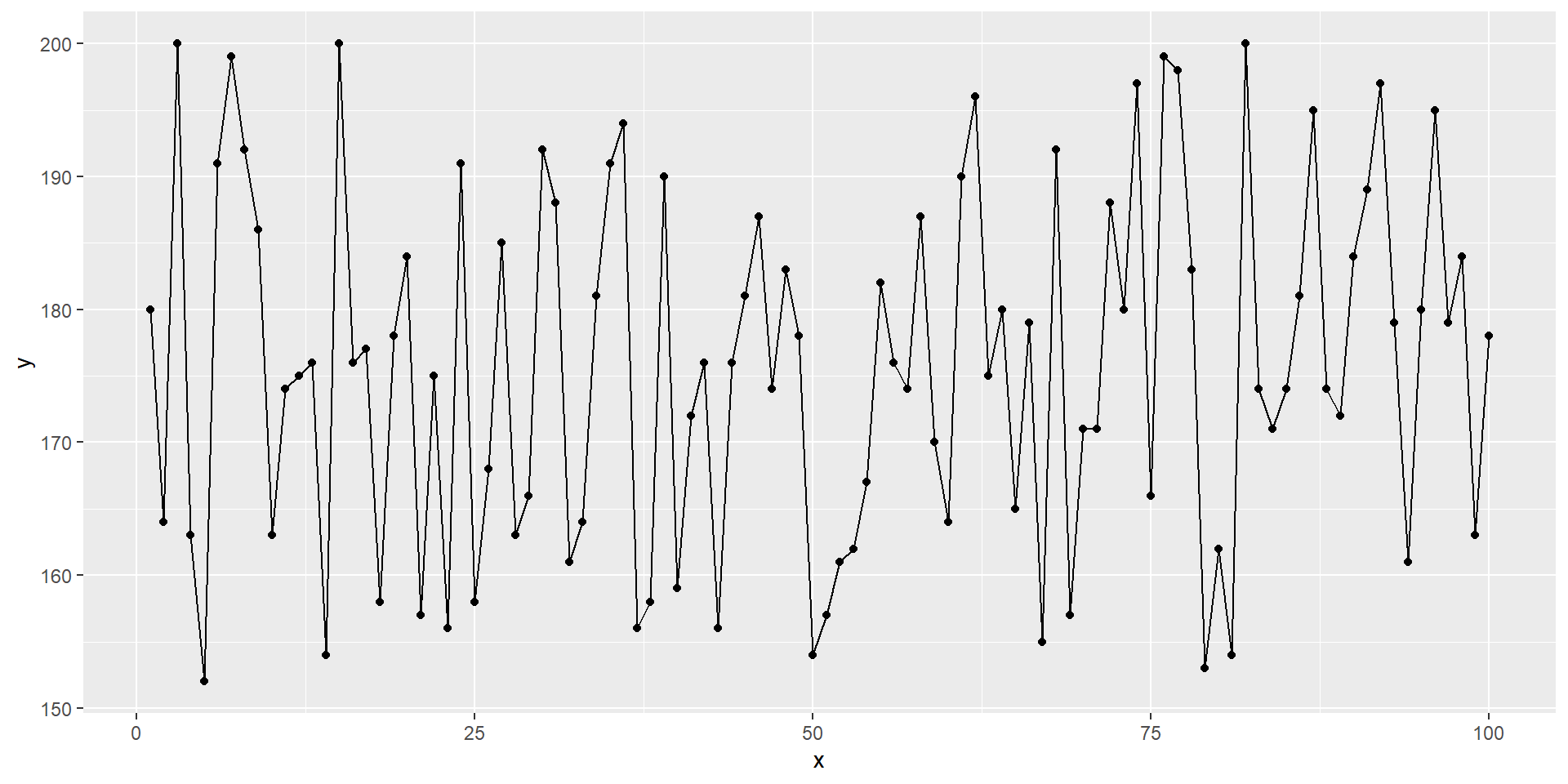
  • Erhebung der Körpergröße von Studierenden

  • Stichprobengröße n = 100

  • Überlegen Sie: Was ist eine geeignete deskriptive Darstellung?

  • Vorschläge?!

    • Unsortierte Beobachtungsreihe der Werte (= Urliste)
    • Sortierte Urliste
    • Grafisch vs. nummerisch
    • …

Verschiedene Optionen

  • Liniendiagramm: Ohne Struktur entlang der X-Achse sinnlos
  • Sortierte Punkte
  • Histogramm: Anzahl der Kategorien (= Bins) entscheidend
  • Boxplot: innere Box reicht vom 25. zum 75. Perzentil mit dem Median als Strich in der Mitte; Striche zeigen Min und Max an – außer es gibt sehr große oder kleine Werte (= Outlier)

Histogramm

Grundlgendes zu Histogrammen

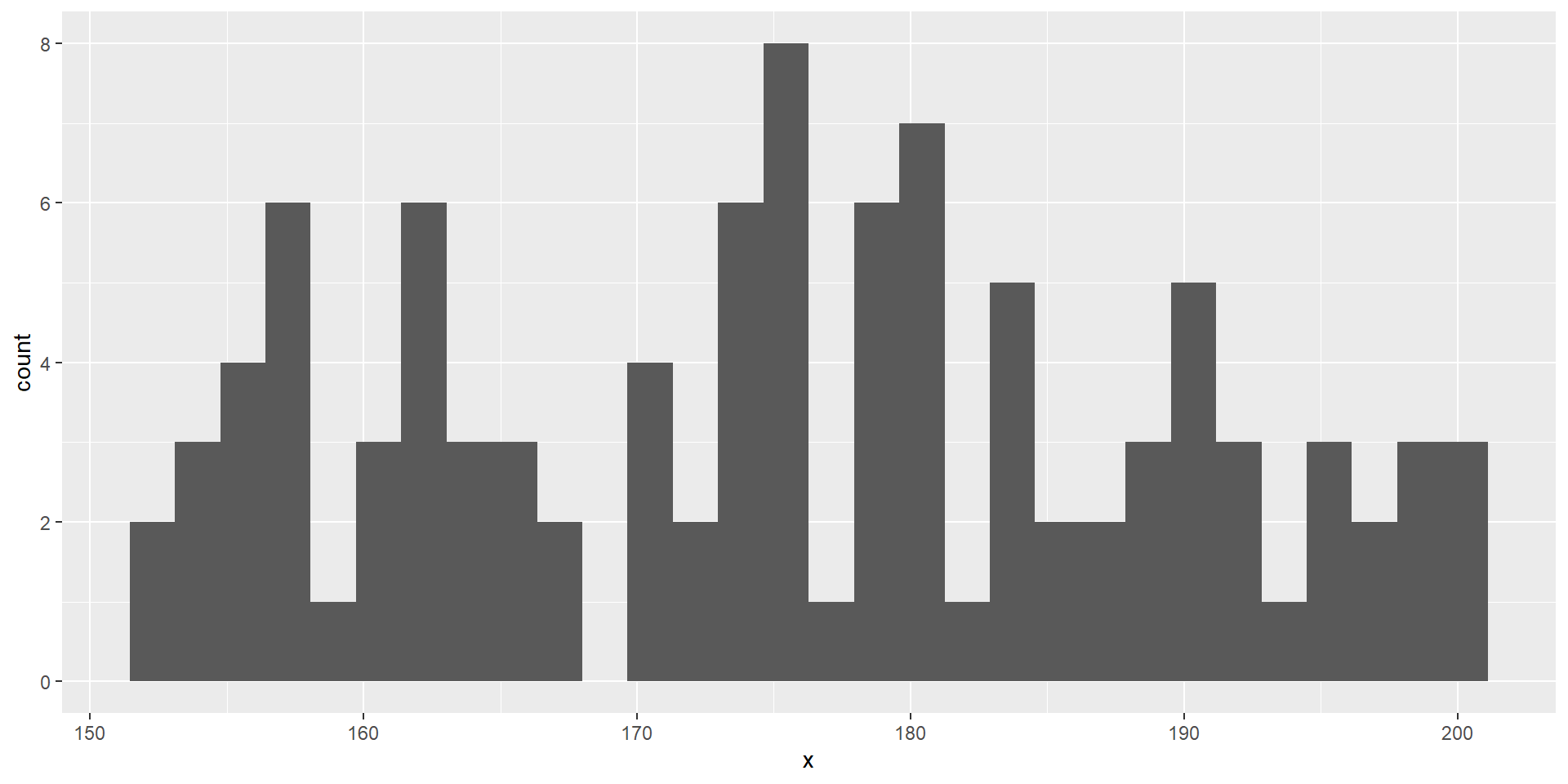
  • X-Achse: (meist) metrische Variable (Intervall-, Verhältnisskala)

  • Y-Achse: Häufigkeiten der Kategorien

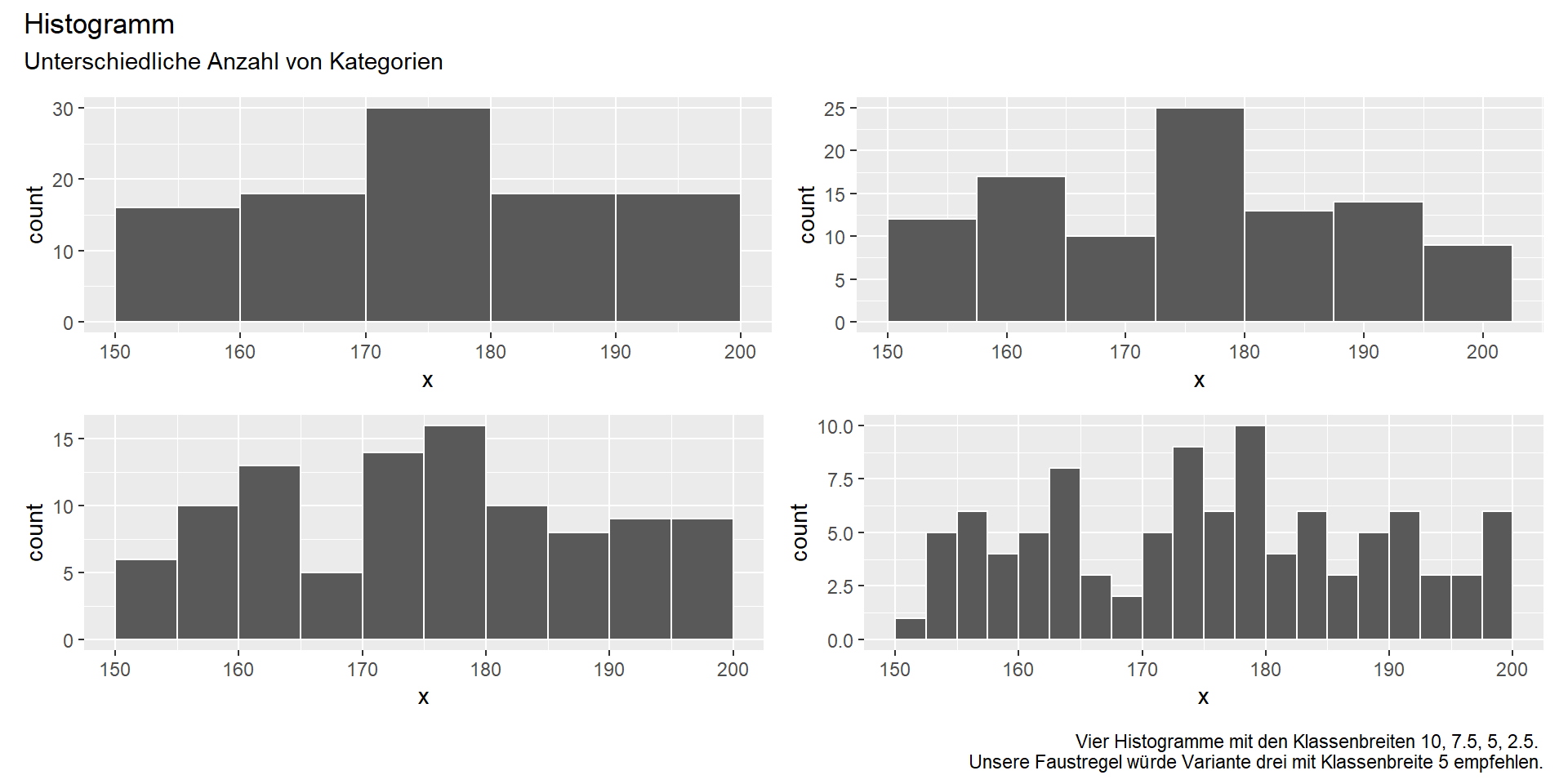
  • Anzahl der Kategorien geeignet wählen

  • Empfehlung: \(k = min(\sqrt{n}, 10 \cdot log_{10}(n))\)
    → “Berechnen der Stichprobengröße n; Berechnen des Logarithmus von n zur Basis 10 (‘10 hoch welche Zahl ergibt n?’) + Multiplikation mit 10; die kleinere der beiden Zahlen ist die Anzahl der Kategorien k.”

  • Vier Darstellungen mit unterschiedlichen Klassenbreiten: 10, 7.5, 5, und 2.5 [cm].

Histogram nach Klassenbreite

Boxplot

Grundlegendes zu Boxplots (1)

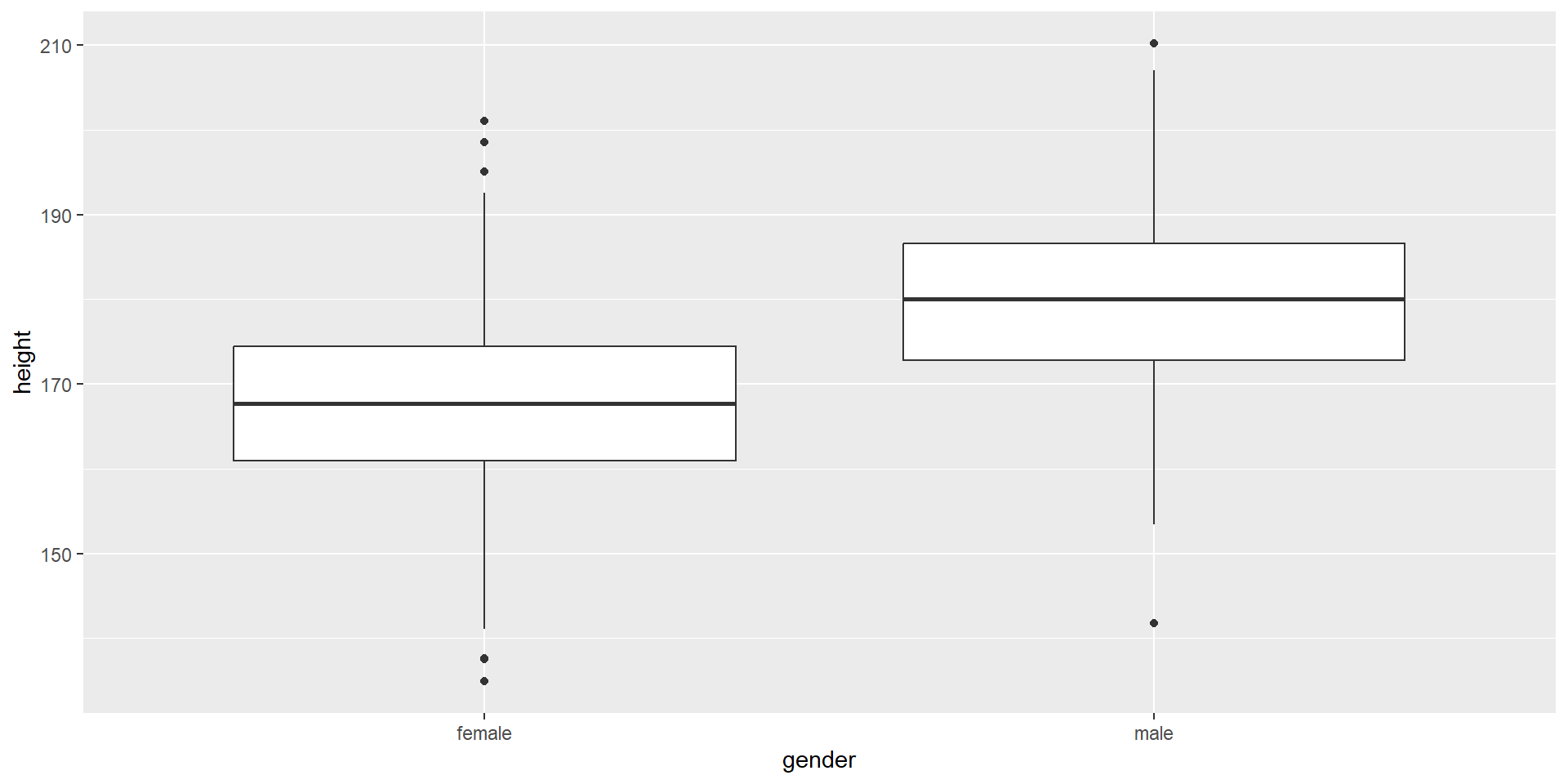
  • Stammt von John Tukey (→ bit)

  • Grafische Darstellung von fünf wichtigen Werten der Verteilung einer mind. ordinalskalierten Variablen

  • Das Rechteck in der Mitte der Darstellung ist die “Box”

  • Kann keine mehrgipfligen (z. B. bimodale) Verteilungen darstellen

  • Median

    • Teilt einen Datensatz in zwei gleich große Teile
    • Steht “in der Mitte” einer sortierten Urliste
    • 50% aller Werte sind kleiner, 50% sind größer als der Median

  • Ermittlung:

    • Daten der Größe nach sortieren
    • Wenn die Anzahl der Werte ungerade ist: Median ist die mittlere Zahl
    • Wenn die Anzahl der Werte gerade ist: Median ist Mittelwert der beiden mittleren Zahlen

Grundlegendes zu Boxplots (2)

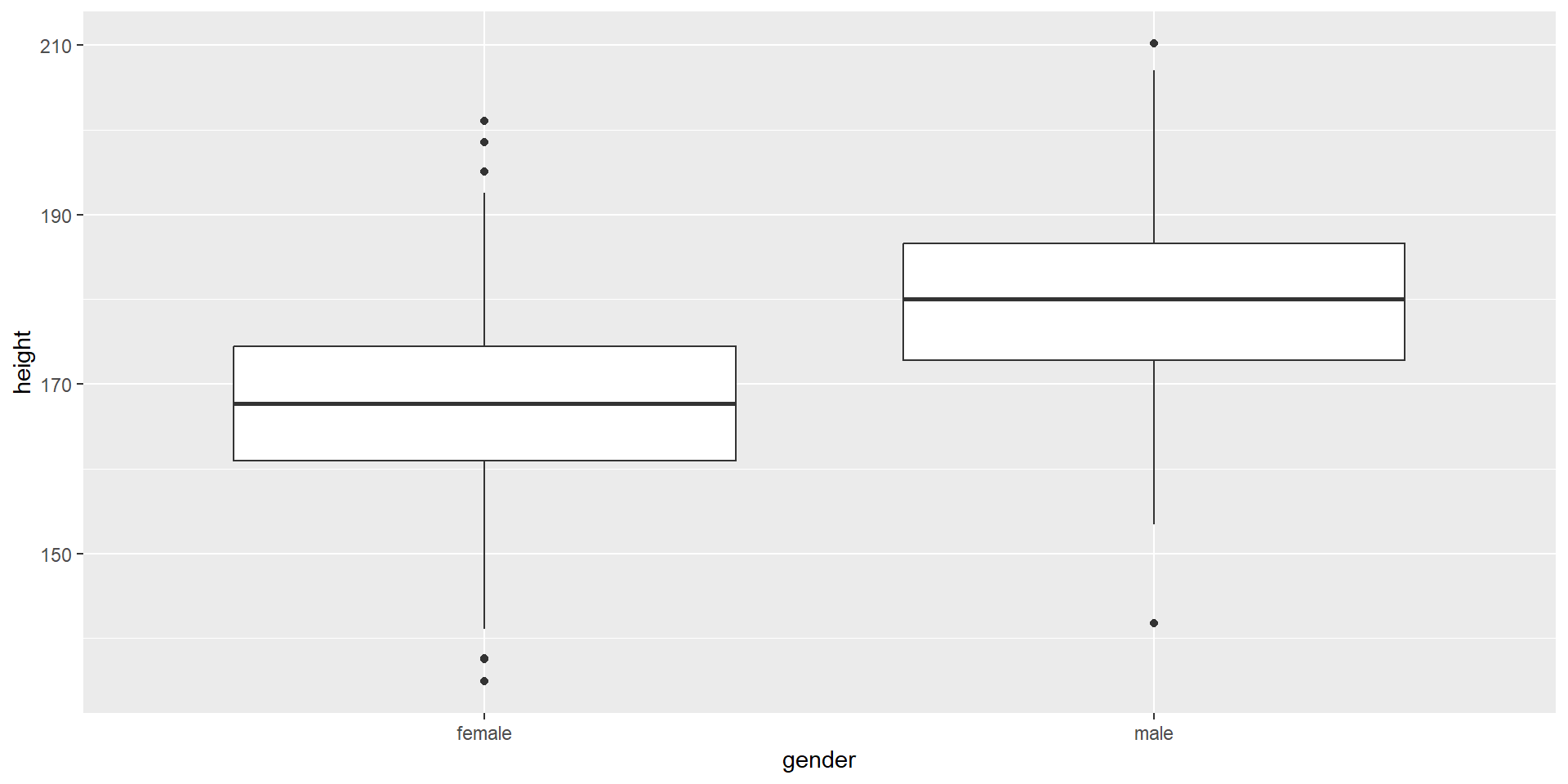
Vergleich zweier Darstellungsvarianten

Variante 1 Variante 2 – robust
Minimum Kleinster Wert, der kein Ausreißer ist
25. Perzentil 25. Perzentil
Median Median
75. Perzentil 75. Perzentil
Maximum Größter Wert, der kein Ausreißer ist

Hinweise:

  • Median (= 50. Perzentil, P50 = 2. Quartil); 25. Perzentil, P25 (= 1. Quartil); 75. Perzentil, P75 (= 3. Quartil); Maximum (= 100. Perzentil, P100 = 4. Quartil)

  • Strich in der Mitte der Box ist der Median

  • Box: von P25 bis P75

  • Die Ausreißer bei Variante 2 werden separat gekennzeichnet; Folge: Darstellung robuster gegenüber Ausreißern; Ausreißer sind kleiner als P25 - 1.5 IQR oder größer als P75 + 1.5 IQR

  • Standard in R: Variante 2 (robust)

Boxplot mit Ausreißer

Zwei Variable: Zusammenhänge

Streudiagramm

  • Voraussetzung: Zwei Variable auf mind. Intervallskalenniveau

  • Je “enger” die Daten (je schmaler eine gedachte Ellipse um die Daten), desto größer der Zusammenhang (= Korrelation)

  • Beispiel: Drei Variablen (V1, V2, V3) mit Zufallswerten und festgelegten Zusammenhängen

Statistische Kennwerte

Lagemaße

= Maße der zentralen Tendenz

  • Mittelwert
  • Median
  • Modalwert = Modus

Mittelwert

  • Geläufige Abkürzungen: \(\mu\), \(\overline{x}\), \(M\), \(\textit{MW}\)

  • Die Summe der Werte wird durch ihre Anzahl geteilt:

\[ \overline{x} = \frac{\sum\limits_{i=1}^{n}x_i}{n} \]

# Die Funktion c(...) fasst die Werte in einem Vektor zusammen
dv <- c(8,8,9,2,4,6)  

# Funktion für Mittelwert: mean()
mean(dv)
[1] 6.166667

Median – kennen wir schon

  • Geläufige Abkürzungen: \(\textit{MD}\), \(\textit{MED}\), \(\widetilde{x}\)
  • Für eine sortierte Stichprobe mit ungerader Anzahl von Elementen: \(n=2m + 1\) \[ \widetilde{x} = x_{m+1} \]
  • Für eine sortierte Stichprobe mit gerader Anzahl von Elementen: \(n=2m\) \[ \widetilde{x} = \frac{1}{2}(x_{m} + x_{m+1}) \]
dv_gerade <- c(8,8,9,2,4,6)  

# Funktion für Median: mean()
median(dv_gerade)
[1] 7
dv_ungerade <- c(8,8,9,2,4,6,10) 
median(dv_ungerade)
[1] 8

Modus

  • Geläufige Abkürzungen: \(\textit{MOD}\), \(D\), \(x_M\), \(x_{\textit{MOD}}\)
  • Der am häufigsten auftretende Wert in einer Stichprobe (sinnvoll meist nur bei ganzzahligen Werten)
  • Gipfel der Häufigkeitsverteilung
  • Im Histogramm: Mitte der häufigsten Kategorie
  • Im folgenden Beispiel ist der Modus = 175:

Schiefe von Verteilungen

Schiefe von Verteilungen in Abhängigkeit der Lagemaße

Lagemaße und Skalenniveaus

  • Modalwert
    • Nominalskala
    • Ordinalskala
    • Intervallskala
    • Verhältnisskala
  • Median
    • Ordinalskala
    • Intervallskala
    • Verhältnisskala
  • Mittelwert
    • Intervallskala
    • Verhältnisskala

Streuungsmaße

  • Enge Verbindung zu Lagemaßen
  • Um den Mittelwert:
    • Varianz
    • Standardabweichung
    • Variationskoeffizient
    • Mittlere absolute Abweichung
  • Um den Median:
    • Interquartilsabstand
  • Spannweite

Varianz

= “durchschnittlicher quadrierter Abstand vom Mittelwert”

  • Geläufige Abkürzungen: \(Var\), \(s²\), \(\sigma²\), \(\hat{\sigma}²\)

  • Formel: \(s² = \hat{\sigma}² = \frac{\sum\limits_{i=1}^{n}(x_i - \overline{x})²}{n-1}\)

  • Problem der Einheit: EUR \(\rightarrow\) EUR²

Standardabweichung

  • Geläufige Abkürzungen: \(\textit{SD}\), \(s\), \(\sigma\), \(\hat{\sigma}\)

  • Wurzel der Varianz

  • Formel: \(s = \hat{\sigma} = \sqrt{\hat{\sigma}²} = \sqrt{\frac{\sum\limits_{i=1}^{n}(x_i - \overline{x})²}{n-1}}\)

  • Kein Problem mehr mit den Einheiten

Weitere Streuungsmaße

  • Variationskoeffizient \[ \operatorname {VarK}(X)={\frac {{\mathrm {Standardabweichung}}(X)}{{\mathrm {Erwartungswert}}(X)}}={\frac {{\sqrt {\operatorname {Var}(X)}}}{\operatorname {E}(X)} = \frac{\textit{SD}}{\overline{x}}} \]

  • Mittlere absolute Abweichung \[ \textit{MAD} = {\displaystyle d_{\overline {x}}(x)={\frac {1}{n}}\sum _{i=1}^{n}|x_{i}-{\overline {x}}|} \]

  • Interquartilsabstand = Abstand zwischen 25. und 75. Perzentil \[ \textit{IQA} = \textit{IQR} =x_{0{.}75}-x_{0{.}25} \]

  • Spannweite \[ {\displaystyle R=x_{\mathrm {max} }-x_{\mathrm {min} }} \]