Grundlagen: Daten, Messen, Skalenniveaus
_Statistik
06.10.2025
Messen
- Messen ist die Zuordnung von Zahlen zu Merkmalsausprägungen von Objekten nach festgelegten Regeln
- Kernaspekt:
- strukturtreue (= homomorphe) Abbildung empirisch → numerisch
- Die Struktur der empirischen und der numerischen Seite sollen möglichst übereinstimmen
- strukturtreue (= homomorphe) Abbildung empirisch → numerisch
- Unterschied physikalische Messung (PM) – sozialwissenschaftliche Messung (SM)
- PM: Operationalisierung steckt im Messgerät; 1:1-Beziehung zwischen latenter und manifester Variablen (= Messgerät)
- SM: Güte der Operationalisierung muss argumentiert werden
- Gemeinsamkeit: Güte der numerischen Zuordnung muss argumentiert werden (vgl. Skalenniveaus)
Nominalskala
- Eine Nominalskala ordnet den Merkmalsausprägungen Zahlen so zu, dass gleiche Merkmalsausprägungen gleiche Zahlen und unterschiedliche Merkmalsausprägungen verschiedene Zahlen erhalten.
- Die Struktur, die erhalten werden muss, ist die Äquivalenz bzw. Unterscheidbarkeit der Elemente auf der empirischen Seite.
- Zahlen entsprechen Namen
- Jede eindeutige Transformation der zugeordneten Zahlen ist erlaubt.
- „Qualitative Variable”
- Zweistufige (meist nominale) Variable: dichotom, binär
- Mittelwerte sind sinnlos, da alle Zahlenzuordnungen erlaubt sind, die die Eindeutigkeit erhalten.
- Beispiele: Geschlecht, Rückennummern von Sportlern, Händigkeit
Ordinalskala
Eine Ordinalskala ordnet den Merkmalsausprägungen Zahlen so zu, dass die größeren Merkmalsausprägung die größere Zahl erhält.
Die Struktur, die erhalten werden muss, ist die Rangreihe der Elemente auf der empirischen Seite. Dabei muss auch die Gleichheit festgelegt werden können.
Jede Transformation, die diese Rangreihe in den zugeordneten Zahlen erhält, ist erlaubt: monotone Transformationen.
Mittelwerte sind sinnlos, da alle Zahlenzuordnungen erlaubt sind, die die Reihenfolge erhalten
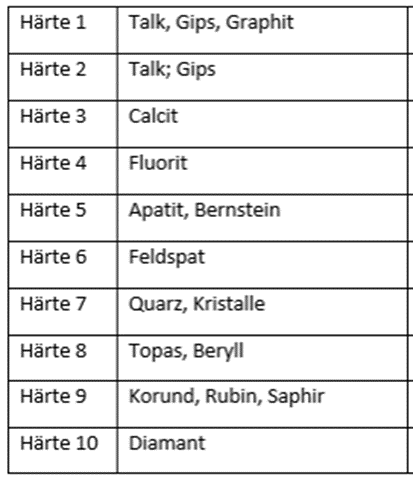
Beispiele: Position in einer Unternehmenshierarchie, Offiziersränge, Schulabschlüsse, Härtegrade
Intervallskala
- Eine Intervallskala ordnet Merkmalsausprägungen Zahlen so zu, dass die Rangordnung der Zahlendifferenzen zwischen je zwei Merkmalsausprägungen der Rangordnung der Merkmalsunterschiede zwischen je zwei Objekten entspricht.
- Die Struktur, die erhalten werden muss, sind die Abstände zwischen den Elementen auf der empirischen Seite.
- Erlaubt sind lineare Transformationen:
z. B. Fahrenheit = 1.8 × Celsius + 32 - Eine Intervallskala hat keinen natürlichen Nullpunkt.
- Mit Intervallskalendaten können sinnvoll Differenzen, Summen und Mittelwerte berechnet werden.
- Beispiele: Ratingskalen, viele psychologischen Messverfahren (IQ-Test)
Verhältnisskala
- Eine Verhältnisskala ordnet Merkmalsausprägungen Zahlen so zu, dass das Verhältnis zwischen je zwei Zahlen dem Verhältnis der Merkmalsausprägungen entspricht.
- Die Struktur, die erhalten werden muss, ist das Verhältnis der Merkmalsausprägungen der Elemente auf der empirischen Seite.
- Empirische Verknüpfung ≙ numerische Addition
- Erlaubt sind multiplikative Transformationen (= Ähnlichkeitstrafo.) der Art Y = k × X; z.B. Umrechnung m → cm; cm → inch
- Eine Verhältnisskala hat einen natürlichen Nullpunkt
- Beispiele: viele physikalische Messverfahren
Absolutskala
- Eine besondere Form der Verhältnisskala
- Maßeinheit ist natürlich gegeben; meist „Stück”
→ kann nicht frei gewählt werden;
→ keine Transformationen möglich - Beispiele: Pulsschläge pro Minute; Anzahl Menschen in einem Raum
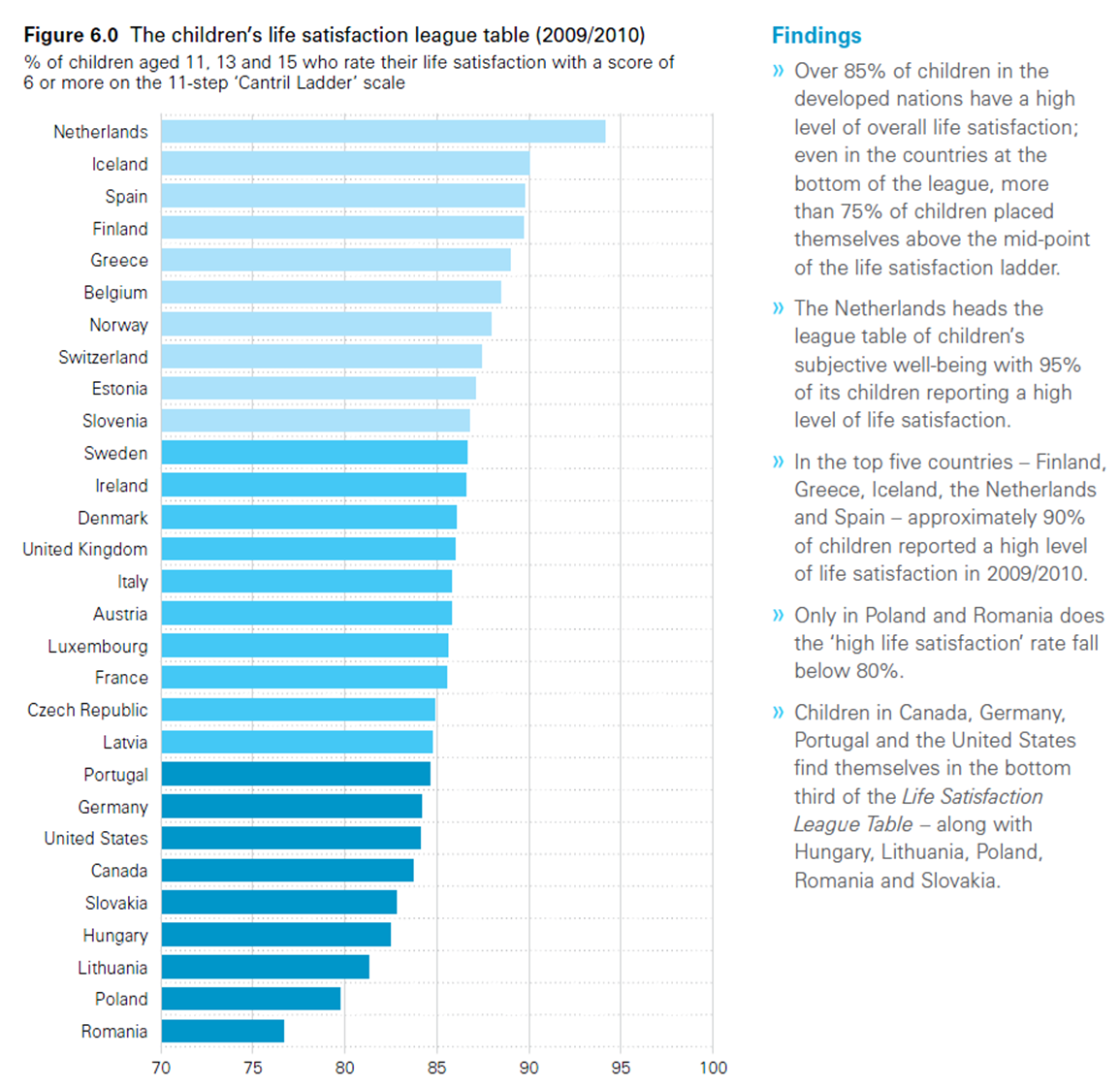
Lebenszufriedenheit von Kindern
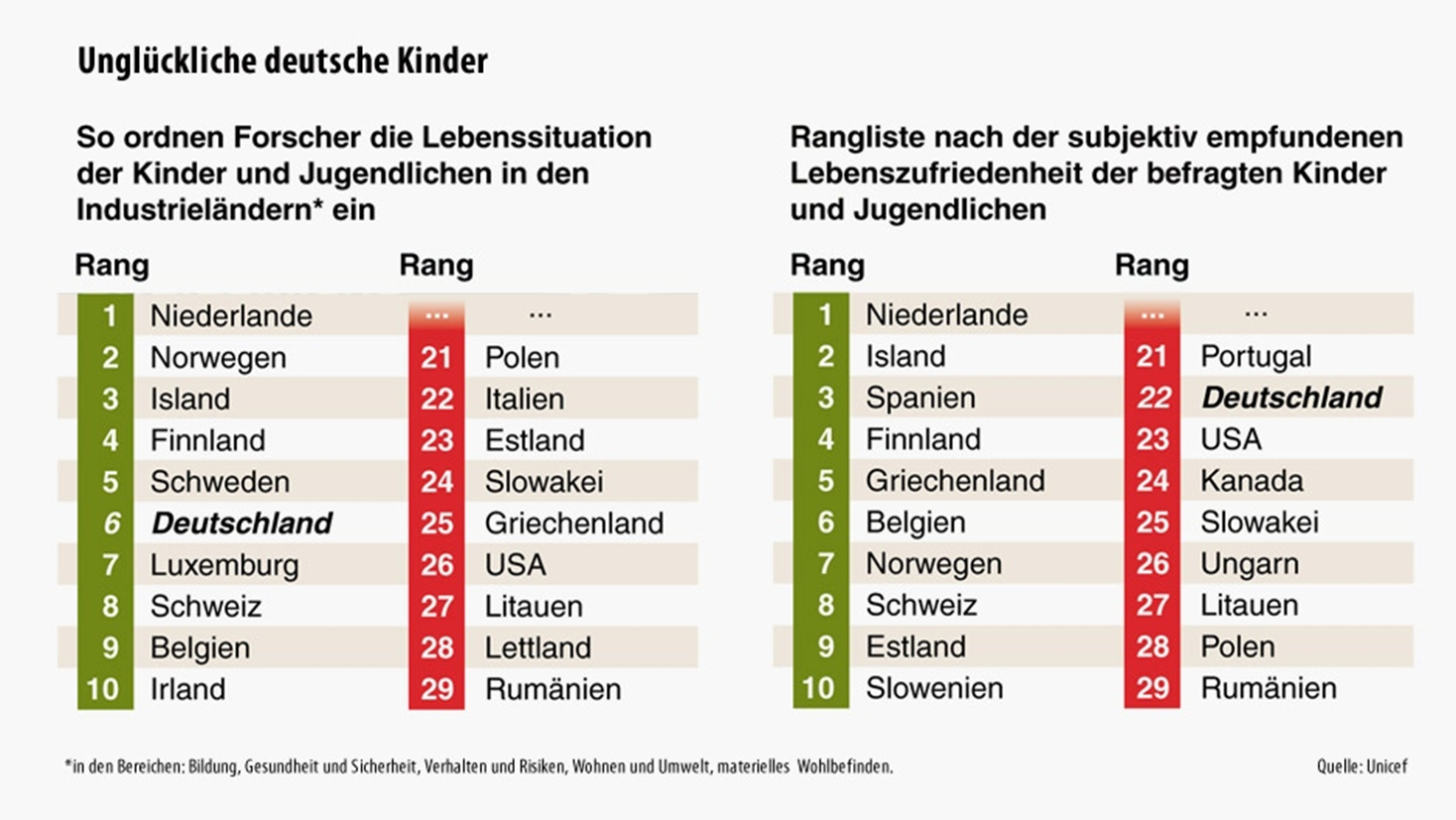
Lebenszufriedenheit (2)
